Geospatial Interpolation and Mapping of Tropospheric Ozone Pollution Using Geostatistics
Abstract
:1. Introduction
2. Experimental Section
2.1. Description of the Study Area
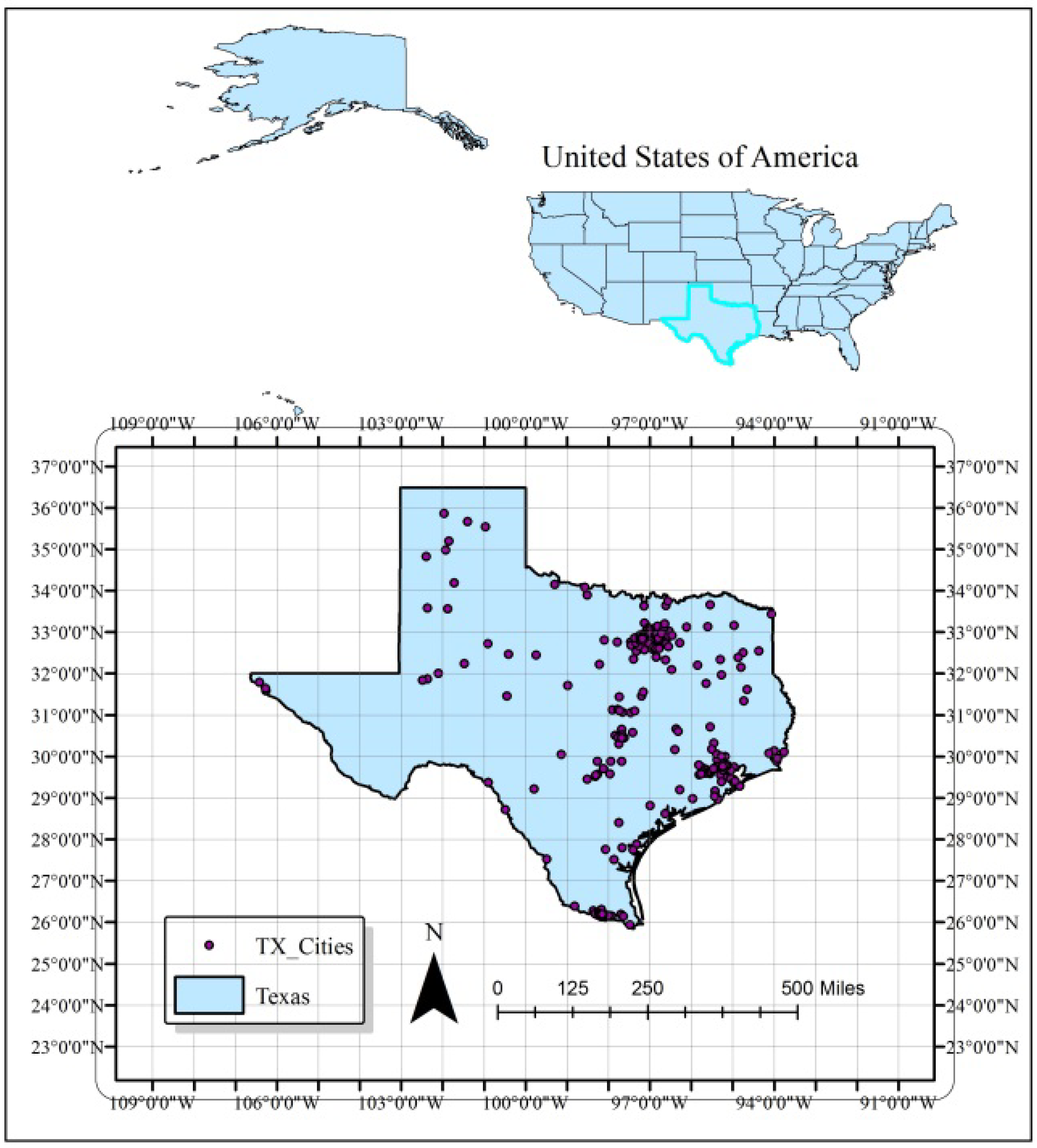
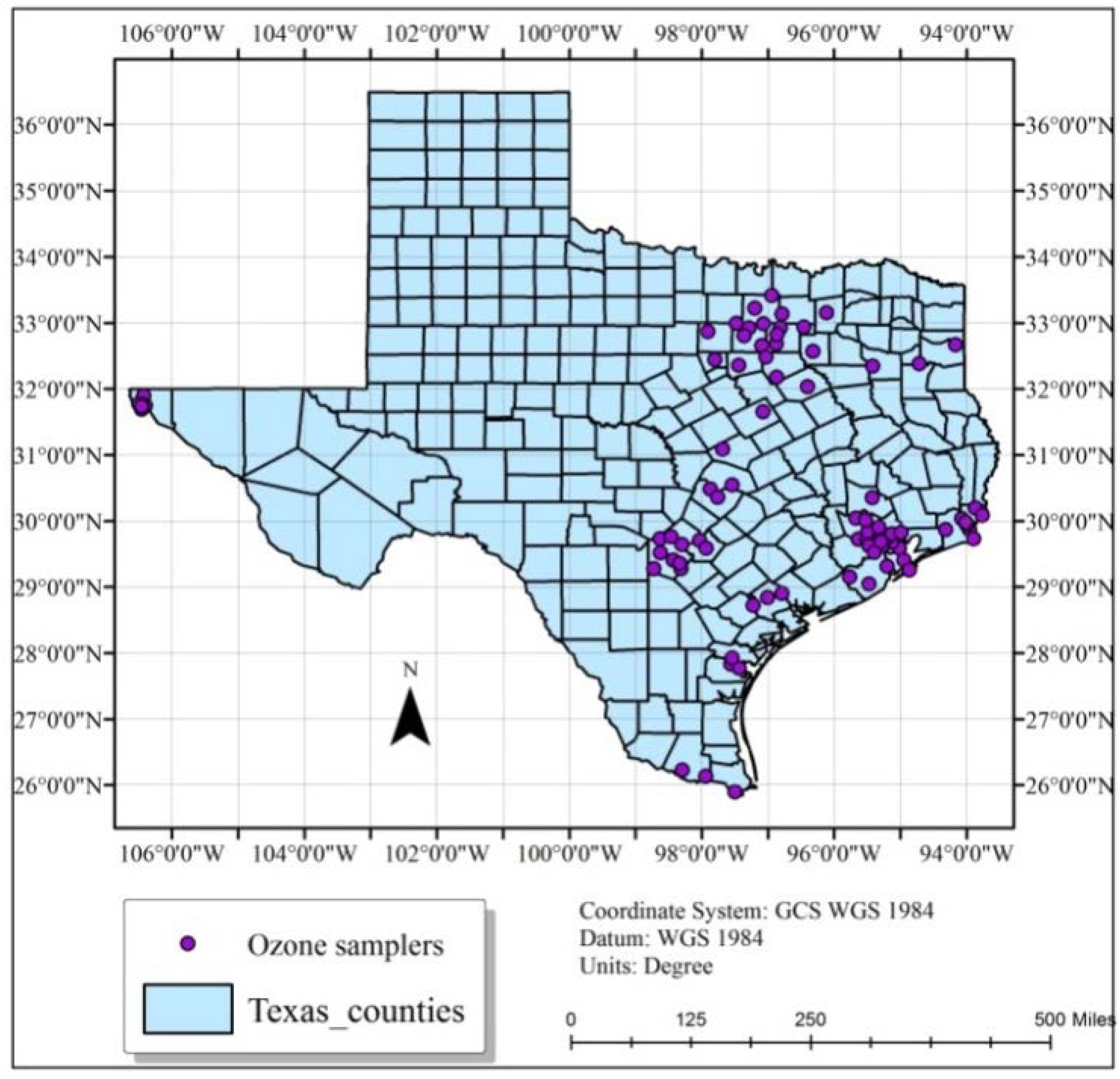
2.2. Data Sources and Software
2.3. Methodology
2.3.1. Exploration of Spatial Data
- (1)
- Use of histogram to represent the distribution:O3 values were split into ten classes (X-Axis values were redrawn to a scale of 10). In each class, the frequency was represented by the height of the bar.
- (2)
- Use of QQ plot to compare the data distribution to the standard normal distribution:Data are said to be normal if they follow a “45°” straight line. For all the studied hours, QQ plots were drawn in which quantiles of O3 data were plotted against the quantiles of the standard normal distribution.
2.3.2. Global Trends in Data
2.3.3. Spatial Correlation in Data
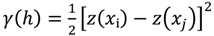
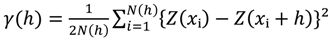
2.3.4. Cross Validation
3. Results and Discussion
3.1. Normality and Checking for Errors
3.1.1. Histogram
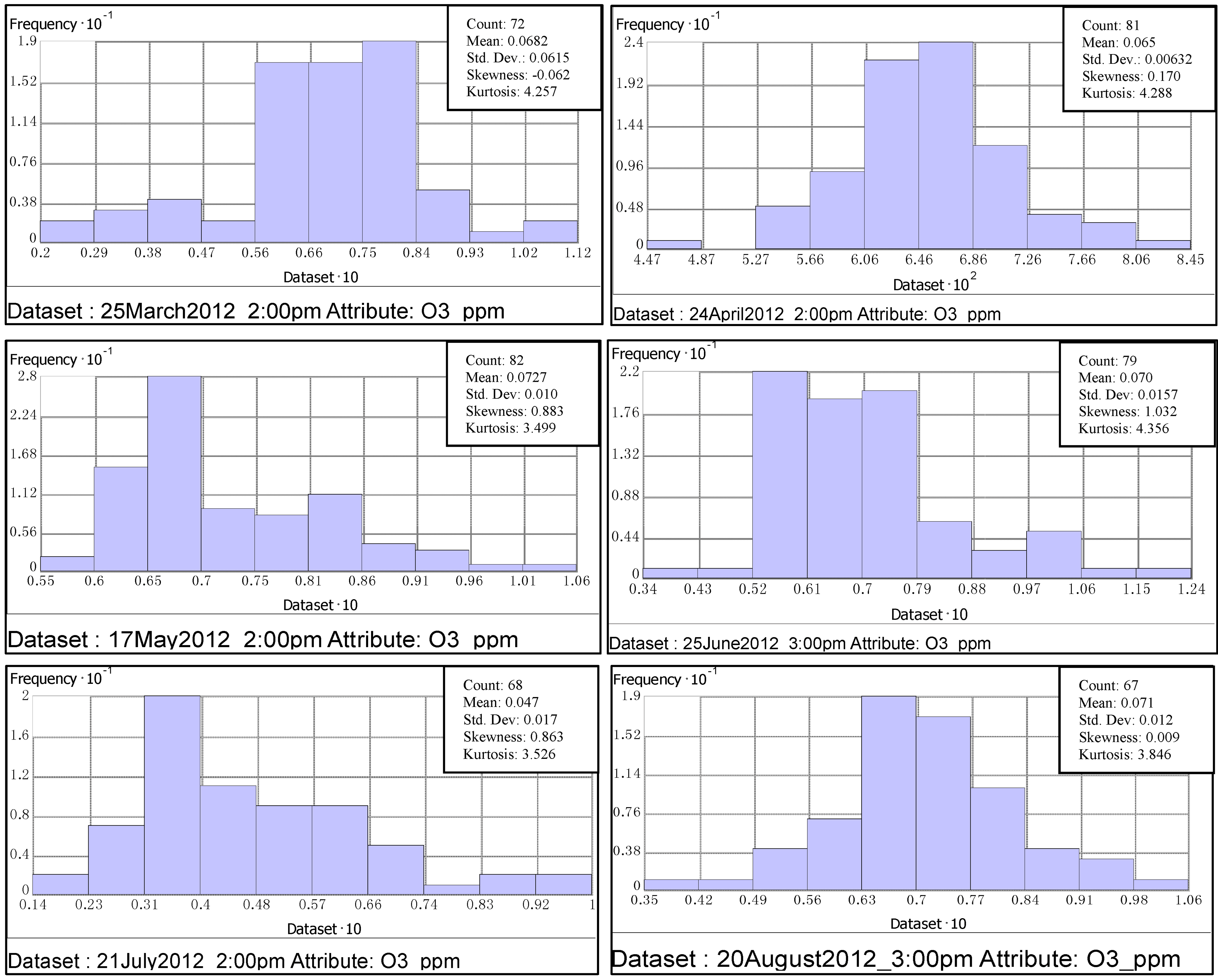
3.1.2. Quantile-Quantile Plot
| 25 March 2012 at 2:00 pm | 24 April 2012 at 2:00 pm | 17 May 2012 at 2:00 pm | 25 June 2012 at 3:00 pm | 21 July 2012 at 2:00 pm | 20 August 2012 at 3:00 pm |
|---|---|---|---|---|---|
| Dallas/Fort Worth, Houston, and Beaumont | Houston and Dallas/Fort Worth | Houston, Austin, Dallas/Fort worth, San Antonio, Beaumont, and Corpus Christi | Dallas/Fort Worth, Houston | Dallas/Fort Worth | Dallas/Fort Worth, Houston, and San Antonio |
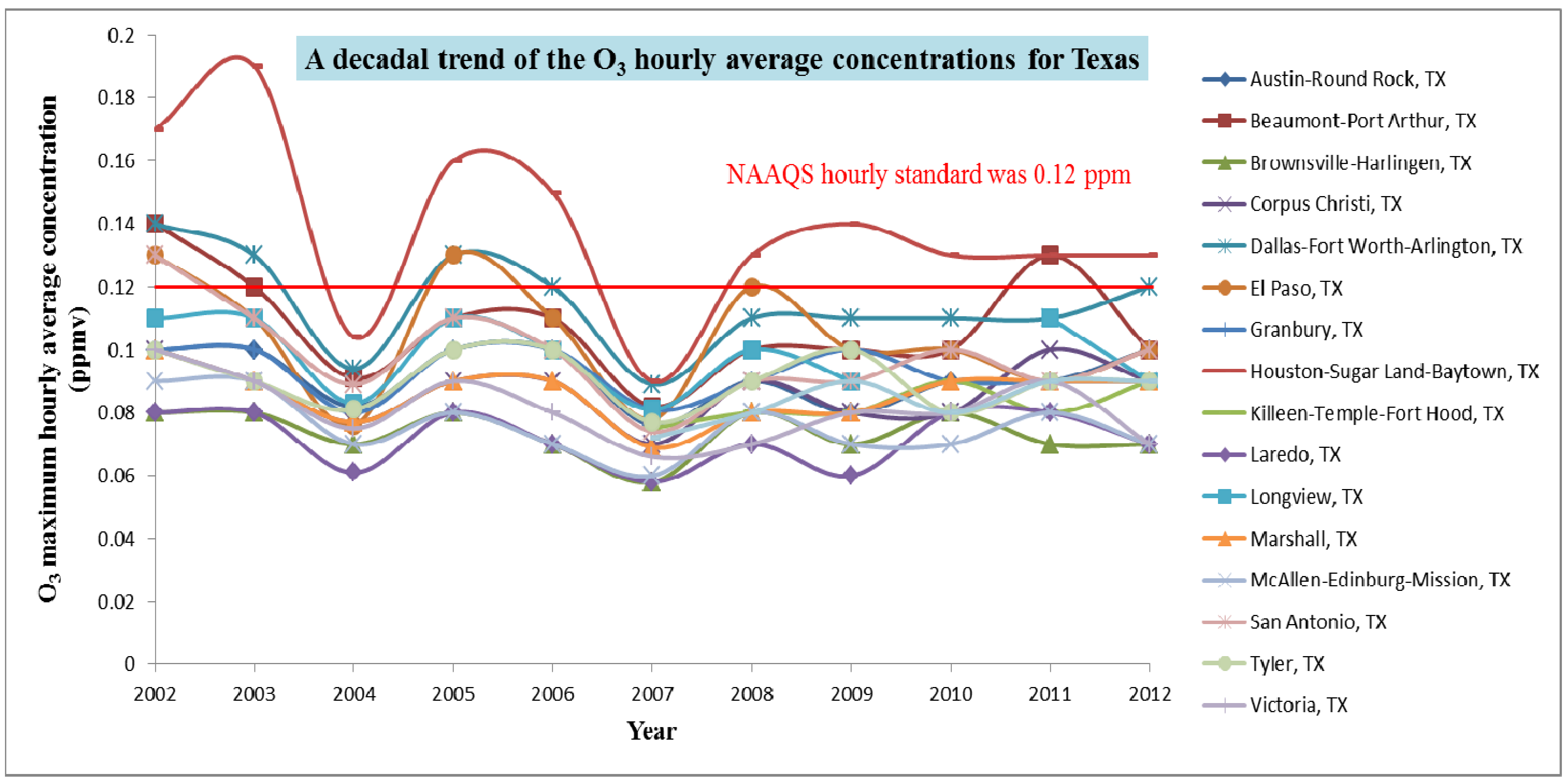
3.2. Global Trend Analysis

3.3. Spatial Correlation

3.4. Cross Validation Results
| Prediction Errors | 25 March 2012 at 2:00 pm | 24 April 2012 at 2:00 pm | 17 May 2012 at 2:00 pm | 25 June 2012 at 3:00 pm | 21 July 2012 at 2:00 pm | 20 August 2012 at 3:00 pm |
|---|---|---|---|---|---|---|
| Samples | 72 of 72 | 81 of 81 | 88 of 88 | 79 of 79 | 68 of 68 | 67 of 67 |
| Mean | −0.0000078 | 0.0000022 | −0.000166 | −0.0000385 | 0.000407 | 0.000306 |
| Root-Mean-Square | 0.00825 | 0.004823 | 0.006229 | 0.00915 | 0.00876 | 0.00956 |
| Mean Standardized | −0.00572 | 0.000444 | −0.02046 | −0.00914 | 0.0270 | 0.0207 |
| Root-Mean-Square Standardized | 0.829 | 0.917 | 0.714 | 1.093 | 1.099 | 1.047 |
| Average Standard Error | 0.0102 | 0.00527 | 0.00977 | 0.0105 | 0.0084 | 0.00927 |
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Cross-State Air Pollution Rule; U.S. EPA: Washington, DC, USA, 2011. Available online: http://www.epa.gov/airtransport/index.html (accessed on 15 November 2012).
- Cooper, O.R.; Parrish, D.D.; Stohl, A.; Trainer, M.; Nédélec, P.; Thouret, V.; Cammas, J.P.; Oltmans, S.J.; Johnson, B.J.; Tarasick, D.; et al. Increasing springtime ozone mixing ratios in the free troposphere over western North America. Nature 2010, 463, 344–348. [Google Scholar] [CrossRef]
- Morris, G.A.; Hersey, S.; Thompson, A.M.; Pawson, S.; Nielsen, J.E.; Colarco, P.R.; McMillan, W.W.; Stohl, A.; Turquety, S.; Warner, J.; et al. Alaskan and Canadian forest fires exacerbate ozone pollution over Houston, Texas, on 19 and 20 July 2004. J. Geophy. Res. 2006, 111. [Google Scholar] [CrossRef]
- Stutz, J.; Alicke, B.; Ackermann, R.; Geyer, A.; White, A.; Williams, E. Vertical profiles of NO3, N2O5, O3, and NOX in the nocturnal boundary layer: 1. Observations during Texas Air Quality Study 2000. J. Geophy. Res. 2004, 109. [Google Scholar] [CrossRef]
- Banta, R.M.; Senff, C.J.; Nielsen-Gammon, J.; Darby, L.S.; Ryerson, T.B.; Alvarez, R.J.; Sandberg, S.P.; Williams, E.J.; Trainer, M. A bad air day in Houston. Bull. Amer. Meteorol. Soc. 2005, 86, 657–669. [Google Scholar] [CrossRef]
- Zhou, W.; Cohan, D.S.; Henderson, B.H. Slower ozone production in Houston, Texas following emission reductions: Evidence from Texas Air Quality Studies in 2000 and 2006. Atmos. Chem. Phys. Discuss. 2013, 13, 19085–19120. [Google Scholar] [CrossRef]
- Moral García, F.J.; González, P.V.; Rodríguez, F.L. Geostatistical analysis and mapping of ground-level ozone in a medium sized urban area. Int. J. Civil Environ. Eng. 2010, 2, 71–82. [Google Scholar]
- Brody, S.D.; Mitchell Peck, B.; Highfield, W.E. Examining localized patterns of air quality perception in Texas: A spatial and statistical analysis. Risk Anal. 2004, 24, 1561–1574. [Google Scholar] [CrossRef]
- Developing Spatially Interpolated Surfaces and Estimating Uncertainty; U.S. EPA: Washington, DC, USA, 2004. Available online: http://www.epa.gov/airtrends/specialstudies/dsisurfaces.pdf (accessed on 10 December 2012).
- Diem, J.E. A critical examination of ozone mapping from a spatial-scale perspective. Environ. Pollut. 2003, 125, 369–383. [Google Scholar] [CrossRef]
- Daum, P.H.; Kleinman, L.I.; Springston, S.R.; Nunnermacker, L.J.; Lee, Y.-N.; Weinstein-Lioyd, J.; Zheng, J.; Berkowitz, C.M. Origin and properties of plumes of high ozone observed during the Texas 2000 air quality study (TexAQS 2000). J. Geophy. Res. 2003, 109. [Google Scholar] [CrossRef]
- Fraczek, W.; Bytnerowicz, A. Automating the Use of Geostatistical Tools for Lake Tahoe Area Study. ArcUser. 2007. Available online: http://www.esri.com/news/arcuser/0807/ga_network.html (accessed on 19 December 2013).
- Yerramilli, A.; Dodla, V.B.; Desamsetti, S.; Challa, S.V.; Young, J.H.; Patrick, C.; Baham, J.M.; Hughes, R.L.; Yerramilli, S.; Tuluri, F.; Hardy, M.G.; Swanier, S.J. Air Quality Modeling for Urban Jackson, Mississippi Region Using a High Resolution WRF/Chem Model. Int. J. Environ. Res. Public Health 2011, 8, 2470–2490. [Google Scholar] [CrossRef]
- Geostatistical Analyst Tutorial; Environmental Systems Research Institute: Redlands, CA, USA, 2012; pp. 1–57.
- Maroko, A.; Maantay, J.A.; Grady, K. Using geovisualization and geospatial analysis to explore respiratory disease and environmental health justice in New York City. In Geospatial Analysis of Environmental Health; Maantay, J.A., McLafferty, S., Eds.; Springer: New York, NY, USA, 2011; pp. 39–66. [Google Scholar]
- ArcGIS™ Geostatistical Analyst: Statistical Tools for Data Exploration, Modeling, and Advanced Surface Generation; An ESRI White Paper; Environmental Systems Research Institute: Redlands, CA, USA, 2001.
- U.S. Department of Commerce, Economics and Statistics Administration, U.S. Census Bureau. 2010 Census: Texas profile. Available online: http://www.census.gov/geo/www/2010census (accessed on 5 November 2012).
- U.S. Energy Information Administration. State Energy Data System: Texas State Energy Profile. 2010. Available online: http://www.eia.gov/beta/state/print.cfm?sid=TX (accessed on 24 October 2012).
- The New York Times. 2011 Proving to be a Bad Year for Air Quality in Texas. 2011. Available online: http://www.nytimes.com/2011/12/11/us/2011-proving-to-be-a-bad-year-for-airquality.html?_ r=0 (accessed on 24 October 2012).
- Miller, H.J. Tobler’s first law and spatial analysis. Ann. Assoc. Amer. Geograph. 2004, 94, 284–289. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Chang, K.T. Introduction to Geographic Information Systems, 4th ed.; McGraw-Hill Publishers: New York, NY, USA, 2008; pp. 326–356. [Google Scholar]
- Moral, F.J.; Rebollo, F.J.; Valiente, P.; López, F.; De la Peńa, A.M. Modelling ambient ozone in an urban area using an objective model and geostatistical algorithms. Atmosph. Environ. 2012, 63, 86–93. [Google Scholar] [CrossRef]
- Fraczek, W.; Bytnerowicz, A.; Legge, A. Optimizing a monitoring network for assessing ambient air quality in the Athabasca oil sands region of Alberta, Canada. In Alpine Space-Man and Environment, Global Change and Sustainable Development in Mountain Regions; Innsbruck University Press: Innsbruck, Austria, 2009; Volume 7, pp. 127–142. [Google Scholar]
- Wong, D.W.; Yuan, L.; Perlin, S.A. Comparison of spatial interpolation methods for the estimation of air quality data. J. Expos. Analysis Environ. Epid. 2004, 14, 404–415. [Google Scholar] [CrossRef]
- Negreiros, J.; Painho, M.; Aguilar, F.; Aguilar, M. Geographical information systems principles of ordinary kriging interpolator. J. Appl. Sci. 2010, 10, 852–867. [Google Scholar] [CrossRef]
- Johnston, K.; Ver Hoef, J.M.; Krivoruchko, K.; Lucas, N. Exploratory spatial data analysis. In Using ArcGIS™ Geostatistical Analyst; Environmental Systems Research Institute: Redlands, CA, USA, 2003; Chapter 4; pp. 81–112. [Google Scholar]
- Air quality statistics report; U.S. EPA: Washington, DC, USA, 2013. Available online: http://www.epa.gov/airdata/ad_rep_con.html (accessed on 26 November 2013 ).
- Sexton, K.; Linder, S.H.; Marko, D.; Bethel, H.; Lupo, P.J. Comparative assessment of air pollution-related health risks in Houston. Environ. Health Persp. 2007, 115, 1388–1393. [Google Scholar]
- National Ambient Air Quality Standards (NAAQS); U.S. EPA: Washington, DC, USA, 2012. Available online: www.epa.gov/air/criteria.html#3 (accessed on 26 November 2013).
- Regulatory Impact Analysis: Final National Ambient Air Quality Standard for Ozone; U.S. EPA: Washington, DC, USA, 2011. Available online: http://www.epa.gov/glo/pdfs/201107_OMBdraft-OzoneRIA.pdf (accessed on 27 November 2013).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kethireddy, S.R.; Tchounwou, P.B.; Ahmad, H.A.; Yerramilli, A.; Young, J.H. Geospatial Interpolation and Mapping of Tropospheric Ozone Pollution Using Geostatistics. Int. J. Environ. Res. Public Health 2014, 11, 983-1000. https://doi.org/10.3390/ijerph110100983
Kethireddy SR, Tchounwou PB, Ahmad HA, Yerramilli A, Young JH. Geospatial Interpolation and Mapping of Tropospheric Ozone Pollution Using Geostatistics. International Journal of Environmental Research and Public Health. 2014; 11(1):983-1000. https://doi.org/10.3390/ijerph110100983
Chicago/Turabian StyleKethireddy, Swatantra R., Paul B. Tchounwou, Hafiz A. Ahmad, Anjaneyulu Yerramilli, and John H. Young. 2014. "Geospatial Interpolation and Mapping of Tropospheric Ozone Pollution Using Geostatistics" International Journal of Environmental Research and Public Health 11, no. 1: 983-1000. https://doi.org/10.3390/ijerph110100983
APA StyleKethireddy, S. R., Tchounwou, P. B., Ahmad, H. A., Yerramilli, A., & Young, J. H. (2014). Geospatial Interpolation and Mapping of Tropospheric Ozone Pollution Using Geostatistics. International Journal of Environmental Research and Public Health, 11(1), 983-1000. https://doi.org/10.3390/ijerph110100983






