Mapping Disease at an Approximated Individual Level Using Aggregate Data: A Case Study of Mapping New Hampshire Birth Defects
Abstract
:1. Introduction
- (1)
- (2)
- (3)
- Unrealistic geographical assumptions: The mapping either assumes that the subjects are evenly distributed across the areal unit or all are concentrated on one point, e.g., the centroid of the polygon [18]; and
- (4)
- Unidentifiable spatial uncertainty: While it is a known fact that data aggregation causes spatial uncertainty due to location imprecision (use a polygon to represent a point) and inaccuracy (use the polygon centroid to represent all locations in the polygon), with a conventional polygon map, there is no effective way to estimate, represent, and present this uncertainty [18,19].
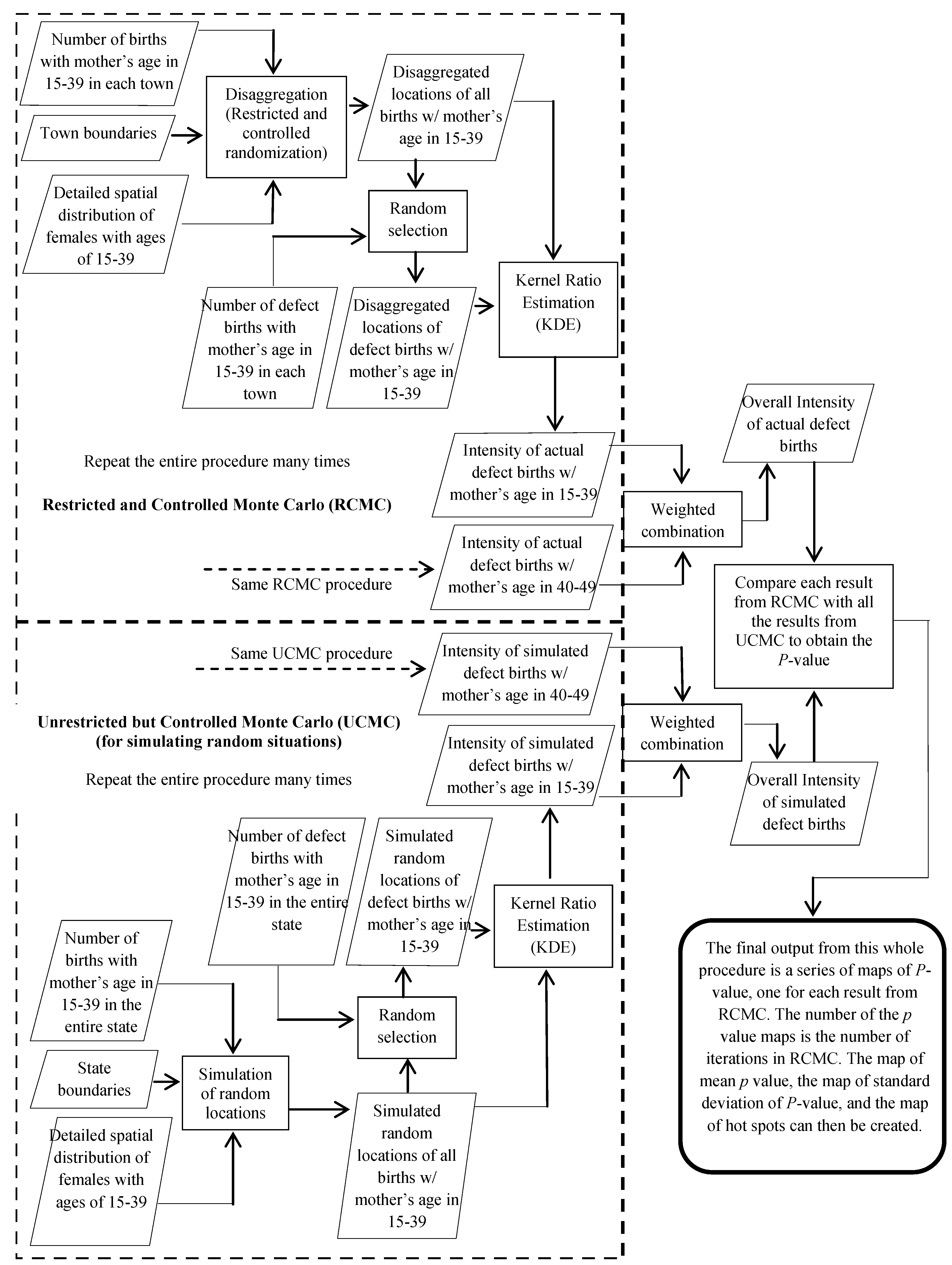
- (1)
- In the previous studies, this method was employed to deal with the situation that the location data is a mixture of point-level and polygon-level data (typically P.O. Box numbers), in which the primary function of RCMC is to disaggregate the polygon-level portion to make them compatible with the point-level data, so that the following disease mapping process (e.g., kernel density estimation or KDE) can be applied. In this study, we further pushed this method to the situation that the data are entirely aggregate in the first place, which is more common in disease mapping practice. By doing this, conceptually we took this method as a general approach to incorporating auxiliary information (e.g., detailed background population data) for the purpose of improving and evaluating spatial certainty of the data used for disease mapping, as well as mitigating the problems associated with mapping based on irregularly defined large areal units.
- (2)
- In previous studies, the RCMC method was applied to a disease (lung cancer) that has a broad cohort (i.e., not limited to a specific category in population), and therefore the background data (expected count) were able to be directly derived from the data of general population and represented as raster. Technically, in those studies the RCMC for disease cases and the following KDE were directly run over the raster backgrounds. Differently, the diseases we addressed in this study, birth defects, have a very specific cohort (infants) rather than general population. The location data of cohort are also aggregate and need to be disaggregated through RCMC. The disaggregation of disease cases and the following KDE need to be based on the disaggregated cohort locations, instead of directly on the general population (or its derivatives). In other words, instead of the case-background two-level structure in the previous studies, in this study we were dealing with a case-cohort-population three-level hierarchy. The extra layer of cohort brings about a great complexity to the implementation of the RCMC method.
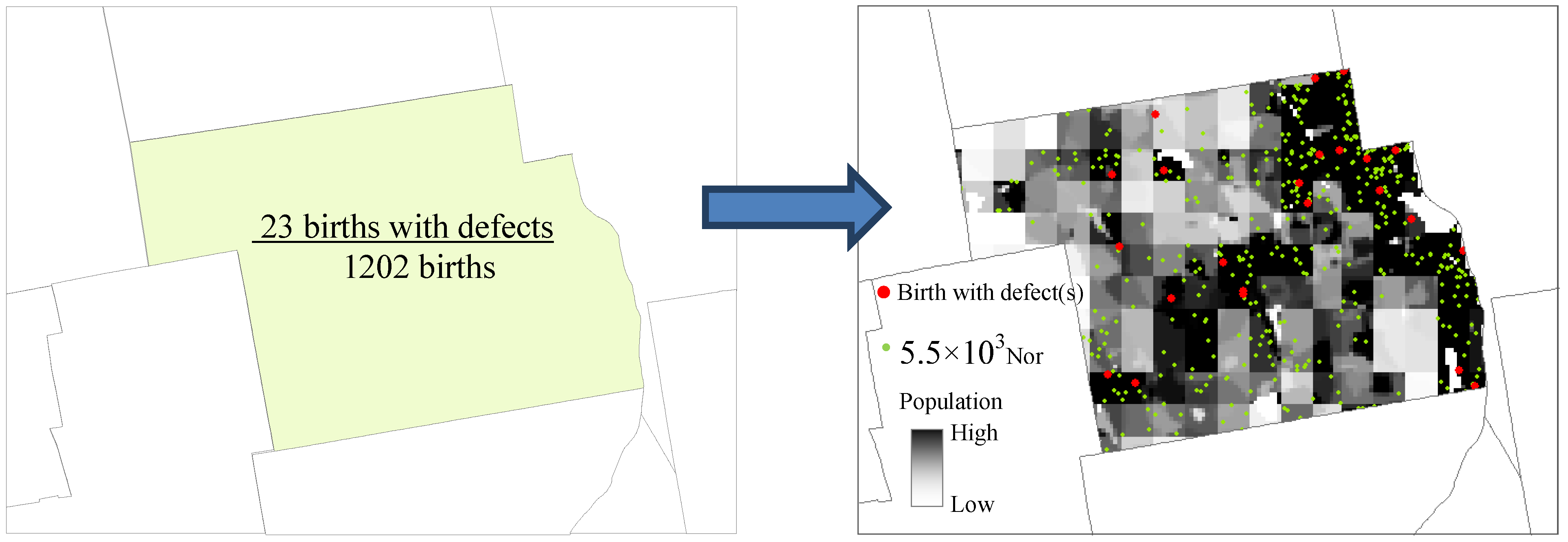
2. Data
2.1. Birth Defect Data and All-Birth Data
| Age | BD Infants | All Births | Ratio |
|---|---|---|---|
| 15–19 | 83 | 5,909 | 0.0140 |
| 20–24 | 322 | 18,823 | 0.0171 |
| 25–29 | 391 | 26,369 | 0.0148 |
| 30–34 | 361 | 27,180 | 0.0133 |
| 35–39 | 180 | 13,625 | 0.0132 |
| 40–44 | 55 | 2,840 | 0.0194 |
| 45–49 | * | <200 | 0.0208 |
| Two-Category Division: | |||
| 15–39 | 1,337 | 91,906 | 0.0145 |
| 40–49 | <100 | <3,000 | 0.0194 |
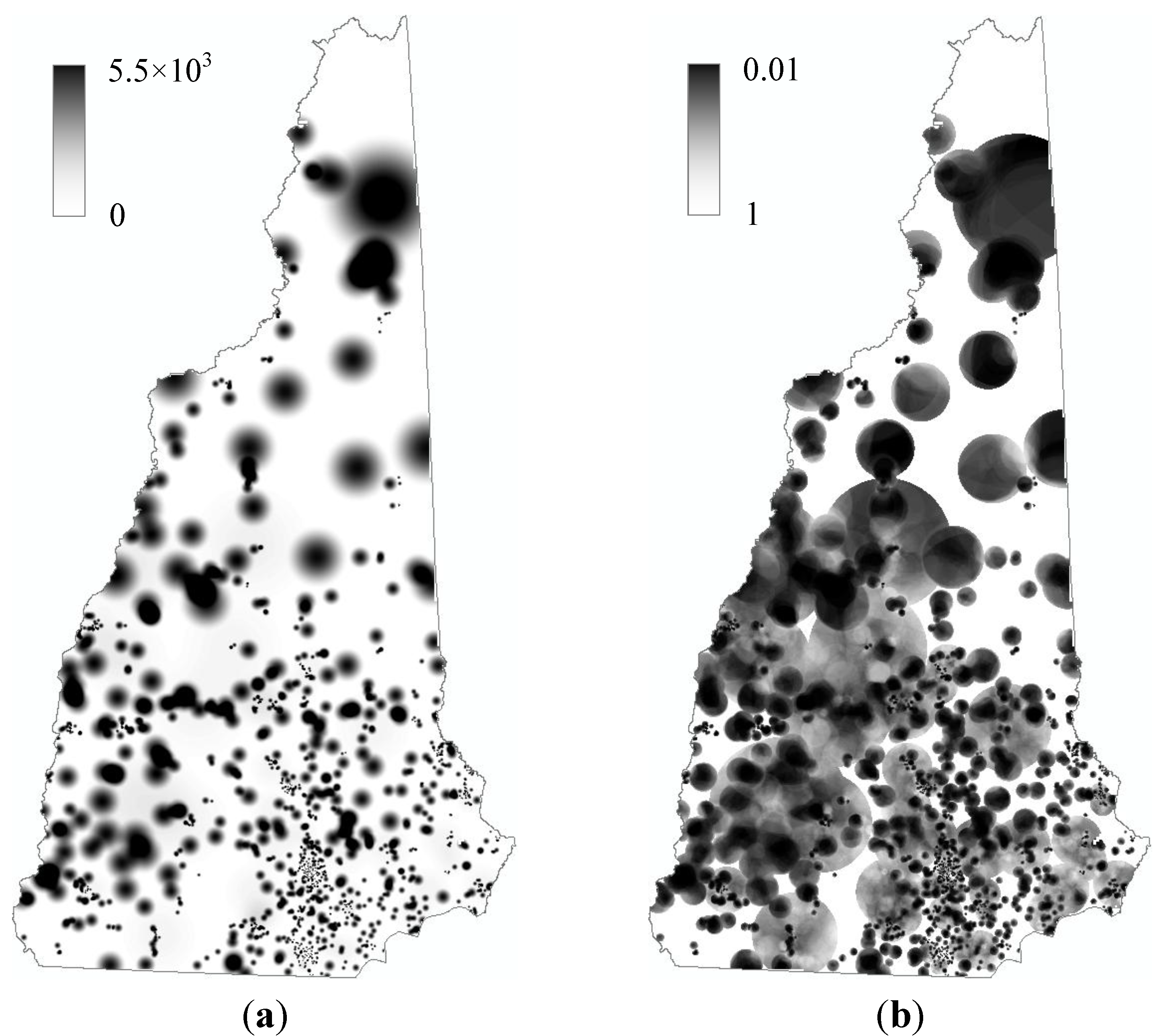
2.2. Spatially Detailed Population Data
3. Method
3.1. Disaggregation
3.2. Intensity Estimation
3.3. Statistical Significance and Spatial Uncertainty
4. Results

5. Discussion and Conclusions
- (1)
- The disaggregation allows analytical processes designed for individual data to be applied, which avoids or mitigates the problems associated with aggregate data.
- (2)
- The resulting raster maps have resolutions at the pixel level (100 m in this study), which presents more detailed spatial distribution of disease, compared with the conventional polygon map. Those details give the raster maps advantage in detecting spatial associations between birth defects and certain environmental factors.
- (3)
- The RCMC process maximizes the use of available spatial information. First of all, restricting the randomization with the smallest aggregate units maximizes the use of the spatial information represented by the polygon. Furthermore, controlling the randomization with the background data layer provides an open mechanism ready to take into account any available information that can help reduce spatial uncertainty and improve analysis quality. In this study, the background data layer of females in a certain age category eventually incorporates rich information from different sources, including the total number of people from the LandScan data and age and sex information from the Census data. The LandScan data are a product of a sophisticated model that incorporates information about population, land use, terrain, night lights, traffic, and others [39,40]. Other information, if available, can find its way into the background layer used by RCMC. For example, if a socioeconomic factor is known to be a confounding factor of a disease, and detailed information about its spatial distribution is available, it can be incorporated into the background layer.
- (4)
- The RCMC process explicitly quantifies the spatial uncertainty caused by data aggregation. Little, if any, information about the spatial uncertainty in a polygon map can be conveyed to the user of the map. RCMC resolves this problem by running the randomization iteration many times. The variance in the results from these iterations represents the uncertainty caused by aggregation, which can be explicitly and easily quantified. Essentially, this is an approach based on the idea of sensitivity analysis that empirically models variance through intensive computation.
Acknowledgments
Conflicts of Interest
References
- Waller, L.A.; Gotway, C.A. Applied Spatial Statistics for Public Health Data; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Cromley, E.K.; McLafferty, S.L. GIS and Public Health, 2nd ed.; Guilford: New York, NY, USA, 2011. [Google Scholar]
- Stallones, L.; Nuckols, J.R.; Berry, J.K. Surveillance around hazardous waste sites: Geographic information systems and reproductive outcomes. Environ. Res. 1992, 59, 81–92. [Google Scholar] [CrossRef]
- Rushton, G.; Lolonis, P. Exploratory spatial analysis of birth defect rates in an urban population. Statist. Med. 1996, 15, 717–726. [Google Scholar] [CrossRef]
- Rushton, G.; Krishnamurthy, R.; Krishnamurti, D.; Lolonis, P.; Song, H. The spatial relationship between infant mortality and birth defect rates in a U.S. city. Statist. Med. 1996, 15, 1907–1919. [Google Scholar] [CrossRef]
- Ihrig, M.M.; Shalat, S.L.; Baynes, C. A hospital-base case-control study of stillbirths and environmental exposure to arsenic using an atmospheric dispersion model and a geographical information system. Epidemiology 1998, 9, 290–274. [Google Scholar] [CrossRef]
- Tango, T.; Fujita, T.; Tanihata, T.; Minowa, M.; Doi, Y.; Kato, N.; Kunikane, S.; Uchiyama, I.; Tanaka, M.; Uehata, T. Risk of adverse reproductive outcomes associated with proximity to municipal solid waste incinerators with high dioxin emission levels in Japan. J. Epidemiol. 2004, 14, 83–93. [Google Scholar] [CrossRef]
- Gilboa, S.M.; Mendola, P.; Olshan, A.F.; Langlois, P.H.; Savitz, D.A.; Loomis, D.; Herring, A.H.; Fixler, D.E. Relation between ambient air quality and selected birth defects, seven county study, Texas, 1997–2000. Am. J. Epidemiol. 2005, 162, 238–252. [Google Scholar] [CrossRef]
- Gilboa, S.M.; Mendola, P.; Olshan, A.F.; Harness, C.; Loomis, D.; Langlois, P.H.; Savitz, D.A.; Herring, A.H. Comparison of residential geocoding methods in population-based study of air quality and birth defect. Environ. Res. 2006, 101, 256–262. [Google Scholar] [CrossRef]
- Chi, W.; Wang, J.; Li, X.; Zheng, X.; Liao, Y. Analysis of geographical clustering of birth defects in Heshun county, Shanxi province. Int. J. Environ. Health Res. 2008, 18, 243–252. [Google Scholar] [CrossRef]
- Vinceti, M.; Malagoli, C.; Fabbi, S.; Teggi, S.; Rodolfi, R.; Garavelli, L.; Astolfi, G.; Rivieri, F. Risk of congenital anomalies around a municipal solid waste incinerator: A GIS-based case-control study. Int. J. Health Geograph. 2009, 8. [Google Scholar] [CrossRef]
- Root, E.D.; Meyer, R.E.; Emch, M.E. Evidence of localized clustering of gastroschisis births in North Carolina, 1999–2004. Soc. Sci. Med. 2009, 68, 1361–1367. [Google Scholar] [CrossRef]
- Bai, H.; Ge, Y.; Wang, J.-F. Using rough set theory to identify villages affected by birth defects: the example of Heshun, Shanxi, China. Int. J. Geograph. Inform. Sci. 2010, 24, 559–576. [Google Scholar] [CrossRef]
- Liao, Y.-L.; Wang, J.-F.; Guo, Y.; Zheng, X.Y. Risk assessment of human neural tube defects using a Bayesian belief network. Stoch. Environ. Res. Risk Assess. 2010, 24, 93–100. [Google Scholar] [CrossRef]
- Liao, Y.-L.; Wang, J.-F.; Wu, J.-L.; Wang, J.J.; Zheng, X.Y. A comparison of methods for spatial relative risk mapping of human neural tube defects. Stoch. Environ. Res. Risk Assess. 2011, 25, 99–106. [Google Scholar] [CrossRef]
- Openshaw, S. The Modifiable Areal Unit Problem; Geo Books: Norwich, UK, 1984. [Google Scholar]
- Cressie, N. Change of support and the modifiable areal unit problem. Geograph. Syst. 1996, 3, 159–180. [Google Scholar]
- Shi, X. Evaluating the Uncertainty Caused by P.O.Box Addresses in Environmental Health Studies: A restricted Monte Carlo Approach. Int. J. Geograph. Inform. Sci. 2007, 21, 325–340. [Google Scholar] [CrossRef]
- Shi, X. A GeoComputation process for characterizing the spatial pattern of lung cancer incidence in New Hampshire. Ann. Assoc. Amer. Geograph. 2009, 99, 521–533. [Google Scholar] [CrossRef]
- Jacquez, G.M.; Waller, L.A. The effect of uncertain locations on disease cluster statistics. In Quantifying Spatial Uncertainty in Natural Resources: Theory and Applications for GIS and Remote Sensing; Mowrer, H.T., Congalton, R.G., Chelsea, M.I., Eds.; Sleeping Bear Press: Chelsea, MI, USA, 1999; pp. 53–64. [Google Scholar]
- Luo, L.; McLafferty, S.; Wang, F. Analyzing spatial aggregation error in statistical models of late-stage cancer risk: A Monte Carlo simulation approach. Int. J. Health Geograph. 2010, 9. [Google Scholar] [CrossRef]
- Schmiedel, S.; Blettner, M.; Schüz, J. Statistical power of disease cluster and clustering tests for rare diseases: A simulation study of point sources. Spat. Spatiotemp. Epidemiol. 2012, 3, 235–242. [Google Scholar] [CrossRef]
- Canfield, M.A.; Honein, M.A.; Yuskiv, N.; Xing, J.; Mai, C.T.; Collins, J.S.; Devine, O.; Petrini, J.; Ramadhani, T.A.; Hobbs, C.A.; Kirby, R.S. National estimates and race/ethnic-specific variation of selected birth defects in the United States, 1999–2001. Birth Defects Res A Clin Mol Teratol. 2006, 76, 747–56. [Google Scholar]
- Bithell, J.F. A classification of disease mapping methods. Statist. Med. 2000, 19, 2203–2215. [Google Scholar] [CrossRef]
- Kelsall, J.E.; Diggle, P.J. Kernel estimation of relative risk. Bernoulli 1995, 1, 3–16. [Google Scholar] [CrossRef]
- Kelsall, J.E.; Diggle, P.J. Non–parametric estimation of spatial variation in relative risk. Statist. Med. 1995, 14, 2335–2342. [Google Scholar] [CrossRef]
- Shi, X. Selection of bandwidth type and adjustment side in kernel density estimation over inhomogeneous backgrounds. Int. J. Geograph. Inform. Sci. 2010, 24, 643–660. [Google Scholar] [CrossRef]
- Openshaw, S.; Charlton, M.; Wymer, C.; Craft, A.W. Developing a mark 1 geographical analysis machine for the automated analysis of point data sets. Int. J. Geograph. Inform. Syst. 1987, 1, 335–358. [Google Scholar] [CrossRef]
- Openshaw, S.; Charlton, M.; Craft, A.W.; Birch, J.M. Investigation of leukaemia clusters by the use of a geographical analysis machine. Lancet 1988, 1, 272–273. [Google Scholar]
- Openshaw, S. Geographical information systems and tropical diseases. Trans. Roy. Soc. Trop. Med. Hyg. 1996, 90, 337–339. [Google Scholar] [CrossRef]
- Openshaw, S. Using a geographical analysis machine to detect the presence of spatial clustering and the location of clusters in synthetic data. In Methods for Investigating Localized Clustering of Disease; Alexander, F.E., Boyle, P., Eds.; IARC Scientific: Lyon, France, 1996; pp. 68–86. [Google Scholar]
- Openshaw, S.; Turton, I.; Macgill, J. Using the geographical analysis machine to analyze limiting long-term illness census data. Geograph. Environ. Model. 1999, 3, 83–89. [Google Scholar]
- Wheeler, D. A comparison of spatial clustering and cluster detection techniques for childhood leukemia incidence in Ohio, 1996–2003. Int. J. Health Geograph. 2007, 6. [Google Scholar] [CrossRef]
- Kloog, I.; Haim, A.; Portnov, B.A. Using kernel density function as an urban analysis tool: Investigating the association between nightlight exposure and the incidence of breast cancer in Haifa, Israel. Comput. Environ. Urban Syst. 2009, 33, 55–63. [Google Scholar] [CrossRef]
- Fang, L.-Q.; de Vlas, S.J.; Feng, D.; Liang, S.; Xu, Y.-F.; Zhou, J.-P.; Richardus, J.H.; Cao, W.-C. Geographical spread of SARS in mainland China. Trop. Med. Int. Health 2009, 14 (suppl. 1), 14–20. [Google Scholar]
- Pathak, E.B.; Reader, S.; Tanner, J.P.; Casper, M.L. Spatial clustering of non-transported cardiac decedents: The results of a point pattern analysis and an inquiry into social environmental correlates. Int. J. Health Geograph. 2011, 10. [Google Scholar] [CrossRef]
- Oppong, J.R.; Tiwari, C.; Ruckthongsook, W.; Huddleston, J.; Arbona, S. Mapping late testers for HIV in Texas. Health Place 2012, 18, 568–575. [Google Scholar] [CrossRef]
- Cai, Q.; Rushton, G.; Bhaduri, B. Validation tests of an improved kernel density estimation method for identifying disease clusters. J. Geograph. Syst. 2012, 14, 243–264. [Google Scholar] [CrossRef]
- Bhaduri, B.; Bright, E.; Coleman, P.; Dobson, J.E. LandScan: Locating people is what matters. Geoinformatics 2002, 5, 34–37. [Google Scholar]
- Dobson, J.E.; Bright, E.A.; Coleman, P.R.; Bhaduri, B.L. LandScan: A global population database for estimating populations at risk. Photogram. Eng. Remote Sens. 2000, 66, 849–857. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shi, X.; Miller, S.; Mwenda, K.; Onda, A.; Rees, J.; Onega, T.; Gui, J.; Karagas, M.; Demidenko, E.; Moeschler, J. Mapping Disease at an Approximated Individual Level Using Aggregate Data: A Case Study of Mapping New Hampshire Birth Defects. Int. J. Environ. Res. Public Health 2013, 10, 4161-4174. https://doi.org/10.3390/ijerph10094161
Shi X, Miller S, Mwenda K, Onda A, Rees J, Onega T, Gui J, Karagas M, Demidenko E, Moeschler J. Mapping Disease at an Approximated Individual Level Using Aggregate Data: A Case Study of Mapping New Hampshire Birth Defects. International Journal of Environmental Research and Public Health. 2013; 10(9):4161-4174. https://doi.org/10.3390/ijerph10094161
Chicago/Turabian StyleShi, Xun, Stephanie Miller, Kevin Mwenda, Akikazu Onda, Judy Rees, Tracy Onega, Jiang Gui, Margaret Karagas, Eugene Demidenko, and John Moeschler. 2013. "Mapping Disease at an Approximated Individual Level Using Aggregate Data: A Case Study of Mapping New Hampshire Birth Defects" International Journal of Environmental Research and Public Health 10, no. 9: 4161-4174. https://doi.org/10.3390/ijerph10094161
APA StyleShi, X., Miller, S., Mwenda, K., Onda, A., Rees, J., Onega, T., Gui, J., Karagas, M., Demidenko, E., & Moeschler, J. (2013). Mapping Disease at an Approximated Individual Level Using Aggregate Data: A Case Study of Mapping New Hampshire Birth Defects. International Journal of Environmental Research and Public Health, 10(9), 4161-4174. https://doi.org/10.3390/ijerph10094161




