Detection of Human Impacts by an Adaptive Energy-Based Anisotropic Algorithm
Abstract
:1. Introduction
2. Methods and Materials
2.1. Functional Specifications of a Reliable Falling Monitor
- It must guarantee a sensitivity value near 100%, with a very low rate of false alarms (high specificity), in all situations and environments where the supervised subject lives.
- The system must be emotionally accepted by target subjects. A well-known derived requirement is the unobtrusive character of the system [21].
- Personalization. The monitor should be customized to the subject under surveillance. The changing nature of human behavior and health suggests that the system must evolve with the subject. We call this an “adaptive monitor” since it is able to follow the associated subject in a continuous way.
- Physical Risk Events (PRE) detector. Falls can be classified in impact-based PREs and non-impact-based PREs. Body impacts must trigger the analysis of activity around the event, to detect impact-based PREs.
- Computational architecture functionally partitioned. A distributed processing architecture, with a division of modules on account of functional tasks, should be a solution to the current limitations on the processing capacity of unobtrusive smart monitors.
- Attention to personal preferences and needs. This requirement agrees with the necessity to allow changes in the position of the sensor, because of health conditions (e.g., dermatitis).
2.2. Laboratory Study
2.3. Accelerometer Sensor Hardware Used in the Study
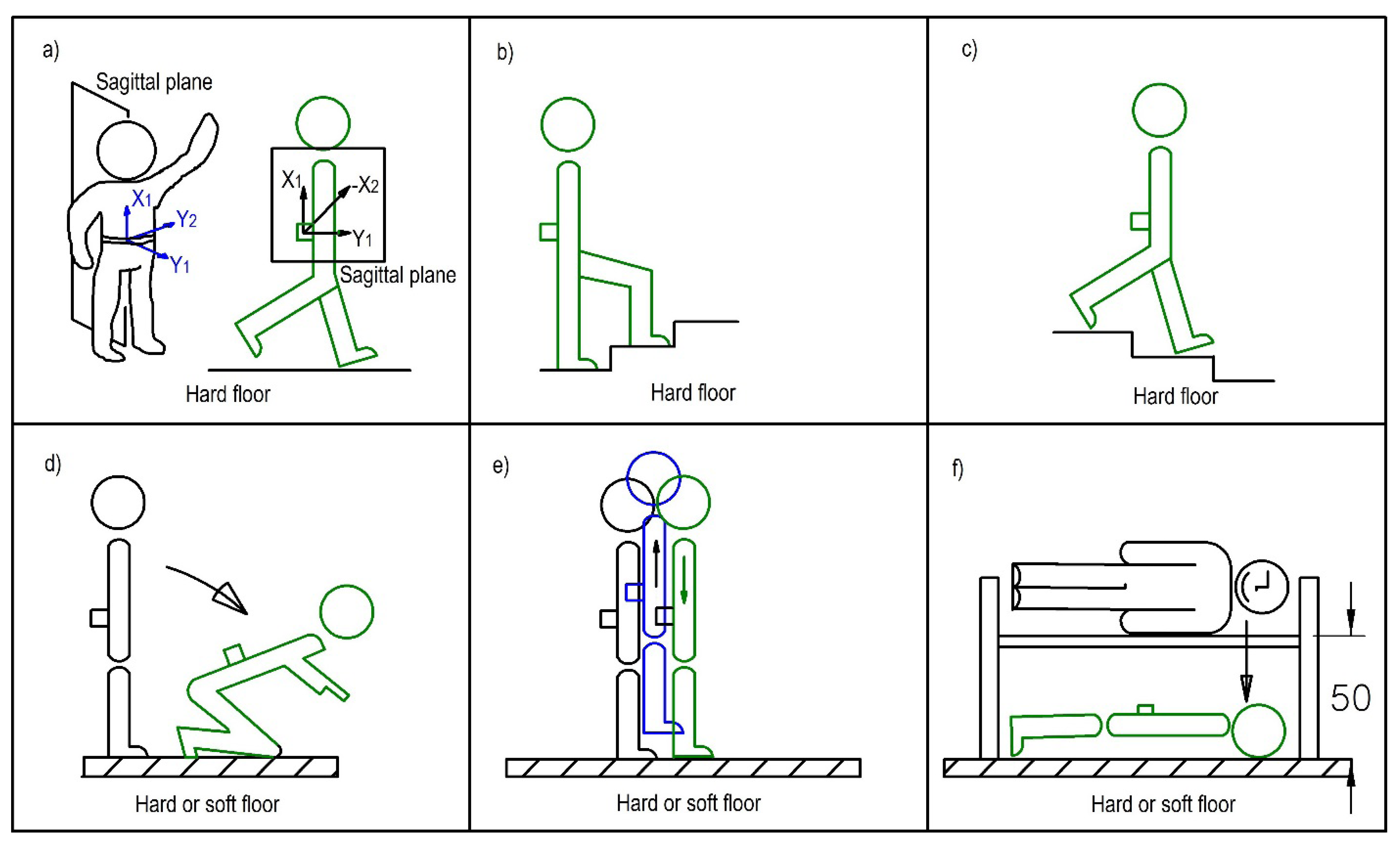
2.4. Algorithms for Impact-Based PRE Detection: Definition and Evaluation
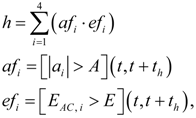
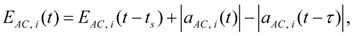
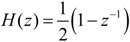
2.5. Smart Monitor Sketch
3. Results
- Personalization. It is shown that personalization improves the sensitivity and specificity of the isotropic algorithm, which can be considered a dichotomic classifier of activities (impact, no impact).
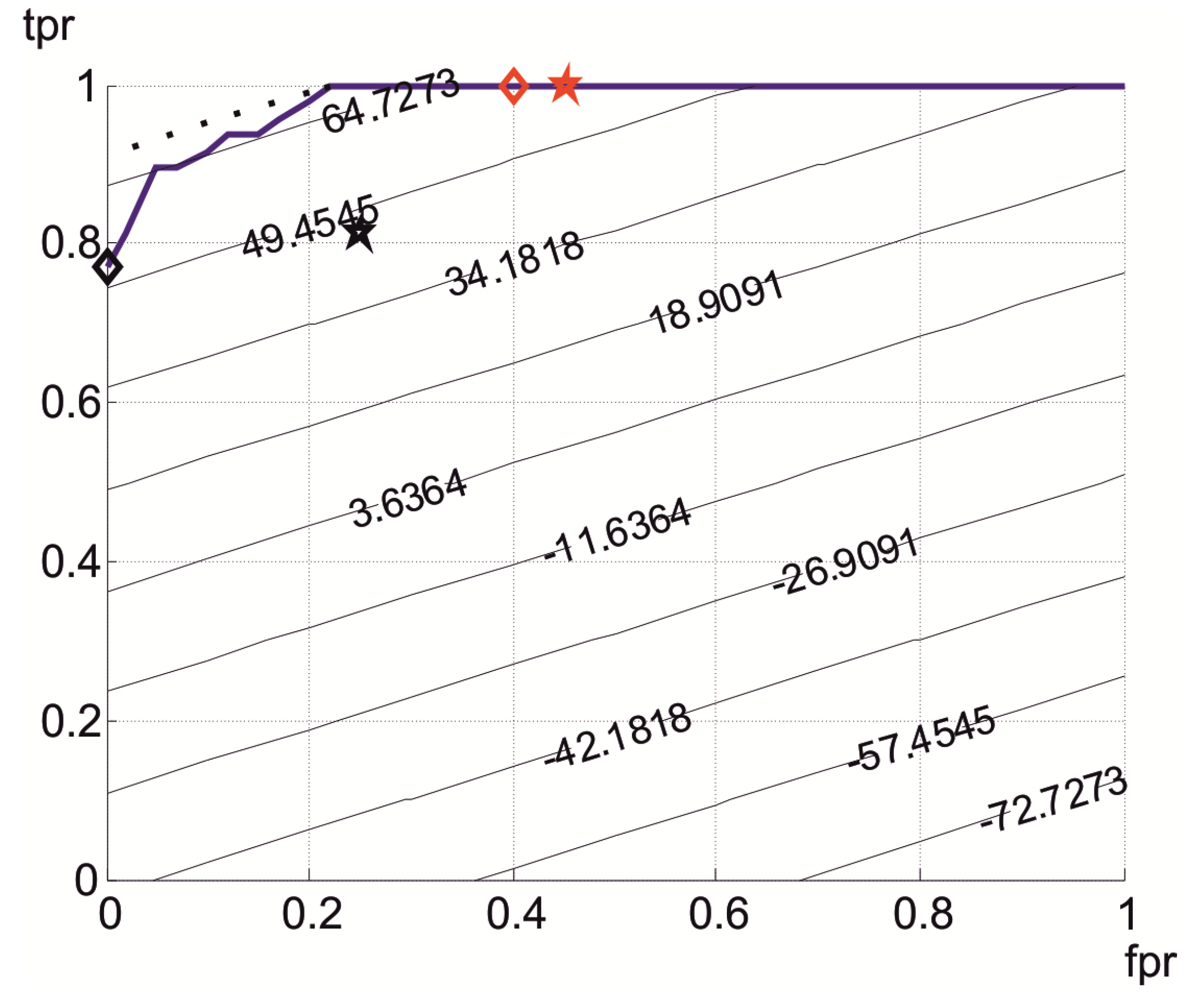
- Optimal parameter region. It is shown that there is an optimal region in the parameter space of the algorithm, Ropt, defined by a sensitivity of 100%, and a high specificity (low rate of false positives), which is robust.
- Functional partition. The analysis of the efficiency of the algorithm inside Ropt will support the functional partition of the computational architecture of the monitor.
- Reachability. It is shown that Ropt is reachable by means of an unsupervised continuous learning technique, with very low computational load, which provides the adaptive feature of the algorithm.
- Anisotropic Algorithm. We verified that the performance of the 3-axis anisotropic algorithm surpasses that of the isotropic algorithm, although it keeps the remaining properties.
3.1. Stage I. Personalization
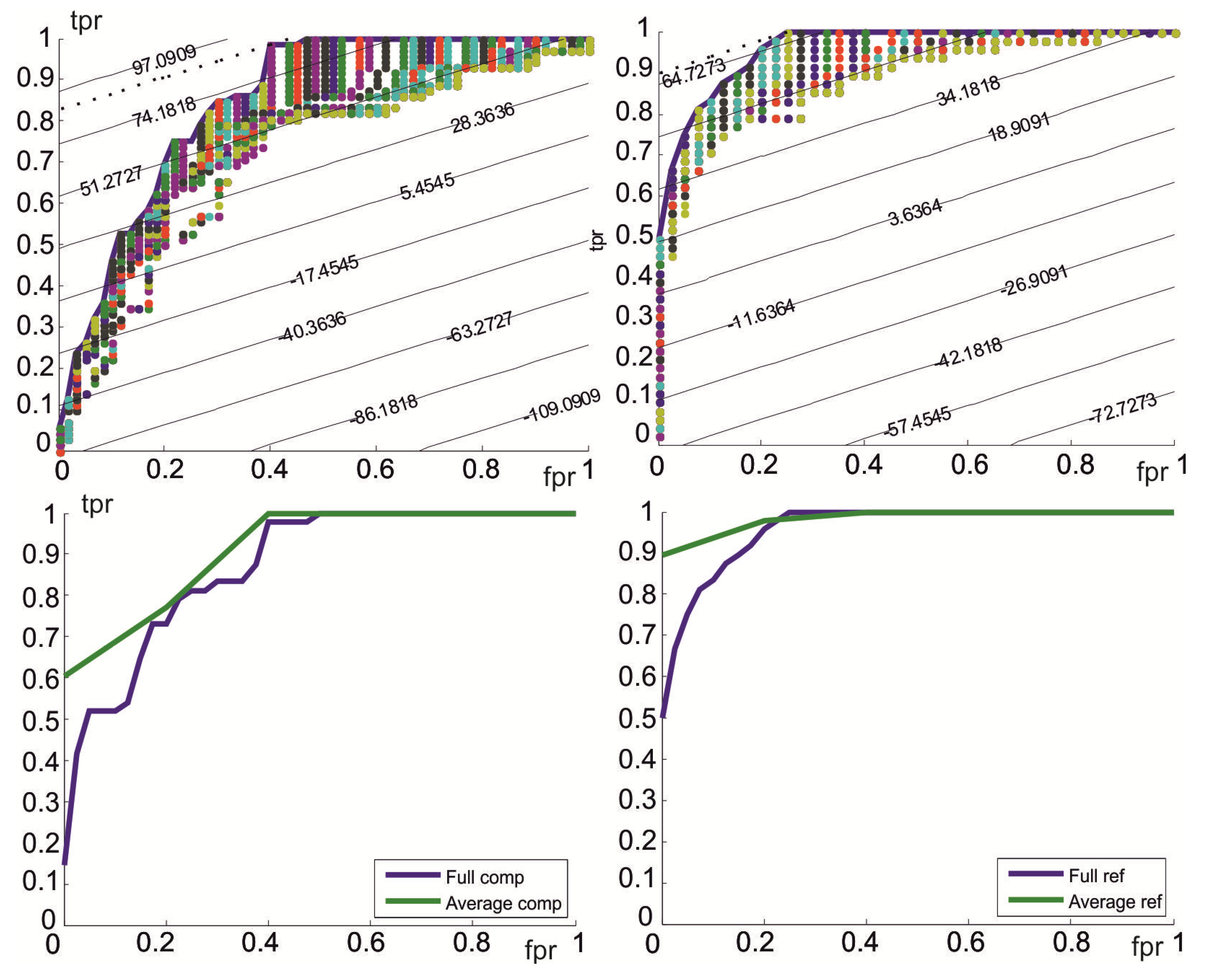
3.2. Stage II. Optimal Parameter Region


3.3. Stage III. Functional Partition
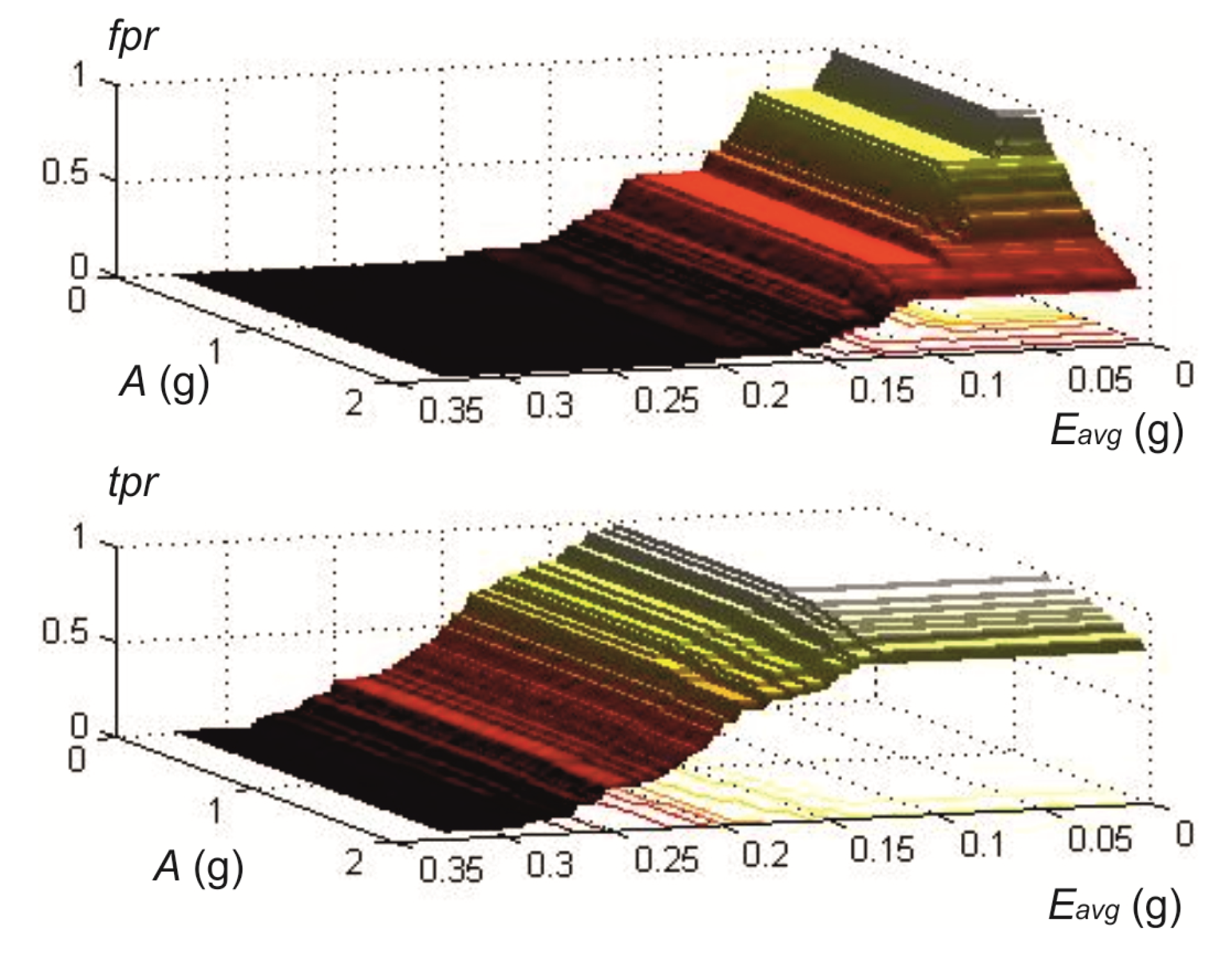
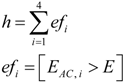
3.4. Stage IV. Reachability
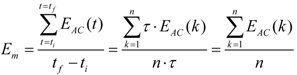
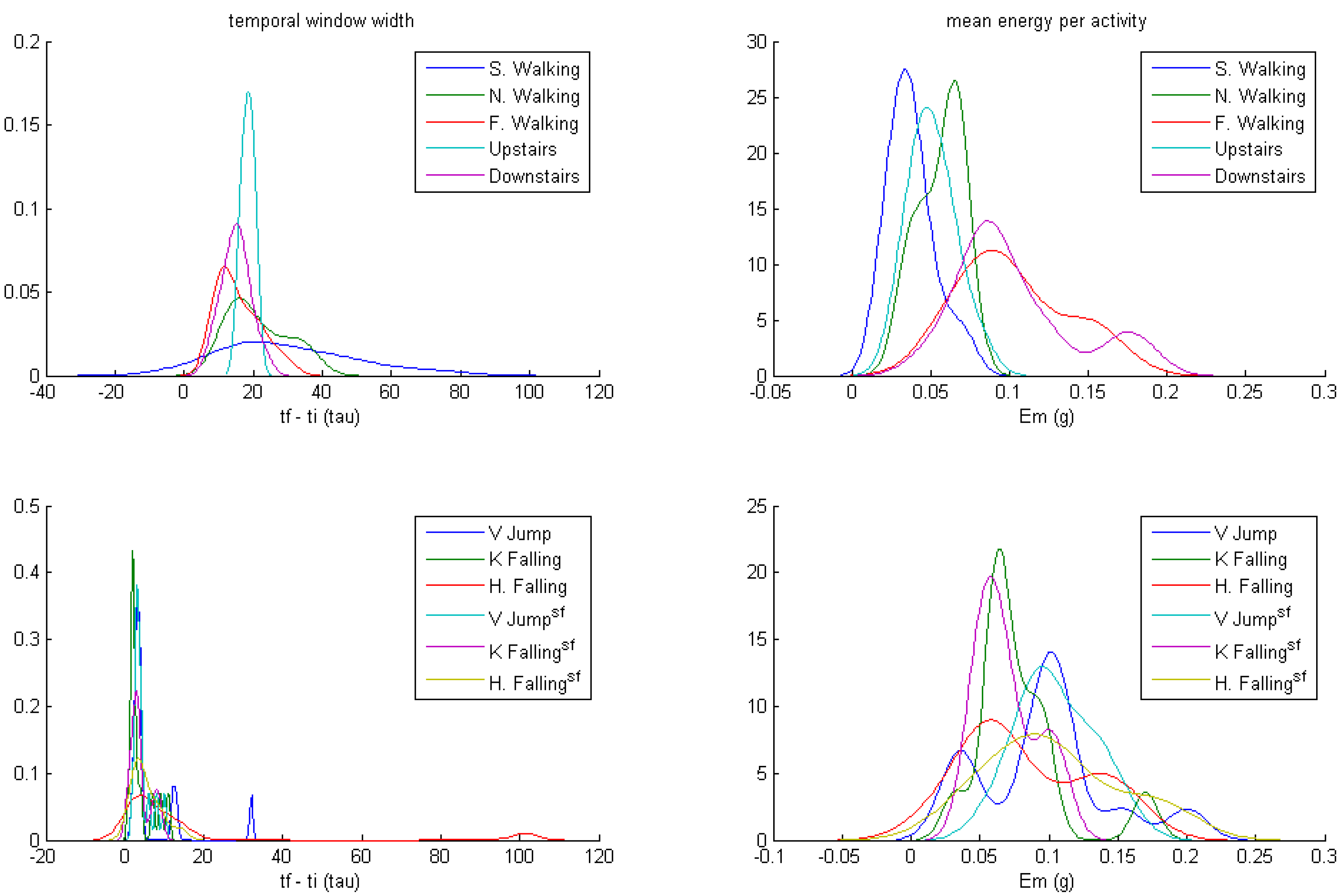

| Activity | tf − ti | Em | Emmax& | EACmax | tf − ti | Em | Emmax | EACmax |
|---|---|---|---|---|---|---|---|---|
| Slow walking | 62.5 ± 10.7 | 0.023 ± 0.002 | 0.025 0.027 | 0.038 | 29.6 ± 19.0 | 0.038 ± 0.014 | 0.071 | 0.101 |
| Normal walking | 29.1 ± 1.8 | 0.046 ± 0.004 | 0.053 0.049 | 0.082 | 21.4 ± 8.5 | 0.056 ± 0.014 | 0.089 | 0.142 |
| Fast walking | 22.1 ± 1.7 | 0.103 ± 0.012 | 0.115 0.090 | 0.200 | 15.8 ± 6.3 | 0.102 ± 0.033 | 0.160 | 0.252 |
| Going upstairs | 17.1 ± 1.9 | 0.048 ± 0.005 | 0.057 0.043 | 0.081 | 18.4 ± 1.7 | 0.051 ± 0.014 | 0.092 | 0.127 |
| Going downstairs | 14.4 ± 2.9 | 0.094 ± 0.012 | 0.108 0.072 | 0.191 | 15.0 ± 4.1 | 0.103 ± 0.039 | 0.189 | 0.312 |
| Vertical jump | 3.2 ± 0.4 | 0.130 ± 0.022 | 0.160 | 0.257 | 7.2 ± 8.6 | 0.097 ± 0.048 | 0.200 | 0.298 |
| Knee falling | 2.9 ± 0.6 | 0.072 ± 0.010 | 0.081 | 0.163 | 3.9 ± 3.3 | 0.078 ± 0.034 | 0.170 | 0.239 |
| Horizontal falling | 3.2 ± 1.3 | 0.115 ± 0.026 | 0.160 | 0.284 | 14.2 ± 27.7 | 0.083 ± 0.046 | 0.162 | 0.315 |
| Vertical jump sf | 4.6 ± 2.0 | 0.121 ± 0.032 | 0.163 | 0.264 | 4.4 ± 2.4 | 0.0105 ± 0.027 | 0.162 | 0.282 |
| Knee falling sf | 2.9 ± 1.0 | 0.096 ± 0.020 | 0.115 | 0.203 | 3.9 ± 2.6 | 0.069 ± 0.021 | 0.158 | 0.189 |
| Horizontal falling sf | 3.2 ± 1.3 | 0.125 ± 0.043 | 0.203 | 0.373 | 5.4 ± 3.7 | 0.103 ± 0.048 | 0.186 | 0.380 |
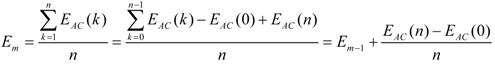

3.5. Stage V. Anisotropic Algorithm
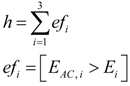
3.6. Adaptive “Divide and Conquer” Smart Monitor (DCSM)
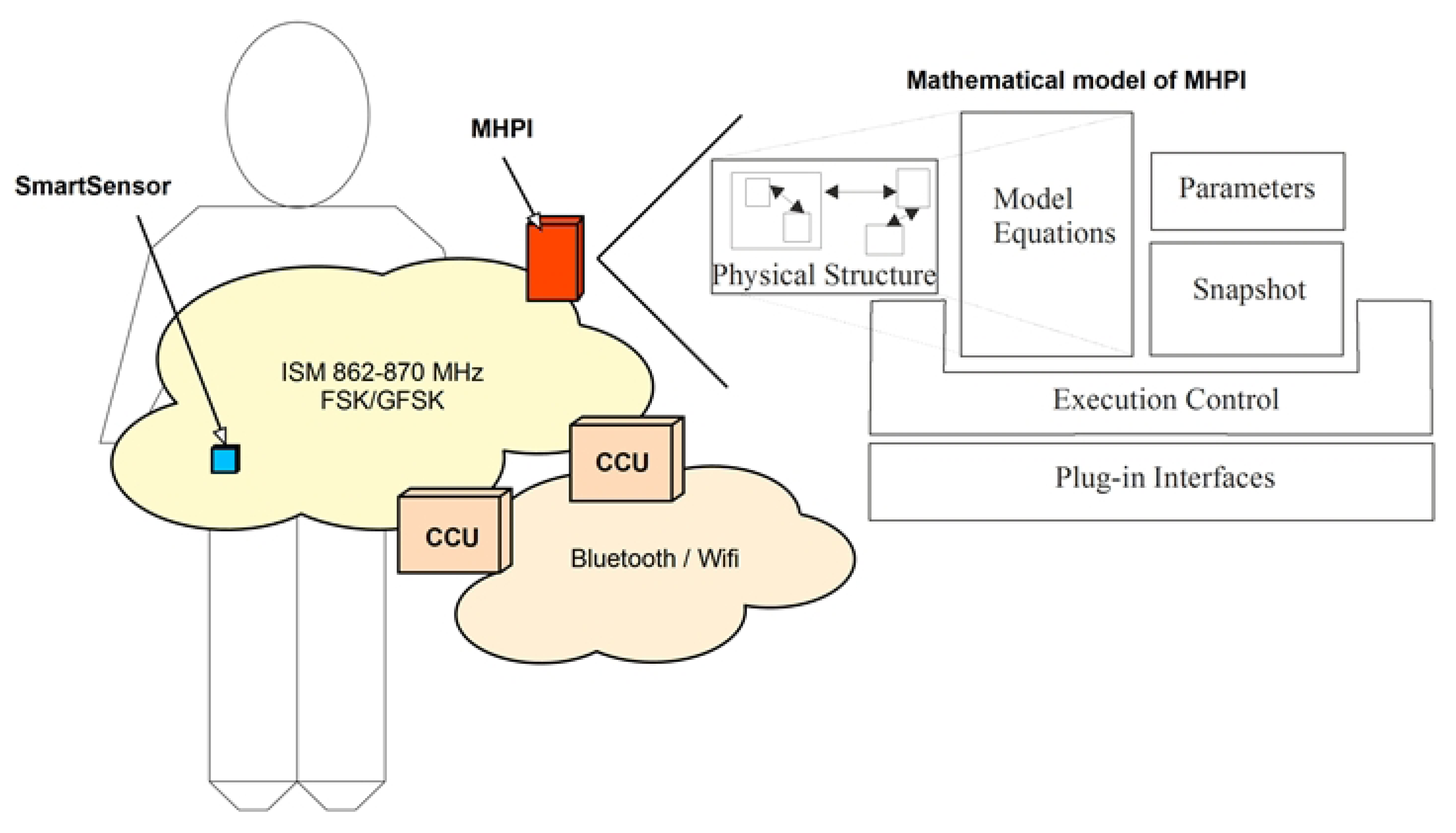
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Cumming, R.G.; Salkeld, G.; Thomas, M.; Szonyi, G. Prospective study of the impact of fear of falling on activities of daily living, SF-36 scores, and nursing home admission. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2000, 55, M299–M305. [Google Scholar] [CrossRef]
- Lord, S.R.; Sherrington, C.; Menz, H.B. Falls in Older People: Risk Factors and Strategies for Prevention; Cambridge University Press: Cambridge, UK, 2001; p. 260. [Google Scholar]
- Al-Aama, T. Falls in the elderly: Spectrum and prevention. Can. Fam. Physician 2011, 57, 771–776. [Google Scholar]
- Abdel-Rahman, E.M.; Turgut, F.; Turkmen, K.; Balogun, R.A. Falls in elderly hemodialysis patients. QJM 2011, 104, 829–838. [Google Scholar] [CrossRef]
- DeGoede, K.M.; Ashton-Miller, J.A.; Schultz, A.B. Fall-related upper body injuries in the older adult: A review of the biomechanical issues. J. Biomech. 2003, 36, 1043–1053. [Google Scholar] [CrossRef]
- Kannus, P.; Parkkari, J.; Niemi, S.; Palvanen, M. Fall-induced deaths among elderly people. Am. J. Public Health 2005, 95, 422–424. [Google Scholar] [CrossRef]
- Heinrich, S.; Rapp, K.; Rissmann, U.; Becker, C.; König, H.H. Cost of falls in old age: A systematic review. Osteoporos. Int. 2010, 21, 891–902. [Google Scholar] [CrossRef]
- Stevens, J.A.; Corso, P.S.; Finkelstein, E.A.; Miller, T.R. The costs of fatal and non-fatal falls among older adults. Inj. Prev. 2006, 12, 290–295. [Google Scholar] [CrossRef]
- De Bruin, E.D.; Hartmann, A.; Uebelhart, D.; Murer, K.; Zijlstra, W. Wearable systems for monitoring mobility-related activities in older people: A systematic review. Clin. Rehabil. 2008, 22, 878–895. [Google Scholar] [CrossRef]
- Scanaill, C.; Carew, S.; Barralon, P.; Noury, N.; Lyons, D.; Lyons, G. A review of approaches to mobility telemonitoring of the elderly in their living environment. Ann. Biomed. Eng. 2006, 34, 547–563. [Google Scholar] [CrossRef]
- Weiss, A.; Shimkin, I.; Giladi, N.; Hausdorff, J.M. Automated detection of near falls: Algorithm development and preliminary results. BMC Res. Notes 2010, 3. [Google Scholar] [CrossRef]
- Williams, G.; Doughty, K.; Cameron, K.; Bradley, D.A. A Smart Fall and Activity Monitor for Telecare Applications. In Proceedings of the 20nd Annual International Conference of the IEEE, Hong Kong, China, 1 November 1998; Engineering in Medicine and Biology Society, Ed.; IEEE: Hong Kong, China, 1998. [Google Scholar]
- Philips. Philips Lifeline. Available online: http://www.lifelinesys.com (accessed on 17 January 2012).
- Zenio. Zenio Fall Detector. Available online: http://www.zenio.be/product/8.html (accessed on 18 January 2012).
- Miguel, A.A.J.; Gorka, E.L.; Guillaume, P.; David, S.F.; Javier, Y.L. System for analysing a person’s activity and for automatic fall detection. EP1779772 (A1), 3 June 2009. [Google Scholar]
- Noury, N.; Fleury, A.; Rumeau, P.; Bourke, A.K.; Laighin, G.; Rialle, V.; Lundy, J.E. Fall detection—Principles and Methods. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2007, 1, 1663–1666. [Google Scholar]
- Prado, M.; Roa, L.M.; Reina-Tosina, J. Viability study of a personalized and adaptive knowledge-generation telehealthcare system for nephrology (NEFROTEL). Int. J. Med. Inf. 2006, 75, 646–657. [Google Scholar] [CrossRef]
- Prado-Velasco, M.; del Río-Cidoncha, M.G.; Ortiz-Marín, R. The Inescapable Smart Impact detection System (ISIS): An Ubiquitous and Personalized Fall Detector Based on a Distributed “Divide and Conquer Strategy”. In Proceedings of Personalized Healthcare through Technology30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, British Columbia, Canada, 20–25 August 2008; pp. 3332–3335.
- Prado, M.; Roa, L.M.; Reina-Tosina, J.; Rovayo, M. Wearable Human Movement Monitoring Device Aimed at Providing Personalized Support in Healthcare. In Microtechnologies for the New Millenium. Smart Sensors, Actuators, and MEMS II; SPIE Proceedings: Sevilla, Spain, 2005; Volume 5836, pp. 570–578. [Google Scholar]
- Prado-Velasco, M.; Ortiz Marín, R.; del Rio Cidoncha, M.G. New Approaches in Personalized E-Health: A Wearable Human Avatar-Based Monitor for Ubiquitous Care. In Proceedings of the 3rd International Symposium on Applied Sciences in Biomedical and Communication Technologies (ISABEL), Rome, Italy, 7–10 November 2010; pp. 1–5.
- Kaye, J.A.; Maxwell, S.A.; Mattek, N.; Hayes, T.L.; Dodge, H.; Pavel, M.; Jimison, H.B.; Wild, K.; Boise, L.; Zitzelberger, T.A. Intelligent systems for assessing aging changes: Home-based, unobtrusive, and continuous assessment of aging. J. Gerontol. B Psychol. Sci. Soc. Sci. 2011, 66B, i180–i190. [Google Scholar] [CrossRef]
- Prado, M.; Reina-Tosina, J.; Roa, L. Distributed Intelligent Architecture for Falling Detection and Physical Activity Analysis in the Elderly. In Proceedings of the 24th Annual International Conference of the IEEE-EMBS and Annual Fall Meeting of the BMES, Houston, TX, USA, 23–26 October 2002; IEEE: Houston, TX, USA, 2002; pp. 1910–1911. [Google Scholar]
- Prado-Velasco, M. Shares to the Telehealthcare in Renal Patients. New Methodological and Technological Solutions to the Renal Telehealthcare, and to the Improvement of Hemodialysis Adequacy and Hemodialyzers Efficiency. Ph.D. Thesis, University of Seville, Seville, Spain, December 2003. [Google Scholar]
- Prado-Velasco, M.; Reina-Tosina, L.J.; Roa, L. Sistema portable para la monitorización de movimiento, estado postural y actividad física de humanos durante las 24 horas del día (Wearable System for Monitoring of Movement, Posture and Physical Activity in Humans during 24 Hours). P200201710, 18 July 2002. [Google Scholar]
- Rorabaugh, C.B. Digital Filter Designer’s Handbook: Featuring C Routines; McGraw-Hill Education, Europe: Blue Ridge Summit, PA, USA, 1993; p. 332. [Google Scholar]
- Bouten, C.V.C.; Koekkoek, K.T.M.; Verduin, M.; Kodde, R.; Janssen, J.D. A triaxial accelerometer and portable data processing unit for the assessment of daily physical activity. IEEE Trans. Biomed. Eng. 1997, 44, 136–147. [Google Scholar] [CrossRef]
- Fawcett, T. ROC Graphs: Notes and Practical Considerations for Researchers. In HP Laboratories: Page Mill Road; HP: Palo Alto, CA, USA, 2004; p. 38. [Google Scholar]
- Prado, M.; Roa, L.; Reina-Tosina, J.; Palma, A.; Milán, J.A. Virtual center for renal support: Technological approach to patient physiological image. IEEE Trans. Biomed. Eng. 2002, 49, 1420–1430. [Google Scholar] [CrossRef]
- Fernández Peruchena, C.M.; Prado-Velasco, M. Smart sensors and virtual physiology human approach as a basis of personalized therapies in diabetes mellitus. Open Biomed. Eng. J. 2010, 4, 236–249. [Google Scholar] [CrossRef]
- Lee, R.Y.W.; Carlisle, A.J. Detection of falls using accelerometers and mobile phone technology. Age Ageing 2011, 40, 690–696. [Google Scholar] [CrossRef]
- Boissy, P.; Choquette, S.; Hamel, M.; Noury, N. User-based motion sensing and fuzzy logic for automated fall detection in older adults. Telemed. J. E. Health 2007, 13, 683–693. [Google Scholar] [CrossRef]
- Dinh, A.; Shi, Y.; Teng, D.; Ralhan, A.; Chen, L.; dal Bello-Haas, V.; Basran, J.; Ko, S.; McCrowsky, C. A fall and near-fall assessment and evaluation system. Open Biomed. Eng. J. 2009, 3, 1–7. [Google Scholar] [CrossRef]
- Bourke, A.K.; Lyons, G.M. A threshold-based fall-detection algorithm using a bi-axial gyroscope sensor. Med. Eng. Phys. 2008, 30, 84–90. [Google Scholar] [CrossRef]
- Kangas, M. Development of Accelerometry-Based Fall Detection: From Laboratory Environment to Real life; University of Oulu: Oulu, Finland, 2011. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Prado-Velasco, M.; Marín, R.O.; Del Rio Cidoncha, G. Detection of Human Impacts by an Adaptive Energy-Based Anisotropic Algorithm. Int. J. Environ. Res. Public Health 2013, 10, 4767-4789. https://doi.org/10.3390/ijerph10104767
Prado-Velasco M, Marín RO, Del Rio Cidoncha G. Detection of Human Impacts by an Adaptive Energy-Based Anisotropic Algorithm. International Journal of Environmental Research and Public Health. 2013; 10(10):4767-4789. https://doi.org/10.3390/ijerph10104767
Chicago/Turabian StylePrado-Velasco, Manuel, Rafael Ortiz Marín, and Gloria Del Rio Cidoncha. 2013. "Detection of Human Impacts by an Adaptive Energy-Based Anisotropic Algorithm" International Journal of Environmental Research and Public Health 10, no. 10: 4767-4789. https://doi.org/10.3390/ijerph10104767





