1. Introduction
Robust operation of a resonant sensor, such as a vibratory gyroscope, requires the resonator to be driven at resonance with constant amplitude. However, both the amplitude and resonant frequency can vary due to environmental factors, such as changes in temperature or stiffness aging. Therefore, some form of oscillation control is needed to track the constantly changing resonant frequency or to tune it to a specified frequency while keeping the amplitude constant.
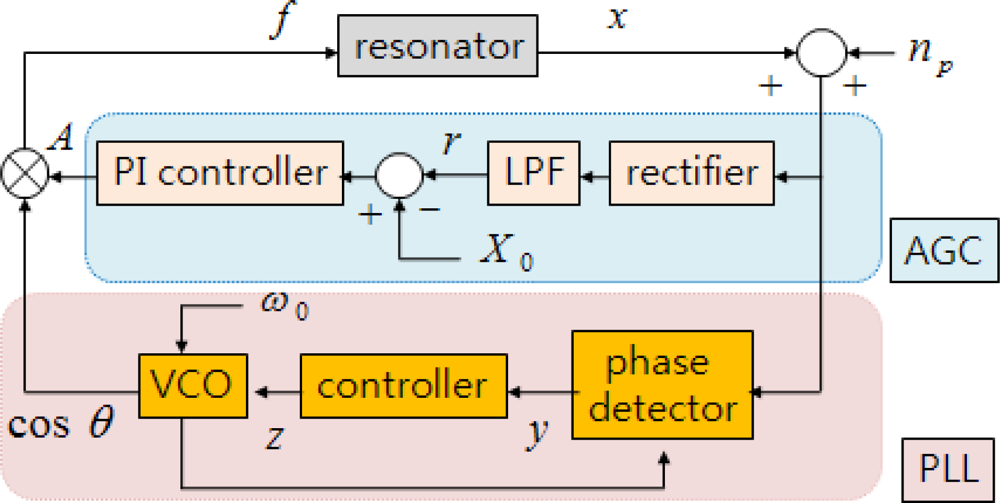
Automatic gain control (AGC) has generally been used to excite the resonator to track the reference amplitude. The application of AGC to the drive axis of a vibratory gyroscope is reported in [
1], where velocity measurement is used to control the velocity amplitude to maintain the reference amplitude. It also presented stability analysis results and AGC performance, but did not provide the noise analysis. Typically the velocity sensing circuitry produces larger noise than the displacement sensing circuitry does. A phase-locked loop (PLL) has been also used to track a resonant frequency in [
2], where stability and resolution analysis results of PLL frequency tracking system for MEMS fatigue testing are reported. However, it did not suggest a method to sustain the specified amplitude.
There have also been a few studies on controllers which, instead of tracking the resonant frequency, tune it to a specified frequency chosen by the designer. The advantages of this method are that it can maintain consistent performance, since the sensor can retain the dynamic characteristics regardless of environmental factors such as temperature changes, and simplify the signal processing loop that uses the resonant frequency as its carrier frequency. In the literature, only Lyapunov based adaptive control schemes for vibratory gyroscopes are reported to place the resonant frequency at a specified frequency [
3,
4].
This paper presents two algorithms for controlling the frequency and amplitude of oscillation. One control algorithm tracks the resonant frequency and the other algorithm tunes it to the specified resonant frequency by altering the resonator dynamics. Both algorithms maintain the specified amplitude of oscillations. In the first algorithm, AGC and PLL structures are used to control the amplitude and track the resonant frequency. The displacement measurement is used to avoid using noisy velocity measurement. The second algorithm is similar to [
3,
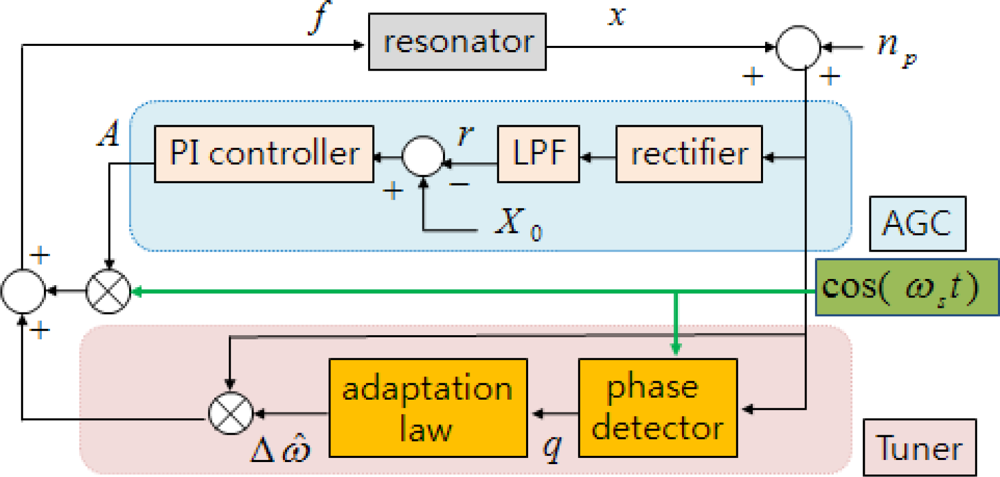
4], in that the reference frequency is chosen and then resonant frequency is adapted to it. However, it is different in some ways. First, our algorithm modifies the PLL structure to tune the resonant frequency and uses conventional AGC to regulate the amplitude, making it simpler than an adaptive control approach. Second, our algorithm can adapt only the frequency to the reference and set amplitude free rather than regulating it, which makes it applicable to mode tuning on the sense axis of a vibratory gyroscope, whereas an adaptive control approach cannot.
The averaging method is used to analyze the stability of the entire feedback system and the effects of the displacement measurement noise on tracking and estimation of the resonant frequency. The proposed control algorithms are applied to two important problems in a vibratory gyroscope to evaluate their performance. The first one is the leading-following resonator problem in the drive axis of a MEMS dual-mass vibratory gyroscope without a mechanical linkage between the two proof-masses. Adopting the proposed control algorithms enables the implementation of the following resonator which precisely traces the oscillation pattern of the leading resonator. The second one is the on-line modal frequency matching problem in a general vibratory gyroscope. Applying the first algorithm on the drive axis and the second algorithm on the sense axis enables the resonant frequencies of the drive and sense axes to be matched precisely, which significantly improves the gyroscope performance.
4. Application to the Drive Axis of a Dual-Mass Gyroscope
In general, a dual-mass gyroscope has two proof-masses linked to each other by a mechanical beam and is designed to oscillate in anti-phase with the same resonant frequency and amplitude [
5]. The Coriolis force acts along opposite directions for each of the two masses, and an external force acts in the same direction, enabling cancellation of the acceleration and other common mode effects. However, because of issues such as the difficulties in the drive axis alignment due to the connecting beam, possibility of unexpected vibration mode, and high production cost induced by high precision process, it has been proposed to remove the connecting beam and have the controller oscillate the two masses in anti-phase with the same resonant frequency and amplitude [
6].
To evaluate the control performance, the proposed control algorithms are applied to the drive axis of a dual-mass gyroscope without a mechanical linkage between the proof-masses. The equation of motion for the drive axis of a dual-mass gyroscope is described by two second-order differential equations as follows:
where subscript 1 and 2 denote the first and the second proof-mass, respectively,
x1,
x2 are the displacements of each proof-mass,
d1,
d2 are normalized damping coefficients,
ω1,
ω2 are natural frequencies, and
f1,
f2 are control inputs.
The first proof-mass is set as the leading resonator, and the second one is set as the following resonator, which precisely traces the oscillation pattern of the leading resonator. The proposed frequency and amplitude controls are applied to each mass. The dual-mass gyroscope parameters are taken from a prototype fabricated at Sejong University, and the parameters are:
Considering likely manufacturing errors, 10% error is added to
ω1 for
ω2 calculation, and 10% error is added to
d1 for
d2 calculation. The PSD of the displacement measurement noise is assumed to be
. The control law applied to the first proof-mass is frequency tracking and amplitude control and is written as:
where
A1 and
θ1 are calculated from (3) and (4), respectively. The control law for the second proof-mass is frequency tuning and amplitude control. In anti-phase, the second proof-mass should oscillate with the same resonant frequency as the first proof-mass, so the control law (25) is modified as:
where
θ1 is identical to (41) and
A2 and Δ
ω̂ are calculated from (3) and (26).
The control parameters are selected to meet the stability conditions in (18) and (36).
Table 1 shows the values of the control parameters used in the simulations. Note that the values in
Table 1 are non-dimensionalized based on length 1 μm and time 1/
ω1 (sec).
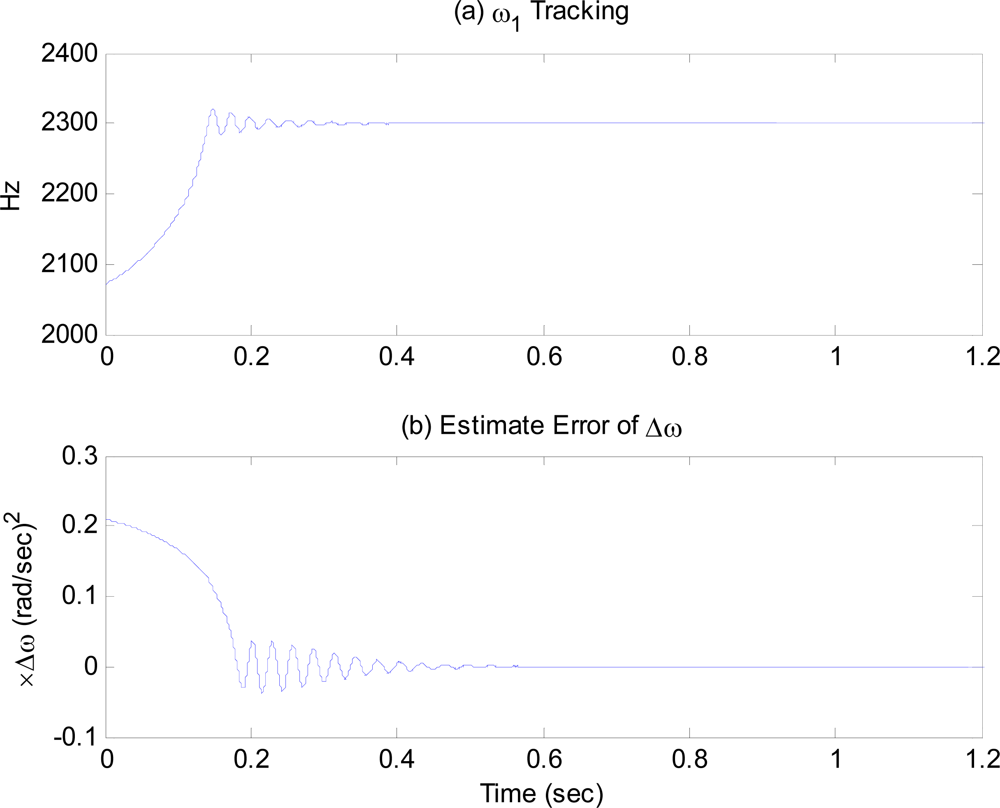
Figure 3(a) shows that the frequency tracking control on the first proof-mass tracks the resonant frequency. The excitation frequency starting from free oscillation frequency of PLL,
ω0 = 0.9
ω1, reaches the resonant frequency of the proof-mass in 0.4 second and then maintain its value. The averaged resolution of the excitation frequency from (23) is σ
1 ≈ 0.004 Hz.
Figure 3(b) shows the response of the estimation error, Δ
ω̃, showing that it converges to zero around 0.6 second.
As soon as the estimation error becomes zero, the dynamic characteristic of the second proof-mass begins to have the same resonant frequency as the first proof-mass, as observed in
Figures 4. The estimation error of Δ
ω calculated from (38), is less than σ
2 ≈ 0.01% ×Δ
ω̃.
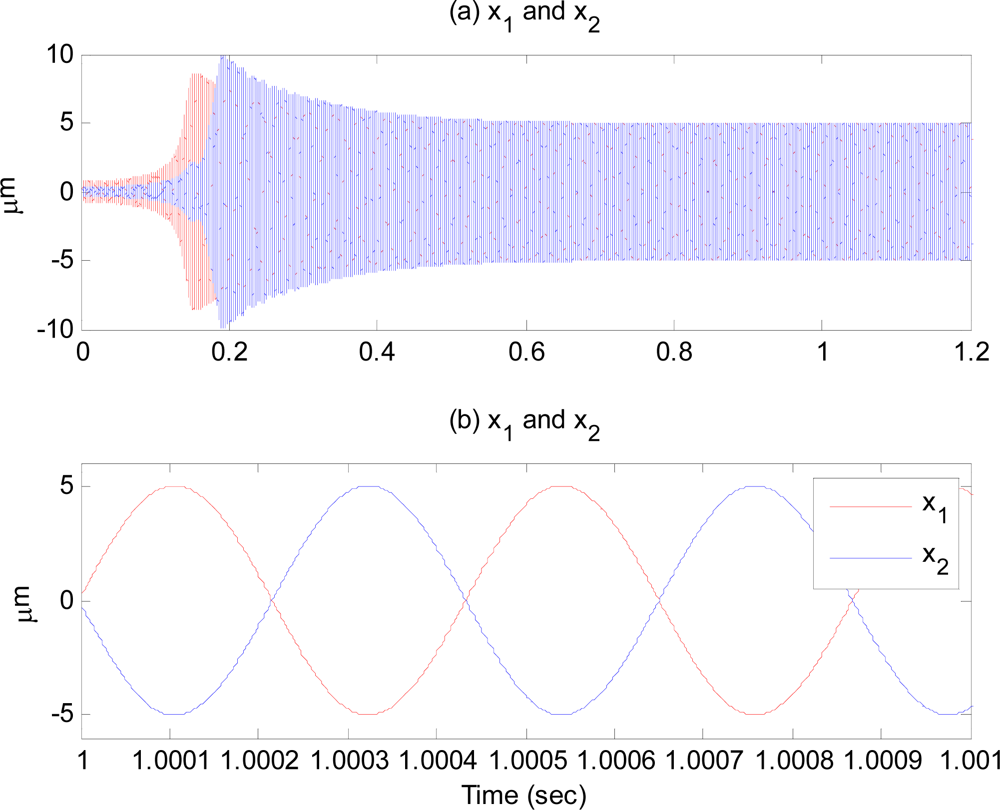
Figure 4(a) is the displacement response of the proof-mass. Its amplitude is maintained at the specified value,
X0 = 5 μm, after some time.
Figure 4(b) zooms in the response plotted in
Figure 4(a) for 1 msec, showing that the two proof-masses oscillate in anti-phase with same resonant frequency and amplitude.
5. Application to Mode Matching for a Vibratory Gyroscope
Most vibratory gyroscopes rely on matching the resonant frequencies of drive and sense axes for high performance. However, manufacturing imperfections result in deviations of the resonant frequencies from their design values. Therefore, various tuning methods have been developed [
7,
8] and the most commonly employed method is to alter the resonator stiffness by applying bias voltages with dedicated electrodes. In this method, the bias voltage should be maintained under the change in the operating conditions, such as temperature variations.
An alternative mode matching method is presented in this section using the proposed oscillation control algorithms. This method is adaptive to changes in the environment such that if the resonant frequency of sense axis is deviated from that of drive axis, the controller will continually compensate the frequency deviation. Therefore it can be used for on-line implementation.
In this method, the frequency tracking and amplitude control is used in the drive axis, and the frequency tuning control in the sense axis. The amplitude control is not used in the sense axis because the amplitude should be allowed to change according to the input angular rate. Since the drive axis control is same as that in previous section, only the sense axis is considered here. The sense axis of a vibratory gyroscope is modeled as:
where
y is the sense axis displacement,
ẋ is the drive axis velocity,
dy is the normalized damping coefficient,
ωy is the natural frequency of sense axis, Ω is the input angular rate about z-axis, and
fy is the control input for sense axis.
Because the frequency tuning control relies on the displacement measurement, it is required to excite the sense axis continually regardless of the presence of an angular rate input. Therefore we propose to insert fictitious angular rate into the sense axis, and the control law (25) is modified as follows:
where
ωx and
θx are drive axis resonant frequency and its integral resulting from drive axis control, respectively. Ω
0 is a fictitious angular rate,
X0 is the amplitude of drive axis oscillation, and Δ
ω̂y is the estimate of
, which is calculated from (26). The first term in (44) is equal to 2Ω
0ẋ if the drive axis is at resonance using the drive axis control (41). By substituting (44) into (43), and modifying (34) and calculating the averaged equilibrium point yield:
where
a0 is the magnitude of sense axis oscillation, which is proportional to input angular rate.
Simulations are conducted with the same gyroscope data given by (40), where subscript 1 and 2 are replaced by
x and
y. Fictitious input angular rate is assumed to be 10 deg/sec.
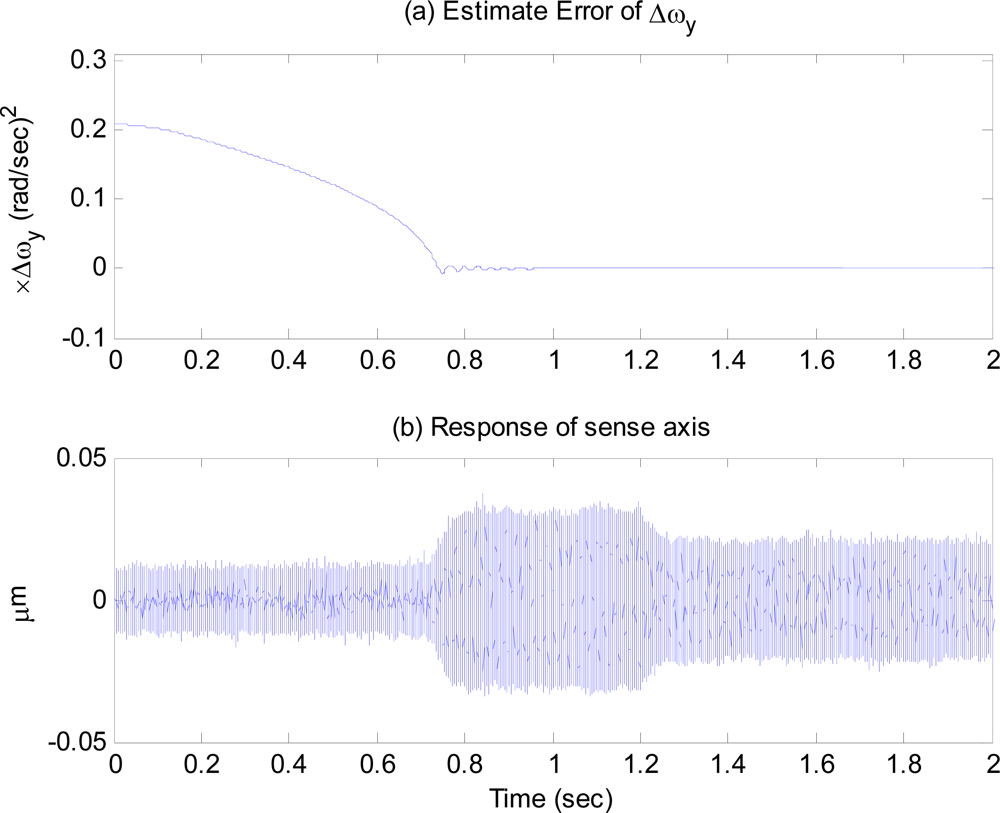
Figure 5(a) shows the time response of the frequency tuning estimation error.
Figure 5(b) shows the time response of the sense axis to a step input angular rate of 5 deg/sec applied at 1.2 sec. It is observed that as soon as the tuning estimation error becomes zero around 0.8 sec, the dynamic characteristic of the sense axis begins to have the same resonant frequency as the drive axis, and the gyroscope is ready to work, with the response of sense axis after 0.8 sec larger than that before.
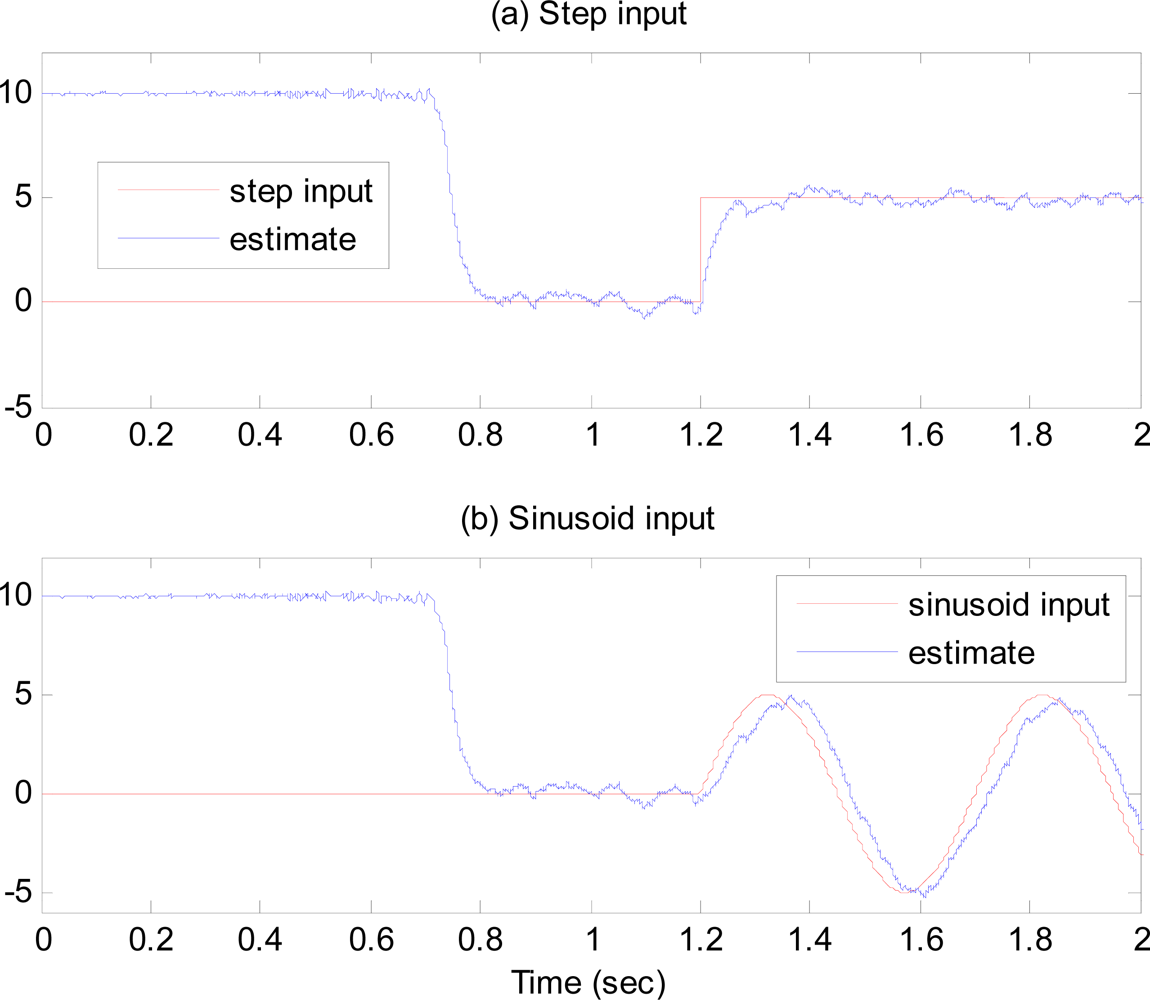
Figure 6 shows the estimates of the angular rate response to step and sinusoidal input angular rates when the modes are matched. These simulation results illustrate that the resonant frequencies of the drive and sense axes are precisely matched, and the gyroscope performance is greatly improved.
6. Conclusions
In this paper, two frequency and amplitude control algorithms are presented. One control algorithm excites the resonator at its own resonant frequency, and the other alters the resonator dynamics to place the resonant frequency at a specified frequency which is chosen by the designer. These control algorithms maintain specified amplitude of oscillations. The stability of the entire feedback system was analyzed using the averaging method, and the stability criteria were proposed so that it can be used as guidelines for selecting the control parameters. In addition, the effects of displacement measurement noise on the tracking and estimation of the resonant frequency were analyzed.
In order to evaluate the performance of the proposed control algorithms, we apply them to two important applications. The first one was application to the drive axis control loop for a dual-mass gyroscope without a mechanical linkage between two proof-masses. The second one was application to modal frequency matching in a vibratory gyroscope for high performance operation.
Simulation results agreed well with analytical analysis, and demonstrated the effectiveness of the proposed control algorithms. In addition, both the analytical and simulation studies showed that it is possible to make the two proof-masses of a dual-mass gyroscope without mechanical linkage to oscillate in anti-phase at the same resonant frequency and with the same amplitude. The proposed controller also enables the resonant frequencies of the drive and sense axes to be matched precisely by continual compensation the frequency deviations, which greatly improves the gyroscope performance.