1. Introduction
Largely because of the MEMS technology, inertial sensors (accelerometers and gyroscopes) are becoming smaller and cheaper [
1], which makes it possible to use inertial sensors in many applications. Inertial sensors are used in motion trackers [
2], personal navigation systems [
3] and remote control systems [
4].
In some applications such as body motion trackers (for example, the product ‘Moven’ by XSENS), inertial sensors are used to track body movement. As the number of inertial sensors increases, the size of sensor data increases accordingly. The sensor data is transmitted to the microprocessor board through wired or wireless communication channels. In a wireless communication channel, the transmission speed is relatively low compared with a wired communication channel. The size of the sensor data needs to be reduced if it exceeds the capacity of the communication channel. For example, the transmission rate of raw sensor data for one MTx (commercial inertial and magnetic sensor) could be as high as 72 Kbps: 9 sensor outputs (3 accelerometers, 3 gyroscopes, and 3 magnetic sensors) × 500 Hz (maximum sampling rate) × 16 bits (16 bit A/D conversion for each sensor). If four MTx are used, the size of the sensor data exceeds the capacity of Zigbee (maximum rate is 250 Kbps [
5]). More applications are expected as networked control and monitoring systems are becoming more popular [
6].
One way to reduce the size of the sensor data is to compress the sensor data before transmission and decompress the received data in the microprocessor board. Data compression has been extensively studied in many areas [
7]. In applications such as body motion trackers, real-time compression is preferable, in order to avoid delayed sensor data transmission and consequently the delay in motion estimation. One of the most popular real-time compression methods is ADPCM (Adaptive Differential Pulse Coded Modulation) [
8], which is optimized for voice data. In [
9], a simplified ADPCM method is used for inertial sensor data compression, where the maximum error (the difference between the original data and the compressed-and-then-decompressed data) is only relatively bounded (e.g., 1% of the sensor data).
The performance indices of data compression are the bit rate and the quality of compressed data. In voice data compression, the quality of compressed data is evaluated by listening to the compressed-and-then-decompressed voice data. This rather subjective evaluation makes sense since the final destination of compressed data is the human ear. On the other hand, the final destination of compressed inertial sensor data is usually a filter (such as a Kalman filter), where orientation is estimated. Thus the quality of compression should be judged by how the compression affects the estimation error.
In this paper, a modified ADPCM method is proposed, where the absolute maximum error bound is explicitly given. Also, we investigate how this error affects the estimation error. A part of this paper was presented in [
10].
2. Inertial and Magnetic Sensor Data Compression and Estimation
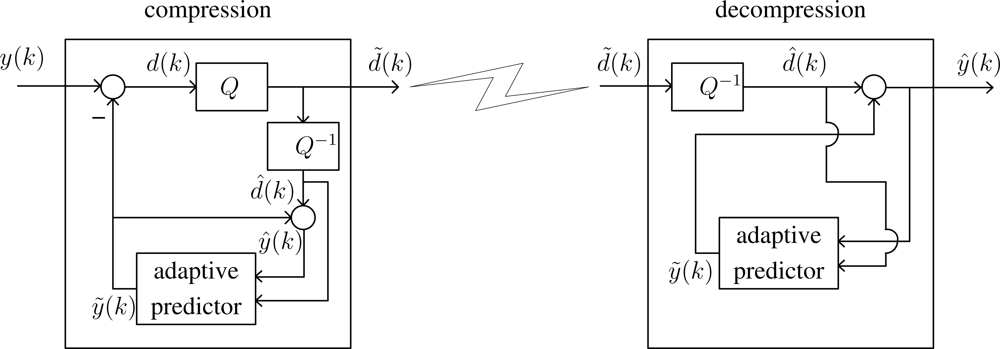
The overall process of compression and estimation is given in
Figure 1, where
k is a discrete time index. The objective is to estimate some states
x(
k) (attitude, heading, position, etc.) using inertial sensor data
y(
k) at a limited data transmission rate. The inertial sensor data
y(
k) is compressed into
d̃(
k) and transmitted to the microprocessor board. The compressed data is decompressed into
ŷ(
k) and the state
x(
k) is estimated using a filter.
Since the objective is to find a good estimator of
x(
k), the quality of compression is considered good if the estimation error
x(
k) −
x̂(
k) is small. The quality of the compression algorithm is evaluated using the following estimation error covariance:
where
x̂(
ŷ) is an estimator when
ŷ is used as an output.
Note that Perror depends on the filter algorithm used to compute x̂(ŷ) in addition to the compression algorithm.
The ideal compression algorithm minimizes both Perror and the bit rate. However, usually if Perror is small, the bit rate tends to be large. In Section 4, we propose a compression algorithm where the maximum compression error is bounded. The maximum compression error bound plays a role of design parameter to adjust Perror and the bit rate.
3. Modified ADPCM Algorithm
The ADPCM block scheme is given in
Figure 2. We assume that
y(
k) is the output of
ny bit uniform quantizer, where
y(
k) satisfies
Let the quantization size
δ of
y(
k) be defined by
If there is more than one sensor, we need one encoder for each sensor.
The sensor data
y(
k) is compared with the predictor output
ỹ(
k). The difference
d(
k) is coded into
d̃(
k) and this
d̃(
k) is transmitted to the estimator board. In the standard ADPCM,
d̃(
k) is a quantization index
i(
k). In this paper,
d̃(
k) consists of one bit mode information
m(
k) and a quantization index
i(
k):
In the decoder, the decompressed data is
ŷ(
k) =
ỹ(
k)+
d̂(
k). The predictor output
ỹ(
k) can be computed from
d̂(
k) and thus does not need to be transmitted.
The adaptive predictor uses the same pole-zero configuration as that in CCITT G.726 ADPCM, which is an ADPCM speech compressor/decompressor protocol proposed in 1990 [
11] :
From the assumption (2), if
ỹ(
k)
> ymax from (5), we set
ỹ(
k) =
ymax. Similarly, if
ỹ(
k)
< −
ymax, we set
ỹ(
k) = −
ymax.
The adaptive algorithm in the G.726 protocol is used to adjust
ai and
bi and the detail is given in [
11]; the tone and transition detector part was omitted since the part is only for voice data.
The compression error
ec(
k) is the difference between the original signal
y(
k) and the decompressed signal
ŷ(
k):
Standard ADPCM algorithms [
8] will be modified so that the maximum error is bounded as follows:
Now
d̃(
k) coding is explained. The mode bit
m(
k) in
d̃(
k) is used to ensure (7). If the compression error
ec(
k) of a standard ADPCM method satisfies (7), then the mode is 0 (i.e.,
m(
k) = 0). As will be seen in Section 3.1, this is true if
|d(
k)|
< 2
ys(k)δ, where
ys(
k) is an adaptive scaling factor. On the other hand, if the compression error
ec(
k) of a standard ADPCM method does not satisfy (7), then the mode is 1 (i.e.,
m(
k) = 1) and a special uniform quantizer is used as in Section 3.2. Thus the mode
m(
k) is given by
where
ys(
k) is an adaptive scaling factor.
The quantization index i(k) is defined differently when m(k) = 0 and when m(k) = 1.
3.1. Quantization index when m(k) = 0
If
m(
k) = 0, a signal
d(
k) is quantized with
nd bits with a logarithm quantizer with an adaptive scaling factor
ys(
k), where the quantized index
i(
k) (1 ≤ |
i| ≤ 2
nd−1) satisfies
The sign of the index
i(
k) is the same as that of
d(
k). If
d(
k) = 0, then
i = 1.
Coefficients
fi in (9) are computed from
μ law [
8] so that
fi satisfies the following:
In this paper,
μ = 5 is used and
fi values for the case of
nd = 5 is given in
Table 1:
The scaling adaptation factor
ys(
k) is computed similarly with the standard ADPCM algorithm except that
ys(
k) is bounded as follows:
We note that
ȳs is chosen so that (7) is satisfied. First we are going to derive the upper bound of
ec(
k) when
ȳs is given.
The decompressed signal
d̂(
k) is computed as follows:
where
The error
ec(
k) is then
From the fact that
fi is monotonically increasing and (10), we have
Given
emax, to satisfy (7),
ȳs should satisfy the following
Thus if
ȳs is chosen to satisfy (12), the quantization error is always smaller than
emax when
m(
k) = 0. We also note that in addition to the global bound
emax, if index
i(
k) is known, we have a less conservative bound given in (11):
This bound will be used later in the estimation problem.
3.2. Quantization index when m(k) = 1
From (8), m(k) = 1 if |d(k)| > 2ys(k)δ. If m(k) = 1, then the logarithm quantizer used cannot guarantee the maximum error (7). Noting that d(k) = y(k) − ỹ(k), we can see that the mode is 1 if the difference between the output y(k) and the predicted value ỹ(k) is large, which happens when the signal change is not smooth but instead rather abrupt.
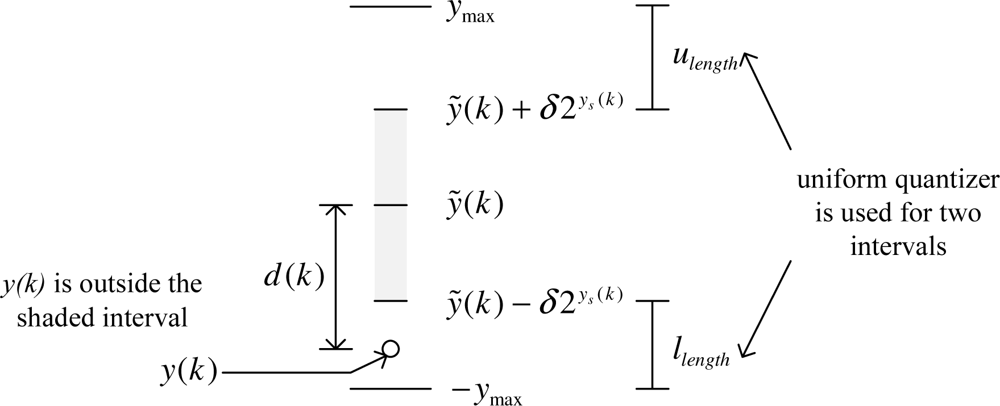
To ensure the maximum error condition (7), we introduce a uniform quantizer when the mode is 1. An example is given in
Figure 3, where
y(
k) is outside the [
ỹ(
k) −
δ2
ys(k), ỹ(
k) +
δ2
ys(k)] interval and the mode is 1. The upper and lower intervals of the mode 1 interval (the mode 0 interval is the shaded area) are quantized with a uniform quantizer (quantization size is 2
emax). The formal definition of the index in mode 1 is given as follows. Let
ulength and
llength be defined by
Let
ulevel (the number of quantization levels for the upper interval
ulength) be defined by
ceil(
α) is the smallest integer no smaller than
α.
The index
i(
k) is given by
where floor(
α) is the largest integer no larger than
α.
The decomposed signal
d̂(
k) is computed as follows.
Since a uniform quantizer is used, the compression error
ec(
k) in mode 1 is bounded by
Note that the number of bits for the index
i(
k) is given by
When
m(
k) = 1,
ni(
k) changes depending on
ỹ(
k) and
y(
k). Note that when
m(
k) = 0,
nd (the number of bits for
i(
k)) is constant. Also note that
ni can be computed in the estimation board and thus does not need to be transmitted.
4. Kalman Filter Compensating the Compression Error
In Section 3, a compression method is proposed, where the maximum compression error is emax. Also if m(k) and i(k) are known, bounds of the compression error are given by (13) and (15). In this section, we use this information in a Kalman filter.
We assume that
y(
k) is generated by a linear system
where
x ∈ Rn is the state,
y ∈ Rp is the output, and
w(
k) and
v(
k) are uncorrelated, zero-mean, white Gaussian noises that satisfy
In the standard Kalman filter,
x(
k) is estimated using
y(
k). If
y(
k) is compressed,
ŷ(
k) =
y(
k) −
ec(
k) is used instead. From (13) and (15),
ēc(
k) can be computed, which is used to reduce the estimation error. If we assume
ec,i(
k) (
i-th element of
ec(
k)) has a uniform distribution,
. By treating the compression error
ec(
k) as measurement noise in
y(
k), the following model can be used for an estimator.
where
Since the compression error is compensated in the estimation algorithm, we can expect a smaller estimation error, which is verified through the simulations in Section 5. When a Kalman filter is used for (17), the estimation error covariance
P(
k) = E{(
x(
k) −
x̂(
k))(
x(
k) −
x̂(
k))′} can be computed from a Riccati equation [
12].
Since
R̄(
k) depends on
ŷ(
k), we cannot compute
P(
k) before simulation. To evaluate the estimation error covariance without simulation, we use an upper bound of
R̄(
k):
Using this
R̄max in place of
R̄(
k), we can find a steady-state solution to (19).
P̄ can be considered as an upper bound of
P(
k) in (19). From
P̄, we can see how
emax,i affects the estimation error.
A similar idea is used in [
13], where a networked estimation problem is considered.
5. Simulation
We compared three data sets using the proposed compression algorithm. Original data is 1600 bits/s for each sensor : 16 bit A/D converted data (i.e., ny = 16) with the sampling rate being 100 Hz. We used nb = 5: that is, the number of bits for the quantization index when m(k) = 0 is 5. emax for each sensor is chosen so that emax = 300δ, where δ is different for each type of sensors. ȳs = 12 is found to satisfy (12).
Bit rates for the three compressed data sets are given in
Table 2. All three data sets are obtained using XSENS MTx (3 accelerometer, 3 gyroscopes, and 3 magnetic sensors). Holding MTx with a hand, we moved MTx slowly (data set 1) and fast (data set 2). Data set 3 is obtained from a personal navigation system, where MTx is attached on the shoe of a pedestrian [
3].
The bit rates of data set 3 is the largest because the change of data is the most abrupt. In particular, when the shoe contacts the floor, there is a large change in the accelerometer and gyroscope outputs, and consequently the compression algorithm becomes m(k) = 1 more often.
To see how the compression error affects the estimation error, a simple one dimensional attitude estimation problem is considered. An attitude (
θ) is estimated using two outputs:
yi is an inclinometer output and
yg is a gyroscope output, where
where
vi and
vg are measurement noises and
and
.
An indirect Kalman filter ([
12]) is used to estimate
θ using
yi and
yg. In the indirect Kalman filter, the gyroscope output is integrated to compute
θi, i.e.,
Defining
θδ as
we obtain
In the indirect Kalman filter,
θδ is first estimated and
θ̂ is obtained indirectly from
θ̂ = θi −
θ̂δ.By discretizing (22) with the sampling period
T (
T = 0.01
sec), we have
Now the proposed compression algorithm is used to compress
yi and
yg. The maximum compression errors
emax,i (
emax for
yi) and
emax,g (
emax for
yg) affect both the bit rate and the estimation error. If
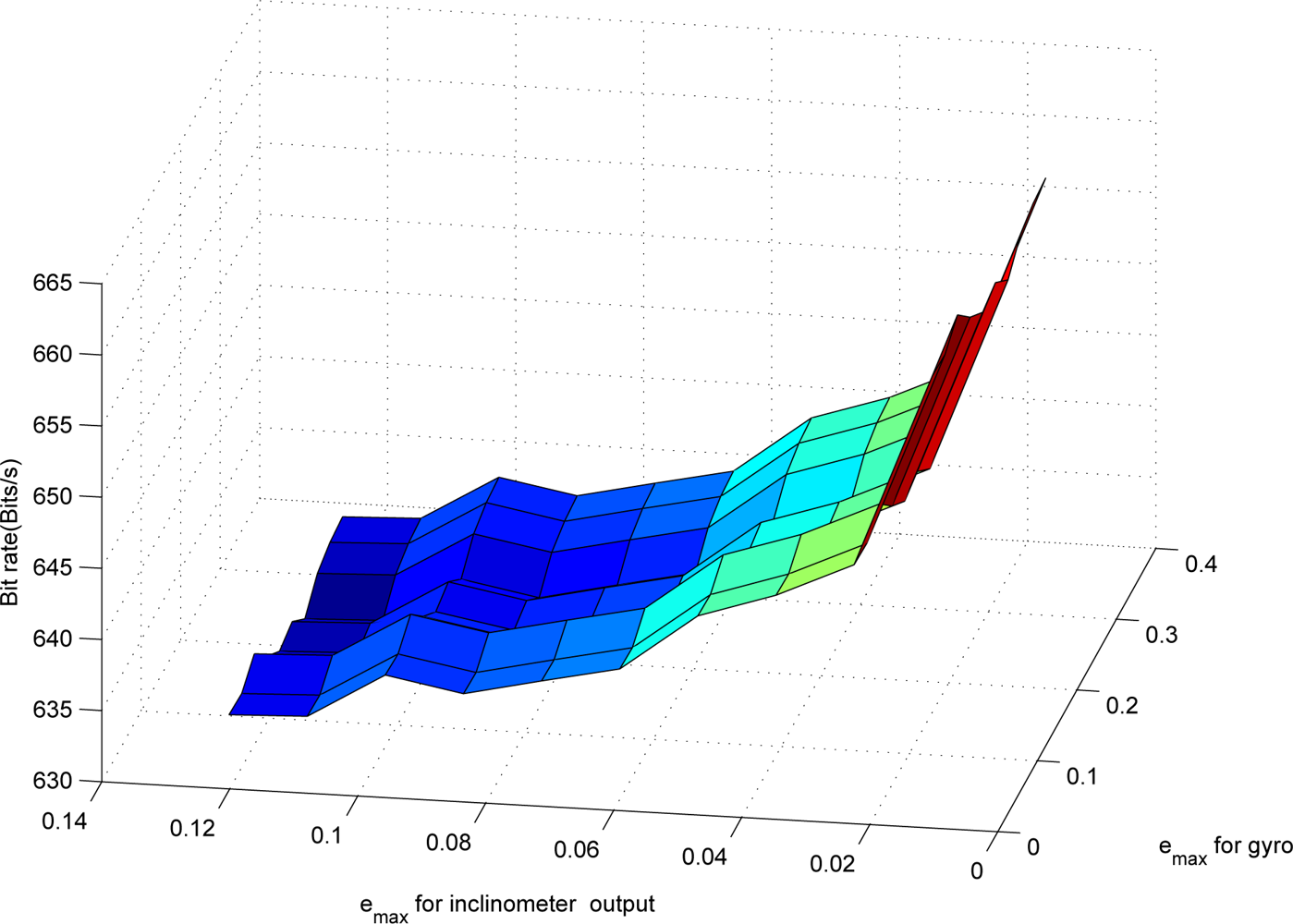
emax is small, the chance that the mode becomes 1 increases. Thus the bit rate becomes large. How the bit rate changes with the changing
emax is given in
Figure 4. The data
yi and
yg are generated using Matlab.
From
Figure 4, we can see that the bit rate of the inclinometer outputs increases rapidly as
emax,i is decreased. On the other hand, the bit rate of the gyroscope outputs does not change much as
emax,g is decreased. The bit rate depends on how often the mode becomes 1: note that
ni (the number of bits needed for the quantized data when the mode is 1) is generally larger than
nd (the number of bits needed when the mode is 0). If the original signal is sufficiently smooth,
d(
k) is small since the predicted value
ỹ(
k) is very close to
y(
k). Thus even if we decrease
emax,
d(
k) still satisfies
|d(
k)|
≤ 2
ys(k)δ condition in (8).
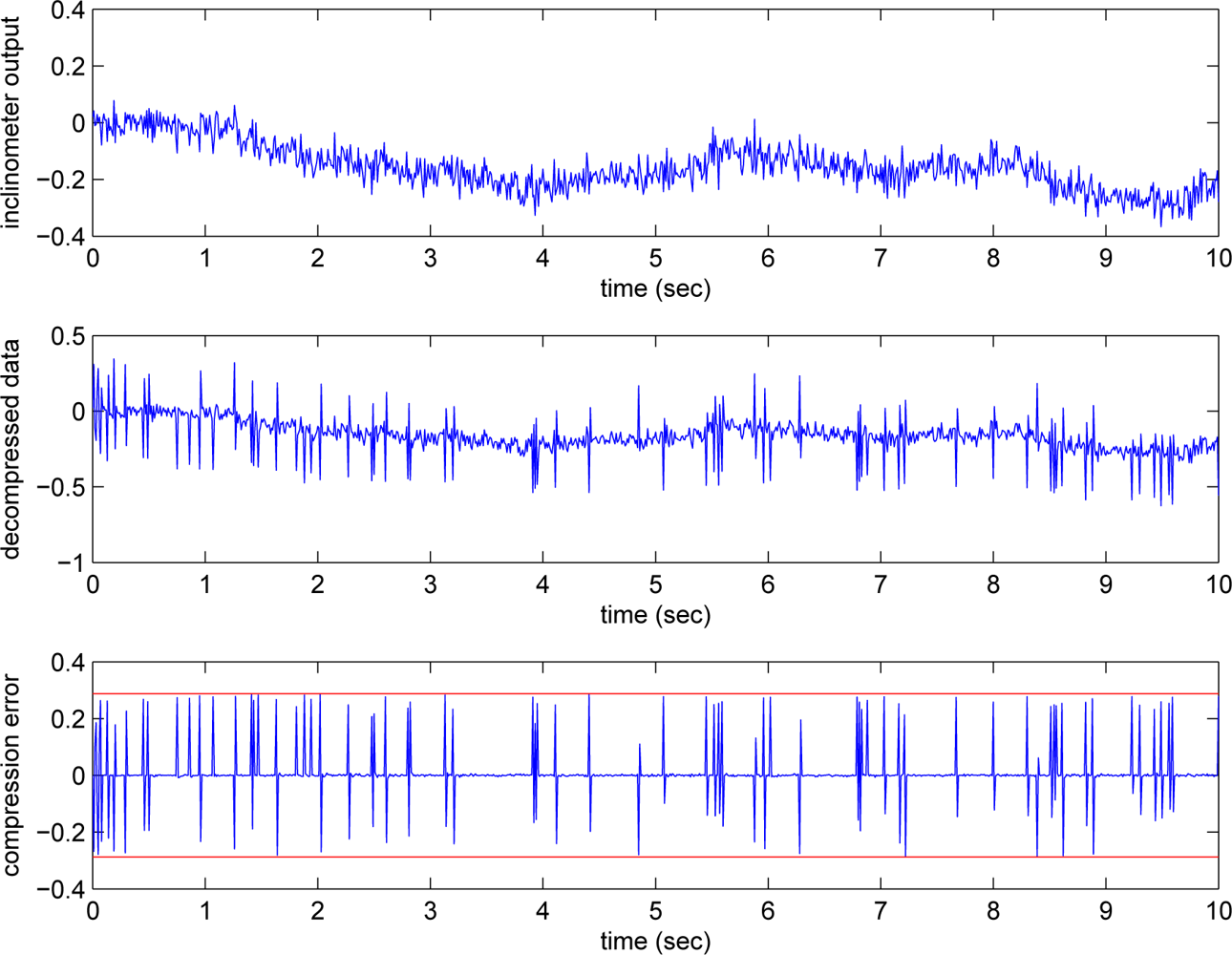
The
yi and
yg signals and the compressed signals are given in
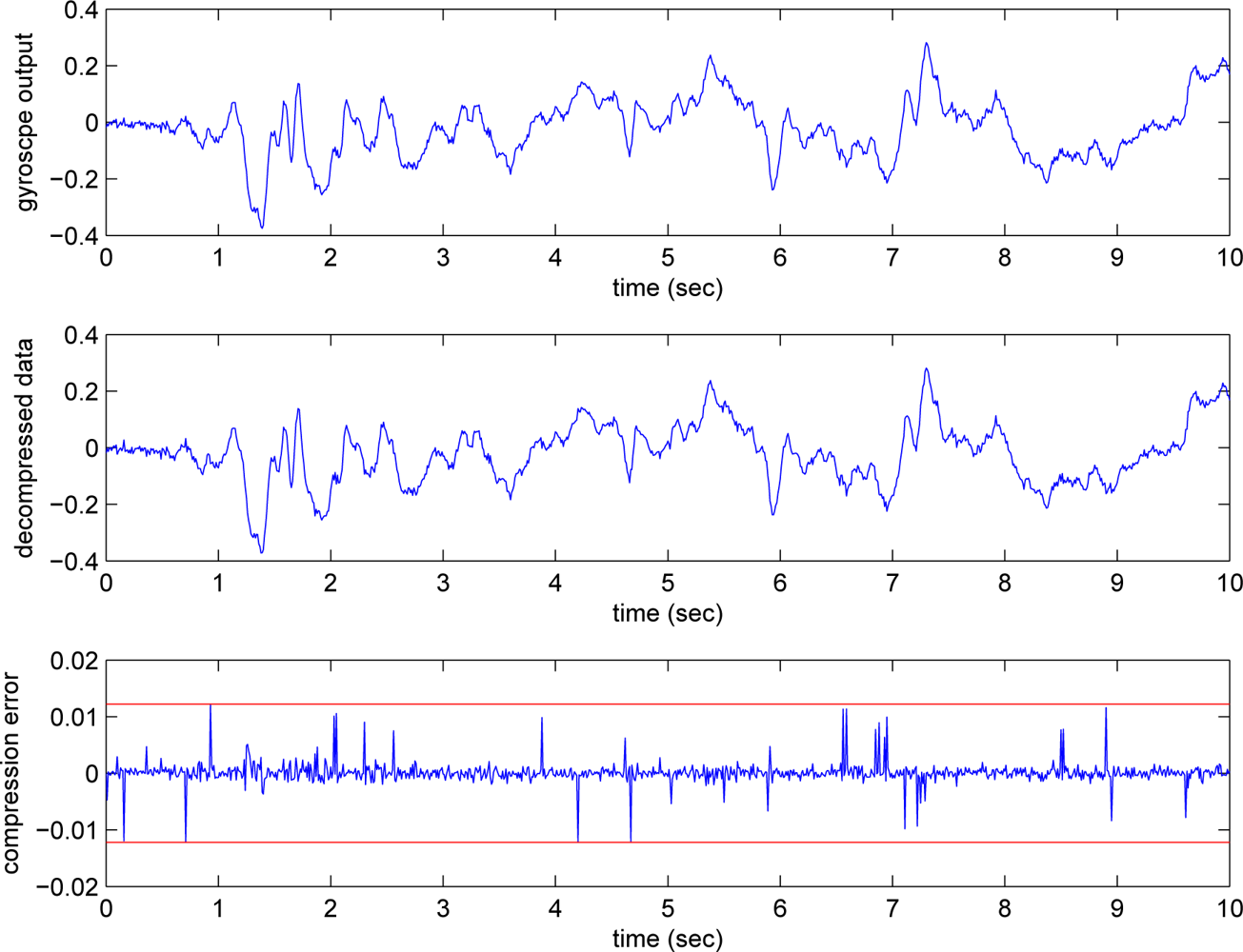
Figures 5 and
6, where
emax,i = 0.2876 and
emax,g = 0.0122. We can see that the gyroscope output is relatively smooth compared with the inclinometer output. Thus the bit rate of the gyroscope output is relatively insensitive to the changes in
emax,g.
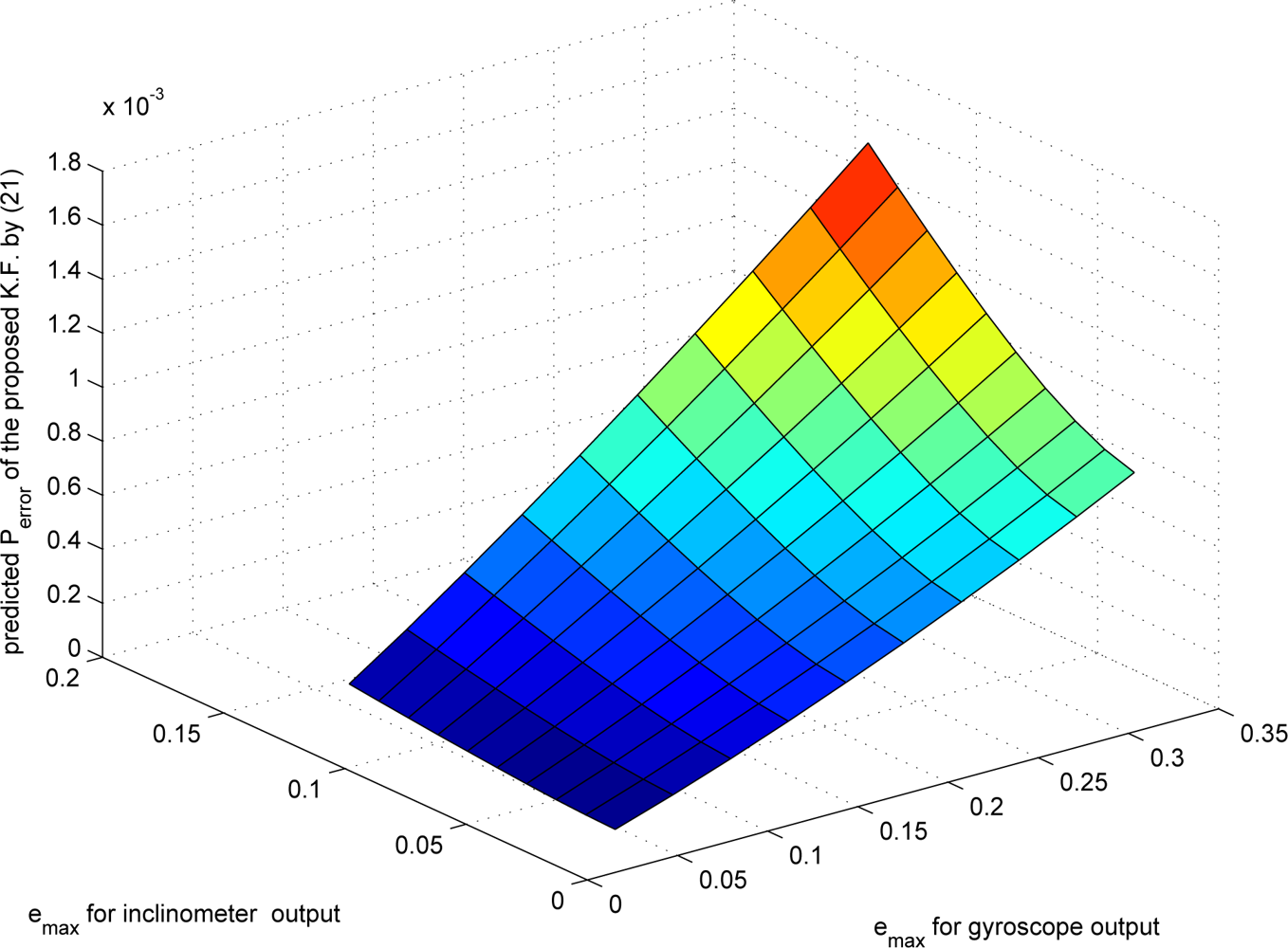
The effects of changes in
emax on the estimation error are given in
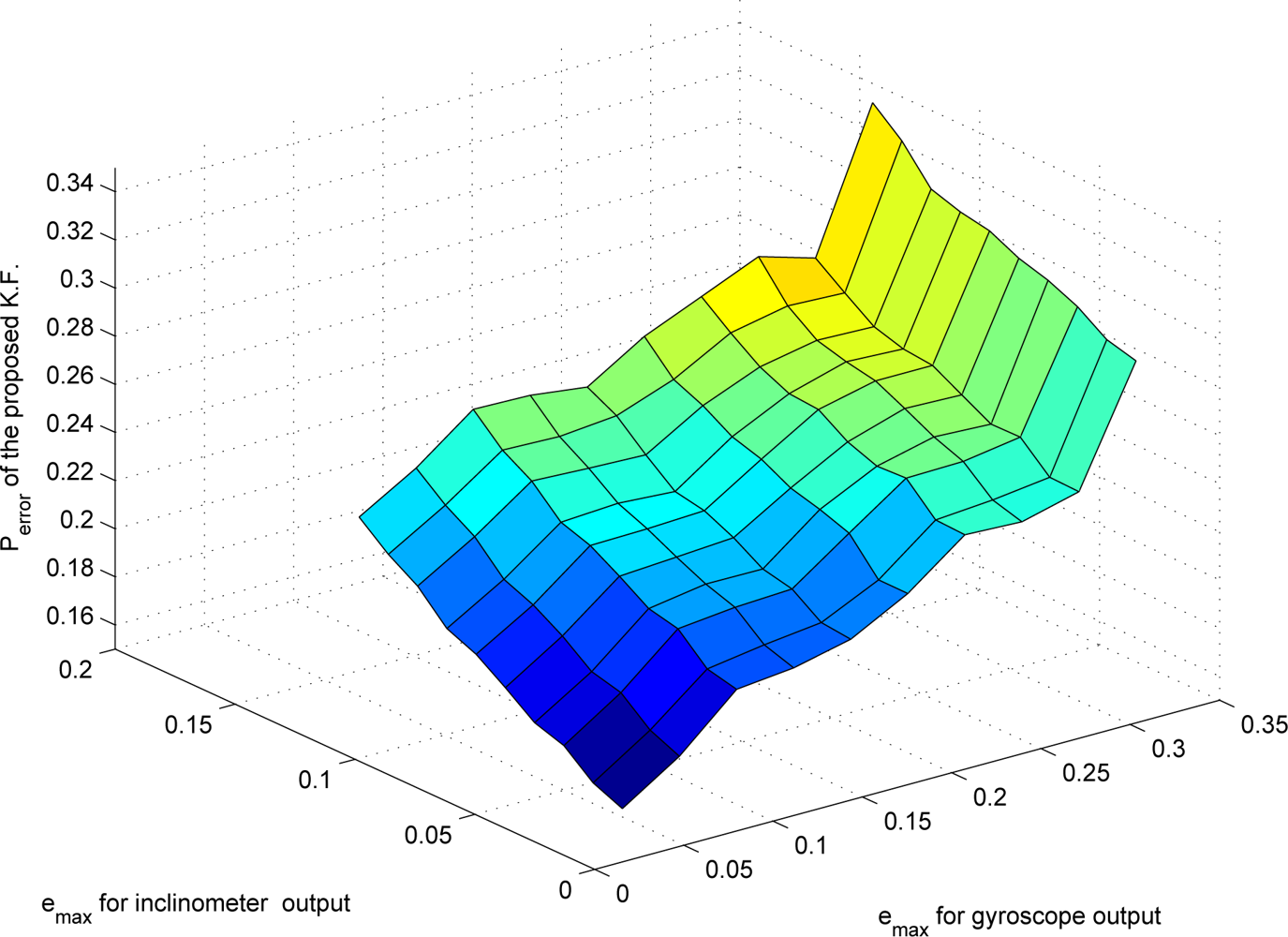
Figure 7, where the estimation error is predicted using (20). Actual estimation error from simulation is given in
Figure 8, where
is computed.
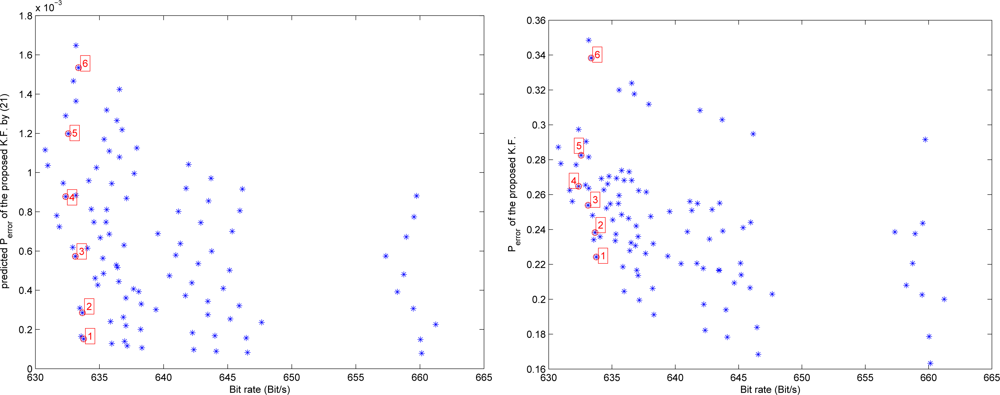
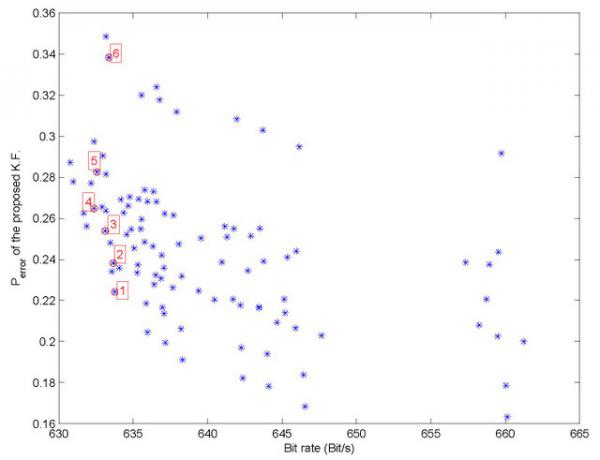
The relationship between bit rates and estimation error is presented in
Figure 9, where data are from
Figures 4,
7 and
8. In the left graph, the points 1–6 have similar bit rates but different
Perror. Thus in the following simulation, we chose the point 1, which corresponds to
emax,i = 0.2876 and
emax,g = 0.0122. We compared three different filters: (a) a standard Kalman filter using
yi and
yg; (b) a Kalman filter using
ŷi and
ŷg with compression error compensation (proposed in Section 4); (c) a Kalman filter using
ŷi and
ŷg without compression error compensation. We randomly generated 12 data sets and the results are given in
Table 3.
It is not surprising that the Perror of the standard Kalman filter is the smallest because the original data yi and yg are used for measurements. We can also see that the Perror of the proposed filter is smaller than that of the filter (c). On average, the estimation error of the proposed filter is smaller by 18.81% compared with that of the filter (c). Note that the proposed filter (b) and the filter (c) use the same decompressed data ŷi and ŷg for measurements. However, in the proposed filter, the compression error information (13) and (15) are explicitly used in (18), whereas they are ignored in the filter (c). In summary, the estimation error reduction was possible because of two facts: (1) the proposed compression method provides the compression error bound (13) and (15), and (2) the proposed filter algorithm explicitly uses the error compression bound.