CoCMA: Energy-Efficient Coverage Control in Cluster-Based Wireless Sensor Networks Using a Memetic Algorithm
Abstract
:1. Introduction
2. Preliminaries
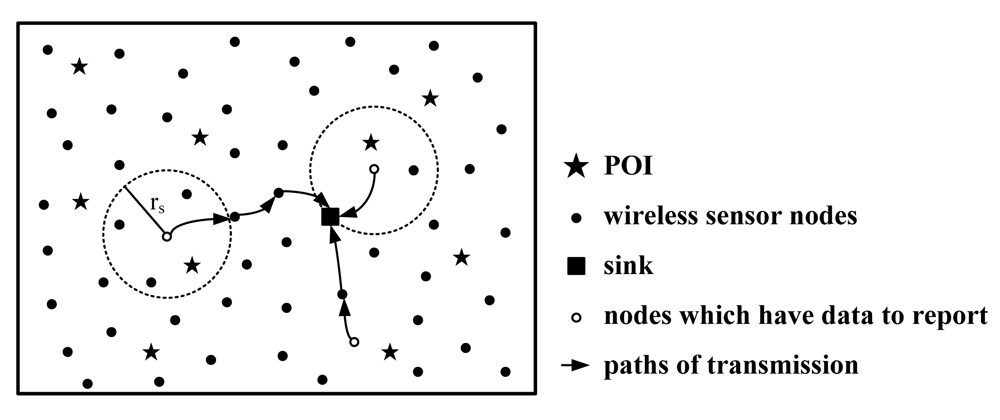
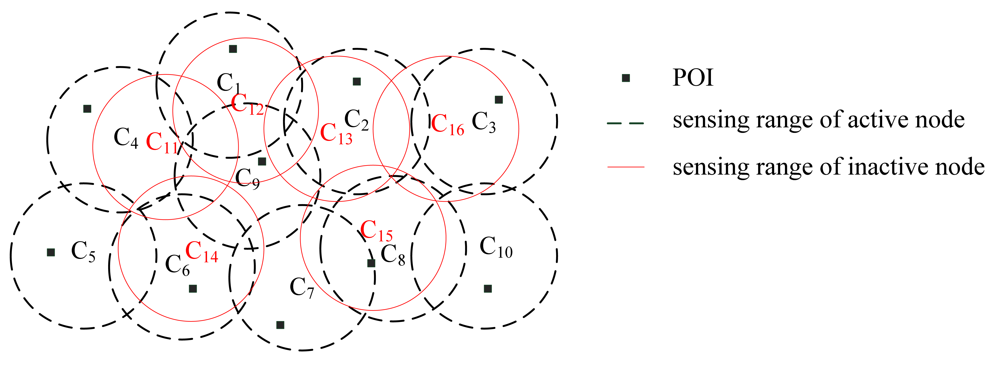
2.1. Sensing Coverage Model
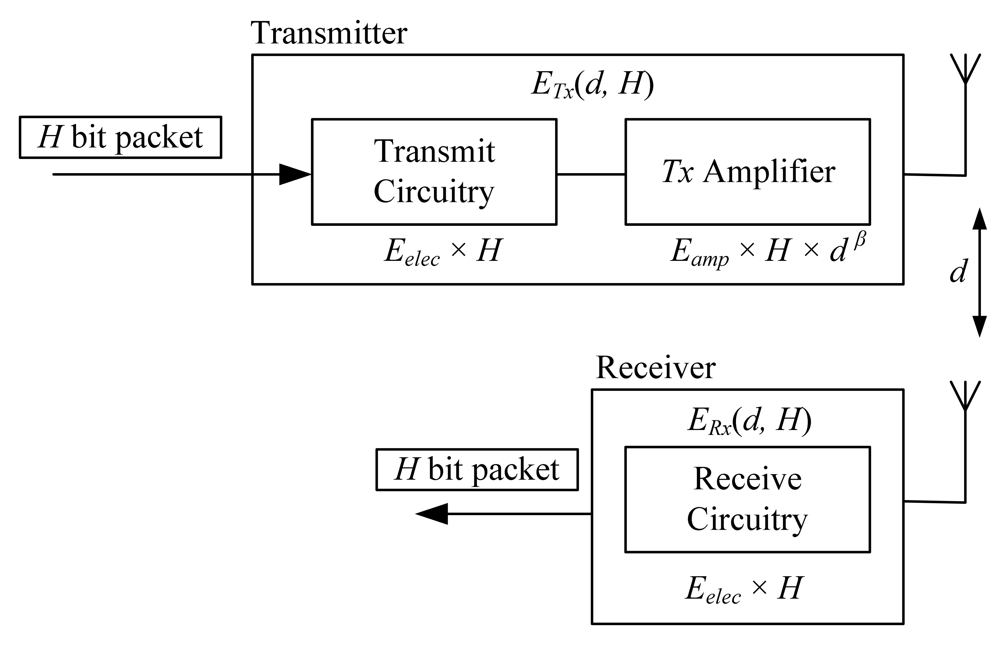
2.2. Energy Consumption Model
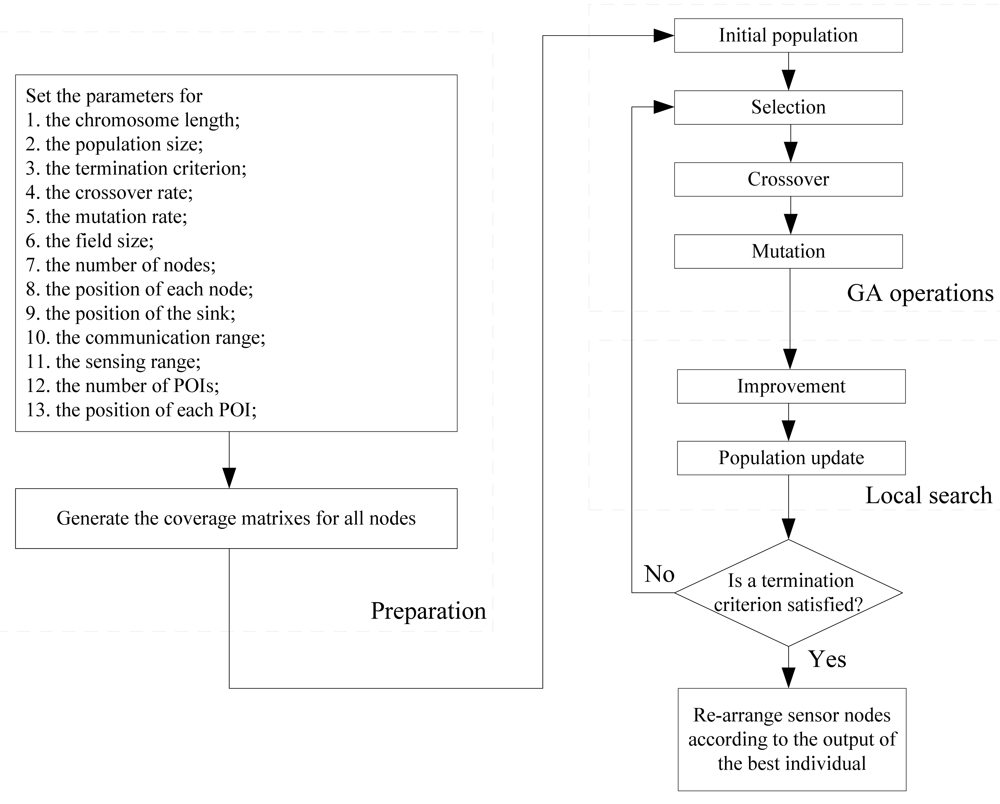
3. Coverage Control Using Memetic Algorithm
3.1. The Set Covering Problem (SCP)
3.2. The CoCMA Proposed for Cluster-based WSNs
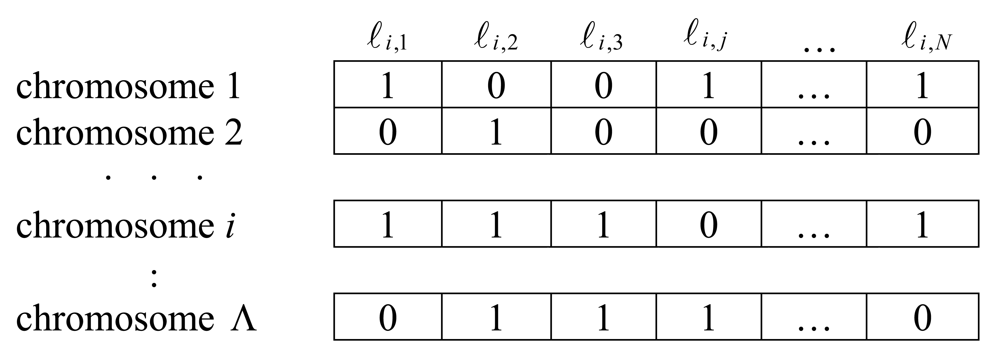
3.2.1. Genetic Representation
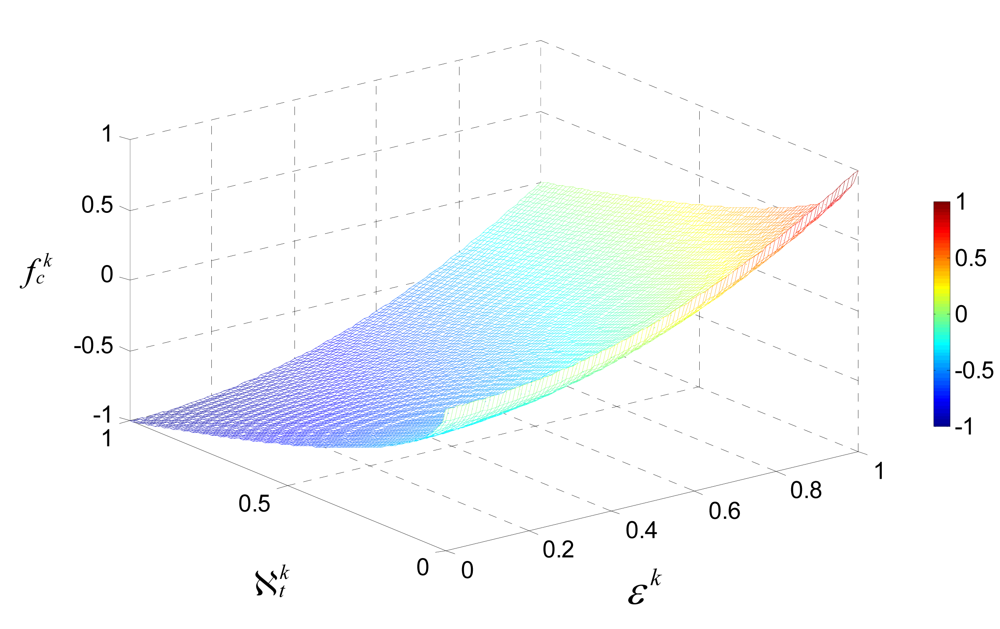
3.2.2. Fitness Function
3.2.3. Genetic Operations
3.2.4. Local Search Scheme
Pseudo code of the proposed local search scheme
- Step 1: Input a population Popk = { u1, u2, …, uρ }k to the local search unit.
Step 2: Let ui be the i-th chromosome in Popk, and N be the length of ui. According to the definition of allele ℓi,j, we know that ui is a binary string composed of ℓi,j, where ∀ i, 1≤ j ≤ N. For i = 1 to ρ do For j = 1 to N do If the value of ℓi,j is equal to one then Record the allele ℓi,j in the array Si. End End End Step 3: For y = 1 to ρ do Let h be the length of Sy. For l = 1 to h do fitness1 = fit(uy);//fit() is the fitness function. In uy, let the allele ctmp, corresponding to the h element in Sy, be zero. fitness2 = fit(uy); // Re-evaluate the fitness If fitness1 > finess2 then Let ctmp equal to one. End End End - Step 4: Output the improved Popk.
3.2.5. MA Termination
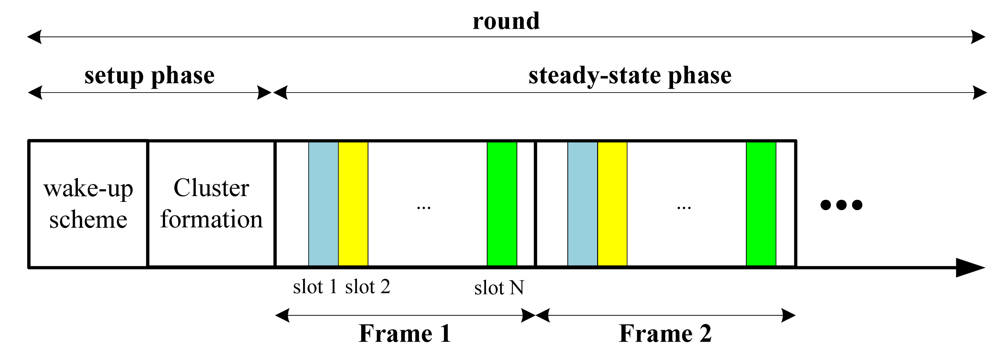
3.3. Wake-up Scheme
Definition 1
Definition 2
Definition 3
Procedure of the wake-up scheme
| variable best_comb, best_value = 0; |
| map, res = [0, 0, …,0], length = M; |
| If node ni has exhausted its energy and can not work correctly then |
| For k = 1 to χ do |
| For every element d of sψi,k do |
| map = πd ∪ map; |
| End |
| If then |
| best_comb= sψ,k; |
| End |
| End |
| output = best_comb; |
| End |
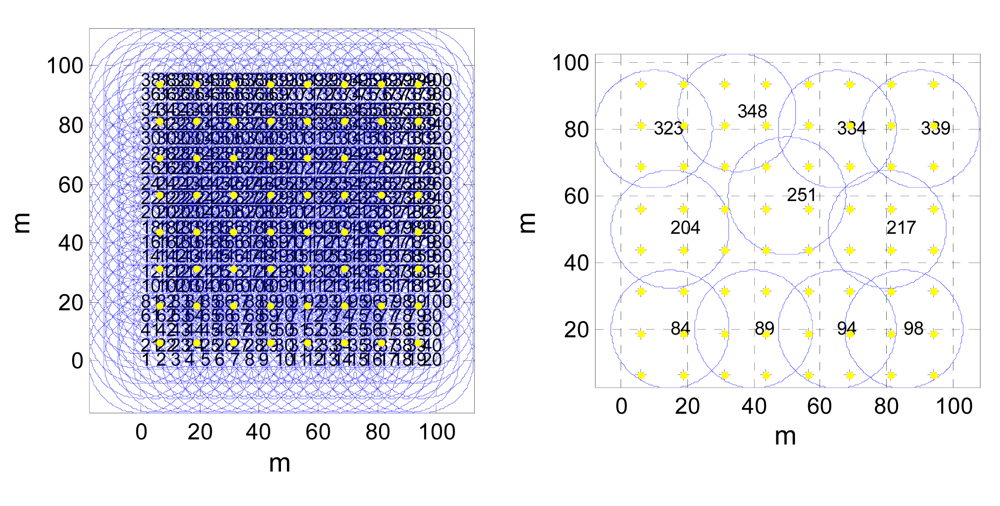
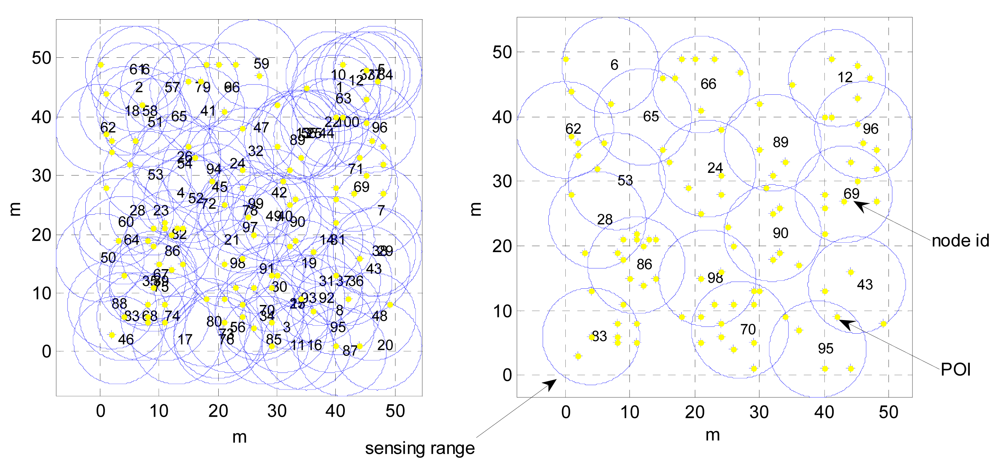
4. Performance Evaluation
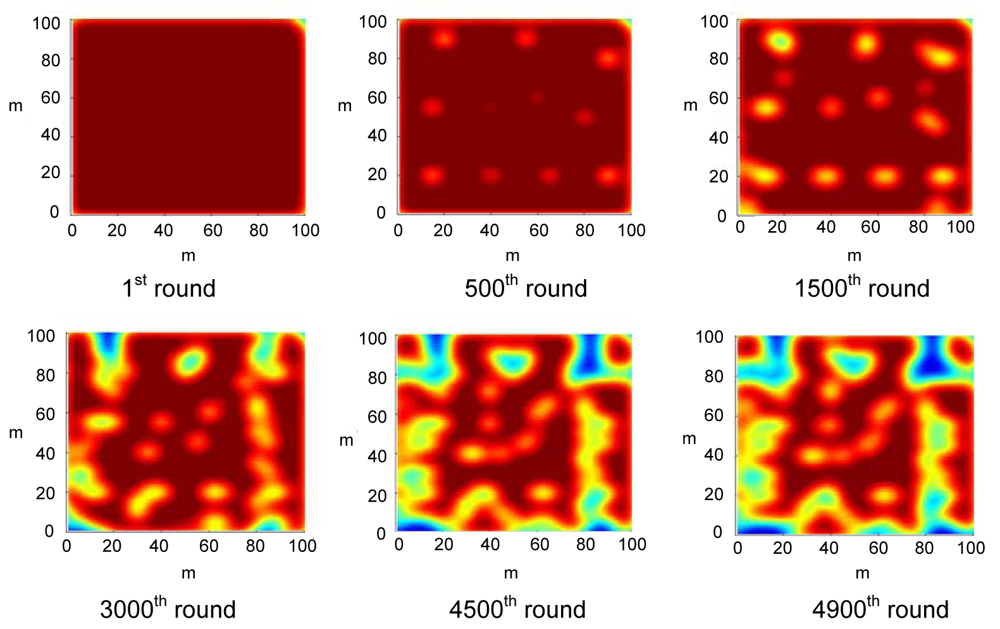
4.1. Convergence of the CoCMA
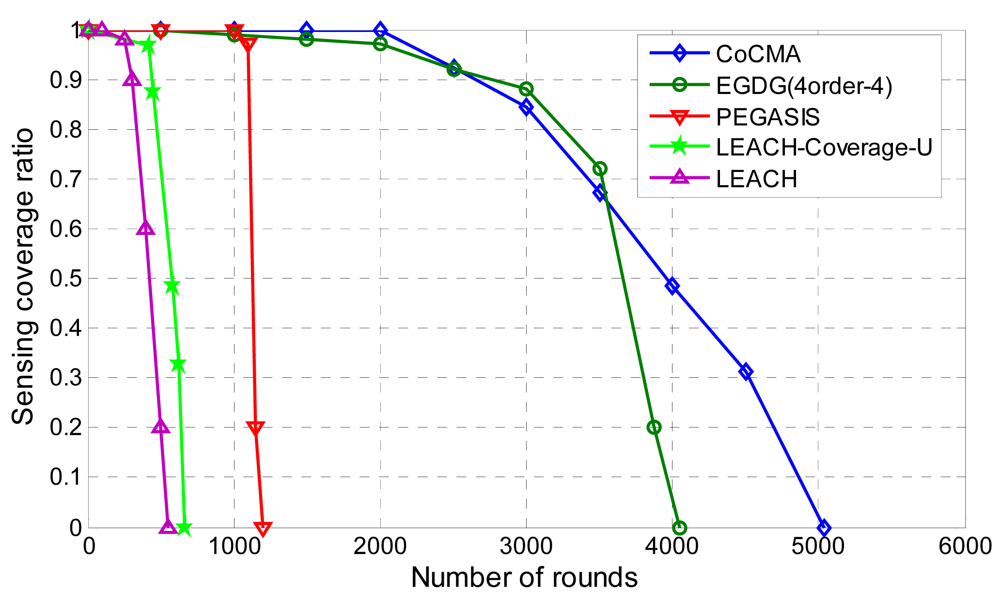
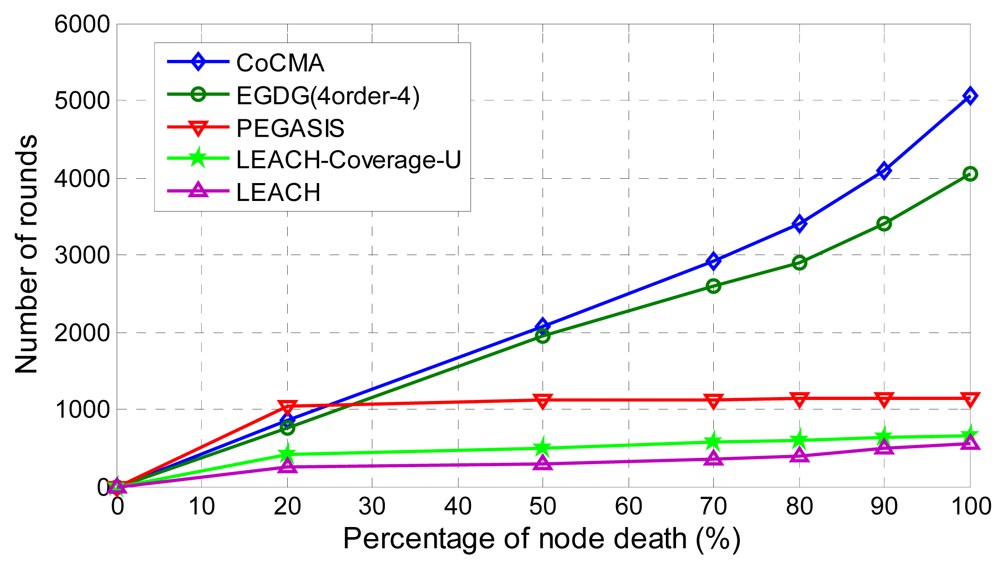
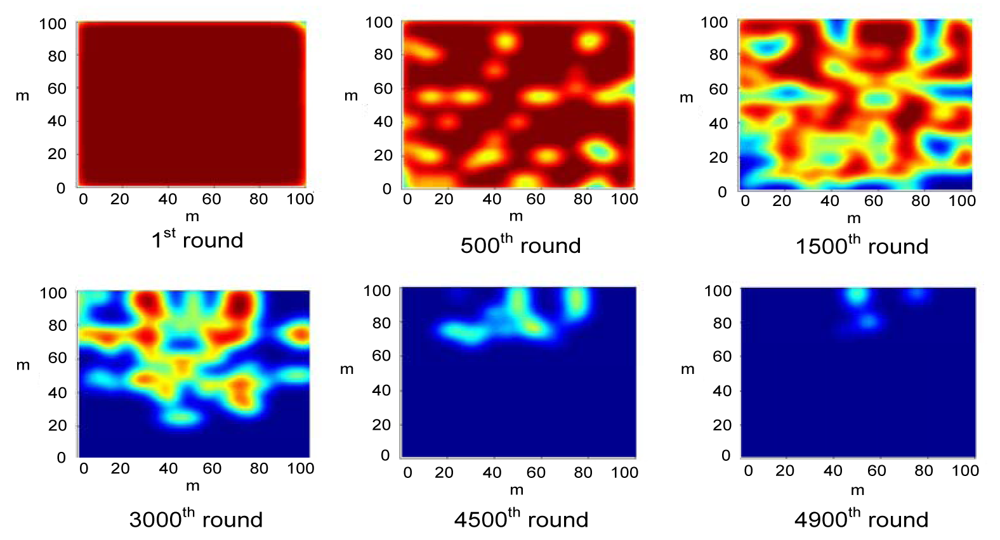
4.2. Network Lifetime Prolongation and Coverage Preservation
5. Conclusions
Acknowledgments
References and Notes
- Shu, T.; Krunz, M. Energy-efficient power/rate control and scheduling in hybrid TDMA/CDMA wireless sensor networks. Comput. Netw. 2009, 53, 1395–1408. [Google Scholar]
- Chen, C.P.; Chuang, C.L.; Tseng, C.L.; Yang, E.C.; Liu, M.Y.; Jiang, J.A. A novel energy-efficient adaptive routing protocol for wireless sensor network. J. Chin. Soc. Mech. Eng. 2009, 30, 59–65. [Google Scholar]
- Vemula, M.; Bugallo, M.F.; Djuric, P.M. Sensor self-localization with beacon position uncertainty. Signal Process. 2009, 89, 1144–1154. [Google Scholar]
- Kim, J.; Park, K.H. An energy-efficient, transport-controlled MAC protocol for wireless sensor networks. Comput. Netw. 2009, 53, 1879–1902. [Google Scholar]
- Chen, J.; Koutsoukos, X. Survey on coverage problems in wireless ad hoc sensor networks. In Proceedings of IEEE southeastCon.; Richmond, VA, USA, 2007. [Google Scholar]
- Huang, C.F.; Tseng, Y.C. The Coverage Problem in a Wireless Sensor Network. Proceedings of the 2nd ACM international conference on Wireless sensor networks and applications, San Diego, CA, USA, September 19, 2003; pp. 115–121.
- Arora, A.; Dutta, P.; Bapat, S.; Kulathumani, V.; Zhang, H.; Naik, V.; Mittal, H.C.; Demirbas, M.; Gouda, M.; Choi, Y. A line in the sand: a wireless sensor network for target detection, classification, and tracking. Comput. Netw. 2004, 46, 605–634. [Google Scholar]
- Chung, W.Y.; Lee, B.G.; Yang, C.S. 3D virtual viewer on mobile device for wireless sensor network-based RSSI indoor tracking system. Sens. Actuat. B: Chem. 2009, 140, 35–42. [Google Scholar]
- Buczak, A.; Jin, Y.; Darabi, H.; Jafari, M. Genetic algorithm based sensor network optimization for target tracking. In Intelligent Engineering Systems through Artificial Neural Networks; Dagli, C.H., Buczak, A., Ghosh, J., Embrechs, M., Ersoy, O., Eds.; ASME Press: New York, NY, USA, 1999; Volume 9, pp. 349–354. [Google Scholar]
- Liu, Y.; Pu, J.; Zhang, S.; Liu, Y.; Xiong, Z. A Localized coverage preserving protocol for wireless sensor networks. Sensors 2009, 9, 281–302. [Google Scholar]
- Bellur, U.; Jaiswal, N. Power aware duty scheduling in wireless sensor networks. Lect. Note comput. Sci. 2006, 4308, 546–551. [Google Scholar]
- Boukerche, A.; Fei, X.; Araujo, R.B. An optimal coverage-preserving scheme for wireless sensor networks based on local information exchange. Comput. Commun. 2007, 30, 2708–2720. [Google Scholar]
- Zalyubovskiy, V.; Erzin, A.; Astrakov, S.; Choo, H. Energy-efficient area coverage by sensors with adjustable ranges. Sensors 2009, 9, 2446–2460. [Google Scholar]
- Daskin, M.S. Network and Discrete Location: Models, Algorithms, and Applications.; Wiley: New York, NY, USA, 1995. [Google Scholar]
- de A Silva, R.M.; Ramalho, G.L. Ant System for the Set Covering Problem. Proceedings of 2001 IEEE International Conference on Systems, Man, and Cybernetics, Tucson, AZ, USA, October 2001; pp. 3129–3133.
- Lin, L.; Wang, H.J.; Xu, Z. Coverage Control In Wireless Sensor Network Based On Improved Ant Colony Algorithm. Proceedings of 2008 IEEE Conference on Cybernetics and Intelligent Systems, Chengdu, China; 2008; pp. 865–868. [Google Scholar]
- Jia, J.; Chen, J.; Chang, G.; Li, J.; Jia, Y. Coverage Optimization based on Improved NSGA-II in Wireless Sensor Network. Proceedings of the 2007 IEEE International Conference on Integration Technology, Shenzhen, China; 2007; pp. 614–618. [Google Scholar]
- Wang, B.; Chua, K.C.; Srinivasan, V. Connected sensor cover for area information coverage in wireless sensor networks. Int. J. Comp. Integ. Manu. 2008, 21, 1181–1203. [Google Scholar]
- Moscato, P. On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms. In Caltech Concurrent Computation Program; California Institute of Technology: Pasadena, CA, USA, 1989. [Google Scholar]
- Dawkins, R. The Selfish Gene; Oxford University Press: New York, NY, USA, 1976; pp. 203–215. [Google Scholar]
- Buriol, L.; França, M.P.; Moscato, P. A new memetic algorithm for the asymmetric traveling salesman problem. J. Heuristics 2004, 10, 483–506. [Google Scholar]
- Merz, P.; Freisleben, B. Memetic Algorithms and the Fitness Landscape of the Graph Bi-Partitioning Problem. Proceedings of the 5th International Conference on Parallel Problem Solving from Nature – PPSN, Amsterdam, the Netherlands, September 27-30; 1998; pp. 765–774. [Google Scholar]
- Merz, P.; Freisleben, B. Genetic Algorithms for Binary Quadratic Programming. Proceedings of the Genetic and Evolutionary Computation Conference, Orlando, FL, USA; 1999; pp. 417–424. [Google Scholar]
- Konstantinidis, A.; Yang, K.; Chen, H.H.; Zhang, Q. Energy-aware topology control for wireless sensor networks using memetic algorithms. Comput. Commun. 2007, 30, 2753–2764. [Google Scholar]
- Ferentinos, K.P.; Tsiligiridis, T.A. A memetic algorithm for dynamic design of wireless sensor Networks. Proceedings of 2007 IEEE Congress on Evolutionary Computation (CEC2007), Swissotel, The Stamford, Singapore, September 25-28, 2007; pp. 2774–2781.
- Heinzelman, W.; Chandrakasan, A.; Balakrishnan, H. Energy-Efficient Communication Protocols for Wireless Microsensor Networks. Proceedings of the 33rd Hawaii International Conference on Systems Science, Maui, HI; 2000; pp. 3005–3014. [Google Scholar]
- Hwang, S.F.; Lu, K.H.; Chang, H.N.; Dow, C.R. An efficient grid-based data gathering scheme in wireless sensor networks. Lect. Note Comput. Sci. 2007, 4611, 545–556. [Google Scholar]
- Tsai, Y. Coverage-preserving routing protocols for randomly distributed wireless sensor networks. IEEE Trans. Wirel. Commun. 2007, 6, 1240–1245. [Google Scholar]
- Lindsey, S.; Raghavendra, C.S. PEGASIS: power-efficient gathering in sensor information systems. Proceeding of IEEE Aerospace Conference, Big Sky, MT, USA, March 2003; pp. 1125–1130.
- Available online: http://www.sentilla.com (accessed on April 21, 2008).
- Available online: http://www.xbow.com (accessed on April 21, 2008).
- Osman, I.H.; Kelly, J.P. Meta-Heuristics: Theory & Applications.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Eiben, A.E.; Michalewicz, Z.; Schoenauer, M.; Smith, J.E. Para meter Control in Evolutionary Algorithms. In Parameter Setting in Evolutionary Algorithms, Studies in Computational Intelligence.; Lobo, F.G., Lima, C.F., Michalewicz, Z., Eds.; Springer: New York, NY, USA, 2007; Volume 54, pp. 19–46. [Google Scholar]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs., 3rd ed.; Springer: New York, NY, USA, 1996. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning.; Addison-Wesley Professional: Boston, MA, USA, 1989. [Google Scholar]
- Gu, L.; Stankovic, A.J. Radio-triggered wake-up for wireless sensor networks. Real-time Syst. 2005, 29, 157–182. [Google Scholar]
- Ansari, J.; Pankin, D.; Mahonen, P. Radio-Triggered Wake-ups with Addressing Capabilities for extremely low power sensor network applications. Proceeding of IEEE 19th International Symposium on Personal, Indoor and Mobile Radio Communications, Cannes, France, August 2008; pp. 1–5.
| NODE# 50 | 100 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| fitness | GA | Std. | CoCMA | Std. | fitness | GA | Std. | CoCMA | Std. |
| 0.32 | 3.21 | 11.45 | 0.9 | 0.36 | 0.53 | 2 | 1.7 | 2.14 | 0.09 |
| 0.3 | 0.06 | 0.05 | 0.82 | 0.18 | 0.58 | 0.58 | 0.34 | 2.08 | 0.09 |
| 0.25 | 0.06 | 0.05 | 0.69 | 0.1 | 0.45 | 0.31 | 0.06 | 1.98 | 0.1 |
| NODE# 200 | 300 | ||||||||
| fitness | GA | Std. | CoCMA | Std. | fitness | GA | Std. | CoCMA | Std. |
| 0.59 | 21.21 | 13.31 | 6.23 | 0.14 | 0.55 | 27.34 | 13.37 | 12.99 | 0.41 |
| 0.55 | 6.62 | 3.59 | 6.15 | 0.14 | 0.5 | 6.17 | 1.5 | 12.84 | 0.41 |
| 0.5 | 1.45 | 0.38 | 6.04 | 0.14 | 0.45 | 1.58 | 0.34 | 12.7 | 0.41 |
| NODE# 400 | 500 | ||||||||
| fitness | GA | Std. | CoCMA | Std. | fitness | GA | Std. | CoCMA | Std. |
| 0.52 | 53.49 | 29.81 | 22.43 | 0.49 | 0.5 | 112.8 | 66.8 | 34.64 | 0.78 |
| 0.5 | 24.67 | 8 | 22.36 | 0.49 | 0.45 | 11.64 | 3.74 | 34.41 | 0.79 |
| 0.45 | 4.53 | 1.35 | 22.16 | 0.49 | 0.4 | 2.1 | 0.44 | 34.16 | 0.79 |
|
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jiang, J.-A.; Chen, C.-P.; Chuang, C.-L.; Lin, T.-S.; Tseng, C.-L.; Yang, E.-C.; Wang, Y.-C. CoCMA: Energy-Efficient Coverage Control in Cluster-Based Wireless Sensor Networks Using a Memetic Algorithm. Sensors 2009, 9, 4918-4940. https://doi.org/10.3390/s90604918
Jiang J-A, Chen C-P, Chuang C-L, Lin T-S, Tseng C-L, Yang E-C, Wang Y-C. CoCMA: Energy-Efficient Coverage Control in Cluster-Based Wireless Sensor Networks Using a Memetic Algorithm. Sensors. 2009; 9(6):4918-4940. https://doi.org/10.3390/s90604918
Chicago/Turabian StyleJiang, Joe-Air, Chia-Pang Chen, Cheng-Long Chuang, Tzu-Shiang Lin, Chwan-Lu Tseng, En-Cheng Yang, and Yung-Chung Wang. 2009. "CoCMA: Energy-Efficient Coverage Control in Cluster-Based Wireless Sensor Networks Using a Memetic Algorithm" Sensors 9, no. 6: 4918-4940. https://doi.org/10.3390/s90604918
APA StyleJiang, J.-A., Chen, C.-P., Chuang, C.-L., Lin, T.-S., Tseng, C.-L., Yang, E.-C., & Wang, Y.-C. (2009). CoCMA: Energy-Efficient Coverage Control in Cluster-Based Wireless Sensor Networks Using a Memetic Algorithm. Sensors, 9(6), 4918-4940. https://doi.org/10.3390/s90604918





