Distributed Joint Source-Channel Coding in Wireless Sensor Networks
Abstract
:1. Introduction
2. Distributed Source Coding
2.1. Theory and Practice
2.2. Syndrome-Based and Parity-Based DSC
3. Distributed Joint Source-Channel Coding
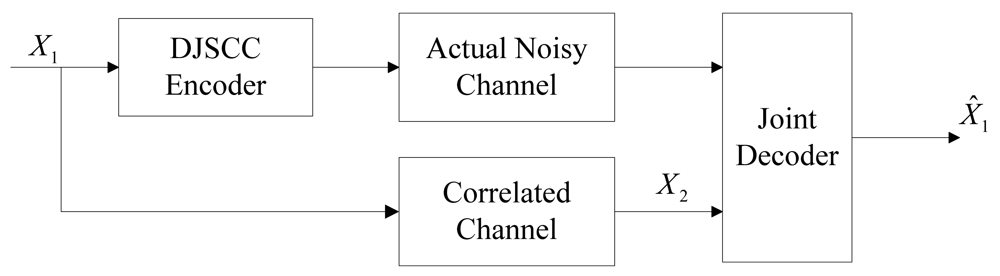
3.1. DJSCC for the Asymmetric Case
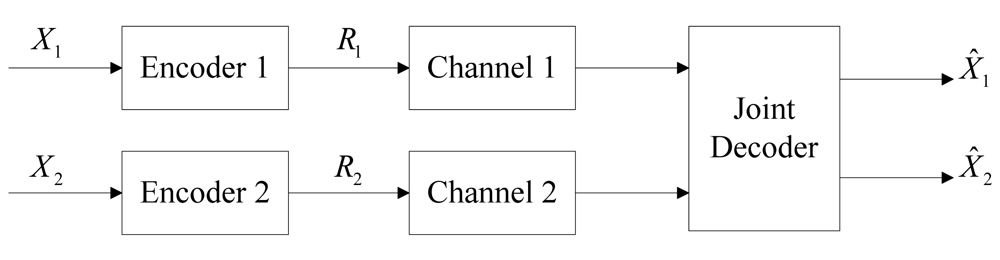
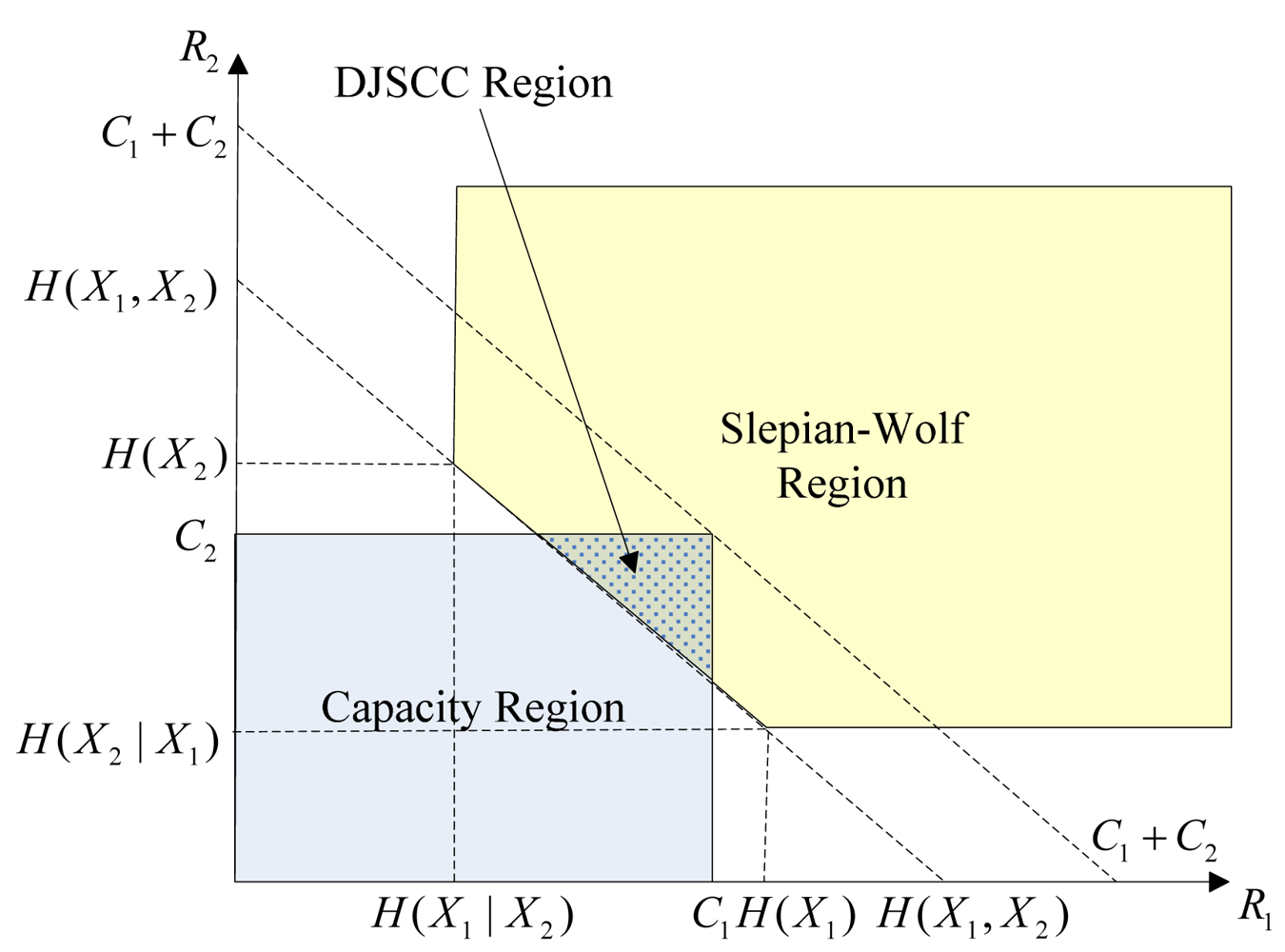
3.2. DJSCC for the Independent Channels Case
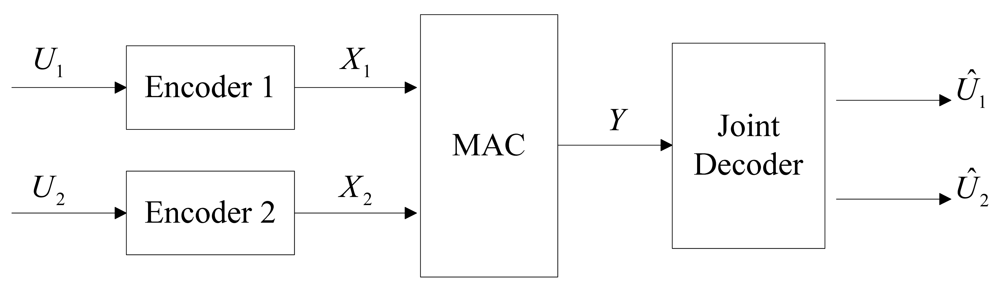
3.3. DJSCC for the Multiple Access Channel Case
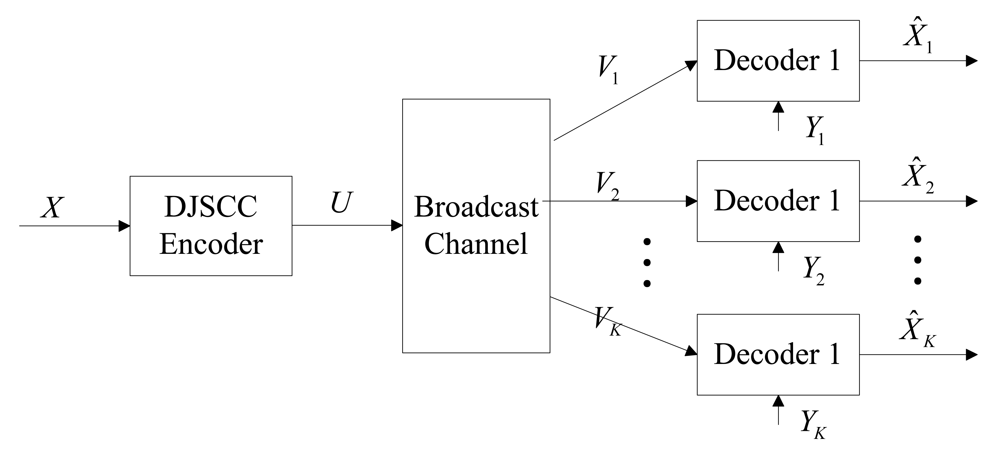
3.4. DJSCC for the Broadcast Channel Case
4. Proposed Scheme of DJSCC for the Independent Channels Case
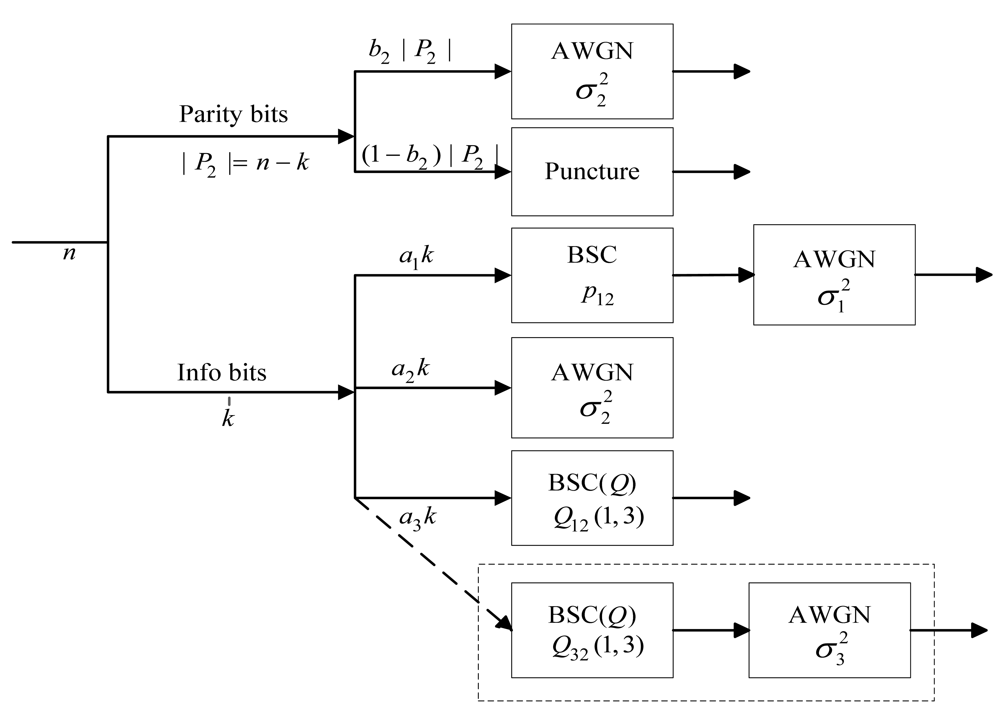
4.1. Proposed Scheme
4.2. Correlation Model and Theoretical Limits
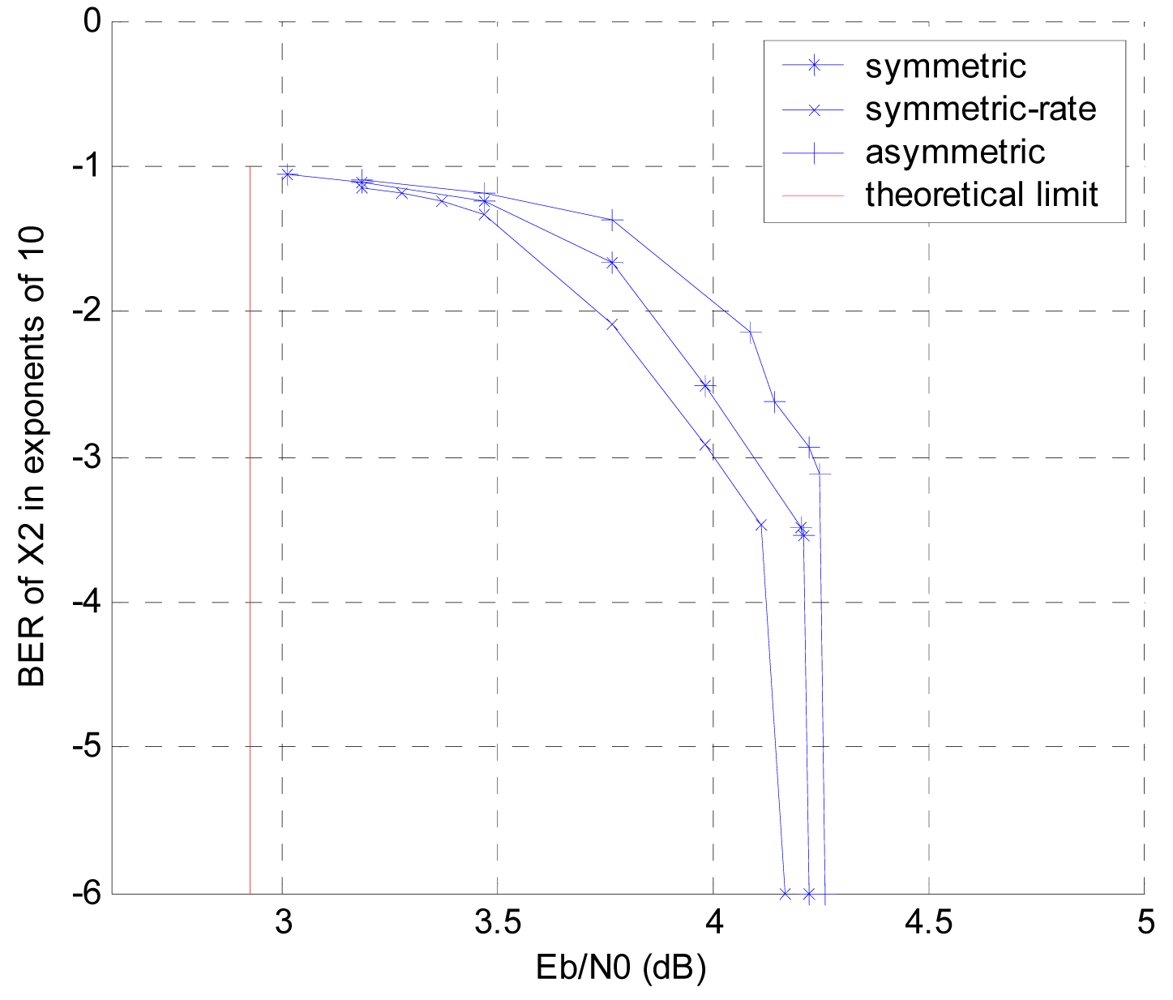
4.3. Simulation Results and Analysis
4.3.1. Two Sources Case
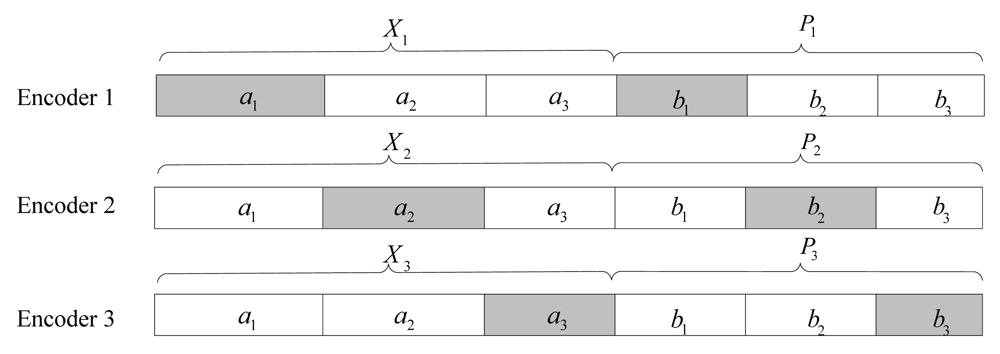
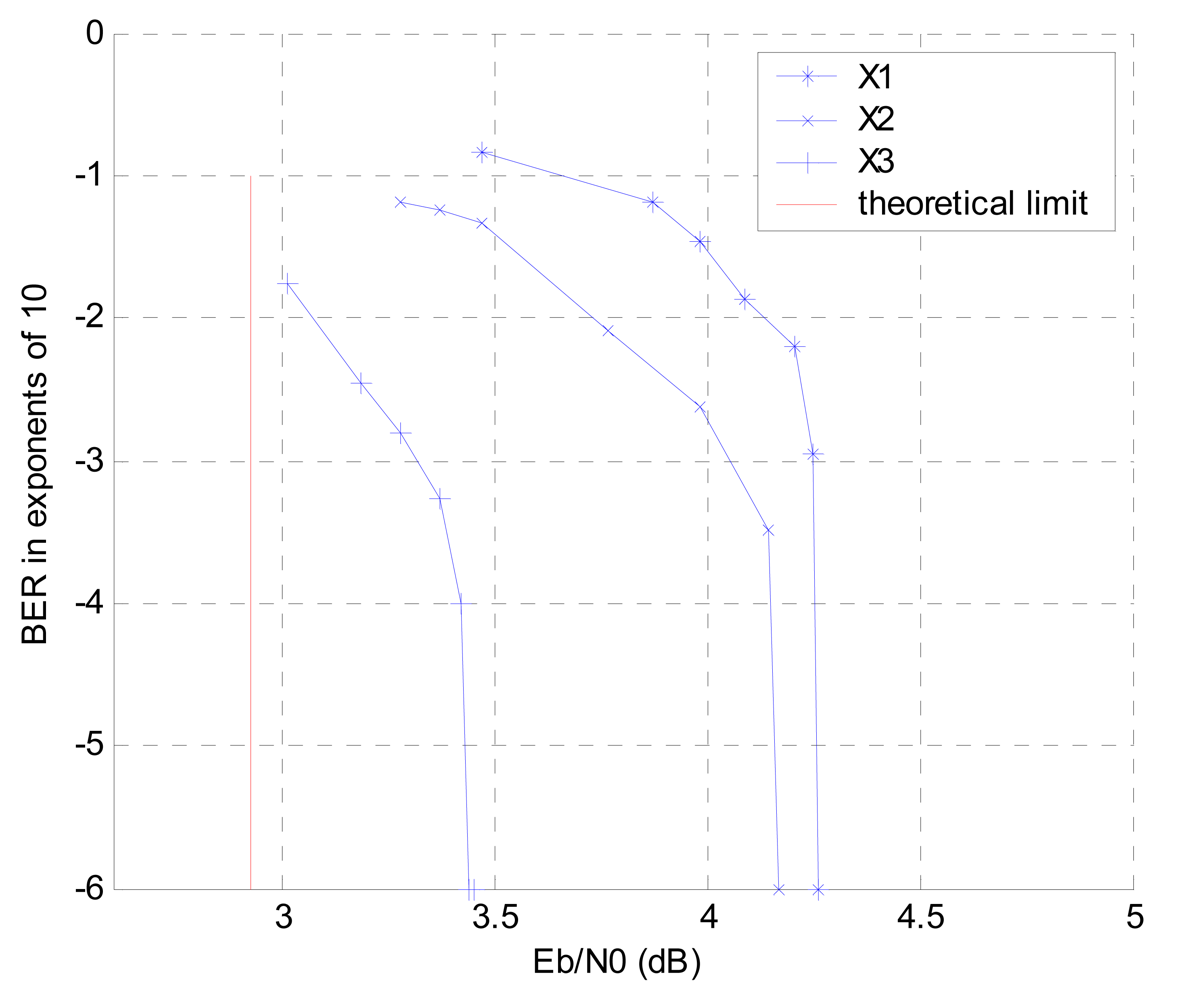
4.3.2. Three Sources Case
5. Conclusions and Future Work
Acknowledgments
References and Notes
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Slepian, D.; Wolf, J.K. Noiseless coding of correlated information sources. IEEE Trans. Inform. Theory 1973, 19, 471–480. [Google Scholar]
- Garcia-Frias, J.; Xiong, Z. Distributed source and joint source-channel coding: from theory to practice. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Philadelphia, PA, USA, March 2005; Vol. 5, pp. v/1093–v/1096.
- Cover, T.M. A proof of the data compression theorem of Slepian and Wolf for ergodic sources. IEEE Trans. Inform. Theory 1975, 22, 226–228. [Google Scholar]
- Wyner, A.; Ziv, J. The rate-distortion function for source coding with side information at the decoder. IEEE Trans. Inform. Theory 1976, 22, 1–10. [Google Scholar]
- Wyner, A.D. Recent results in the Shannon theory. IEEE Trans. Inform. Theory 1974, 20, 2–10. [Google Scholar]
- Pradhan, S.S.; Ramchandran, K. Distributed source coding using syndromes (DISCUS): Design and construction. Proceedings of the IEEE Data Compression Conference (DCC), Snowbird, UT, USA, March 1999; pp. 158–167.
- Garcia-Frias, J.; Zhao, Y. Compression of correlated binary sources using turbo codes. IEEE Commun. Lett. 2001, 5, 417–419. [Google Scholar]
- Liveris, A.D.; Xiong, Z.; Georghiades, C.N. Compression of binary sources with side information at the decoder using LDPC codes. IEEE Commun. Lett. 2002, 6, 440–442. [Google Scholar]
- Aaron, A.; Girod, B. Compression with side information using turbo codes. Proceedings of the IEEE Data Compression Conference (DCC), Snowbird, UT, USA, April 2002; pp. 252–261.
- Stankovic, V.; Liveris, A.D.; Xiong, Z.; Georghiades, C.N. Design of Slepian-Wolf codes by channel code partitioning. Proceedings of the IEEE Data Compression Conference (DCC), Snowbird, UT, USA, March 2004; pp. 302–311.
- Gehrig, N.; Dragotti, P.L. Symmetric and asymmetric Slepian-Wolf codes with systematic and nonsystematic linear codes. IEEE Commun. Lett. 2005, 9, 61–63. [Google Scholar]
- Sartipi, M.; Fekri, F. Distributed source coding in wireless sensor networks using LDPC coding: the entire Slepian-Wolf rate region. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, March 2005; pp. 1939–1944.
- Toto-Zarasoa, V.; Roumy, A.; Guillemot, C. Rate-adaptive codes for the entire Slepian-Wolf region and arbitrarily correlated sources. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, March 30-April 4 2008; pp. 2965–2968.
- Tan, P.; Xie, K.; Li, J. Slepian-Wolf coding using parity approach and syndrome approach. Proceedings of the 41st Annual Conference on Information Sciences and Systems, Baltimore MD, USA, March 2007; pp. 708–713.
- Shamai, S.; Verdu, S. Capacity of channels with uncoded side information. Eur. Trans. Telecomm. 1995, 6, 587–600. [Google Scholar]
- Shamai, S.; Verdu, S.; Zamir, R. Systematic lossy source/channel coding. IEEE Trans. Inform. Theory 1998, 44, 564–579. [Google Scholar]
- Mitran, P.; Bajcsy, J. Turbo source coding: a noise-robust approach to data compression. Proceedings of the IEEE Data Compression Conference (DCC), Snowbird, UT, USA, April 2002; p. 465.
- Liveris, A.D.; Xiong, Z.; Georghiades, C.N. Joint source-channel coding of binary sources with side information at the decoder using IRA codes. In IEEE Workshop on Multimedia Signal Processing; St. Thomas, VI, USA, December 2002; Vol. 9, issue 11, pp. 53–56. [Google Scholar]
- Xu, Q.; Stankovic, V.; Xiong, Z. Distributed joint source-channel coding of video using raptor codes. IEEE J. Sel. Areas Commun. 2007, 25, 851–861. [Google Scholar]
- Ser, J.D.; Crespo, P.M.; Galdos, O. Asymmetric joint source-channel coding for correlated sources with blind HMM estimation at the receiver. EURASIP J. Wirel. Commun. Netw. 2005, 5, 483–492. [Google Scholar]
- Tan, P.; Li, J. Enhancing the robustness of distributed compression using ideas from channel coding. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM), St. Louis, MO, USA, December 2005; 4, pp. 2385–2389.
- Heidarzadeh, A.; Lahouti, F. On robust syndrome-based distributed source coding over noisy channels using LDPC codes. Proceedings of the IEEE International Conference on Signal Processing and Communications (ICSPC), Minneapolis, MN, USA, May 2007; pp. 400–403.
- Jin, H.; Khandekar, A.; McEliece, R. Irregular repeat-accumulate codes. Proceedings of the 2nd International Symposium on Turbo codes and related topics, Brest, France, September 2000; pp. 1–8.
- Shokrollahi, A. Raptor codes. IEEE Trans. Inf. Theory 2006, 52, 2551–2567. [Google Scholar]
- Luby, M. LT codes. Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science (FOCS), Vancouver, Canada, November 2002; pp. 271–280.
- Garcia-Frias, J.; Villasenor, J.D. Joint turbo decoding and estimation of hidden Markov sources. IEEE J. Sel. Areas Commun. 2001, 19, 1671–1679. [Google Scholar]
- Tu, Z.; Li, J.; Blum, R.S. An efficient SF-ISF approach for the Slepian-Wolf source coding problem. Eurasip J. Appl. Sign. Proces. 2005, 6, 961–971. [Google Scholar]
- Barros, J.; Servetto, S.D. The sensor reachback problem. IEEE Trans. Inform. Theory 2003. Submitted. [Google Scholar]
- Barros, J.; Servetto, S.D. Network information flow with correlated sources. IEEE Trans. Inform. Theory 2006, 52, 155–170. [Google Scholar]
- Zhong, W.; Lou, H.; Garcia-Frias, J. LDGM codes for joint source-channel coding of correlated sources. Proceedings of the International Conference on Image Processing (ICIP), Barcelona, Spain, September 2003; pp. 14–17.
- Garcia-Frias, J.; Zhao, Y. Near-Shannon/Slepian-Wolf performance for unknown correlated sources over AWGN channels. IEEE Trans. Commun. 2005, 53, 555–559. [Google Scholar]
- Garcia-Frias, J.; Zhao, Y.; Zhong, W. Turbo-like codes for transmission of correlated sources over noisy channels. IEEE Sign. Proces. Mag. 2007, 24, 58–66. [Google Scholar]
- Daneshgaran, F.; Laddomada, M.; Mondin, M. LDPC-based channel coding of correlated sources with iterative joint decoding. IEEE Trans. Commun. 2006, 54, 577–582. [Google Scholar]
- Cheng, J.-F.; McEliece, R.J. Some high-rate near capacity codecs for the Gaussian channel. Proceedings of the 34th Annual Allerton Conference on Communications, Control and Computing, Allerton, IL, USA, October 1996; pp. 494–503.
- Cover, T.M.; El Gamal, A.; Salehi, M. Multiple access channels with arbitrarily correlated sources. IEEE Trans. Inform. Theory 1980, 26, 648–657. [Google Scholar]
- Dueck, G. A note on the multiple access channel with correlated sources. IEEE Trans. Inform. Theory 1981, 27, 232–235. [Google Scholar]
- Pradhan, S.S.; Suhan, C.; Ramchandran, K. A graph-based framework for transmission of correlated sources over multiple-access channels. IEEE Trans. Inf. Theory 2007, 53, 4583–4604. [Google Scholar]
- Gunduz, D.; Erkip, E. Transmission of correlated sources over multiuser channels with receiver side information. Information Theory and Applications Workshop, San Diego, CA, USA, January 2007; pp. 197–201.
- Rajesh, R; Varshneya, V.K.; Sharma, V. Distributed joint source channel coding on a multiple access channel with side information. IEEE International Symposium on Information Theory (ISIT), Toronto, Ontario, Canada, July 2008; pp. 2707–2711.
- Zhong, W.; Zhao, Y.; Garcia-Frias, J. Turbo-like codes for distributed joint source-channel coding of correlated senders in multiple access channels. Conference Record of the Thirty-Seventh Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, November 2003; 1, pp. 840–844.
- Zhong, W.; Chai, H.; Garcia-Frias, J. LDGM codes for transmission of correlated senders over MAC. Proceedings of the Allerton Conference on Communication, Control, and Computing, Allerton, IL, USA, October 2005. invited paper.
- de Bruyn, K.; Prelov, V.; van der Meulen, E. Reliable transmission of two correlated sources over an asymmetric multiple-access channel. IEEE Trans. Inf. Theory 1987, 33, 716–718. [Google Scholar]
- Gunduz, D.; Erkip, E. Correlated sources over an asymmetric multiple access channel with one distortion criterion. Proceedings of the 41st Annual Conference on Information Sciences and Systems (CISS), Baltimore MD, USA; 2007; pp. 325–330. [Google Scholar]
- Han, T.S.; Costa, M.H.M. Broadcast channels with arbitrarily correlated sources. IEEE Trans. Inf. Theory 1987, 33, 641–650. [Google Scholar]
- Suhan, C.; Pradhan, S.S. Representation of correlated sources into graphs for transmission over broadcast channels. IEEE International Symposium on Information Theory, Seattle, WA, USA, July 2006; pp. 2418–2422.
- Suhan, C.; Pradhan, S.S. A graph-based framework for transmission of correlated sources over broadcast channels. IEEE Trans. Inf. Theory 2008, 54, 2841–2856. [Google Scholar]
- Tuncel, E. Slepian-Wolf coding over broadcast channels. IEEE Trans. Inf. Theory 2006, 52, 1469–1482. [Google Scholar]
- Costa, M.H.M. Writing on dirty paper. IEEE Trans. Inf. Theory 1983, 29, 439–441. [Google Scholar]
- Nayak, J.; Tuncel, E.; Gunduz, D. Wyner-Ziv coding over broadcast channels. In 2008 IEEE Information Theory Workshop; Porto, Portugal, 5-9 May 2008; pp. 179–183. [Google Scholar]
- Gunduz, D.; Nayak, J.; Tuncel, E. Wyner-Ziv coding over broadcast channels using hybrid digital/analog transmission. IEEE International Symposium on Information Theory, Toronto, Canada, July 2008; pp. 1543–1547.
- Liveris, A.D.; Lan, C.; Narayanan, K.R.; Xiong, Z.; Georghiades, C.N. Slepian-Wolf coding of three binary sources using LDPC codes. Proceedings of the International Symposium on Turbo Codes and Related Topics, Brest, France; 2003; pp. 63–66. [Google Scholar]
- Lajnef, K.; Guillemot, C.; Siohan, P. Distributed coding of three binary and Gaussian correlated sources using punctured turbo codes. Sign. Proces. 2006, 86, 3131–3149. [Google Scholar]
- Sartipi, M.; Fekri, F. Distributed source coding using short to moderate length rate-compatible LDPC codes: the entire Slepian-Wolf rate region. IEEE Trans. Commun. 2008, 56, 400–411. [Google Scholar]
- Chung, S.-Y. On the construction of some capacity-approaching coding schemes. Ph.D. Dissertation., Massachusetts Institute of Technology, Cambridge, MA, USA, 2000. [Google Scholar]

© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhu, X.; Liu, Y.; Zhang, L. Distributed Joint Source-Channel Coding in Wireless Sensor Networks. Sensors 2009, 9, 4901-4917. https://doi.org/10.3390/s90604901
Zhu X, Liu Y, Zhang L. Distributed Joint Source-Channel Coding in Wireless Sensor Networks. Sensors. 2009; 9(6):4901-4917. https://doi.org/10.3390/s90604901
Chicago/Turabian StyleZhu, Xuqi, Yu Liu, and Lin Zhang. 2009. "Distributed Joint Source-Channel Coding in Wireless Sensor Networks" Sensors 9, no. 6: 4901-4917. https://doi.org/10.3390/s90604901



