A Small-Displacement Sensor Using Total Internal Reflection Theory and Surface Plasmon Resonance Technology for Heterodyne Interferometry
Abstract
:1. Introduction
2. Principle
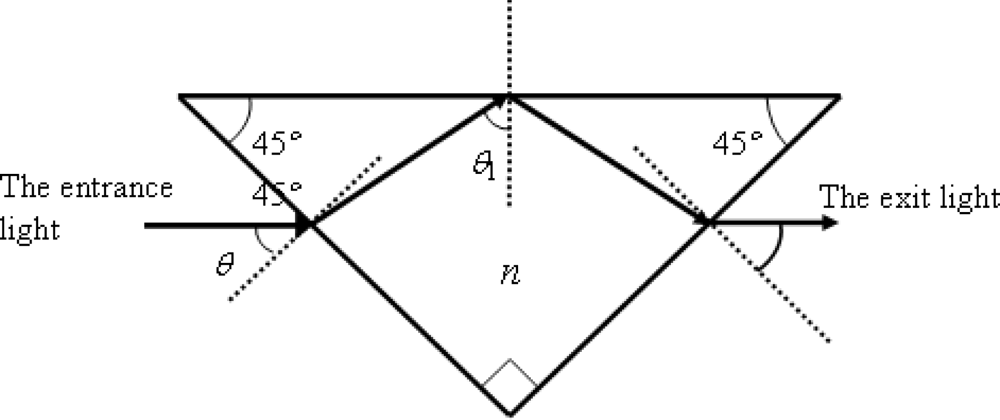
2.1. The phase difference at the TIR effect
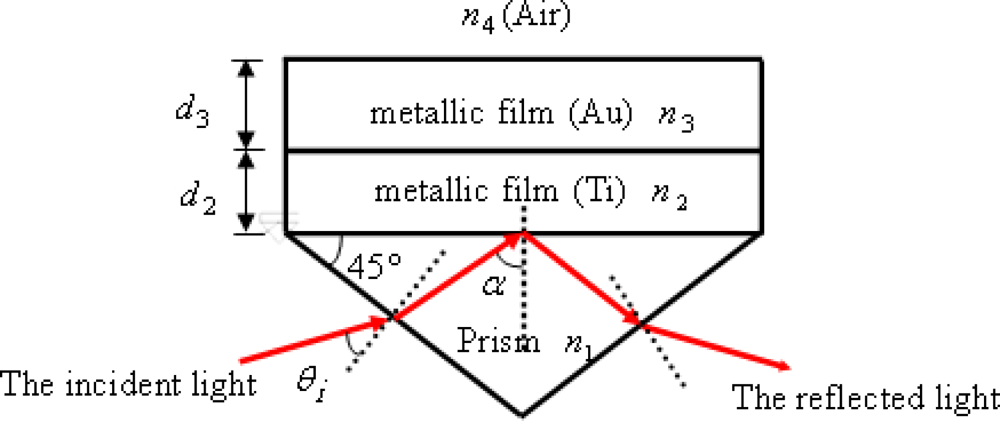
2.2. The basic principle of SPR technology
2.3. The basic principle of the displacement probe (DP)
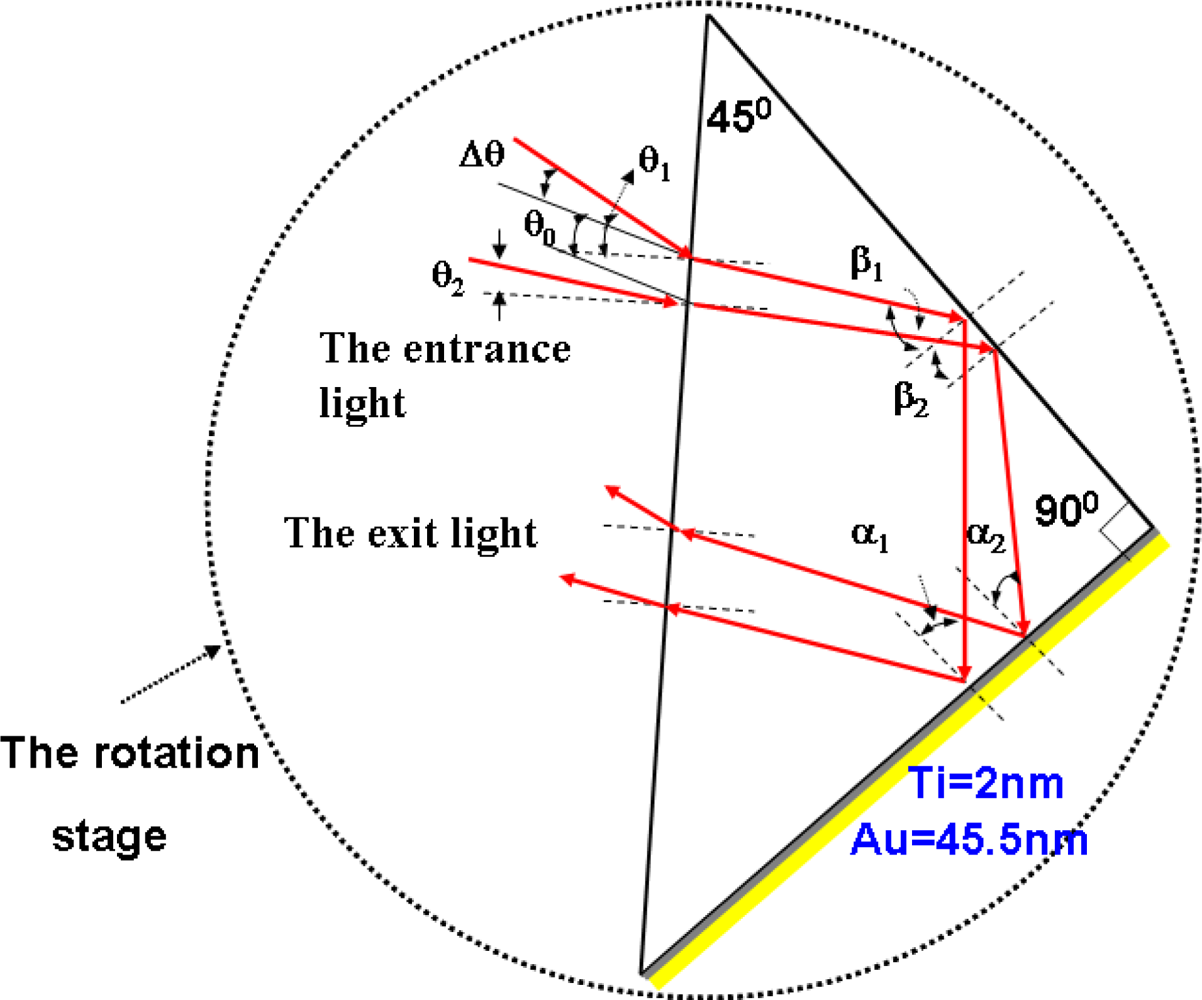
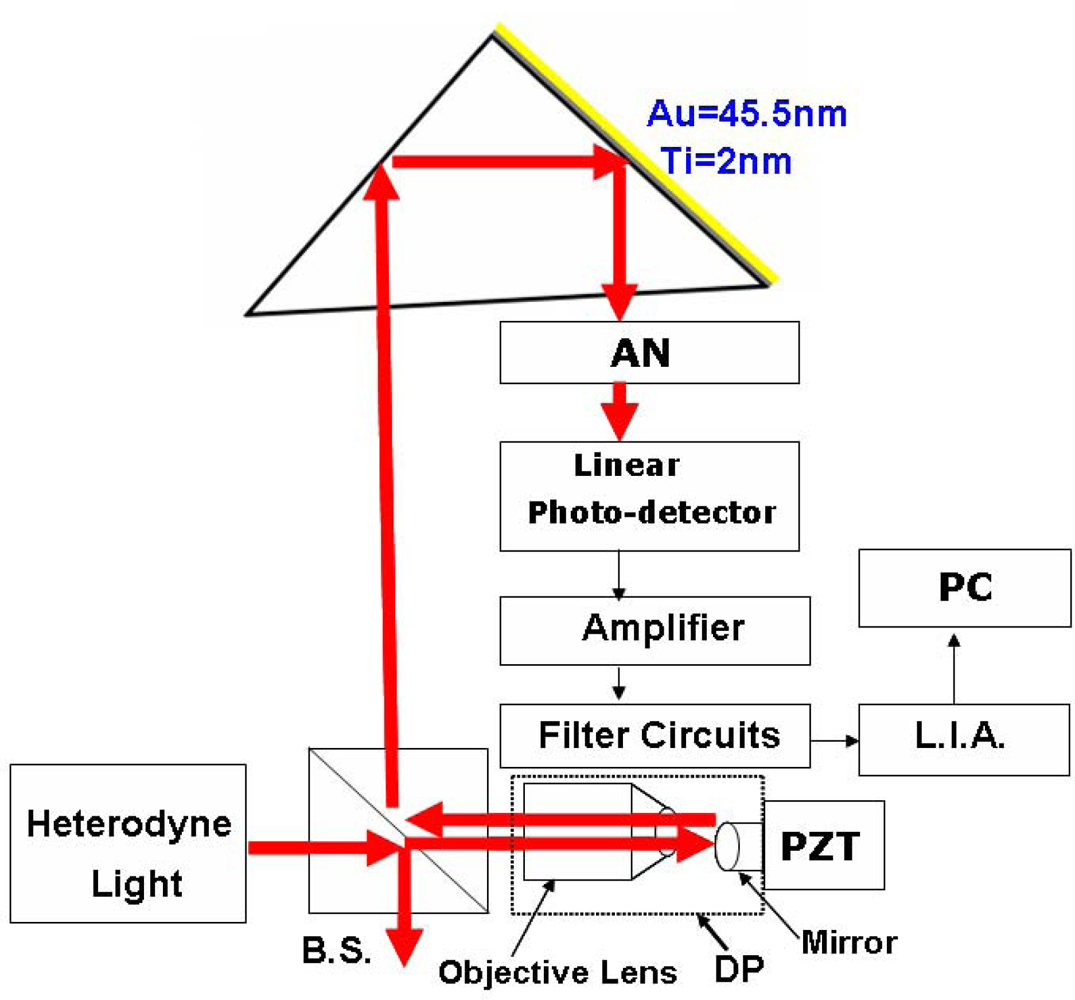
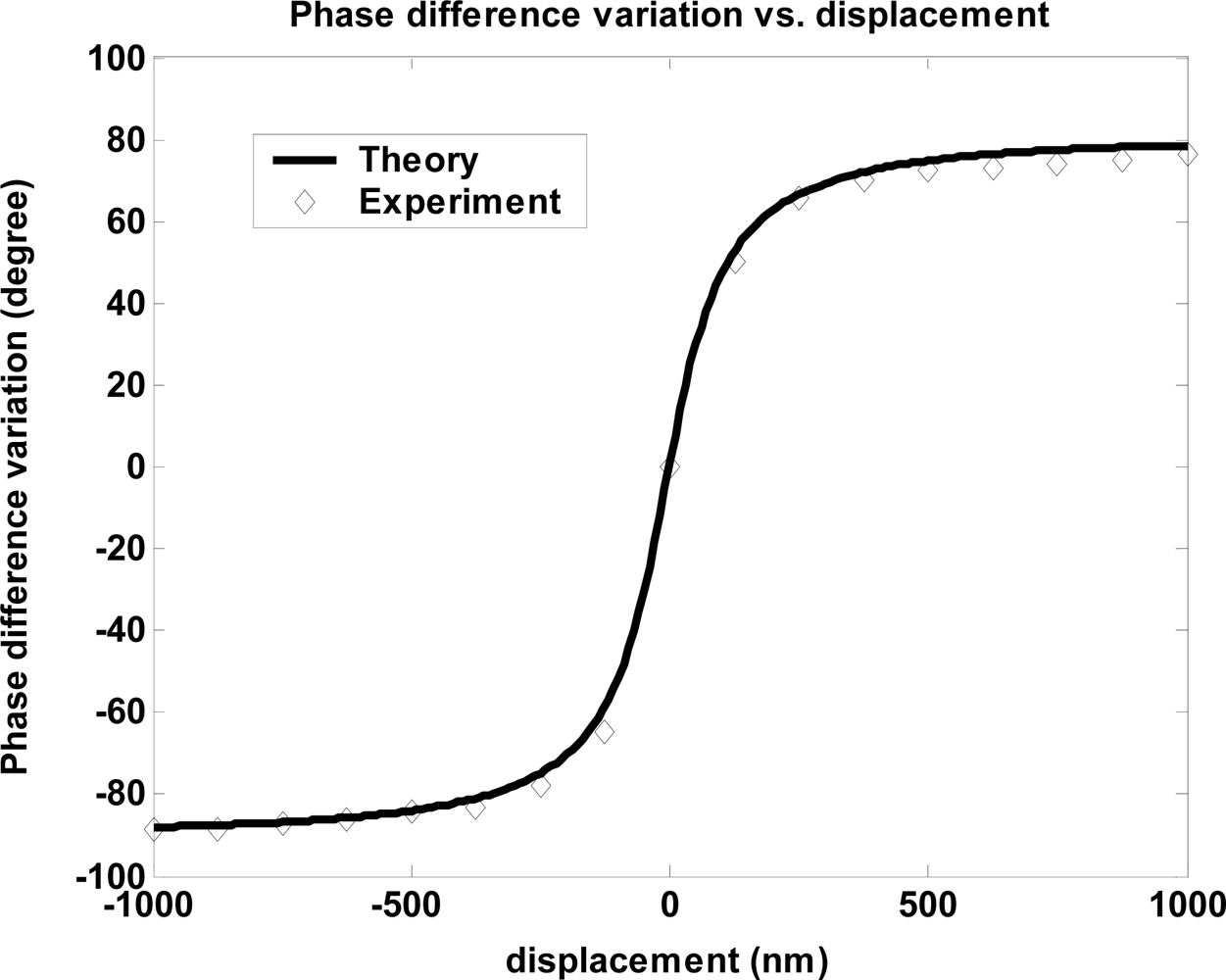
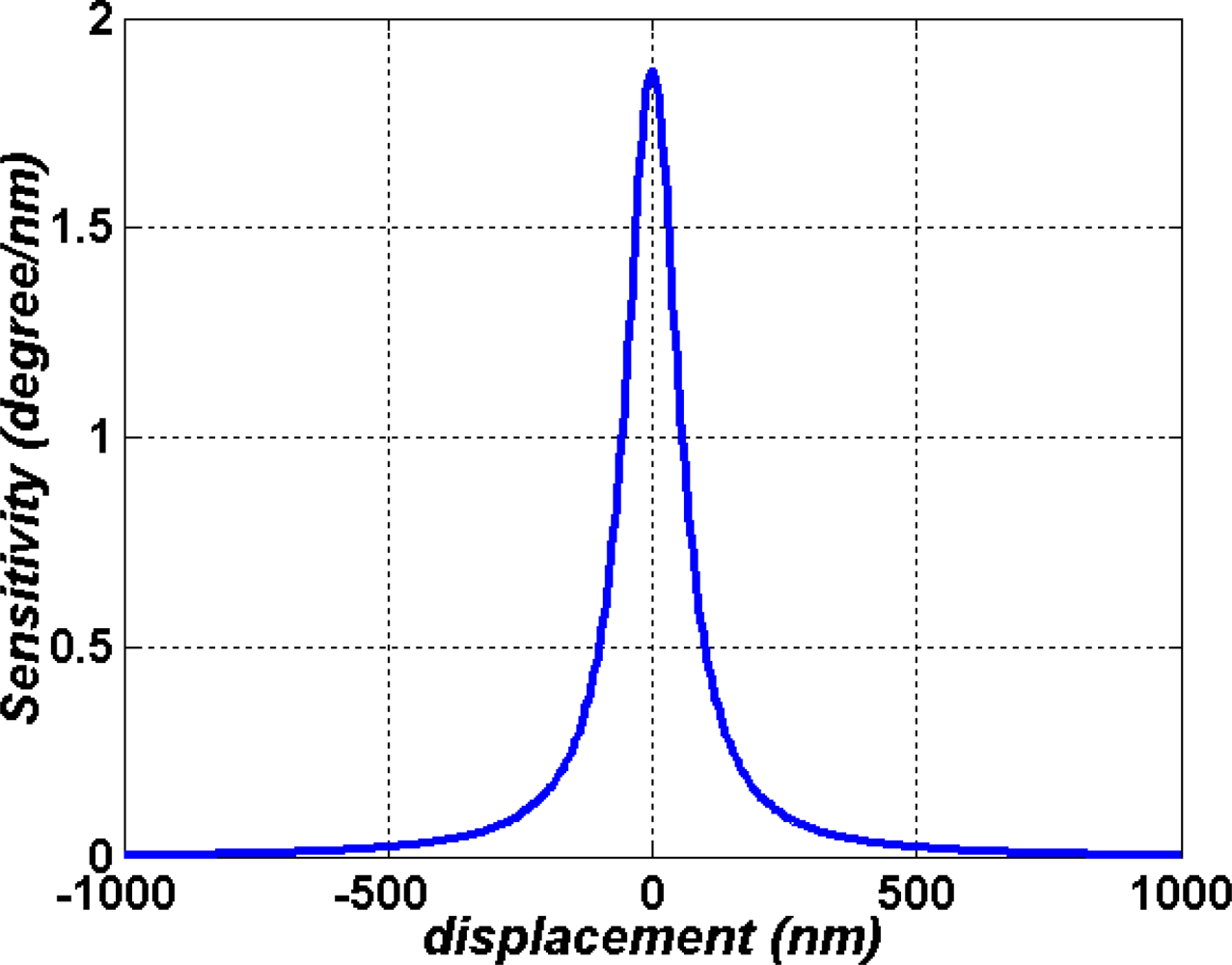
3. Experimental Apparatus and Results
4. Discussion
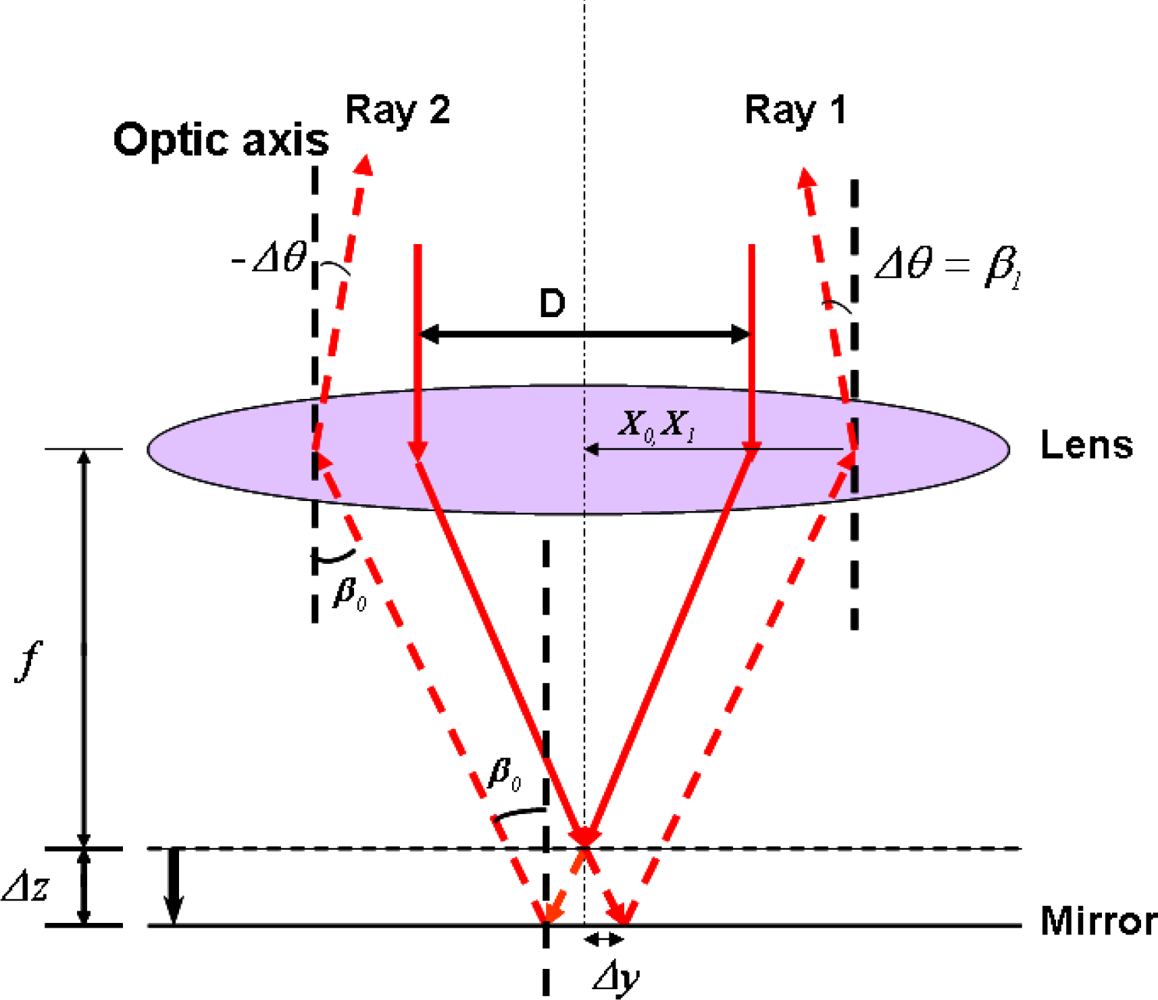
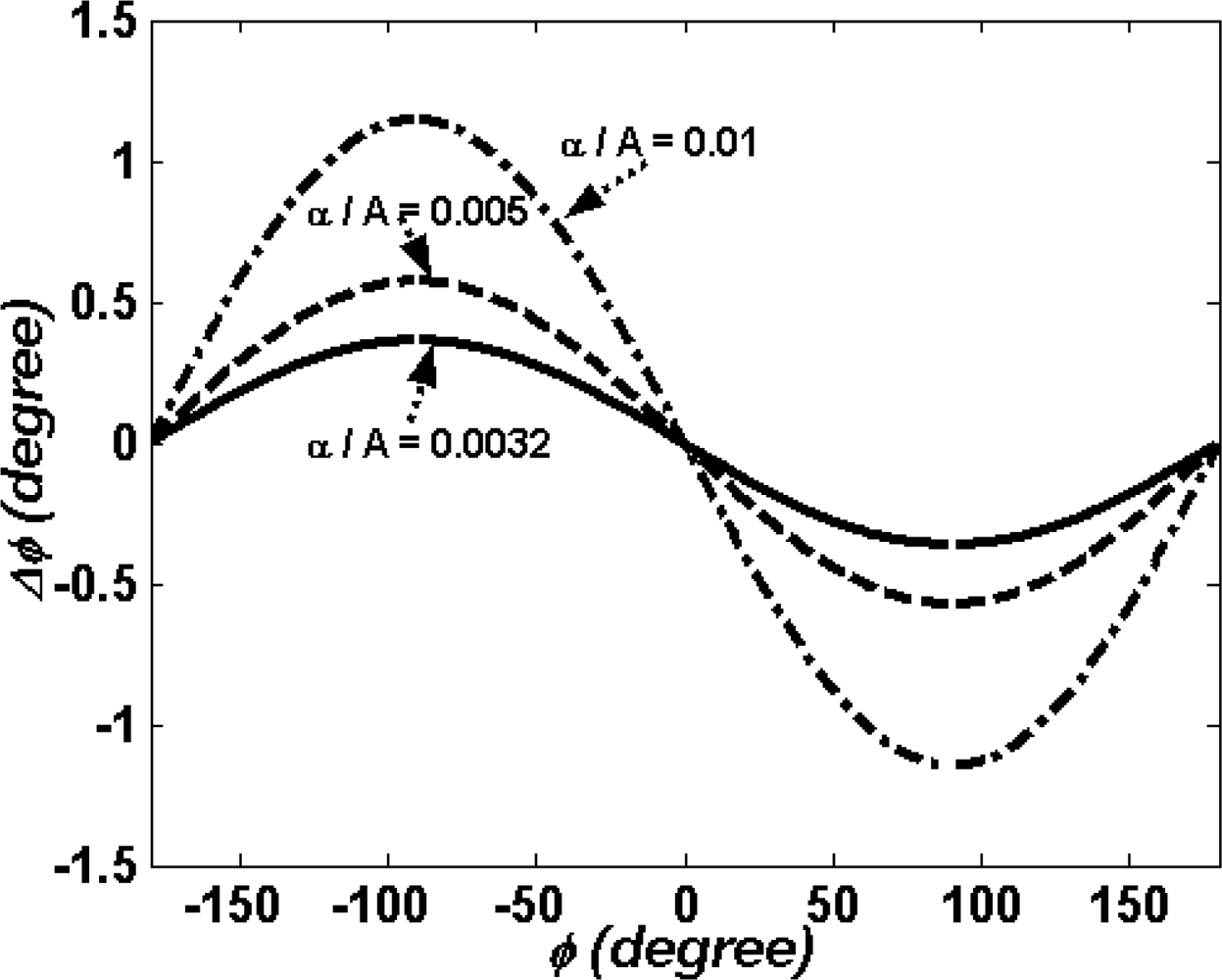
(a). The First Order Error
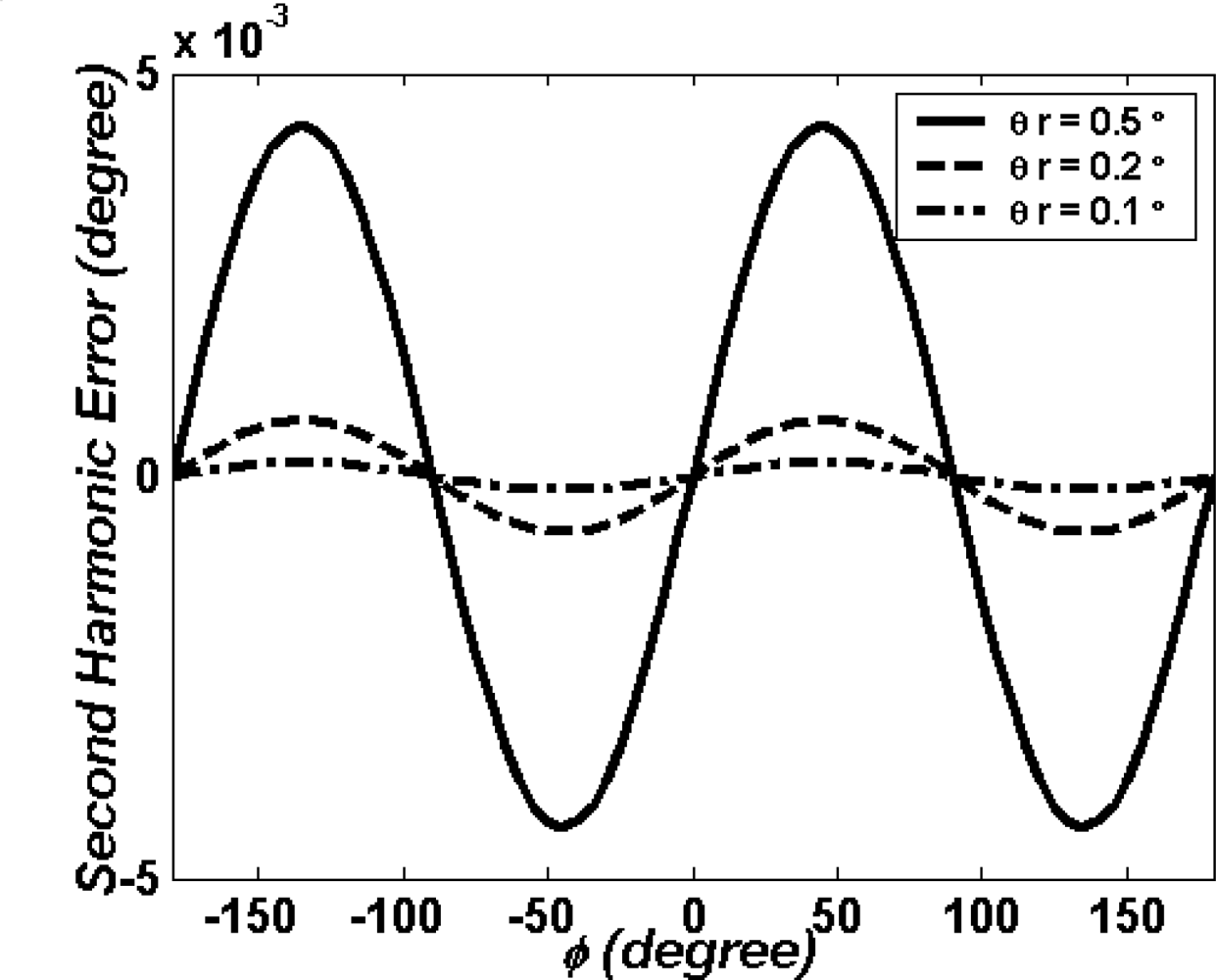
(b). Second Harmonic Error
5. Conclusions
Acknowledgments
References and Notes
- Nesci, A.; Dändliker, R.; Herzig, H.P. Quantitative amplitude and phase measurement by use of a heterodyne scanning near-field optical microscope. Opt. Lett 2001, 26, 208–210. [Google Scholar]
- Liu, X.; Clegg, W.; Jenkins, D.F.L.; Liu, B. Polarization interferometer for measuring small displacement. IEEE Trans. Instrum. Meas 2001, 50, 868–871. [Google Scholar]
- Liao, S.J.; Wang, S.F.; Chiu, M.H. A new method for measuring a small displacement by using the critical angle method and confocal technology. SPIE 2005, 5635, 211–218. [Google Scholar]
- Chiu, M.H.; Shih, B.Y.; Lai, C.W.; Shyu, L.H.; Wu, T.H. Small absolute distance measurement with nanometer resolution using geometrical optics principles and a SPR angular sensor. Sens. Act. A 2008, 141, 217–223. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 6th Ed ed; Pergamon Press: Oxford, UK, 1980; pp. 45–50. [Google Scholar]
- Kretshmann, E. Die Bestimmung optischer Konstanten von Metallen durch Anregung von Oberflächenplasmaschwingungen. Z. Phys 1971, 241, 313–324. [Google Scholar]
- Raether, H. Surface plasmons on smooth and rough surfaces and on gratings; Springer-Verlag: Berlin, Heidelberg, Germany, 1988; pp. 10–13. [Google Scholar]
- Wang, S.F.; Chiu, M.H; Lai, C.W.; Chang, R.S. High-sensitivity small-angle sensor based on the SPR technology and heterodyne interferometry. Applied Optics 2006, 45, 6702–6707. [Google Scholar]
- Chiu, M.H.; Wang, S.F.; Chang, R.S. Instrument for measuring small angles by use of multiple total internal reflections in heterodyne interferometry. Applied Optics 2004, 43, 5438–5442. [Google Scholar]
- Hou, W.; Wilkening, G. Investigation and compensation of the nonlinearity of heterodyne interferometers. Prec.Eng 1992, 14, 91–98. [Google Scholar]
- Bobroff, N. Recent advances in displacement measuring interferometry. Meas. Sci. Technol 1993, 4, 907–926. [Google Scholar]
- Hou, W.; Zhao, X. Drift of nonlinearity in the heterodyne interferometer. Prec. Eng 1994, 16, 25–35. [Google Scholar]
- Bobroff, N. Residual errors in laser interferometry fromair turbulence and nonlinearity. Applied Optics 1987, 26, 2676–2682. [Google Scholar]
- Badami, V.G.; Patterson, S.R. A frequency domain method for the measurement of nonlinearity in heterodyne interferometry. Prec.Eng 2000, 24, 41–49. [Google Scholar]
- Freitas, J.M.D.; Player, M.A. Importance of rotational beam alignment in the generation of second harmonic errors in laser heterodyne interferometry. Meas. Sci. Technol 1993, 4, 1173–1176. [Google Scholar]


© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, S.-F. A Small-Displacement Sensor Using Total Internal Reflection Theory and Surface Plasmon Resonance Technology for Heterodyne Interferometry. Sensors 2009, 9, 2498-2510. https://doi.org/10.3390/s90402498
Wang S-F. A Small-Displacement Sensor Using Total Internal Reflection Theory and Surface Plasmon Resonance Technology for Heterodyne Interferometry. Sensors. 2009; 9(4):2498-2510. https://doi.org/10.3390/s90402498
Chicago/Turabian StyleWang, Shinn-Fwu. 2009. "A Small-Displacement Sensor Using Total Internal Reflection Theory and Surface Plasmon Resonance Technology for Heterodyne Interferometry" Sensors 9, no. 4: 2498-2510. https://doi.org/10.3390/s90402498



