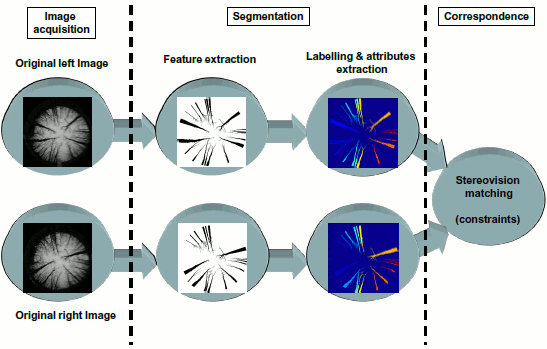
A Featured-Based Strategy for Stereovision Matching in Sensors with Fish-Eye Lenses for Forest Environments
Abstract
:1. Introduction
1.1. Constraints Applied in Stereovision Matching
1.2. Techniques in Stereovision Matching
1.3. Motivational Research and Contribution
Area-Based
- The matching is carried out pixel-by-pixel following the epipolar lines. It does not require a previous knowledge about if the pixel under matching belongs to a trunk or not.
- The correspondence is established by similarity among the properties of the pixels under matching. The main drawback is that in our images, the trunks and the grass in the soil display similar spectral signatures. They are both dark grey for the images in Figure 1 and green for the images of Figure 2. Hence, in the common parts where soil and trunks are confused the identification of the trunks becomes a difficult task.
- The part of the image associated to the sky is very homogeneous and the matching pixel by pixel also becomes difficult.
- Because of the above difficulties, if the correspondence were carried out pixel-by-pixel, after matching we would need to identify the pixels belonging to the trunks.
Feature-Based
- It is the natural choice that a human-based system will use. Indeed, the matching should be carried out by comparing tree-by-tree in both images.
- The above implies that the human matches the trunks by applying shape similarities between them and also by considering its location in the image based on the epipolar constraint provided by the sensor. The ordering constraint also helps to make the matching.
- The near radial orientation of the trunks towards the optical centre in the images could be exploited for matching.
- The main drawback of feature-based in our specific problem, for the automation process, is that the trunks must be identified previously and then a set of properties extracted for their identification.
- Segmentation: both images are processed so that a set of regions, corresponding to the trunks, are extracted and then labelled. Each region is identified by a set of attributes, including the Hu invariant moments [28], the position and orientation of the centroid and the area.
- Correspondence: based on these attributes and applying the stereovision matching constraints, where the sensor geometry is specifically considered, the matching between the regions in both images can be established.
1.4. Paper Organization
2. Segmentation Process
- The Charge Coupled Device (CCD), in both cameras, is rectangular, but the projection of the scene through the fish-eye lenses result on a circular area of the scene, which is the valid image to be processed.
- In the central part of the image, until a given level, the sky and the trunks are easily distinguished because of its contrast. Unfortunately this does not occur in the outer part of the valid circumference because the trunks and the grass in the soil display both similar spectral signatures in the RGB colour space. They are dark gray in the image in Figure 1 and green in the enhanced image of Figure 2.
- The trunks display an orientation towards the centre; this means that in the 3D scene they are near vertical. Nevertheless, there are some of them that are not exactly vertical and even capricious forms could appear. This must be taken into account because it impedes us to apply exactly the geometrical radial property during the segmentation.
- The trees are clean of leaves in the branches, this facilitates their identification.
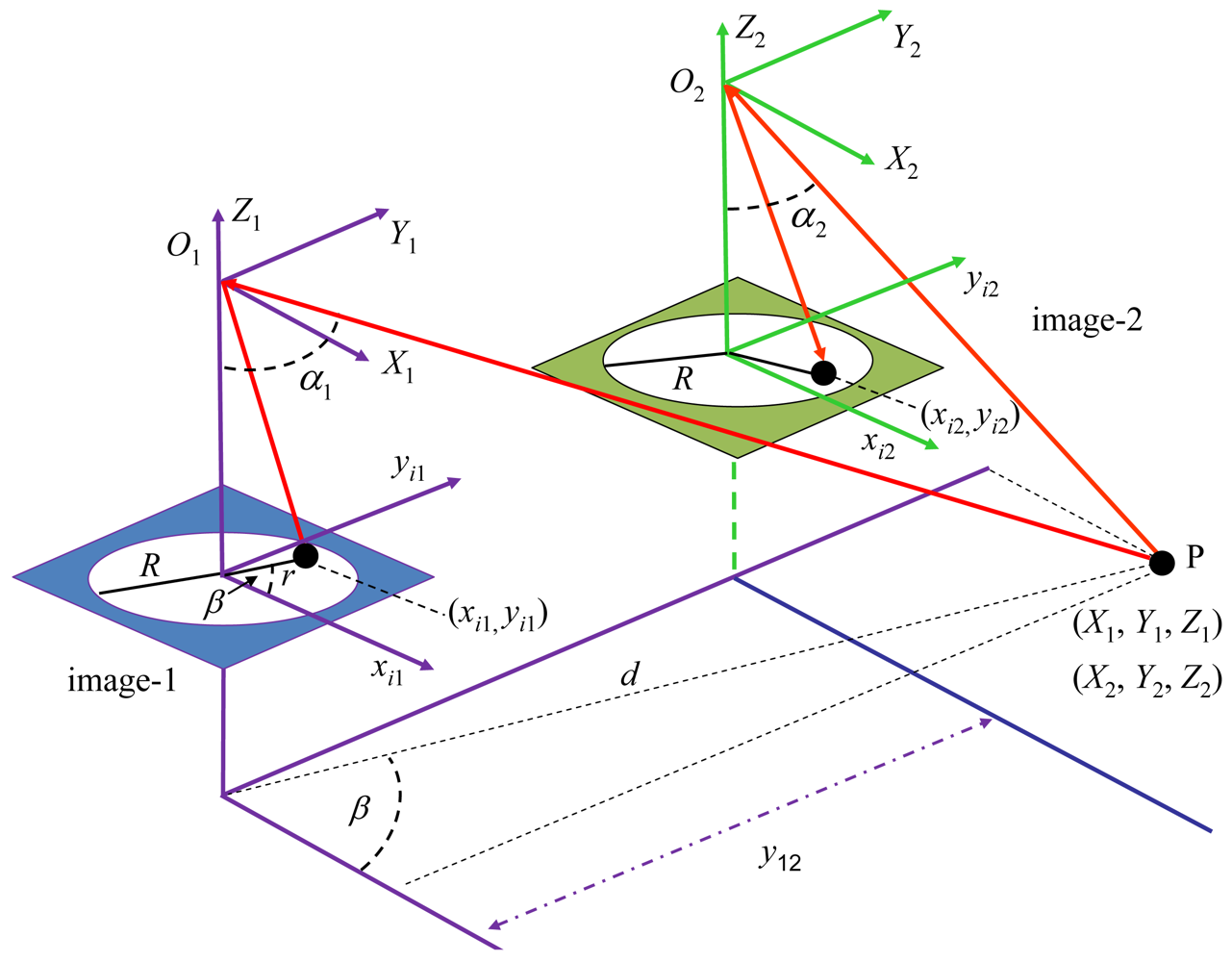
- Because the cameras in the stereovision sensor are separated by the base-line, 1 m in our sensor, the same tree is not located in the same spatial position in both images. A relative displacement, measured in degrees of angle, appears between corresponding matches. This displacement is greater for the trees near the sensor than for those who are far.
- Depending on the position of each tree with respect each camera, the images of the trees appear under different sizes, affecting the area of the imaged trunk in both images. A tree near the left camera appears with an area in the left image greater than the area in the right one and vice versa.
- Step 1 Valid image: each CCD has 1,616 × 1,616 pixels in width and height dimensions respectively. Considering the origin of coordinates in the left bottom corner, the centre of the image is located in the coordinates (808, 808). The radius R of the valid image from the centre is 808 pixels. So, during the process only the image region inside the area limited by the given radius is to be considered. Moreover, we work with the intensity image I in the HSI colour space obtained after the transformation from RGB to HSI. This is because, as mentioned before, we have not achieved satisfactory results with the studied colour spaces and the image I contains the spectral information of the three R, G and B spectral channels. The region growing process, applied later, works better in the original image, Figure 1, than in the enhanced one, Figure 2, because of the similarity on the intensity values in the original one. This justifies the use of the original images instead of the enhanced ones. Later, in section 4, we give details about the protocol for measuring a sample plot in the forest, where the sensor is located in the centre of a circle with radius ranging from 5 m to 25 m. Hence, only the trunks inside circles with radius below 25 m are of interest and they are imaged with an appropriate area for their treatment, the remainder ones are projected with small areas and their treatments become complicated.
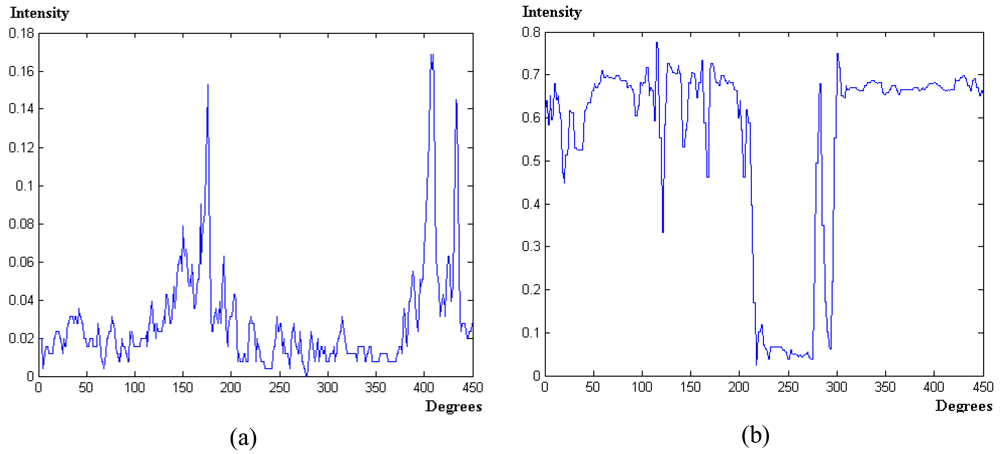
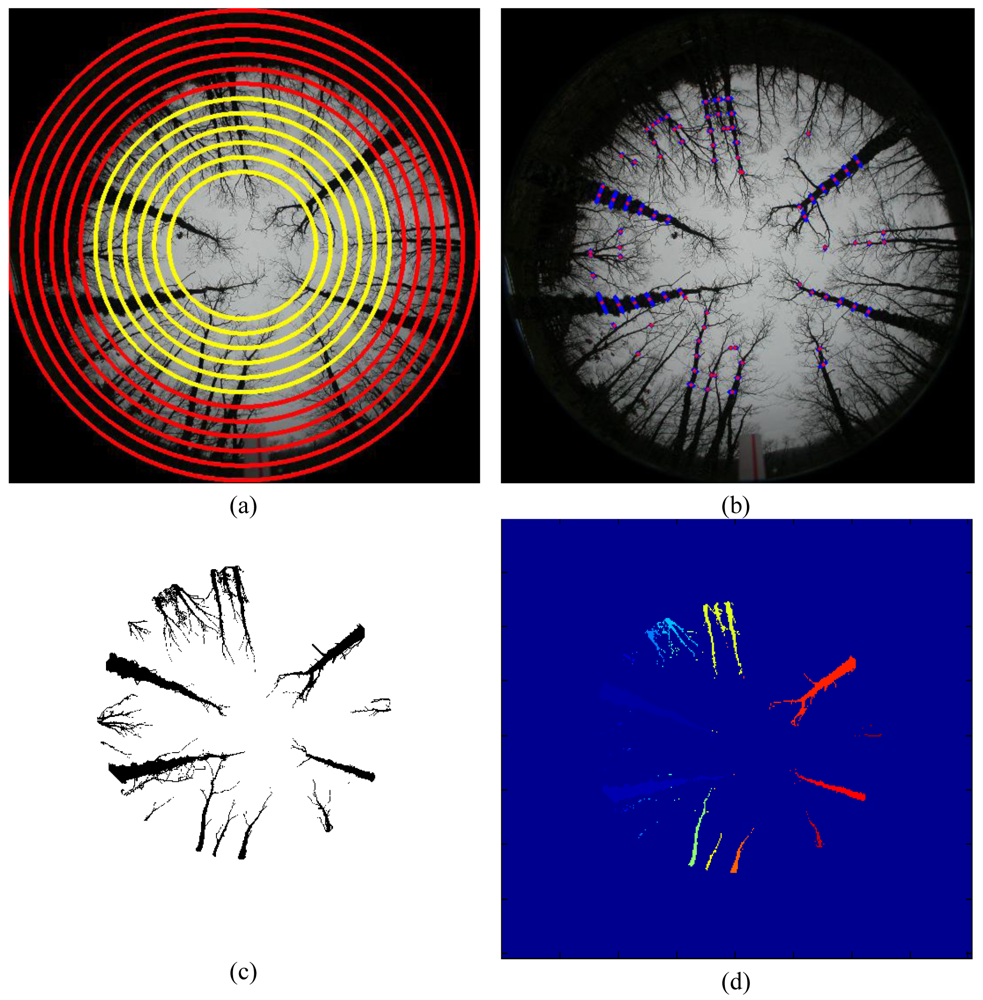
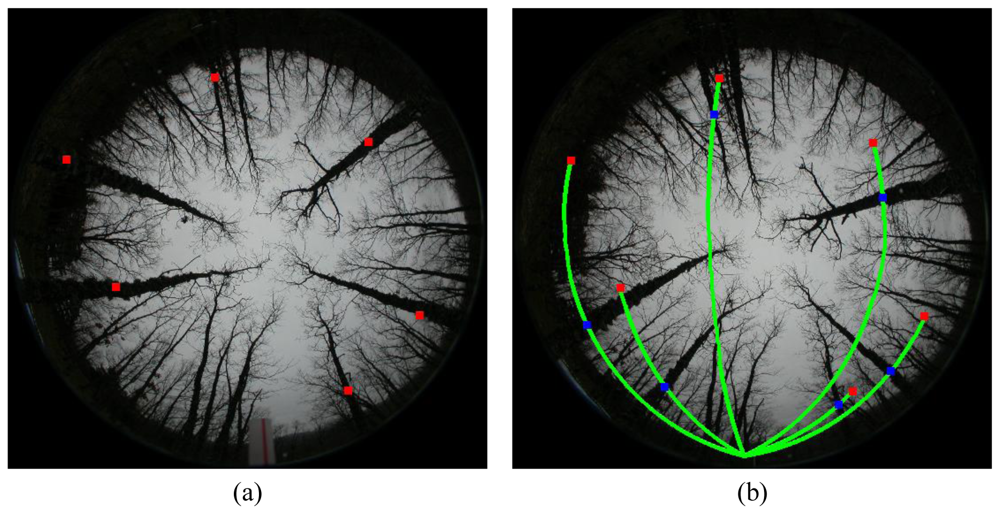
- Step 2 Concentric circumferences: we draw concentric circumferences on the original image, starting with a radius r = 250 pixels with increases of 50 pixels until r = R. For each circumference, we obtain the intensity profile. There are two main types of circumferences, namely: those in zones where all trunks are well contrasted with respect the background and those in zones where the background and the trunks get confused. Figure 5(a) displays both types of zones, the first ones are drawn in yellow and the second ones in red. As one can see, the yellow circumferences cross areas with the trunks over the sky and the red ones cross zones where the trunks and the soil appear with similar intensity levels.
- Step 3 Intensity profiles and detection of crossed dark regions: following the circumference paths, we draw the associated intensity profile for each one. Figure 4 displays two intensity profiles covering a range of 45° in this representation from 135° to 180°. In the profile appear low and high intensity levels. The low ones are associated to trunks or soil and the high ones to the sky. Based on the above, if large dark areas appear in the profile, this means that the circumference cross a region where the trunks and the soil cannot be distinguished and this circumference is labelled as red. This occurs in the Figure 4(a) which represents low intensity values ranging from 0 to 0.18 over a range of [0,1] i.e., a large dark area. If no large dark areas are identified, the circumference is labelled as yellow. On the contrary if a relative small dark area appears limited by two clear areas, it represents a trunk; Figure 4(b).
- Step 4 Putting seeds in the trunks: considering the yellow circumferences, we are able to detect the trunks positions crossed by them, which are dark homogeneous regions in the profile limited by clear zones, Figure 4(b). This allows choosing a pixel for each dark homogeneous region; such pixel is considered a seed. Also, because we know the transition from clear to clear crossing a dark homogeneous region, we obtain the average intensity value and standard deviation for it. In summary, from each dark homogeneous region in a yellow circumference, we select a seed and obtain its average intensity value and standard deviation.
- Step 5 Region filtering: we are only interested in specific dark regions, considered as those that represent trunks of interest. The process of selecting them is as follows, Figure 5(b).
- We consider only those dark regions in the profile where the intersection with yellow circumferences produces a line with more than T1 pixels. This is to guarantee that the trunk analyzed is wide enough. Its justification is because we assume that this kind of trunks belong to the area of interest under analysis, i.e., to the circle with radius lesser than 25m.
- Also, based on the yellow circumferences, we only consider the regions with intensity levels less than T2 because we are dealing with dark homogeneous regions (trunks).
- Considering the outer yellow circumference ci, we select only dark regions whose intersection with this circumference gives a line with a number of pixels lower than T3. The maximum value in pixels of all lines of intersection is . Then for the next yellow circumference towards the centre of the image, ci+1, T3 is now set to , which is the value used when the next circumference is processed and so on until the inner yellow circumference is reached. This is justified because the thickness of the trunks always diminishes towards the centre.
In this work, T1, T2 and T3 are set to 10, 0.3 and 120 respectively, after experimentation. - Step 6 Region growing: this process is based on the procedure described in [28], we start in the outer yellow circumference by selecting the seed pixels obtained in this circumference. From these seed points we append to each seed those neighbouring pixels that have a similar intensity value than the seed. The similarity is measured as the difference between the intensity value of the pixel under consideration and the mean value in the zone where the seed belongs to, they do not differ more than the standard deviation computed in step 4 for that zone. The region growing ends when no more similar neighbouring pixels are found for that seed between this circumference and the centre of the image. This allows obtaining a set of regions as displayed in Figure 5(c).
- Step 7 Labelling: before the labelling, an opening morphologic operation is applied. The aim is to break joined links, to avoid that some branches of the trees overlapping other branches or trunks lead to label two trees or trunks as a unique region. The structural element during the opening is the classical 3 × 3 matrix of ones because it is symmetric operating in all spatial directions. The regions extracted during the previous region growing are labelled following the procedure described in [32]. Figure 5(d) displays this step.
- Step 8 Regions and seeds association: for each one of the seeds in the outer yellow circumference, we make to correspond to each seed its region identified before. It is possible that more than one seed turns out to be belonging to the same region. If this occurs, we create new regions, so that finally we obtain the same number of regions than seeds. After this step, each region has assigned a unique seed.
- Step 9 Seeds association: we check for the other seeds in the remainder yellow circumferences. If a seed fulfils that it is the nearest in terms of pixel distance and its angle in degrees the most similar to the angle of the previously checked seed, then it belongs to the same region that the seed checked previously, which is the reference. The angle in degrees is the θ value in polar coordinates (ρ,θ) with respect the seed location in Cartesian coordinates (x,y). This process allows establishing correspondences among the seeds of the different yellow circumferences depending on the region to which they belong, Figure 6(a), i.e., to identify seeds that belong probably to the same region (trunk). We compute the average orientation, s̄, for all seeds belonging to the same region identified according to the process described in this point.
- Step 10 Estimation of the seeds locations in the red circumferences: it consists of three sub steps, prediction, correction and measurement:
- Prediction: the pixels belonging to a trunk crossed by a red circumference must have identical orientation, in degrees, that the seed in the outer yellow circumference crossing the same trunk. So, we obtain the seeds in red circumferences fulfilling this and starting from the inner one.
- Correction: since there are trunks that are not aligned towards the centre, the prediction can introduce mistakes. An offset value is applied to this location, which is exactly s̄, computed in step 9, Figure 6(b).
- Measurement: after the offset correction, we verify if the estimated seed in each red circumference belongs to a trunk. This is only possible if the red circumference crosses a region with low intensity values limited by zones with high intensity values and the estimated seed location is inside the region with low values. With this, we assume that the seed belongs to the same trunk that the seed in the yellow circumference. Because of the contrast in the intensity profile for the red region in the specific trunk, we can measure the exact seed location in the central part of the low intensity region. The estimated seed location is replaced by the measured one and used for estimating the next seed location in the next red circumference. If the profile does not display low and high intensity values, no measurements can be taken and the next seed location is the previously estimated by prediction and correction.
- Step 11 New region growing: starting on the outer yellow circumference, we apply again a new region growing process as the one described in the step 6, but now controlled by several iterations (so many iterations as red circumferences). For each iteration, the region growing has its upper limit given by the radius of the nearest red circumference. Once the outer red circumference is reached, i.e., maximum number of iterations, the region growing ends; at this moment an opening morphologic operation is applied trying to break links between regions (trunks) which could be still joined. The structural element used for the opening is the same that the one used in step 7. Figure 6(c) displays this step.
- Step 12 Relabeling: this process is similar to the one described in step 7. We re-label each one of the regions that have appeared after the region growing process in step 11, Figure 6(d).
- Step 13 Attributes extraction: once all regions have been relabelled, for each region we extract the following attributes: area (number of pixels), centroid (xy-averaged pixel positions in the region), angles in degrees of each centroid and the seven Hu invariant moments [28].
3. Correspondence Process
3.1. Epipolar: Centroid
3.2. Similarity: Areas and Hu Moments
- . This means that the minimum distance is indeed obtained for and and it is smaller than a fixed threshold T1, i.e., only small distances are accepted. T1 is set to 0.3 after trial and error.
- . This means that the minimum distance is smaller enough than the mean of the distances from all other distances between features, where is the mean value of and T2 is a threshold ranging from 0 to 1. It has been set to 0.5 in our experiments, because we have verified that it suffices as in [16].
- the rate between and the second minimum distance with h = 1, 2, …, NR and h ≠ j, is smaller than a threshold T3, set to 0.3 in our experiments. This guarantees that a gap between the absolute minimum distance and the second one exists.As mentioned before, because the sensor is built with two cameras, with a given base-line, the same tree in the 3D scene can be imaged under different areas in both images. This issue has been addressed in [35] where an exhaustive study is made about the different shapes in the images of the same 3D surface in conventional sensors. Here, it is stated that there is not a unique correspondence between a pixel in one image an other pixel in the other image. This is an important reason for using regions as a feature-based approach instead of area-based because the above problem does not occur. Now two trunks, which are true matches, one belonging to an image and the other to the second, can display different areas. Therefore, we formulate the following condition for matching two regions by considering both areas:
- The areas Ai and Aj do not differ between them more than the 33%.
3.3. Ordering: Angles
3.4. Summary of the Full Correspondence Process
Correspondence Left to Right
- 1.
- Apply epipolar constraint: we only consider potential matches of Li those Rj regions that fulfil the epipolarity, as defined in the subsection 3.1. After this step, Li has as potential candidates a list li of n regions in the right image, say li ≡ Li → {Rj1, .., Rjn}, where j1, jn ∈ {1, …, NR}.
- 2.
- Apply the condition D given in Section 3.2 to the list li. Exclude from li those candidates that do not fulfil such condition D.
- 3.
- Apply conditions A to C given in Section 3.2 to the current list li. For each pair (Li, Rjn) obtained from li, determine if Li and Rjn match based on the kth Hu moment according to such conditions A to C. Define lk as the number of these individual matches.
Correspondence Right to Left
- 4.
- For each region Rj in the right image we search for candidates Lj in the left image, following similar steps to the previous ones. Now a list rj of candidates is built and a number rk of individual matches is obtained according to the Hu invariant moments. The epipolar constraint is applied following the same lines than those used for Left to Right but in the reverse sense.
Final Decision: Simple majority and Uniqueness
- 5.
- We say that Li matches with Rj, iif lk + rk > U, where U has been set to 7 in our experiments. This value has been fixed taking into account that the maximum value that the sum lk + rk can achieve is 14, i.e., a value greater than 7 represents the majority.
- 6.
- If the matching between Li and Rj is unambiguous the correspondence between both features is solved; otherwise in the ambiguous case, where the above condition is fulfilled by more than one match, then we apply the ordering constraint based on the unambiguous correspondences which have been already solved. This implies the application of both ordering and uniqueness constraints simultaneously.
4. Results
4.1. Segmentation
- The regions have been well separated, even if there were regions very near among them. This occurs with the regions 10 and 11 or 18 and 20 in the left image and also with the regions 8 and 10 in the right one.
- The procedure is able to extract regions corresponding to trunks, which are relatively far from the sensor, i.e., out of the area of the sample plot, which is the area of interest. This occurs with the regions labelled as 4, 5, 18, 19 and 20 in the left image and 2, 17, 18 and 19 in the right image. Although such regions are out of the interest, we have preferred include them for matching, because in the future perhaps the sensed area could be extended to an area greater than 25 m and also to verify the robustness of the correspondence process. Its exclusion is an easy task because they all fulfil that their areas are below a value of 6,400 pixels, which is the threshold T4 applied for the ordering constraint.
- Through the morphological operations, the process is able to break links between regions, allowing their identification. This occurs between regions 5 and 8 in the right, where two branches are overlapped. Without this breaking, both regions are labelled as a unique region and its matching with the corresponding regions in the left image, which are separated, is not possible.
4.2. Correspondence
- We can see that regions labelled as 2, 1 and 3 in the left image match with regions 1, 5 and 3 respectively in the right image. Without the limitation of the ordering constraint with respect heights and areas of the regions, section 3.3, this constraint should be violated by the region 3 in the left image because the ordering with respect the couple 1 with 5 is not preserved. In this case, the ordering is applied only between regions 2, 1 in the left image and 1 and 5 in the right one. The heights and areas fulfil the requirements given in section 3.3. The ordering constraint is violated for the case of regions 19, 18 and 20 in the left image, which correspond to 18, 17 and 19, while the order is 18, 19 and 17. Based on the requirements in Section 3.3, they fulfil that the areas do not differ more than the 33% but they fails for the requirement that the areas must overpass the threshold T4, i.e., in this case the ordering constraint is not applied.
- Occlusions: we have found a clear occlusion that has been correctly handled. The region 6 is visible in the left image and its corresponding match is occluded by 5 in the right image. Our approach does not find its match, as expected.
- Ambiguities: there are two types of ambiguities which arise inside the area of interest in the sample plot and outside this area. To the first case belongs the ambiguity between the region 13 in the left image and regions 12 and 7 in the right image. To the second case belong the regions 18 and 20 in the left image, where both have as preferred matches the regions 17 and 19. The first case is solved thanks to the application of the ordering constraint. Unfortunately, in the second case this constraint does not solve the ambiguity causing erroneous matches. Nevertheless, we still consider that its application is favourable because it works properly in the area of interest. Although this could be a limit for extending the area of interest.
- The percentage of successful correspondences in the stereo pair displayed in this paper is the 90%. On average, the percentage of success for the sixteen stereo pairs of images analyzed with similar characteristics is the 88.4%.
5. Conclusions
Acknowledgments
References
- Pita, P.A. El Inventario en la Ordenación de Montes; INIA: Ministerio de Agricultura, Pesca y Alimentación: Madrid, Spain, 1973. [Google Scholar]
- Pardé, J.; Bouchon, J. Dendrométrie; l'École National du Génie Rural des Eaux et des Forêts: Nancy, France, 1987. [Google Scholar]
- Mandallaz, D.; Ye, R. Forest inventory with optimal two-phase, two-stage sampling schemes based on the anticipated variance. Can. J. Forest Res. 1999, 29, 1691–1708. [Google Scholar]
- Montes, F.; Hernández, M.J.; Cañellas, I. A geostatistical aproach to cork production sampling estimation in Quercus suber L. forests. Can. J. Forest Res. 2005, 35, 2787–2796. [Google Scholar]
- Abraham, S.; Förstner, W. Fish-eye-stereo calibration and epipolar rectification. Photogram. Remote Sens. 2005, 59, 278–288. [Google Scholar]
- Wulder, M.A.; Franklin, S.E. Remote Sensing of Forest Environments: Concepts and Case Studies; Kluwer Academic Publishers: Boston, MA, USA, 2003. [Google Scholar]
- Montes, F.; Ledo, A.; Rubio, A.; Pita, P.; Canellas, I. Use of estereoscopic hemispherical images for forest inventories. Proceedings of the International Scientific Conference Forest, Wildlife and Wood Sciences for Society development, Faculty of Forestry and Wood Sciences; Czech University of Life Sciences: Prague, Czech Republic, 2009. [Google Scholar]
- Gregoire, T.G. Design-based and model-based inference in survey sampling: apreciating the difference. Can. J. Forest Res. 1998, 28, 1429–1447. [Google Scholar]
- Barnard, S.; Fishler, M. Computational Stereo. ACM Comput. Surv. 1982, 14, 553–572. [Google Scholar]
- Scharstein, D.; Szeliski, A. Taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vision 2002, 47, 7–42. [Google Scholar]
- Tang, L.; Wu, C.; Chen, Z. Image dense matching based on region growth with adaptive window. Pattern Recognit. Lett. 2002, 23, 1169–1178. [Google Scholar]
- Grimson, W.E.L. Computational experiments with a feature-based stereo algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 7, 17–34. [Google Scholar]
- Ruichek, Y.; Postaire, J.G. A neural network algorithm for 3-D reconstruction from stereo pairs of linear images. Pattern Recognit. Lett. 1996, 17, 387–398. [Google Scholar]
- Medioni, G.; Nevatia, R. Segment based stereo matching. Comput. Vision Graph. Image Process 1985, 31, 2–18. [Google Scholar]
- Pajares, G; Cruz, J.M. Fuzzy cognitive maps for stereo matching. Pattern Recognit. 2006, 39, 2101–2114. [Google Scholar]
- Scaramuzza, D.; Criblez, N.; Martinelli, A.; Siegwart, R. Robust feature extraction and matching for omnidirectional images. In Field and Service Robotics; Laugier, C., Siegwart, R., Eds.; Springer: Berlin, Germany, 2008; Volume 42, pp. 71–81. [Google Scholar]
- McKinnon, B.; Baltes, J. Practical region-based matching for stereo vision. Proceedings of 10th International Workshop on Combinatinal Image Analysis (IWCIA'04); Klette, R., Zunic, J., Eds.; Springer: Berlin, Germany, 2004; pp. 726–738, LNCS 3322. [Google Scholar]
- Marapane, S.B.; Trivedi, M.M. Region-based stereo analysis for robotic applications. IEEE Trans. Syst. 1989, 19, 1447–1464. [Google Scholar]
- Wei, Y.; Quan, L. Region-based progressive stereo matching. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'04), Washington, DC, USA, June 27, 2004; Vol. 1. pp. 106–113.
- Chehata, N.; Jung, F.; Deseilligny, M.P.; Stamon, G. A region-based matching approach for 3D-roof reconstruction from HR satellite stereo Pairs. Proceedings of VIIth Digital Image Computing: Techniques and Applications, Sydney, Australia; 2003; pp. 889–898. [Google Scholar]
- Kaick, O.V.; Mori, G. Automatic classification of outdoor images by region matching. Proceedings of the 3rd Canadian Conference on Computer and Robot Vision (CRV'06), Quebec, Canada, June 7–9, 2006; p. 9.
- Renninger, L.W.; Malik, J. When is scene recognition just texture recognition? Vision Res. 2004, 44, 2301–2311. [Google Scholar]
- Hu, Q.; Yang, Z. Stereo matching based on local invariant region identification. Proceedings of the International Symposium on Computer Science and Computational Technology, Shanghai, China, December 20–22, 2008; Vol. 2. pp. 690–693.
- Premaratne, P.; Safaei, F. Feature based Stereo correspondence using Moment Invariant. Proceedings of the 4th International Conference on Information and Automation for Sustainability (ICIAFS'08), Colombo, Sri Lanka, December 12–14, 2008; pp. 104–108.
- Lopez, M.A.; Pla, F. Dealing with segmentation errors in region-based stereo matching. Pattern Recognit. 2000, 8, 1325–1338. [Google Scholar]
- Wang, Z.F.; Zheng, Z.G. A region based stereo matching algorithm using cooperative optimization. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR'08), Anchorage, AK, USA; 2008; pp. 1–8. [Google Scholar]
- El Ansari, M.; Masmoudi, L.; Bensrhair, A. A new regions matching for color stereo images. Pattern Recognit. Lett. 2007, 28, 1679–1687. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd Ed. ed; Prentice-Hall: Bergen County, NJ, USA, 2008. [Google Scholar]
- Trias-Sanz, R.; Stamon, G.; Louchet, J. Using colour, texture, and hierarchical segmentation for high-resolution remote sensing. ISPRS J. Photogram. Remote Sens. 2008, 63, 156–168. [Google Scholar]
- Bandzi, P.; Oravec, M.; Pavlovicova, J. New statistics for texture classification based on gabor filters. Radioengineering 2007, 16, 133–137. [Google Scholar]
- Herrera, P.J.; Pajares, G.; Guijarro, M.; Ruz, J.J.; de la Cruz, J.M. Combination of attributes in stereovision matching for fish-eye lenses in forest analysis. ACIVS 2009; Springer-Verlag: Berlin, Germany, 2009; pp. 277–287, LNCS 5807. [Google Scholar]
- Haralick, R.M.; Shapiro, L.G. Computer and Robot Vision; Addison-Wesley: Reading, MA, USA, 1992; Volume I–II. [Google Scholar]
- Schwalbe, E. Geometric modelling and calibration of fisheye lens camera systems. Proceedings of the 2nd Panoramic Photogrammetry Workshop, International Archives of Photogrammetry and Remote Sensing, Dresden, Germany, February 19–22, 2005. Vol. 36.
- Elias, R. Sparse view stereo matching. Pattern Recognit. Lett. 2007, 28, 1667–1678. [Google Scholar]
- Ogale, A.S.; Aloimonos, Y. Shape and the stereo correspondence problem. Int. J. Comput. Vision 2005, 65, 147–162. [Google Scholar]
- Shah, S.; Aggarwal, J.K. Mobile robot navigation and scene modeling using stereo fish-eye lens system. Mach. Vision Appl. 1997, 10, 159–173. [Google Scholar]




| Left image regions Li | Corresponding right image regions (Rj) | lk | rk | Final decision matching |
|---|---|---|---|---|
| 1 | 5 | 7 | 7 | S |
| 2 | 1 | 7 | 7 | S |
| 3 | 3 | 7 | 7 | S |
| 4 | 2 | 7 | 7 | S |
| 5 | 4 | 7 | 7 | S |
| 6 | no match (hidden by 5) | 0 | 0 | S (unmatched) |
| 7 | 6 | 7 | 7 | S |
| 8 | 8 | 4 | 5 | S |
| 9 | 10 | 6 | 7 | S |
| 10 | 7 | 7 | 1 | S |
| 11 | 9 | 7 | 7 | S |
| 12 | 11 | 7 | 3 | S |
| 13 | 12 | 1 | 7 | S |
| 14 | 13 | 7 | 7 | S |
| 15 | 14 | 7 | 7 | S |
| 16 | 15 | 7 | 7 | S |
| 17 | 16 | 7 | 7 | S |
| 18 | 17 | 2 | 4 | F |
| 19 | 18 | 5 | 6 | S |
| 20 | 19 | 4 | 3 | F |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Herrera, P.J.; Pajares, G.; Guijarro, M.; Ruz, J.J.; Cruz, J.M.; Montes, F. A Featured-Based Strategy for Stereovision Matching in Sensors with Fish-Eye Lenses for Forest Environments. Sensors 2009, 9, 9468-9492. https://doi.org/10.3390/s91209468
Herrera PJ, Pajares G, Guijarro M, Ruz JJ, Cruz JM, Montes F. A Featured-Based Strategy for Stereovision Matching in Sensors with Fish-Eye Lenses for Forest Environments. Sensors. 2009; 9(12):9468-9492. https://doi.org/10.3390/s91209468
Chicago/Turabian StyleHerrera, Pedro Javier, Gonzalo Pajares, Maria Guijarro, José J. Ruz, Jesús M. Cruz, and Fernando Montes. 2009. "A Featured-Based Strategy for Stereovision Matching in Sensors with Fish-Eye Lenses for Forest Environments" Sensors 9, no. 12: 9468-9492. https://doi.org/10.3390/s91209468