Testing Multivariate Adaptive Regression Splines (MARS) as a Method of Land Cover Classification of TERRA-ASTER Satellite Images
Abstract
:1. Introduction
2. Materials
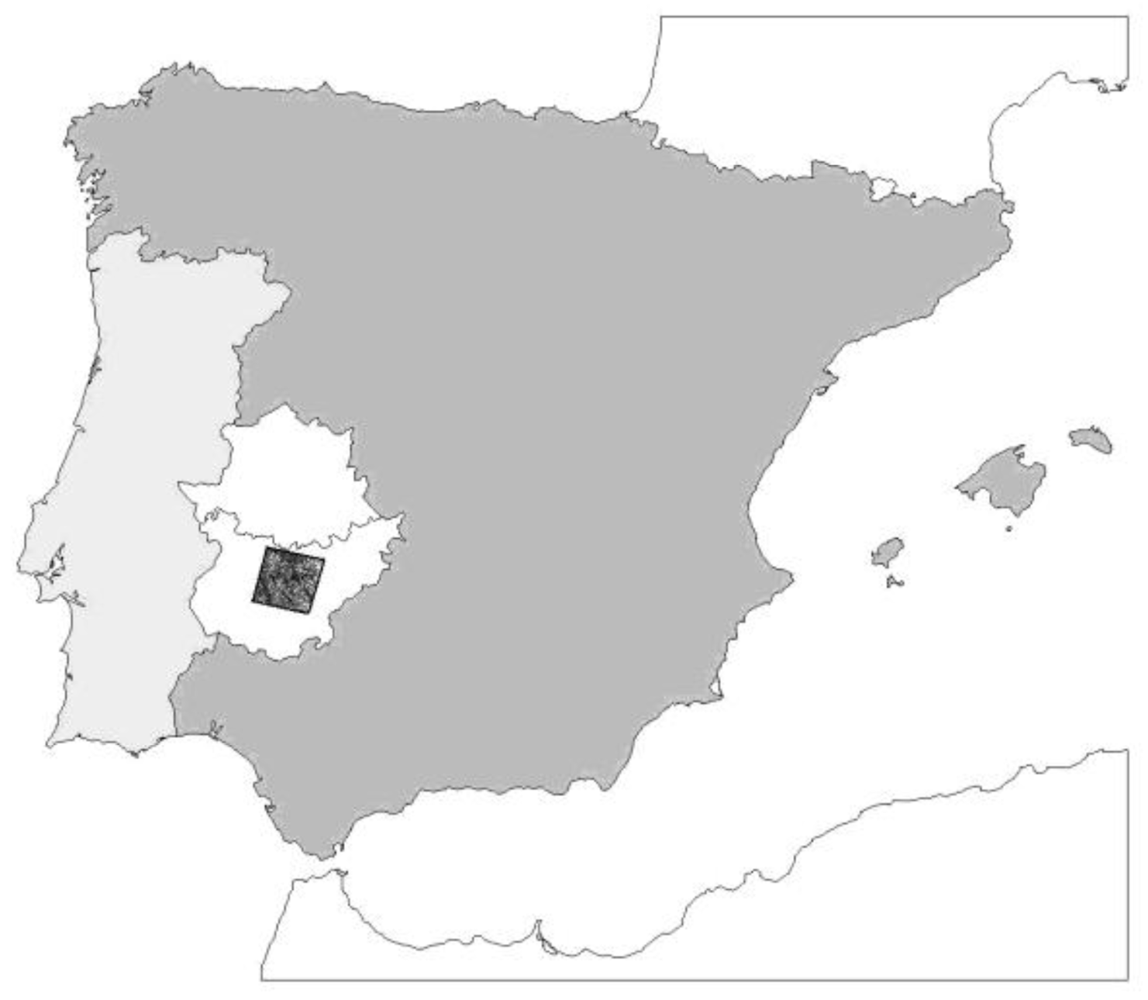
2.1. TERRA-ASTER scene
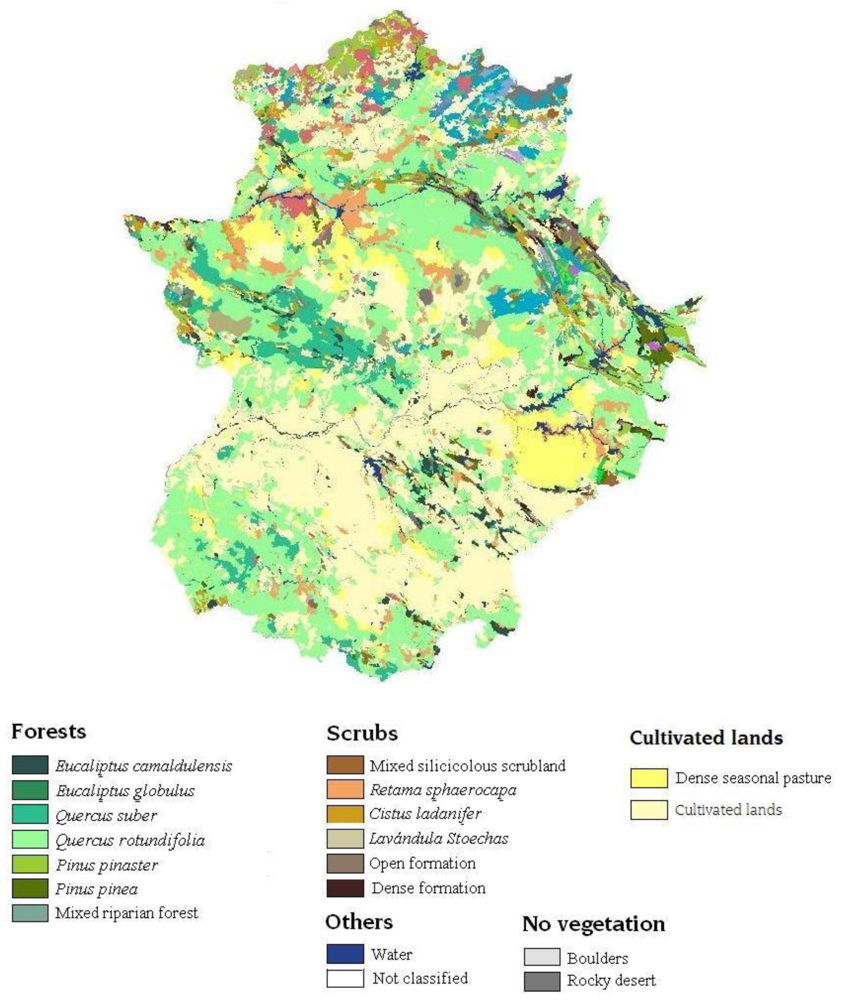
2.2. Vegetation map
2.3. Software
3. Methods
3.1. Image preprocessing
3.2. Introduction to the MARS algorithm
- The selection of basic functions from the initial set is achieved by determining a constant function h0(X) = 1 so that all functions from set C are candidates. New pairs of functions are considered at each stage until the model has the maximum number of terms set by the user at the beginning of the process.
- The backward removal is performed by suppressing those model terms that contribute to a minimal residual error. This stage consists of reducing the complexity of the model complexity by increasing its generalisability [7]. This process can be conducted by means of generalised cross-validation (GCV).With this GCV function, the optimum number of model terms (λ) can be estimated with:The value M(λ) is the effective number or parameters in the model, and it is expressed in terms of r (i.e., the number of linearly independent basic functions) and K (i.e., the number of knots selected in the forward process).The process stops when the number of model terms reaches GCV(λ).
- Finally, smoothing is necessary for removing discontinuities within regional borders and ensuring the continuity of first and second derivatives.
3.3. Classification maps
3.3.1. ML classification
3.3.2. Parallelepiped classification
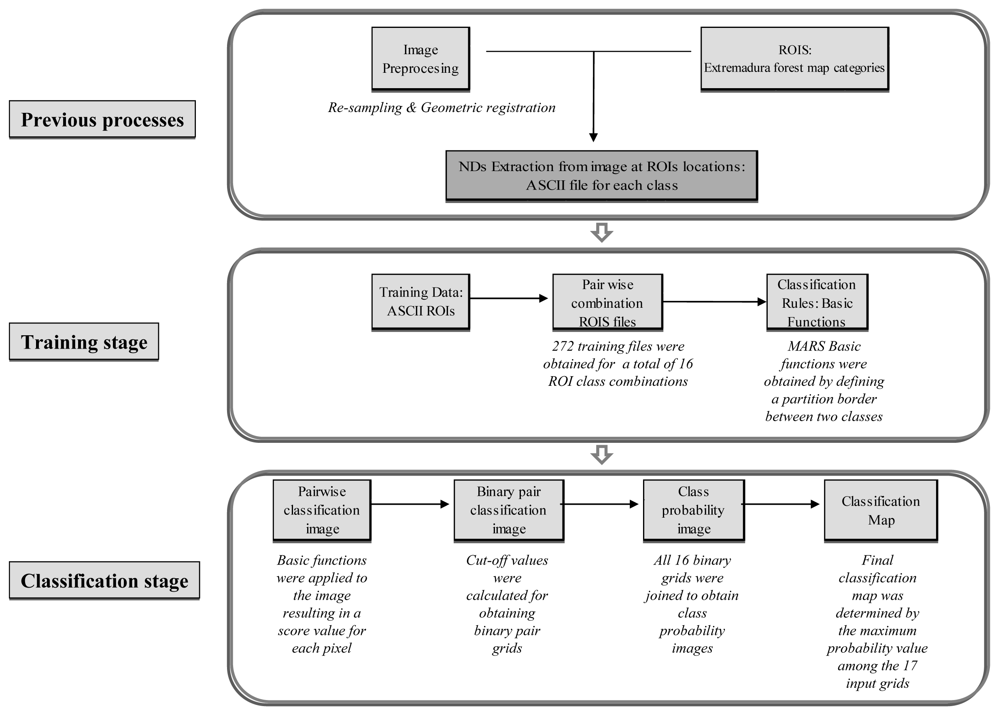
3.3.3. MARS classification
a) Training stage
a.1. Pairwise combination of ROI ASCII files
a.2. Obtaining basic functions
b) Classification stage
b.1. Application of pairwise basic functions to the entire scene
b.2. Generating binary pair classification images
- Maximise correct classification probabilities
- Minimise incorrect classification probabilities
b.3. Generating the class probability image
b.4. Obtaining the final classification image
3.4. Probabilities maps
3.4.1. The ML probability maps
3.4.2. Parallelepiped probability maps
3.4.3. MARS probability maps
4. Results and Discussion
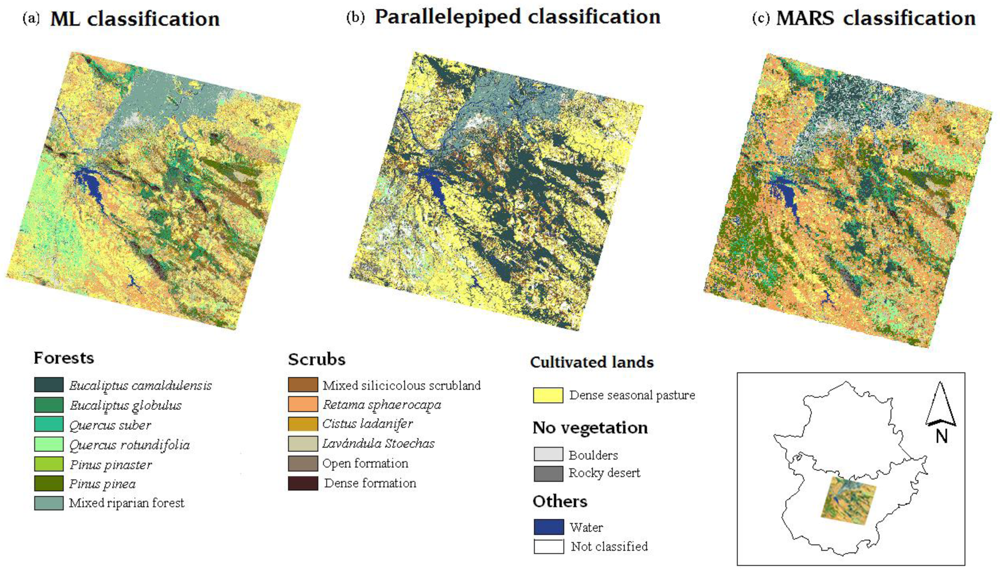
4.1. Classification maps
4.2. Comparison of classification maps
5. Conclusions
Acknowledgments
References
- Ruiz, L.A. Introducción al tratamiento digital de imágenes en teledetección; Servicio de publicaciones de la Universidad Politécnica de Valencia: Valencia, Spain, 1998. [Google Scholar]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar]
- Sarunas, R. On dimensionality, sample size, and classification error of nonparametric linear classification algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 667–671. [Google Scholar]
- Cortijo, F.J.; de la Blanca, N.P. The performance of regularized discriminant analysis versus non-parametric classifiers applied to high-dimensional image classification. Int. J. Remote Sens. 1999, 20, 3345–3365. [Google Scholar]
- Hill, T.; Lewicki, P. Statistics: Methods and Applications. A Comprehensive Reference for Science, Industry and Data Minining; StatSoft: Tulsa, OK, USA, 2006. [Google Scholar]
- Friedman, J.H. Multivariate adaptive regression splines; Salford Systems: San Diego, CA, USA, 1990. [Google Scholar]
- Bonilla, M.; Olmeda, I.; Puertas, R. Modelos paramétricos y no paramétricos en problemas de credit scoring. Revista Española de Financiación y Contabilidad 2003, 31, 833–869. [Google Scholar]
- Heikkinen, R.K.; Luoto, M.; Kuussaari, M.; Toivonen, T. Modelling the spatial distribution of a threatened butterfly: Impacts of scale and statistical technique. Landsc. Urban Plan. 2007, 79, 347–357. [Google Scholar]
- Leathwick, J.R.; Elith, J.; Hastie, T. Comparative performance of generalized additive models and multivariate adaptive regression splines for statistical modelling of species distributions. Ecol. Modell. 2006, 199, 188–196. [Google Scholar]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar]
- Felicísimo, A.M.; Gómez, A.; Munoz, J. Potential distribution of forest species in dehesas of Extremadura. In Sustainability of agrosilvopastoral systems: Dehesas, montados; Schnabel, S., Ferreira, A., Eds.; Catena Verlag: Reiskirchen, Germany, 2004; pp. 231–246. [Google Scholar]
- Moisen, G.G.; Frescino, T.S. Comparing five modelling techniques for predicting forest characteristics. Ecol. Modell. 2002, 157, 209–225. [Google Scholar]
- Muñoz, J.; Felicísimo, A.M. Comparison of statistical methods commonly used in predictive modelling. J. Veg. Sci. 2004, 15, 285–292. [Google Scholar]
- Francis, L.; FCAS; MAAA. Martian Chronicles: Is MARS Better than Neural Networks? Available online: http://www.salfordsystems.com/publications.php (accessed June 8, 2008).
- Dwinnell, W. Exploring MARS: An Alternative to Neural Networks. Available online: http://www.salfordsystems.com/publications.php (accessed June 8, 2008).
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference and Prediction; Springer-Verlag: New York, NY, USA, 2001. [Google Scholar]
- Duda, R.; Hart, P.; Stork, D. Pattern Classification; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Molina, R.; de la Blanca, N.P.; Taylor, C.C. Modern statistical techniques. In Machine Learning, Neural and Statistical Classification; Michie, D.J., Spiegelhalter, D.J., Eds.; Ellis Horwood: Upper Saddle River, NJ, USA, 1994; pp. 29–49. [Google Scholar]
- Solberg, A.H. Flexible nonlinear contextual classification. Pattern Recognit. Lett. 2004, 25, 1501–1508. [Google Scholar]
- Kato, M.; Syoji, M.; Oyanagi, M. Aster status and data application use. Proceedings of the 22nd Asian Conference on Remote Sensing, Singapore, November, 2001.
- Stefanov, W.L.; Netzband, M. Assessment of ASTER land cover and MODIS NDVI data at multiple scales for ecological characterization of an arid urban center. Remote Sens. Environ. 2005, 99, 31–43. [Google Scholar]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Balick, L.; Gillespie, A.R.; Sabol, D.A.; Gustafson, W.T. Accuracy of ASTER level-2 thermal-infrared standard products of an agricultural area in Spain. Remote Sens. Environ. 2007, 106, 146–153. [Google Scholar]
- Muukkonen, P.; Heiskanen, J. Estimating biomass for boreal forests using ASTER satellite data combined with standwise forest inventory data. Remote Sens. Environ. 2005, 99, 434–447. [Google Scholar]
- Barry, R.G. The status of research on glaciers and global glacier recession: A review. Prog. Phys. Geogr. 2006, 30, 285–306. [Google Scholar]
- Khromova, T.E.; Osipova, G.B.; Tsvetkov, D.G.; Dyurgerov, M.B.; Barry, R.G. Changes in glacier extent in the eastern Pamir, central Asia, determined from historical data and ASTER imagery. Remote Sens. Environ. 2006, 102, 24–32. [Google Scholar]
- Tralli, D.M.; Blom, R.G.; Zlotnicki, V.; Donnellan, A.; Evans, D.L. Satellite remote sensing of earthquake, volcano, flood, landslide and coastal inundation hazards. ISPRS-J. Photogramm. Remote Sens. 2005, 59, 185–198. [Google Scholar]
- Gillespie, T.W.; Chu, J.; Frankenberg, E.; Thomas, D. Assessment and prediction of natural hazards form satellite imagery. Prog. Phys. Geogr. 2007, 31, 459–470. [Google Scholar]
- Liu, Y.; Hiyama, T.; Yamaguchi, Y. Scaling of land surface temperature using satellite data: A case examination on ASTER and MODIS products over a heterogeneous terrain area. Remote Sens. Environ. 2006, 105, 115–128. [Google Scholar]
- Pu, R.; Gong, P.; Michishita, R.; Sasagawa, T. Assessment of multi-resolution and multi-sensor data for urban surface temperature retrieval. Remote Sens. Environ. 2006, 104, 211–225. [Google Scholar]
- Jianwen, M.; Bagan, H. Land-use classification using ASTER data and self-organized neutral networks. Int. J. Appl. Earth Obs. Geoinf. 2005, 7, 183–188. [Google Scholar]
- Fawcett, T. ROC Graphs: Notes and Practical Considerations for Researchers; HP Laboratories: Palo Alto, CA, USA, 2004. [Google Scholar]
- Huang, J.; Ling, C.X. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans. Knowl. Data Eng. 2005, 17, 299–310. [Google Scholar]
- Ling, C.X.; Huang, J.; Zhang, H. AUC: A statistically consistent and more discriminating measure than accuracy. Proceedings of the International Joint Conference on Artificial Intelligence, Acapulco, Mexico, August, 2003.
- Marchant, J.A.; Andersen, H.J.; Onyango, C.M. Evaluation of an imaging sensor for detecting vegetation using different waveband combinations. Comput. Electron. Agric. 2001, 32, 101–117. [Google Scholar]
- Tu, T.M.; Chen, C.H.; Chang, C.I. A posteriori least squares orthogonal subspace projection approach to desired signature extraction and detection. IEEE Trans. Geosci. Remote Sens. 1997, 35, 127–139. [Google Scholar]
- Abrams, M.; Hook, S. ASTER User Handbook; JPL-NASA: Pasadena, CA, USA, 2001. [Google Scholar]
- de la Torre, J.R. Mapa forestal de Espana. Escala 1:200.000. Memoria general; Ministerio de agricultura, pesca y alimentación: Madrid, Spain, 1990. [Google Scholar]
- Nedjah, N.; de Macedo Mourelle, L. Fuzzy Systems Engineering: Theory and Practice; Springer: New York, NY, USA, 2005. [Google Scholar]
- Stone, C.J.; Hansen, M.H.; Kooperberg, C.; Truong, Y.K. Polynomial splines and their tensor products in extended linear modelling: 1994 Wald memorial lecture. Ann. Stat. 1997, 25, 1371–1470. [Google Scholar]
- Girard, M.C. Processing of Remote Sensing Data; Taylor & Francis: Paris, France, 2003. [Google Scholar]
- Tso, B.; Mather, P.M. Classification Method for Remotely Sensed Data; CRC: New York, NY, USA, 2001. [Google Scholar]
- Richards, J.A.; Jia, X. Remote Sensing Digital Image Analysis: An Introduction; Springer-Verlag: New York, NY, USA, 2006. [Google Scholar]

| Sub-system | Band n° | Spectral range (mm) | Spatial resolution (m) | Quantization levels |
|---|---|---|---|---|
| Visible & Near infrared (VNIR) | 1 | 0.52–0.60 | 15 | 8 bits |
| 2 | 0.63–0.69 | |||
| 3N | 0.78–0.86 | |||
| 3B | 0.78–0.86 | |||
| Shortwave infrared (SWIR) | 4 | 1.60–1.70 | 30 | 8 bits |
| 5 | 2.145–2.185 | |||
| 6 | 2.185–2.225 | |||
| 7 | 2.235–2.285 | |||
| 8 | 2.295–2.365 | |||
| 9 | 2.360–2.430 | |||
| Thermal infrared (TIR) | 10 | 8.125–8.475 | 90 | 12 bits |
| 11 | 8.475–8.825 | |||
| 12 | 8.925–9.275 | |||
| 13 | 10.25–10.95 | |||
| 14 | 10.95–11.65 | |||
| Forest map cod. | Legend | Total area (Km2) | Percentage of the area under study |
|---|---|---|---|
| 999 | Water | 49.6 | 1.3% |
| 547 | Mixed silicicolous scrubland | 47.5 | 1.2% |
| 534 | Agricultural land | 2,422.9 | 61.4% |
| 507 | Mixed riparian forest | 23.5 | 0.6% |
| 458 | Dense seasonal pasture | 135.6 | 3.4% |
| 454 | Open formation | 8.7 | 0.2% |
| 453 | Dense formation | 8.6 | 0.2% |
| 337 | Boulders | 2.1 | 0.1% |
| 329 | Rocky desert | 42.2 | 1.1% |
| 309 | Retama sphaerocapa | 109.2 | 2.8% |
| 303 | Cistus ladanifer | 22.0 | 0.6% |
| 221 | Lavandulas stoechas | 10.4 | 0.3% |
| 62 | Eucaliptus camaldulensis | 194.7 | 4.9% |
| 61 | Eucaliptus globulus | 10.1 | 0.3% |
| 46 | Quercus suber | 53.5 | 1.4% |
| 45 | Quercus rotundifolia | 786.0 | 19.9% |
| 26 | Pinus pinaster | 1.4 | 0.0% |
| 23 | Pinus pinea | 17.8 | 0.5% |
| Forest map cod. | Legend | Category areas at image (km2) | ROI areas (km2) | ROI area percentages |
|---|---|---|---|---|
| 999 | Water | 49.6 | 33.3 | 67.19% |
| 547 | Mixed silicicolous scrubland | 47.5 | 28.4 | 59.73% |
| 507 | Mixed riparian forest | 23.5 | 11.6 | 49.18% |
| 458 | Dense seasonal pasture | 135.6 | 52.2 | 38.47% |
| 454 | Open formation | 8.7 | 2.8 | 31.89% |
| 453 | Dense formation | 8.6 | 5.6 | 64.68% |
| 337 | Boulders | 2.1 | 0.8 | 36.22% |
| 329 | Rocky desert | 42.2 | 23.5 | 55.82% |
| 309 | Retama sphaerocapa | 109.2 | 69.6 | 63.69% |
| 303 | Cistus ladanifer | 22.0 | 10.6 | 48.33% |
| 221 | Lavandula stoechas | 10.4 | 8.1 | 78.18% |
| 62 | Eucaliptus camaldulensis | 194.7 | 140.6 | 72.25% |
| 61 | Eucaliptus globulus | 10.1 | 5.7 | 55.93% |
| 46 | Quercus suber | 53.5 | 26.0 | 48.48% |
| 45 | Quercus rotundifolia | 786.0 | 544.2 | 69.23% |
| 26 | Pinus pinaster | 1.4 | 0.7 | 52.24% |
| 23 | Pinus pinea | 17.8 | 12.1 | 67.92% |
| Forest map cod. | Legend | ROI areas (km2) | MARS | ML | Parallelepiped |
|---|---|---|---|---|---|
| AUC | AUC | AUC | |||
| 999 | Water | 33.3 | 0.952 | 0.945 | 0.793 |
| 547 | Mixed silicicolous scrubland | 28.4 | 0.852 | 0.813 | 0.754 |
| 507 | Mixed riparian forest | 11.6 | 0.936 | 0.936 | 0.814 |
| 458 | Dense seasonal pasture | 52.2 | 0.844 | 0.714 | 0.687 |
| 454 | Open formation | 2.8 | 0.978 | 0.929 | 0.954 |
| 453 | Dense formation | 5.6 | 0.985 | 0.961 | 0.971 |
| 337 | Boulders | 0.8 | 0.963 | 0.969 | 0.791 |
| 329 | Rocky desert | 23.5 | 0.890 | 0.884 | 0.701 |
| 309 | Retama sphaerocapa | 69.6 | 0.724 | 0.699 | 0.670 |
| 303 | Cistus ladanifer | 10.6 | 0.856 | 0.826 | 0.728 |
| 221 | Lavandula stoechas | 8.1 | 0.906 | 0.898 | 0.657 |
| 62 | Eucaliptus camaldulensis | 140.6 | 0.908 | 0.856 | 0.834 |
| 61 | Eucaliptus globulus | 5.7 | 0.949 | 0.939 | 0.870 |
| 46 | Quercus suber | 26.0 | 0.864 | 0.841 | 0.766 |
| 45 | Quercus rotundifolia | 544.2 | 0.688 | 0.577 | 0.600 |
| 26 | Pinus pinaster | 0.7 | 0.957 | 0.976 | 0.903 |
| 23 | Pinus pinea | 12.1 | 0.952 | 0.960 | 0.924 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Quirós, E.; Felicísimo, Á.M.; Cuartero, A. Testing Multivariate Adaptive Regression Splines (MARS) as a Method of Land Cover Classification of TERRA-ASTER Satellite Images. Sensors 2009, 9, 9011-9028. https://doi.org/10.3390/s91109011
Quirós E, Felicísimo ÁM, Cuartero A. Testing Multivariate Adaptive Regression Splines (MARS) as a Method of Land Cover Classification of TERRA-ASTER Satellite Images. Sensors. 2009; 9(11):9011-9028. https://doi.org/10.3390/s91109011
Chicago/Turabian StyleQuirós, Elia, Ángel M. Felicísimo, and Aurora Cuartero. 2009. "Testing Multivariate Adaptive Regression Splines (MARS) as a Method of Land Cover Classification of TERRA-ASTER Satellite Images" Sensors 9, no. 11: 9011-9028. https://doi.org/10.3390/s91109011
APA StyleQuirós, E., Felicísimo, Á. M., & Cuartero, A. (2009). Testing Multivariate Adaptive Regression Splines (MARS) as a Method of Land Cover Classification of TERRA-ASTER Satellite Images. Sensors, 9(11), 9011-9028. https://doi.org/10.3390/s91109011





