Autonomous Distributed Self-Organization for Mobile Wireless Sensor Networks
Abstract
:1. Introduction
2. Related Work
3. The Self-Adaptive Mobile Clustering Algorithm (SAMCA)
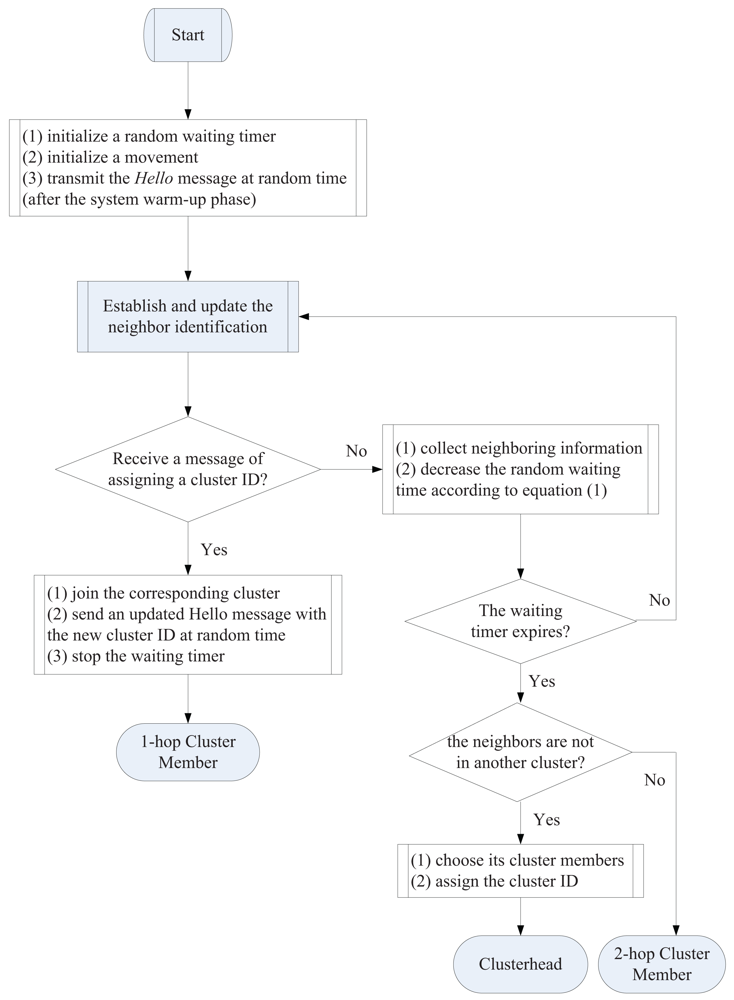
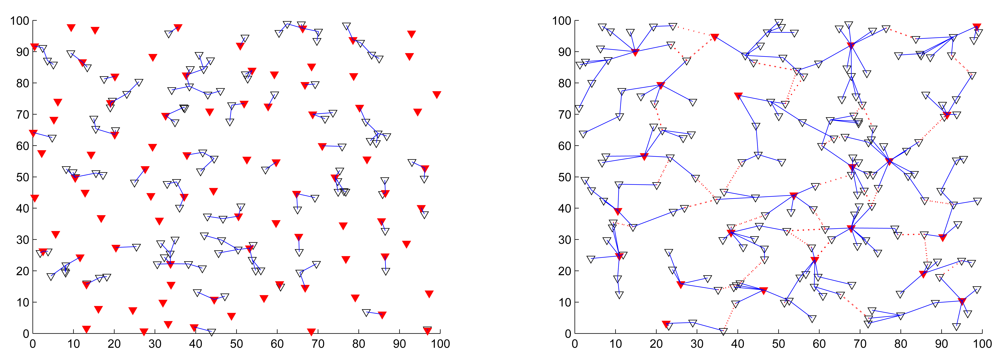
3.1. Phase I: Cluster Formation
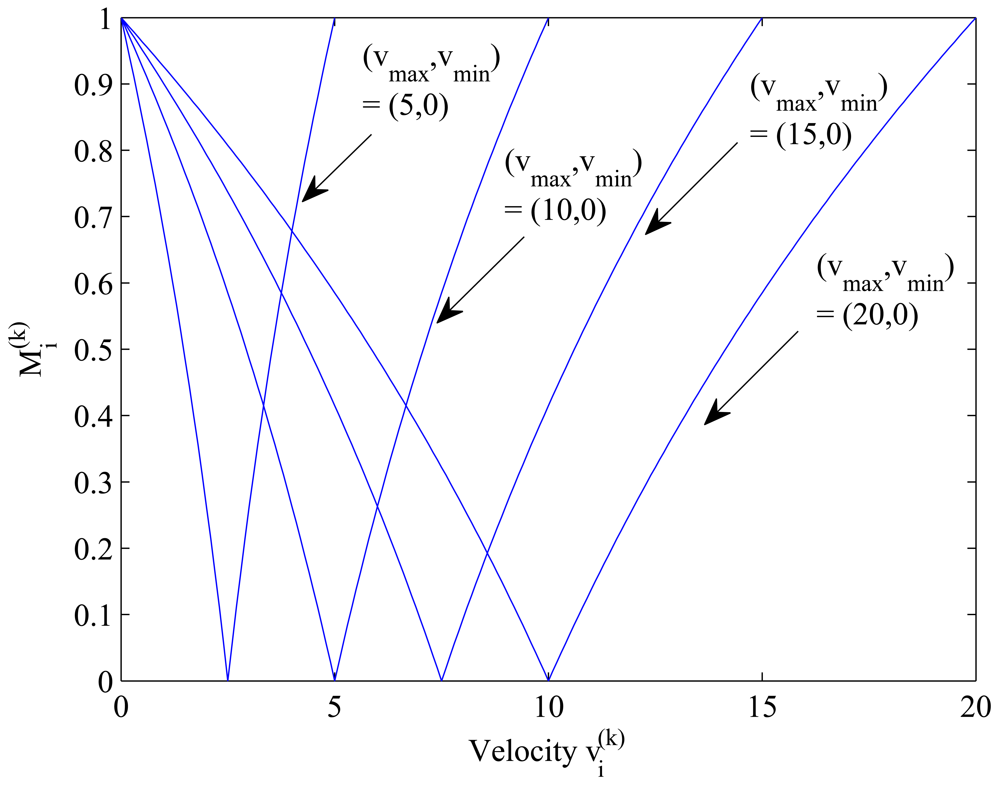
Clusterhead Selection
Gateway Selection
3.2. Phase II: Cluster Reformation
Joining/Leaving A Cluster
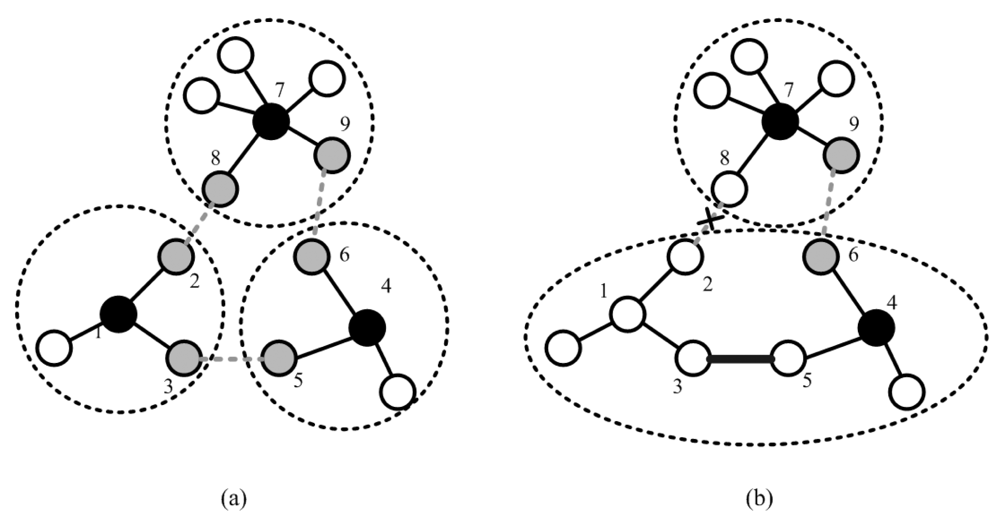
Merging Clusters
Splitting Clusters
Clusterhead Reselection
Gateway Reselection
4. Performance Analysis
4.1. Analysis of Neighboring Sensor Properties
Theorem 1
Theorem 2
4.2. Analysis of Node Density Change
Link Available Time
The Lindeberg Theorem
Theorem 3
Analysis of Density Change
4.3. Simplified Methods of Cluster Formation
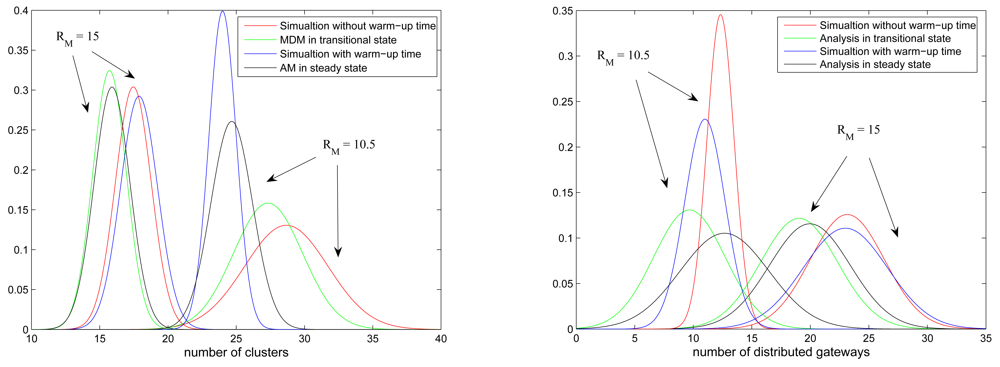
The Transitional Phase
The Steady Phase
5. Energy Consumption and Complexity Analysis
5.1. Cluster Formation
Clusterhead Selection
Gateway Selection
Complexity Analysis
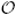 (2) rounds. For gateway selection process, the clusterhead initiates the selection operation and 2 rounds of local flooding are applied in the 2-hop cluster structure. Next, the border sensors and gateway sensors generate another 2 rounds of local flooding for broadcasting the weighting values and gateway information, respectively. Thus, the time complexity is
(2) rounds. For gateway selection process, the clusterhead initiates the selection operation and 2 rounds of local flooding are applied in the 2-hop cluster structure. Next, the border sensors and gateway sensors generate another 2 rounds of local flooding for broadcasting the weighting values and gateway information, respectively. Thus, the time complexity is
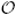 (4) rounds. Given the energy consumption analysis above, both the clusterhead selection process and the gateway selection process have a communication complexity of
(4) rounds. Given the energy consumption analysis above, both the clusterhead selection process and the gateway selection process have a communication complexity of
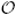 (n). Therefore, the communication complexity due to cluster formation is
(n). Therefore, the communication complexity due to cluster formation is
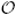 (n) +
(n) +
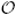 (n) =
(n) =
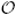 (n).
(n).5.2. Cluster Reformation
Cluster Merging/Splitting
Complexity Analysis
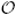 (n). Thus, the communication complexity due to cluster reformation is
(n). Thus, the communication complexity due to cluster reformation is
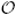 (n).
(n).6. Simulations and Discussion
6.1. Experimental Settings
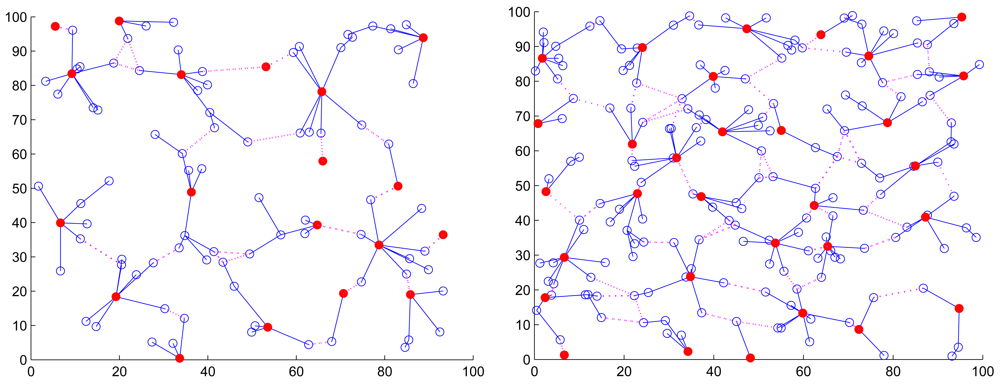
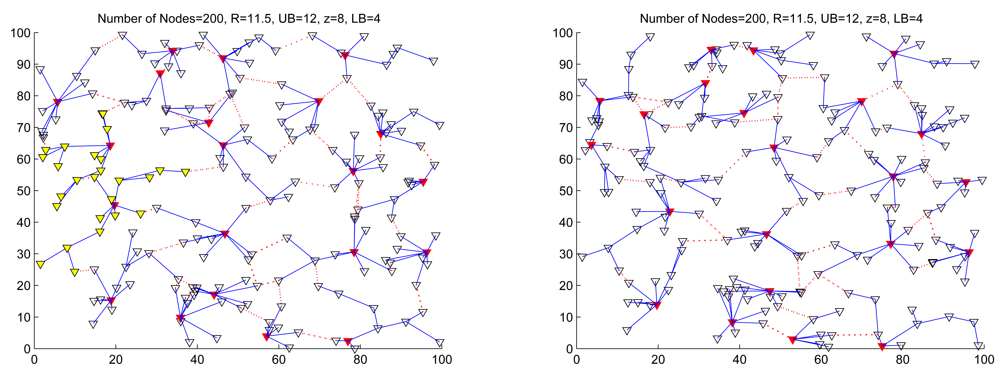
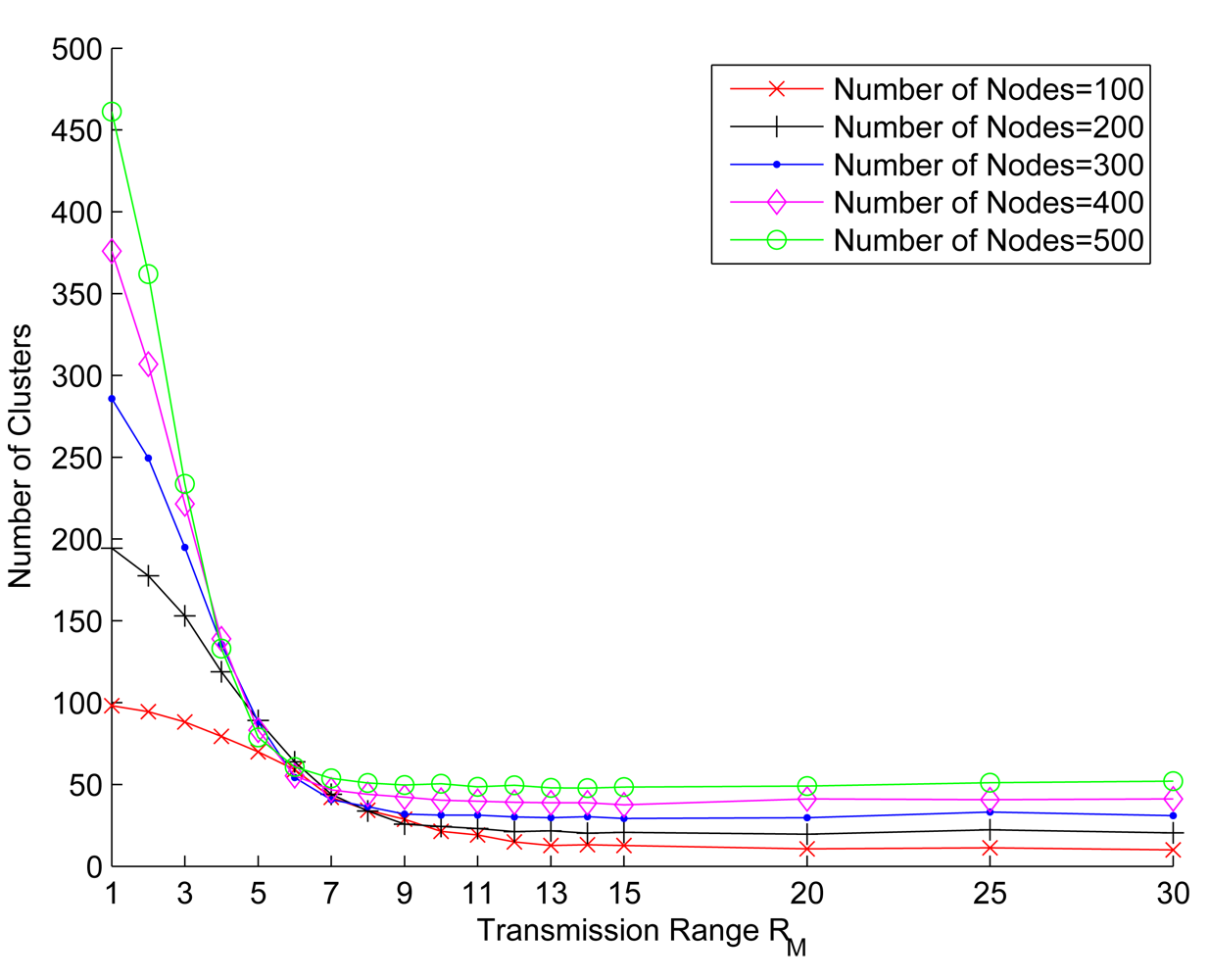
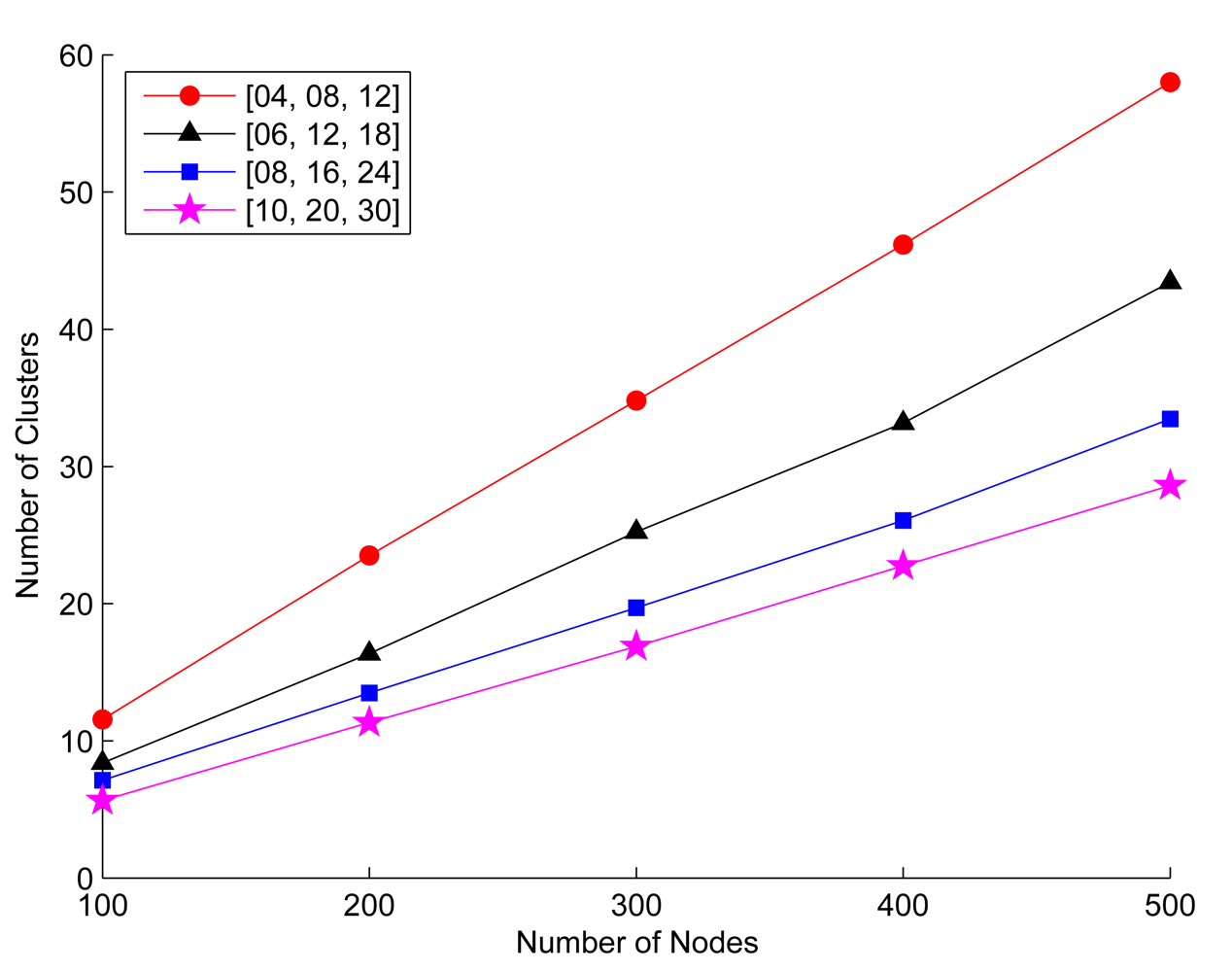
6.2. The Number of Clusters
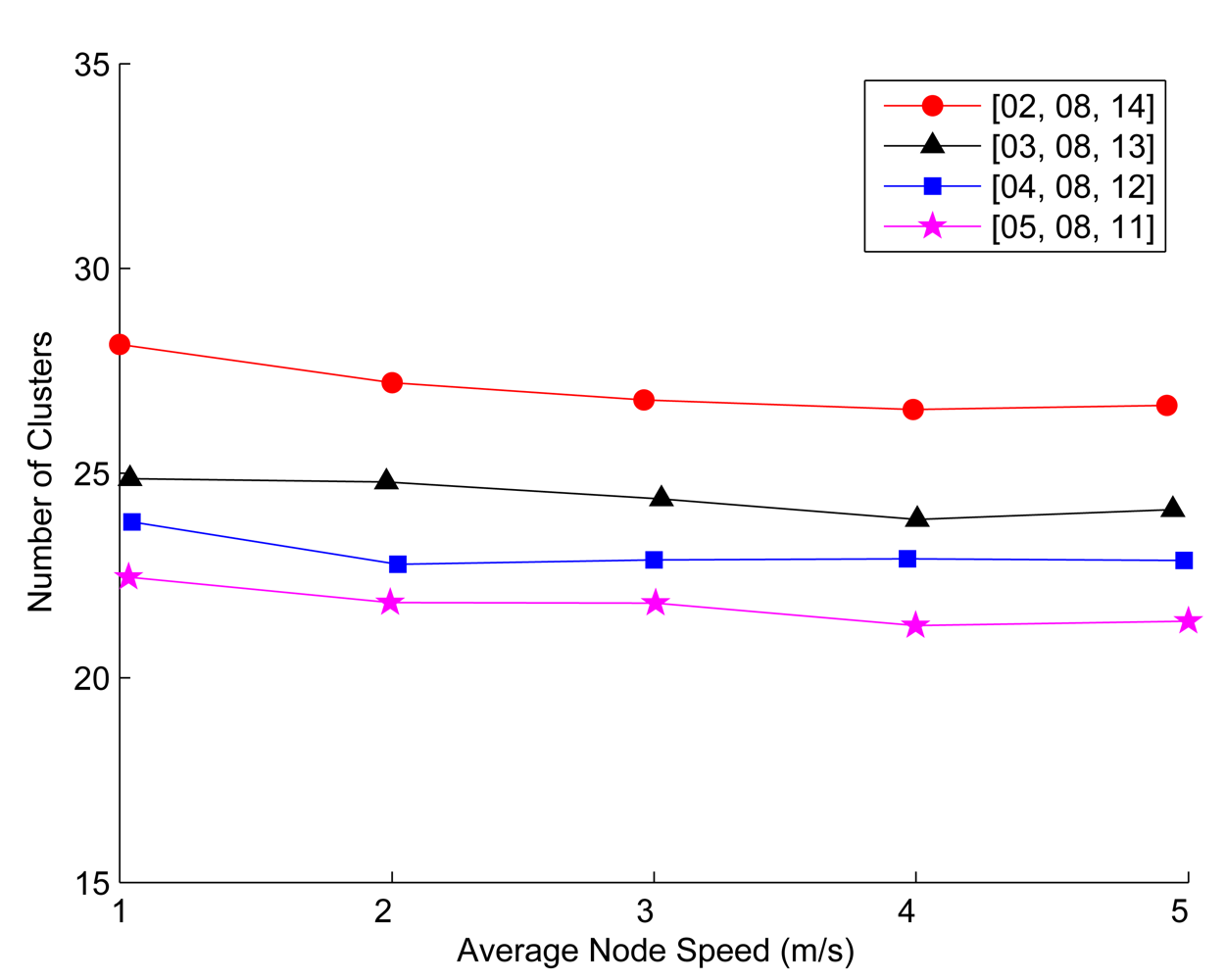
6.3. Setting Cluster Parameters
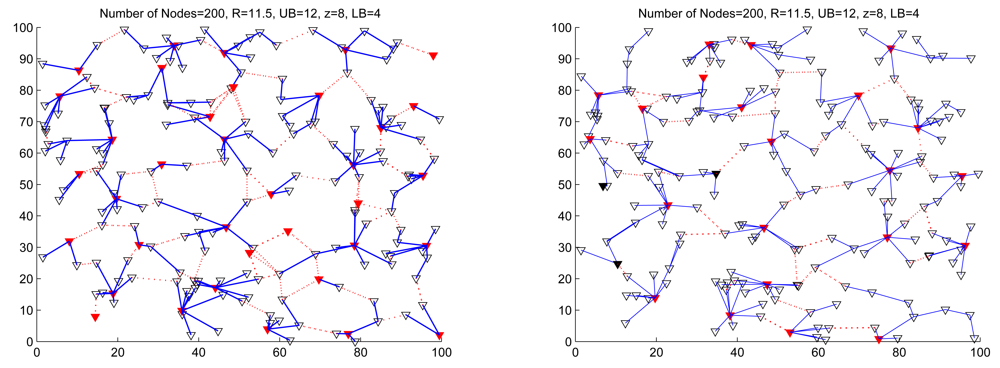
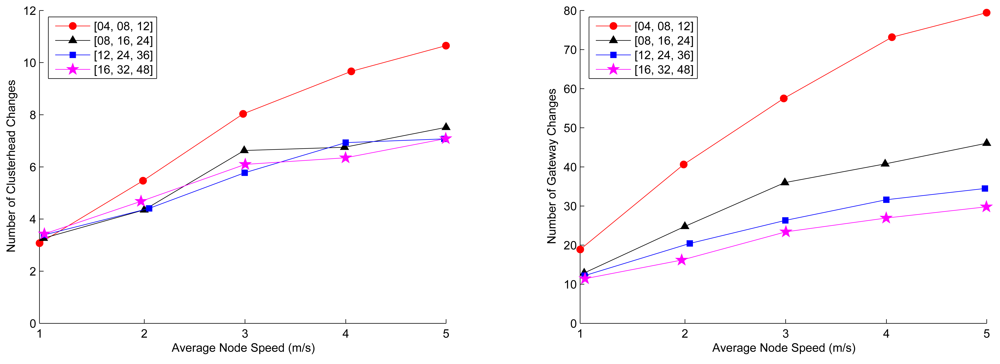
6.4. The Number of Clusterhead/Gateway Changes
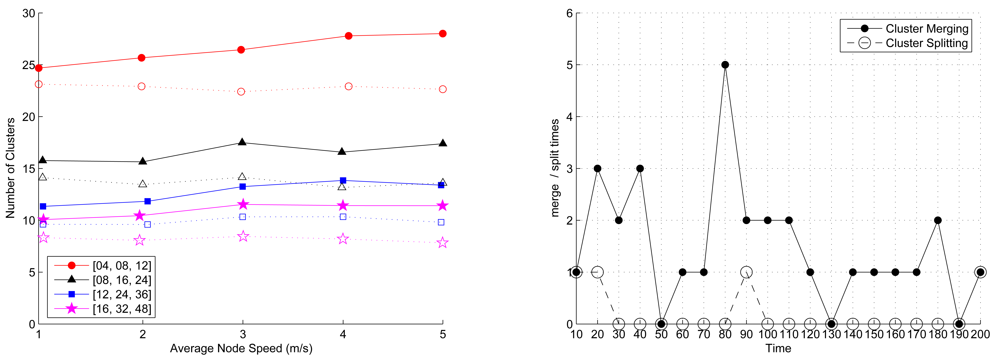
6.5. The Effect of Merging/Splitting Clusters
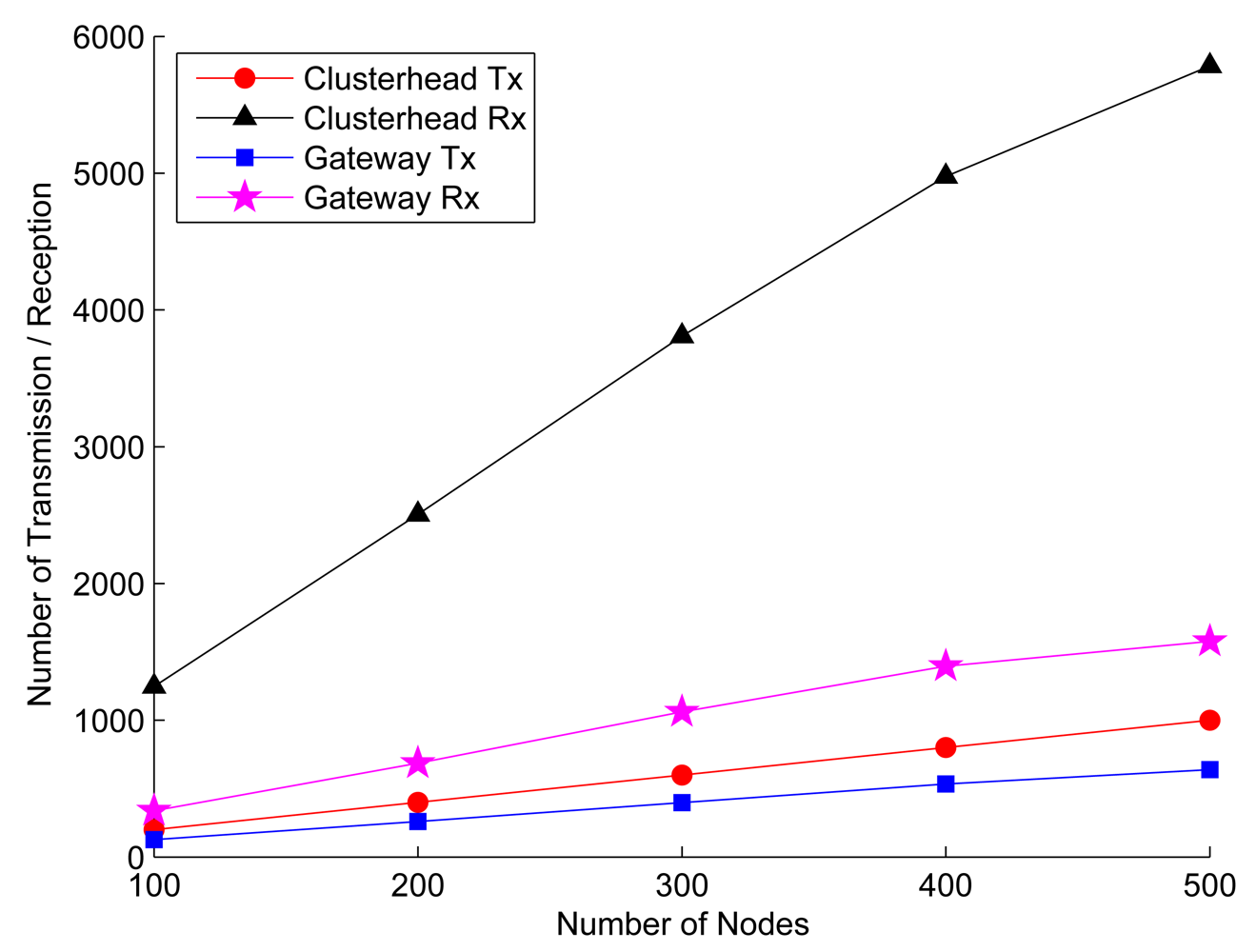
6.6. Energy Consumption
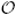 (4),
(4),
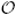 (n)) for cluster formation is demonstrated to be comparable to Lowest-ID algorithm (
(n)) for cluster formation is demonstrated to be comparable to Lowest-ID algorithm (
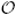 (1),
(1),
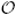 (n)) [21], the Max-Min heuristic (
(n)) [21], the Max-Min heuristic (
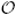 (D),
(D),
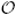 (n)) [16], and the tree-partitioning technique for grouping sensors (
(n)) [16], and the tree-partitioning technique for grouping sensors (
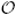 (S),
(S),
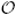 (n)) [51] in terms of the time complexity and the communication complexity, where n is the number of sensors in the network, D is the maximum number of hops that an ordinary node can be away from its clusterhead, and S is the predefined cluster size.
(n)) [51] in terms of the time complexity and the communication complexity, where n is the number of sensors in the network, D is the maximum number of hops that an ordinary node can be away from its clusterhead, and S is the predefined cluster size.6.7. Comparison of Analysis and Simulation
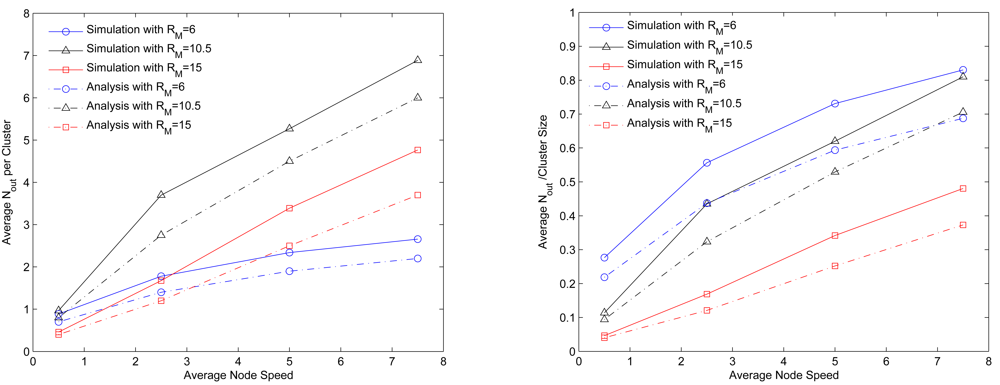
Link Dynamics (Nout)
Simulations vs. Simplified Models
6.8. Comparison of Cluster-Based Self-Organization Schemes
7. Conclusion
References and Notes
- Murthy, C. S. R.; Manoj, B. Ad Hoc Wireless Networks: Architectures and Protocols; Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Belding-Royer, E.M. Hierarchical routing in ad hoc mobile networks. Wirel. Commun. Mobile Comp. 2002, 2, 515–532. [Google Scholar]
- Lin, C.R.; Gerla, M. Adaptive clustering for mobile wireless networks. IEEE JSAC 1997, 15, 1265–1275. [Google Scholar]
- Kozat, U.C.; Kondylis, G.; Ryu, B.; Marina, M.K. Virtual dynamic backbone for mobile ad hoc networks. Proceedings of IEEE ICC, Helsinki, Finland, June 11–14, 2001; pp. 250–255.
- Pearlman, M.R.; Haas, Z.J. Determining the optimal configuration for the zone routing protocol. IEEE JSAC 1999, 17, 1395–1414. [Google Scholar]
- Iwata, A.; Chiang, C.-C.; Pei, G.; Gerla, M.; Chen, T.-W. Scalable routing strategies for ad hoc wireless netw. IEEE JSAC 1999, 17, 1369–1379. [Google Scholar]
- Chen, W.; Jain, N.; Singh, S. ANMP: Ad hoc network management protocol. IEEE JSAC 1999, 17, 1506–1531. [Google Scholar]
- Wen, C.-Y.; Sethares, W.A. Automatic decentralized clustering for wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2005, 5, 686–697. [Google Scholar]
- Santi, P. Topology Control in Wireless Ad Hoc and Sensor Networks; John-Wiley & Sons: Chichester, UK, 2005. [Google Scholar]
- Amis, A.D.; Prakash, R. Load-balancing clusters in wireless ad hoc networks. Proceedings of ASSET, Richardson, TX, USA, March 24–25, 2000; pp. 25–32.
- Basagni, S. Distributed clustering for ad hoc networks. Proceedings of International Symposium on Parallel Architectures, Algorithms and Networks, Fremantle, Australia, June 23–25, 1999; pp. 310–315.
- Bao, L.; Garcia-Luna-Aceves, J.J. Topology management in ad hoc networks. Proceedings of MobiHoc'03, Annapolis, MD, USA, June 1–3, 2004; pp. 129–140.
- Baker, D.J.; Ephremides, A.; Flynn, J.A. The design and simulation of a mobile radio network with distributed control. IEEE JSAC 1984, 2, 226–237. [Google Scholar]
- Parekh, A.K. Selecting routers in ad hoc wireless networks. Proceedings of the SBT/IEEE International Telecommunications Symposium, ITS 1994, Rio de Janeiro, Brazil, August 22–26, 1994; pp. 420–424.
- Gerla, M.; Tsai, T.-C. Multicluster, mobile, multimedia radio network. Wirel. Netw. 1995, 1, 255–265. [Google Scholar]
- Amis, A.D.; Prakash, R.; Vuong, T. H.P.; Huynh, D.T. Max-min d-cluster formation in wireless ad hoc networks. Proceedings of IEEE INFOCOM, Tel-Aviv, Israel, March 26–30, 2000; pp. 32–41.
- Chiasserini, C.F.; Chlamtac, I.; Monti, P.; Nucci, A. Energy efficient design of wireless ad hoc networks. Proceedins of European Wireless, Florence, Italy, February 25–27, 2002; pp. 376–386.
- Cardei, M.; Wu, J.; Yang, S.-H. Topology control in ad hoc wireless networks using cooperative communication. IEEE Trans. Mob. Comput. 2006, 5, 711–724. [Google Scholar]
- Ye, M.; Li, C.; Chen, G.; Wu, J. An energy efficient clustering scheme in wireless sensor networks. Int. J. Ad Hoc Sens. Wirel. Netw. 2005, 1, 1–21. [Google Scholar]
- Younis, O.; Fahmy, S. Heed: a hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks. IEEE Trans. Mob. Comput. 2004, 3, 366–379. [Google Scholar]
- Ephremides, A.; Wieselthier, J.; Baker, D. A design concept for reliable mobile radio network with frequency hopping signaling. Proc. IEEE 1987, 75, 56–79. [Google Scholar]
- Liu, C.-M.; Lee, C.-H.; Wang, L.-C. Distributed clustering algorithms for data-gathering in wireless mobile sensor networks. J. Paral. Distrib. Comput. 2007, 67, 1187–1200. [Google Scholar]
- Venkataraman, G.; Emmanuel, S.; Srikanthan, T. A novel distributed cluster maintenance technique for high mobility ad-hoc networks. Proceedings of the First International Symposium on Wireless Communication Systems, Mauritius, September 20–22, 2004; pp. 225–229.
- Er, I.I.; Seah, W.K.G. Mobility-based d-hop clustering algorithm for mobile ad hoc networks. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC'04), Atlanta, GA, USA, March 21–25, 2004; pp. 2359–2364.
- Wei, D.; Chan, H.A. Clustering Ad Hoc Networks: Schemes and Classifications. Proceedings of IEEE SECON, Restone, VA, USA, September 25–28, 2006; pp. 920–926.
- Nain, P.; Towsley, D.; Liu, B.Y.; Liu, Z. Properties of random direction models. Proceedings of IEEE INFOCOM, Miami, FL, USA, March 13–17, 2005; pp. 1897–1907.
- Joa-Ng, M.; Lu, I.-T. A peer-to-peer zone-based two-level link state routing for mobile ad hoc networks. IEEE J. Sel. Areas Commun. 1999, 17, 1415–1425. [Google Scholar]
- Heinzelman, W.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless micro sensor networks. Proceedings of the Hawaii International Conference on System Sciences (HICSS'00), Maui, HI, USA, January 4–7, 2000; pp. 8020–8029.
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. An application specific protocol architecture for wireless microsensor network. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar]
- Handy, M.; Haase, M.; Timmermann, D. Low energy adaptive clustering hierarchy with deterministic cluster-head selection. Proceedings of the 4th International Workshop on Mobile and Wireless Communications Network, Stockholm, Sweden, September 9–11, 2002; pp. 368–372.
- Halgamuge, M.N.; Guru, S.M.; Jennings, A. Energy efficient cluster formation in wireless sensor networks. Proceedings of the 10th International Conference on Telecommunications, Tahiti, Papeete, French Polynesia, Febuary 23–March 1, 2003; pp. 1571–1576.
- Basu, P.; Khan, N.; Little, T.D.C. Mobility based metric for clustering in mobile ad hoc networks. Proceedings of Workshop on Distributed Computing Systems, Phoenix, AZ, USA, April 16–19, 2001; pp. 413–418.
- Chatterjee, M.; Das, S.K.; Turgut, D. Wca: A weighted clustering algorithm for mobile ad hoc networks. J. Cluster Comput. 2002, 5, 193–204. [Google Scholar]
- Lundelius, J.; Lynch, N. An upper and lower bound for clock synchronization. Inform. Contr. 1984, 62, 190–204. [Google Scholar]
- Turgut, D.; Robinson, K.; Chatterjee, M. Entropy based clustering in mobile ad hoc networks. JUCI 2007, 1, 101–109. [Google Scholar]
- Basagni, S.; Mastrogiovanni, M.; Panconesi, A.; Petrioli, C. Localized protocols for ad hoc clustering and backbone formation: A performance comparison. IEEE Trans. Paral. Distrib. Sys. 2006, 17, 292–306. [Google Scholar]
- McDonald, A.B.; Znati, T. A mobility based framework for adaptive clustering in wireless ad-hoc networks. IEEE J. Sel. Area. Commun. 1999, 17, 1466–1487. [Google Scholar]
- Ohta, T.; Inoue, S.; Kakuda, Y. An adaptive multihop clustering scheme for highly mobile ad hoc networks. Proceedins of the Sixth International Symposium on Autonomous Decentralized Systems (ISADS'03), Pisa, Italy, April 9–11, 2003; pp. 293–300.
- Nocetti, F.; Gonzalez, J.; Stojmenovic, I. Connectivity based k-hop clustering in wireless networks. Telecommun. Syst. 2003, 22, 205–220. [Google Scholar]
- Fernandess, Y.; Malkhi, D. K-clustering in wireless ad-hoc networks. Proceedins of the 2nd ACM Workshop on Principles of Mobile Computing (POMC'02), Toulouse, France, October 30–31, 2002; pp. 31–37.
- Lin, H.C.; Chu, Y.H. A clustering technique for large multihop mobile wireless networks. Proceedings of the IEEE Vehicular Technology Conference, Tokyo, Japan, May 15–18, 2000; pp. 15–18.
- Chiang, C.-C.; Wu, H.-K.; Liu, W.; Gerla, M. Routing in clustered multihop, mobile wireless networks with fading channel. Proceedings of IEEE Singapore International Conference on Networks (SICON), Kent Ridge, Singapore, September 9–12, 1997; pp. 197–211.
- Lehsaini, M.; Guyennet, H.; Feham, M. A novel cluster-based self-organization algorithm for wireless sensor networks. Proceedins of International Symposium on Collaborative Technologies and Systems (CTS 2008), Irvine, CA, USA, May 19-23, 2008; pp. 19–26.
- Yu, J.Y.; Chong, P.H.J. A survey of clustering schemes for mobile ad hoc networks. IEEE Commun. Surv. Tutorial 2005, 7, 32–48. [Google Scholar]
- Dressler, F. Self-Organization in Sensor and Actor Networks; John-Wiley & Sons: NY, USA, 2007. [Google Scholar]
- Wen, C.-Y.; Sethares, W.A. Adaptive decentralized re-clustering for wireless sensor networks. Proceedings of IEEE International Conference on Systems, Man, and Cybernetics, Taipei, Taiwan, October 8–11, 2006; pp. 2709–2716.
- Bai, F.; Sadagopan, N.; Helmy, A. IMPORTANT: a framework to systematically analyze the impact of mobility on performance of routing protocols for adhoc networks. Proceedings of IEEE INFOCOM, San Franciso, CA, USA, March 30–April 3, 2003; pp. 825–835.
- Yu, D.; Li, H. Influence of mobility models on node distribution in ad hoc networks. Proceedings of ICCT2003, Beijing, China, April 9–11, 2003; pp. 985–989.
- Billingsley, P. Probability and Measure; John-Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Yu, D.; Li, H.; Gruber, I. Path availability in ad hoc network. Proceedings of the 10th International Conference on Telecommunications, Tahiti, Papeete, French Polynesia, Febuary 23–March 1, 2003; pp. 383–387.
- Venkataraman, G.; Emmanuel, S.; Thambipillai, S. Size-restricted cluster formation and cluster maintenance technique for mobile ad hoc networks. Int. J. Netw. Manag. 2007, 17, 171–194. [Google Scholar]




|
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wen, C.-Y.; Tang, H.-K. Autonomous Distributed Self-Organization for Mobile Wireless Sensor Networks. Sensors 2009, 9, 8961-8995. https://doi.org/10.3390/s91108961
Wen C-Y, Tang H-K. Autonomous Distributed Self-Organization for Mobile Wireless Sensor Networks. Sensors. 2009; 9(11):8961-8995. https://doi.org/10.3390/s91108961
Chicago/Turabian StyleWen, Chih-Yu, and Hung-Kai Tang. 2009. "Autonomous Distributed Self-Organization for Mobile Wireless Sensor Networks" Sensors 9, no. 11: 8961-8995. https://doi.org/10.3390/s91108961





