Clock Synchronization in Wireless Sensor Networks: An Overview
Abstract
:1. Introduction
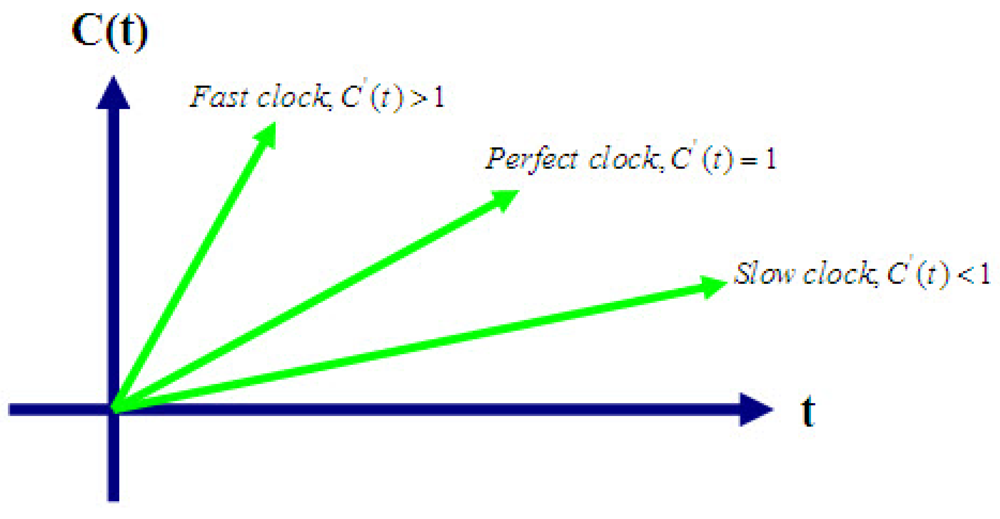
2. General Clock Model
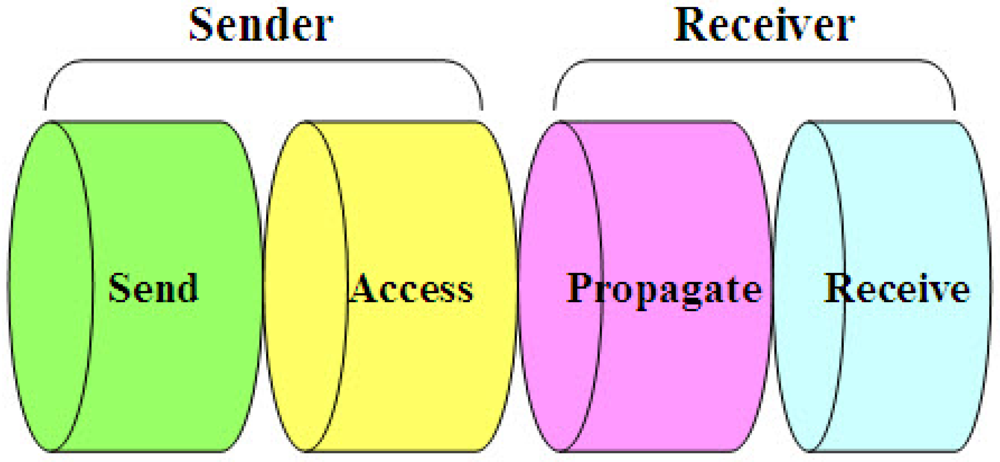
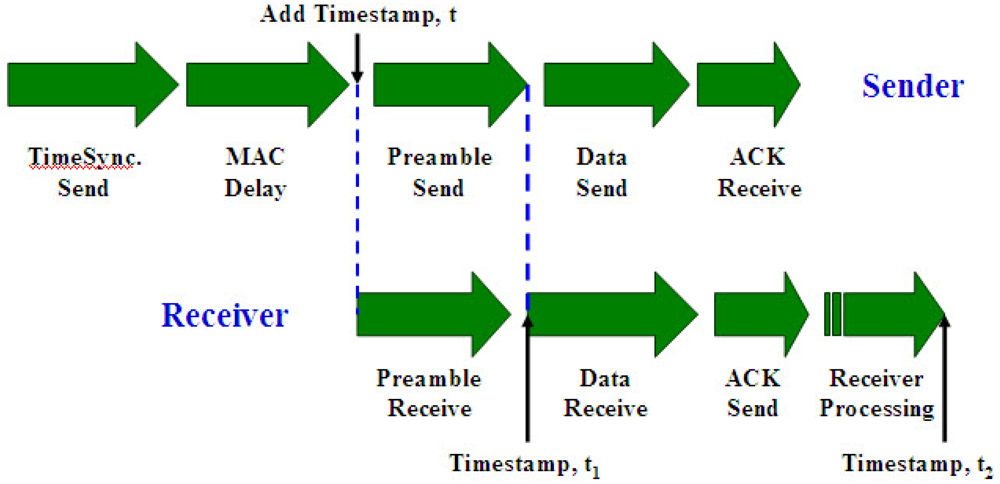
- Send Time: This is the time spent by the sender to construct the message, including kernel protocol processing and variable delays introduced by the operating system, e.g., context switches and system call overhead incurred by the synchronization application. This time also accounts for the time needed to transfer the message from the host to its network interface.
- Access Time: This is the delay incurred while waiting for access to the transmission channel. Access Time is very MAC (Medium Access Control)-specific. Contention-based MACs must wait for the channel to be clear before transmitting, and retransmit in case that a collision happened. Wireless RTS/CTS schemes such as those in 802.11 networks need an exchange of control packets before data transmission. TDMA channels require the sender to wait for its slot before transmitting.
- Propagation Time: This is the time for the message to travel from the sender to the destination node through the channel since it left the sender. In case that the sender and the receiver share access to the same physical media (e.g., neighbors in an ad-hoc wireless network or a LAN), this time is very small as it is simply the physical propagation time of the message through the medium. In contrast, Propagation Time dominates the delay in wide-area networks, where it includes queuing delay and switching delay at each router as the message transits through the network.
- Receive Time: This is the time for the network interface on the receiver side to get the message and notify the host of its arrival. This is typically the time required for the network interface to generate a message reception signal. If the arrival time is time-stamped at a low enough level in the host's operating system kernel (e.g., inside of the network driver's interrupt handler), Receive Time does not include the overhead of system calls, context switches, or even the transfer of the message from the network interface to the host and so can be kept small.
3. Clock Synchronization Protocols for Wireless Sensor Networks
- Synchronization issues
- Master-slave versus peer-to-peer synchronization
- -
- Master-slave: This protocol assigns one node as the master and the other nodes as slaves. The slave nodes regard the local clock reading of the master node as the reference time and try to synchronize with the master. The representative examples in this class are the protocol of Mock et al. [41] and Ping's protocol [42].
- -
- Peer-to-peer: Any node can communicate directly with other nodes in the network. Such an approach removes the risk of the master node failure. Therefore these class of protocols are more flexible but also more uncontrollable. RBS [25] and the time diffusion protocol (TDP) [43] assume peer-to-peer configurations.
- Internal synchronization versus external synchronization
- -
- Internal synchronization: A global time base is not available from within the system and therefore the protocol attempts to minimize the maximum difference between the readings of local clocks of the sensors. The protocol of Mock et al. [41] belongs to this scheme.
- -
- External synchronization: A standard time such as UTC (Universal Time Controller) is available and is used as a reference time. The local clocks of sensors seek to synchronize to this reference time. NTP [23] is the representative example.
- Probabilistic versus deterministic synchronization
- -
- Probabilistic synchronization: This method gives a probabilistic guarantee on the maximum clock offset with a failure probability that can be bonded or determined. In a wireless environment where energy is scarce, this can be very expensive. The protocol of PalChaudhuri et al. [44] is a probabilistic variation of RBS [25].
- -
- Deterministic synchronization: Arvind [45] defined deterministic algorithms as those guaranteeing an upper bound on the clock offset with certainty. Most protocols are deterministic and so are RBS and TDP.
- Sender-to-receiver versus receiver-to-receiver versus receiver-only synchronization
- -
- Sender-to-receiver synchronization (SRS): The sender node periodically sends a message with its local time as a timestamp to the receiver and then the receiver synchronizes with the sender using the timestamp received from the sender.
- -
- Receiver-to-receiver synchronization (RRS): This method uses the property that if any two receivers receive the same message in a single-hop transmission, they receive it at approximately the same time. Receivers exchange the time at which they received the same message and compute their offset based on the difference in reception times.
- -
- Receiver-only synchronization (ROS): A group of nodes can be simultaneously synchronized by only listening to the message exchanges of a pair of nodes.
- Clock correction versus untethered clocks
- -
- Clock correction: The local clocks of nodes participating in the network are corrected either instantaneously or continually to keep the entire network synchronized. Timing-sync protocol for sensor networks (TPSN) [29] uses this approach.
- -
- Untethered clocks: Every node maintains its own clock as it is, and keeps a time-translation table relating its clock to the clock of the other nodes. Local timestamps are compared using the table. A global timescale is maintained in this way with the clocks untethered. RBS belongs to this approach.
- Pairwise Synchronization versus network-wide synchronization
- -
- Pairwise synchronization: The protocols are primarily designed to synchronize two nodes, although they usually can be extended to deal with the synchronization of a group of nodes.
- -
- Network-wide synchronization: The protocols are mainly designed to synchronize a large number of nodes in the network.
- Application-dependent features
- Single-hop versus multi-hop networks
- -
- Single-hop communication: A sensor node can directly communicate and exchange messages with any other sensor in a single-hop network. The protocol of Mock et al. [41] is a representative example. However, it can be extended to multi-hop communication.
- -
- Multi-hop communication: Sensors in a domain communicate with sensors in another domain via an intermediate sensor relating to both domains. Communication can also occur as a sequence of hops through a chain of pairwise-adjacent sensors. RBS and TDP can be suitably extended to deal with multi-hop communication.
- Stationary networks versus mobile networks
- -
- Stationary networks: Sensors do not move. The protocols such as RBS and TPSN, and Mock et al.'s protocol are geared to stationary networks.
- -
- Mobile networks: Sensors have the ability to move, and they connect with other sensors only when entering the geographical scope of those sensors. The changing topology is often a problem because it needs resynchronization of nodes and re-computation of the neighborhoods or clusters.
- Reference Broadcast Synchronization (RBS) [25]
- Timing-Sync Protocol for Sensor Networks (TPSN) [29]
- Delay Measurement Time Synchronization for Wireless Sensor Networks (DMTS) [42]
- Flooding Time Synchronization Protocol (FTSP) [46]
- Probabilistic clock synchronization service in sensor networks [44]
- Time Diffusion Synchronization Protocol (TDP) [43]
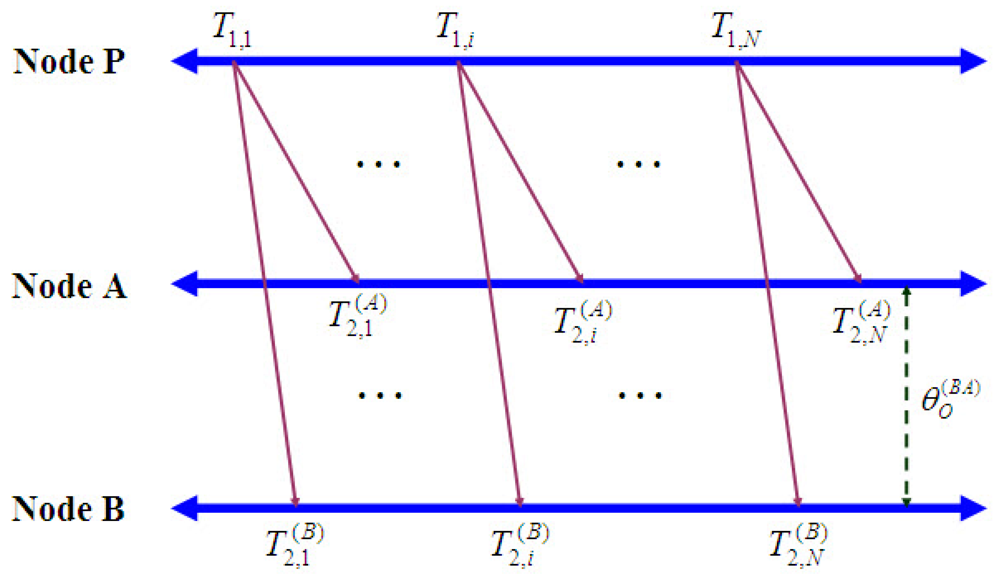
3.1. Reference Broadcast Synchronization [25]
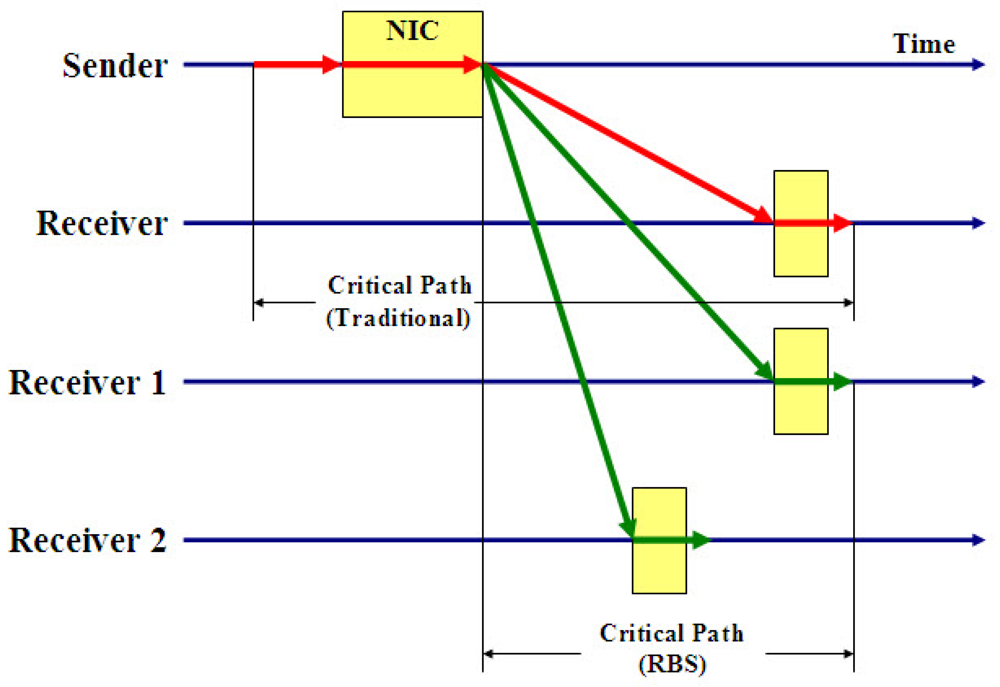
- The largest sources of nondeterministic latency can be eliminated from the critical path by using the broadcast channel to synchronize receivers with one another. This leads to significantly better precision synchronization than algorithms that measure round-trip delay.
- Multiple broadcasts enable tighter synchronization because residual errors tend to follow well-behaved distributions, and also allow estimation of clock skew and extrapolation of past phase offsets.
- Outliers and lost packets are handled gracefully; the best fit line can be drawn even if some points are missing.
- RBS allows nodes to construct local timescales. This is useful for sensor networks and other applications that require synchronized time but may not have an absolute time reference available.
- This protocol is not applicable to point-to-point networks; a broadcasting medium is needed.
- For a single-hop network of n nodes, RBS requires O(n2) message exchanges, which is computationally expensive in the case of large scale networks.
- Convergence time, which is the time taken to synchronize the network, can be high because of the large number of message exchanges.
- The reference node is left unsynchronized in this protocol. In some sensor networks, if the reference node needs to be synchronized, it will result in a considerable waste of energy.Now we take a look at a method for joint estimation of clock offset and skew in RBS.
3.1.1 Estimation of clock offset and clock skew
3.2. Timing-Sync Protocol for Sensor Networks [29]
Level Discovery Phase
Synchronization Phase
- It is scalable and the synchronization precision does not deteriorate significantly as the size of the network increases.
- Network-wide synchronization is computationally less expensive in comparison with such protocols as NTP [23].
- Energy conservation is not so effective since a physical clock correction needs to be performed on the local clocks of sensors while achieving synchronization.
- The protocol is not suitable for applications with highly mobile nodes because it requires a hierarchical infrastructure.
- TPSN does not support multi-hop communication.
3.2.1 Estimation of Clock Offset
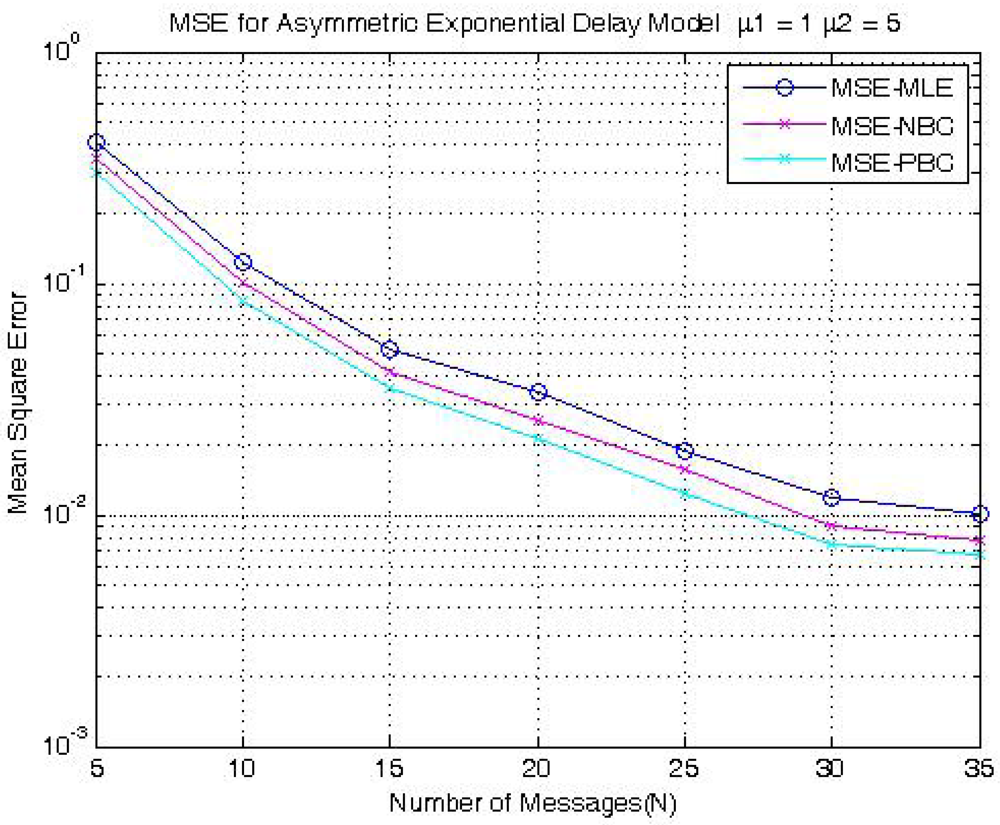
3.2.2 Clock Offset Estimation Using Bootstrap Bias Correction
The Nonparametric Bootstrap
- Step 0. Conduct the experiment to obtain the random sample X = {X1, X2,… Xn} and calculate the estimate θ̂ from the sample X.
- Step 1. Construct the empirical distribution F̂, which puts equal mass 1/n at each observation X1 = x1, X2 = x2,… Xn = xn.
- Step 2. From F̂, draw a sample , called the bootstrap resample.
- Step 3. Approximate the distribution of θ̂ by the distribution of θ̂* derived from the bootstrap resample X*.
The Parametric Bootstrap
The Bootstrap Estimate of Bias
◆ Bias Correction
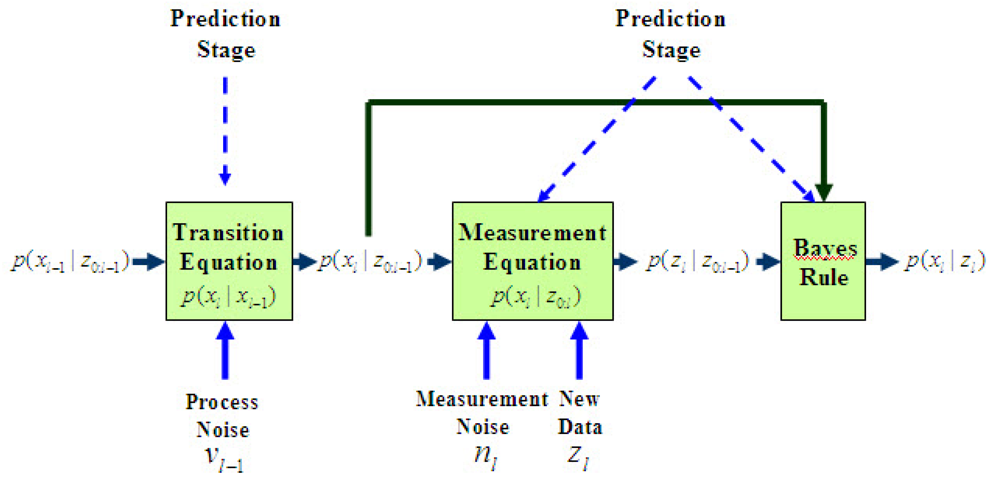
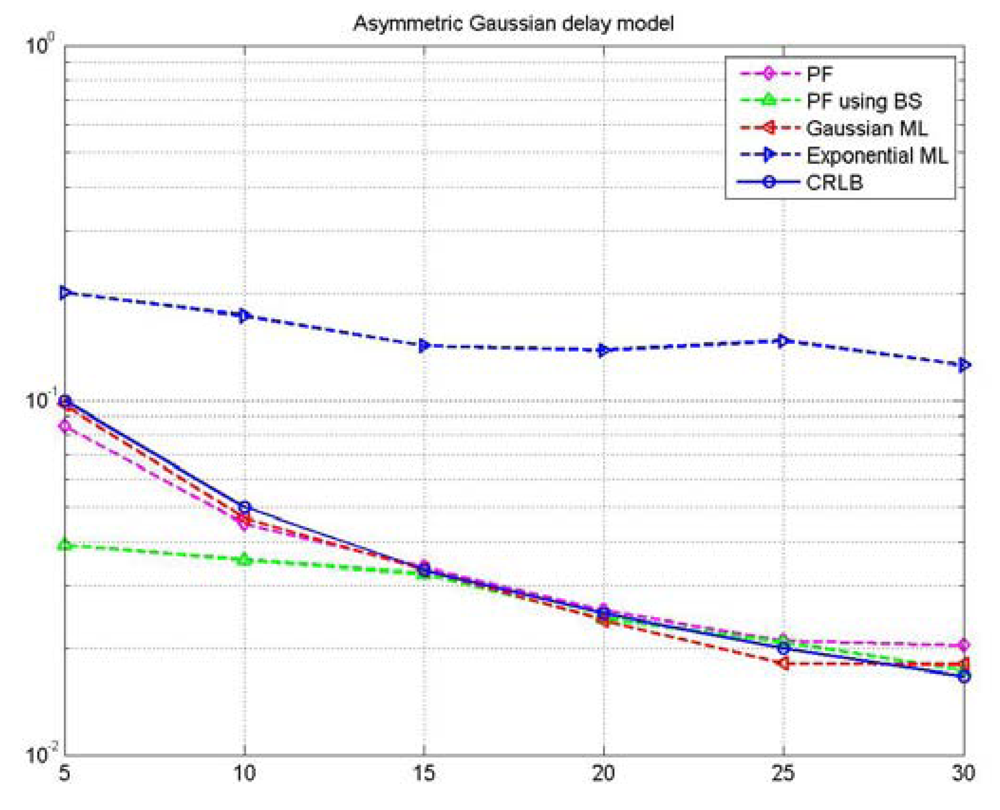
3.2.3 Clock Offset Estimation via Particle Filtering
| Algorithm 1. PF algorithm. |
| Initialize weights (k = 0) |
| • Draw |
| Step.1) Prediction : predict via the state model (23) |
| Step.2) Measurement Update : |
| • Evaluate the weights according to the likelihood function as (30), i = 1:N |
| • Normalize the weights |
| Step.3) Resampling Stage |
| • If Neff < Nth |
| - take N samples with replacement from the set where the probability to take sample i is . Let . |
| Step.4) Output : MMSE |
| Step.5) Continue: set k → k + 1 and iterate to Step. 2. |
| Algorithm 2. PF with BS algorithm. |
| Conduct the experiment to obtain the random sample Z = {Z1, ⋯ ZK} and calculate the estimate θ̂ from the sample Z. |
| Step 1) Construct the empirical distribution Ĥ, which puts equal mass 1/n at each observation {Z1 = z1, ⋯, Zn = zn}. |
| Step 2) From Ĥ, draw a sample , called the bootstrap resample. |
| Step 3) From the bootstrap resample Z*, estimate the clock offset x̂ by PF. |
3.3. Delay Measurement Time Synchronization for Wireless Sensor Networks (DMTS) [42]
3.4. Flooding Time Synchronization Protocol (FTSP) [46]
3.5. Probabilistic Clock Synchronization [44]
- A probabilistic guarantee reduces both the number of messages exchanged among nodes and the computational load on each node.
- There is a tradeoff between synchronization accuracy and resource cost.
- This protocol supports multi-hop networks, which span several domains.
- In case of safety-critical applications (for example, nuclear plant monitoring), a probabilistic guarantee on accuracy may not be proper.
- The protocol is sensitive to message losses. Nevertheless, it does not consider provisions for message losses.
3.6. Time Diffusion Synchronization Protocol [43]
- This protocol is tolerant to message losses.
- A network-wide equilibrium time is achieved across all nodes and involves all the nodes in the synchronization process.
- The diffusion does not count on static level-by-level transmissions and thus it exhibits flexibility and fault-tolerance.
- The protocol is geared towards mobility.
- The convergence time tends to be high in case that no external precise time servers are used.
- Clocks may run backward. This can happen whenever a clock value is suddenly adjusted to a lower value.
4. Conclusions
References and Notes
- Hill, J.; Horton, M.; Kling, R.; Krishnamurthy, L. The platforms enabling wireless sensor networks. Commun. ACM 2004, 6, 41–46. [Google Scholar]
- The Intel Mote. Intel Corporation Homepage. http://www.intel.com/research/exploratory/motes.htm (accessed November 10, 2008).
- SmartDust. Autonomous sensing and communication in a cubic millimeter Homepage. http://robotics.eecs.berkeley.edu/~pister/SmartDust/ (accessed November 10, 2008).
- TinyOS. An operating system for networked sensors Homepage. http://www.tinyos.net (accessed November 10, 2008).
- Akyildiz, I; Su, W.; Sankarasubramanian, Y; Cayirci, E. Wireless sensor networks: a survey. Comput. Netw. 2002, 4, 393–422. [Google Scholar]
- Distributed Surveillance Sensor Network. ONR SPAWAR Systems Center, San Diego Homepage. http://www.spawar.navy.mil/robots/undersea/dssn/dssn.html (accessed November 10, 2008).
- CENS: Monitoring of marine microorganisms Homepage. http://www.cens.ucla.edu/Research/Applications/momm.htm (accessed November 10, 2008).
- CENS: Seismic monitoring and structural response Homepage. http://www.cens.ucla.edu/Research/Applications/seismicmonitor.htm (accessed on November 15, 2008).
- Szewczyk, R.; Osterweil, E.; Polastre, J.; Hamilton, M.; Mainwaring, A.; Estrin, D. Habitat monitoring with sensor networks. Commun. ACM 2004, 6, 34–40. [Google Scholar]
- Johnson, P.; et al. Remote continuous physiological monitoring in the home. J. Telemed. Telecare. 1996, 2, 107–113. [Google Scholar]
- Akyildiz, I.F.; Akan, O.; Chen, C.; Fang, J.; Su, W. InterPlaNetary Internet: state-of-the-art and research challenges. Comput. Netw. 2003, 2, 75–112. [Google Scholar]
- Burleigh, S.; Cerf, V.; Durst, R.; Fall, K.; Hooke, A.; Scott, K.; Weiss, H. The InterPlaNetary Internet: a communications infrastructure for Mars exploration. 53rd International Astronautical Congress, The World Space Congress, Houston, Texas, October 2002.
- Lemmerman, L.; Delin, K.; Hadaegh, F.; Lou, M.; Bhasin, K.; Bristow, J.; Connerton, R.; Pasciuto, M. Earth science vision: platform technology challenges. Proceedings of International Geoscience and Remote Sensing Symposium (IGARSS 2001), Sydney, Australia; 2001. [Google Scholar]
- The sensor web project, NASA Jet Propulsion Laboratory Homepage. http://sensorwebs.jpl.nasa.gov (accessed November 10, 2008).
- The deep space sensor network, NASA Jet Propulsion Laboratory Homepage. http://deepspace.jpl.nasa.gov/dsn (accessed November 15, 2008).
- Space Missions Homepage. http://www.galacticsurf.net/missionsGB.htm (accessed November 15, 2008).
- Chart on the Web. Maryland Department of Transportation Homepage. http://www.chart.state.md.us/ (accessed November 10, 2008).
- Li, Q.; DeRosa, M.; Rus, D. Distributed algorithms for guiding navigation across a sensor network. Proceedings of Ninth Annual International Conference on Mobile Computing and Networking, San Diego, CA, USA, September 2003; pp. 313–326.
- Want, R; Hopper, A.; Falcao, V.; Gibbons, J. The active badge location system. ACM Trans. Inf. Syst. 1992, 1, 91–102. [Google Scholar]
- Werb, J.; Lanzl, C. Designing a positioning system for finding things and people indoors. IEEE Spectr. 1998, 9, 71–78. [Google Scholar]
- Sundararaman, B.; et al. Clock synchronization for wireless sensor networks: a survey. Ad Hoc Netw. 2005, 3, 281–323. [Google Scholar]
- Zhao, F.; Guibas, L. Wireless Sensor Networks: An Information Processing Approach.; Morgan Kaufmann: San Francisco, CA, USA, 2004; pp. 107–117. [Google Scholar]
- Mills, D.L. Internet time synchronization: the network time protocol. IEEE Trans. Commun. 1991, 10, 1482–1493. [Google Scholar]
- Bulusu, N.; Jha, S. Wireless Sensor Networks: A Systems Perspective; Artech House: Norwood MA, USA, 2005. [Google Scholar]
- Elson, J.; Girod, L.; Estrin, D. Fine-grained network time synchronization using reference broadcasts. Procedings. of the Fifth Symposium on Operating System Design and Implementation, Boston, MA, USA, Dec. 2002.
- Elson, J.; Estrin, D. Time synchronization for wireless sensor networks. Proceedings of International Parallel and Distributed Processing Symposium (IPDPS 2001), Workshop on Parallel and Distributed Computing Issues in Wireless Networks and Mobile Computing, San Francisco, CA, USA, April 2001.
- Noh, K.L.; Serpedin, E.; Qaraqe, K. A new approach for time synchronization in wireless sensor networks: pairwise broadcast synchronization. IEEE Trans. Wireless Commun. 2008, 9, 3318–3322. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing, Vol. I. Estimation Theory.; Prentice Hall: New York, NY, USA, 1993. [Google Scholar]
- Ganeriwal, S.; Kumar, R; Srivastava, M.B. Timing-sync protocol for sensor networks. Proceedings of the 1st international conference on Embedded networked sensor systems, Los Angeles, CA, USA, Nov. 2003; pp. 138–149.
- Verissimo, P.; Rodrigues, L.; Casimiro, A. CesiumSpray: a precise and accurate global time service for large-scale systems. Journal of Real-Time Systems 1997, 3, 243–294. [Google Scholar]
- Narasimhan, S.; Kunniyur, S.S. Effect of network parameters on delay in wireless ad-hoc networks. University of Pennsylvania Technical Report 2004. [Google Scholar]
- Papoulis, A. Probability, Random Variables and Stochastic Processes., 3rd Ed ed; McGraw-Hill: Columbus, OH, USA, 1991. [Google Scholar]
- Leon-Garcia, A. Probability and Random Processes for Electrical Engineering., 2nd Ed ed; Addison-Wesley: Reading, MA, USA, 1993. [Google Scholar]
- Paxson, V. On calibrating measurements of packet transit times. ACM Sigmetrics Perf. Eval. Rev. 1998, 26, 11–21. [Google Scholar]
- Abdel-Ghaffar, H.S. Analysis of synchronization algorithm with time-out control over networks with exponentially symmetric delays. IEEE Trans. Commun. 2002, 10, 1652–1661. [Google Scholar]
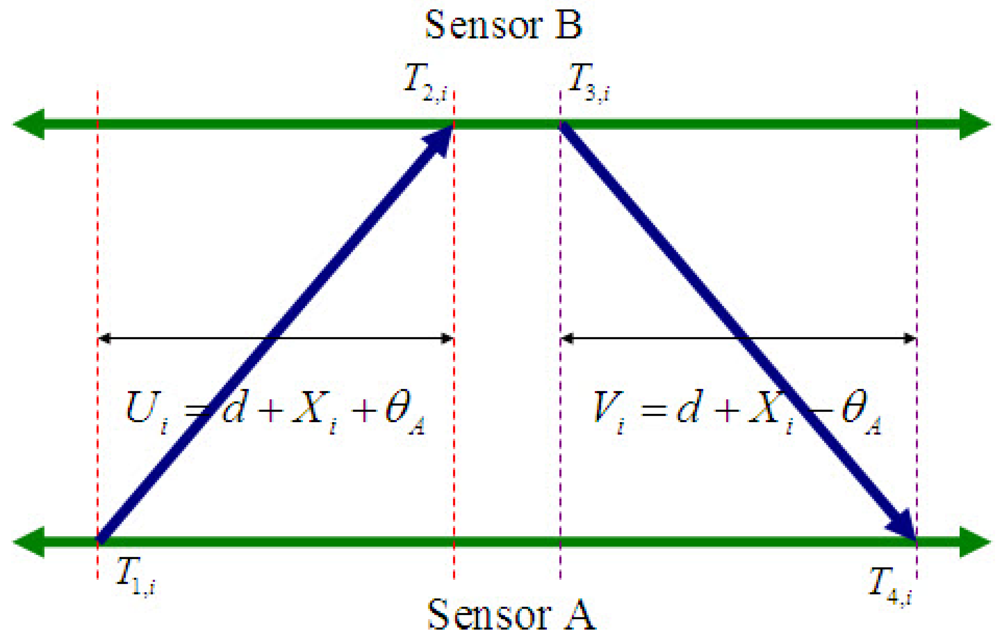
- Noh, K.L.; Chaudhari, Q.; Serpedin, E; Suter, B. Novel clock phase offset and skew estimation using two-way timing message exchanges for wireless sensor networks. IEEE Trans. Commun. 2007, 4, 766–777. [Google Scholar]
- Jeske, D.R. On the maximum likelihood estimation of clock offset. IEEE Trans. Commun. 2005, 1, 53–54. [Google Scholar]
- Lee, J.; Kim, J.; Serpedin, E. Clock offset estimation in wireless sensor networks using bootstrap bias correction. Proceedings of the International Conference on Wireless Algorithms, Systems, and Applications (WASA'08), Dallas, TX, USA, October 26-28, 2008.
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap.; Chapman & Hall: Boca Raton, 1993. [Google Scholar]
- Zoubir, A.M.; Iskander, D.R. Bootstrap Techniques for Signal Processing; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Mock, M.; Frings, R.; Nett, E.; Trikaliotis, S. Continuous clock synchronization in wireless real-time applications. Proceedings of 19th IEEE Symposium on Reliable Distributed Systems (SRDS'00), October 2000; pp. 125–133.
- Ping, S. Delay measurement time synchronization for wireless sensor networks. Intel Research, IRB-TR-03-013.
- Su, W.; Akyildiz, I.F. Time-diffusion synchronization protocol for wireless sensor networks. IEEE/ACM Trans. Netw. 2005, 2, 384–397. [Google Scholar]
- PalChaudhuri, S.; Saha, A.; Johnson, D.B. Probabilistic clock synchronization service in sensor networks. Technical Report TR 03-418, Department of Computer Science, Rice University: Houston, TX, USA, 2003. [Google Scholar]
- Arvind, K. Probabilistic clock synchronization in distributed systems. IEEE Trans. Parallel Distrib. Syst. 1994, 5, 474–487. [Google Scholar]
- Maroti, M.; Kusy, B.; Simon, G.; Ledeczi, A. The flooding time synchronization protocol. In Conference On Embedded Networked Sensor Systems, Proceedings. of the 2nd International Conference on Embedded Networked Sensor Systems, Baltimore, MD, USA; ACM: New York, NY, USA, 2004; pp. 39–49. [Google Scholar]
- Caffery, J.; Stuber, G.L. Nonlinear multiuser parameter estimation and tracking in CDMA systems. IEEE Trans. Commun. 2000, 12, 2053–2063. [Google Scholar]
- Doucet, A. Monte Carlo methods for Bayesian estimation of hidden Markov models. Applications to Radiation Signals. PhD thesis, University Paris-Sud, Orsay, France, Chapters 4 and 5. 1997. [Google Scholar]
- Doucet, A.; de Freitas, N.; Gordon, N. Sequential Monte-Carlo Methods in Practice; Springer-Verlag: New York, 2001. [Google Scholar]
- Bergman, N. Recursive Bayesian estimation: navigation and tracking applications. PhD Thesis, Linkoping University, Linkoping, Sweden, 1999. [Google Scholar]
- Arulampalam, M.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for on-line nonlinear/non-Gaussian Bayesian Tracking. IEEE Trans. Signal Process. 2002, 2, 174–188. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R. Estimation and Tracking: Principles, Techniques and Software.; Artech House: Boston, MA, USA, 1998. [Google Scholar]
- Chaudhari, Q.; Serpedin, E.; Qaraqe, K. On maximum likelihood estimation of clock offset and skew in networks with exponential delays. IEEE Trans. Signal Process. 2008, 4, 1685–1697. [Google Scholar]
- Jeske, D.R.; Sampath, A. Estimation of clock offset using bootstrap bias-correction techniques. Technometrics 2003, 3, 256–261. [Google Scholar]
- Jeske, D.R.; Chakravartty, A. Effectiveness of bootstrap bias correction in the context of clock offset estimators. Technometrics 2006, 4, 530–538. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rhee, I.-K.; Lee, J.; Kim, J.; Serpedin, E.; Wu, Y.-C. Clock Synchronization in Wireless Sensor Networks: An Overview. Sensors 2009, 9, 56-85. https://doi.org/10.3390/s90100056
Rhee I-K, Lee J, Kim J, Serpedin E, Wu Y-C. Clock Synchronization in Wireless Sensor Networks: An Overview. Sensors. 2009; 9(1):56-85. https://doi.org/10.3390/s90100056
Chicago/Turabian StyleRhee, Ill-Keun, Jaehan Lee, Jangsub Kim, Erchin Serpedin, and Yik-Chung Wu. 2009. "Clock Synchronization in Wireless Sensor Networks: An Overview" Sensors 9, no. 1: 56-85. https://doi.org/10.3390/s90100056



