HyBloc: Localization in Sensor Networks with Adverse Anchor Placement
Abstract
:1. Introduction
2. Related Works
2.1. Distributed Algorithms
2.2. Centralized algorithms
3. Our Hybrid Approach: HyBloc
3.1. Overview
3.2. The Protocol
- Phase Ia: Identification of secondary anchorsDue to the different properties of uniform and anisotropic networks, we adopt different ways to assign secondary anchors. Secondary anchors are spread apart in uniform networks but are relatively close in anisotropic networks.
- Uniform NetworksIn uniform networks, secondary anchors can be more widely spread and can be farther away from the primary anchors than in anisotropic networks. Each primary anchor sends an invitation packet containing its unique ID, two counters initialized to zero and a value ks controlling the number of secondary anchors, to one of its neighbours. One of the counters marks how many secondary anchors have been selected so far while the other marks the hop count that the invitation packet has travelled since the last secondary anchor is selected. Each invitation packet should identify ks secondary anchors. Normal sensor receiving this packet will perform a Bernoulli trial with a success rate of p only if the invitation packet has travelled for at least x hops away from the last secondary anchor or primary anchor. The success rate p and the x-hop restriction roughly controls the separation between secondary anchors so that they will not be clustered together. The values of p and x can be included in the packet sent by primary anchors or stored in sensor nodes before deployment. If the outcome is true, the normal sensor increments the counter by one and becomes a secondary anchor. The packet will be forwarded to another neighbour until the counter equals to ks. If a secondary anchor receives a packet originated from other primary anchors, the packet will be forwarded to another node. Thus the total number of primary and secondary anchors will be kp × (ks + 1), kp primary anchors and kp * ks secondary anchors.
- Anisotropic NetworksIn a C-shaped network, path distance is an unreliable Euclidean distance estimate when nodes are far apart. Thus unlike an uniform network, nodes close to the anchors are chosen as secondary anchors. Each primary anchor is responsible to choose ks secondary anchors. A primary anchor first selects secondary anchors from its direct neighbours. If the number of one hop neighbours is less than ks, the residue vacancies will be filled up by the two-hop neighbours or three-hop neighbours until ks secondary anchors are selected. The total number of primary and secondary anchors is also kp × (ks + 1).
- Phase Ib: Localization of Secondary AnchorsIn this step, secondary anchors have to acquire the proximity information between every pair of primary and secondary anchors. After sending the invitation packet, each primary anchor sends packets containing its unique ID and coordinates to all of its neighbours. The packet also bears a field marking the proximity, i.e. the distance or hop count the packet has travelled. The value is initialized to be zero. Secondary anchors will simply repeat the operation of primary anchors, that is sending out packets with its unique ID but leaving the coordinates field blank.Every node (including anchors) receiving a proximity packet from an anchor (either primary or secondary) will store its ID and the proximity value. If a packet from a particular anchor has been received before, the node examines the proximity and checks whether it is larger than the stored proximity. If it is larger than the stored value, the packet will be discarded. Otherwise, the stored value and the proximity field of the packet will be updated and the packet will be forwarded to other neighbours. Thus the stored proximity always reflects the shortest path distance or hop count from a particular anchor.After an anchor x has discovered its proximities to all anchors, it will send the proximities it has collected to other anchors and wait for other anchors to repeat the same step. When all anchors have distributed the proximities to their counterparts, each anchor knows the proximity information between every pair of anchors. Now, every secondary anchor can determine its location through the classical MDS.
- Phase IIa: Anchor Nodes Proximity-Distance Map CalculationAfter calculating its physical position using MDS, each secondary anchor also knows the position estimates of other secondary anchors since MDS provides a configuration about the primary and secondary anchors. Thus the proximity-distance map T among both primary and secondary anchors can be calculated immediately as follows according to [8]:Let P be the proximity matrix that pij is the proximity measure between anchors i and j where pii = 0. The proximity measure can be hop count or cumulative path distance between anchors. Similarly, let L be a geographical distance matrix that lij is the geographical distance between anchors i and j. lij can be calculated by utilizing the position estimates obtained from the previous step. P and L are square matrices with size m × m where m is the total number of primary and secondary anchors (kp × (ks + 1)). The PDM T is defined as a linear mapping that maps matrix P to matrix L in which the following error is minimized:whereand ti is the i-th row of T,The mapping T can be calculated by using singular value decomposition (SVD). Every secondary anchor calculates the PDM. The mapping and the position estimates of secondary anchors obtained from the first phase are distributed to the normal nodes nearby.
- Phase IIb: Localization of Normal NodesEach normal sensor node s uses the mapping T to process the proximity vector ps it has stored when it aided anchors exchanging proximity information.Finally, the node position is calculated by multilateration with the processed proximity vector and the position information of primary and secondary anchors.
3.3. Computational Complexity
4. Simulation
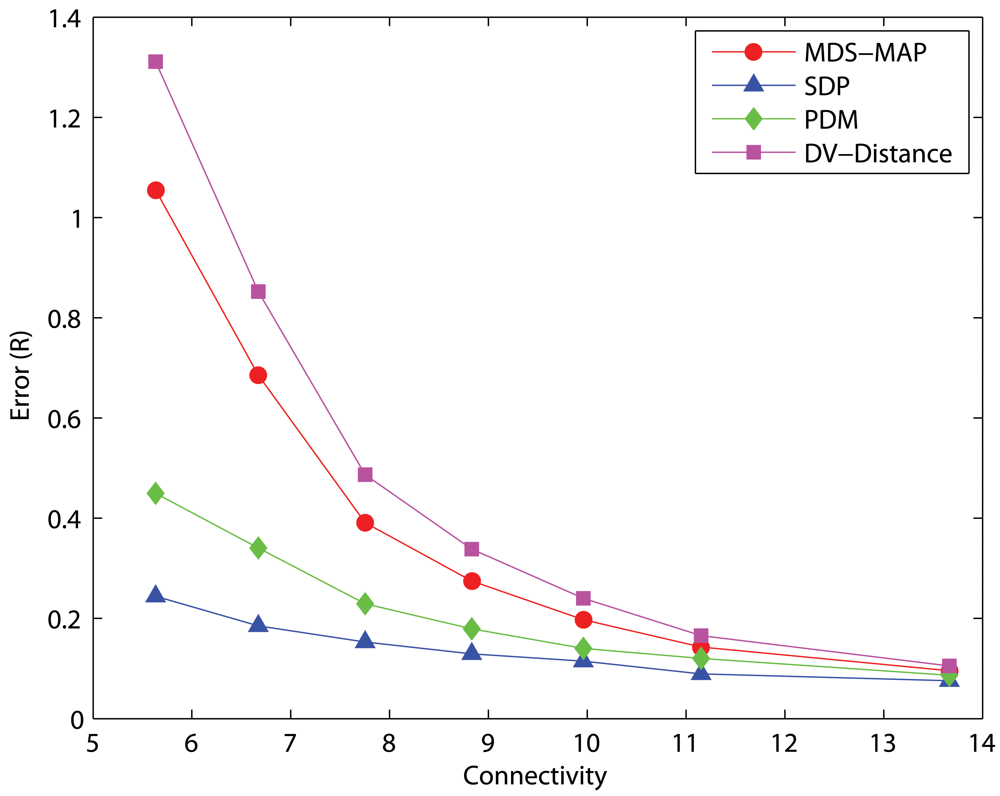
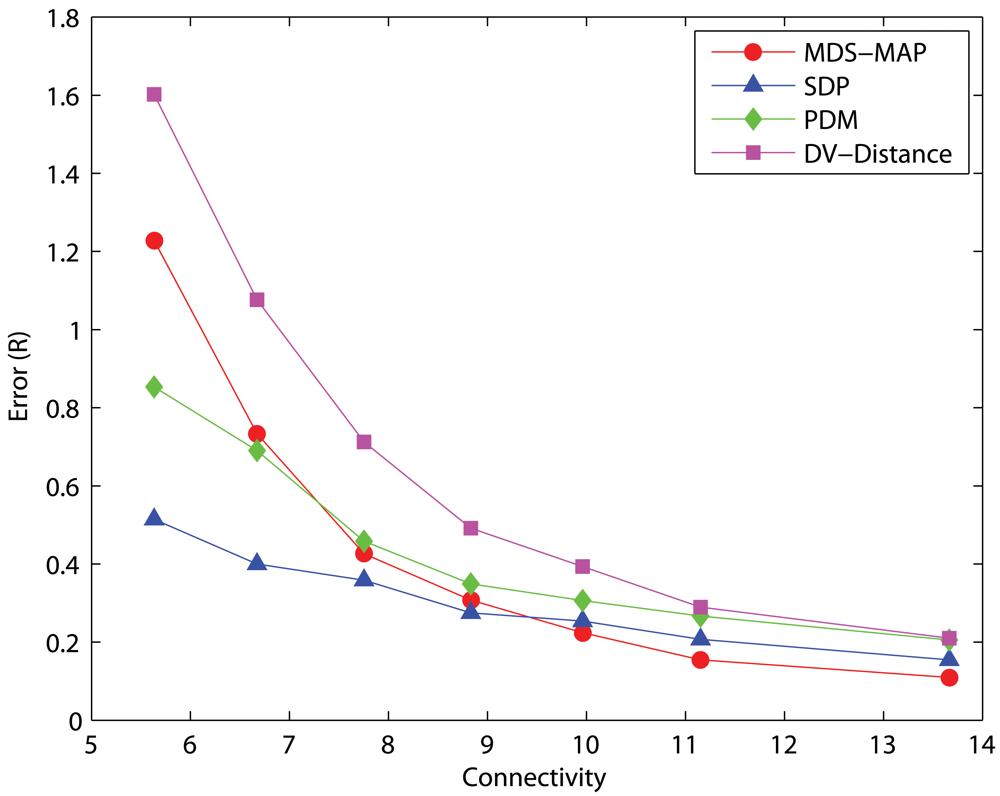
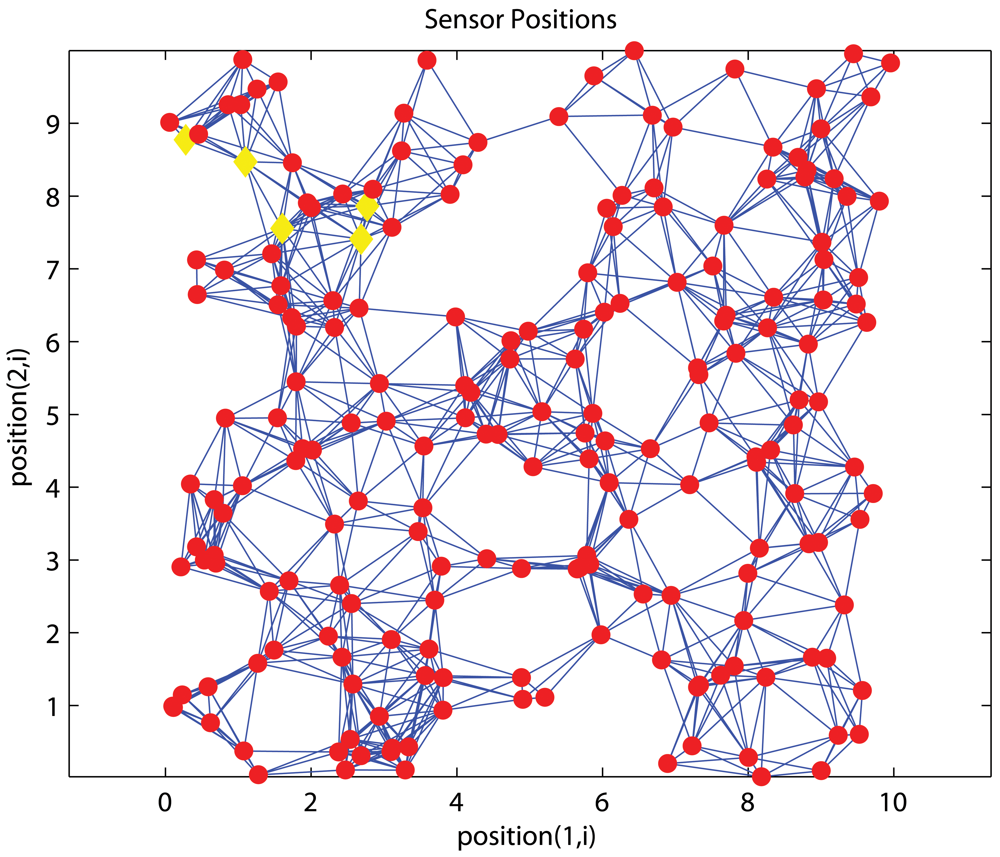
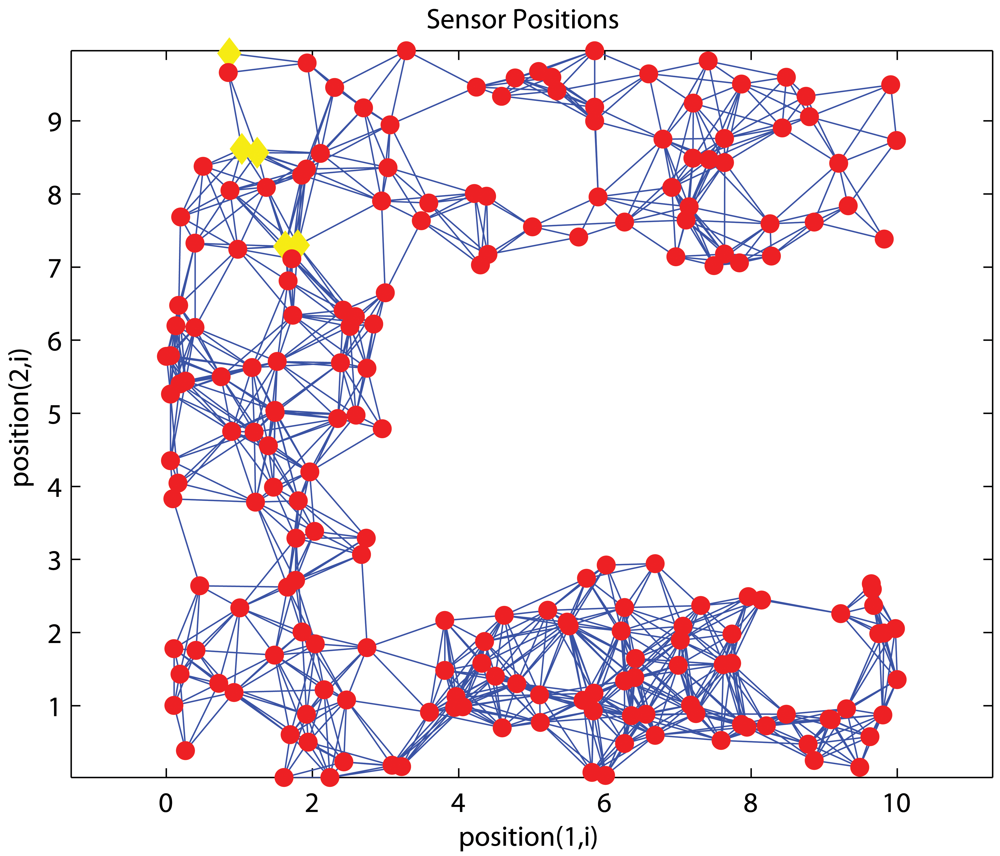
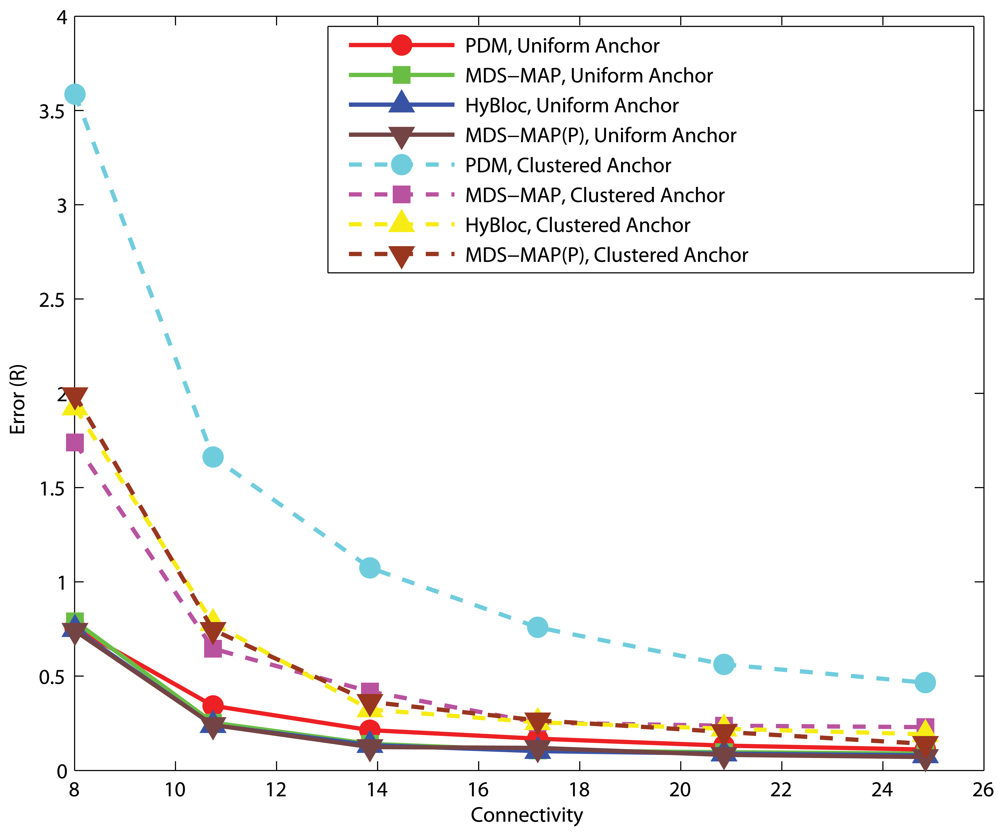
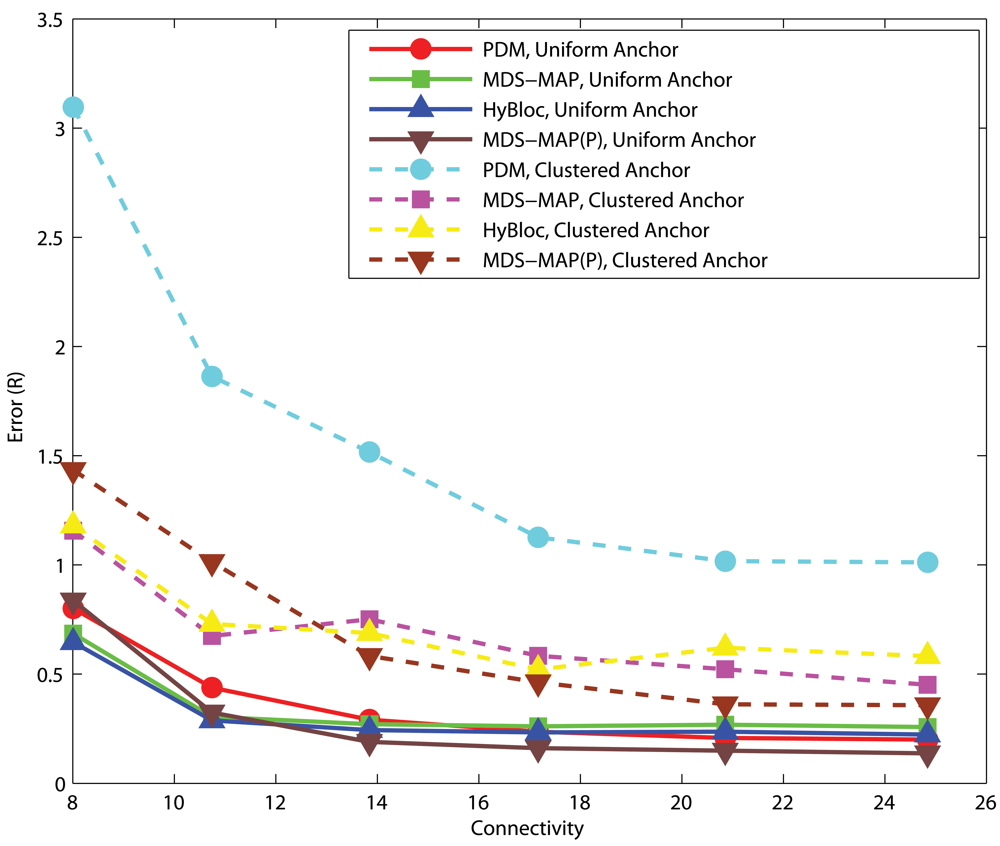
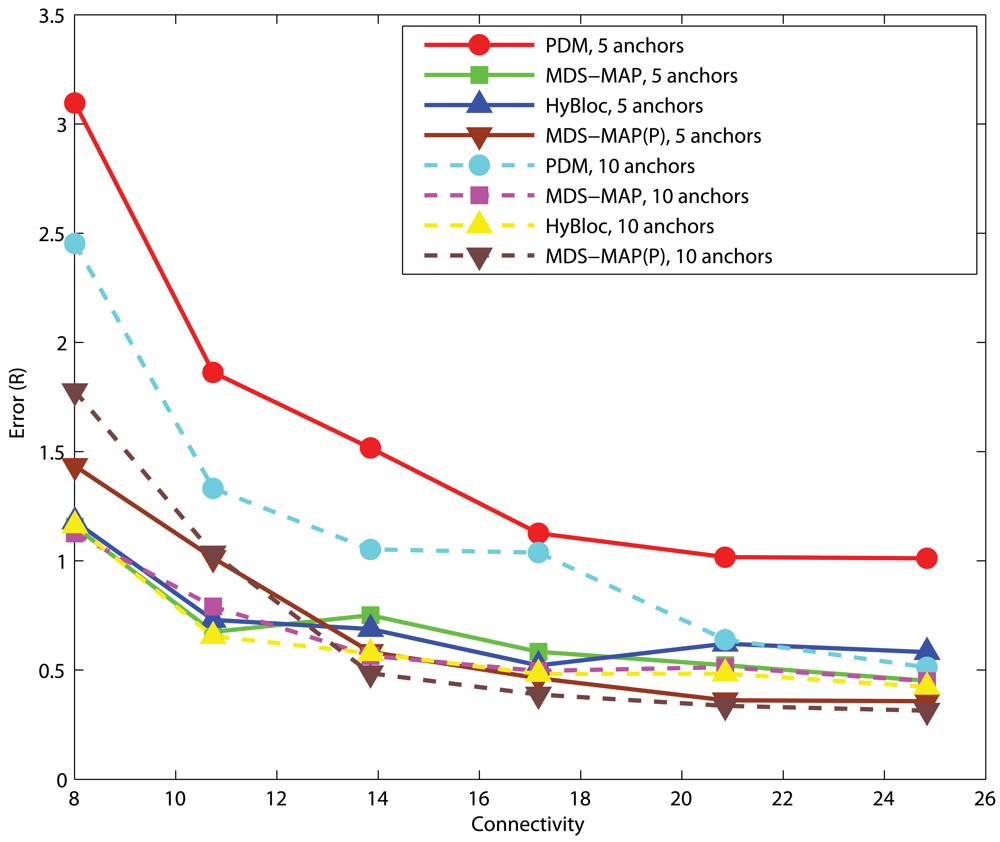
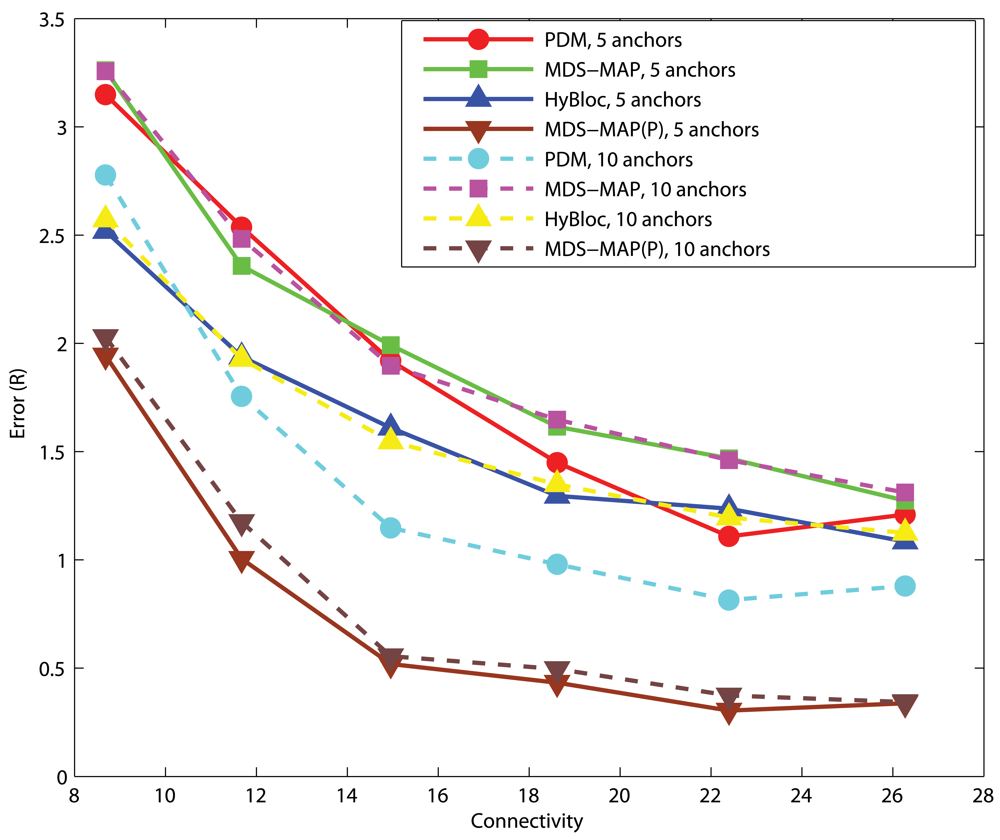
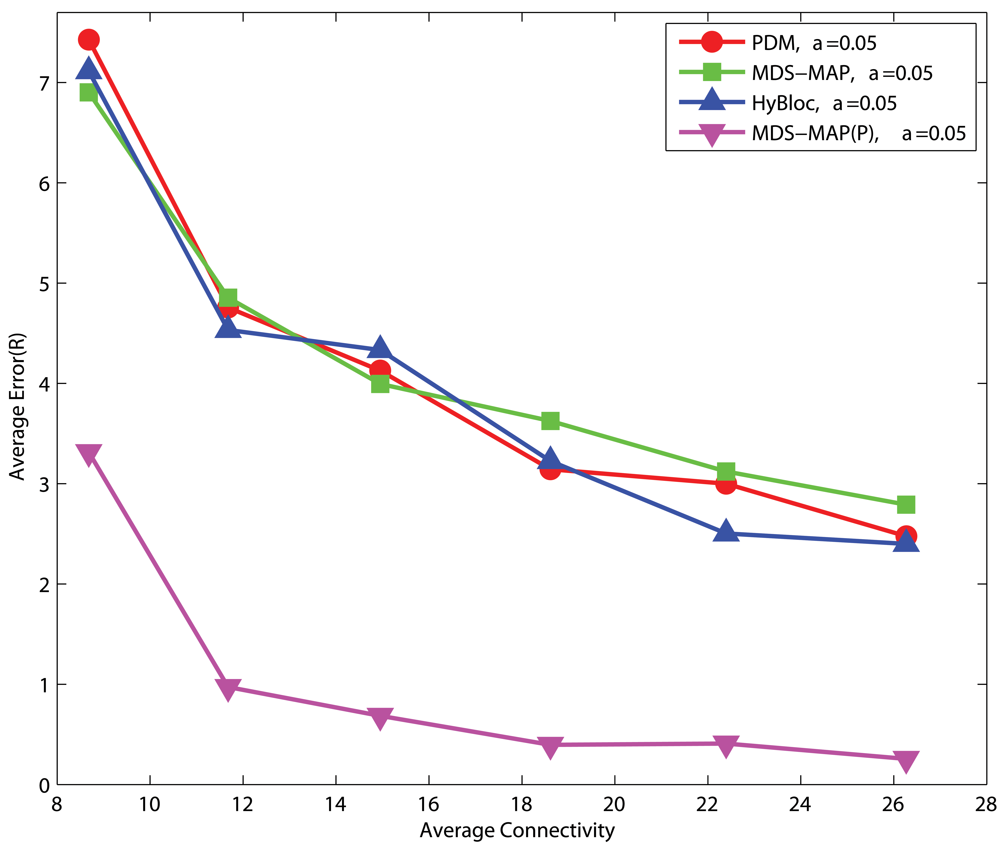
4.1. Effects of anchor placement
Uniform Networks
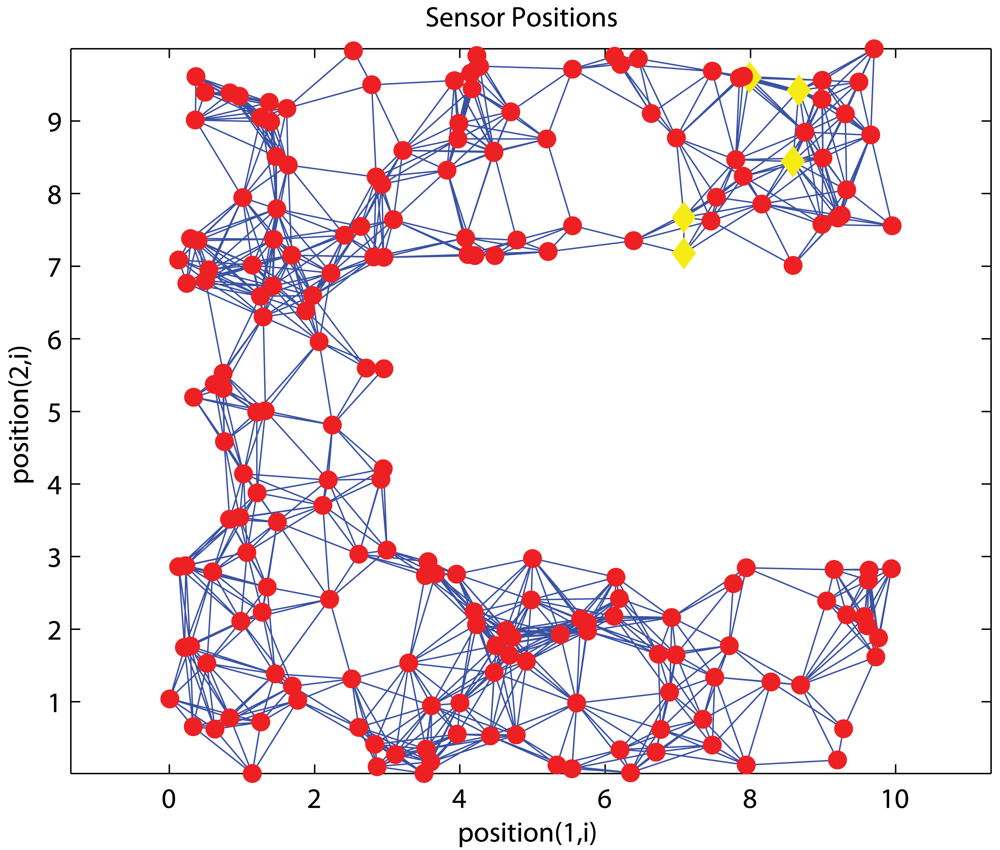
C-shaped Networks
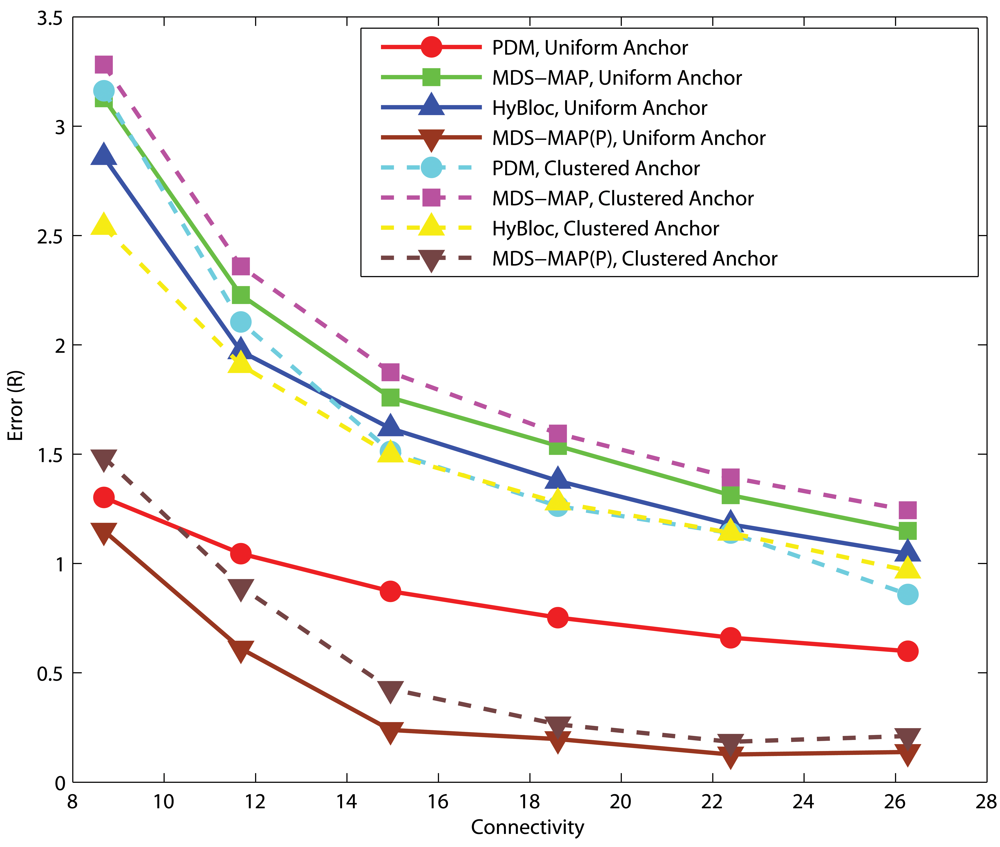
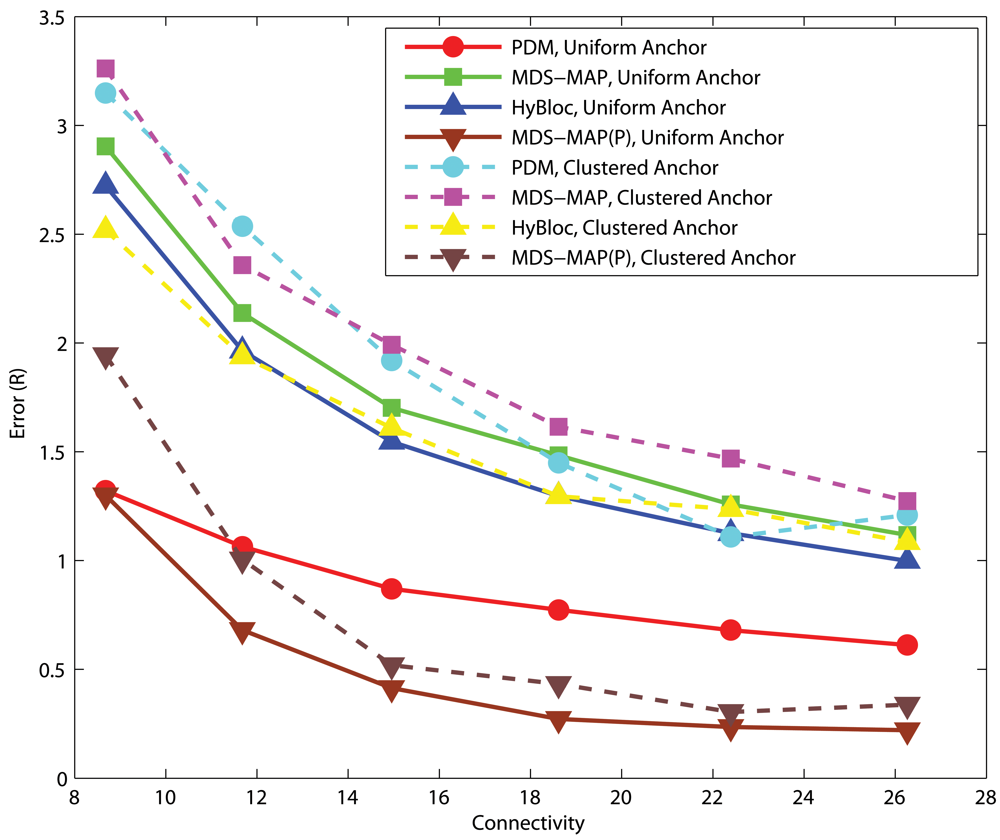
4.2. Effects of the number of primary anchors
Uniform Networks
C-shaped Networks
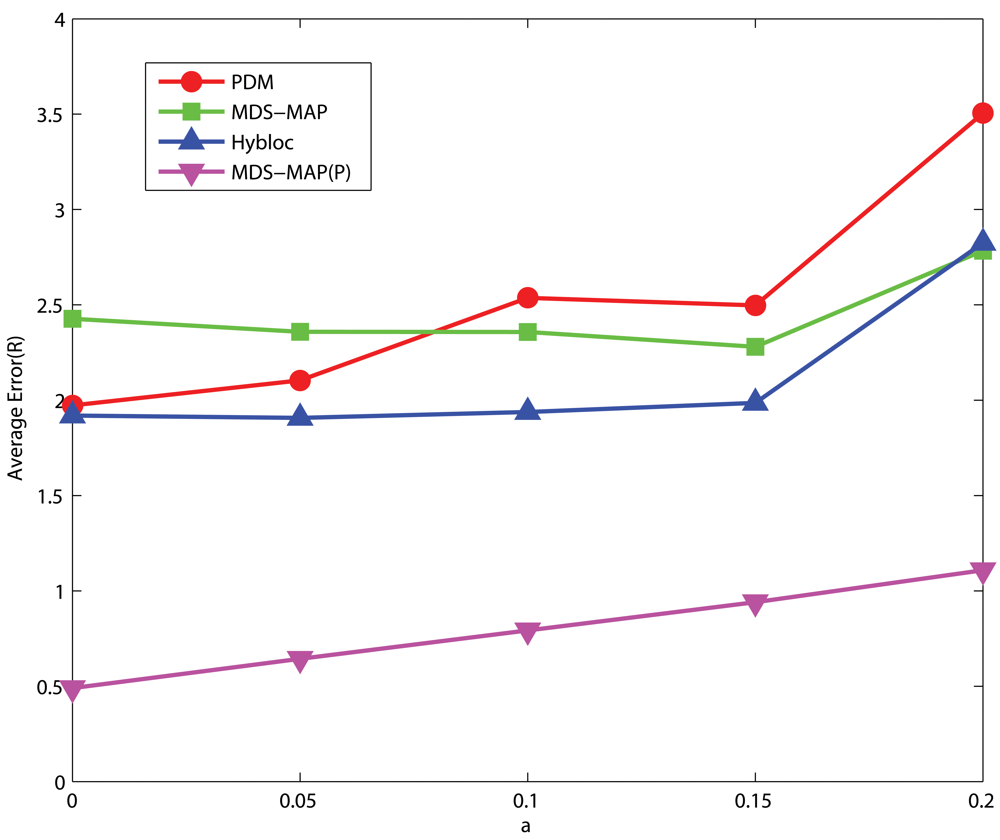
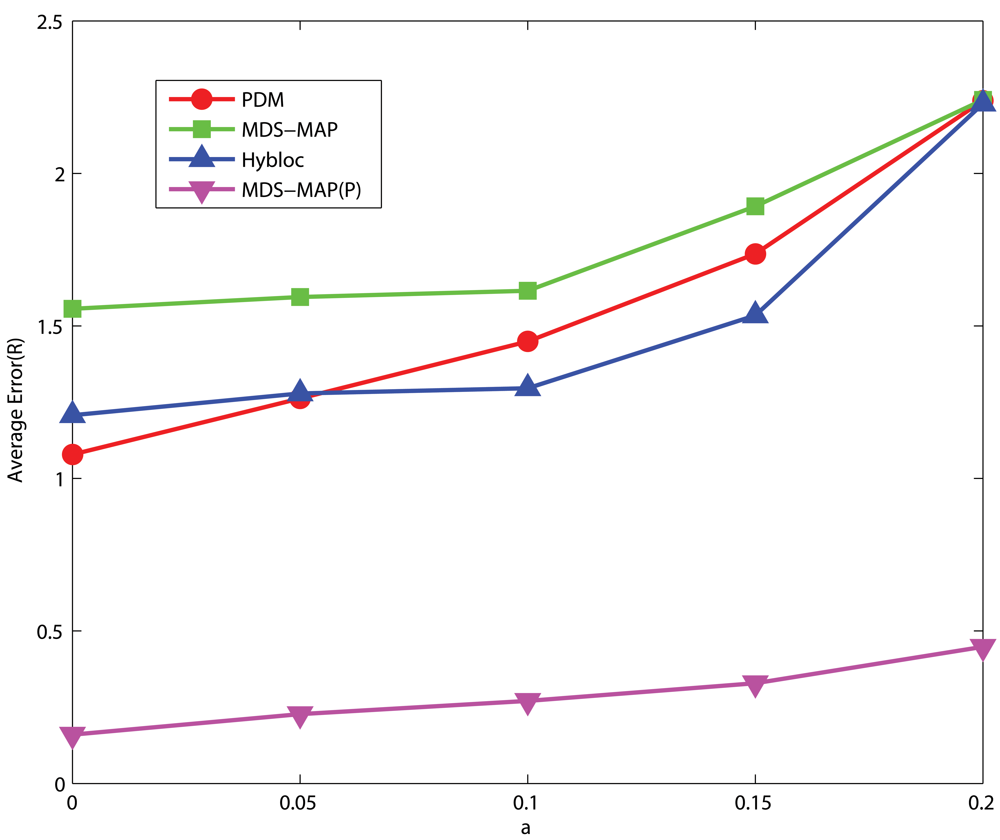
4.3. Sensitivity to noise
Uniform Networks
C-shaped Networks
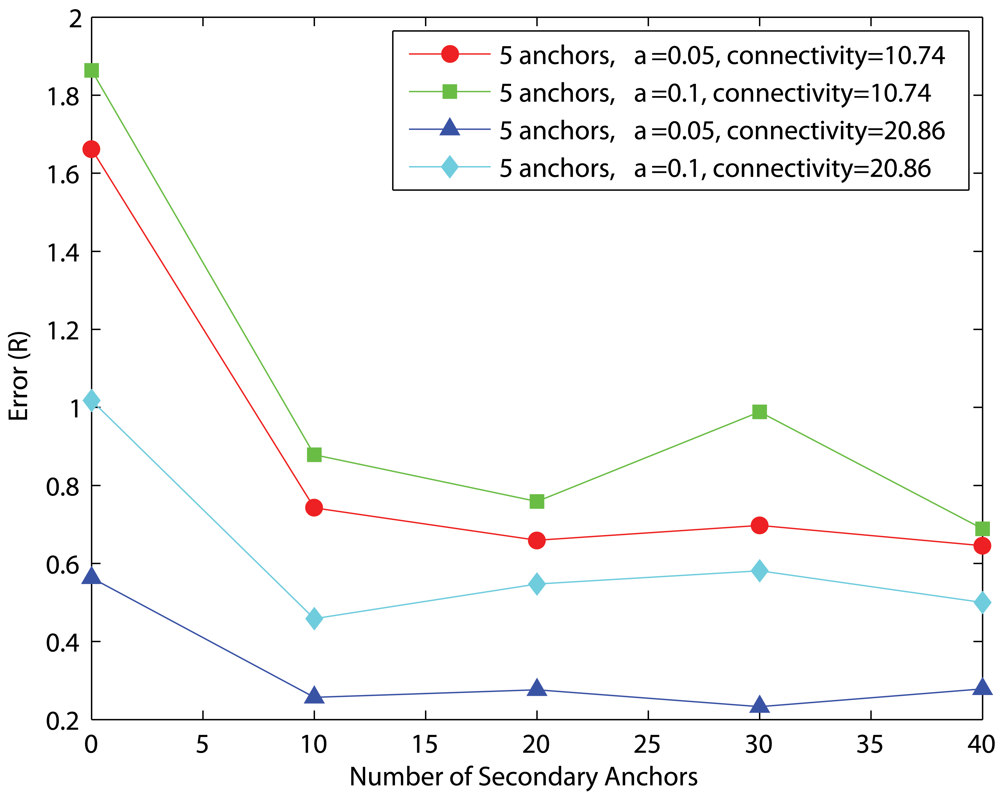
4.4. Effects of the number of secondary anchors
4.5. Effects on the position of anchor cluster
Uniform Networks
C-shaped Networks
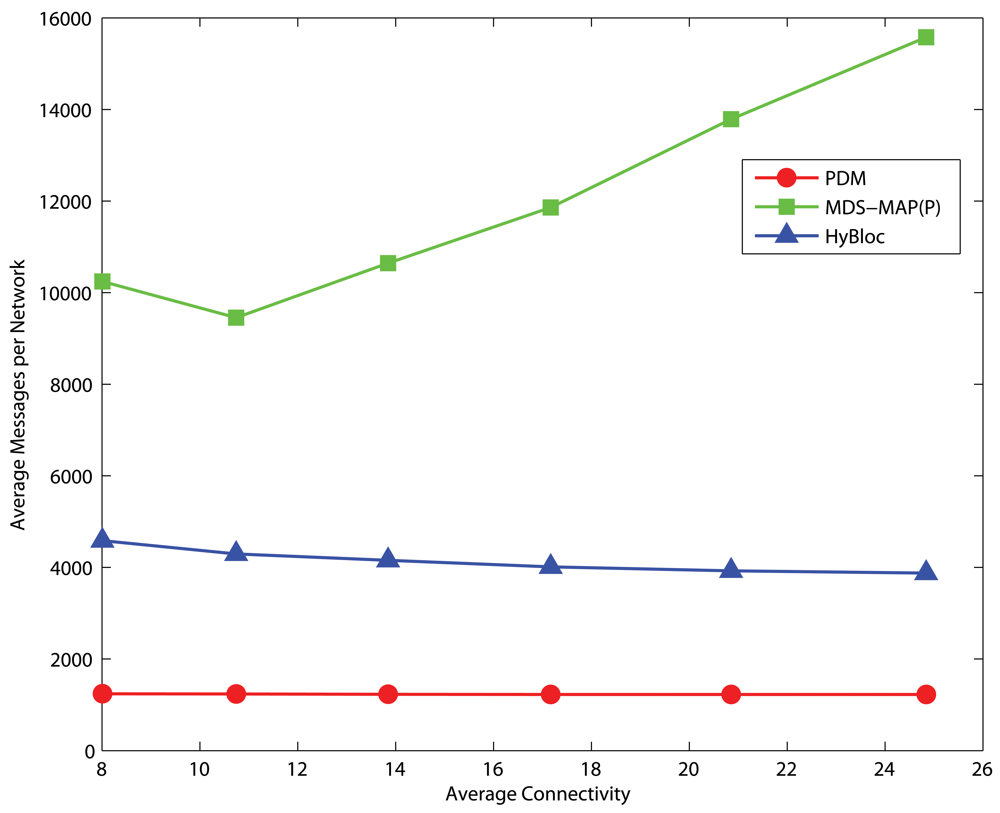
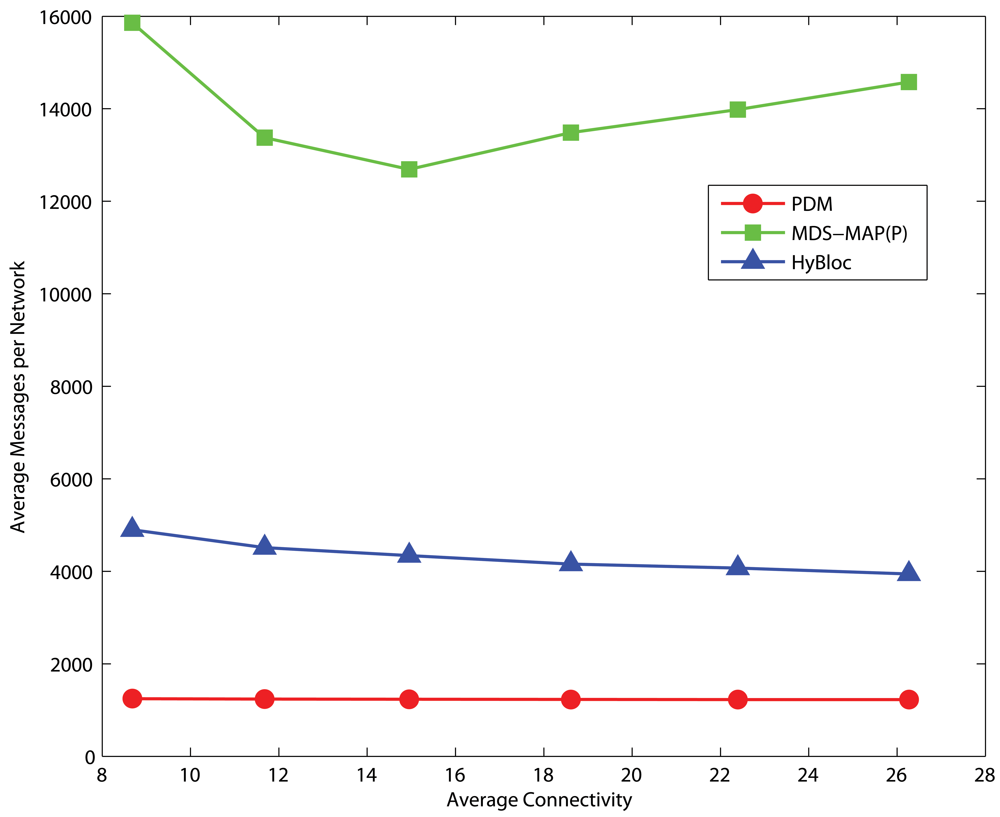
4.6. Communication Overheads
5. Conclusion
Acknowledgments
References and Notes
- Niculescu, D.; Nath, B. Ad hoc positioning system (APS). In IEEE Globecom.; san Antonio, November 2001; pp. 2926–2931, 1., 2.1. [Google Scholar]
- Gentile, C. Sensor location through linear programming with triangle inequality constraints. IEEE International Conference on Communications (ICC'05), Seoul, Korea, May 2005; 5, pp. 3192–3196, 1.
- Shang, Y.; Ruml, W.; Zhang, Y.; Fromherz, M. Localization from mere connectivity. In ACM MobiHoc; Annapolis, MD, USA, June 1-3 2003; pp. 201–212, 1., 2.2., 4. [Google Scholar]
- Shang, Y.; Ruml, W. Improved MDS-based localization. Proceedings of the 23rd Conference of the IEEE Communicatons Society (Infocom 2004), Piscataway NJ, March 7-11, 2004; 5, pp. 2640–2651, 1., 2.2., 4.
- Savvides, A.; Park, H.; Srivastava, M. The bits and flops of the n-hop multilateration primitive for node localization problems. In ACM International Workshop on Wireless Sensor Networks and Applications (WSNA '02); Atlanta, USA, Sept. 2002; pp. 112–121, 2.1. [Google Scholar]
- Biswas, P.; Ye, Y. Semidefinite programming for ad hoc wireless sensor network localization. IEEE IPSN 2004, 46–54, 1., 2.2. [Google Scholar]
- Savarese, C.; Rabaey, J.; Langendoen, K. Robust positioning algorithm for distributed ad-hoc wireless sensor networks. USENIX Technical Annual Conference, Berkeley, CA; Ellis, C.S., Ed.; 2002; pp. 317–327, 2.1. [Google Scholar]
- Lim, H.; Hou, J. C. Localization for anisotropic sensor networks. In IEEE INFOCOM; Miami, FL, USA, March 2005; 1., 2.1., 3., 3.1., 3, 4. [Google Scholar]
- Goldenberg, D. K.; Bihler, P.; Cao, M.; Fang, J.; Anderson, B. D.; Morse, A. S.; Yang, Y. R. Localization in sparse networks using sweeps. In ACM MobiCom; Los Angeles, CA, USA, 2006; pp. 110–121, 1., 2.1. [Google Scholar]
- Doherty, L.; Pister, K.; Ghaoui, L. Convex position estimation in wireless sensor networks. In IEEE INFOCOM; Anchorage, April 2001; 1., 2.2. [Google Scholar]
- Langendoen, K.; Reijers, N. Distributed localization in wireless sensor networks: a quantitative comparison. Computer Networks: The International Journal of Computer and Telecommunications Networking 2003, 43. [Google Scholar]
- Savvides, A.; Garber, W.; Adlakha, S.; Moses, R.; Srivastava, M. B. On the error characteristics of multihop node localization in ad-hoc sensor networks. In IEEE IPSN; PARC, Palo Alto, April 2003; pp. 317–332. [Google Scholar]
- Shang, Y.; Shi, H.; Ahmed, A.A. Performance study of localization methods for ad-hoc sensor networks. IEEE International Conference on Mobile Ad-hoc and Sensor Systems, Fort Lauderdale, Florida, USA, Oct. 25-27, 2004.
- Cheng, K.-Y.; Lui, K.-S.; Tam, V. Localization in sensor networks with limited number of anchors and clustered placement. In IEEE WCNC; Hong Kong, March 11-15 2007. [Google Scholar]
- Costa, J.; Patwari, N.; Hero, A. Distributed weighted-multidimensional scaling for node localization in sensor networks. ACM Trans. Sens. New. 2006, 2, 39–64, 2.1. [Google Scholar]
- Aspnes, J.; Eren, T.; Goldenberg, D. K.; Morse, A. S.; Whiteley, W.; Yang, YR.; Anderson, B.D.; Belhumeur, P.N. A theory of network localization. IEEE Trans. Mobile Comput. 2006, 1663–1678, 2.1. [Google Scholar]
- Ahmed, A. A.; Shi, H.; Shang, Y. Sharp: A new approach to relative localization in wireless sensor networks. In IEEE ICDCS; Columbus, OH, USA, June 6-10 2005; pp. 892–898, 2.2. [Google Scholar]
- Borg, I.; Groenen, P. Modern Multidimensional Scaling, Theory and Applications., 2nd edition; Springer: New York, 2005; p. 3. [Google Scholar]







| PDM | MDS-MAP, MDS-MAP(P) | HyBloc |
|---|---|---|
|
|
|
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cheng, K.-Y.; Lui, K.-S.; Tam, V. HyBloc: Localization in Sensor Networks with Adverse Anchor Placement. Sensors 2009, 9, 253-280. https://doi.org/10.3390/s90100253
Cheng K-Y, Lui K-S, Tam V. HyBloc: Localization in Sensor Networks with Adverse Anchor Placement. Sensors. 2009; 9(1):253-280. https://doi.org/10.3390/s90100253
Chicago/Turabian StyleCheng, King-Yip, King-Shan Lui, and Vincent Tam. 2009. "HyBloc: Localization in Sensor Networks with Adverse Anchor Placement" Sensors 9, no. 1: 253-280. https://doi.org/10.3390/s90100253
APA StyleCheng, K.-Y., Lui, K.-S., & Tam, V. (2009). HyBloc: Localization in Sensor Networks with Adverse Anchor Placement. Sensors, 9(1), 253-280. https://doi.org/10.3390/s90100253





