A One-Layer Satellite Surface Energy Balance for Estimating Evapotranspiration Rates and Crop Water Stress Indexes
Abstract
:1. Introduction
2. Description of the modeling approach
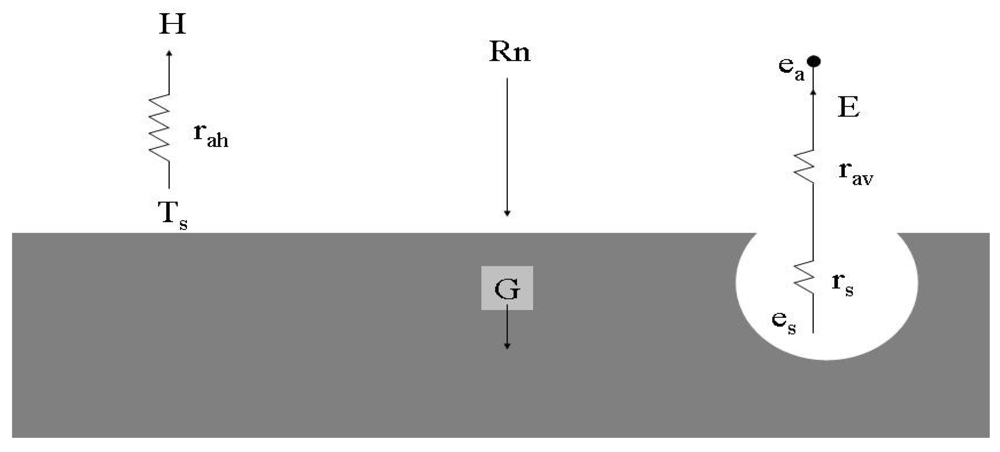
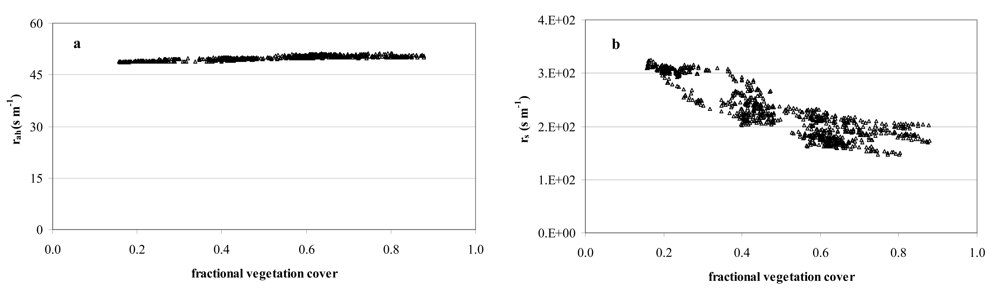
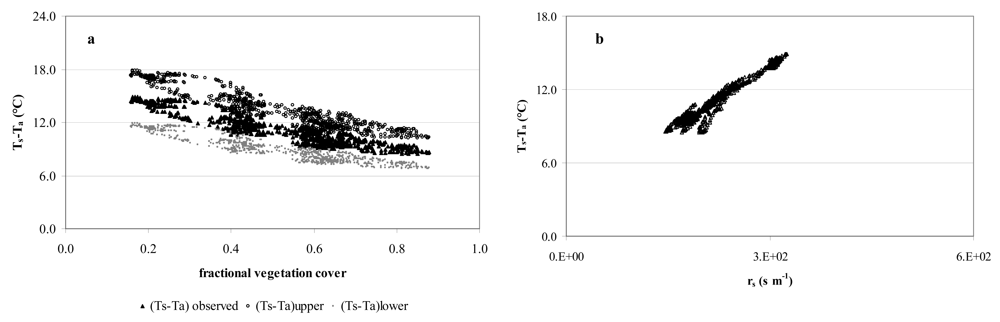
2.1. The surface energy balance approach
2.2. The crop water stress index
2.3. The Kc reflectance-based approach
3. Application of the proposed approach
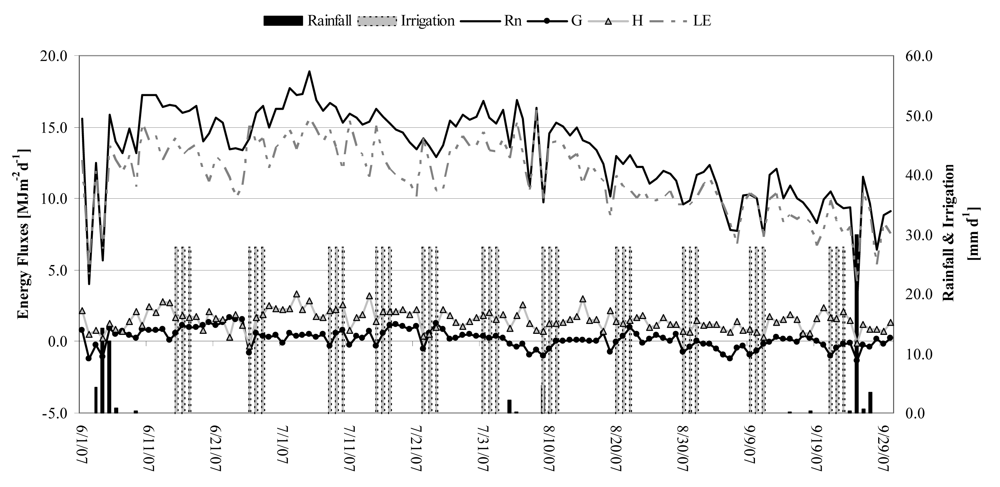
3.1. Experimental site and micrometeorological energy fluxes
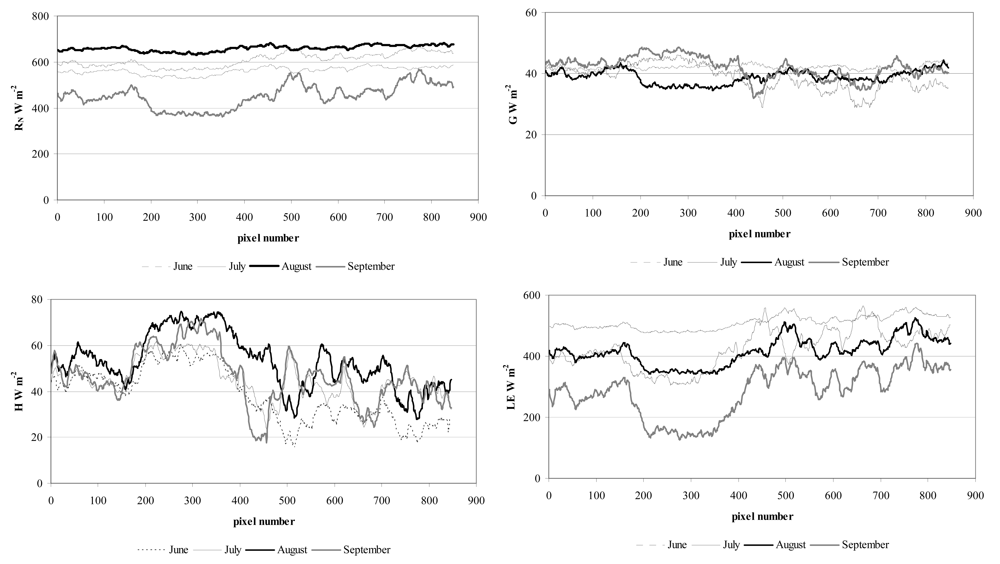
3.2. Processing satellite-based data
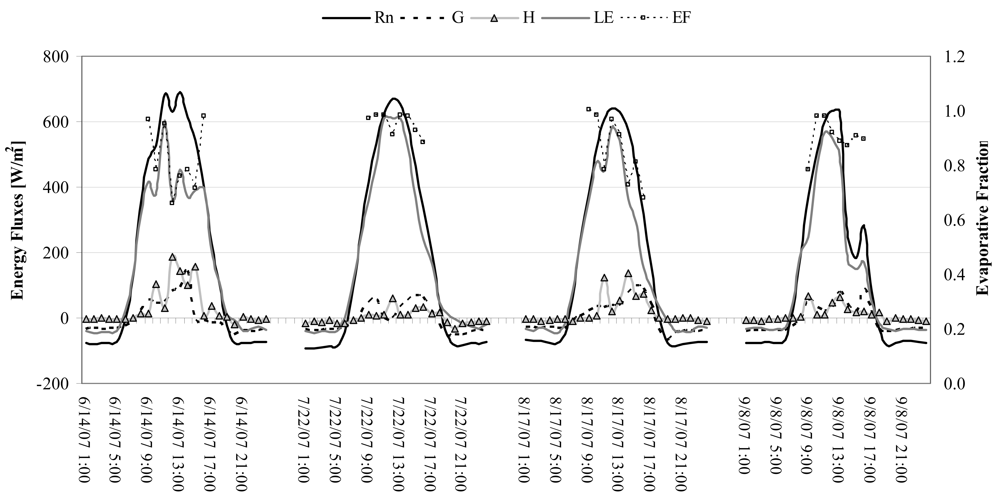
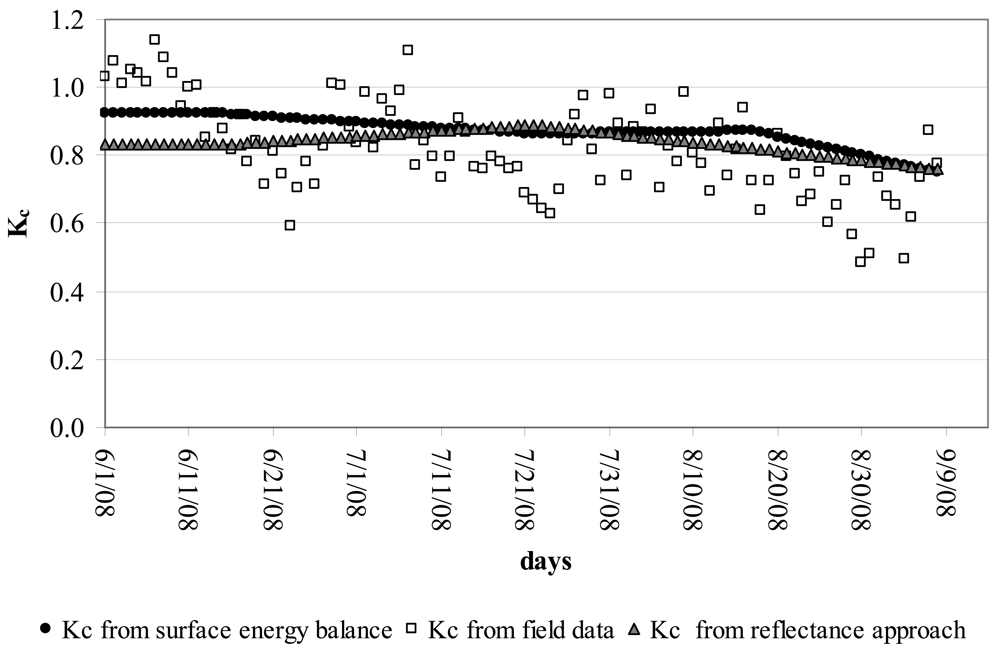
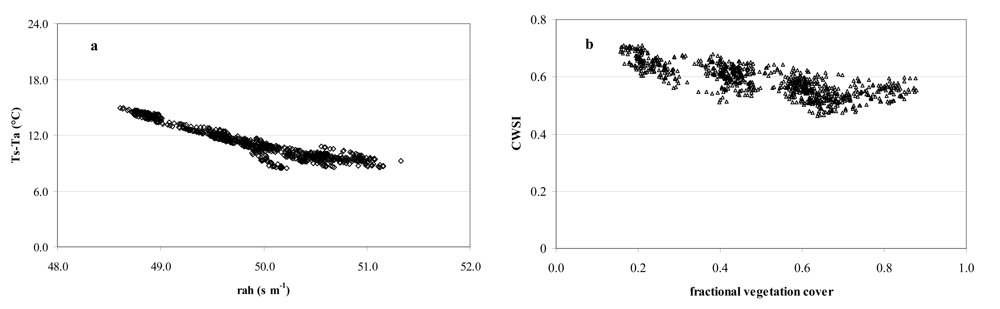
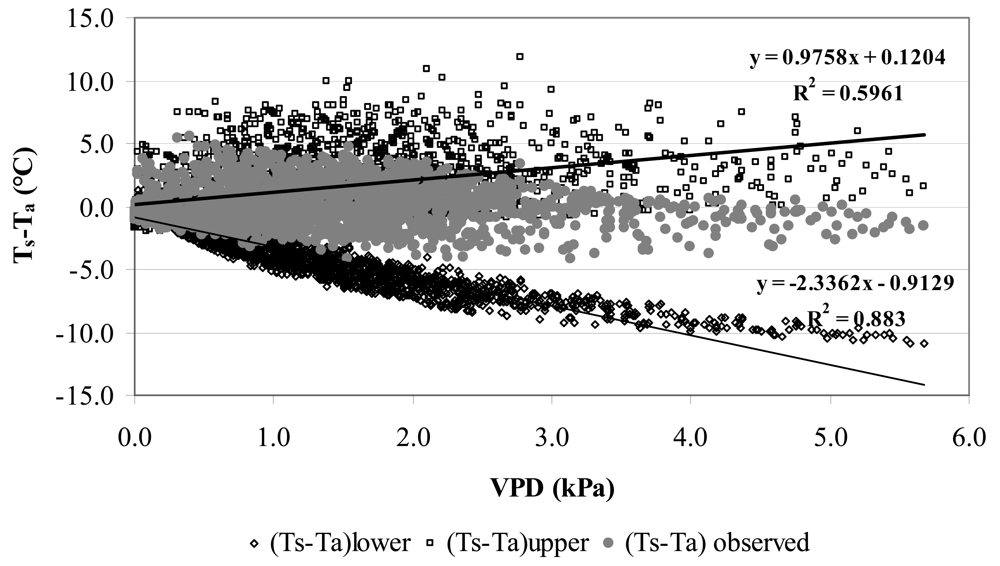
4. Results and Discussion
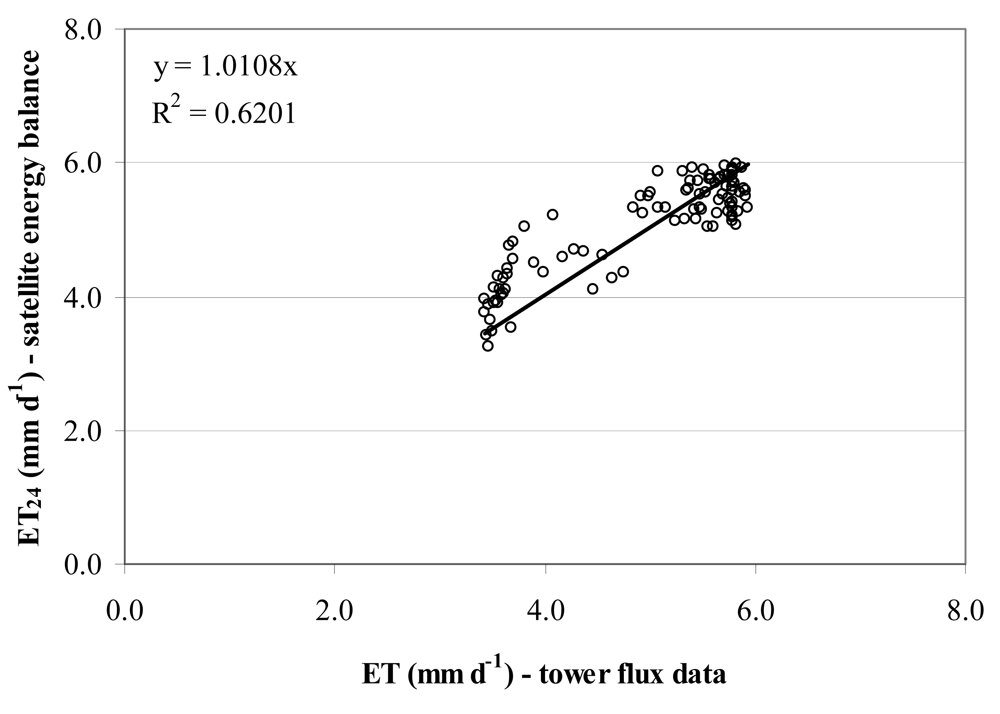
4.1. Comparing the model estimates of energy flux with micrometeorological measurements
4. Conclusions
Acknowledgments
References and Notes
- Abdelghani, C.; Hoedjes, J.C.B.; Rodriguez, J-C.; Watts, C.J.; Garatuza, J.; Jacob, F.; Kerr, Y.H. Using remotely sensed data to estimate area-averaged daily surface fluxes over a semi-arid mixed agricultural land. Agric. Forest Meteorol. 2007, 148, 330–342. [Google Scholar]
- Betts, A.K.; Chen, F.; Mitchell, K.E.; Janjic, Z.I. Assessment of the land surface and boundary layer models in two operational versions of the NCEP ETa Model using FIFE data. Mon. Weather Rev. 1997, 125, 2896–2916. [Google Scholar]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar]
- Moran, M.S. Thermal infrared measurement as an indicator of planet ecosystem health. In Thermal Remote Sensing in Land Surface Processes; Quattrocchi, D., Ed.; CRC-Taylor & Francis: Oxfordshire, UK, 2004; pp. 257–282. [Google Scholar]
- Boegh, E.; Soegaard, H. Estimation of evapotranspiration from a millet crop in the Sahel combining sap flow, leaf area index and eddy correlation technique. J. Hydro. 1995, 166, 265–282. [Google Scholar]
- Garrat, J.R. Transfer characteristics for a heterogeneous surface of large aerodynamic roughness. Q. J. R. Meteorol. 1978, 27, 973–988. [Google Scholar]
- Stull, R.B. Boundary layer meteorology.; Kluver Academic Dordrecht: the Netherlands, 1988. [Google Scholar]
- Boegh, E.; Soegaard, H.; Thomsen, A. Evaluating evapotranspiration rates and surface conditions using Landsat TM to estimate atmospheric resistance and surface resistance. Remote Sens. Environ. 2002, 79, 329–343. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. A two-source approach for estimating soil and vegetation energy fluxes from observations of directional radiometric surface temperature. Agric. Forest Meteorol. 1995, 80, 87–109. [Google Scholar]
- Zhang, L.; Lemeue, R.; Goutorbe, J.P. A one-layer resistance model for estimating regional evapotranspiration using remote sensing data. Agric. Forest Meteorol. 1995, 77, 241–261. [Google Scholar]
- Calera, A.; Jochum, A.M.; Cuesta, A.; Montoro, A.; Lopez, P. Irrigation management from space: towards user-friendly products. Irrig. Drainage Syst. 2005, 9, 337–353. [Google Scholar]
- D'Urso, G. Simulation and Management of On-Demand Irrigation Systems: a combined agro-hydrological approach. Ph.D. Thesis., Wageningen University, Wageningen, The Netherlands, 2001; p. 174. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R. A Landsat-based energy balance and evapotranspiration model in western US water rights regulation and planning. Irrig. Drainage Syst. 2005, 19, 251–268. [Google Scholar]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslang, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL): 1 Formulation. J. Hydrol. 1998, 212-213, 198–212. [Google Scholar]
- Neal, C.M.U.; Bausch, W.; Heermann, D. Development of reflectance based crop coefficients for corn. Trans. ASAE 1989, 30, 703–709. [Google Scholar]
- Neal, C.M.U.; Vinukollu, R.K.; Ramsey, R.D. A hybrid surface energy balance approach for the estimation of evapotranspiration in agricultural areas. AIP Conference Proceedings 2004 852, 138–145.
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops-an energy combination theory. Quart. J.R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar]
- Friedl, M.A. Forward and inverse modelling of land surface energy balance using surface temperature measurements. Remote Sens. Environ. 2002, 79, 344–354. [Google Scholar]
- Monteith, J.L.; Ong, C.K.; Corlett, J.E. Microclimatic interactions in agroforestry systems. Forest Ecol. Manage. 1991, 45, 31–44. [Google Scholar]
- Price, J. Quantitavive aspects of remote sensing in the thermal infrared. In Theory and Applications of Optical Remote Sensing; Asrar, G., Ed.; Wiley: New York, 1989; pp. 578–603. [Google Scholar]
- Rouse, J.M.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the vernal advancement of retrogradation of natural vegetation; NASA/GSFC Final report: Greenbelt, MD, 1974; p. 371. [Google Scholar]
- Clevers, J.G.P.W. The application of a weighted infrared-red vegetation index for estimation leaf area index by correcting for soil moisture. Remote Sens. Environ. 1989, 29, 25–37. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ 1988, 25, 295–309. [Google Scholar]
- Menenti, M. Physical aspect and determination of evaporation in desert applying remote sensing techniques. ICW Report n.10 (Special issue). 1984.
- Kustas, W.P.; Daughtry, C.S.T. Estimation of the soil heat flux/net radiation ratio from spectral data. Agric. Forest Meteorol. 1990, 49, 205–223. [Google Scholar]
- Chodhury, B.J.; Idso, S.B.; Reginato, R.J. An analysis of infrared temperature observations over wheat and calculation of laten heat flux. Agric. Forest Meteorol. 1986, 37, 75–88. [Google Scholar]
- Huband, N.D.S.; Monteith, J.L. Radiative surface temperature and energy balance of a what canopy. Part I: Comparison of radiative and aerodynamic canopy temperature. Boundary-Layer Meteorol. 1986, 6, 1–17. [Google Scholar]
- Sobrino, J.A.; Raissouni, N.; Li, Z. A comparative study of land surface emissivity retrieval from NOAA data. Remote Sens. Environ. 2001, 75, 256–266. [Google Scholar]
- Chander, C.; Markham, B. Revised Landsat-5 TM radiometric calibration procedures and postcalibration dynamic ranges. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2674–2677. [Google Scholar]
- Schneider, K.; Mauser, W. Processing and accuracy of Landsat Thematic Mapper data for lake surface temperature measurements. Int. J. Remote Sens. 1996, 17, 2027–2041. [Google Scholar]
- Sobrino, J.A.; Jiménez-Mu˜oz, J.C.; El-Kharraz, J.; Gómez, M.; Romaguera, M.; Sòria, G. Single-channel and two channel methods for land surface temperature retrieval from DAIS data and its application to the Barrax site. Int. J. Remote Sens. 2004, 25, 215–230. [Google Scholar]
- Brutsaert, W. Evaporation into the atmosphere: Theory, History and Applications; Springer: Boston, MA, 1982. [Google Scholar]
- Sugita, M.; Brutsaert, W. Regional surface fluxes from remote sensed surface skin temperature and lower boundary layer measurements. Water Resour. Res. 1990, 26, 2937–2944. [Google Scholar]
- Businger, J.A. A note on the Businger-Dyer profiles. Boundary-Layer Meteorol. 1988, 42, 145–151. [Google Scholar]
- Idso, S.B.; Jackson, R.D.; Pinter, P.J.; Hatfield, J.L. Normalizing the stress-degree-day parameter for environmental variability. Agric. Meteorol. 1981, (24), 45–55. [Google Scholar]
- Jackson, R.D.; Kustas, W.P.; Choudhury, B.J. A reexamination of the Crop Water Stress Index. Irrig. Sci. 1988, 9, 309–317. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements. In Irrig & Drainage Paper 56.; FAO: Rome, 1998. [Google Scholar]
- Stanghellini, C.; Bosma, A.H.; Gabriels, P.C.J.; Werkhoven, C. The water consumption of agricultural crops: how crop coefficients are affected by crop geometry and microclimate. Acta Hort. 1990, 278, 509–515. [Google Scholar]
- Kustas, W.O.; Moran, M.S.; Humes, K.S.; Stannard, D.I.; Pinter, P.J., Jr; Hipps, L.E.; Swiatek, E.; Goodrich, D.C. Surface energy balance estimates at local and regional scales using optical remote sensing from an aircraft platform and atmospheric data collected over semiarid rangelands. Water Resour. Res. 1994, 30, 1241–1259. [Google Scholar]
- Consoli, S.; D'urso, G.; Toscano, A. Remote sensing to estimate ET-fluxes and the performance of an irrigation district in southern Italy. Agric. Water Manage 2006, 81, 295–314. [Google Scholar]
- Gao, W.; Shaw, R.H.; Paw U, K.T. Observation of organized structure in turbulent flow within and above a forest canopy. Boundary-Layer Meteorol. 1989, 47, 349–377. [Google Scholar]
- Paw U, K.T.; Qiu, J.; Su, H.B.; Watanabe, T.; Brunet, Y. Surface renewal analysis: a new method to obtain scalar fluxes without velocity data. Agric. Forest Meteorol. 1995, 74, 119–137. [Google Scholar]
- Snyder, R.L.; Spano, D.; Paw U, K.T. Surface Renewal analysis for sensible and latent heat flux density. Boundary-Layer Meteoro. 1996, 77, 249–266. [Google Scholar]
- Spano, D.; Snyder, R.L.; Duce, P.; Paw U, K.T. Surface renewal analysis for sensible heat flux density using structure functions. Agric. Forest Meteorol. 1997, 86, 259–271. [Google Scholar]
- Van Atta, C.W. Effect of coherent structures on structure functions of temperature in the atmopheric boundary layer. Arch Mech. 1977, 29, 161–171. [Google Scholar]
- ASCE-EWRI. The ASCE Standardized Reference Evapotranspiration Equation. Environmental and Water Resources Institute of ASCE Standardization of Reference Evapotranspiration. In Task Committee.; American Society of Civil Engineers: Reston, VA, 2005; p. 216. [Google Scholar]
- Soil Conservation Service. Procedures for collecting soil samples and methods of analysis for soil survey. Soil survey investigation report 1.; SCS: Washington D.C., 1982. [Google Scholar]
- Jensen, J.R. Introductory digital image processing: A remote sensing perspective.; Cliff, N.J., Ed.; Prentice-Hall: Englewood, NJ, U.S.A, 1986. [Google Scholar]
- Richter, R.; Mueller, A.; Heiden, U. Aspects of operational atmospheric correction of hyperspectral imagery. Int. J. Remote Sens. 23, 145–157.
- Nagler, P.L.; Glenn, E.P.; Kim, H.; Emmerich, W.; Scott, R.L.; Huxman, T.E.; Huete, A.R. Relationship between evapotranspiration and precipitation pulse in a semiarid rangeland estimated by moisture flux towers and MODIS vegetation indices. J. Arid. Env. 2007, 70, 443–462. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. Crop water requirements. In Irrig & Drainage Paper 24.; revised; FAO: Rome, 1977. [Google Scholar]
- Mahrt, L.; Ek, M. Spatial variability of turbulent fluxes and roughness lengths in HAPEX- MOBILHY. Boundary-Layer Meteorol. 1993, 65, 381–400. [Google Scholar]
- Soegaard, H. Fluxes of carbon dioxide, water vapour and sensible heat in a boreal agricultural area of Sweden - scaled from canopy to landscape level. Agric. Forest Meteorol. 1999, 98-99, 463–478. [Google Scholar]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar]
- Kar, G.; Kumar, A. Surface energy fluxes and crop water stress index in groundnut under irrigated ecosystem. Agric. Forest Meteorol. 2007, 146, 94–106. [Google Scholar]
- Orta, H.A.; Erdem, Y.; Tolga, E. Crop water stress index for watermelon. J. Scientia 2003, 98, 121–130. [Google Scholar]

| Indicators* | Expression | Parameters | Reference |
|---|---|---|---|
| Normalized Difference Vegetation Index | [21] | ||
| Weighted Difference Vegetation Index | [22] | ||
| Leaf Area Index | α*, WDVI∞ | [22] | |
| Soil Adjusted vegetation index | SAVI = (ρi − ρr)/(ρi + ρr + 0.5) | [23] | |
| Spectrally integrated hemispherical reflectance (albedo) | r = ∑λ wλ · ρλ | wλ | [24] |
| Corner coordinates (WGS 84) | X | Y |
|---|---|---|
| Upper left | 472006 | 4155746 |
| Upper right | 508658 | 4155746 |
| Lower left | 472006 | 4127050 |
| Lower right | 508658 | 4127050 |
| Sensor | Pixel size (m) | Band | Band range (μm) | Gain* (W m-2 sr-1 μm-1) | Offset (W m-2 sr-1 μm-1) |
|---|---|---|---|---|---|
| Landsat 5 TM | 30 | 1 | 0.45-0.52 | 0.6023 | -1.50 |
| 2 | 0.52-0.60 | 1.1749 | -2.80 | ||
| 3 | 0.63-0.69 | 0.8058 | -1.20 | ||
| 4 | 0.76-0.90 | 0.8145 | -1.50 | ||
| 5 | 1.55-1.75 | 0.1087 | -0.37 | ||
| 120 | 6 | 10.4-12.5 | 0.0551 | 1.20 | |
| 30 | 7 | 2.08-2.35 | 0.0569 | -0.15 |
| Satellite-based indicators | Mean values | |||||||
|---|---|---|---|---|---|---|---|---|
| June 14th | July 22nd | August 17th | September 8th | |||||
| M | CV | M | CV | M | CV | M | CV | |
| albedo (α) | 0.18 | 0.08 | 0.16 | 0.05 | 0.17 | 0.04 | 0.12 | 0.07 |
| emissivity (ε) | 0.96 | 0.05 | 0.96 | 0.03 | 0.96 | 0.03 | 0.97 | 0.05 |
| Leaf area index (LAI) | 1.68 | 0.17 | 1.79 | 0.21 | 1.55 | 0.15 | 1.38 | 0.15 |
| NDVI | 0.50 | 0.07 | 0.55 | 0.09 | 0.60 | 0.08 | 0.45 | 0.06 |
| SAVI | 0.23 | 0.06 | 0.23 | 0.08 | 0.23 | 0.05 | 0.19 | 0.07 |
| WDVI | 0.17 | 0.11 | 0.20 | 0.07 | 0.24 | 0.14 | 0.17 | 0.10 |
| Field measurements of LAI | 1.45 | 0.16 | 1.40 | 0.15 | 1.55 | 0.17 | 1.35 | 0.18 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Barbagallo, S.; Consoli, S.; Russo, A. A One-Layer Satellite Surface Energy Balance for Estimating Evapotranspiration Rates and Crop Water Stress Indexes. Sensors 2009, 9, 1-21. https://doi.org/10.3390/s90100001
Barbagallo S, Consoli S, Russo A. A One-Layer Satellite Surface Energy Balance for Estimating Evapotranspiration Rates and Crop Water Stress Indexes. Sensors. 2009; 9(1):1-21. https://doi.org/10.3390/s90100001
Chicago/Turabian StyleBarbagallo, Salvatore, Simona Consoli, and Alfonso Russo. 2009. "A One-Layer Satellite Surface Energy Balance for Estimating Evapotranspiration Rates and Crop Water Stress Indexes" Sensors 9, no. 1: 1-21. https://doi.org/10.3390/s90100001
APA StyleBarbagallo, S., Consoli, S., & Russo, A. (2009). A One-Layer Satellite Surface Energy Balance for Estimating Evapotranspiration Rates and Crop Water Stress Indexes. Sensors, 9(1), 1-21. https://doi.org/10.3390/s90100001





