Modelling Amperometric Biosensors Based on Chemically Modified Electrodes
Abstract
:1. Introduction
2. Mathematical Model
2.1. Governing Equations
2.2. Initial Conditions
2.3. Boundary Conditions
2.4. Biosensor Response
3. Numerical Solution
4. Model Validation
5. Dimensionless Model
6. Results and Discussion
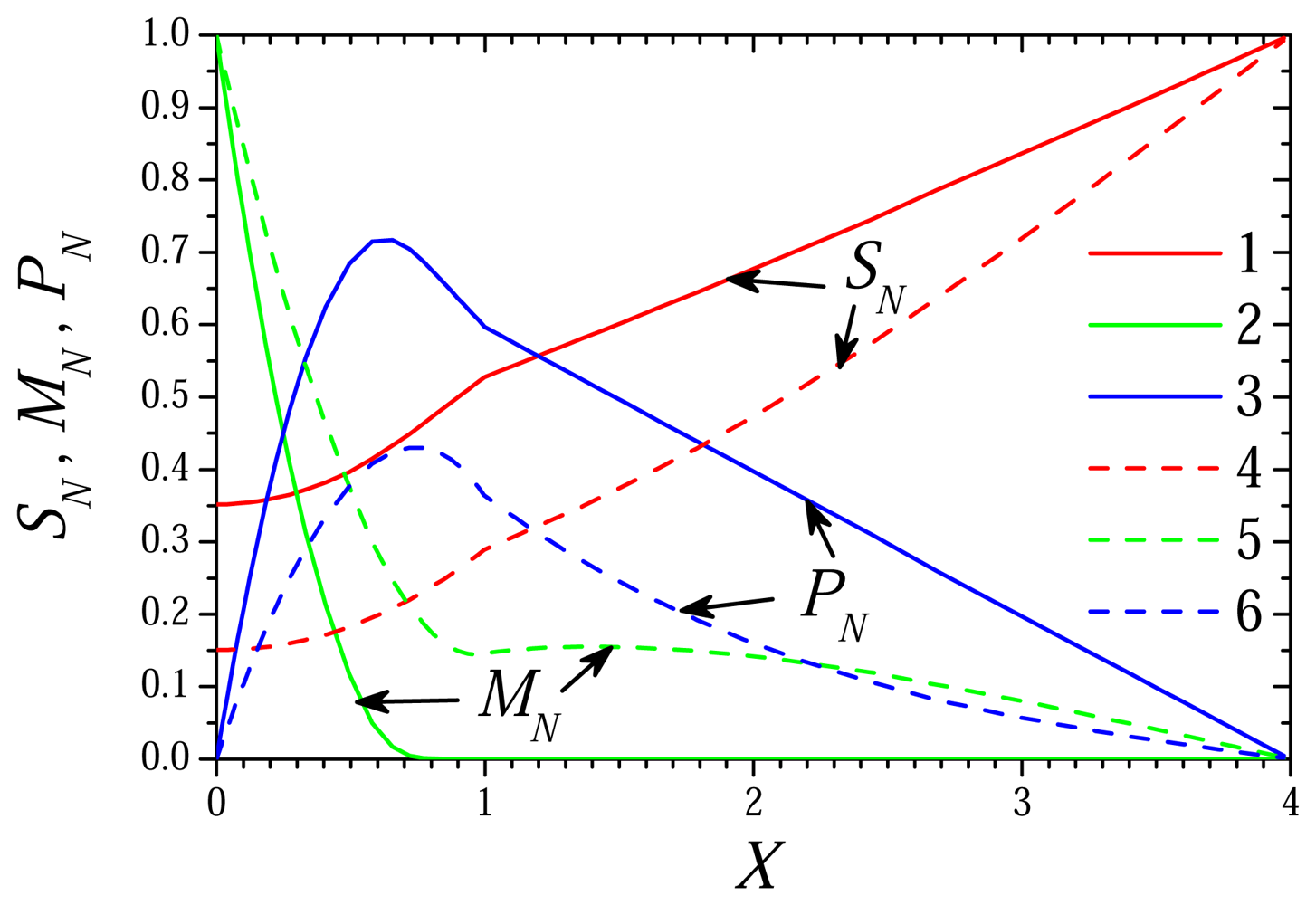
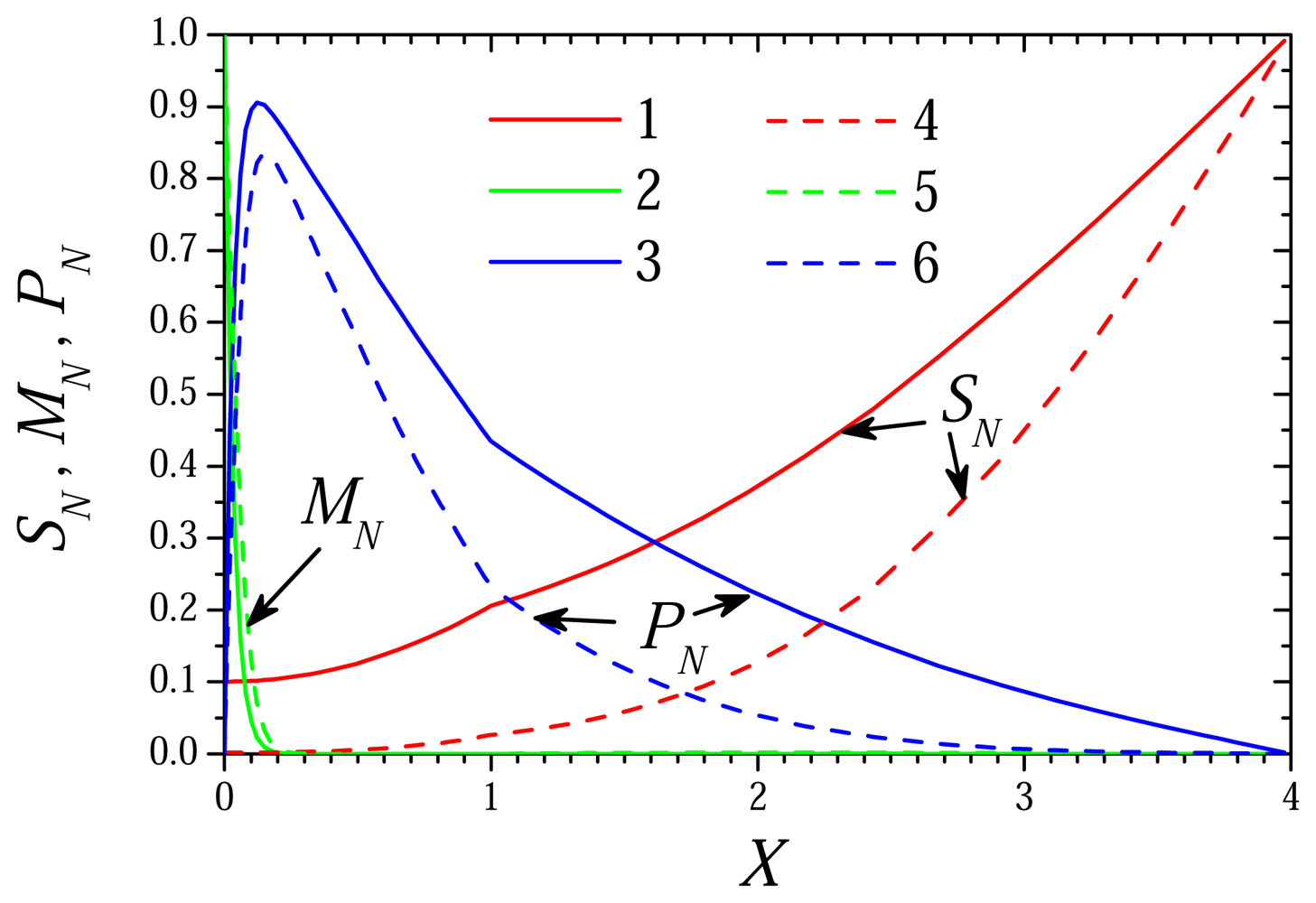
6.1. The Dynamics of the Biosensor Action
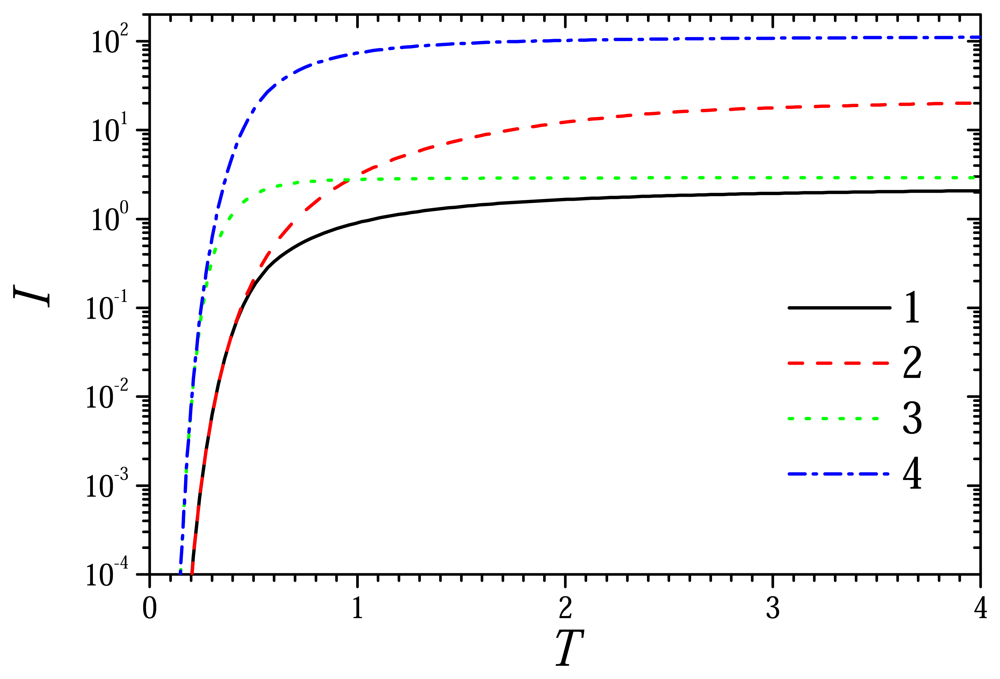
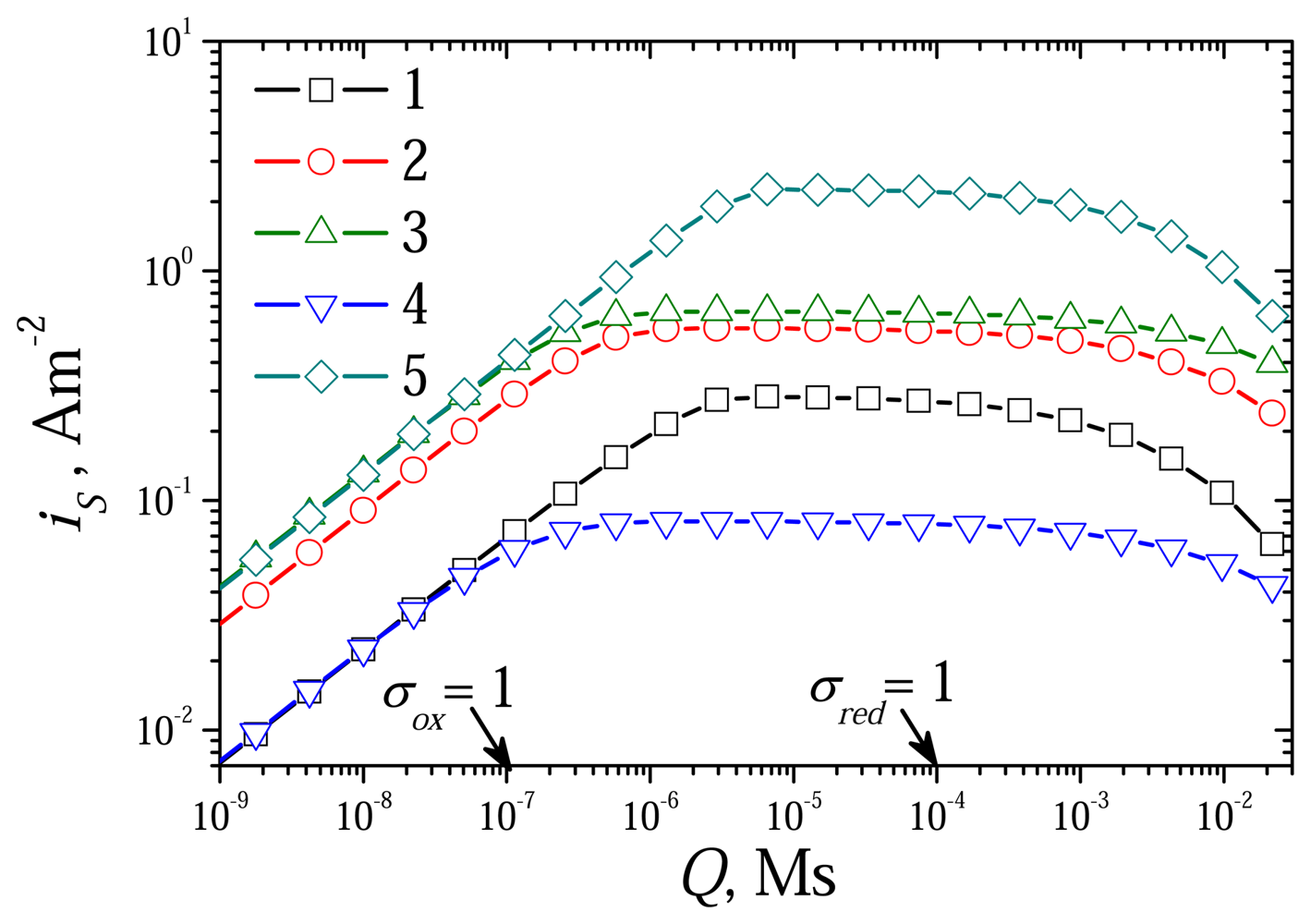
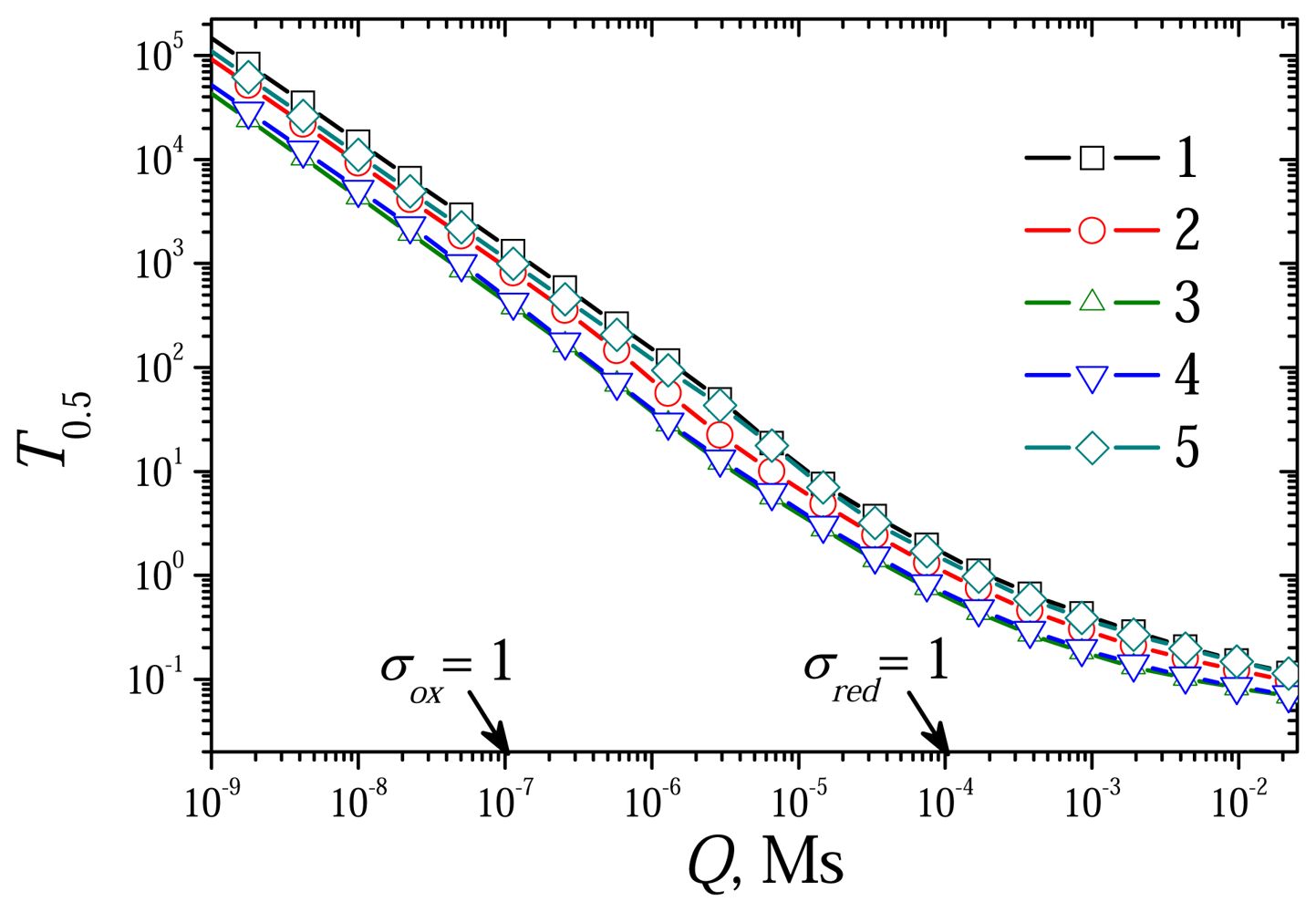
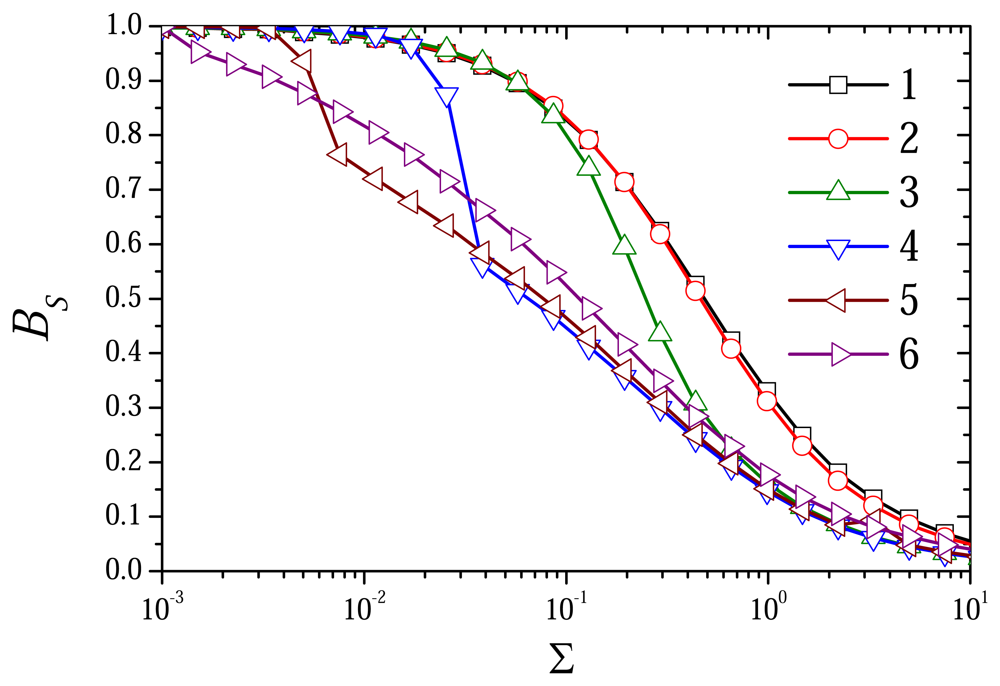
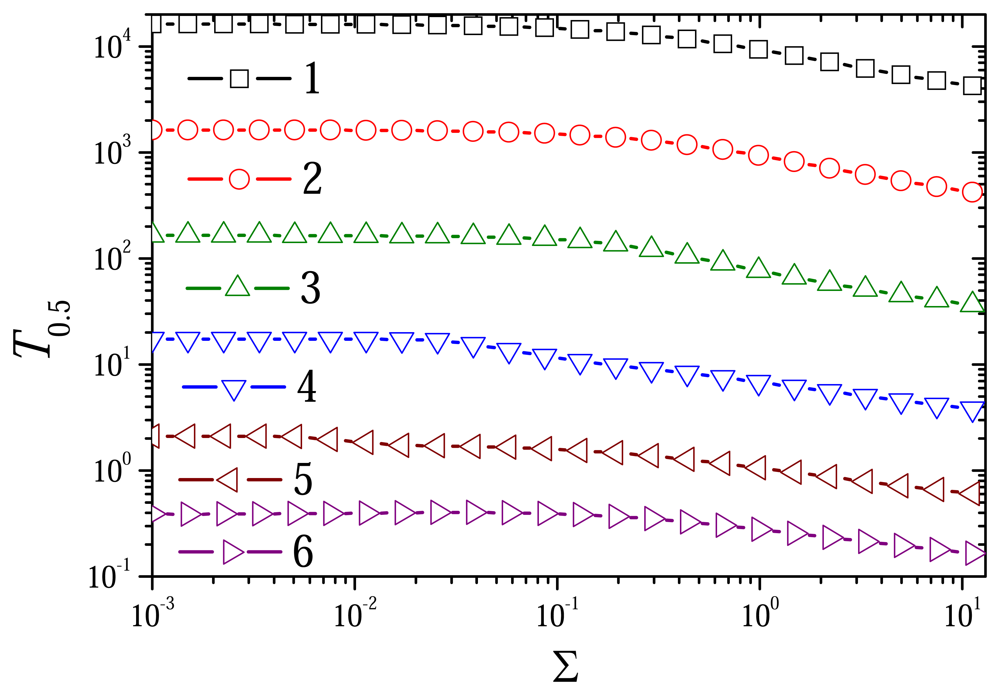
6.2. The Impact of the Diffusion Modulus
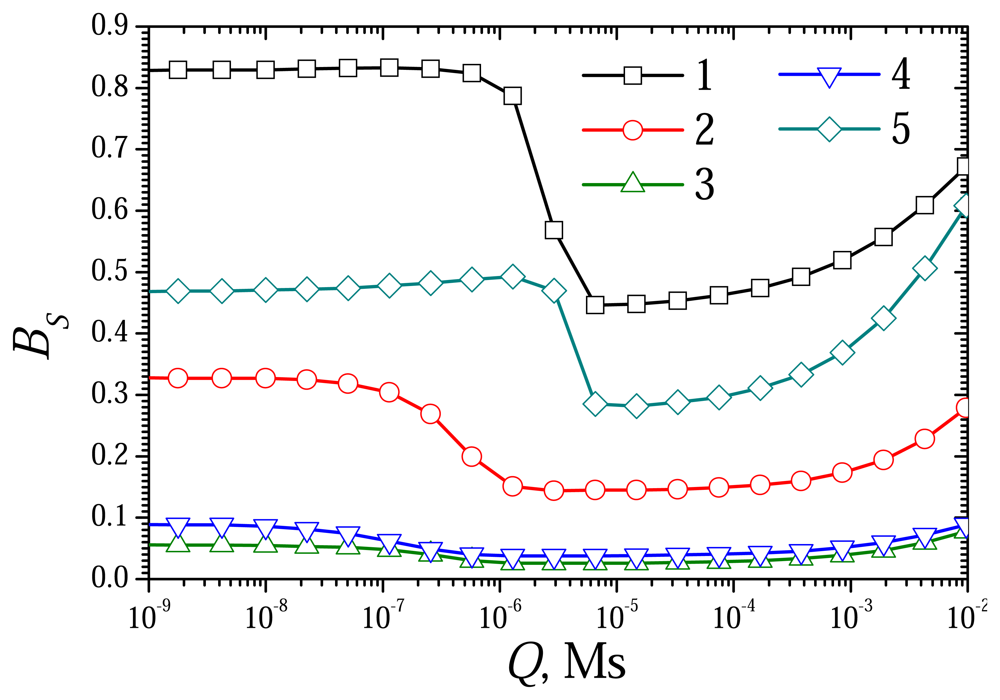
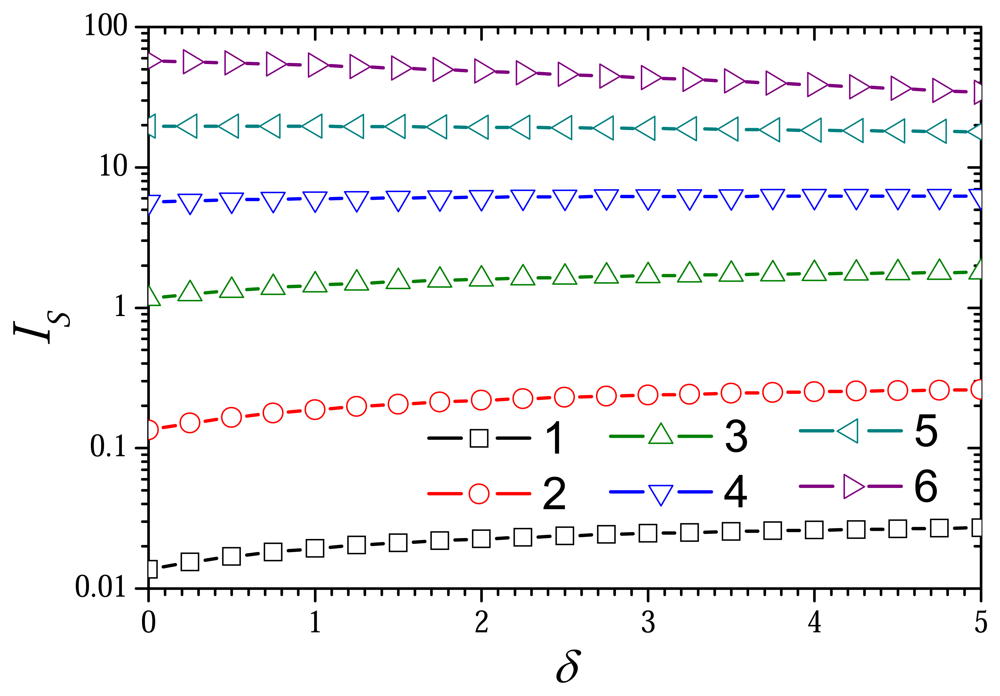
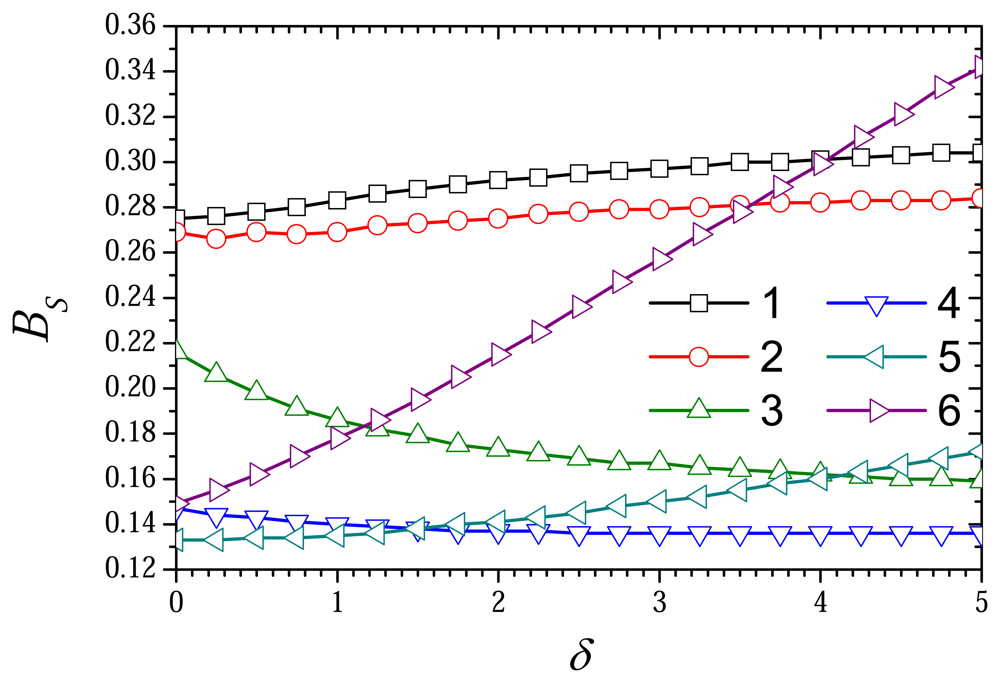
6.3. The Impact of the Thickness of the External Diffusion Layer
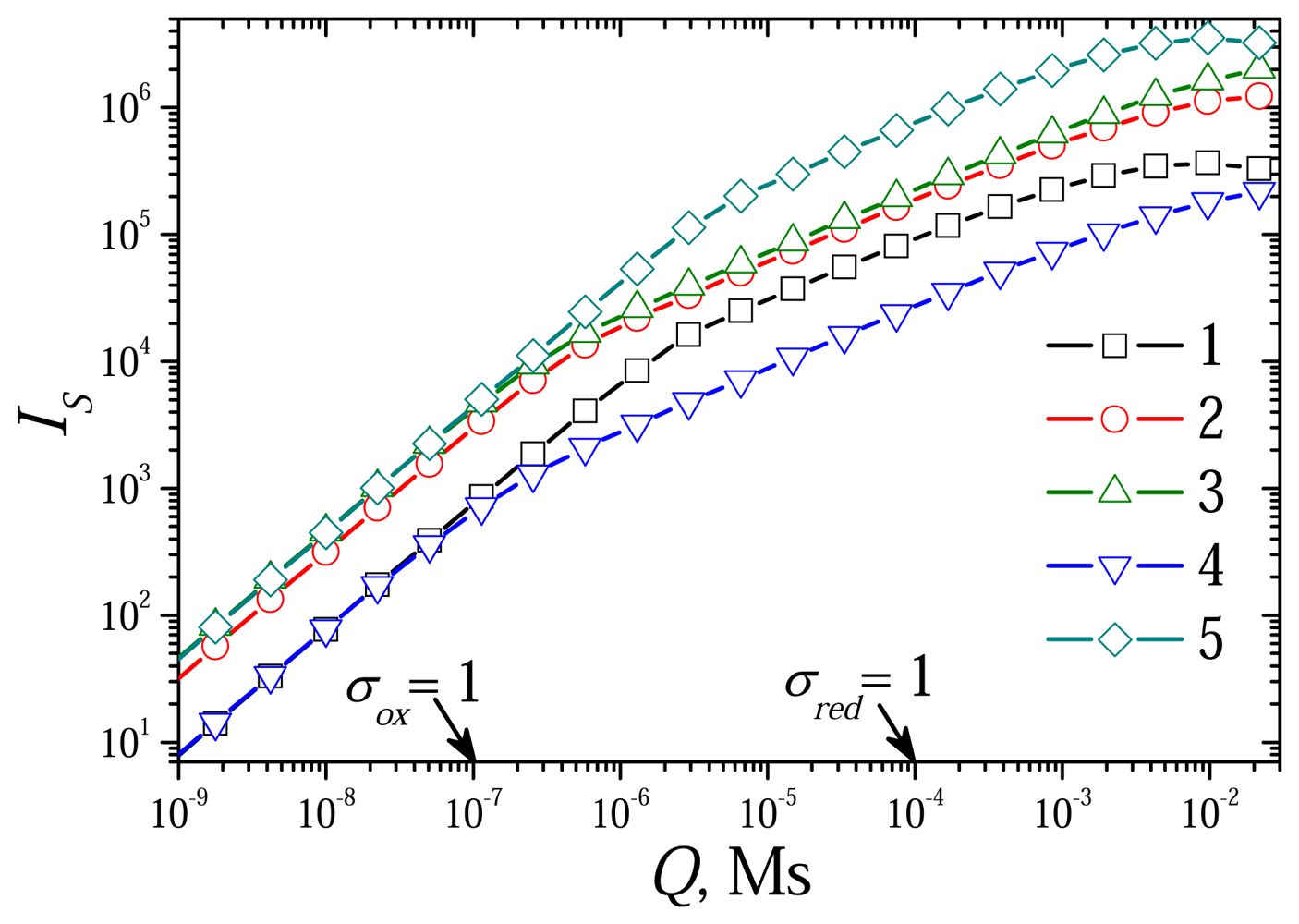
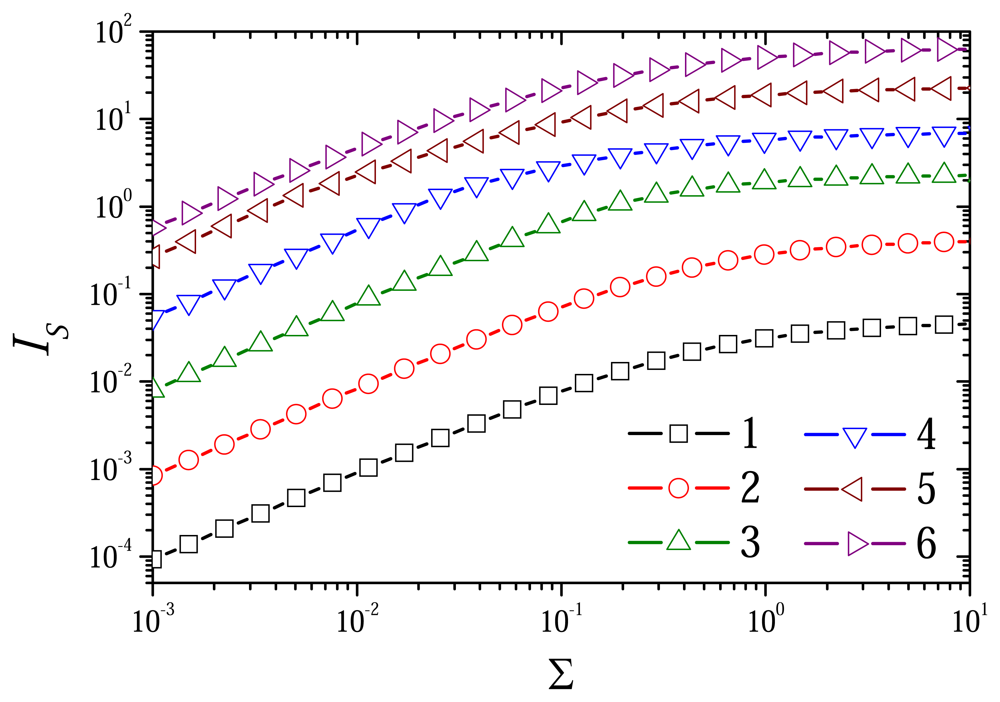
6.4. The Impact of the Outer Substrate Concentration
7. Conclusions
Acknowledgments
References and Notes
- Turner, A. P. F.; Karube, I.; Wilson, G. S. Biosensors: Fundamentals and Applications.; Oxford University Press: Oxford, 1987. [Google Scholar]
- Scheller, F.; Schubert, F. Biosensors.; Elsevier: Amsterdam, 1992. [Google Scholar]
- Chaubey, A.; Malhotra, B. D. Mediated biosensors. Biosens. Bioelectron. 2002, 17(6), 441–456. [Google Scholar]
- Wollenberger, U.; Lisdat, F.; Scheller, F. W. Frontiers in Biosensorics 2. Practical Applications.; Birkhauser Verlag: Basel, 1997. [Google Scholar]
- Knopf, G. K.; Bassi, A. S. Smart Biosensor Technology.; CRC Press: New York, 2007. [Google Scholar]
- Cenas, N. K.; Kulys, J. J. Biocatalytic oxidation of glucose on the conductive charge transfer complexes. Bioelectrochem. Bioenerg. 1981, 8, 103–113. [Google Scholar]
- Sapelnikova, S.; Dock, E.; Solna, R.; Skladal, P.; Ruzgas, T.; Emnéus, J. Screen-printed multienzyme arrays for use in amperometric batch and flow systems. Anal. Bioanal. Chem. 2003, 376(7), 1098–1103. [Google Scholar]
- Hart, J. P.; Crew, A.; Crouch, E.; Honeychurch, K. C.; Pemberton, R. M. Some recent designs and developments of screen-printed carbon electrochemical sensors/biosensors for biomedical, environmental, and industrial analyses. Anal. Lett. 2004, 37(5), 789–830. [Google Scholar]
- Forrow, N. J.; Bayliff, S. W. A commercial whole blood glucose biosensor with a low sensitivity to hematocrit based on an impregnated porous carbon electrode. Biosens. Bioelectron. 2005, 21(4), 3581–587. [Google Scholar]
- Renedo, O. D.; Alonso-Lomillo, M. A.; Martinez, M. J. A. Recent developments in the field of screen-printed electrodes and their related applications. Talanta 2007, 73(2), 202–219. [Google Scholar]
- Tudorache, M.; Bala, C. Biosensors based on screen-printing technology, and their applications in environmental and food analysis. Anal. Bioanal. Chem. 2007, 388(3), 565–578. [Google Scholar]
- Murray, R. W. Chemically modified electrodes. Accts. Chem. Res. 1980, 13(5), 135–141. [Google Scholar]
- Mizutani, F. Application of enzyme-modified electrodes to biosensors. Bunseki Kagaku 1999, 48, 809–821. [Google Scholar]
- Svancara, I.; Vytras, K.; Barek, J.; Zima, J. Carbon paste electrodes in modern electroanalysis. Crit. Rev. Anal. Chem. 2001, 31(4), 311–345. [Google Scholar]
- Mello, L. D.; Kubota, L. T. Review of the use of biosensors as analytical tools in the food and drink industries. Food Chem. 2002, 77(2), 237–256. [Google Scholar]
- Ferreira, L. S.; Souza, M. B. D.; Trierweiler, J. O.; Broxtermann, O.; Folly, R. O. M.; Hitzmann, B. Aspects concerning the use of biosensors for process control: experimental and simulation investigations. Comp. Chem. Engng. 2003, 27(8), 1165–1173. [Google Scholar]
- Corcuera, J. R. D.; Cavalieri, R.; Powers, J.; Tang, J. Amperometric enzyme biosensor optimization using mathematical modeling. Proceedings of the 2004 ASAE / Csae Annual International Meeting, page Paper No. 047030. Ottawa, Ontario, Canada, (August 1-4 2004).
- Amatore, C.; Oleinick, A. I.; Svir, I. Construction of optimal quasi-conformal mappings for the 2d-numerical simulation of diffusion at microelectrodes. part 1: Principle of the method and its application to the inlaid disk microelectrode. J. Electroanal. Chem. 2006, 597(1), 69–76. [Google Scholar]
- Stamatin, I.; Berlic, C.; Vaseashta, A. On the computer-aided modelling of analyte-receptor interactions for an efficient sensor design. Thin Solid Films 2006, 495, 312–315. [Google Scholar]
- Mell, C. D.; Maloy, J. T. A model for the amperometric enzyme electrode obtained through digital simulation and applied to the glucose oxidase system. Anal. Chem. 1975, 47, 299–307. [Google Scholar]
- Kernevez, J. P. Enzyme Mathematics. Studies in Mathematics and its Applications.; Elsevier Science: Amsterdam, 1980. [Google Scholar]
- Kulys, J. The development of new analytical systems based on biocatalysts. Anal. Lett. 1981, 14, 377–397. [Google Scholar]
- Bartlett, P. N.; Pratt, K. F. E. Modelling of processes in enzyme electrodes. Biosens. Bioelectron. 1993, 8(9-10), 451–462. [Google Scholar]
- Lyons, M. E. G.; Greer, J. C.; Fitzgerald, C. A.; Bannon, T.; Barlett, P. N. Theoretical analysis of time dependent diffusion, reaction and electromigration in membranes. Analyst 1996, 121, 715–731. [Google Scholar]
- Pérusse, P.; Leech, D. Dual electrode cyclic voltammetry under computer control using graphical programming of a bipotentiostat. Instrum. Sci. Technol. 2000, 28(1), 59–70. [Google Scholar]
- Schulmeister, T. Mathematical modelling of the dynamic behaviour of amperometric enzyme electrodes. Select. Electr. Rev. 1990, 12, 203–260. [Google Scholar]
- Lyons, M. E. G. Mediated electron transfer at redox active monolayers. Sensors 2001, 1(7), 215–228. [Google Scholar]
- Yokoyama, K.; Koide, S.; Kayanuma, Y. Cyclic voltammetric simulation of electrochemically mediated enzyme reaction and elucidation of blosensor behaviors. Anal. Bioanal. Chem. 2002, 372(2), 248–253. [Google Scholar]
- Kulys, J.; Tetianec, L. Synergistic substrates determination with biosensors. Biosens. Bioelectron. 2005, 21(1), 152–158. [Google Scholar]
- Chen, L. C.; Tseng, K. S.; Ho, K. C. General kinetic model for amperometric sensors based on prussian blue mediator and its analogs: Application to cysteine detection. Electroanalysis 2006, 18(13-14), 1313–1321. [Google Scholar]
- Naujikas, R.; Malinauskas, A.; Ivanauskas, F. Modeling of electrocatalytic processes at conducting polymer modified electrodes. J. Math. Chem. 2007, 42(4), 1069–1084. [Google Scholar]
- Aris, R. The Mathematical Theory of Diffusion and Reaction in Permeable Catalysts. The Theory of the Steady State.; Clarendon Press: Oxford, 1975. [Google Scholar]
- Britz, D. Digital Simulation in Electrochemistry.Springer-Verlag: Berlin, 3rd edition; 2005. [Google Scholar]
- Kulys, J.; Samalius, A. S.; Svirmickas, G.-J. S. Electron exchange between the enzyme active center and organic metal. FEBS Lett. 1980, 114, 7–10. [Google Scholar]
- Samarskii, A. A. The Theory of Difference Schemes.; Marcel Dekker: New York-Basel, 2001. [Google Scholar]
- Baronas, R.; Kulys, J.; Ivanauskas, F. Computational modelling of biosensors with perforated and selective membranes. J. Math. Chem. 2006, 39(2), 345–362. [Google Scholar]
- Gaidamauskaite, E.; Baronas, R. A comparison of finite difference schemes for computational modelling of biosensors. Nonlinear Anal. Model. Contr. 2007, 12(3), 359–369. [Google Scholar]
- Moreira, J. E.; Midkiff, S. P.; Gupta, M.; Artigas, P. V.; Snir, M.; Lawrence, R. D. Java programming for high-performance numerical computing. IBM Syst. J. 2000, 39(6), 21–56. [Google Scholar]
- Baronas, R.; Ivanauskas, F.; Kulys, J. The influence of enzyme membrane thickness on the response of amperometric biosensors. Sensors 2003, 3(7), 248–262. [Google Scholar]
- Baronas, R.; Ivanauskas, F.; Kulys, J. The effect of diffusion limitations on the response of amperometric biosensors with substrate cyclic conversion. J. Math. Chem. 2004, 35(3), 199–213. [Google Scholar]
- Baronas, R.; Gaidamauskaite, E.; Kulys, J. Modelling a peroxidase-based optical biosensor. Sensors 2007, 7(11), 2723–2740. [Google Scholar]
- Ivanauskas, F.; Baronas, R. Modelling an amperometric biosensor acting in a flowing liquid. Int. J. Numer. Meth. Fluids 2008, 56(8), 1313–1319. [Google Scholar]
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Baronas, R.; Kulys, J. Modelling Amperometric Biosensors Based on Chemically Modified Electrodes. Sensors 2008, 8, 4800-4820. https://doi.org/10.3390/s8084800
Baronas R, Kulys J. Modelling Amperometric Biosensors Based on Chemically Modified Electrodes. Sensors. 2008; 8(8):4800-4820. https://doi.org/10.3390/s8084800
Chicago/Turabian StyleBaronas, Romas, and Juozas Kulys. 2008. "Modelling Amperometric Biosensors Based on Chemically Modified Electrodes" Sensors 8, no. 8: 4800-4820. https://doi.org/10.3390/s8084800



