Interferometric Synthetic Aperture Microscopy: Computed Imaging for Scanned Coherent Microscopy
Abstract
:1. Introduction
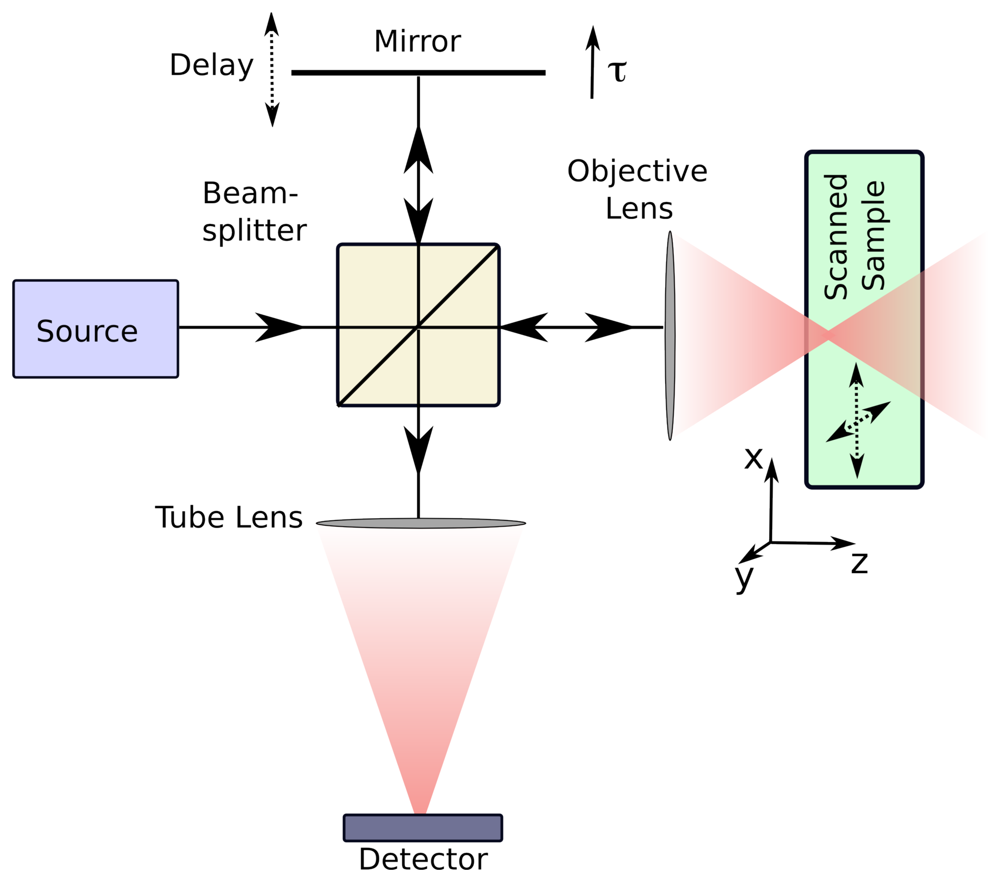
2. Optical Coherence Tomography
3. General Framework
3.1. The Back-Scattered Field
3.2. Signal Detection in Radar
3.3. Signal Detection in Time-Domain OCT and ISAM
3.4. Signal Detection in Fourier-Domain OCT and ISAM
4. System Modeling
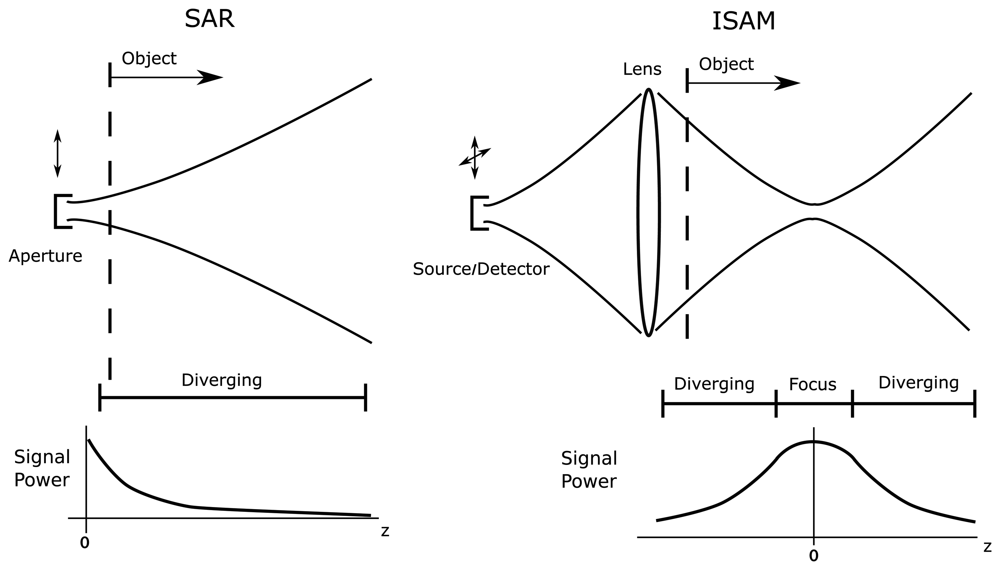
4.1. Radar and OCT
4.2. SAR and ISAM
5. The Inverse Problem for SAR and ISAM
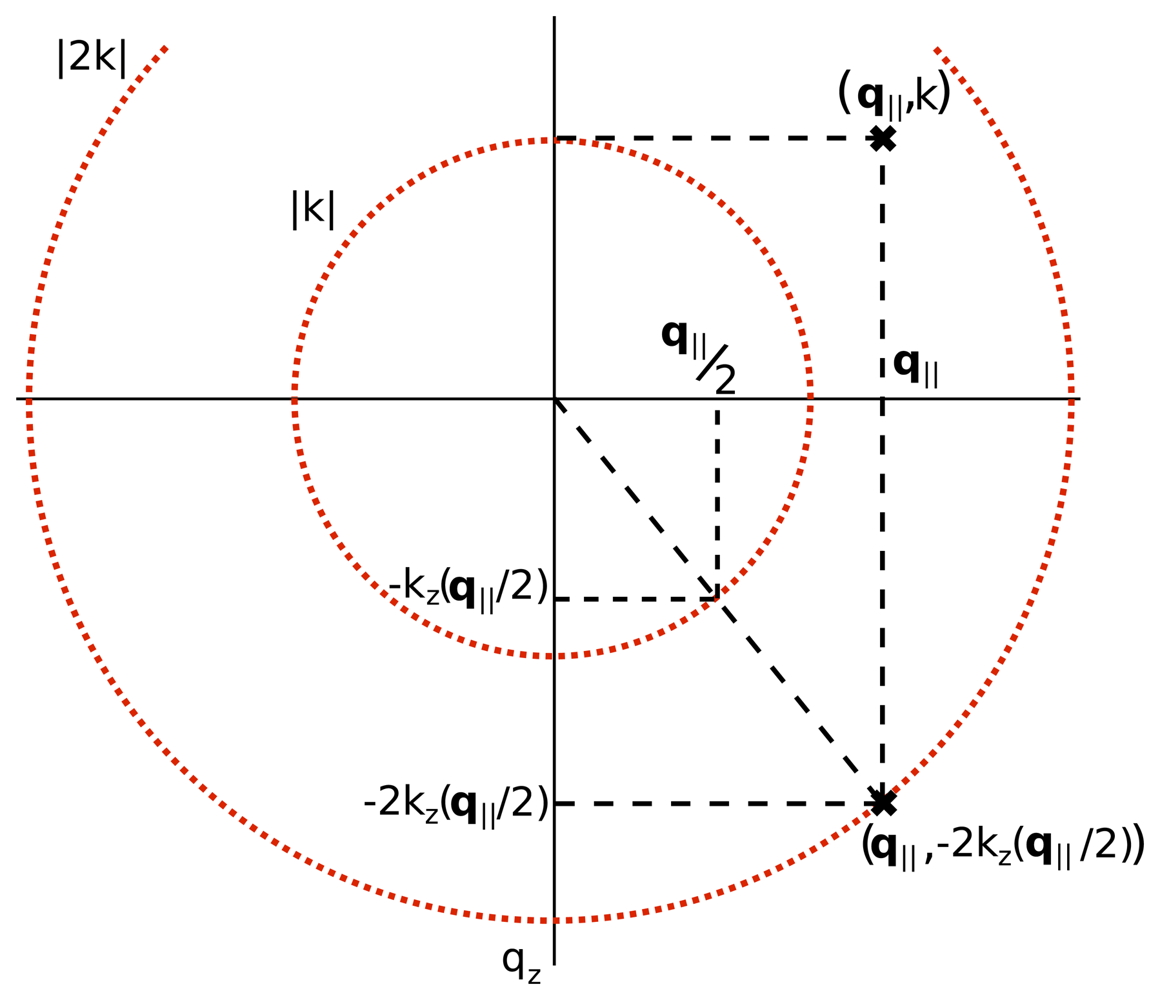
5.1. Transverse Spatial Fourier Representation of the Model
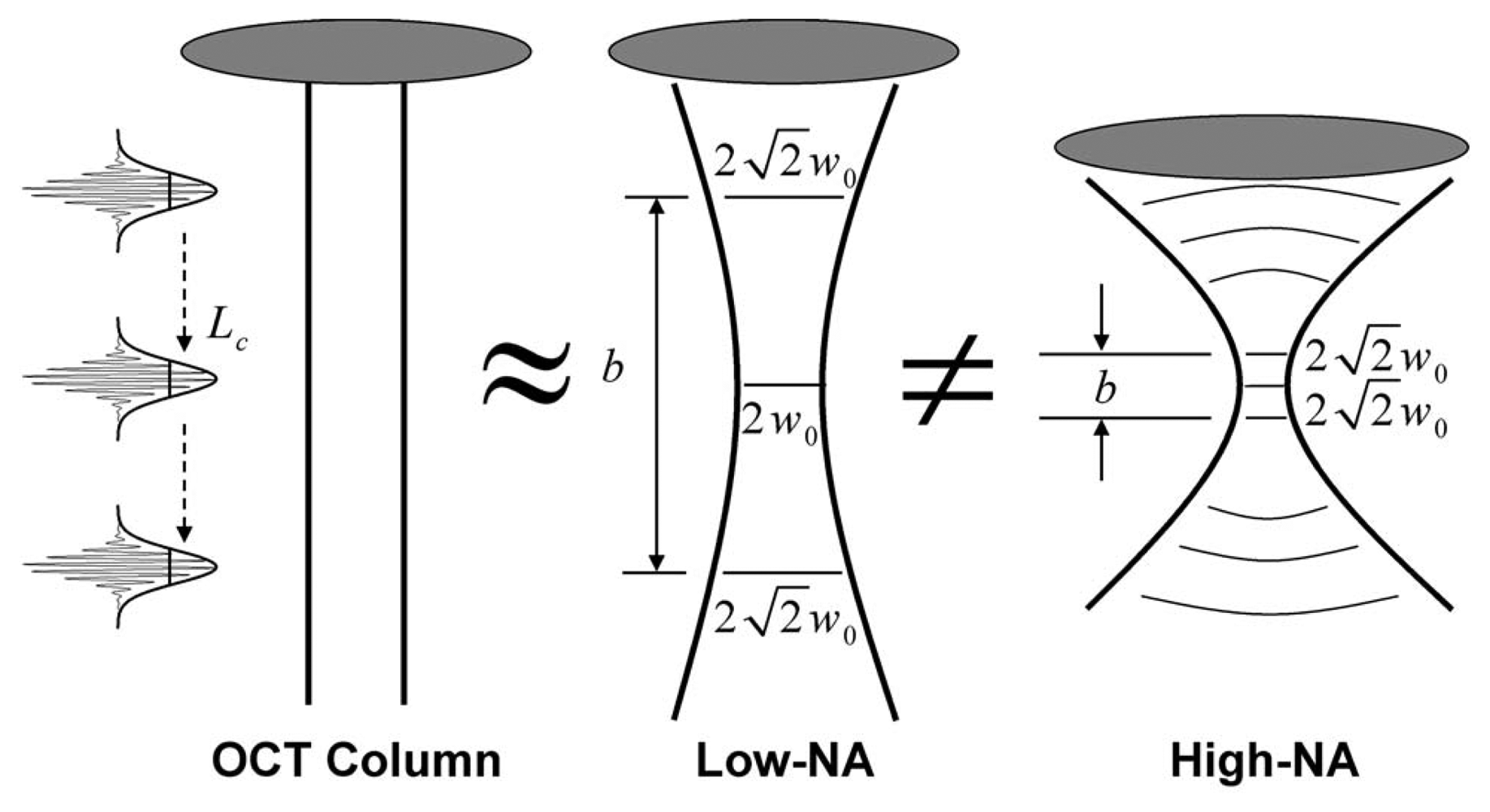
5.2. Model Approximation in Diverging Regions
5.3. Model Approximation in Focused Regions
5.4. Reduction to Resampling
- Starting with the complex data S(ρ‖, ω), collected as described in Sec. 3, take the transverse spatial Fourier transform to get S̃(q‖, ω).
- Implement a linear filtering, i.e., a Fourier-domain multiplication of a transfer function with S̃ (q‖, ω), to compensate for the bandpass shape given by A(ω) H(−q‖, ω) in Eq. (25). This step may often be omitted without significant detriment to the resulting image.
- Warp the coordinate space of S̃ (q‖, ω) so as to account for the Stolt mapping illustrated in Fig. 4. Resample the result back to a regular grid to facilitate numerical processing.
- Take the inverse three-dimensional Fourier transform to get an estimate of η(r)/R(z), the object with an attenuation away from focus.
- If required, multiply the resulting estimate by R(z) to compensate for decay of the signal away from focus.
6. Results
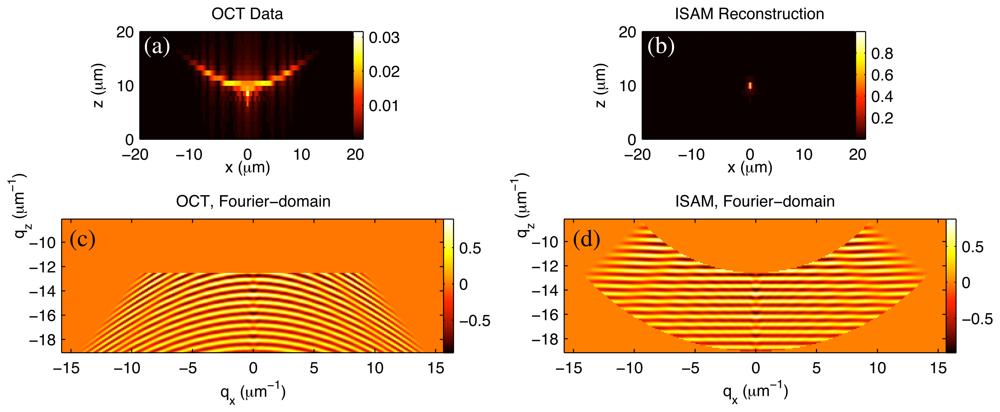
6.1. Simulations
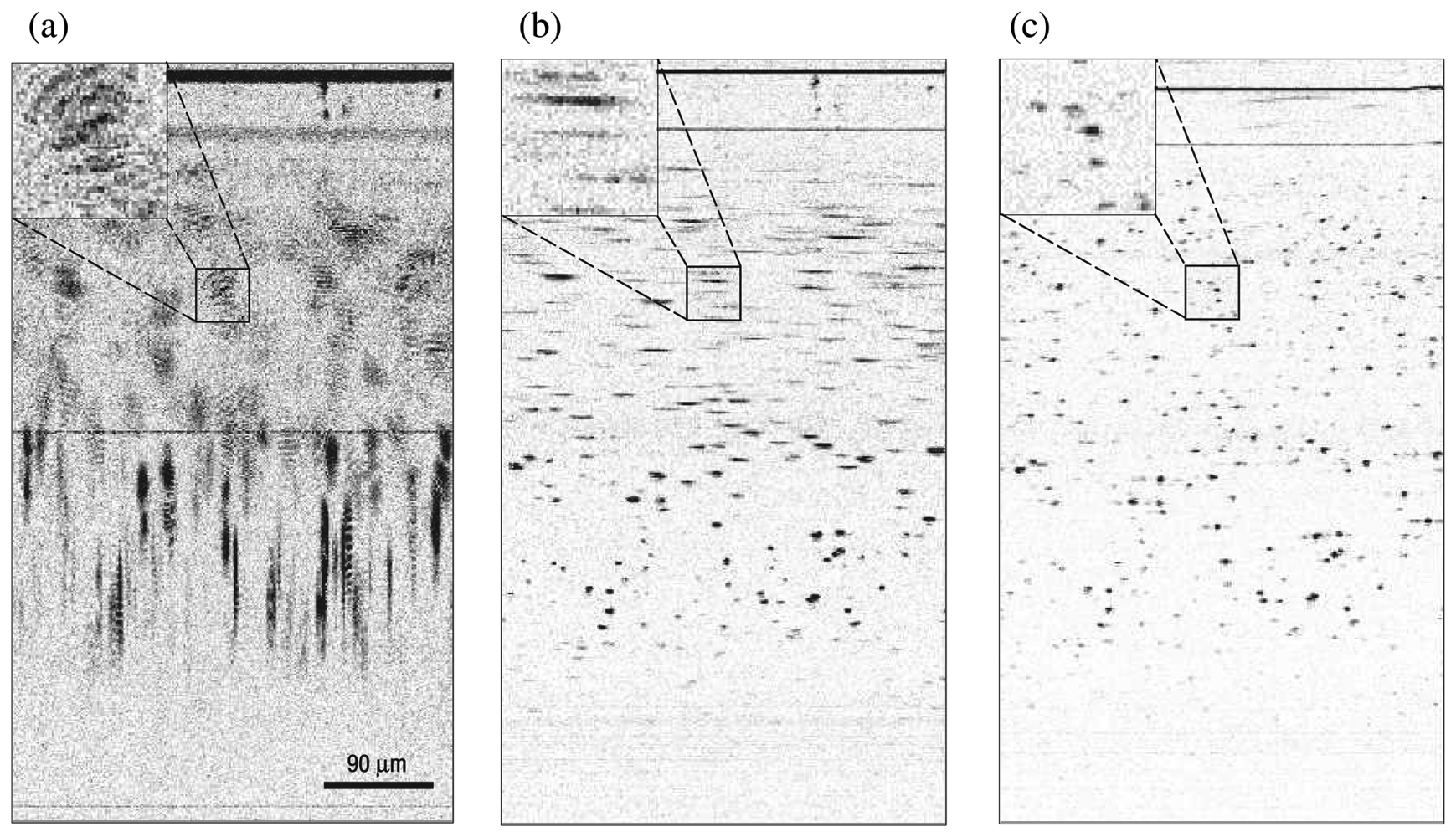
6.2. Imaging a Phantom
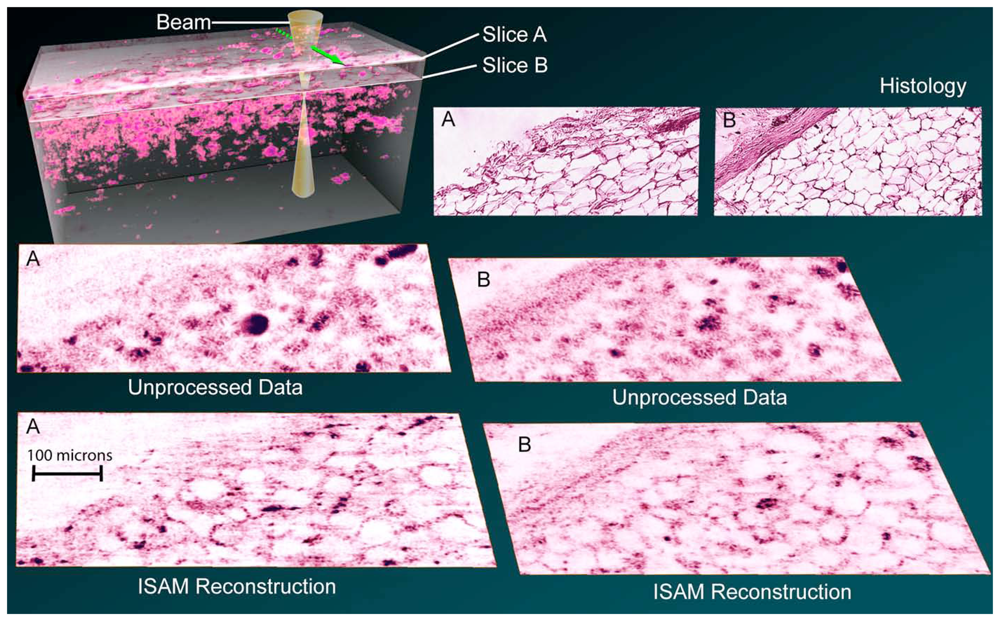
6.3. Imaging Tissue
7. Alternate ISAM Modalities
7.1. Vector ISAM
7.2. Full-Field ISAM
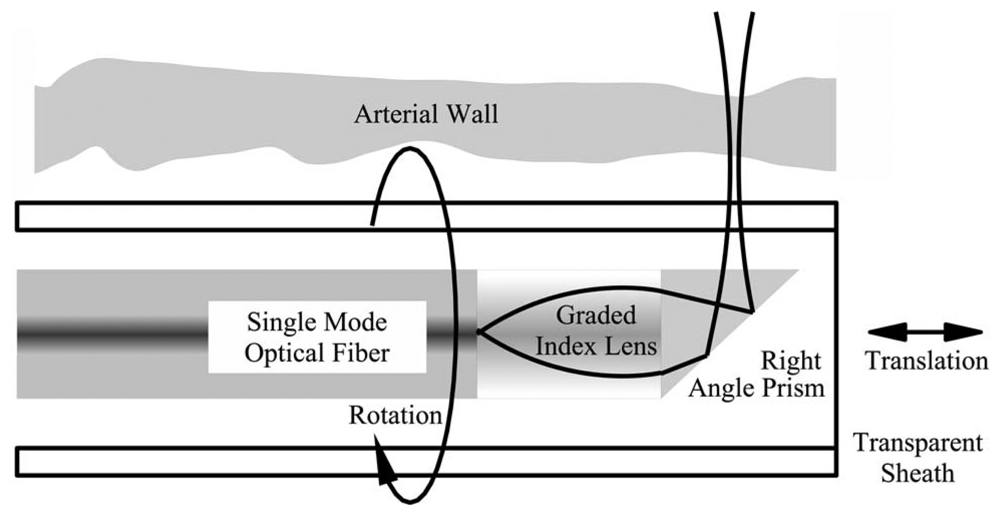
7.3. Rotationally-Scanned ISAM
7.4. Partially-Coherent ISAM
8. Conclusions
Acknowledgments
References
- Röntgen, W. C. On a new kind of rays. Nature 1896, 1369, 274–276. [Google Scholar]
- Bloch, F.; Hansen, W. W.; Packard, M. The nuclear induction experiment. Phys. Rev. 1946, 70, 474–485. [Google Scholar]
- Carr, H. Y.; Purcell, E. M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 1954, 94, 630–638. [Google Scholar]
- Buderi, R. The Invention That Changed the World.Abacus, second edition; 1998. [Google Scholar]
- Sabra, A. I. The Optics of Ibn Al-Haytham.; The Warburg Institute, 1989. [Google Scholar]
- Schaller, R. R. Moore's law: past, present and future. IEEE Spectrum 1997, 34(6), 52–59. [Google Scholar]
- Cormack, A. M. Representation of a function by its line integrals, with some radiological applications. J. Appl. Phys. 1963, 34, 2722–2727. [Google Scholar]
- Hounsfield, G. N. Computerized transverse axial scanning (tomography): part I. Description of system. Br. J. Radiol. 1973, 46, 1016–1022. [Google Scholar]
- Lauterbur, P. C. Image formation by induced local interactions: examples employing nuclear magnetic resonance. Nature 1973, 242, 190–191. [Google Scholar]
- Curlander, J. C.; McDonough, R. N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley-Interscience, 1991. [Google Scholar]
- Gough, P. T.; Hawkins, D. W. Unified framework for modern synthetic aperture imaging algorithms. Int. J. Imag. Syst. Technol. 1997, 8, 343–358. [Google Scholar]
- Carrara, W. G.; Goodman, R. S.; Majewski, R. M. Spotlight Synthetic Aperture Radar Signal Processing Algorithms.; Artech House, 1995. [Google Scholar]
- Davis, B. J.; Ralston, T. S.; Marks, D. L.; Boppart, S. A.; Carney, P. S. Autocorrelation artifacts in optical coherence tomography and interferometric synthetic aperture microscopy. Opt. Lett. 2007, 32, 1441–1443. [Google Scholar]
- Davis, B. J.; Schlachter, S. C.; Marks, D. L.; Ralston, T. S.; Boppart, S. A.; Carney, P. S. Nonparax-ial vector-field modeling of optical coherence tomography and interferometric synthetic aperture microscopy. J. Opt. Soc. Am A 2007, 24, 2527–2542. [Google Scholar]
- Marks, D. L.; Ralston, T. S.; Boppart, S. A.; Carney, P. S. Inverse scattering for frequency-scanned full-field optical coherence tomography. J. Opt. Soc. Am A 2007, 24, 1034–1041. [Google Scholar]
- Marks, D. L.; Ralston, T. S.; Carney, P. S.; Boppart, S. A. Inverse scattering for rotationally scanned optical coherence tomography. J. Opt. Soc. Am A 2006, 23, 2433–2439. [Google Scholar]
- Ralston, T. S.; Marks, D. L.; Carney, P. S.; Boppart, S. A. Inverse scattering for optical coherence tomography. J. Opt. Soc. Am A 2006, 23, 1027–1037. [Google Scholar]
- Ralston, T. S.; Marks, D. L.; Carney, P. S.; Boppart, S. A. Interferometric synthetic aperture microscopy. Nat. Phys. 2007, 3, 129–134. [Google Scholar]
- Ralston, T. S.; Marks, D. L.; Boppart, S. A.; Carney, P. S. Inverse scattering for high-resolution interferometric microscopy. Opt. Lett. 2006, 24, 3585–3587. [Google Scholar]
- Ralston, T. S.; Marks, D. L.; Carney, P. S.; Boppart, S. A. Real-time interferometric synthetic aperture microscopy. Opt. Express 2008, 16, 2555–2569. [Google Scholar]
- Wheatstone, C. Contributions to the physiology of vision. Part the first. On some remarkable, and hitherto unobserved, phenomena of binocular vision. Philos. T. Roy. Soc. 1838, 128, 371–394. [Google Scholar]
- Kellermann, K. I.; Moran, J. M. The development of high-resolution imaging in radio astronomy. Annu. Rev. Astrophys. 2001, 39, 457–509. [Google Scholar]
- Markel, V. A.; Schotland, J. C. Inverse problem in optical diffusion tomography. I. Fourier-Laplace inversion formulas. J. Opt. Soc. Am. A 2001, 18, 1336–1347. [Google Scholar]
- Milstein, A. B.; Oh, S.; Webb, K. J.; Bouman, C. A.; Zhang, Q.; Boas, D. A.; MIllane, R. P. Fluorescence optical diffusion tomography. Appl. Opt. 2003, 42, 3081–3094. [Google Scholar]
- Boas, D. A.; Brooks, D. H.; Miller, E. L.; DiMarzio, C. A.; Kilmer, M.; Gaudette, R. J.; Zhang, Q. Imaging the body with diffuse optical tomography. IEEE Signal Proc. Mag. 2001, 18(6), 57–75. [Google Scholar]
- Ollinger, J. M.; Fessler, J. A. Positron-emission tomography. IEEE Signal Proc. Mag. 1997, 14(1), 43–55. [Google Scholar]
- Donoho, D. L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar]
- Cande's, E. J.; Romberg, J.; Tao, T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar]
- Takhar, D.; Laska, J. N.; Wakin, M. B.; Duarte, M. F.; Baron, D.; Sarvotham, S.; Kelly, K. F.; Bara-niuk, R. G. A new compressive imaging camera architecture using optical-domain compression. In Proc. Computational Imaging IV; volume 6065, SPIE, 2006. [Google Scholar]
- Sato, T.; Ueda, M.; Fukuda, S. Synthetic aperture sonar. J. Acoust. Soc. Am. 1973, 54, 799–802. [Google Scholar]
- Williams, R. E. Creating an acoustic synthetic aperture in the ocean. J. Acoust. Soc. Am. 1976, 60, 60–73. [Google Scholar]
- Hayes, M. P.; Gough, P. T. Broad-band synthetic aperture sonar. IEEE J. Oceanic Eng. 1992, 17, 80–94. [Google Scholar]
- Gray, S. H.; Etgen, J.; Dellinger, J.; Whitmore, D. Seismic migration problems and solutions. Geophysics 2001, 66, 1622–1640. [Google Scholar]
- Bleistein, N.; Cohen, J. K.; Stockwell, J. W. Mathematics of Multidimensional Seiesmic Imaging, Migration and Inversion; Springer, 2001. [Google Scholar]
- Angelsen, B. A. J. Ultrasound Imaging: Waves, Signals and Signal Processing.; Emantec, 2000. [Google Scholar]
- Nelson, T. R.; Pretorius, D. H. Three-dimensional ultrasound imaging. Ultrasound Med. Biol. 1998, 24, 1243–1270. [Google Scholar]
- Profio, A. E.; Doiron, D. R. Transport of light in tissue in photodynamic therapy. Photochem. Photobiol. 1987, 46, 591–599. [Google Scholar]
- Huang, D.; Swanson, E. A.; Lin, C. P.; Schuman, J. S.; Stinson, W. G.; Chang, W.; Hee, M. R.; Flotte, T.; Gregory, K.; Puliafito, C. A.; Fujimoto, J. G. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar]
- Schmitt, J. M. Optical coherence tomography (OCT): a review. IEEE J. Select. Topics Quantum Electron. 1999, 5, 1205–1215. [Google Scholar]
- Brezinski, M. E. Optical Coherence Tomography: Principles and Applications.; Academic Press, 2006. [Google Scholar]
- Zysk, A. M.; Nguyen, F. T.; Oldenburg, A. L.; Marks, D. L.; Boppart, S. A. Optical coherence tomography: a review of clinical development from bench to bedside. J. Biomed. Opt. 2007, 12. (051403). [Google Scholar]
- Young, T. A Course of Lectures on Natural Philosophy and the Mechanical Arts.; Joseph Johnson: London, 1807. [Google Scholar]
- Michelson, A. A.; Morley, E. W. On the relative motion of the Earth and the luminiferous ether. Am. J. Sci. 1887, 34, 333–345. [Google Scholar]
- Hariharan, P. Optical Interferometry.; Academic Press, 2003. [Google Scholar]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University, 1995. [Google Scholar]
- Saleh, B. E. A.; Teich, M. C. Fundamentals of Photonics; chapter 3; pp. 80–107. John Wiley and Sons, 1991. [Google Scholar]
- Gabor, D.; Goss, W. P. Interference microscope with total wavefront reconstruction. J. Opt. Soc. Am. 1966, 56, 849–858. [Google Scholar]
- Arons, E.; Leith, E. Coherence confocal-imaging system for enhanced depth discrimination in transmitted light. Appl. Opt. 1996, 35, 2499–2506. [Google Scholar]
- Leith, E. N.; Mills, K. D.; Naulleau, P. P.; Dilworth, D. S.; Iglesias, I.; Chen, H. S. Generalized confocal imaging and synthetic aperture imaging. J. Opt. Soc. Am. A 1999, 16, 2880–2886. [Google Scholar]
- Chien, W.-C.; Dilworth, D. S.; Elson, L.; Leith, E. N. Synthetic-aperture chirp confocal imaging. Appl. Opt. 2006, 45, 501–510. [Google Scholar]
- Davis, B. J.; Ralston, T. S.; Marks, D. L.; Boppart, S. A.; Carney, P. S. Interferometric synthetic aperture microscopy: physics-based image reconstruction from optical coherence tomography data. In International Conference on Image Processing; volume 4, pp. 145–148. IEEE, 2007. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics.Cambridge University, 6 edition; 1980. [Google Scholar]
- Turin, G. An introduction to matched filters. IEEE Trans. Inf. Theory 1960, 6, 311–329. [Google Scholar]
- Wahl, D. E.; Eichel, P. H.; Ghiglia, D. C.; Jakowatz, C. V., Jr. Phase gradient autofocus—a robust tool for high resolution SAR phase correction. IEEE Trans. Aero. Elec. Sys. 1994, 30, 827–835. [Google Scholar]
- Ralston, T. S.; Marks, D. L.; Carney, P. S.; Boppart, S. A. Phase stability technique for inverse scattering in optical coherence tomography. 3rd International Symposium on Biomedical Imaging; 2006; pp. 578–581. [Google Scholar]
- Fercher, A. F.; Hitzenberger, C. K.; Kamp, G.; El-Zaiat, S. Y. Measurement of intraocular distances by backscattering spectral interferometry. Opt. Commun. 1996, 117, 43–48. [Google Scholar]
- Choma, M. A.; Sarunic, M. V.; Yang, C.; Izatt, J. A. Sensitivity advantage of swept source and Fourier domain optical coherence tomography. Opt. Express 2003, 11, 2183–2189. [Google Scholar]
- Leitgeb, R.; Hitzenberger, C. K.; Fercher, A. F. Performance of Fourier domain vs. time domain optical coherence tomography. Opt. Express 2003, 11, 889–894. [Google Scholar]
- Bhargava, R.; Wang, S.-Q.; Koenig, J. L. FTIR microspectroscopy of polymeric systems. Adv. Polym. Sci. 2003, 163, 137–191. [Google Scholar]
- Griffiths, P. R.; De Haseth, J. A. Fourier Transform Infrared SpectrometryWiley-Interscience, second edition; 2007. [Google Scholar]
- Papoulis, A.; Pillai, S. U. Probability, Random Variables and Stochastic Processes; chapter 11.4; pp. 513–522. McGraw-Hill, 2002. [Google Scholar]
- Zhao, Y.; Chen, Z.; Saxer, C.; Xiang, S.; de Boer, J. F.; Nelson, J. S. Phase-resolved optical coherence tomography and optical Doppler tomography for imaging blood flow in human skin with fast scanning speed and high velocity sensitivity. Opt. Lett. 2000, 25, 114–116. [Google Scholar]
- Potton, R. J. Reciprocity in optics. Rep. Prog. Phys. 2004, 67, 717–754. [Google Scholar]
- Marks, D. L.; Oldenburg, A. L.; Reynolds, J. J.; Boppart, S. A. A digital algorithm for dispersion correction in optical coherence tomography. Appl. Opt. 2003, 42, 204–217. [Google Scholar]
- Marks, D. L.; Oldenburg, A. L.; Reynolds, J. J.; Boppart, S. A. Autofocus algorithm for dispersion correction in optical coherence tomography. Appl. Opt. 2003, 42, 3038–3046. [Google Scholar]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system. Proc. R. Soc. London A 1959, 253, 358–379. [Google Scholar]
- Hansen, P. C. Numerical tools for analysis and solution of Fredholm integral equations of the first kind. Inverse Prob. 1992, 8, 849–872. [Google Scholar]
- Karl, W. C. Handbook of Image and Video Processing; chapter Regularization in Image Restoration and Reconstruction; pp. 141–161. Academic, 2000. [Google Scholar]
- Vogel, C. R. Computational Methods for Inverse Problems.; SIAM, 2002. [Google Scholar]
- Wiener, N. Extrapolation, Interpolation, and Smoothing of Stationary Time Series; The MIT Press, 1964. [Google Scholar]
- Gazdag, J.; Sguazzero, P. Migration of seismic data. Proc. IEEE 1984, 72, 1302–1315. [Google Scholar]
- Stolt, R. H. Migration by Fourier transform. Geophysics 1978, 43, 23–48. [Google Scholar]
- Langenberg, K. J.; Berger, M.; Kreutter, T.; Mayer, K.; Schmitz, V. Synthetic aperture focusing technique signal processing. NDT Int. 1986, 19, 177–189. [Google Scholar]
- Mayer, K.; Marklein, R.; Langenberg, K. J.; Kreutter, T. Three-dimensional imaging system based on Fourier transform synthetic aperture focusing technique. Ultrasonics 1990, 28, 241–255. [Google Scholar]
- Schmitz, V.; Chakhlov, S.; Müller. Experiences with synthetic aperture focusing technique in the field. Ultrasonics 2000, 38, 731–738. [Google Scholar]
- Passmann, C.; Ermert, H. A 100-MHz ultrasound imaging system for dermatologic and ophthal-mologic diagnostics. IEEE Trans. Ultrason. Ferr. 1996, 43, 545–552. [Google Scholar]
- Cafforio, C.; Prati, C.; Rocca, F. SAR data focusing using seismic migration techniques. IEEE Trans. Aero. Elec. Sys. 1991, 27, 194–207. [Google Scholar]
- Ralston, T. S.; Marks, D. L.; Kamalabadi, F.; Boppart, S. A. Deconvolution methods for mitigation of transverse blurring in optical coherence tomography. IEEE Trans. Image Proc. 2005, 14, 1254–1264. [Google Scholar]
- Charvat, G. L. A Low-Power Radar Imaging System. PhD thesis, Michigan State University, 2007. [Google Scholar]
- Charvat, G. L.; Kempel, L. C.; Coleman, C. A low-power, high sensitivity, X-band rail SAR imaging system. (to be published). IEEE Antenn. Propag. Mag. 2008, 50. [Google Scholar]
- Izatt, J. A.; Hee, M. R.; Owen, G. M.; Swanson, E. A.; Fujimoto, J. G. Optical coherence microscopy in scattering media. Opt. Lett. 1994, 19, 590–592. [Google Scholar]
- Abouraddy, A. F.; Toussaint, K. C., Jr. Three-dimensional polarization control in microscopy. Phys. Rev. Lett. 2006, 96, 153901. [Google Scholar]
- Beversluis, M. R.; Novotny, L.; Stranick, S. J. Programmable vector point-spread function engineering. Opt. Express 2006, 14, 2650–2656. [Google Scholar]
- Novotny, L.; Beversluis, M. R.; Youngworth, K. S.; Brown, T. G. Longitudinal field modes probed by single molecules. Phys. Rev. Lett. 2001, 86, 5251–5254. [Google Scholar]
- Quabis, S.; Dorn, R.; Leuchs, G. Generation of a radially polarizaed doughnut mode of high quality. Appl. Phys. B 2005, 81, 597–600. [Google Scholar]
- Sick, B.; Hecht, B.; Novotny, L. Orientational imaging of single molecules by annular illumination. Phys. Rev. Lett. 2000, 85, 4482–4485. [Google Scholar]
- Toprak, E.; Enderlein, J.; Syed, S.; McKinney, S. A.; Petschek, R. G.; Ha, T.; Goldman, Y. E.; Selvin, P. R. Defocused orientation and position imaging (DOPI) of myosin V. PNAS 2006, 103, 6495–6499. [Google Scholar]
- Butcher, P. N.; Cotter, D. The Elements of Nonlinear Optics; chapter 5.2; pp. 131–134. Cambridge University, 1990. [Google Scholar]
- Akiba, M.; Chan, K. P.; Tanno, N. Full-field optical coherence tomography by two-dimensional heterodyne detection with a pair of CCD cameras. Opt. Lett. 2003, 28, 816–818. [Google Scholar]
- Dubois, A.; Moneron, G.; Grieve, K.; Boccara, A. C. Three-dimensional cellular-level imaging using full-field optical coherence tomography. Phys. Med. Biol. 2004, 49, 1227–1234. [Google Scholar]
- Dubois, A.; Vabre, L.; Boccara, A.-C.; Beaurepaire, E. High-resolution full-field optical coherence tomography with a Linnik microscope. Appl. Opt. 2002, 41, 805–812. [Google Scholar]
- Laude, B.; De Martino, A.; Drévillon, B.; Benattar, L.; Schwartz, L. Full-field optical coherence tomography with thermal light. Appl. Opt. 2002, 41, 6637–6645. [Google Scholar]
- Považay, B.; Unterhuber, A.; Hermann, B.; Sattmann, H.; Arthaber, H.; Drexler, W. Full-field time-encoded frequency-domain optical coherence tomography. Opt. Express 2006, 14, 7661–7669. [Google Scholar]
- Devaney, A. J. Reconstructive tomography with diffracting wavefields. Inverse Prob. 1986, 2, 161–183. [Google Scholar]
- Pan, S. X.; Kak, A. C. A computational study of reconstruction algorithms for diffraction tomography: interpolations versus filtered backpropagation. IEEE Trans. Acoust. Speech Signal Proc. 1983, ASSP-31, 1262–1275. [Google Scholar]
- Wolf, E. Three-dimensional structure determination of semi-transparent objects from holographic data. Opt. Commun. 1969, 1, 153–156. [Google Scholar]
- Marks, D. L.; Davis, B. J.; Boppart, S. A.; Carney, P. S. Partially coherent illumination in full-field interferometric synthetic aperture microscopy (submitted). J. Opt. Soc. Am. A 2008. [Google Scholar]
- Brigham, E. The Fast Fourier Transform and Its Applications.; Prentice-Hall, 1988. [Google Scholar]



© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Davis, B.J.; Marks, D.L.; Ralston, T.S.; Carney, P.S.; Boppart, S.A. Interferometric Synthetic Aperture Microscopy: Computed Imaging for Scanned Coherent Microscopy. Sensors 2008, 8, 3903-3931. https://doi.org/10.3390/s8063903
Davis BJ, Marks DL, Ralston TS, Carney PS, Boppart SA. Interferometric Synthetic Aperture Microscopy: Computed Imaging for Scanned Coherent Microscopy. Sensors. 2008; 8(6):3903-3931. https://doi.org/10.3390/s8063903
Chicago/Turabian StyleDavis, Brynmor J., Daniel L. Marks, Tyler S. Ralston, P. Scott Carney, and Stephen A. Boppart. 2008. "Interferometric Synthetic Aperture Microscopy: Computed Imaging for Scanned Coherent Microscopy" Sensors 8, no. 6: 3903-3931. https://doi.org/10.3390/s8063903



