Reflectance Modeling for Real Snow Structures Using a Beam Tracing Model
Abstract
:1. Introduction
2. The beam tracing model (BTM)
2.1 Morphology of the scattering medium
2.2 Illumination of the sample
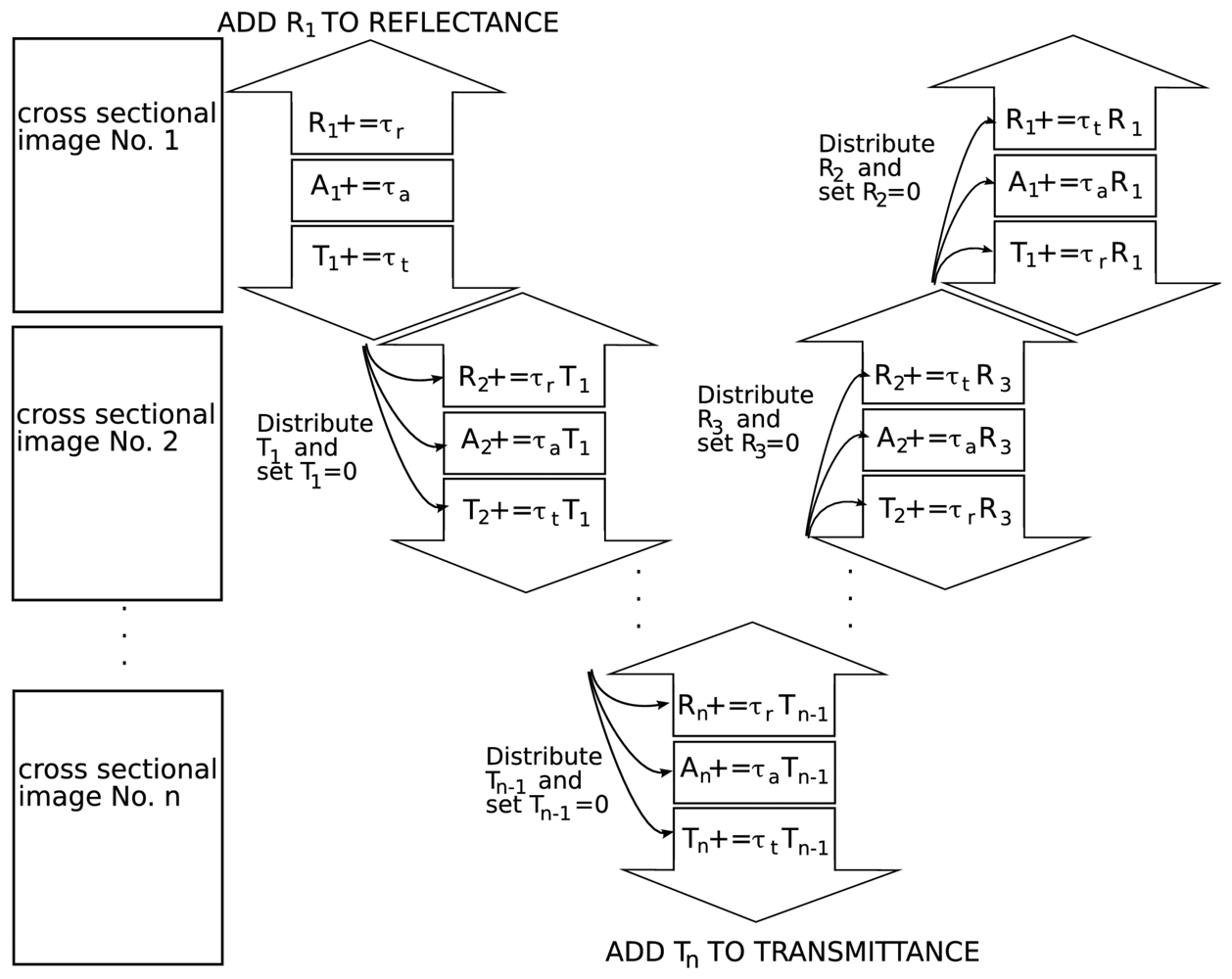
2.3 Beam tracing
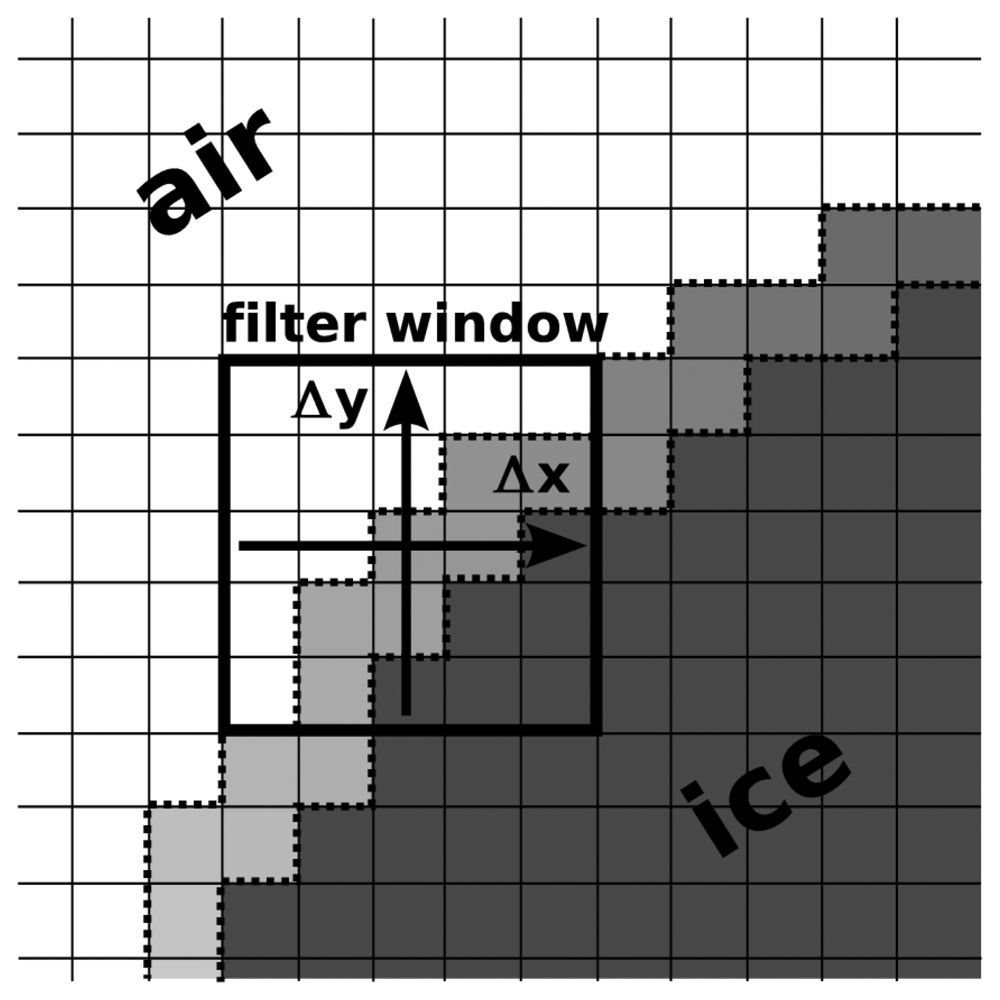
2.4 Snow extension module for BTM – the ladder approximation
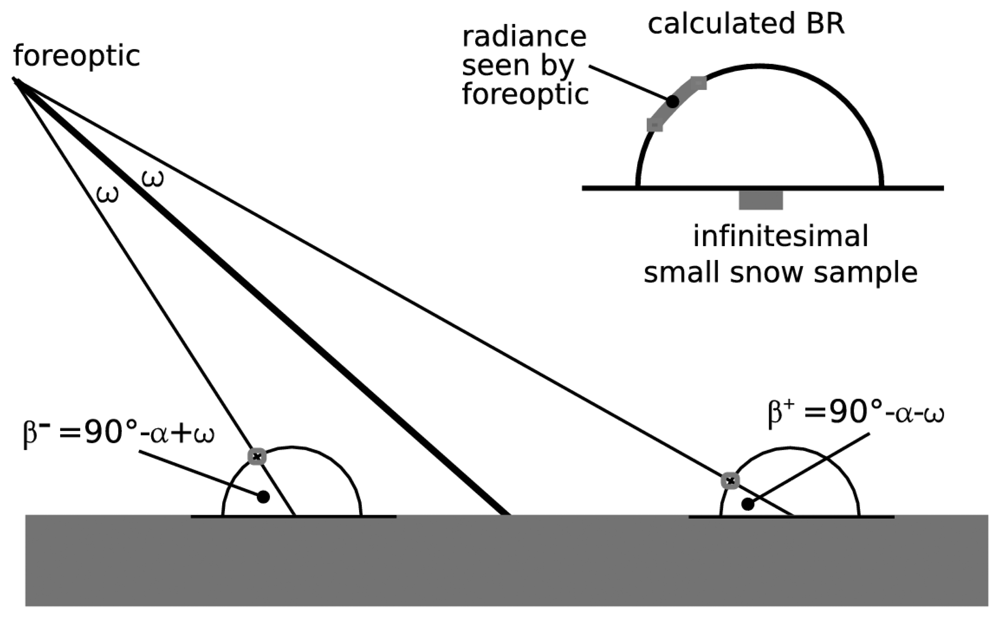
2.5 Sensor
3. Experiment
3.1 Snow sampling
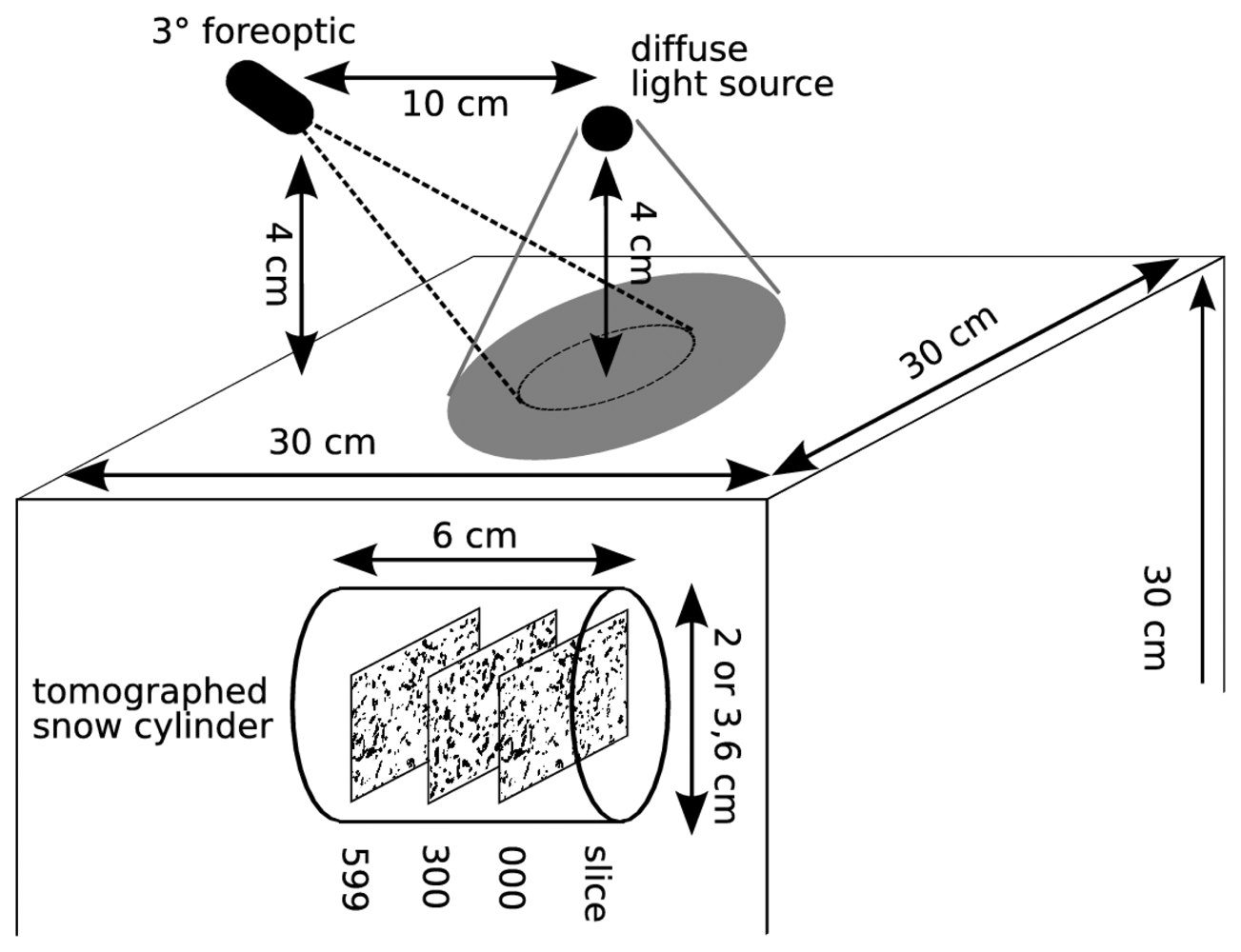
3.2 Snow reflectance measurement
3.3 Snow tomography
4. Results
4.1 Results from measurements
4.2 Results from modeling
5. Discussion
6. Conclusions
Acknowledgments
References and Notes
- Marks, D.; Dozier, J.; Davis, R. Climate and energy exchange at the snow surface in the alpine region of the Sierra-Nevada. 1. Meteorological measurements and monitoring. Water Resources Research 1992, 28, 3029–3042. [Google Scholar]
- Roesch, A.; Wild, M.; Pinker, R.; Ohmura, A. Comparison of spectral surface albedos and their impact on the general circulation model simulated surface climate. Journal of Geophysical Research 2002, 107(D14), ACL13–1–18. [Google Scholar] [CrossRef]
- Nolin, A.; Dozier, J. A hyperspectral method for remotely sensing the grain size of snow. Remote Sensing and Environment 2000, 74, 207–216. [Google Scholar]
- Sturm, M.; McFadden, J.; Liston, G.; Chapin, F.; Racine, C.; Holmgren, J. Snowshrub interactions in Arctic tundra: A hypothesis with climatic implications. Journal of Climate 2001, 14, 336–344. [Google Scholar]
- Giddings, J.; LaChapelle, E. Diffusion theory applied to radiant energy distribution and albedo of snow. Journal of Geophysical Research 1961, 66(1), 181–189. [Google Scholar]
- Wiscombe, J.; Warren, S. A model for spectral albedo of snow 1: Pure snow. Journal of the Atmospheric Sciences 1980, 37, 2712–2733. [Google Scholar]
- Painter, T.; Dozier, J. Measurements of the hemispherical-directional reflectance of snow at fine spectral and angular resolution. Journal of Geophysical Research 2004, 109(D18), 21. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, P.; Gao, B.; Kattawar, G.; Mishchenko, M. Effect of ice crystal shape and effective size on snow bidirectional reflectance. Journal of Quantitative Spectroscopy & Radiative Transfer 2006, 100, 457–469. [Google Scholar] [CrossRef]
- Mishchenko, M.; Liu, L.; Mackowski, D.; Cairns, B.; Videen, G. Multiple scattering by random particle media: exact 3D results. Optics Express 2007, 15, 2822–2836. [Google Scholar]
- Davis, R.; Dozier, J. Stereological characterization of dry alpine snow for microwave remote sensing. Advances in Space Research 1989, 9, 245–251. [Google Scholar]
- Matzl, M.; Schneebeli, M. Areal measurement of specific surface area in snow profiles by near infrared reflectivity. Journal of Glaciology 2006. submitted. [Google Scholar]
- Bohren, C.; Huffman, D. Absorption and scattering of light by small particles.; John Wiley & Sons, 1983. [Google Scholar]
- Grenfell, T.C.; Warren, S.G. Representation of a nonspherical ice particle by a collection of independent spheres for scattering and absorption of radiation. Journal of Geophysical Research 1999, 104(D24), 31,697–31,709. [Google Scholar]
- Mätzler, C. A simple snowpack/cloud reflectance and transmittance model from microwave to ultraviolet: the ice-lamella pack. Journal of Glaciology 2000, 46(152), 20–24. [Google Scholar]
- Leroux, C.; Lenoble, J.; Brogniez, G.; Hovenier, J.; Haan, J. D. A model for the bidirectional polarized reflectance of snow. Journal of Quantitativ Spectroscopy and Radiative Transfer 1999, 61(3), 273–285. [Google Scholar]
- Meirold-Mautner, I.; Lehning, M. Measurements and model calculations of the solar shortwave fluxes in snow on Summit, Greenland. Annals of Glaciology 2004, 38, 279–284. [Google Scholar]
- Macke, A.; Müller, J.; Raschke, E. Single scattering properties of atmospheric ice crystals. Journal of the Atmospheric Sciences 1996, 53. [Google Scholar]
- Hesse, E.; Ulanowski, Z. Scattering from long prisms computed using ray tracing combined with diffraction on facets. Journal of Quantitative Spectroscopy and Radiative Transfer 2003, 79, 721–732. [Google Scholar]
- Peltoniemi, J. Spectropolarised ray-tracing simulations in densely packed particulate medium. Journal of Quantitative Spectroscopy and Radiative Transfer 2007, 108, 180–196. [Google Scholar]
- Schneebeli, M. Three-dimensional snow: How snow really looks like. Proceedings of International Snow Science Workshop 2000, 407–408. [Google Scholar]
- Coleou, C.; Lesaffre, B.; Brzoska, J.; Ludwig, W.; Boller, E. 3-D snow images by X-rays micro-tomography. Annals of Glaciology 2001, 32, 75–81. [Google Scholar]
- Bänninger, D.; Lehmann, P.; Flühler, H. Modelling the effect of particle size, shape and orientation of light transfer through porous media. European Journal of Soil Science 2006, 57, 906–915. [Google Scholar] [CrossRef]
- Volkov, S.; Remizovich, V. Comparative analysis of the propagation of light radiation in 2D and 3D media: II. Transmission of light radiation through strongly absorbing media with large-scale scatters. Laser Physics 1998, 8(6), 1140–1162. [Google Scholar]
- Bohren, C.; Herman, B. Asymptotic scattering efficiency of a large sphere. Journal of Optical Society of America 1979, 69, 1615–1616. [Google Scholar]
- Lai, H.; Wong, W.; Wong, W. Extinction paradox and actual power scattered in light beam scattering: a two-dimensional study. Journal of Optical Society of America A 2004, 21, 2324–2333. [Google Scholar]
- Klette, R.; Zamperoni, P. Handbuch der Operatoren für Bildbearbeitung; Vieweg, 1992. [Google Scholar]
- Warren, S. Optical constants of ice from the ultraviolet to the microwave. Applied Optics 1984, 23, 1026–1225. [Google Scholar]
- Grenfell, T.; Perovich, D. Radiation absorption coefficients of polycrystalline ice from 400-1400nm. Journal of Geophysical Research 1981, 86(C8), 7447–7450. [Google Scholar]
- Schaepman-Strub, G.; Schaepmann, M.; Painter, T.; Dangel, S.; Martonchik, J. Reflectance quantities in optical remote sensing – definitions and case studies. Remote Sensing of Environment 2006, 103, 27–42. [Google Scholar]
- Sandmeier, S.; Müller, C.; Hosgood, B.; Andreoli, G. Sensitivity analysis and quality assessment of laboratory BRDF data. Remote Sensing of Environment 1998, 64, 176–191. [Google Scholar]
- Kaempfer, T.; Schneebeli, M.; Sokratov, S. A microstructural approach to model heat transfer in snow. Geophysical Research Letter 2005, 32, L21503. [Google Scholar] [CrossRef]
- Schneebeli, M.; Sokratov, S. Tomography of temperature gradient metamorphism of snow and associated changes in heat conductivity. Hydrological Processes 2004, 18(18), 3655–3665. [Google Scholar]
- Dobbins, R.A.; Jizmagia, G.S. Optical scattering cross sections for polydispersions of dielectric spheres. Journal of the Optical Society of America 1966, 56(10), 1345–1350. [Google Scholar]
- Dozier, J.; Davis, R.E.; Chang, A.T.C.; Brown, K. The spectral bidirectional reflectance of snow. In Spectral Signatures of Objects in Remote Sensing; pp. 87–92. Paris, 1988; European Space agency. [Google Scholar]
- Hildebrand, T.; Laib, A.; Müller, R.; Dequeker, J.; Rüegsegger, P. Direct three-dimensional morphometric analysis of human cacellous bone: Microstructural data from spine, femur, iliac crest, and calcanens. Journal of Bone and Mineral Research 1999, 14(7), 1167–1174. [Google Scholar]
- Pielmeier, C.; Schneebeli, M. Stratigraphy and changes in hardness of snow measured by hand, ramsonde and snow micro penetrometer; a comparison with planar sections. Cold Regions Science and Technology 2003, 37, 393–405. [Google Scholar]
- Mitchell, D. Effective diameter in radiation transfer: General definition, applications, and limitations. Journal of the Atmospheric Sciences 2002, 59(15), 2330–2346. [Google Scholar]
- O′Hirok, W.; Gautier, C. A three-dimensional radiative transfer model to investigate the solar radiation within a cloudy atmosphere. Part I: Spatial effects. Journal of the Atmospheric Sciences 1998, 55, 2162–2179. [Google Scholar]

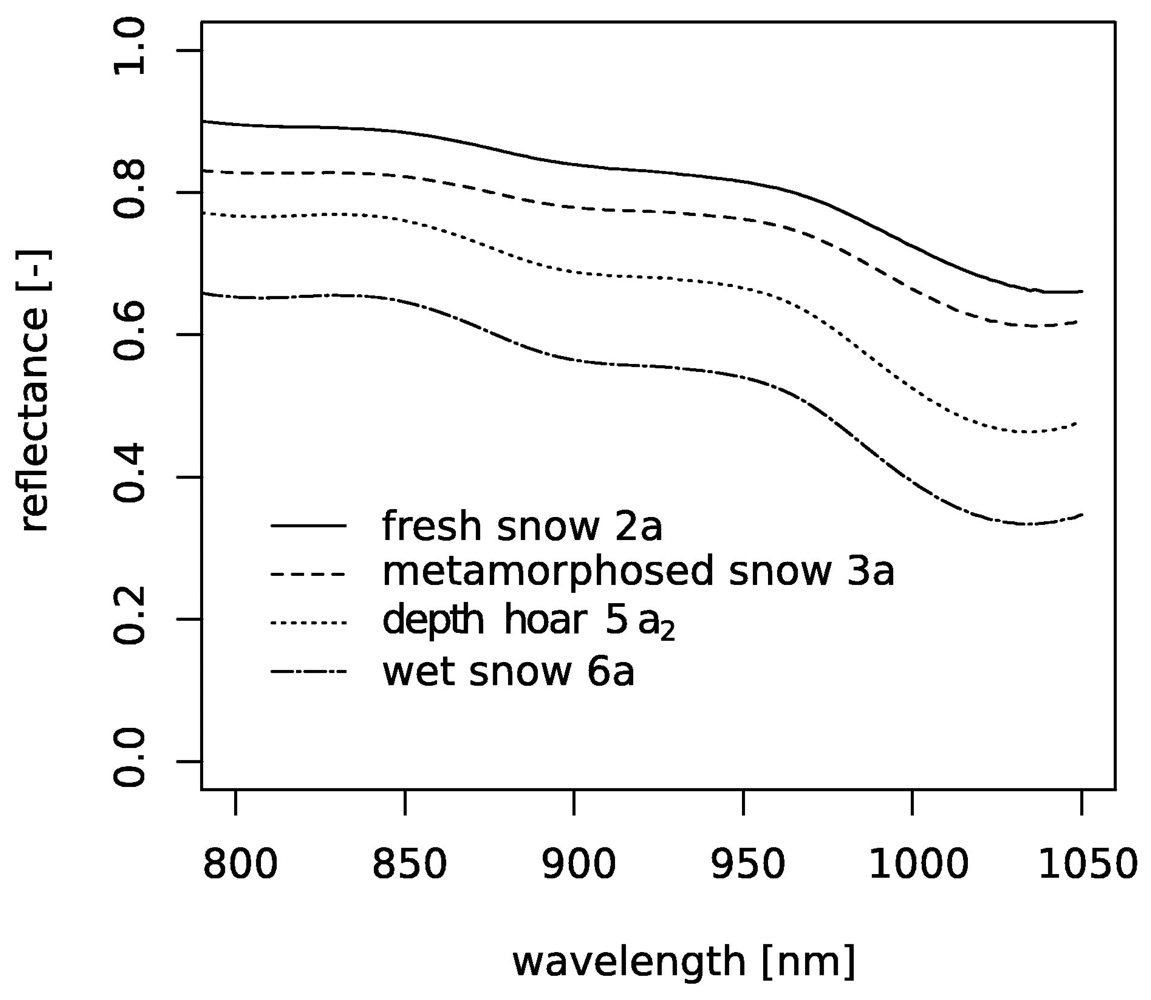

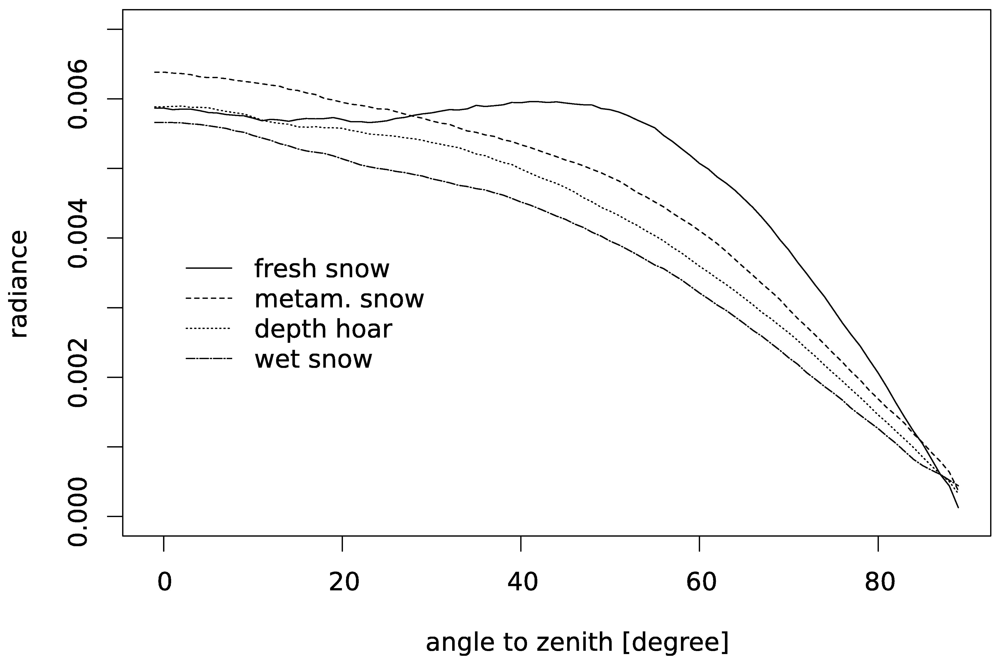
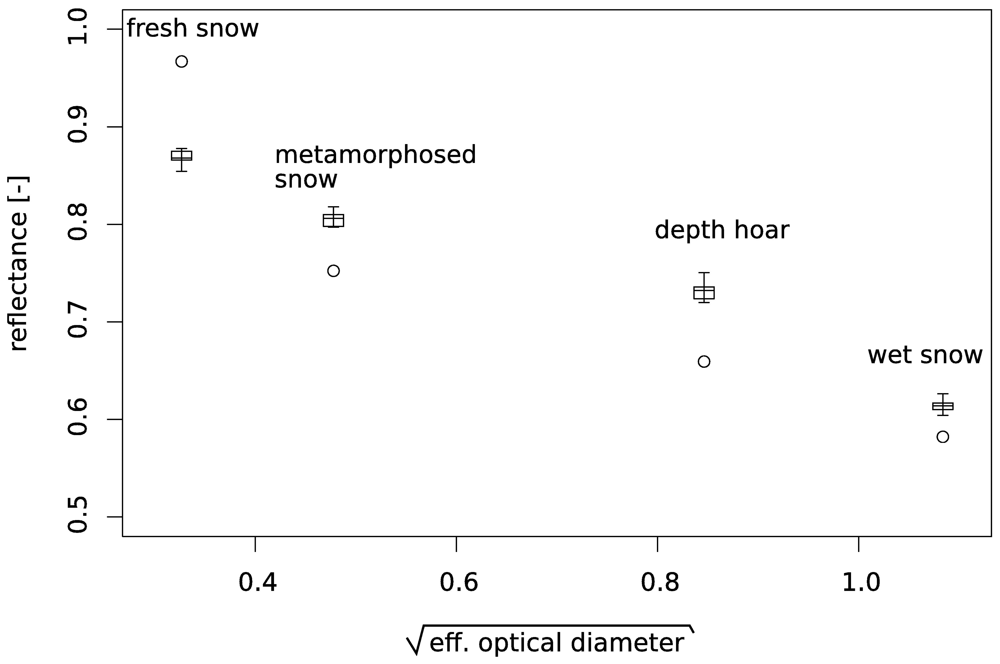
| Snow type (ISC) | Shortcut | density [kg/m3] | SSA [mm-1] | effective radius μ m | cross sectional image size [mm × mm] |
|---|---|---|---|---|---|
| Fresh snow (2a) | fs | 110 | 59.22 | 51 | 6 × 4 |
| metam. snow (3a) | m2 | 194 | 26.29 | 114 | 6 × 4 |
| depth hoar (5a2) | dh | 305 | 8,38 | 358 | 10.8 × 7.2 |
| wet snow (6a) | ws | 535 | 5.11 | 587 | 10.8 × 7.2 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the CreativeCommons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bänninger, D.; Bourgeois, C.S.; Matzl, M.; Schneebeli, M. Reflectance Modeling for Real Snow Structures Using a Beam Tracing Model. Sensors 2008, 8, 3482-3496. https://doi.org/10.3390/s8053482
Bänninger D, Bourgeois CS, Matzl M, Schneebeli M. Reflectance Modeling for Real Snow Structures Using a Beam Tracing Model. Sensors. 2008; 8(5):3482-3496. https://doi.org/10.3390/s8053482
Chicago/Turabian StyleBänninger, Dominik, Claude Saskia Bourgeois, Margret Matzl, and Martin Schneebeli. 2008. "Reflectance Modeling for Real Snow Structures Using a Beam Tracing Model" Sensors 8, no. 5: 3482-3496. https://doi.org/10.3390/s8053482





