1. Introduction
It is known that atmospheric aerosols influence the Earth climate system. Various efforts are being made to investigate the global distribution and concentration of these aerosols and to quantify their forcing on the radiation budget. Numerous data from passive optical Earth observation satellites are used to map aerosol properties on a global scale. Not only atmospheric scientists, but also the remote sensing community relies on aerosol information. Earth observation data in particular have to be corrected for the atmospheric influence in order to provide accurate physical measuring quantities.
During the last two decades, several aerosol retrieval techniques have been developed for satellite instruments. An overview is given by [
1] and recent inter-comparisons are provided for the retrieval over land by [
2] and over sea by [
3], [
4] and [
5]. In general, relatively large discrepancies between different satellite instruments were found, especially on the scale of single pixels [
2]. Even long-term studies over the ocean reveal differences between well established satellite instruments of up to 0.1 aerosol optical depth (AOD or
) and 0.45 Ångstrøm exponent [
4].
State-of-the-art hyperspectral airborne imagers may be able to outperform the limitations of most current satellite instruments. For example, the typical ground sampling distance (GSD) of spaceborne instruments retrieving AOD routinely is in the range of 1
km to 30
km. The resulting uncertainty of the surface reflectance is an important contribution to the inaccuracy of the retrieved AOD over land. On the other hand, the GSD of airborne instruments is in the range of meters. One can therefore assume better performances in AOD retrieval over land because the unmixing of the surface and the atmospheric signal is expected to be less difficult. The increased likelihood of observing a uniform surface within one pixel leads to smaller uncertainties in the assumptions about the surface reflectance. This is a major source of error in most satellite-based AOD retrievals. In addition, the use of a hyperspectral sensor allows the avoidance of atmosphere gaseous absorption bands and the use of the complete spectrum from near-UV to SWIR if desired. Furthermore, the spectral and the spatial domain can be binned (adding bands or pixels together) to achieve the desired signal-to-noise ratio (SNR). The Airborne Prism EXperiment (APEX) [
6] is chosen for this paper as an example for such an airborne hyperspectral instrument.
This study assesses the feasibility of aerosol retrieval with APEX in terms of the SNR and independent of any particular AOD retrieval technique, which was previously proposed by [
7] and [
8]. A model which translates atmospheric conditions and surface reflectance into radiance values at-sensor is essential for the establishment of feasibility. It needs also to address the multiple scattering of light while being as simple as possible to avoid excessive computational time or alternatively the use of precalculated lookup tables. This study analyses the SNR requirements and limitations of aerosol retrieval with a focus on the influence of the surface reflectance.
All calculations are carried out at the commonly used aerosol reference wavelength of 550nm to make the results comparable to other studies. Preliminary analysis at other wavelengths within the visible spectrum did not reveal qualitative differences to the findings at 550nm and are therefore not shown in this paper. The figures are plotted for
on the x-axis because the minimum expected visibility for an airborne remote sensing campaign will be about 5km. Flights usually will be carried out at visibilities of more than 10km.
2. Sensor Characteristics of APEX
APEX is a dispersive push-broom imaging spectrometer, which is expected to provide unique hyper-spectral data to geophysical and biochemical studies on land, water and atmospheric processes. APEX will contribute to the Earth observation community by simulating, calibrating and validating future space- and airborne optical sensors. The expected performance of APEX along with a novel spectral, radiometric and geometric calibration methodology provide an opportunity to overcome limitations of currently available remote sensing instruments. This potential is especially important in addressing the requirements for the remote sensing of aerosols.
APEX features more than 500 spectral bands from 385nm to 2500nm with a sampling interval of 0.4nm to 10nm in the full spectral mode. The standard spectral mode comprises more than 300 bands, where bands are binned together to increase the SNR. The typical gain in SNR is in the order of 40% per domain (spectral or spatial). This corresponds to a factor of 1.42 ≈ 2 for the binning in both domains.
The GSD is governed by 0.028° instantaneous field of view and 1000 pixels across track. It varies from 2.5m to 8m depending on the flight altitude.
Table 1 provides the preflight APEX-specific sensor performance for minimum, average and maximum radiance levels at 550
nm. They correspond to surface reflectances
of 0%, 30% and 100%.
represents a relatively bright surface reflectance, which can be expected during remote sensing campaigns over land. The minimum and maximum surface reflectance was chosen to account for the extreme values following [
9]. The sensor performance is expressed by the noise equivalent spectral radiance difference
. The relation between
and
is given by:
where
SNRλ is the band-specific signal-to-noise ratio or sensor efficiency. It consists of the instrument and photon noise. The latter is mainly a function of the spectral radiance level
.
The actual sensor performance values are going to be measured in mid 2008 during the first full calibration of APEX. This instrument is currently in assembly and its maiden flight is scheduled later in 2008.
3. Radiance Simulation
Some basic radiation transfer equations are needed to simulate the attenuation of the light traveling from the top of the atmosphere down to a surface pixel and upward to the airborne sensor. The upwelling spectral radiance into an instrument (at-sensor-radiance
) is a function of successive orders of radiation interactions within the coupled surface-atmosphere system. In theory, it can be decoupled into a contribution from the atmosphere (path-radiance
) and from the underlying surface
.
can be split into the direct
and the diffuse
reflected spectral radiance from the scattering atmospheric layer:
3.1. Path-Radiance
If we assume a homogeneous scattering layer and the single scattering approximation (SSA), the atmospheric spectral path-radiance can be derived from the well known Radiation Transfer Equation by [
10] as follows:
where the incoming spectral radiance (
I) is reflected by the scattering atmosphere (
II) and scattered directly (single scattering) into the sensor's viewing geometry (
III).
E0λμ0 is the solar spectral irradiance, scaled by the cosine of the solar zenith angle.
μ describes the sensor viewing geometry, where
μ =
cos(0°) = 1 is valid for a nadir viewing instrument, such as APEX. The atmospheric single scattering albedo
ω0 is the ratio of the scattering to the extinction coefficient. The atmospheric phase function
Pλ (Θ) takes care of the amount of light, which is diverted into the sensor viewing direction. For aerosol remote sensing, the atmospheric optical depth can be decomposed into its molecular and particle (aerosol) extinction part, such that
.
The multiple scattering of light at molecules and aerosols is an important contribution to
for
λ < 800
nm. It leads to increasing errors for smaller
λ due to the SSA in
Equation 3. Unfortunately, multiple scattering is difficult to express in form of a simple equation. But its influence can be taken into account by introducing a correction factor
f(
τλ) [
11]:
It represents the ratio of the exact radiance calculation by a multiple scattering radiation transfer code (i.e. [
12] or [
11]) to the SSA radiance calculation.
f(
τλ) can be interpreted in
Figure 1(a) by taking the ratio between the MODTRAN4 [
13] curve and the SSA curve from
Equation 3. One finds that the multiple scattering intensifies
by a factor of 1.5 at
and by a factor of 2.0 at
.
The atmospheric spectral radiance corrected for the multiple scattered light is therefore given by:
3.2. Surface Contribution
Since
is often the dominating contribution to
, one must account for the underlying surface. The ratio of incoming and outgoing spectral irradiance at the surface level yields the homogeneous Lambertian surface reflectance:
. Since
and therefore
we find:
sλ is the spherical albedo and describes the portion of the light scattered back to the surface as a result of isotropic illumination of the atmosphere by the surface. It is therefore also a function of
Tλ and
τλ.
denotes the total spectral transmittance, comprising of the down- and upward direct
and diffuse
scattering transmittance and the absorption transmittance
:
[
14] offers a parameterization by polynomial series with a satisfying accuracy to describe
and
sλ. Additionally, a non-uniform surface could be considered by adjusting
in the denominator of
Equation 6 to incorporate an environment reflectance according to [
15] and [
16] or [
17].
3.3. At-Sensor-Radiance
In the case of an airborne remote sensor, the atmospheric extinction has to be adjusted to the reduced atmospheric path length between the surface and the sensor. An approximating method would be to use the air pressure ratio (p*) between the sensor and the surface level to scale the upward optical depth due to molecular scattering:
, which is equal to
. The extinction by aerosols above the sensor (ie. background volcanic particles in the stratosphere) is neglected here. For this study, p* is set to 0.5, which corresponds to a sensor height of about 5500 meters above sea level using the international standard atmosphere.
Finally, the complete spectral radiance at the sensor level is given by adding
Equations 5 and
6:
3.4. Verification with MODTRAN4
Equation 8 was compared against results from the widely accepted radiation transfer model MOD-TRAN4 [
13] including the multiple stream algorithm DISORT [
12] to account for the multiple scattering. The 1976 U.S. Standard Model Atmosphere was used to describe the vertical profile of gas mixing ratios. The aerosol optical properties within the planetary boundary layer were taken into account in MODTRAN4 by a rural type of aerosol with a mixing ratio of 0.7 small water-soluble and 0.3 large dust-like particles. A tropospheric type with small water soluble particles was used for the free troposphere.
Equation 8 was fed by the Average Continental model from [
18], which adds a few particles of soot (0.06 mixing ratio) to the troposphere type. The results and conclusions of this paper were derived by means of
Equation 8 and they are therefore not affected by differences in the aerosol models. Further parameters used with
Equation 8 and with MODTRAN4 for the verification are given in
Table 2.
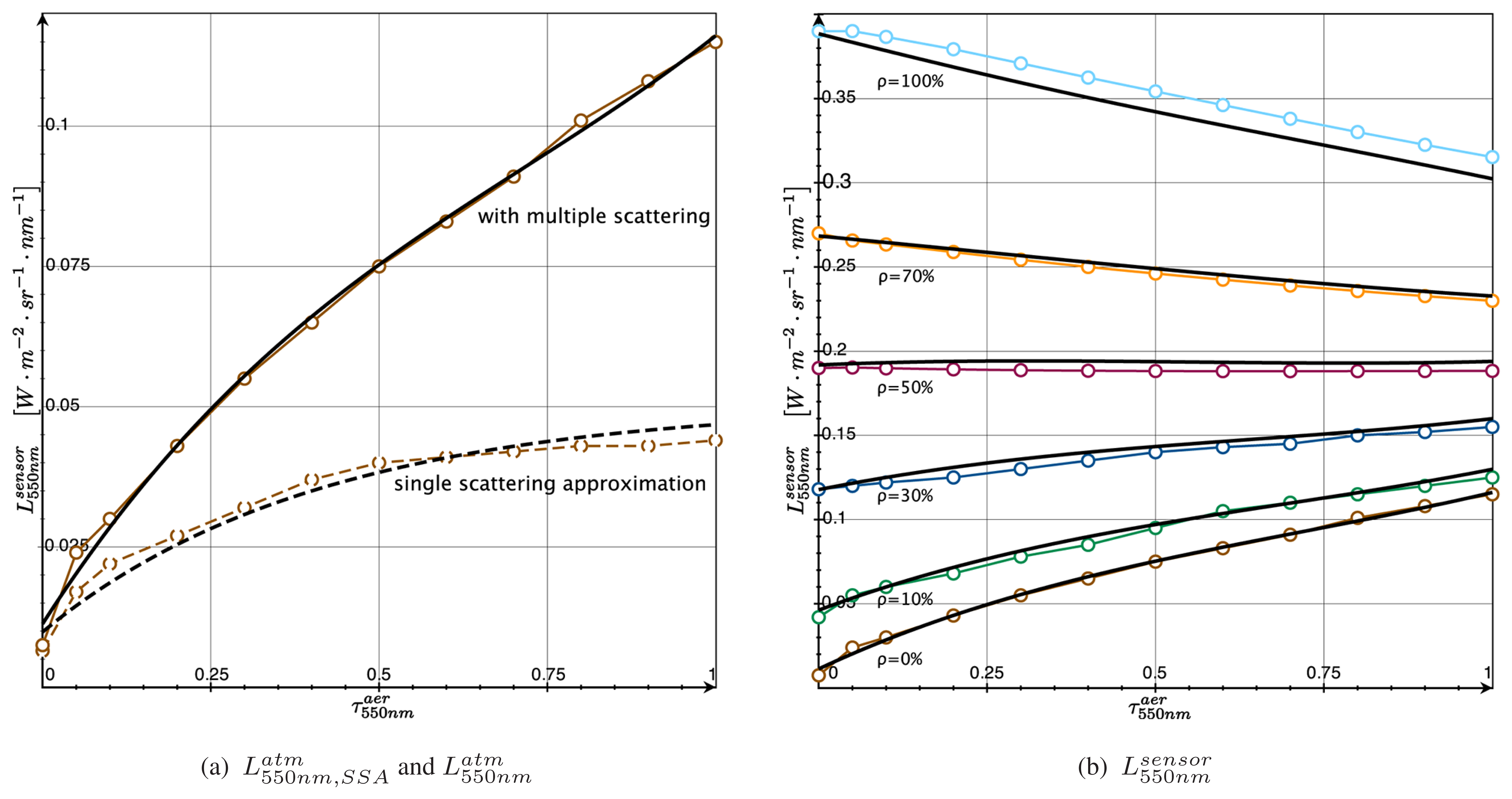
Figure 1 presents the simulation of
as a function of
. The black lines are the results from
Equation 8 over different
while the colored lines with circles referring to the MODTRAN4 reference calculations.
Figure 1(a) shows the intermediate step with the SSA (dashed lines) over a black surface
, which is given by
Equation 3. The influence of the multiple scattering is clearly visible as the offset between the dashed and the solid line. This offset is represented in the multiple scattering correction factor
f(
τλ) used in
Equation 5.
The accuracy of the spectral radiance simulation is given by qualitatively comparing the results for
and
with the MODTRAN4 reference calculations in
Figure 1(a). The effect of the surface contribution by
Equation 6 can be seen in
Figure 1(b), where the complet
from
Equation 8 is given for different surface reflectances along with the MODTRAN4 results.
At
, the model expects to cancel out the change in absorption and the change in scattering due to a changing AOD.
is therefore no longer a function of
, which makes it impossible to retrieve AOD at a surface reflectance of about 50%. Further investigations showed that this critical
varies with the aerosol scattering properties ω0, Pλ (Θ) and with μ0, μ and sλ (not shown).
4. Sensitivity Requirements
4.1. AOD Retrieval Sensitivity Requirements
The atmosphere has a distorting effect on
, which has to be compensated for quantitative remote sensing applications. AOD is a crucial parameter for the atmospheric correction process to derive accurate apparent surface reflectances. We define an accuracy requirement of 1% absolute error in surface reflectance according to [
20]. This can be also expressed in terms of transmittance in order to relate it to AOD. A rough estimation of the allowed application specific error (
ε) in
yields 0.01 transmittance values for dark surfaces, such as water bodies
. The relative influence of
on
is decreasing for increasing
(
Equation 8). For example, at
the
accounts for about 25% of
at
(see
Figure 1(b)) and therefore
ε yields 0.04 transmittance values.
The required retrieval sensitivity of the total optical depth is calculated by:
The exponential dependence of Δ
τλ on the total optical depth and therefore also on AOD is obvious. It is found that
is needed for the worst case of a dark surface and low AOD conditions
. A
is satisfactory for
.
Equation 9 is also used later in
Figures 2 and
3 to define AOD retrieval requirements.
4.2. Sensor Sensitivity Requirements
The results from AOD retrieval sensitivity requirements can now be used to define the performance requirements of an optical remote sensing instrument because they are related to the radiometric resolvability (Δ
Lλ). This is a prerequisite for the successful retrieval of aerosols. For obvious reason, the radiance variation induced due to change in AOD must exceed
NE ΔLλ of a sensor [
21]:
The sensor-specific sensitivity on AOD
is given by means of the simulated
from
Equation 8 and
from
Equations 1 and
10:
5. Results
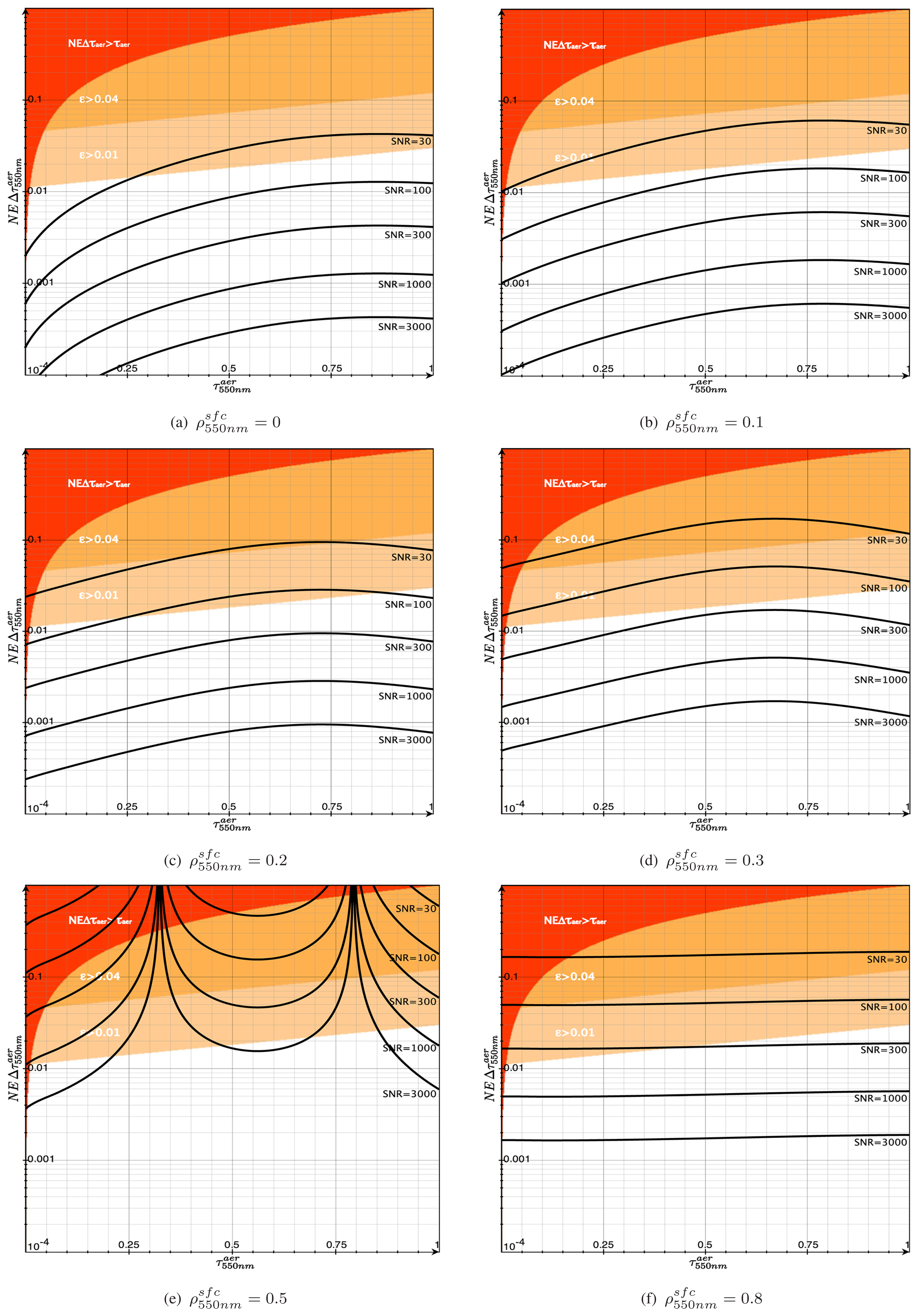
5.1. SNR Requirements
Figure 2 assesses the SNR requirements depending on surface reflectance and AOD. The retrieval of
is feasible as long as
according to
Equation 10. The area where this limit is not fulfilled, because the noise exceeds the signal, is drawn in dark-red in
Figures 2 and
3. The dark orange color denotes the area where the desired minimal aerosol retrieval interval
from
Equation 9 can not be achieved for the
ε = 0.04 requirement. The stricter
ε = 0.01 is met within the white area.
Over dark surfaces, where
dominates
, AOD retrieval sensitivity is best for small AOD. This is because small
can be achieved even for relative low SNR values (
Figures 2(a) and 2(b)). An SNR of less than 100 is enough to fulfill the strict atmospheric correction accuracy requirement of
ε = 0.01, which is needed for dark targets. Assuming a typical case with a surface of
and
, a
of at least 0.008 for SNR = 100 can be expected.
Brighter surfaces
require greater SNR to keep a certain aerosol retrieval sensitivity compared to dark surfaces. This range of surface reflectances is expected to be the typical case for remote sensing over land. To fulfill
ε = 0.01, an SNR between 100 and 300 is now required. In terms of atmospheric correction
ε can be relaxed to 0.04, where an SNR between 30 and 100 is sufficient (
Figures 2(c) and 2(d)). An SNR of 300 allows an aerosol retrieval sensitivity of less than 0.01 with
, which is expected to be the typical condition for most flight campaigns.
Very bright surfaces
are found to be most challenging because
depends weakly on
. Changes in scattering and absorption of light due to a
may cancel each other out. It can be seen in
Figure 1(b),
Equation 8 and MODTRAN4 reveal virtually no influence of the aerosol loading on
in the case of
. Due to the derivation of a local minimum in
Equation 11,
can go to infinity as plotted in
Figure 2(e). This critical surface reflectance of about 50% as well as the position (in terms of
) of
depends on many parameters and can vary between different models. This effect is not analyzed in detail here but shows clearly that aerosol retrieval can be difficult for a certain small range of surface reflectances.
Extremely bright targets, such as snow and clouds, provide adequate sensitivity.
Figure 2(f) shows an example for
, where an SNR of about 100 is sufficient for
ε = 0.04, while 300 is needed for the
ε = 0.01 requirement. The sensitivity is almost constant over the typical range of
at this surface reflectance. This is in contrast to the calculations with low surface reflectance
, where
generally decreases for increasing
.
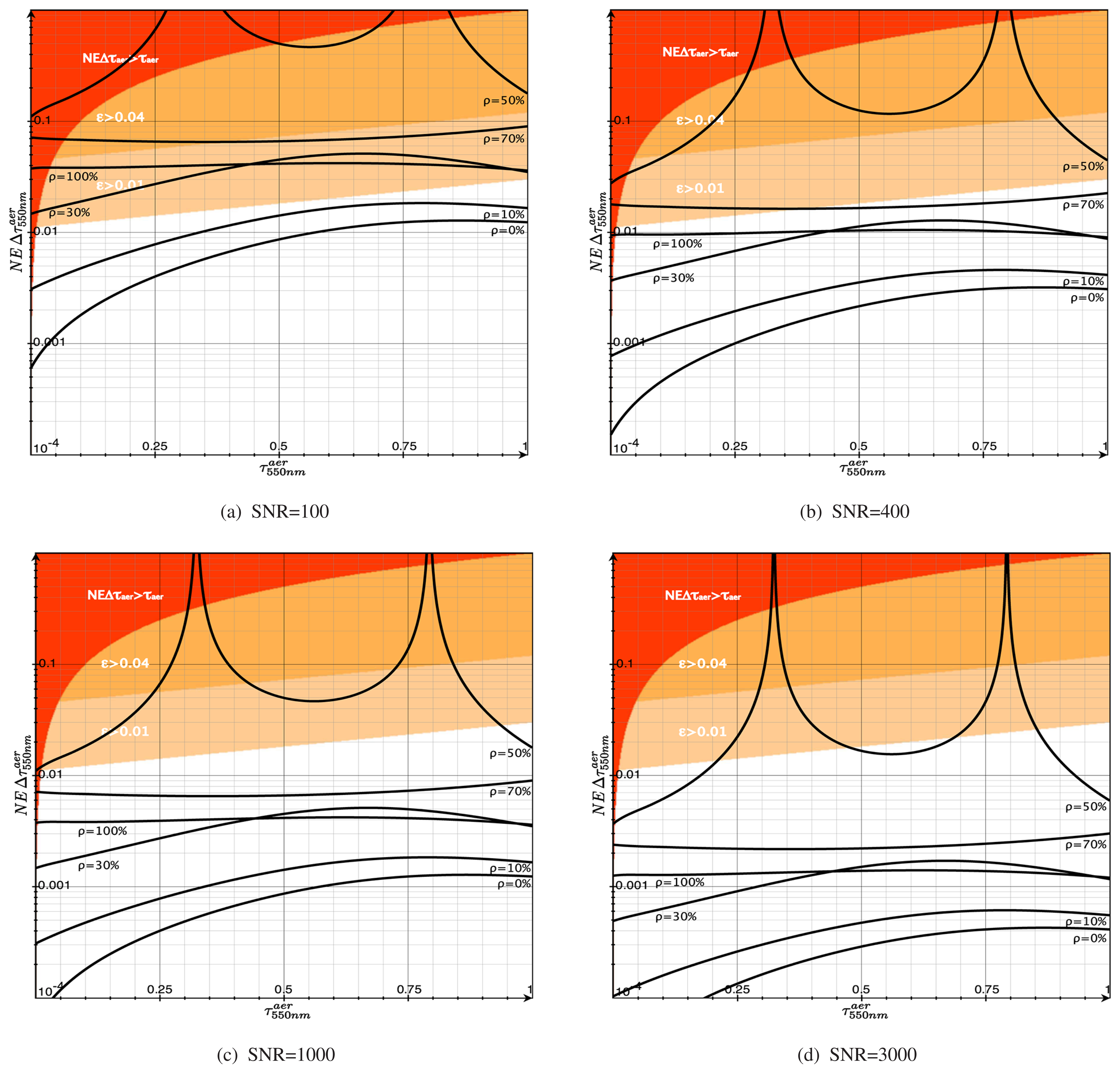
5.2. Influence of the Surface Reflectance
The influence of the surface reflectance on aerosol retrieval is highlighted by
Figure 3. 3(a) reveals clearly that an
SNR ≥ 100 is needed to detect aerosols over typical surfaces. Such an SNR allows achieving
ε = 0.01 with dark surfaces and
ε = 0.04 with
and 1.0.
is mostly unproblematic for instruments with SNR greater than 50. A surface reflectance of
or
requires an instrument with an SNR of about 400 to fulfill the strict requirement (
Figure 3(b)). It is possible to achieve
ε = 0.04 with the same SNR also for
and
. Greater SNR enhances the retrieval sensitivity within the white area, where
ε < 0.01 is given.
Much higher SNR are required in order to detect aerosols over a surface reflectance of around 50%.
Figures 3(c) and 3(d) show that the requirement of
ε = 0.04 can be met within a range of
with an SNR of 1000. This AOD range becomes smaller for a larger SNR.
ε = 0.01 can only be met partially by having an SNR of more than 3000. This can be achieved only by trading off foremost spatial and/or spectral resolution for SNR by binning hyperspectral remote sensing data in these domains.
5.3. Feasibility of Aerosol Retrieval with APEX
The crucial question is whether an aerosol retrieval is possible with an airborne hyperspectral sensor optical system, such as APEX. It must be demonstrated that the required signal sensitivity is provided by the instrument. Since APEX has not yet undergone a complete calibration process, one must use preflight SNR requirements for this analysis. These values are given in
Table 1 with
and the corresponding SNR in
Table 3 along with the retrieval requirements.
The feasibility analysis is based upon three scenarios corresponding to the minimal, average and maximal expected spectral radiance levels according to
Table 1.
Equation 8 was solved for
, 0.3 and 1.0. to find the modeled
. The SNR requirements for aerosol retrieval were interpreted from the data, which are shown in
Figure 2, where the SNR meets the requirement of
ε = 0.01 (
Equation 9).
The comparison in
Table 3 between the retrieval requirement and the SNR of APEX reveals clearly the feasibility of aerosol retrieval for the analysed cases. However, it might be possible that the SNR does not meet the requirements for aerosol retrieval over the critical surface reflectance around
without additional binning.
6. Summary and Conclusions
A spectral radiance simulation at the sensor level has been presented. It is capable of reproducing MODTRAN4 results under the SSA and within typical airborne remote sensing conditions. The multiple scattered path radiance was taken into account by the DISORT code [
12]. This
simulation was used to evaluate the noise equivalent difference aerosol optical thickness
as a function of
for different SNR and surface reflectances at 550
nm. The results reveal the sensor performance requirements for a sufficiently accurate AOD retrieval along with a feasibility analysis regarding APEX.
It has been shown that the detection of aerosols is feasible with APEX for low, average and high spectral radiance levels under the evaluated conditions (ie. solar, viewing and sensor configuration). This finding concerns the sensitivity requirements for an optical remote sensing instrument, such as APEX. The resulting feasibility is based on preflight sensor performance values; the final APEX SNR will be available after full scale calibration during the year 2008. Further investigations will be performed to assess the sensitivity and the limitations of the radiation transfer calculation and the aerosol retrieval algorithm itself.
We found that the spectral SNR is vital for aerosol remote sensing and varies strongly with surface reflectance. The latter strongly influences the intensity of
, which drives the SNR. It has been shown that dark surfaces
have the lowest SNR demands for aerosol retrieval. This is crucial for establishing feasibility because the sensor provides a lower SNR over dark surfaces due to the lower spectral radiance. The analysis showed that APEX is expected to provide sufficiently high SNR values even for black surfaces under the given conditions. More critical are relatively bright surfaces
because
depends only weakly on
. Extremely bright surfaces require again a lower SNR, but the unmixing of
is expected to be more difficult because of errors in the estimation of
become dominant. Due to the small GSD of airborne instruments, it is expected that the identification of pure surface materials could be done with an adequate precision compared to satellite platforms. This allows to reduce the uncertainties in allocating a best-guess
to the observed pixels and therefore alleviate the challenge of the unmixing of
from
.
The finding of indefinitely high SNR requirements might be an artifact of the approximate simulation of
(
Equation 8) for
. It depends strongly upon the aerosol model assumption, in particular the approximation of the phase function and the multiple scattering. Further investigations are needed.
Generally, it was shown that an SNR of 300 or better will provide satisfying aerosol retrieval results for most surface reflectances considered in this analysis. Restricting the ranges to
and
, which are optimal and representative remote sensing conditions, an SNR of 100 is adequate. This is a promising finding in scope of the development of aerosol retrieval methods because most current instruments fulfill such SNR requirements under typical conditions.