An Artificial Neural Network Approach for the Prediction of Absorption Measurements of an Evanescent Field Fiber Sensor
Abstract
:1. Introduction
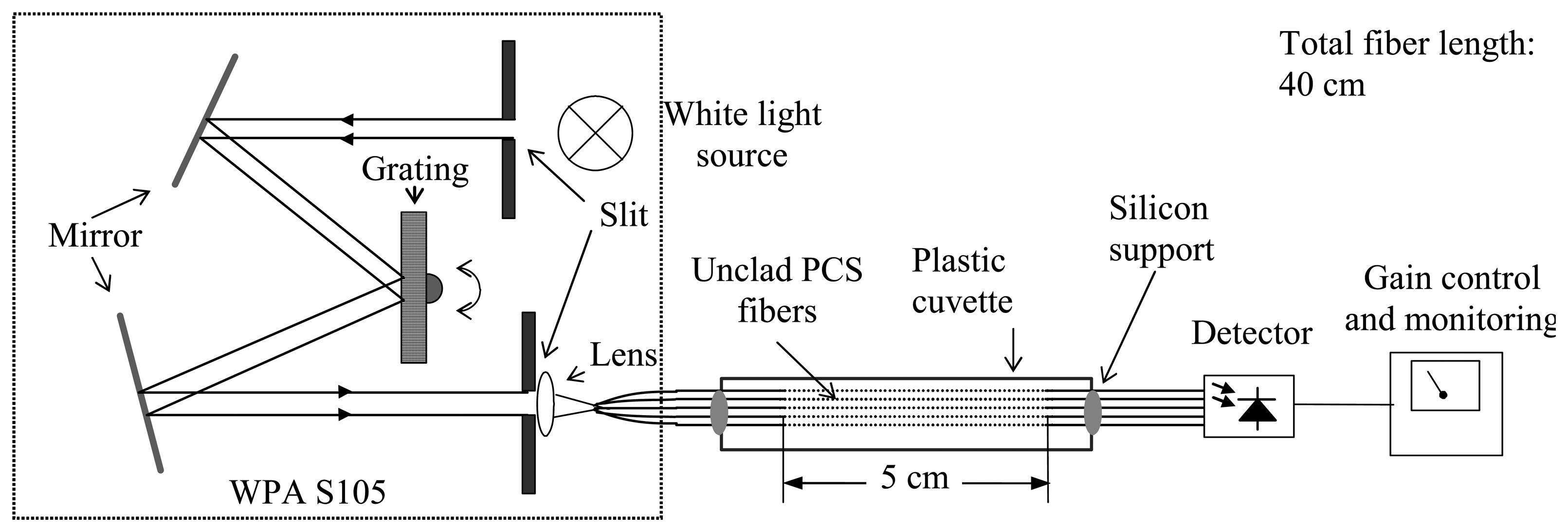
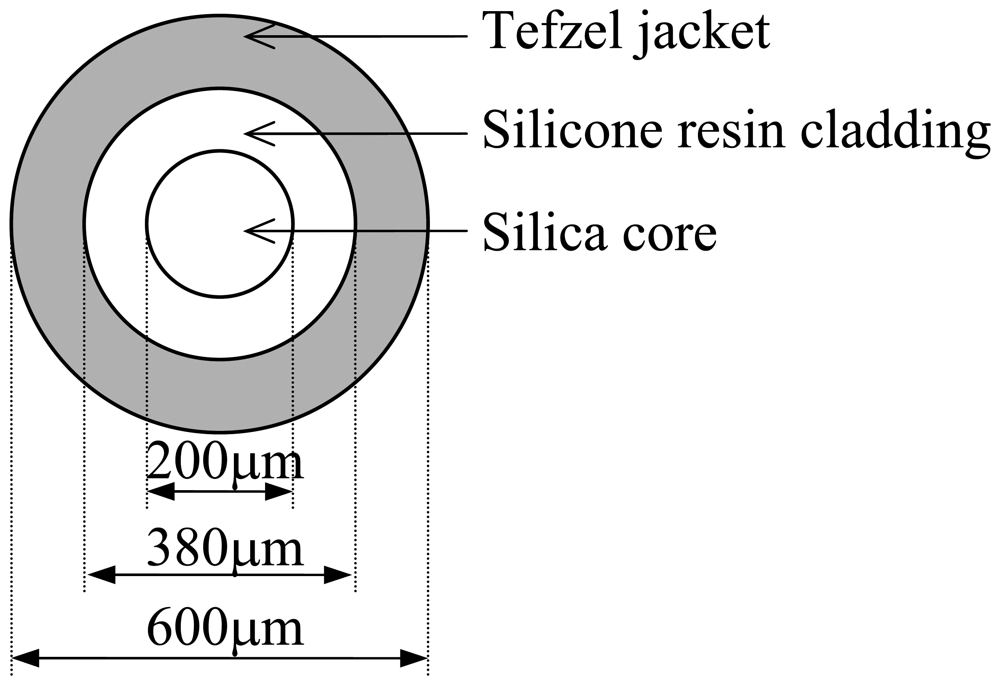
2. EFA Sensor Measurements
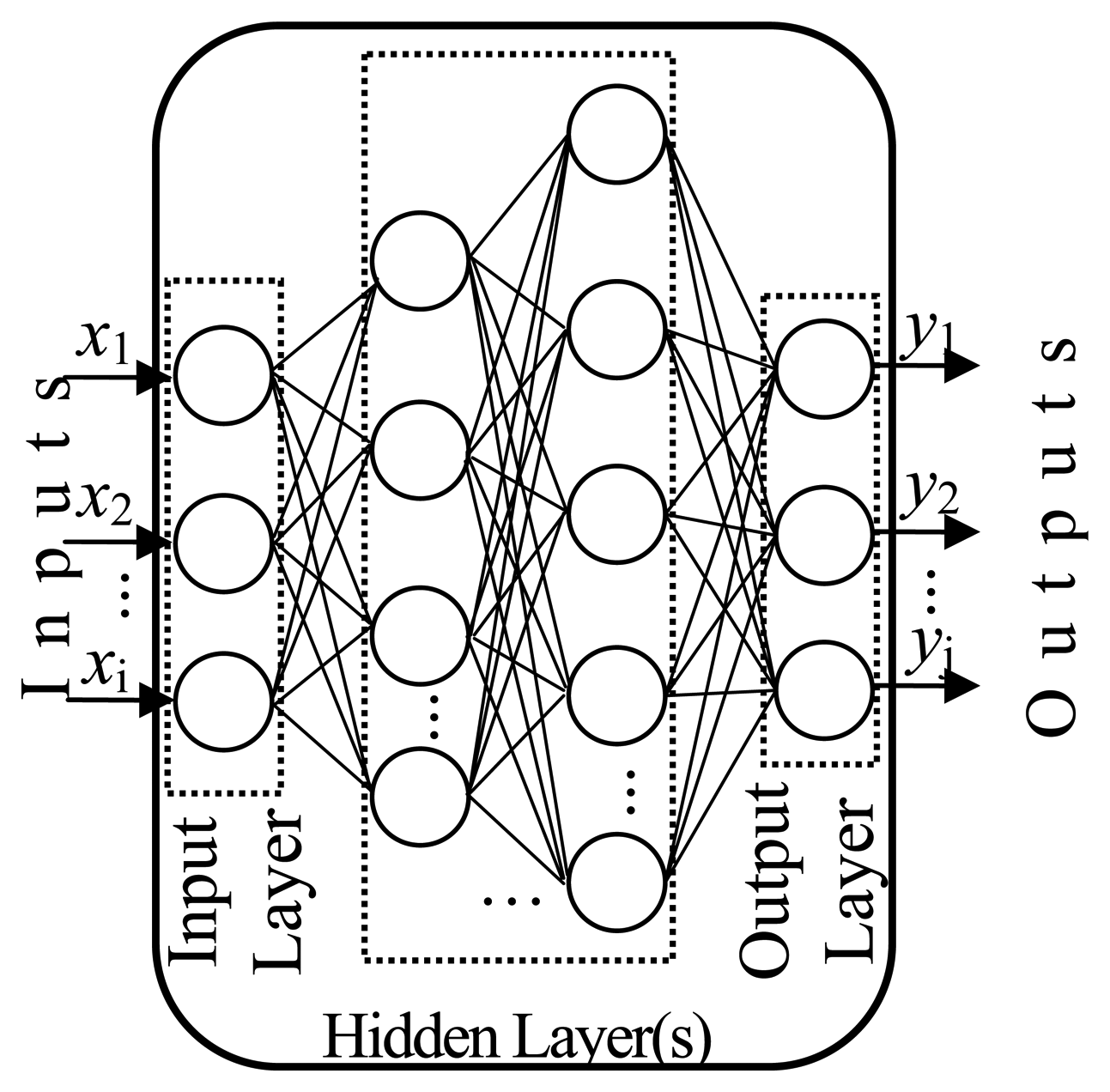
3. Artificial Neural Networks (ANNs)
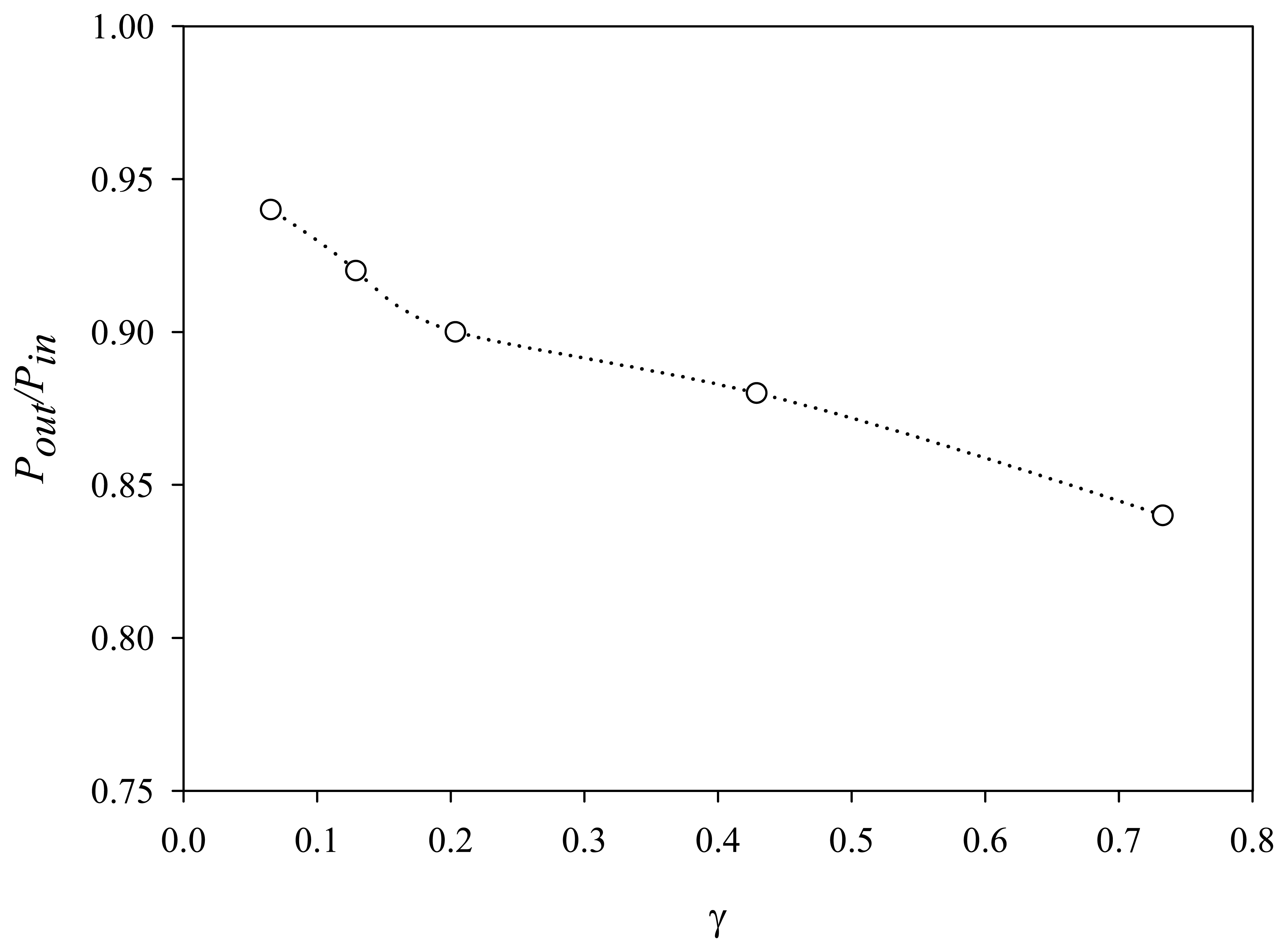
4. Application of ANN and Results
5. Conclusions
References
- DeGrandpre, M.D.; Burgess, L.W. Long path fiber-optic sensor for evanescent field absorbance measurements. Anal. Chem. 1988, 60, 2582–2586. [Google Scholar]
- Wolfbeis, O.S. Fiber-optic chemical sensors and biosensors. Anal. Chem. 2006, 78, 3859–3874. [Google Scholar]
- Gupta, B. D.; Sharma, D. K. Evanescent wave absorption based fiber optic pH sensor prepared by dye doped sol-gel immobilization technique. Opt. Comm. 1997, 140, 32–35. [Google Scholar]
- Choudhury, P.K.; Yoshino, T. On the pH response of fiber optic evanescent field absorption sensor having a U-shaped probe: An experimental analysis. Optik-Int. J. Light Electron Opti. 2003, 114, 13–18. [Google Scholar]
- Lye, P.G.; Boerkamp, M.; Ernest, A.; Lamb, D.W. Investigating the sensitivity of PMMA optical fibres for use as an evanescent field absorption sensor in aqueous solutions. J. Phys. 2005, 15, 262–269. [Google Scholar]
- Khijwania, S.K.; Srinivasan, K.L.; Singh, J.P. An evanescent-wave optical fiber relative humidity sensor with enhanced sensitivity. Sensors Actuat. B 2005, 104, 217–222. [Google Scholar]
- Willer, U.; Scheel, D.; Kostjucenko, I.; Bohling, C.; Schade, W.; Faber, E. Fiber-optic evanescent-field laser sensor for in-situ gas diagnostics. Spectrochim. Acta A: Mol. Biomol. Spectros. 2002, 58, 2427–2432. [Google Scholar]
- Santoyo, A.T.; Shlyagina, M.G.; Jimeneza, F.J.M.; Oyarzabal, L.N.R. Determination of the optimal wavelength for temperature independent detection of commercial gasoline with a polymer cladding optical fiber. Opt. Comm. 2007, 271, 386–390. [Google Scholar]
- Bosch, M.E.; Sánchez, A.J.R.; Rojas, F.R.; Ojeda, C.B. Recent Development in Optical Fiber Biosensors. Sensors 2007, 7, 797–859. [Google Scholar]
- Wu, Y.; Deng, X.; Li, F.; Zhuang, X. Less-mode optic fiber evanescent wave absorbing sensor: Parameter design for high sensitivity liquid detection. Sensors Actuat. B 2007, 122, 127–133. [Google Scholar]
- Lee, S.T.; Kumar, R.D.; Kumar, P.S.; Radhakrishnan, P.; Vallabhan, C.P.G.; Nampoori, V.P.N. Long period gratings in multimode optical fibers: application in chemical sensing. Opt. Comm. 2003, 224, 237–241. [Google Scholar]
- Cao, W.; Duan, Y. Optical fiber-based evanescent ammonia sensor. Sensors Actuat. B 2005, 110, 252–259. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed; Prentice-Hall: Englewood Cliffs, NJ, 1999. [Google Scholar]
- Kröse, B.; Smagt, P.V.D. An introduction to Neural Networks; The University of Amsterdam: Amsterdam, 1996. [Google Scholar]
- Christodoulou, C.G.; Georgiopoulos, M. Application of Neural Networks in Electromagnetics; Artech House: MA, USA, 2001. [Google Scholar]
- Brook, T.E.; Taib, M. N.; Narayanaswamy, R. Extending the range of a fibre-optic relative-humidity sensor. Sensors Actuat. B 1997, 39, 272–276. [Google Scholar]
- Taib, M.N.; Andres, R.; Narayanaswamy, R. Extending the response range of an optical fibre pH sensor using an artificial neural network. Anal. Chim. Acta 1996, 330, 31–40. [Google Scholar]
- Suah, F.B.M.; Ahmad, M.; Taib, M.N. Optimisation of the range of an optical fibre pH sensor using feed-forward artificial neural network. Sensors Actuat. B 2003, 90, 175–181. [Google Scholar]
- Taib, M.N.; Narayanaswamy, R. Multichannel calibration technique for optical-fibre chemical sensor using artificial neural network. Sensors Actuat. B 1997, 39, 365–370. [Google Scholar]
- Yang, Q.; Butler, C. Sensor signal processing using neural networks for a 3-D fibre-optic position sensor. Sensors Actuat. A 1994, 41, 102–109. [Google Scholar]
- Tu, Y.; Huang, S. Two kinds of neural network algorithms suitable for fiber optic sensing array signal processing. Opt. Engin. 1996, 35, 2196–2202. [Google Scholar]
- Borecki, M. Intelligent Fiber Optic Sensor for Estimating the Concentration of a Mixture-Design and Working Principle. Sensors 2007, 7, 384–399. [Google Scholar]
- Saraçoğlu, Ö. G.; Özsoy, S. Implementation of Evanescent Field Absorption Based pH Sensing using Fiber Optic Bundle. Proc. Elect. Electron. Comp. Engin. Symp. in Turkish. 2000, 275–279. [Google Scholar]
- Payne, F.P.; Hale, Z.M. Deviation from Beer's Law in multimode evanescent field sensors. Int. J. Optoelectron. 1993, 8, 743–748. [Google Scholar]
- Saracoglu, O.G.; Ozsoy, S. Simple equation to estimate the output power of an evanescent field absorption-based fiber sensor. Opt. Engin. 2002, 41, 598–600. [Google Scholar]
- http://www.mathworks.com/access/helpdesk_r13/help/toolbox/nnet/nnet.html

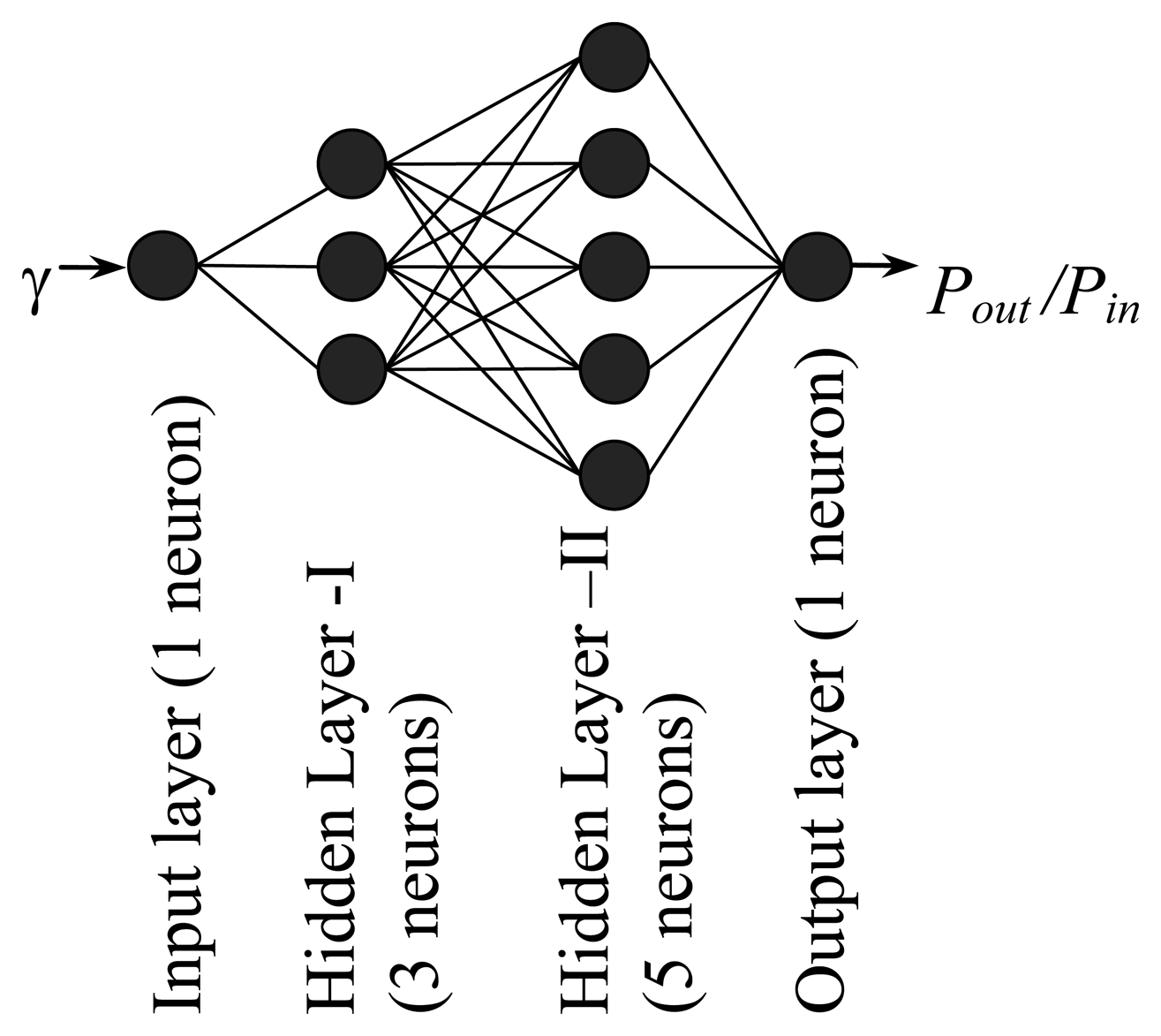
| Algorith m | Number of Artificial Neurons | MSE | |||
|---|---|---|---|---|---|
| Input Layer | Hidden Layer - I | Hidden Layer - II | Output Layer | ||
| LM | 1 | 3 | 5 | 1 | 1.85E-07 |
| SCG | 1 | 2 | 5 | 1 | 9.98E-07 |
| BFGS | 1 | 5 | 4 | 1 | 6.25E-07 |
| BR | 1 | 2 | 2 | 1 | 1.10E-07 |
| CGP | 1 | 4 | 4 | 1 | 3.55E-07 |
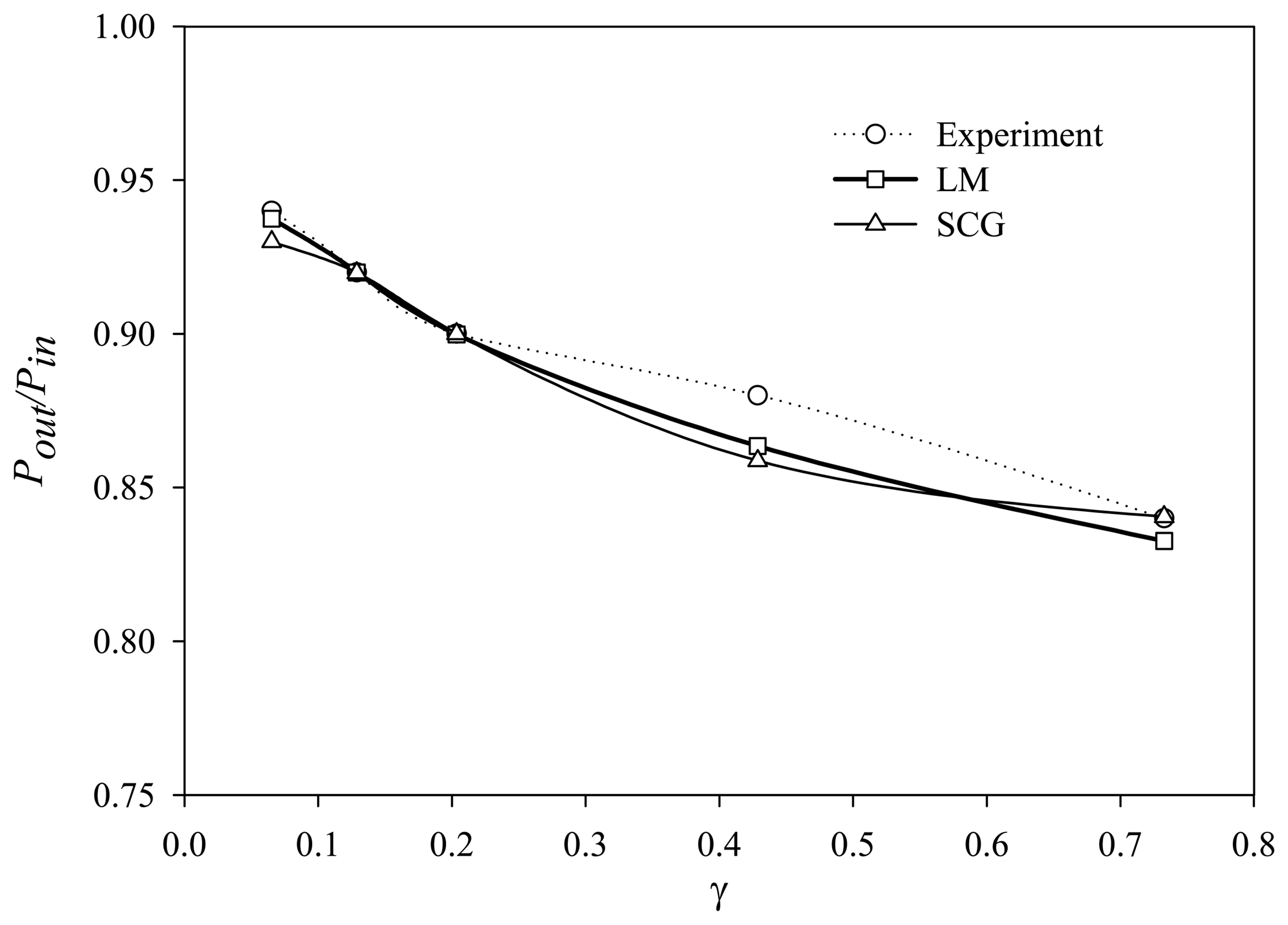
| γ | Sensor Response | ANN Model Outputs | ||||
|---|---|---|---|---|---|---|
| LM | SCG | BFGS | BR | CGP | ||
| 0.7328 | 0.84 | 0.83269 | 0.84053 | 0.84139 | 0.83967 | 0.84130 |
| 0.4288 | 0.88 | 0.86355 | 0.85874 | 0.87051 | 0.85924 | 0.86277 |
| 0.2035 | 0.90 | 0.89983 | 0.90008 | 0.89909 | 0.90004 | 0.90058 |
| 0.1290 | 0.92 | 0.92003 | 0.91987 | 0.91944 | 0.91996 | 0.92030 |
| 0.0653 | 0.94 | 0.93748 | 0.93000 | 0.92248 | 0.93843 | 0.93089 |
| MSE | 0.04389 | 0.07333 | 0.05316 | 0.05762 | 0.05072 | |
| γ | Sensor Response | ANN Model Outputs | ||||
|---|---|---|---|---|---|---|
| LM | SCG | BFGS | BR | CGP | ||
| 0.7328 | 0.84 | 0.83269 | 0.83450 | 0.83705 | 0.87837 | 0.83797 |
| 0.4288 | 0.88 | 0.86355 | 0.86220 | 0.85763 | 0.87837 | 0.85642 |
| 0.2035 | 0.90 | 0.89983 | 0.90040 | 0.89922 | 0.87837 | 0.89999 |
| 0.1290 | 0.92 | 0.92003 | 0.91970 | 0.91939 | 0.87837 | 0.91948 |
| 0.0653 | 0.94 | 0.93748 | 0.92560 | 0.92164 | 0.87837 | 0.92300 |
| MSE | 0.04389 | 0.0738 | 0.1125 | 0.9929 | 0.1129 | |
© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Saracoglu, Ö.G. An Artificial Neural Network Approach for the Prediction of Absorption Measurements of an Evanescent Field Fiber Sensor. Sensors 2008, 8, 1585-1594. https://doi.org/10.3390/s8031585
Saracoglu ÖG. An Artificial Neural Network Approach for the Prediction of Absorption Measurements of an Evanescent Field Fiber Sensor. Sensors. 2008; 8(3):1585-1594. https://doi.org/10.3390/s8031585
Chicago/Turabian StyleSaracoglu, Ö. Galip. 2008. "An Artificial Neural Network Approach for the Prediction of Absorption Measurements of an Evanescent Field Fiber Sensor" Sensors 8, no. 3: 1585-1594. https://doi.org/10.3390/s8031585
APA StyleSaracoglu, Ö. G. (2008). An Artificial Neural Network Approach for the Prediction of Absorption Measurements of an Evanescent Field Fiber Sensor. Sensors, 8(3), 1585-1594. https://doi.org/10.3390/s8031585





