The trick which makes the LGB algorithm possible is to convert the original graph G into its corresponding line graph L(G). The property that the edges of the line graph correspond to the nodes of the original graph enables us to design a new heuristic algorithm which once more finds small edge separators but in the line graph this time. This, in effect, allows us to directly obtain vertex separators for the corresponding original graph.
The LGB algorithm is, in essence, a modified version of KLB in that both the characteristics of the line graph such as the existence of edges, now, that needs to be treated as one and the requirements imposed by the original problem such as the necessity to keep track of the loads of the respective partitions in terms of the weights of the edges rather than nodes are neatly taken into account so as to efficiently compute small edge separators. Assuming that such small edge separators can feasibly be found in the line graph through an algorithm which is going to be described in full detail shortly, it is trivial to derive the corresponding nodal partition induced in the original graph which corresponds exactly to the minimum cut partition obtained by LGB in the line graph.
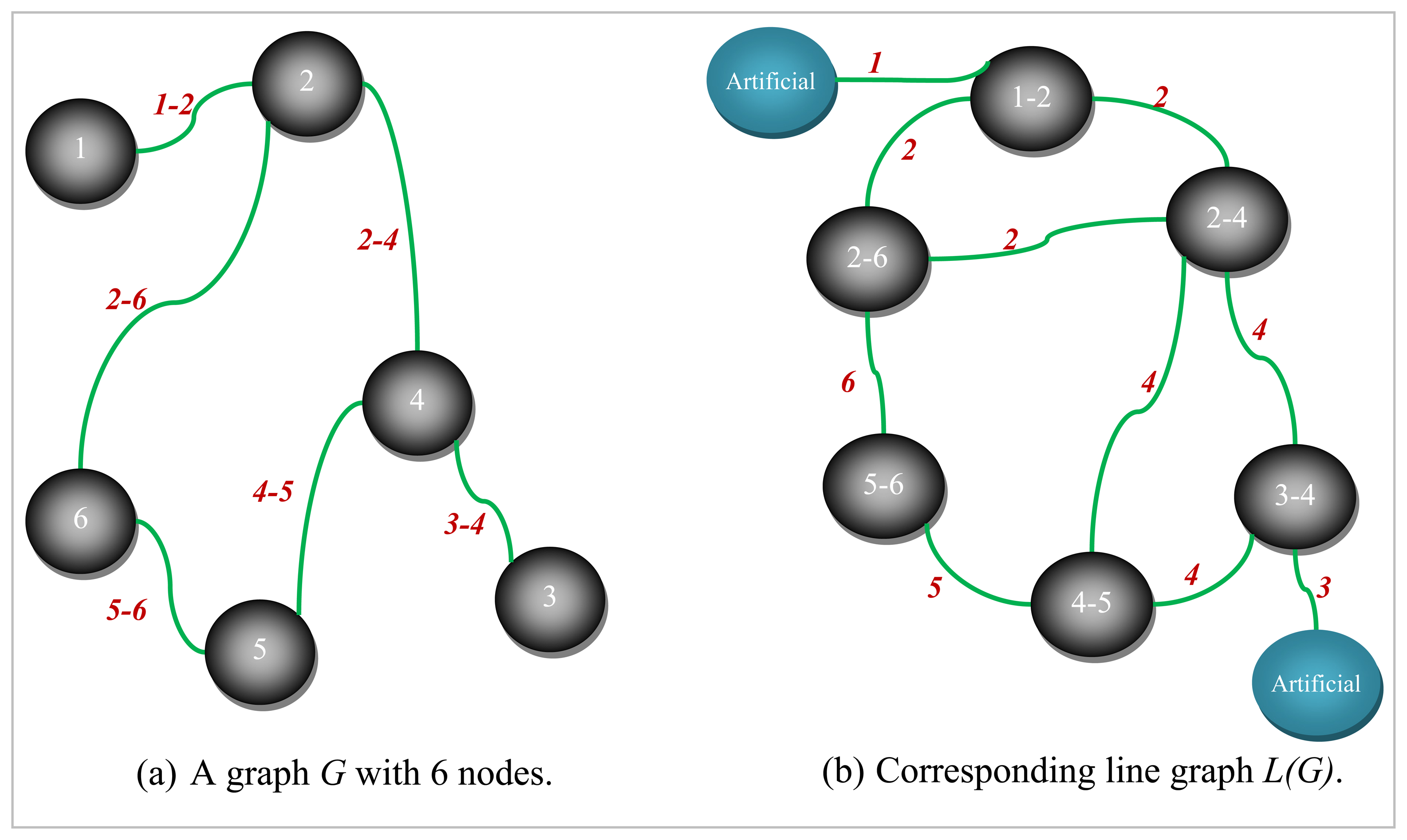
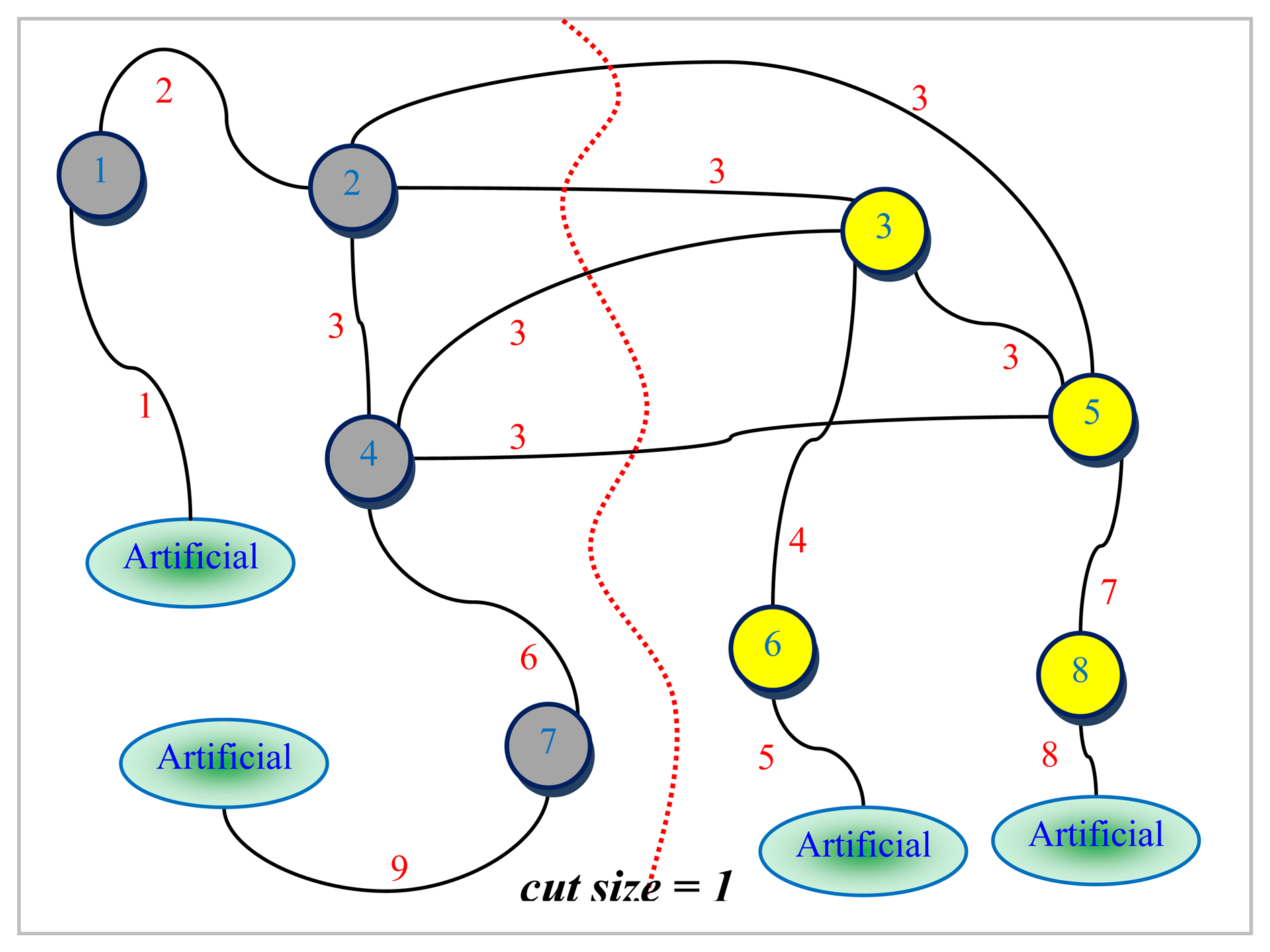
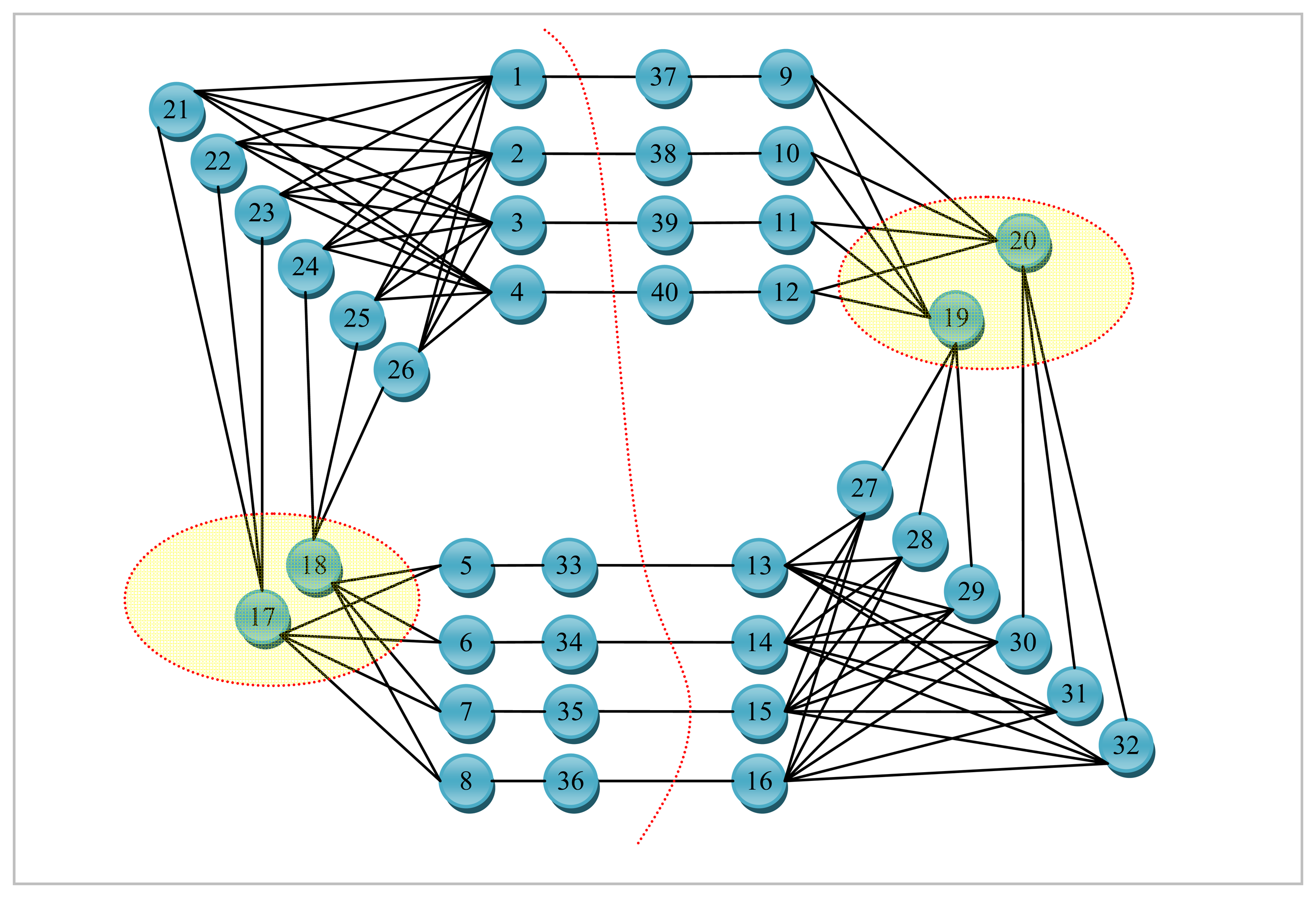
An example graph
G for which a small size vertex separator is sought and its corresponding line graph
L(G) are depicted in
Figures 5 and
6, respectively. The numbers shown next to each edge in
Figure 5 are used to uniquely identify them. All the nodes are assumed to be associated with a weight of one for the example graph
G given in
Figure 5. The dotted line in red seen in
Figure 6 represents the bisection of
L(G) computed by the LGB algorithm. There are a total of four edges in the cut in
Figure 6. These edges have been all labeled the same (i.e.,
3 corresponding to node 3 in
Figure 5). It can easily be seen from
Figure 6 that nodes 1, 2, 4 and 7 shaded in grey together with edges 1, 2, 3, 6, and 9 of
L(G) to the left of the dotted line in red are all pinned in a separate partition. These grey-shaded nodes 1, 2, 4, and 7 in
Figure 6 are actually the edges labeled as 1, 2, 4, and 7 again, respectively in
Figure 5. The edge separator and the partitioning scheme in
Figure 6 obtained by the LGB algorithm, thus, induce the nodal partitioning specified by the configuration of
Figure 5 in which only node 3 ends up in the separator. While nodes in grey (1, 2, 6, 9) are assigned to a partition, nodes in yellow (4, 5, 7, 8) are placed in another which turns out, in this case, to be an optimal vertex partition with respect to both the separator size minimization (just node 3) and the load balance (each have 4 nodes) constraints. It should, however, be noted at that point that the cut size has been treated as one in
Figure 6 by counting only the number of distinct labels of weight one as specified by the example at the cut. As it is quite clear from the discussion of the example, LGB is a modified KLB applied to the line graph. The only modifications needed, apparently, are those which stem from the fact that a number of edges having the same label in the line graph have to be treated as a single edge and the fact that the partition weights implicitly used to control the quality of load balance are, now, a function of the edge weights rather than the node weights. The existence of multiple edges having the same labels in the line graph as seen in
Figure 6 has a direct effect on the way the gain of a node is calculated and updated in the line graph. The efficiency of the proposed LGB algorithm heavily depends on preserving the locality of updates in LGB as is the case in KLB.
For computing vertex separators as outlined in
Figure 7, the original graph
G is first transformed into its line graph equivalent
L(G). The LGB algorithm is, then, applied to obtain the partitions
P1 and
P2 similar to the KLB algorithm. The only exception is, this time, that gain value calculations and updates take place with respect to the labeled edges grouped into two for each node. The vertex separator and the corresponding partitions are, finally, recovered in
G as dictated by the partitioning scheme induced by
P1 and
P2 of
L(G) obtained by an application of LGB. As the corresponding line graph of the original graph has now been partitioned into clusters such that the sum of the weights of the edges with distinct labels across clusters is minimized and the load of each cluster is balanced up to a tolerable amount, the total weight of the vertices in the separator of the original graph corresponding to the distinct labels of the edges in the cut of its line graph have also been minimized effectively. A similar argument holds with respect to the balancing of load over the partitions so long as a modification is incorporated into LGB such that the sum of all the individual weights of the labels in the set of distinct labels of edges instead of the total weight of nodes in respective partitions of
L(G) at any time is used to keep track of the individual weights of the partitions. Such a modification, which certainly frees us from assuming that the number of edges and vertices in the original graph are linearly proportional, is possible as will be explained shortly. The load is, therefore, balanced by LGB up to an amount specified by the tolerance factor
ε.
4.3.2 LGB Algorithm and the Data Structures
The LGB algorithm used in step (2) of Procedure 4.1 to find small vertex separators for partitioning a graph is listed in
Figure 8. Both the data structures used and the algorithm itself are described next in the execution order as explanations are provided in detail.
The input to the Algorithm 4.2 listed in
Figure 8 is the line graph
L(G) of the original graph
G. L(G) is represented as an array of size
e which corresponds to the number of edges in
G.
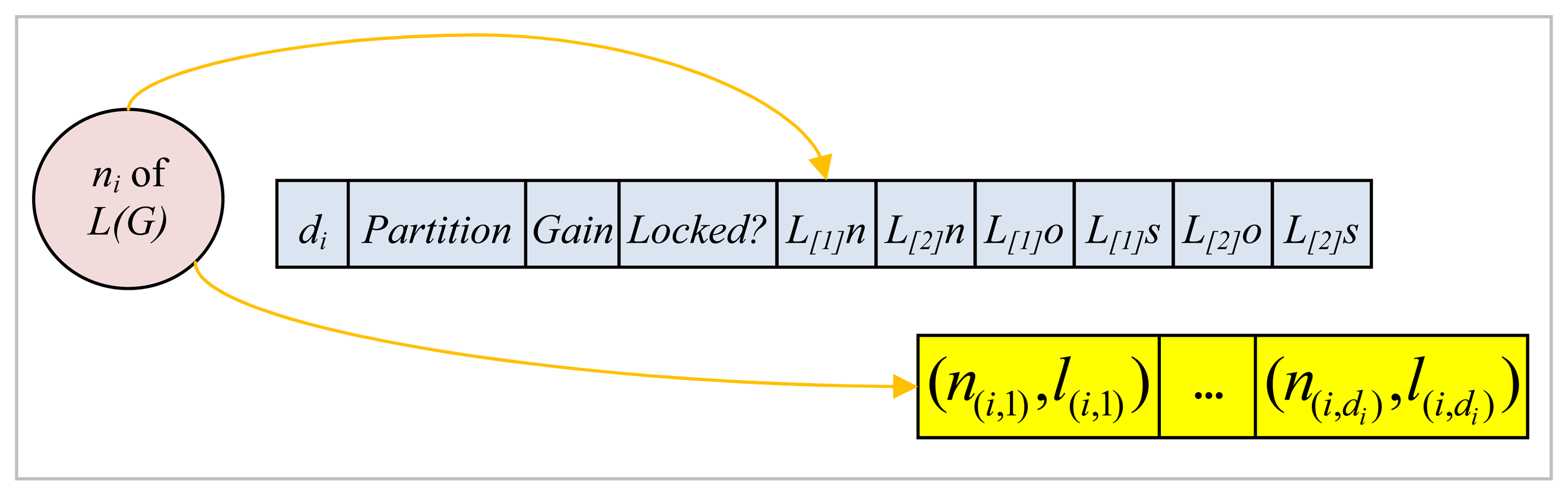
Each slot of the array as shown in
Figure 9 stores information for the corresponding node
ni of
L(G), such as its degree
di; the partition it belongs to which may be either 1 or 2 at any instant corresponding to the two partitions
P1 and
P2, respectively; its gain value; whether it is locked or not at any instant; its
L[1]n and
L[2]n which stand for the names of the two distinct labels of the edges incident on this node; its
L[1]s and
L[2]s which denote the number of adjacent nodes connected with an edge labeled either
L[1]n or
L[2]n respectively that belong exactly to the same partition as the node under consideration; and
L[1]o and
L[2]o which are the number of adjacent nodes connected with an edge labeled either
L[1]n or
L[2]n, respectively, that are, on the other hand, located in the other partition with respect to the node at hand. Each node
ni also points to an array of length
di where a sequence of pairs in the form of
(n(i,j), l(i,j)) where
n(i,j) is an adjacent node and
l(i,j) is the label of the corresponding edge are stored as shown in
Figure 9.
Upon getting the input, LGB obtains an initial partition
P1 and
P2 at step (1) of the Algorithm 4.2. Depending on the initial partition, the number of external and internal edges for each of the two distinct labels, namely,
L[1]o,
L[2]o,
L[1]s, and
L[2]s, are calculated next by a single pass over the line graph
L(G). Steps (3) and (4) detect the set of distinct labels in the cut as well as in partitions
P1 and
P2. This is, in effect, equivalent to finding the vertex separator
S and partitions
A and
B of
G induced by the partitioning of
L(G) obtained initially. It is now time to calculate the initial weights of the partitions
P1 and
P2 and store them as original weights as outlined in steps (5) and (6) before the iterations start. In step (7), all the nodes are marked as unlocked so that they will have a chance of being moved and their gains are all initialized to zero. The initial load difference corresponding to the initial partition is stored at step (8) and the main outer loop starts at step (9) of the algorithm which can be iterated so long as the limit specified by
LIMIT in line (10) is not exceeded and either the cut size or the load balance can be improved upon. LGB is just like Fiduccia and Mattheyses modified KLB, running with the exception that edges with the same label are treated as a single edge with the specified weight with respect to both the cut size and gain calculations performed. At step 9.1 of the outer loop between (9) and (10), a temporary copy of
L(G)'s header section excluding the adjacent nodes shown in
Figure 13 is created so that the results of intermediate moves can be recorded. Step 9.2 initializes the bins used for sorting the gain values of the nodes to make it possible to find maximum gain values in both partitions
P1 and
P2 in
O(1) time via a process called bin sorting.
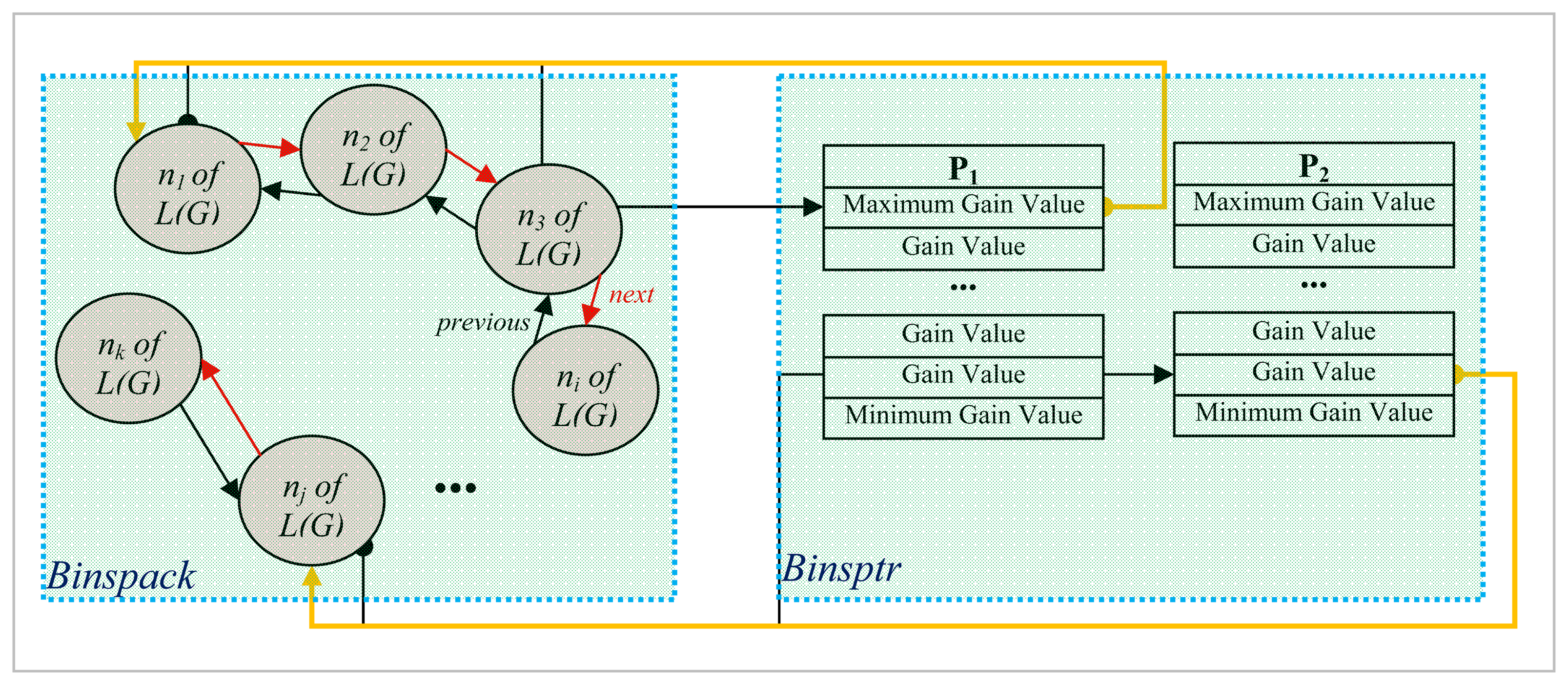
A doubly linked list data structure,
Binspack, shown in
Figure 10 has a slot for every node of the
L(G). It has some fields in every slot for maintaining the current gain values of the corresponding nodes and two pointers named
previous and
next as shown in
Figure 10 which point to the previous and the next nodes with the same gain values, respectively. If there is no previous node, however,
previous is assigned the negative of the bin number pointing to this specific node whose gain value is directly related to the bin number in
Binsptr data structure also shown in
Figure 10.
Binsptr[gv] [2] data structure is used to store the pointers to the first node in
Binspack with a gain value equal to
gv for each different gain value
gv that can possibly be attained by the nodes in
P1 as well as in
P2 at all times during the algorithm. These two data structures enable us to find the node with the maximum gain value in each partition and also update the gains of the adjacent nodes that are affected from a move at each iteration in
O(1) time by keeping the bins sorted. In case it is assumed that the nodes of
G have all a unit weight equal to one, the corresponding edges of
L(G) would, accordingly, have labels whose weights are also one. This would specifically induce a set of five possible gain values in the range of
- 2 through
2 since each node of
L(G) has two distinct labels and the move of such a node may either increase or decrease the cut size by none, one or both of the labels depending on the current configuration.
Binsptr[i] [j], assumingly, would point to a node in the
Binspack data structure with a corresponding gain value of
(i-3) when
i can take on values in the range
0 through
4. However, it should be noted at this point that in the general case where nodes in
G=
(N, E) may have different weights, possible integral values can be in the range specified by [−
gν, +
gν] where
gν = 2 max{
weight(
ni)|
ni ∈
N}.
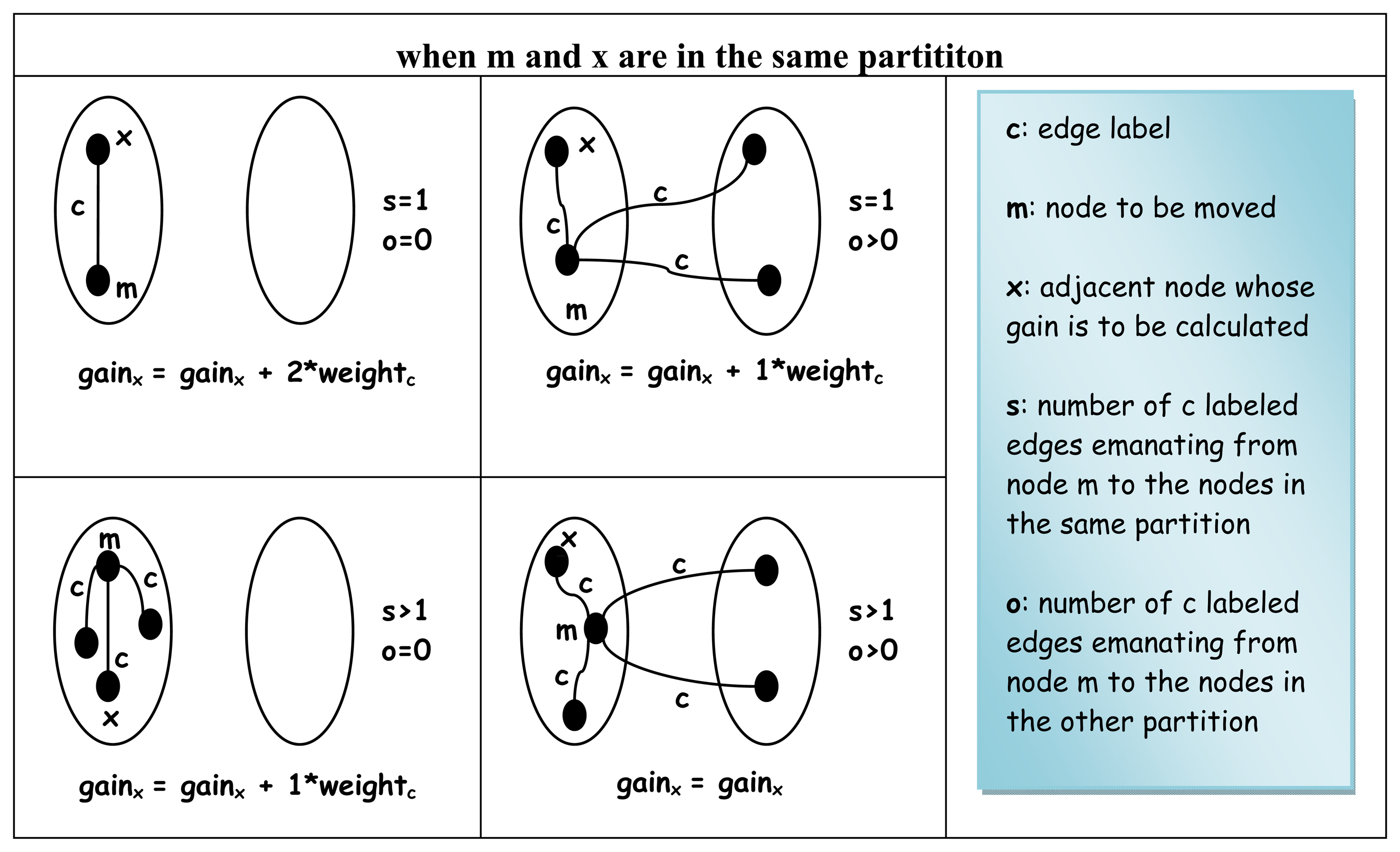
Initial gains are calculated for all nodes in tempL(G) and inserted into the bins at step 9.3 right before the inner loop 9.5 - 9.6 of the algorithm starts moving the nodes. Since each node in L(G) has a labeled degree of two (see Theorem 4.3), the edges emanating from a node can virtually be grouped into two distinctly labeled sets: (1) those labeled by L[1]n and (2) the rest labeled by L[2]n, respectively.
Each set of edges naturally connects to some adjacent nodes that are either in the same partition called
s or in the other partition called
o as seen in
Figure 11 with respect to the node whose gain value is to be calculated.
Definition 4.8: The set of the distinct labels of the edges whose endpoints are not both in the same partition is called the labeled cut set denoted by ℜ within the context of LGB.
Definition 4.9: The sum of the weights of labels in ℜ at any time is called the labeled cut size and denoted by Γ.
Definition 4.10: Gain of a node at any instant of LGB algorithm is defined as the change in the labeled cut size when the node is moved to the other partition.
The Algorithm 4.3 for calculating the initial gain of a node is given in
Figure 12. There are only three cases to be considered for each node whose gain value is to be calculated. The fact that there are actually no more than only three cases can easily be deduced based on Property 4.11.
Property 4.11: If i is a node in the original graph and its degree is k, then k nodes in its line graph will be fully connected by the i labeled edges forming a clique. So the total number of the nodes in a clique connected by the same labeled edges are exactly k*(k-1)/2 in the line graph. This, in turn, implies that if there is an edge labeled ℓ between nodes t1 and t2, t3 has an edge also labeled ℓ incident either on t1 or t2, then there must exist other ℓ labeled edges from t3 to both t1 and t2.
The term
weight(
L[k]n) in
Figure 12 refers to the weight of a node in
G which labels the corresponding edges in
L(G).
After recording the previous load balance difference at step 9.4, the inner loop that performs a sequence of moves from the source partition to the destination partition which has less weight until all the nodes are marked as locked is executed at steps 9.5 through 9.6. For each prospective move found, respective weights of the partitions are updated at step 9.5.3.2 of Algorithm 4.2 as detailed by Algorithm 4.4 shown in
Figure 13.
Having recorded the move together with its sequence number, gain and the new load difference value between the partitions at step 9.5.3.3, it is time for updating the gains affected by this move at step 9.5.3.4. Fortunately, the nodes whose gains need to be updated are only those adjacent to the node just moved. Additionally, the updates are local in that the distinct labels in the cut need not be searched for updates to be done accurately.
Lemma 4.12: There is no need to keep track of the labels in the cut so as to figure out which labels are in the cut after a legal move in L(G).
Proof: The existence of a label in the cut can be instantly discovered according to Property 4.11 when both the number of edges linking to nodes in the same and the other partition are known a priori. The latter is ensured by a local process repeated to adjust the label counts which takes time proportional to the degree of a node in L(G).
This property is exploited for minimizing the number of cases to perform fast updates and minimizes the storage required.
As can be seen from
Figures 14 and
15, updating the gain of each of the adjacent nodes can be performed in
O(1) time. The algorithmic representation corresponding to
Figures 14 and
15 is listed in
Figure 16. After updating the gains of the adjacent nodes, changes are reflected in the bins. The moved node is then locked so that it cannot be moved again and placed in the destination partition. The configuration resulting from this move is finally reflected in
tempL(G) by adjusting the label counts of all the nodes adjacent to the moved node. This is a simple process in which each adjacent node is visited and the number of edges to the same partition and the number of edges to the other partition for each label are either incremented or decremented depending on whether the adjacent nodes are actually in the same or other partition, respectively.
The inner loop is exited to step 9.7 when all the nodes are marked as locked where a sequence number maximizing the expression
gainmove[1]+…+
gainmove[k] is found. Such a strategy avoids getting stuck at local maxima in that it allows for intermediate moves that may cause an increase in the cut size which can be later outscored by better moves. The LGB algorithm, then, realizes the sequence of moves if they are proven to be improving either the cut size or the load balance between the partitions. The next iteration of the outer loop starts at step (9) again with the initial configuration resulting from the previous pass of LGB, and this continues as far as either the quality of the partitioning is improved or a limit to the number of iterations is reached in which case the algorithm stops.
Lemma 4.13: The proposed LGB algorithm takes O(ne) time and O(ne) space, where n is the number of nodes and e is the number of edges in G.
Proof: The line graph
L(G) has, then,
e nodes and
n labels. Referring to the pseudo code in
Figure 8, at each iteration of the inner loop at most
e nodes are locked, and these sub-iterations may be repeated as long as the cut size decreases. At the slowest rate, it may decrease by one per iteration of the outer loop. If the balancing iterations are not allowed, this may be repeated for
O(ne) iterations at most.
It can easily be seen that a single pass of LGB algorithm takes O(e) time just as Fiduccia and Mattheyses modified KLB. Hence, it may be claimed that LGB is fast and has the same characteristics as does KLB. Step 3 of Procedure 4.1 for recovering the corresponding partitions A, B and the vertex separator S in G induced by P1 and P2 of L(G) will be skipped since it has already been covered implicitly.