A Modified Subpulse SAR Processing Procedure Based on the Range-Doppler Algorithm for Synthetic Wideband Waveforms
Abstract
:1. Introduction
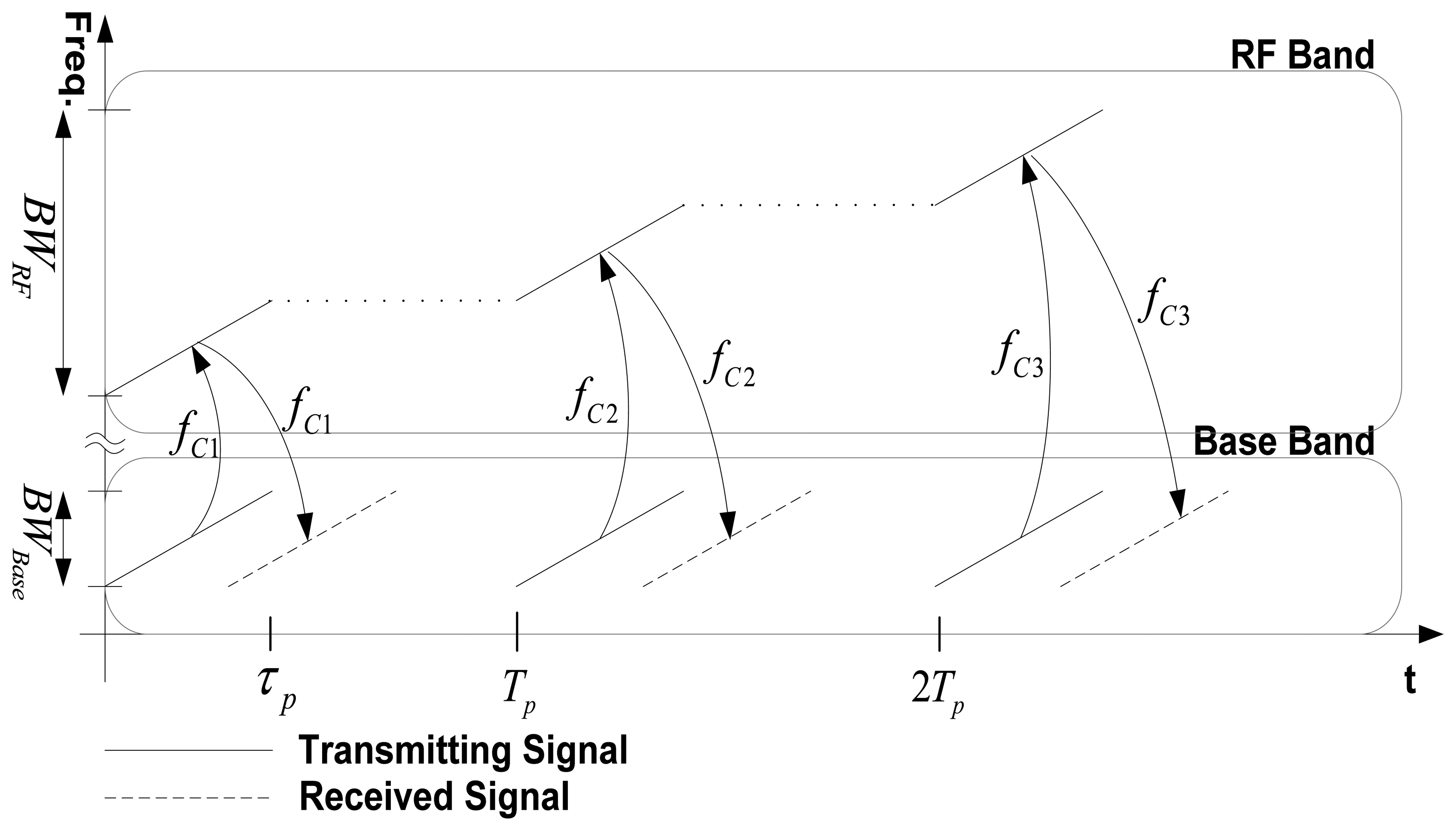
2. Synthetic Wideband Waveform Modeling
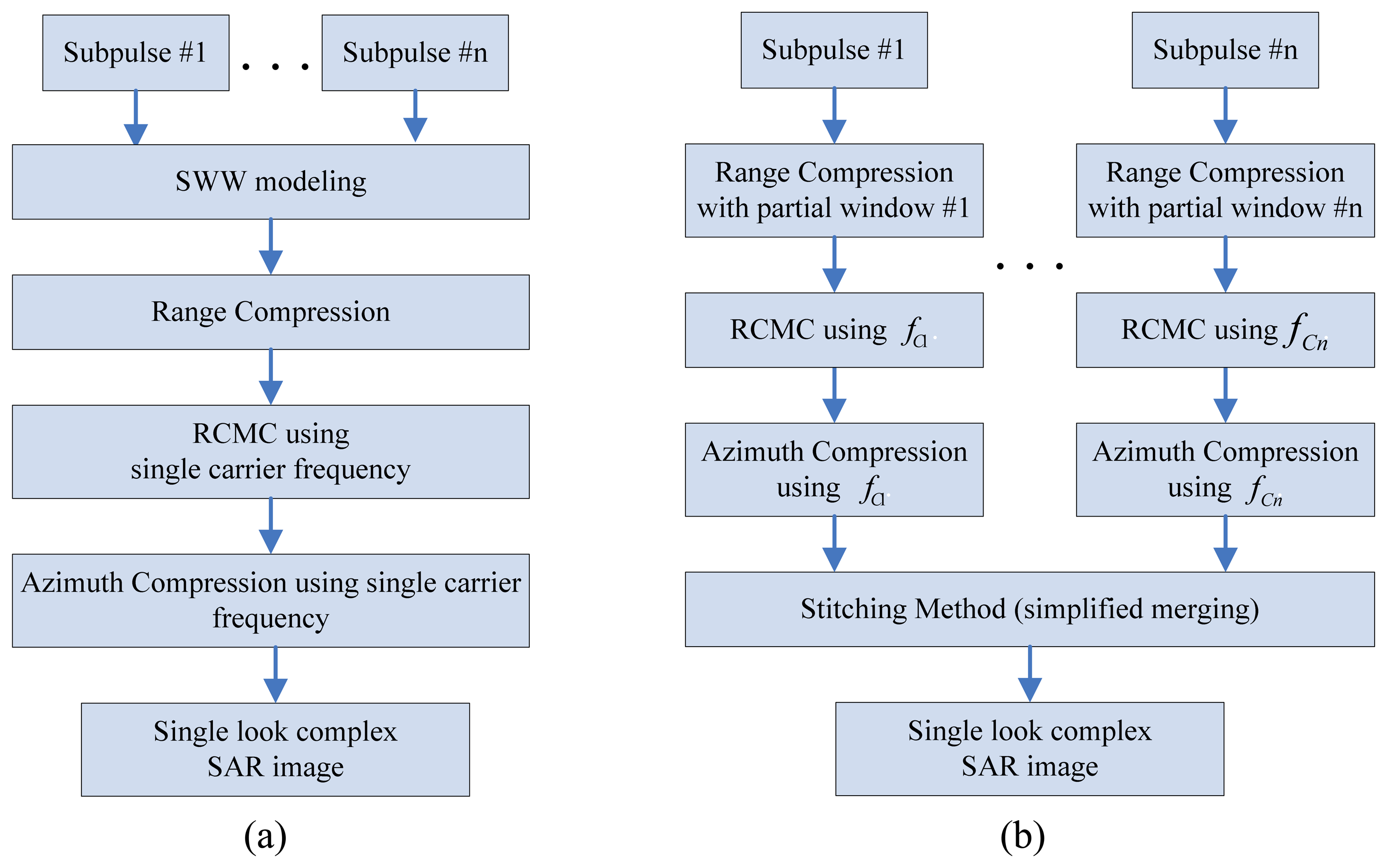
3. Modified RDA Procedure for Synthetic Wideband Signals
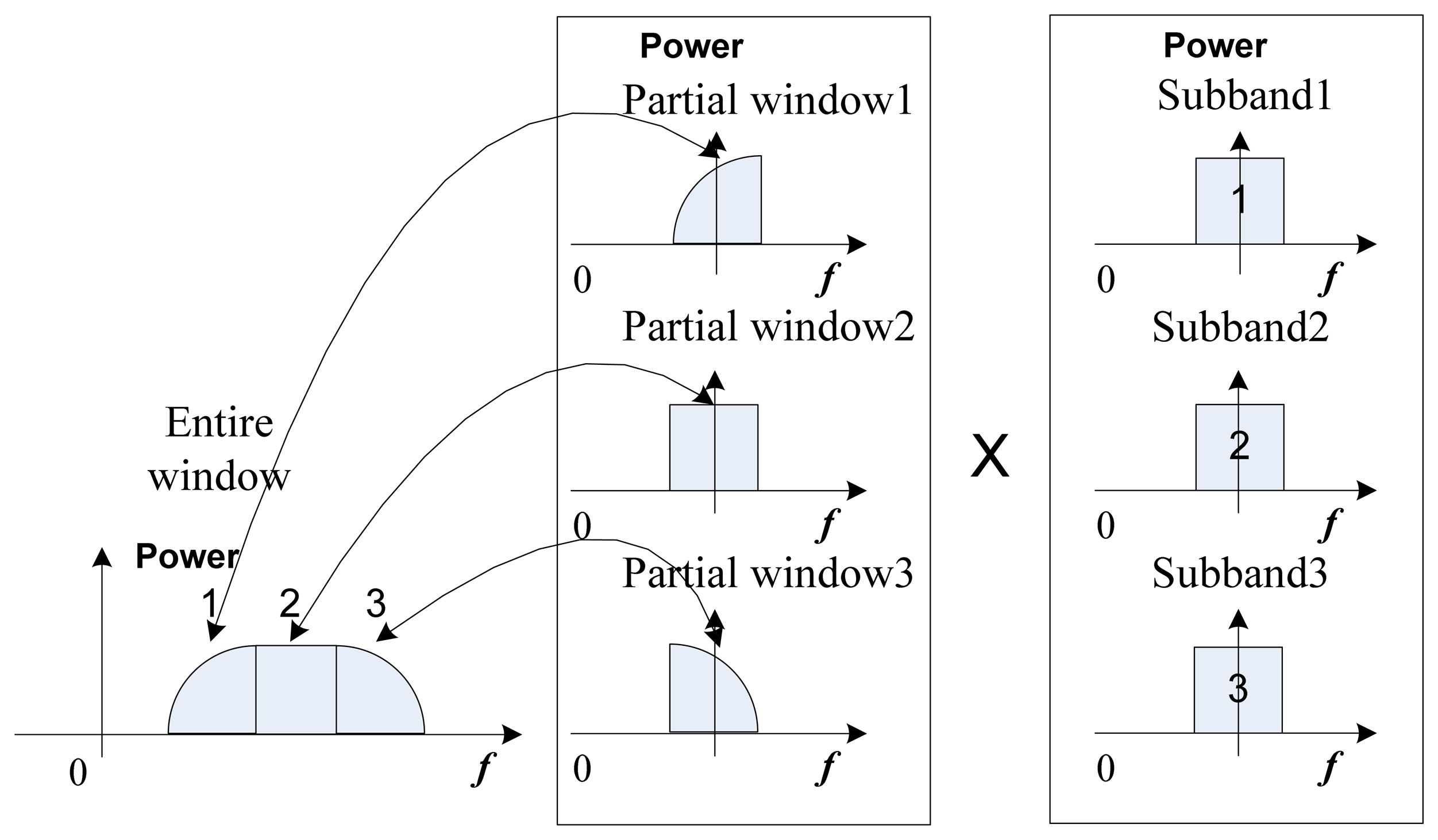
3.1. Range Compression with Partial Windowing
3.2. Range Cell Migration Compensation (RCMC)
3.3. Azimuth Compression
3.4. Stitching
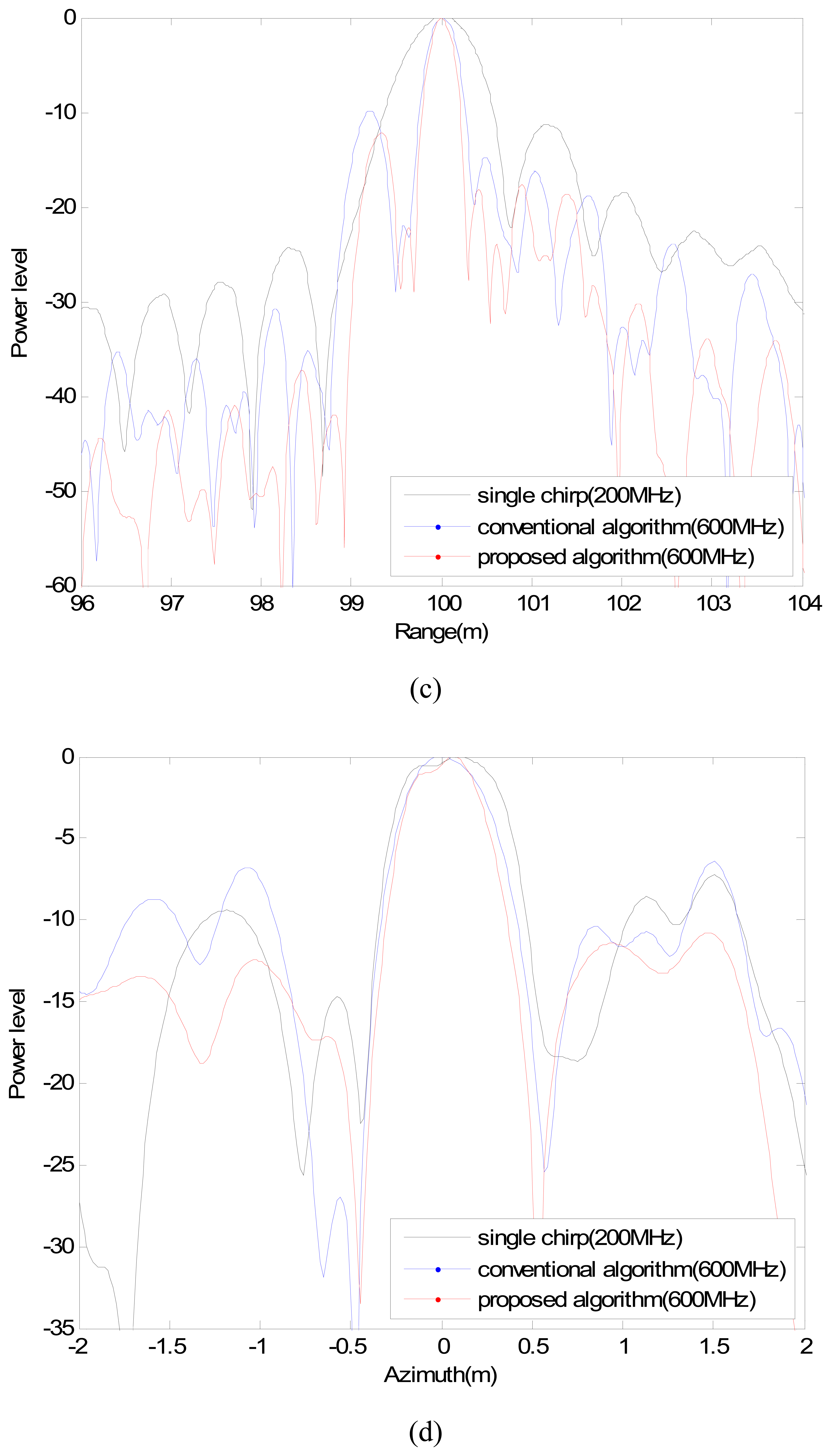
4. Experimental Results
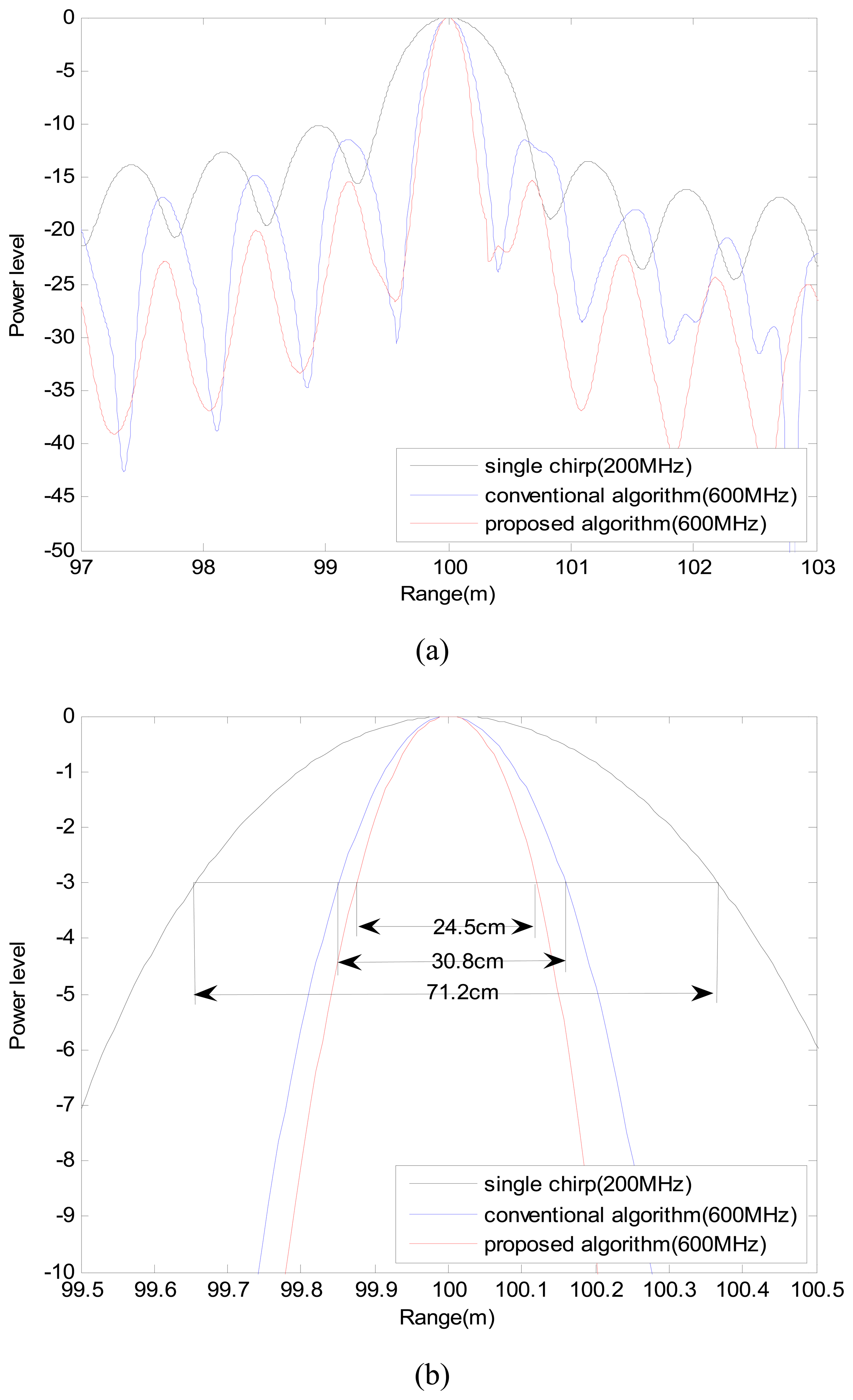
4.1. Single Point Target
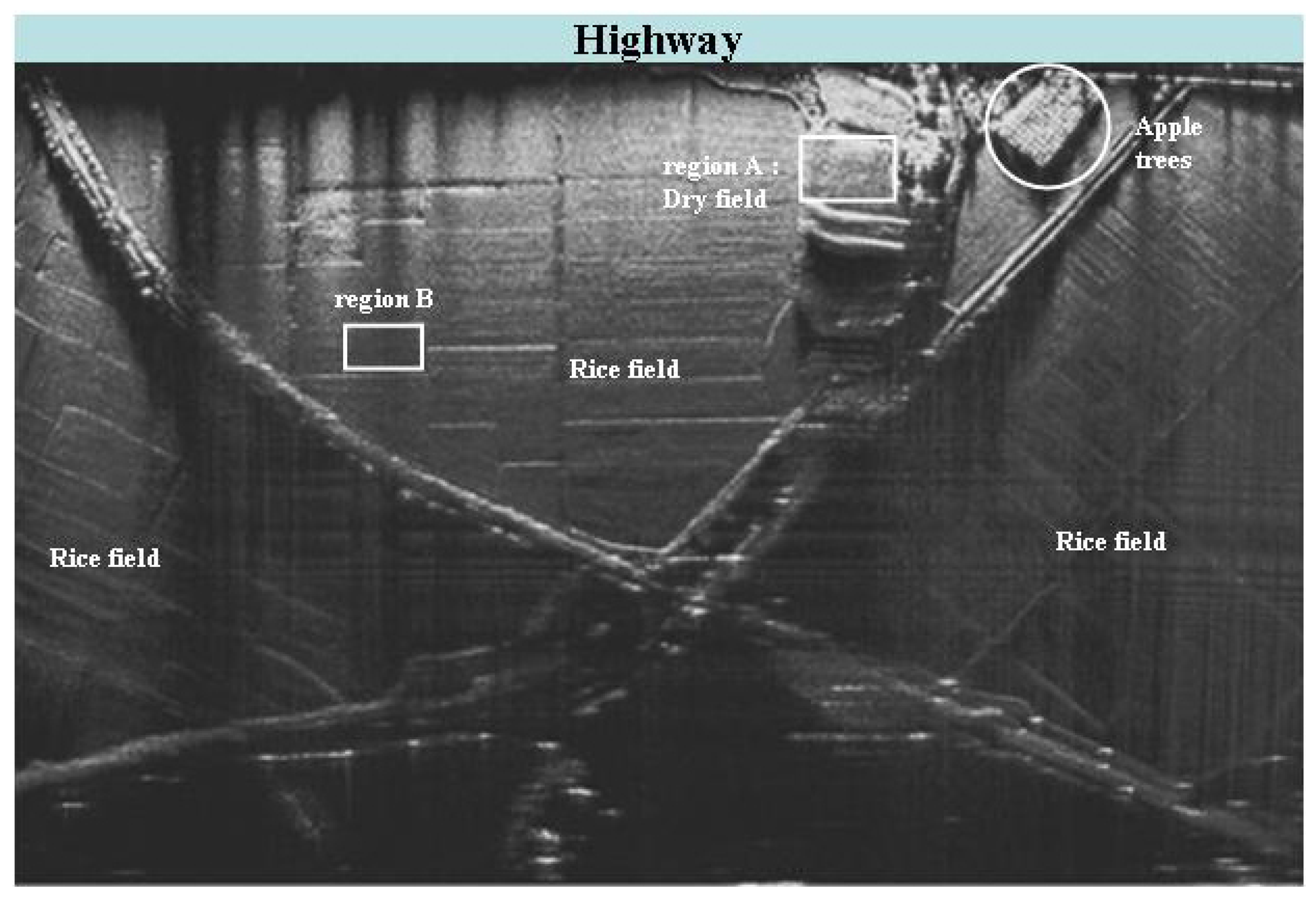
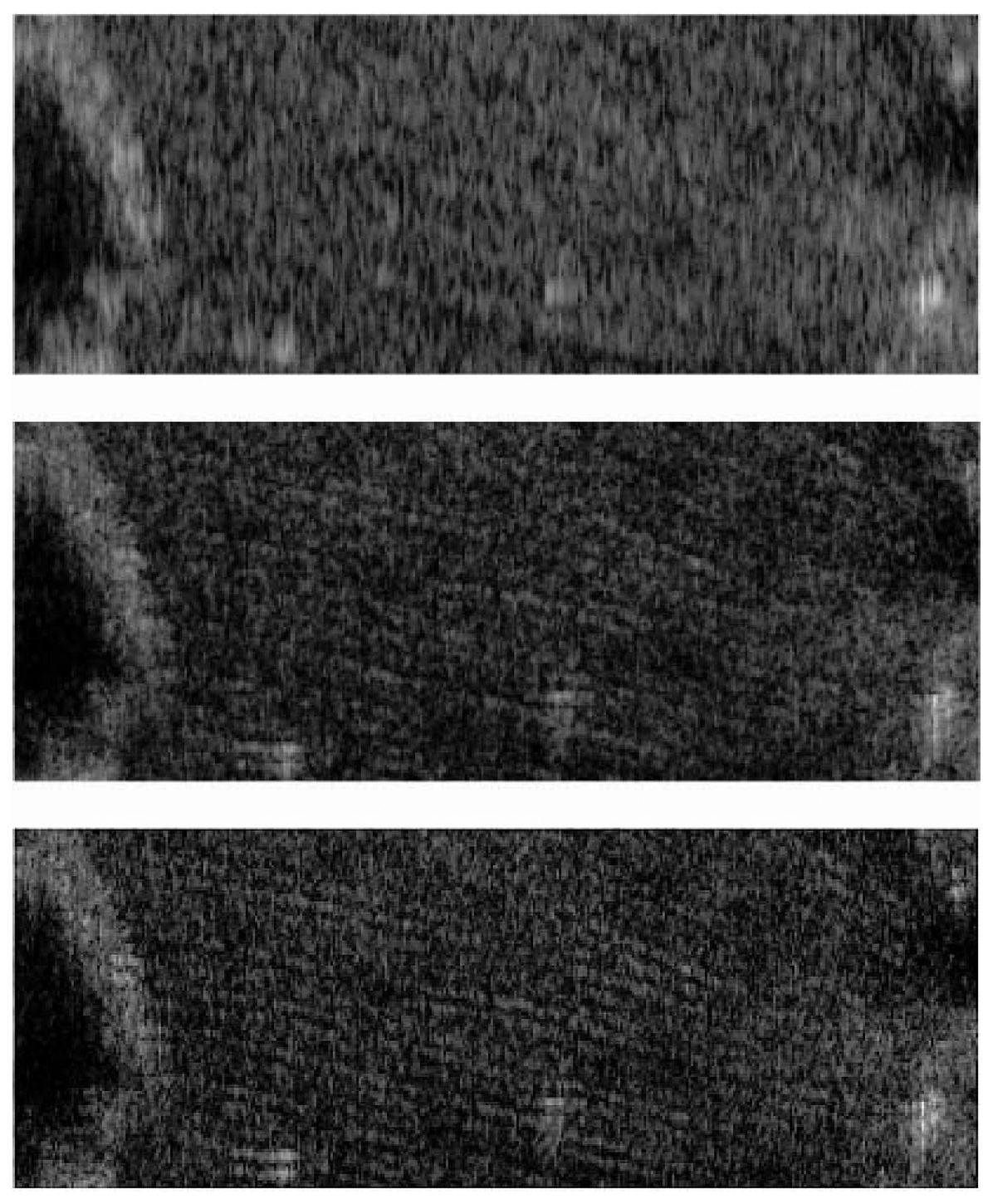
4.2. Distributed Targets
5. Conclusions
Acknowledgments
References and Notes
- McGroary, F.; Lindell, K. A Stepped Chirp Technique for Range Resolution Enhancement. Telesystems Conference, Atlanta, Georgia, USA, March 26–27, 1991; 1, pp. 121–126.
- Lord, R.T.; Inggs, M.R. High Resolution SAR Processing Using Stepped-Frequencies. Proc. IEEE Int. Geosci. Remote S. Symp., Singapore, August 3–8, 1997; pp. 490–492.
- Levanon, N. Stepped-frequency Pulse-train Radar Signal. IEEE P-Radar Son. Nav. 2002, 149, 297–309. [Google Scholar]
- Rabideau, D.J. Nonlinear Synthetic Wideband Waveforms. Proc. IEEE Radar Conforence, Long Beach, Calif, USA, April 2000; 149, pp. 212–219.
- Berens, P. SAR with Ultra-High Range Resolution Using Synthetic Bandwidth. Proc. IEEE Int. Geosci. Remote S. Symp., Hamburg, Germany, June 28–July 2, 1999; pp. 1752–1754.
- Schimpf, H.; Wahlen, A.; Essen, H. High Range Resolution by means of Synthetic Bandwidth Generated by Frequency-stepped Chirps. Electron. Lett. 2003, 39(18), 1346–1348. [Google Scholar]
- Li, H.B.; Zhang, Y.H.; Wu, J. Sidelobes and Grating Lobes Reduction of Stepped-Frequency Chirp Signal. International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Bejing, August 2005; 2, pp. 1210–1213.
- Gladkova, I.; Chebanov, D. Suppression of Grating Lobes in Stepped-Frequency Train. Proc. IEEE Radar Conference, Arlington, USA, May 2005; pp. 371–376.
- Gladkova, I. A General Class of Stepped Frequency Trains. Proc. IEEE Radar Conference, Verona, NY, April 2006; pp. 100–105.
- Maron, D.E. Frequency-Jumped Burst Waveforms with stretch processing. Proc. IEEE Radar Conference, Arlington, USA, May 7–10, 1990; pp. 274–279.
- Cumming, I.G.; Wong, F.H. Digital processing of Synthetic Aperture Radar Data; Artech House: Boston, 2004. [Google Scholar]
- Guillaso, S.; Reigber, A.; Ferro-Famil, L.; Pottier, E. Range Resolution Improvement of Airborne SAR Images. IEEE Geosci. Remote Sens. Lett. 2006, 3(1), 135–139. [Google Scholar]
- Cho, B.L.; Kong, Y.K.; Park, H.G.; Kim, Y.S. Automobile-based SAR/InSAR system for Ground Experiments. IEEE Geosci. Remote Sens. Lett. 2006, 3(3), 401–405. [Google Scholar]
| Parameters | Values |
|---|---|
| Pulse period, Tp | 10 μs |
| Pulse width, τp | 4 μs |
| Carrier frequencies, fCn | 9.45, 9.65, 9.85 GHz |
| RF Bandwidth | up to 600 MHz |
| Baseband Bandwidth | 200 MHz |
| Sampling frequency | 500 MHz |
| Beamwidth (range, azimuthal) | 10°, 5° |
| Azimuth sampling interval | 3 cm |
| Methods | Range resolution (cm) | |||
|---|---|---|---|---|
| Theory | Simulation | Measurement | ||
| Point target | Distributed target (SA) | |||
| Single chirp (200 MHz) | 66.5 | 71.2 | 69.0 | 68.4 |
| Conventional algorithm (600 MHz) | 22.2 | 30.8 | 30.4 | 31.5 |
| Proposed algorithm (600 MHz) | 22.2 | 24.5 | 24.3 | 22.4 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lim, B.-G.; Woo, J.-C.; Lee, H.-Y.; Kim, Y.-S. A Modified Subpulse SAR Processing Procedure Based on the Range-Doppler Algorithm for Synthetic Wideband Waveforms. Sensors 2008, 8, 8224-8236. https://doi.org/10.3390/s8128224
Lim B-G, Woo J-C, Lee H-Y, Kim Y-S. A Modified Subpulse SAR Processing Procedure Based on the Range-Doppler Algorithm for Synthetic Wideband Waveforms. Sensors. 2008; 8(12):8224-8236. https://doi.org/10.3390/s8128224
Chicago/Turabian StyleLim, Byoung-Gyun, Jea-Choon Woo, Hee-Young Lee, and Young-Soo Kim. 2008. "A Modified Subpulse SAR Processing Procedure Based on the Range-Doppler Algorithm for Synthetic Wideband Waveforms" Sensors 8, no. 12: 8224-8236. https://doi.org/10.3390/s8128224




