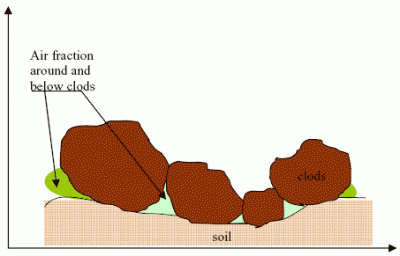
Dielectric Constant Modelling with Soil–Air Composition and Its Effect on Sar Radar Signal Backscattered over Soil Surface
Abstract
:I. Introduction
II. Experimental campaigns
1- Orgeval'94
2- Pays de Caux'98, 99
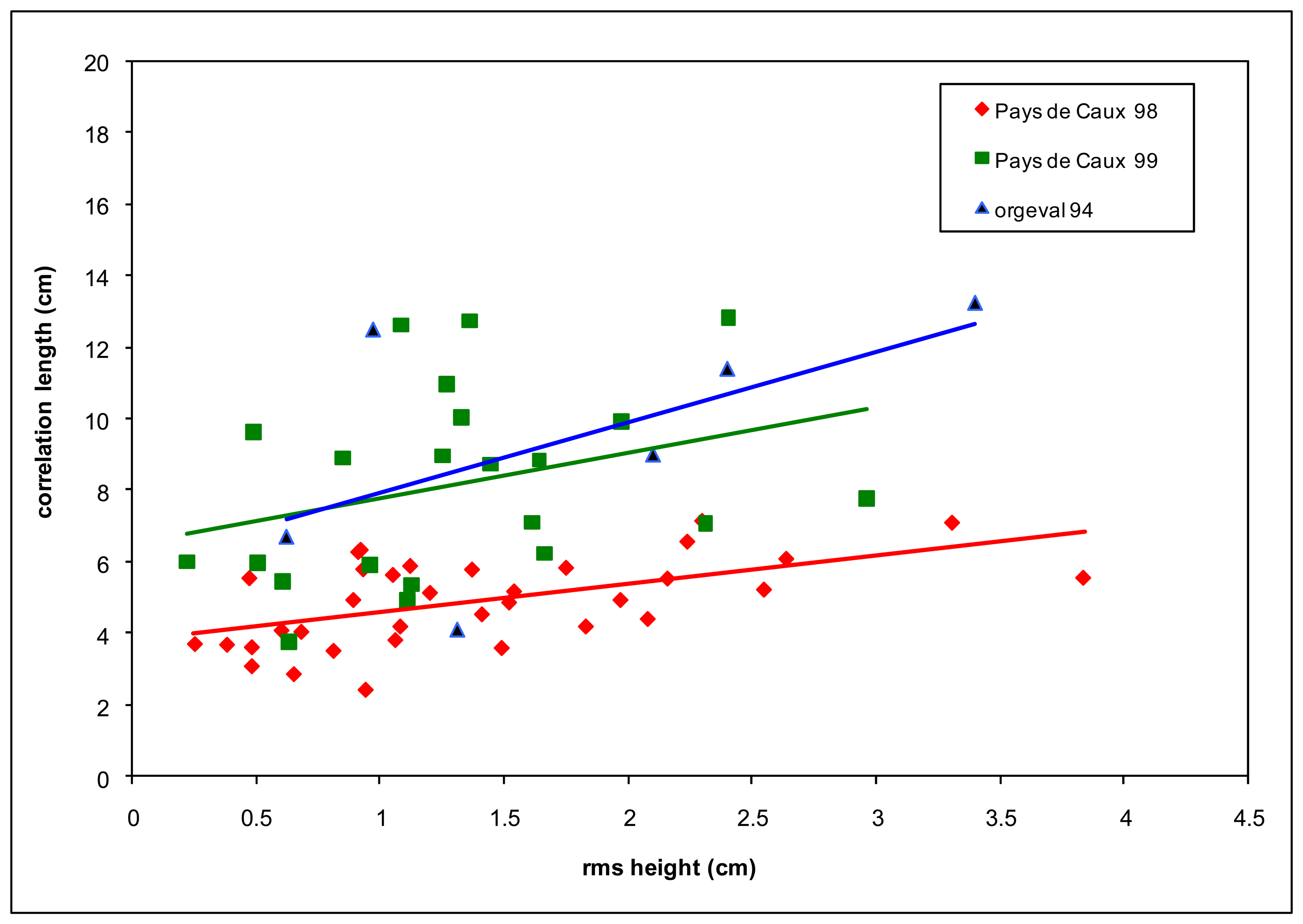
3- Roughness measurement results
III. Backscattering modelling
1- IEM
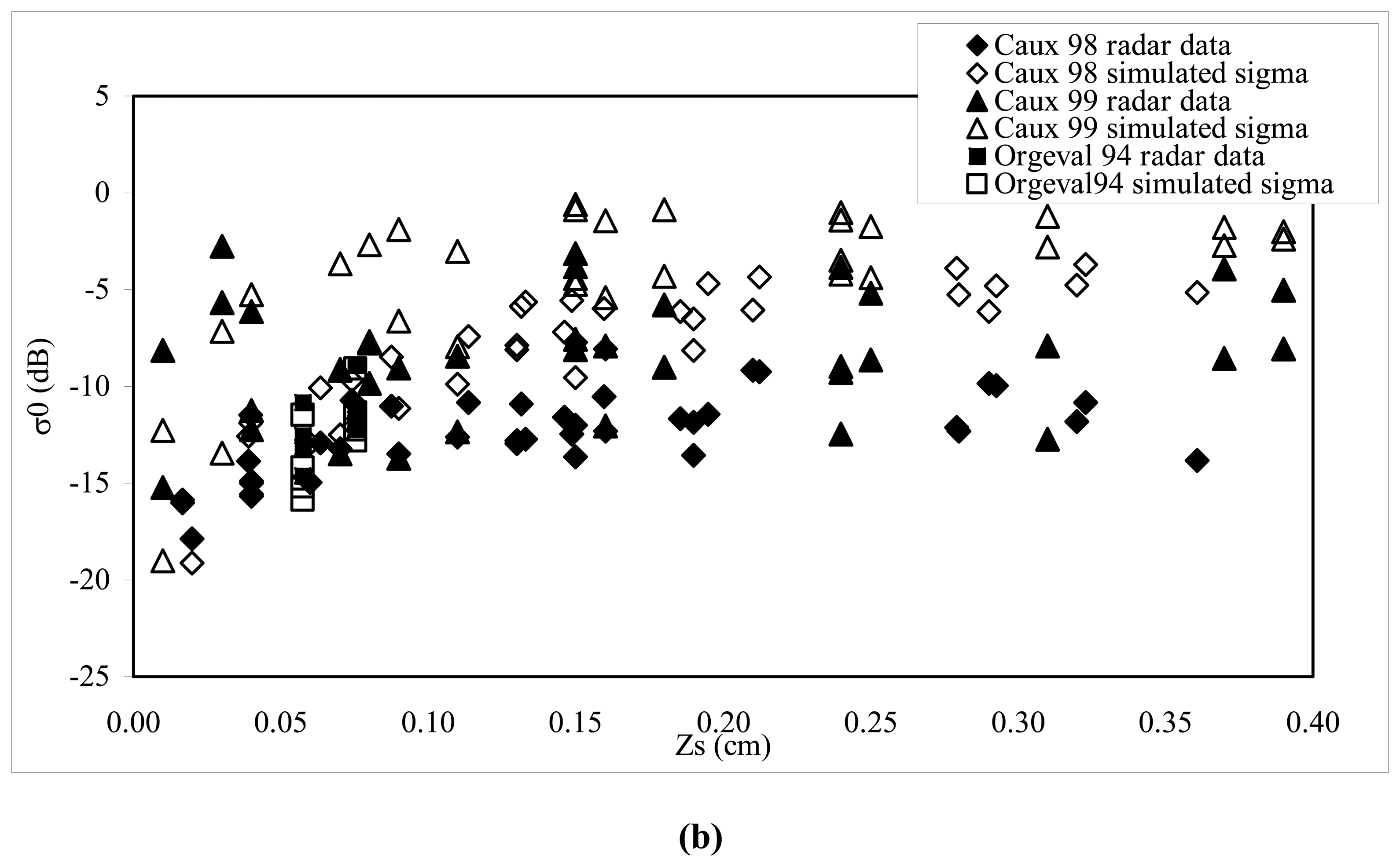
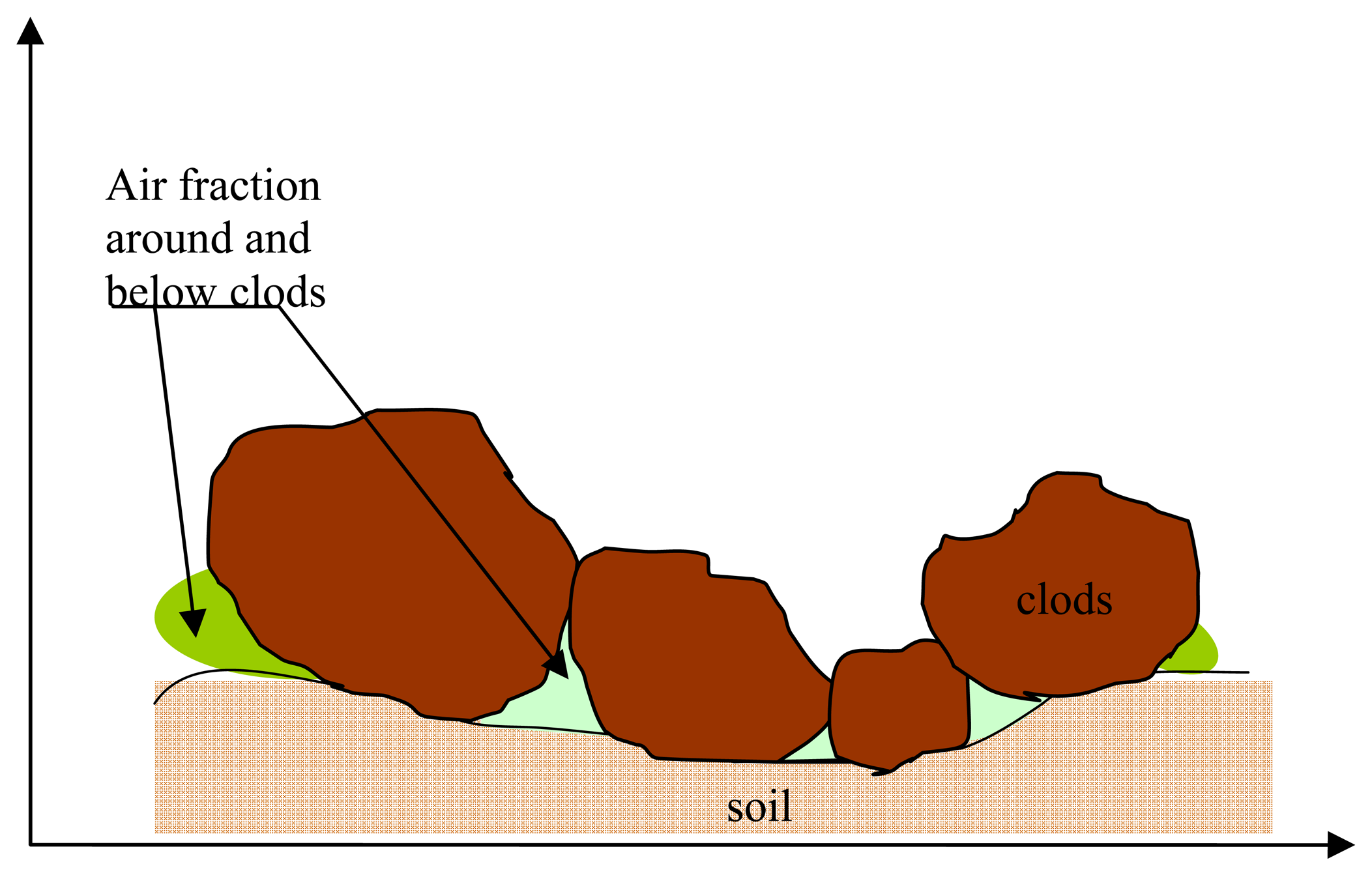
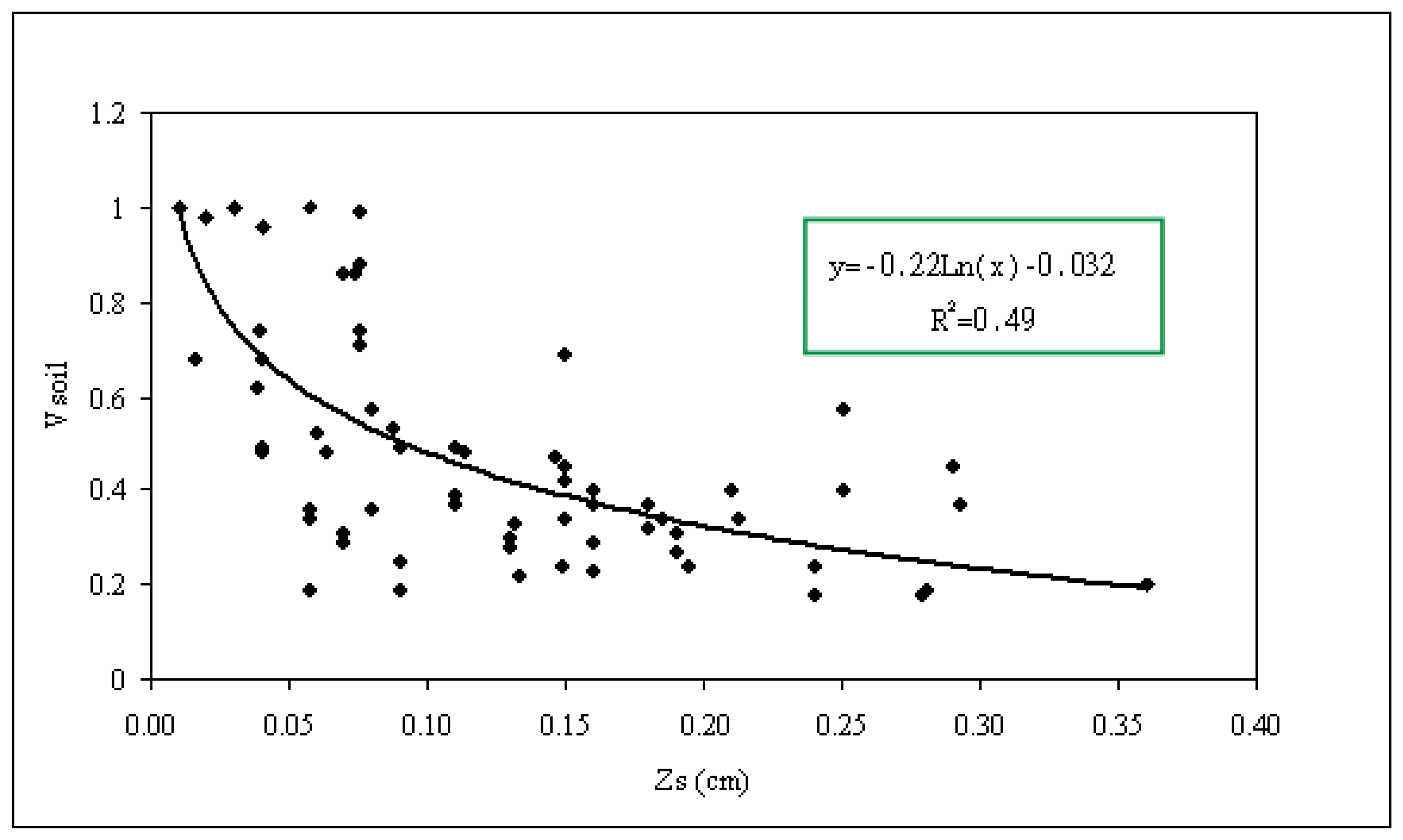
2- Dielectric constant modelling
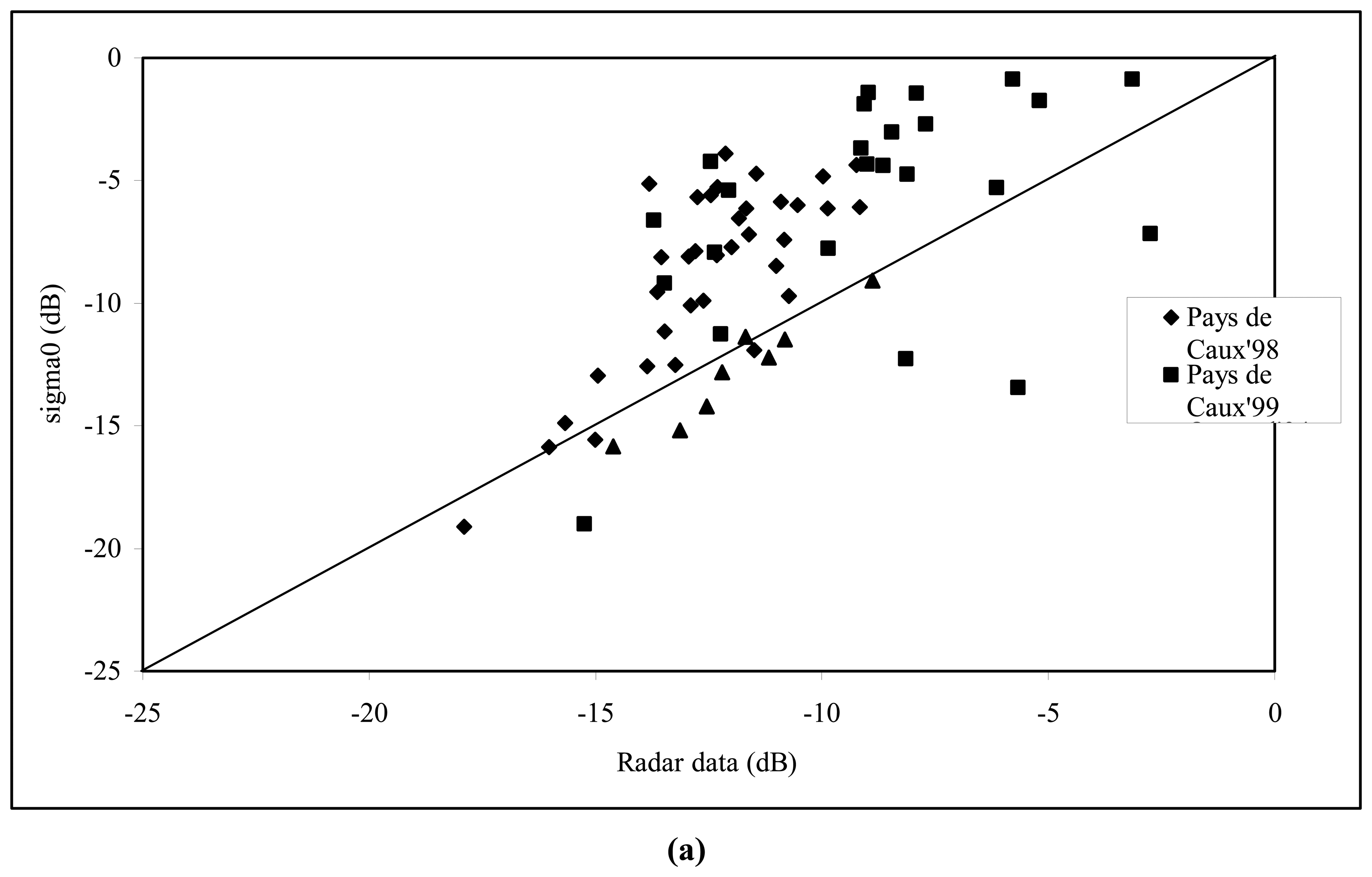
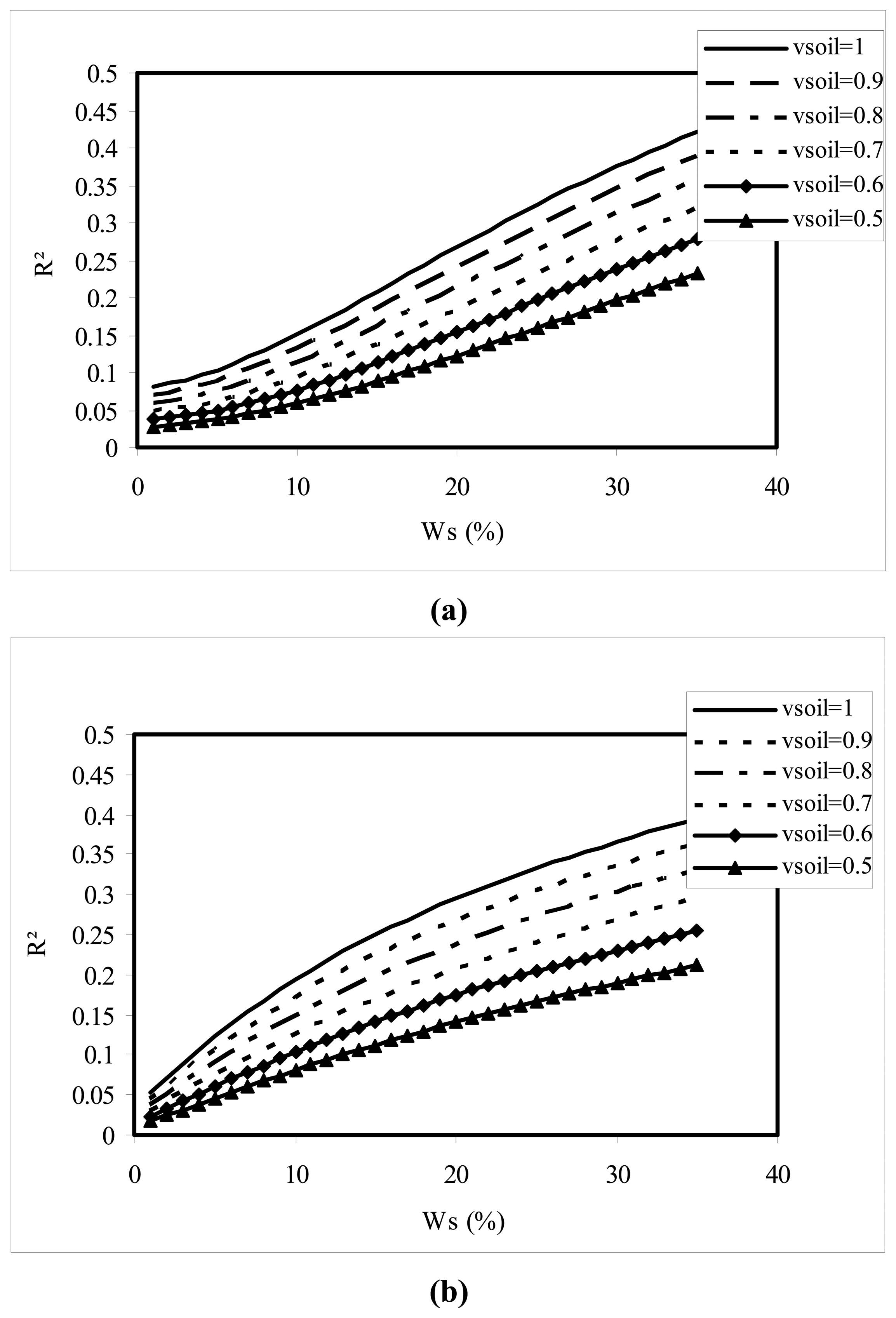
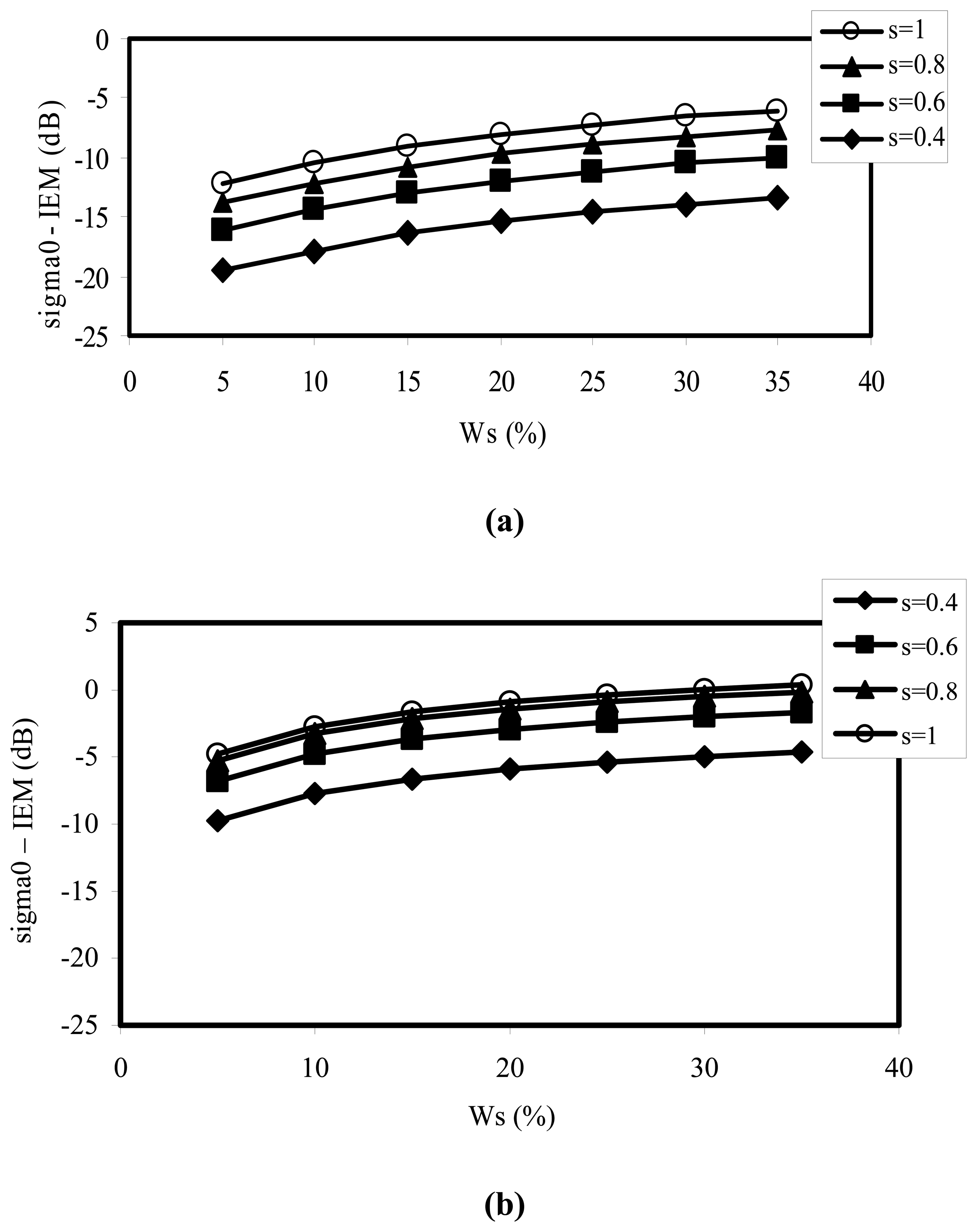
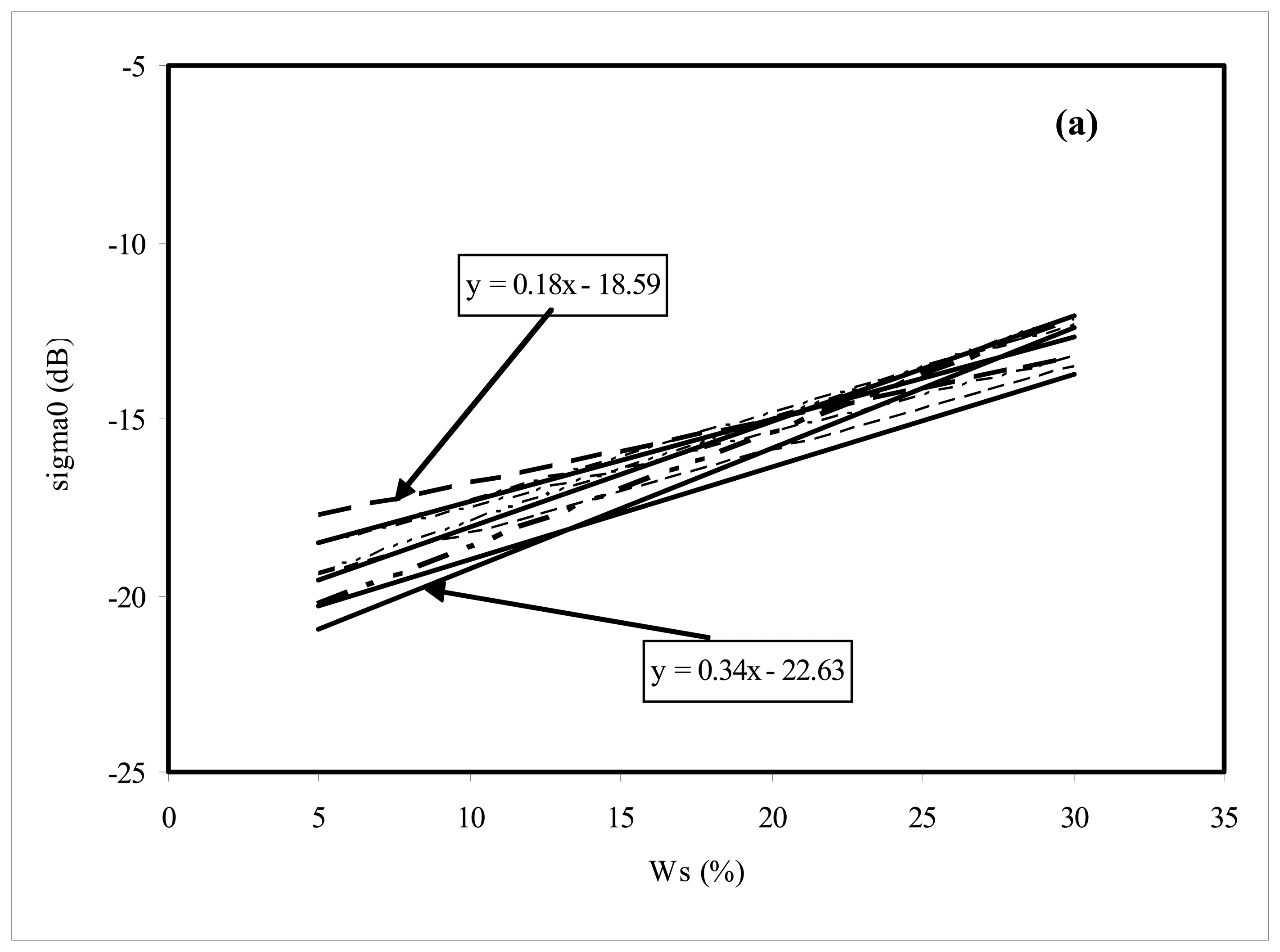
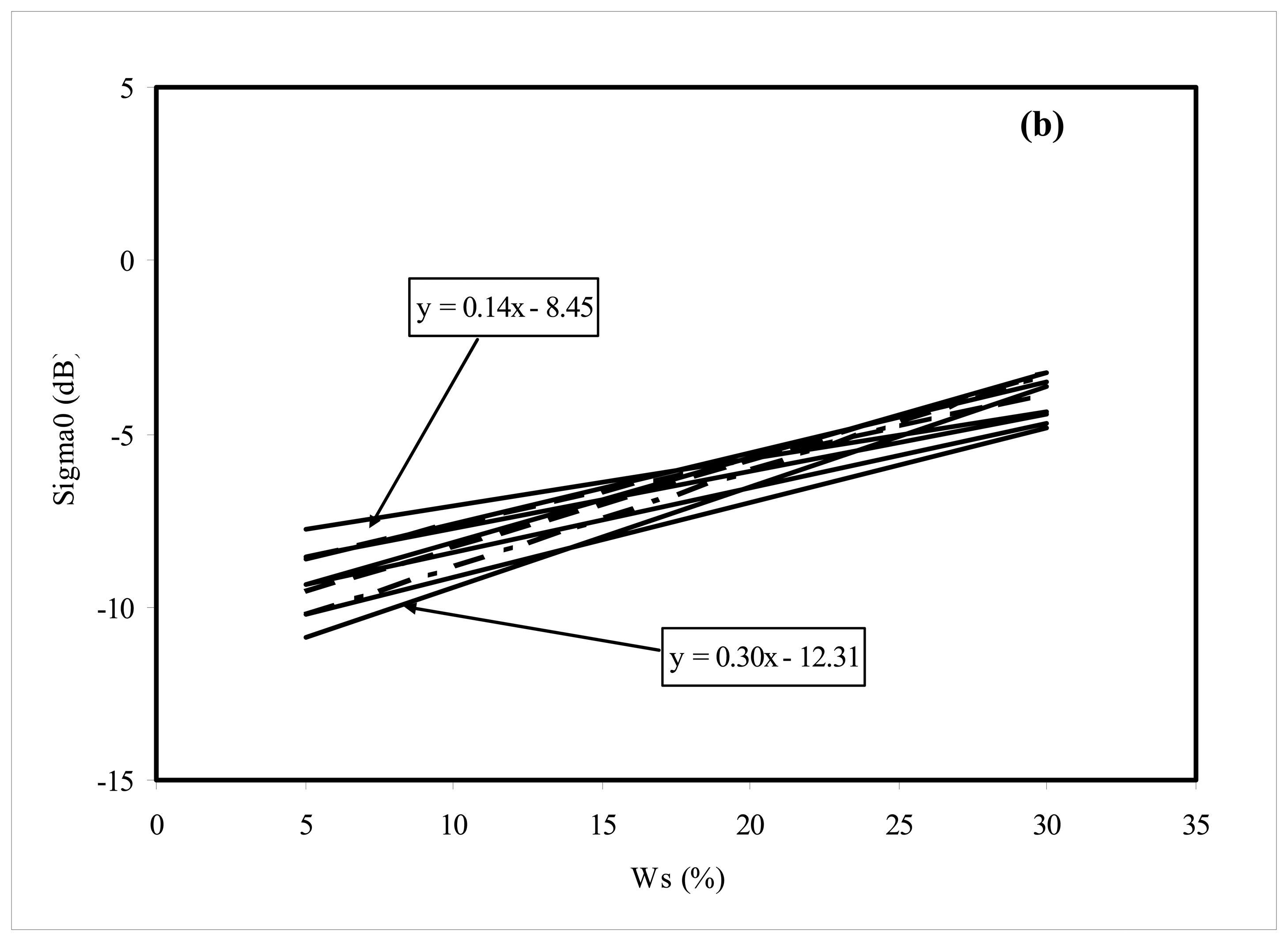
3- Analysis of the correlation between backscattering and moisture measurements
IV. Conclusions
Acknowledgments
References
- Ulaby, F.T.; Moore, M.K.; Fung, A.K. Microwave Remote Sensing, Active and Passive.; Artech House: Norwood, MA, 1986; Vol. 3. [Google Scholar]
- Jackson, T.J.; Schmugge, J.; Engman, E.T. Remote sensing applications to hydrology: soil moisture. Hydrol Sci. 1996, 41, 517–530. [Google Scholar]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from Radar Data. Remote Sens. Environ. 2002, 84, 42–52. [Google Scholar]
- Baghdadi, N.; King, C.; Chanzy, A.; Wigneron, J.P. An empirical calibration of the integral equation model based on SAR data and measurements of soil moisture and surface roughness over bare soils. Int. J. Remote Sens. 2002, 23, 4325–4340. [Google Scholar]
- Baghdadi, N.; Gherboudj, I.; Zribi, M.; Sahebi, M.; King, C.; Bonn, F. Semi-empirical calibration of the IEM backscattering model using radar images and moisture and roughness field measurements. Int. J. Remote Sens. 2004, 25, 3593–3623. [Google Scholar]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar]
- Zribi, M.; Taconet, O.; Le Hégarat-Mascle, S.; Vidal-Madjar, D.; Emblanch, C.; Loumagne, C.; Normand, M. Backscattering behavior and simulation comparison over bare soils using SIRC/XSAR and ERASME 1994 data over Orgeval. Remote Sens. Environ. 1997, 59, 256–266. [Google Scholar]
- Chen, K.S.; Wu, T.D.; Tsay, M.K.; Fung, A.K. A note on the multiple scattering in an IEM model. IEEE Trans. Geosci. Remote Sens. 2000, 38, 249–256. [Google Scholar]
- Wu, T.D.; Chen, K.S.; Shi, J.; Fung, A.K. A transition model for the reflection coefficient in surface scattering. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2040–2050. [Google Scholar]
- Baghdadi, N.; Holah, N.; Zribi, M. Calibration of the Integral Equation Model for SAR data in C-band and HH and VV polarizations. Int. J. Remote Sens. 2006, 27, 805–816. [Google Scholar]
- Mattia, F.; Le Toan, T. Backscattering properties of multi-scale rough surfaces. J. Electromagnet. Wave. 1999, 13, 491–526. [Google Scholar]
- Zribi, M.; Ciarletti, V.; Taconet, O. Validation of a rough surface model based on fractional brownian geometry with SIRC and ERASME radar data over Orgeval site. Remote Sens. Environ. 2000, 73, 65–72. [Google Scholar]
- Li, Q.; Shi, J.C.; Chen, K.S. A generalized Power Law Spectrum and its Applications to the Backscattering of soil surfaces Based on the Integral Equation Model. IEEE Trans. Geosci. Remote Sens. 2002, 40, 271–281. [Google Scholar]
- Zribi, M.; Baghdadi, N.; Holah, N.; Fafin, O.; Guérin, C. Evaluation of a rough soil surface description with ASAR-ENVISAT Radar Data. Remote Sens. Environ. 2005, 95, 67–76. [Google Scholar]
- Quesney, A.; Le Hégarat-Mascle, S.; Taconet, O.; Vidal-Madjar, D.; Wigneron, J.P.; Loumagne, C.; Normand, M. Estimation of watershed soil moisture index from ERS/SAR data. Remote Sens. Environ. 2000, 72, 290–303. [Google Scholar]
- Le Hégarat-Mascle, S.; Zribi, M.; Alem, F.; Weisse, A. Soil moisture estimation from ERS/SAR data: Toward an operational methodology. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2647–2658. [Google Scholar]
- Moran, M.S.; Hymer, D.C.; Qi, J.; Sano, E.E. Soil moisture evaluation using multitemporal synthetic aperture radar (SAR) in semiarid rangeland. Agric. Forest Meteorol. 2000, 105, 69–80. [Google Scholar]
- Moran, M.S.; Peters-Lidard, C.D.; Watts, J.M.; McElroy, S. Estimating soil moisture at the watershed scale with satellite-based radar and land surface models. Can. J. Remote Sens. 2004, 30, 805–826. [Google Scholar]
- Verhoest, N. E.C; Lievens, H.; Wagner, W.; Alvarez-Mozos, J.; Moran, M.S; Mattia, F. On the soil roughness parameterization problem in soil moisture retrieval of bare surfaces from Synthetic Aperture Radar. Sensors 2008, 8, 4213–4248. [Google Scholar]
- Shi, J.; Wang, J.; Hsu, A.Y.; O‘Neill, P.E.; Engmann, T. Estimation of Bare Surface Soil Moisture and Surface Roughness Parameter Using L-Band SAR Image Data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1265. [Google Scholar]
- Callens, M.; Verhoest, N.E.C.; Davidson, M.W.J. Parameterization of tillage-induced single-scale soil roughness from 4-m profiles. IEEE Trans. Geosci. Remote Sens. 2006, 44, 878–888. [Google Scholar]
- Davidson, M.W.J.; Le Toan, T.; Mattia, F.; Satalino, G.; Manninen, T.; Borgeaud, M. On the characterization of agricultural soil roughness for radar remote sensing studies. IEEE Trans. Geosci. Remote Sens. 2000, 38, 630–640. [Google Scholar]
- Oh, Y.; Kay, Y.C. Condition for precise measurement of soil surface roughness. IEEE Trans. Geosci. Remote Sens. 1998, 36, 691–695. [Google Scholar]
- Hallikanen, M.T.; Ulaby, F.T.; Dobson, M.C.; El-Rayes, M.; Wu, L. Microwave dielectric behavior of Wet Soil- Part I: Empirical Models and Experimental Observations. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 25–34. [Google Scholar]
- Sihvola, A. Electromagnetic mixing formulas and applications.; IEEE Electromagnetic Waves Series 47; IEEE: London, 1999. [Google Scholar]
- Schneeberger, K.; Schwank, M.; Stamm, C.; De Rosnay, P.; Matzler, C.; Fluhler, H. Topsoil Structure Influencing Soil Water Retrieval by Microwave Radiometry. Vad. Zone J. 2004, 3, 1169–1179. [Google Scholar]
- Birchak, J.C.; Gardner, J.; Hipp; Victor, J. High dielectric constant microwave probes for sensing soil moisture. Proc. IEEE 1974, 62, 93–98. [Google Scholar]
- Taconet, O.; Vidal-Madjar, D.; Emblanch, C.; Normand, M. Taking into account vegetation effects to estimate soil moisture from C-band radar measurements. Remote Sens. Environ. 1996, 56, 52–56. [Google Scholar]
- Weimann, A.; Von Schonermark, M.; Schumann, A.; Jorm, P.; Gunter, R. Soil moisture estimation with ERS-1 SAR in the East German loess soil area. Int. J. Remote Sens. 1998, 19, 237–243. [Google Scholar]
- Zribi, M.; Baghdadi, N.; Holah, N.; Fafin, O. New methodology for soil surface moisture estimation and its application to ENVISAT-ASAR multi-incidence data inversion. Remote Sens. Environ. 2005, 96, 485–496. [Google Scholar]

| Campaign | Sensor | Date | Configuration |
|---|---|---|---|
| Orgeval 94 | SIR-C | 12/04/94 - 18/04/94 | HH 44°,52°,55 °,57° |
| Pays de Caux 98 | RADARSAT | 24/02/98 09/02/98 08/02/98 | HH 39° HH 47° |
| Pays de Caux 99 | RADARSAT | 07/02/99 04/02/99 | HH 23° HH 40° |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zribi, M.; Le Morvan, A.; Baghdadi, N. Dielectric Constant Modelling with Soil–Air Composition and Its Effect on Sar Radar Signal Backscattered over Soil Surface. Sensors 2008, 8, 6810-6824. https://doi.org/10.3390/s8116810
Zribi M, Le Morvan A, Baghdadi N. Dielectric Constant Modelling with Soil–Air Composition and Its Effect on Sar Radar Signal Backscattered over Soil Surface. Sensors. 2008; 8(11):6810-6824. https://doi.org/10.3390/s8116810
Chicago/Turabian StyleZribi, Mehrez, Aurélie Le Morvan, and Nicolas Baghdadi. 2008. "Dielectric Constant Modelling with Soil–Air Composition and Its Effect on Sar Radar Signal Backscattered over Soil Surface" Sensors 8, no. 11: 6810-6824. https://doi.org/10.3390/s8116810
APA StyleZribi, M., Le Morvan, A., & Baghdadi, N. (2008). Dielectric Constant Modelling with Soil–Air Composition and Its Effect on Sar Radar Signal Backscattered over Soil Surface. Sensors, 8(11), 6810-6824. https://doi.org/10.3390/s8116810