Validating Evapotranspiraiton Equations Using Bowen Ratio in New Brunswick, Maritime, Canada
Abstract
:1. Introduction
2. Material and Methods
2.1. Research site and operating dates
2.2. Bowen Ratio system
2.3. ETo Model descriptions
2.3.1. FAO-56 Penman-Monteith (PM)
2.3.2. Priestley-Taylor (PT)
2.3.3. Penman 1963 (PE)
2.4. Bowen Ratio theory (BR)
2.5. Data analysis and Statistical processing
3. Results and Discussion
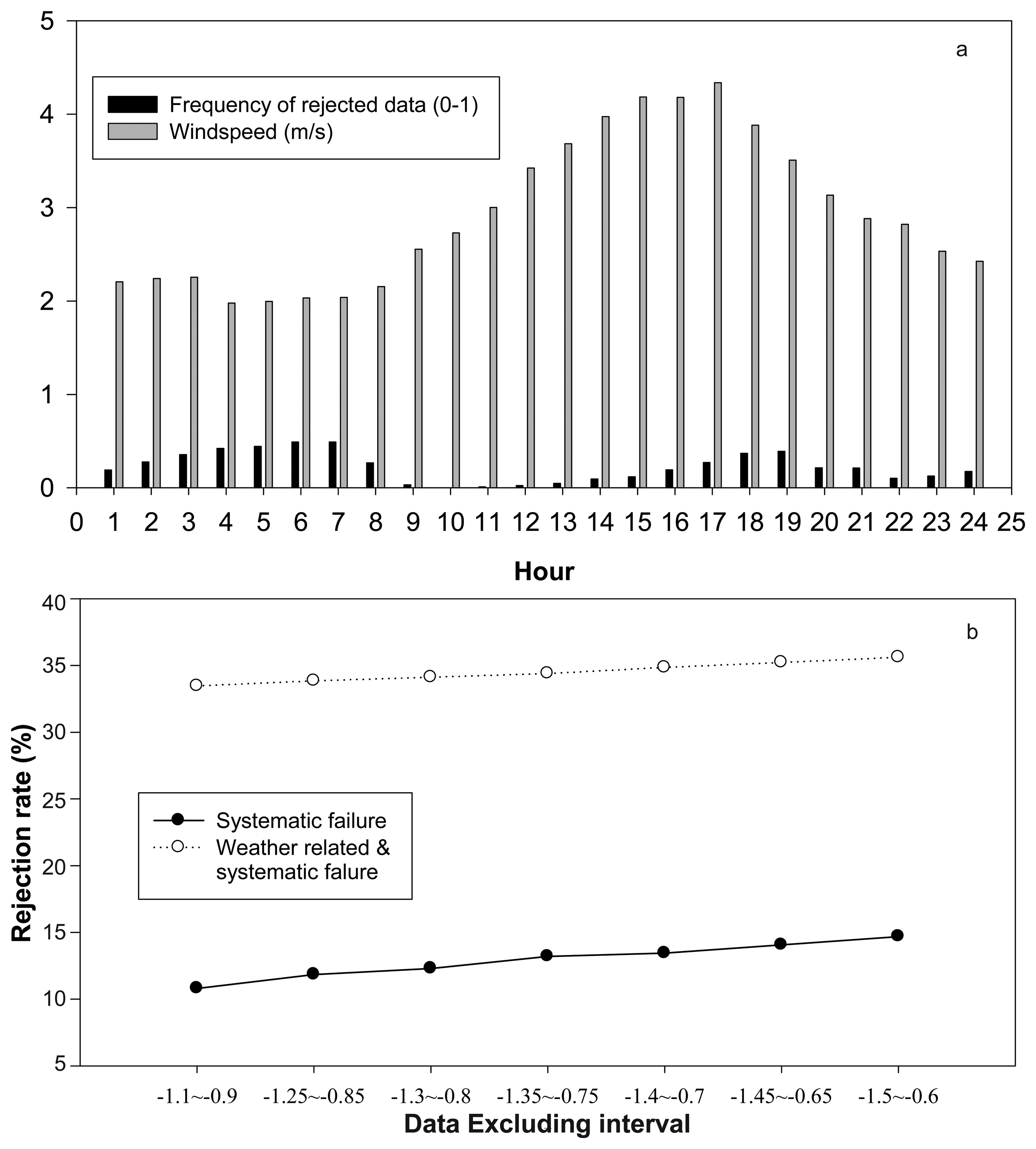
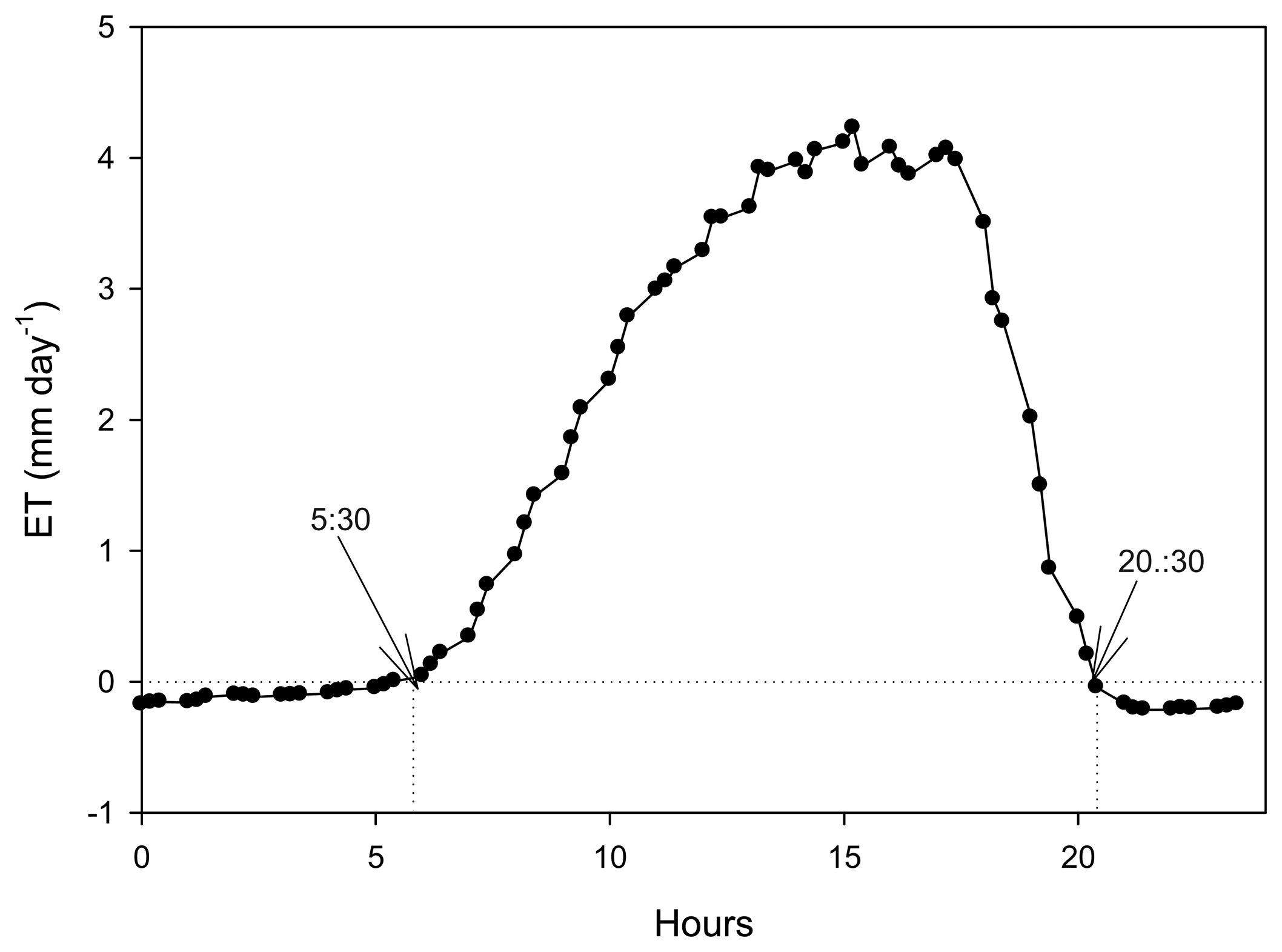
3.1. Bowen ratio method and its performance in the Maritime region
3.2. Comparisons of different ETo methods
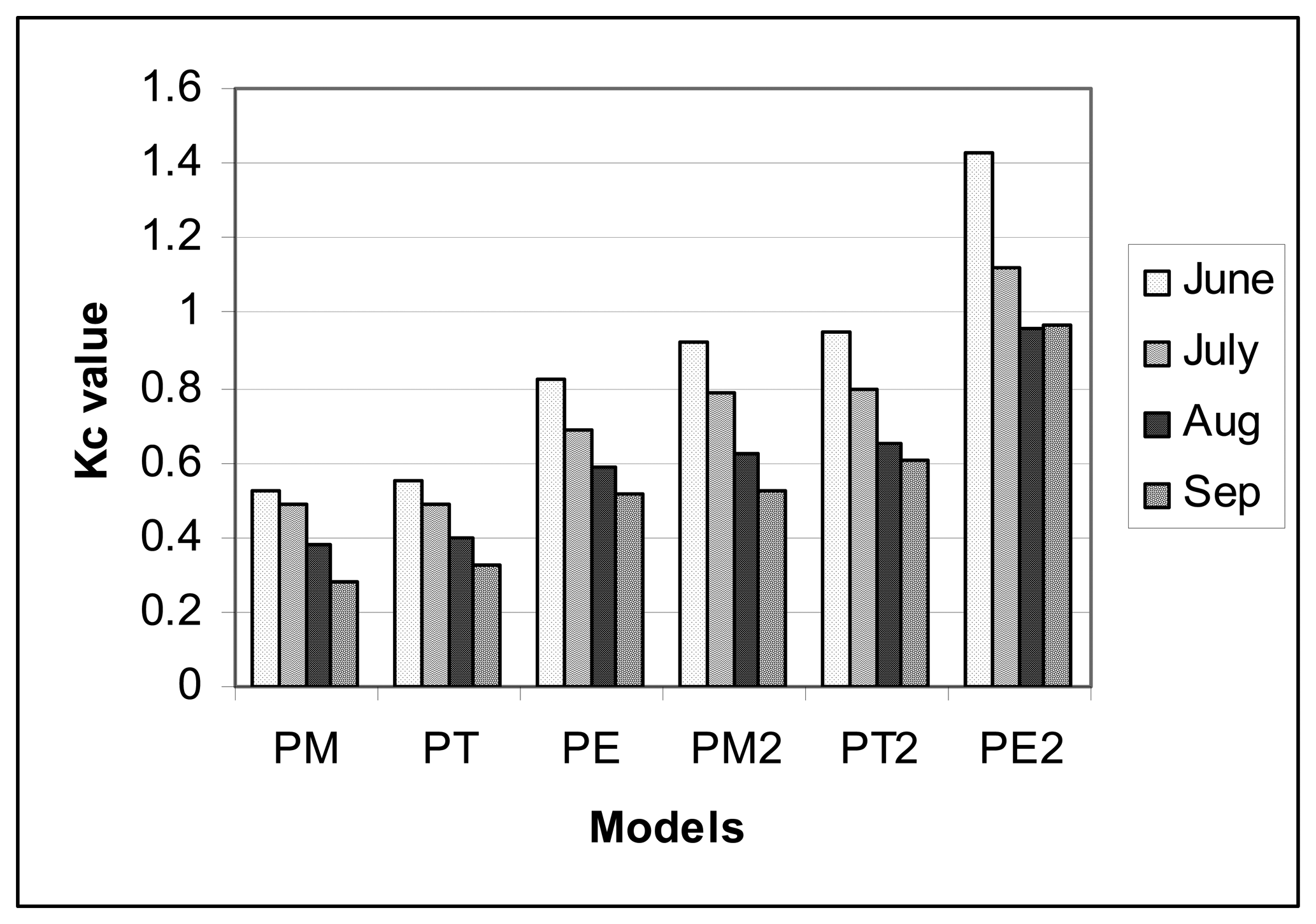
3.3. Kc variability
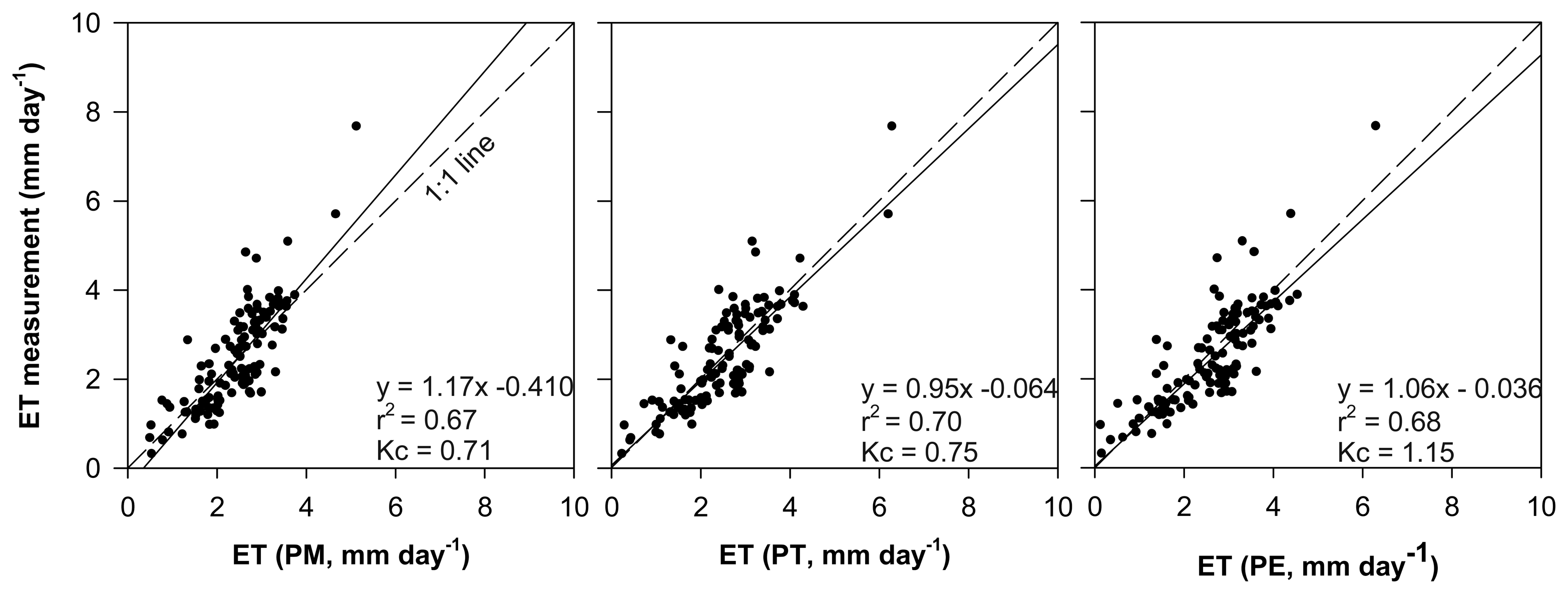
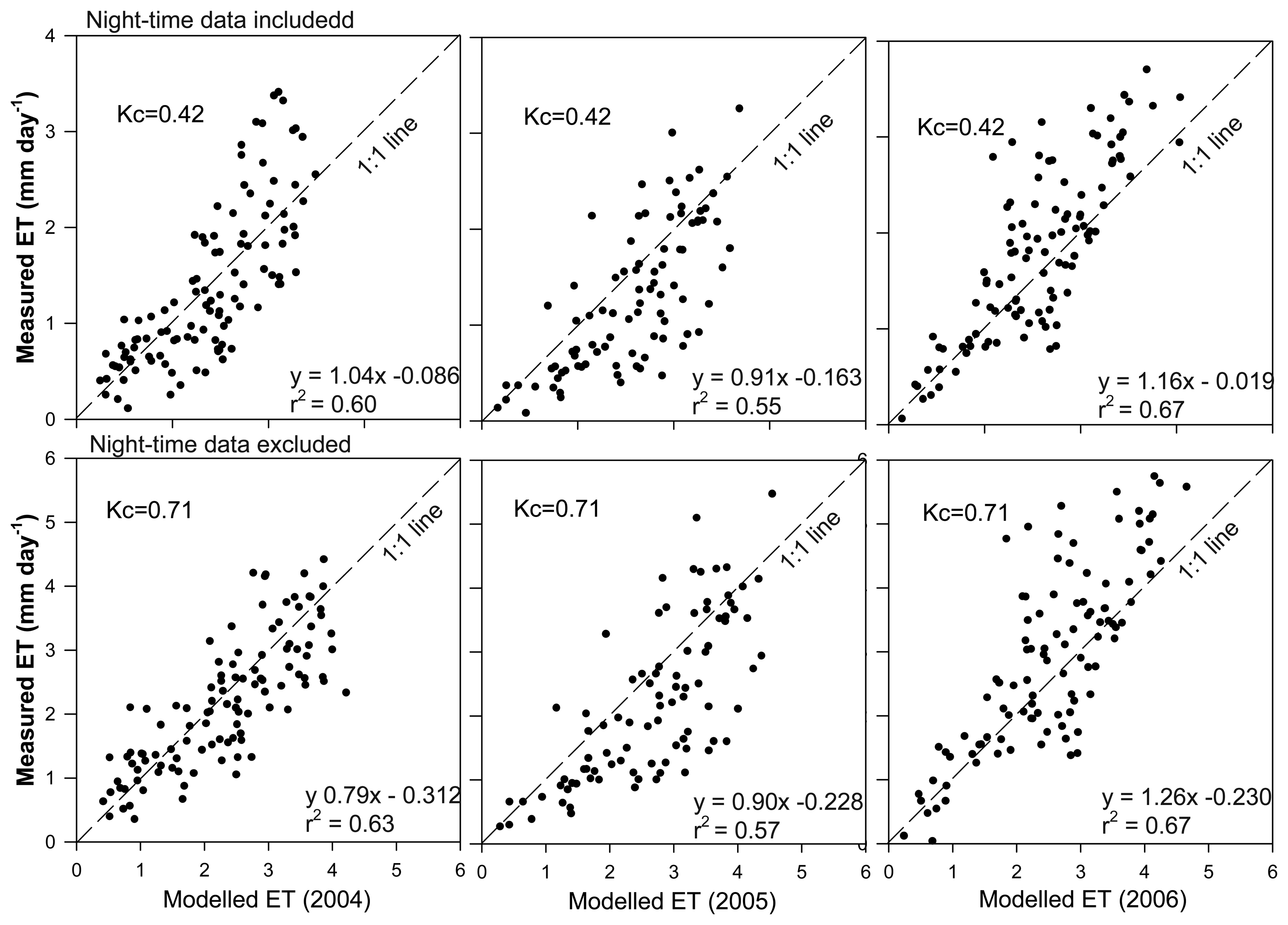
3.4. Inter-annual variability of model performance
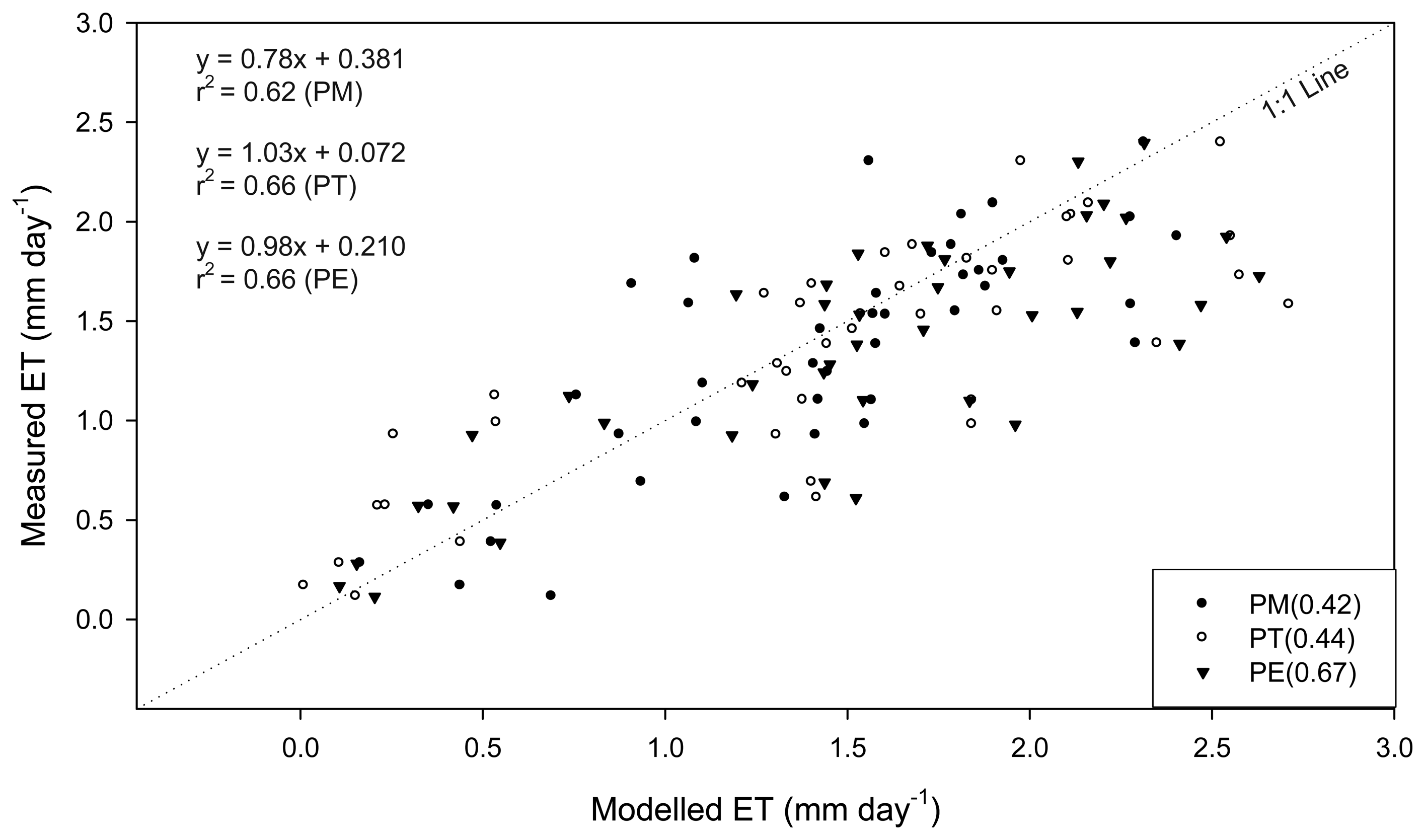
3.5. A comparable validation of the tested model using the data collected in 2007
3.6. A further refinement the PT method in the region
4. Conclusions
References
- López-Urrea, R.; Martin de Santa Olalla, F.; Fabeiro, C.; Moratalla, A. Testing evapotranspiration equations using lysimeter observations in a semiarid climate. Agricultural Water Management 2006, 85, 15–26. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration.Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998; FAO Irrigation and draiange, Paper No. 56. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Applied Engineering Agriculture 1985, 1, 96–99. [Google Scholar]
- Jensen, M. E.; Burman, R. D.; Allen, R. G. Evapotranspiration and irrigation water requirements; Committee on Irrigation Water Requirements of the Irrigation and Draniage Division of ASCE: New York, 1989. [Google Scholar]
- Droogers, P.; Allen, R.G. Estimating Reference Evapotranspiration Under Inaccurate Data Conditions. Irrigation and Drainage Systems 2002, 16, 33–45. [Google Scholar]
- Penman, H.L. Vegetation and hydrology. In Technological Communication 53; Commonweath Bureau of Soils: Harpenden, England, 1963. [Google Scholar]
- Allen, R.G.; Jensen, M.E.; Wright, J.L.; Burman, R.D. Operational estimates of reference evapotranspiration. Agronomy Journal 1989, 81, 650–662. [Google Scholar]
- Steiner, J.L.; Howell, T.A.; Schneider, A.D. Lysimetric evaluation of daily potential evapotranspiration models for grain-sorghum. Agronomy Journal 1991, 83, 240–247. [Google Scholar]
- DehghaniSanij, H.; Yamamoto, T.; Rasiah, V. Assessment of evapotranspiration estimation models for use in semi-arid environments. Agricultural Water Management 2004, 64, 91–106. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat-flux and evaporation using large-scale parameters. Monthly Weather Review 1972, 100, 81–92. [Google Scholar]
- Xing, Z.; Chow, L.; Meng, F-R.; Rees, H.W.; Lionel, S.; Monteith, J. Testing reference evapotranspiration estimation methods using evaporation pan and modeling in Maritime region of Canada. Journal of Irrigation and Drainage Engineering 2007, in press. [Google Scholar]
- Blad, B.L.; Rosenberg, N.J. Lysimetric calibration of the Bowen Ratio-Energy Balance method for evapotranspiration estimation in the central Great Plains. Journal of Applied Meteorology 1974, 13, 227–236. [Google Scholar]
- Ashktorab, H. Partitioning of evapotranspiration using lysimeter and micro-Bowen-ratio system. J. Irrig. and Drain. Engrg. 1994, 120(2), 450–464. [Google Scholar]
- Yrisarry, J.J.B.; Naveso, F.S. Use of weighing lysimeter and Bowen-Ratio Energy-Balance for reference and actual crop evapotranspiration measurements. ISHS Acta Horticulturae 2000, 537. [Google Scholar]
- Viana, T. V.; Folegatti, M. V.; Azevedo, B. M.; Bomfim, G. V.; Elói, W. M. Evapotranspiration through the Bowen ratio system and a weiching lysimeter in greenhouse. IRRIGA 2003, 8(2), 113–119, in Spanish. [Google Scholar]
- Fontenot, R.L. An evaluation of reference evapotranspiration in Lousiana; Louisiana State University and A&M College, 2004; pp. 1–83. [Google Scholar]
- Villar, J.M. Adjusting reference ET using local calibrations by means of a Bowen ratio system; 1992. [Google Scholar]
- Malek, E. Calibration of the Penman wind function using the Bowen ratio energy balance method. J. Hydrol. (Amst.) 1994, 163(3-4), 289–298. [Google Scholar]
- Peacock, C.E.; Hess, T.M. Estimating evapotranspiration from a reedbed using the Bowen ratio energy balance method. Hydrological Processes 2004, 18, 247–260. [Google Scholar]
- Todd, R.W.; Evett, S.R.; Howell, T.A. The Bowen ratio-energy balance method for estimating latent heat flux of irrigated alfalfa evaluated in a semi-arid, advective environment. Agricultural and Forest Meteorology 2000, 103, 335–348. [Google Scholar]
- Gavilan, P. Accuracy of the Bowen ratio-energy balance method for measuring latent heat flux in a semiarid advective environment. Irrigation Science 2007, 25(2), 127–140. [Google Scholar]
- Ohmura, A. Objective criteria for rejecting data for Bowen ratio flux calculations. Journal of Applied Meteorology 1982, 21, 595–598. [Google Scholar]
- Angus, D.E.; Watts, P.J. Evapotranspiration--how good is the Bowen ratio method? Agricultural Water Management 1984, 8, 133–150. [Google Scholar]
- Unland, H.E.; Houser, P.R.; Shuttleworth, W.J.; Yang, Z.L. Surface flux measurement and modelling at a semi-arid Sonoran Desert Site. Agricultural and Forest Meteorology 1996, 82, 119–153. [Google Scholar]
- Perez, P.J.; Castellvi, F.; Ibañez, M.; Rosell, J.I. Assessment of reliability of Bowen ratio method for partitioning fluxes. Agricultural and Forest Meteorology 1999, 97, 141–150. [Google Scholar]
- Ortega-Farias, S. O.; Rojas, V.; Valdés, H.; Gonzaléz, P. Estimation of reference evapotranspiration in the Maule Region of Chile: a comparison between the FAO Penman-Monteith and Bowen ratio methods. Acta Horticulturae 2004, 664, 469–475. [Google Scholar]
- Bowen Ratio Instrumentalion Instruction Manual; Campbell Scientific Inc., 1995.
- Suleiman, A.A.; Hoogenboom, G. Comparison of Priestley-Taylor and FAO-56 Penman-Monteith for daily reference evapotranspiration estimation in Georgia, USA. Journal of Irrigation and Drainage Engineering 2007, 133(2), 175–182. [Google Scholar]
- Stannard, D.I. Comparison of Penman-Monteith, Shuttleworth-Wallace, and modified Priestley-Taylor evapotranspiration models for wildland vegetation in semiarid rangland. Water Resources Management 1993, 29(1993), 1379–1392. [Google Scholar]
- Li, L.; Yu, Q. Quantifying the effects of advection on canopy energy budgets and water use efficiency in an irrigated wheat field in the North China Plain. Agriculture and Water Management 2007, 89, 116–122. [Google Scholar]
- Nichols, J.; Eichinger, W.; Cooper, D.I.; Prueger, J.H.; Hipps, L.E.; Neale, C.M.U.; Bawazir, A.S. Comparison of evaporation estimation methods for a riparian area. Final report. In UHR Technical Report No. 436; College of Engineering, University of Iowa: USA.
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Physics Review 1926, 27, 779–787. [Google Scholar]
- Tanner, C.B. Energy balance in approach to evapotranspiraiton from crops. Soil Science Society of America Proceedings 1960, 24, 1–9. [Google Scholar]
- Verma, S.B.; Rosenberg, N.J.; Blad, B.L. Turbulent exchange coefficients for sensible heat and water vapor under advective conditions. Journal of Applied Meteorology 1978, 17, 330–338. [Google Scholar]
- Allen, R.G.; Hill, R. W.; Srikanth, V. Evapotranspiration parameters for variably sized wetlands. America Society of agricultural and Engineering 1994, 94, 21–32. [Google Scholar]
- Green, A.E. Evapotranspiration from pasture: a comparison of lysimeter and Bowen ratio measurements with Priestley-Taylor estimates. New Zealand Journal of Agricultural Research 1984, 27, 321–327. [Google Scholar]
- Sumner, D.M.; Jacobs, J. M. Utility of Penman-Monteith, Priestley-Taylor, reference evapotranspiration, and pan evaporation methods to estimate pasture. evapotranspiration. Journal of Hydrology 2005, 308, 81–104. [Google Scholar]
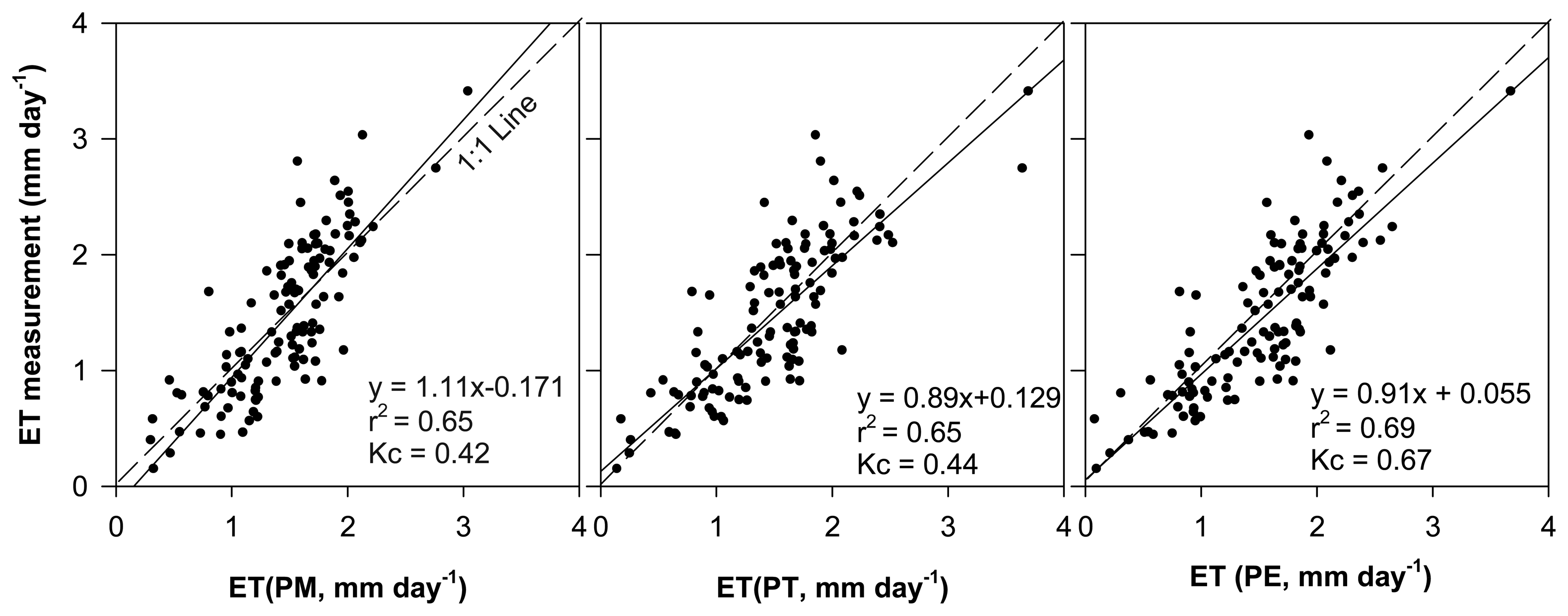
| Methods* | Samples | Mean | Variance | P-value** | F*** | F crit | Kc* | RE(%)**** |
|---|---|---|---|---|---|---|---|---|
| PM | 318 | 1.46 | 0.23 | 0.92 | 0.01 | / | 0.42 | 0.8 |
| PT | 318 | 1.49 | 0.35 | 0.65 | 0.21 | / | 0.44 | 2.5 |
| PE | 318 | 1.53 | 0.36 | 0.32 | 0.97 | / | 0.67 | 5.5 |
| ET | 318 | 1.45 | 0.43 | 3.88 |
| Methods | Samples | Mean | Variance | P-value | F | F crit | Kc | RE(%) |
|---|---|---|---|---|---|---|---|---|
| PM | 318 | 2.46 | 0.64 | 0.98 | 0.00 | / | 0.71 | 0.0 |
| PT | 318 | 2.53 | 1.02 | 0.59 | 0.29 | / | 0.75 | 2.8 |
| PE | 318 | 2.62 | 1.05 | 0.24 | 1.41 | / | 1.15 | 6.9 |
| ET | 2.46 | 1.31 | 3.88 |
© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Xing, Z.; Chow, L.; Meng, F.-R.; Rees, H.W.; Steve, L.; Monteith, J. Validating Evapotranspiraiton Equations Using Bowen Ratio in New Brunswick, Maritime, Canada. Sensors 2008, 8, 412-428. https://doi.org/10.3390/s8010412
Xing Z, Chow L, Meng F-R, Rees HW, Steve L, Monteith J. Validating Evapotranspiraiton Equations Using Bowen Ratio in New Brunswick, Maritime, Canada. Sensors. 2008; 8(1):412-428. https://doi.org/10.3390/s8010412
Chicago/Turabian StyleXing, Zisheng, Lien Chow, Fan-Rui Meng, Herb W. Rees, Lionel Steve, and John Monteith. 2008. "Validating Evapotranspiraiton Equations Using Bowen Ratio in New Brunswick, Maritime, Canada" Sensors 8, no. 1: 412-428. https://doi.org/10.3390/s8010412




