Sensitivity of PZT Impedance Sensors for Damage Detection of Concrete Structures
Abstract
:1. Introduction
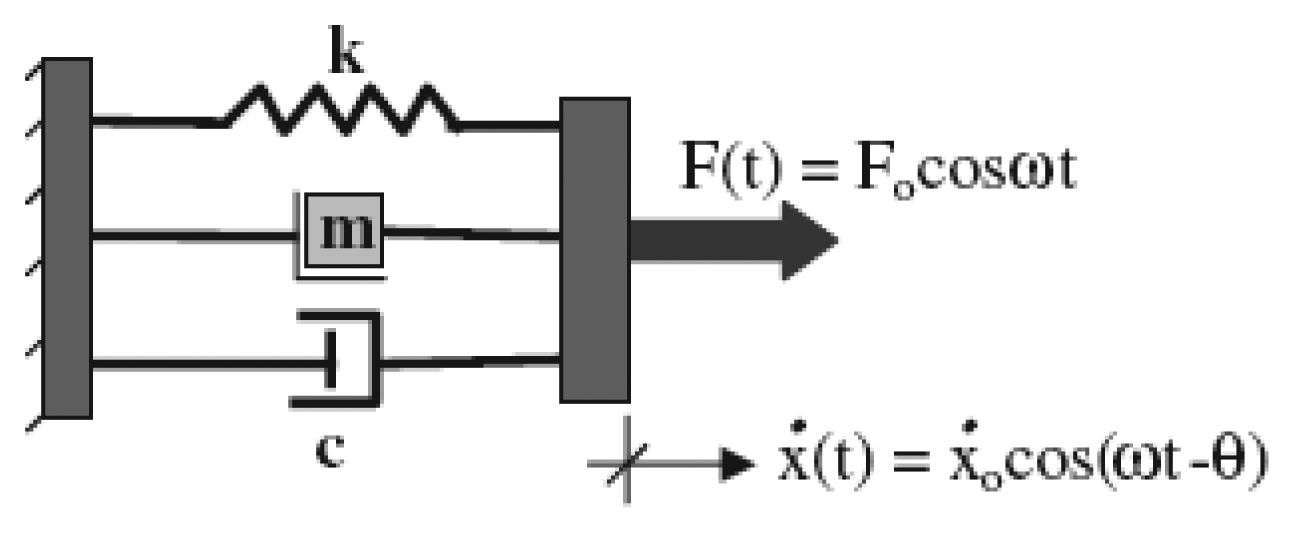
2. Electro-Mechanical Impedance (EMI)
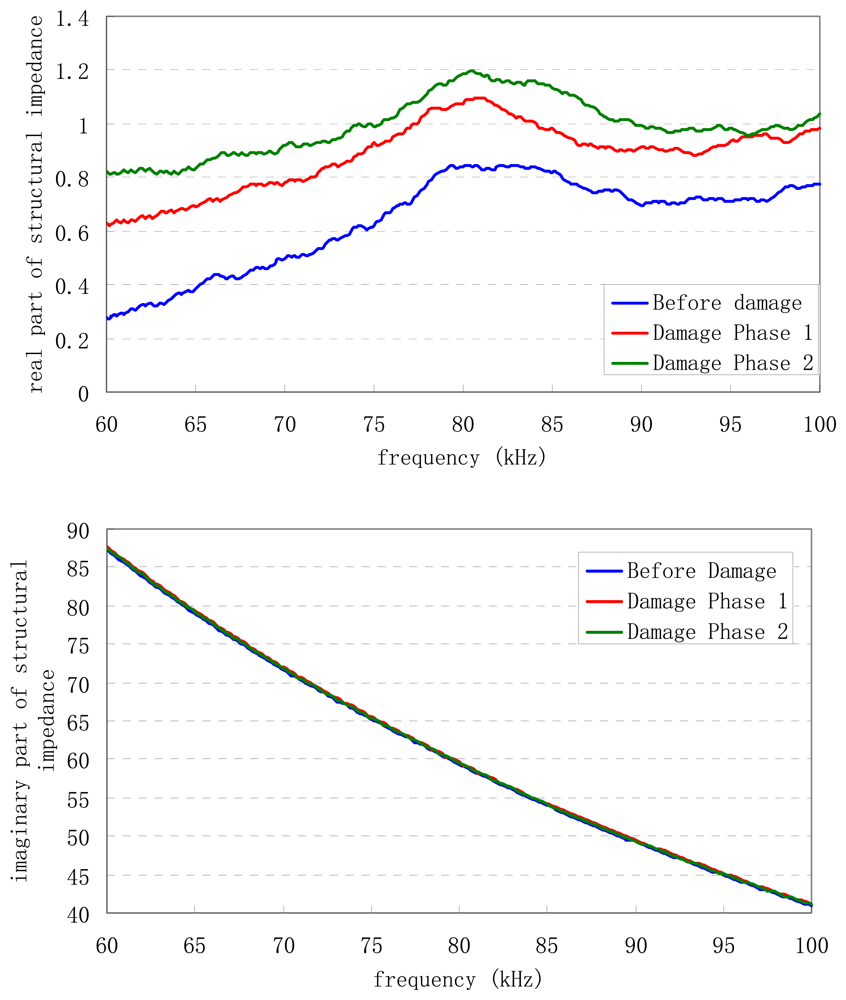
3. Extraction of SMI
4. RMSD for EM Admittance and SMI
5. Modeling of SMI by a Dynamic System
6. Structural Parameters Identification Using Genetic Algorithm
5. Experimental Set-up and Procedure
6. Results and Discussion
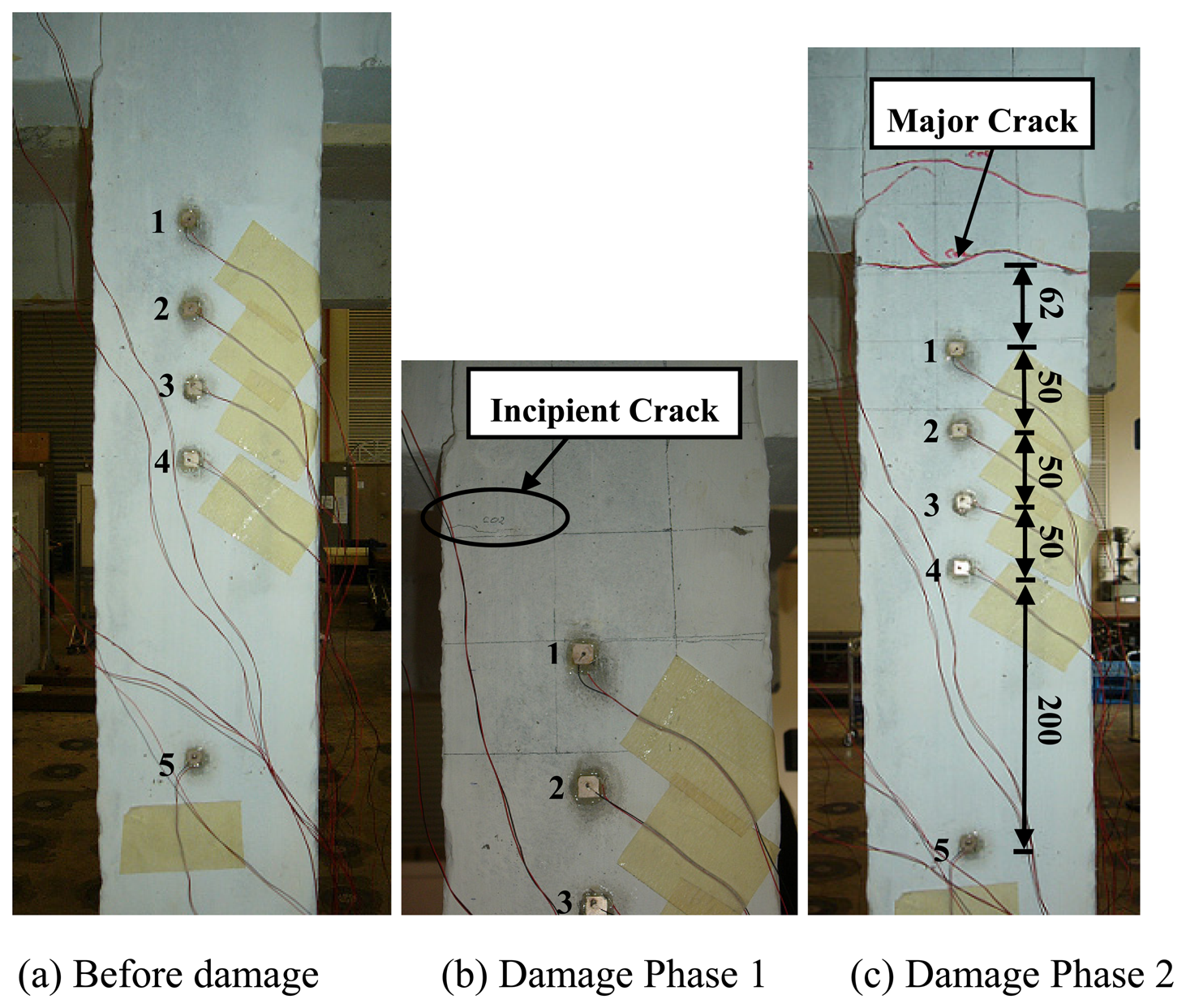
6.1 PZT sensing region in concrete structure
6.2 Changes of structural parameters caused by damages
6.2.1 Application of GAs
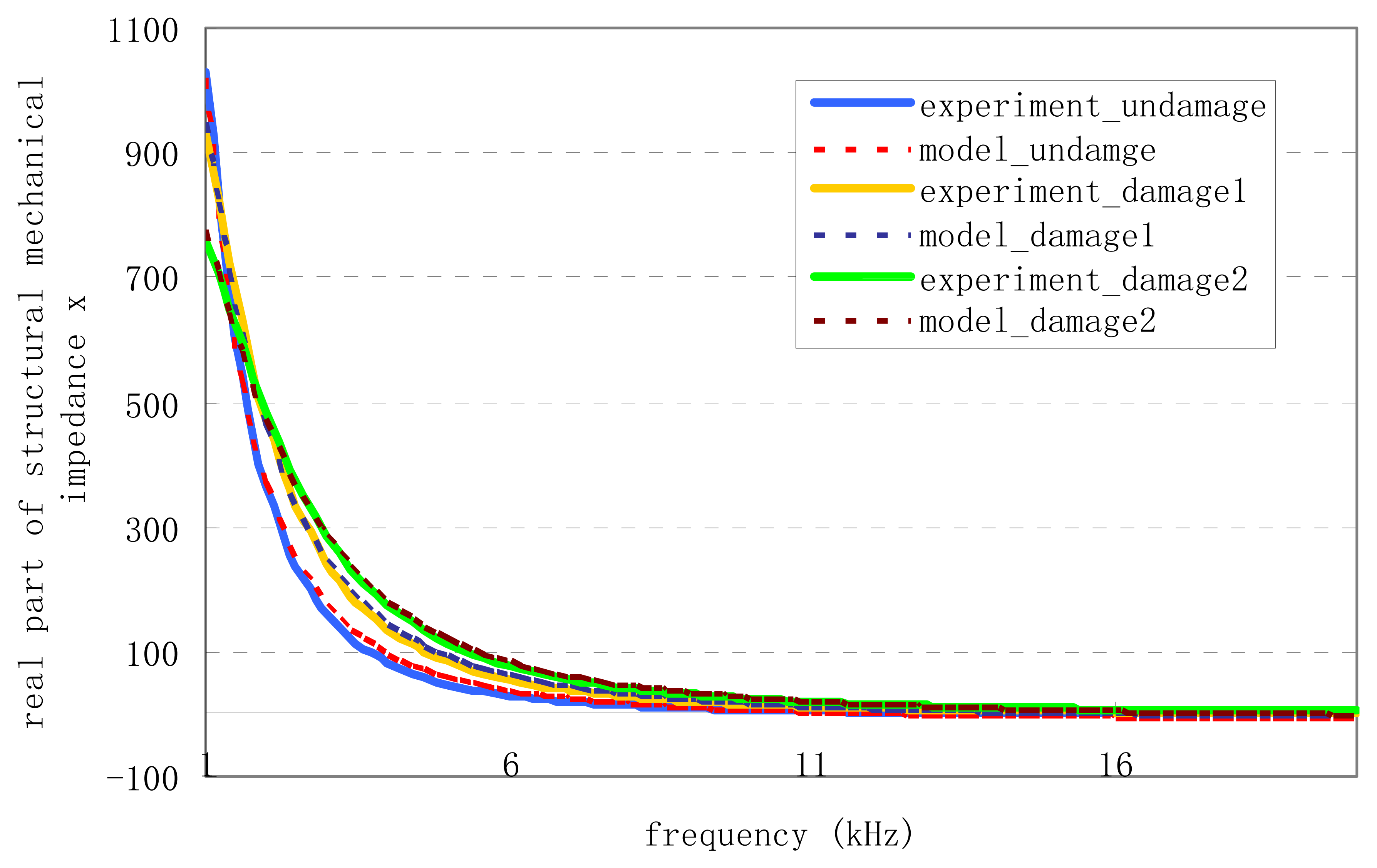
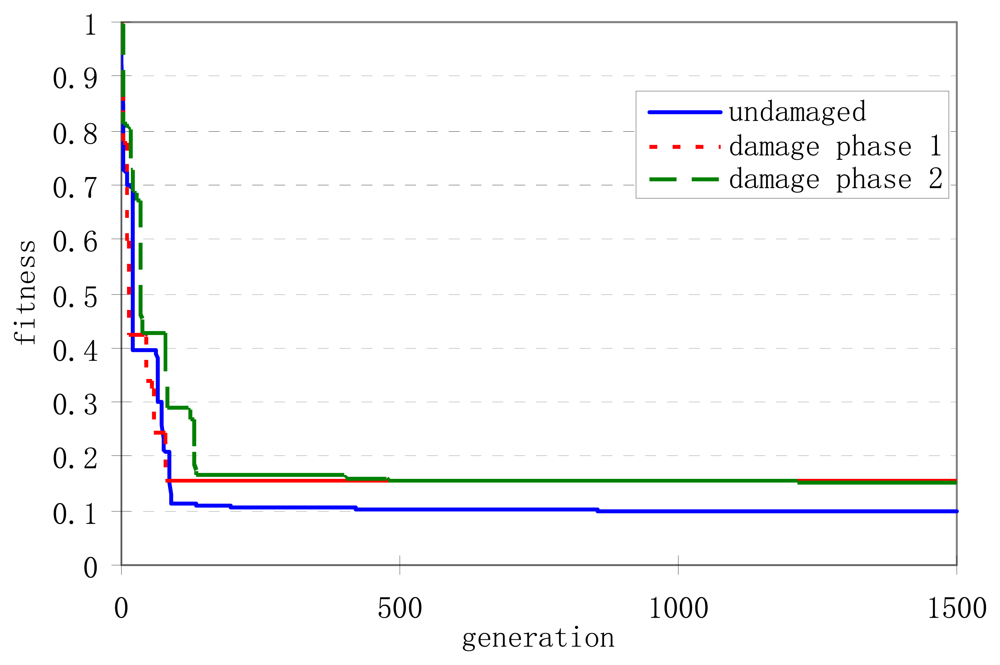
6.2.2 Convergence Performance
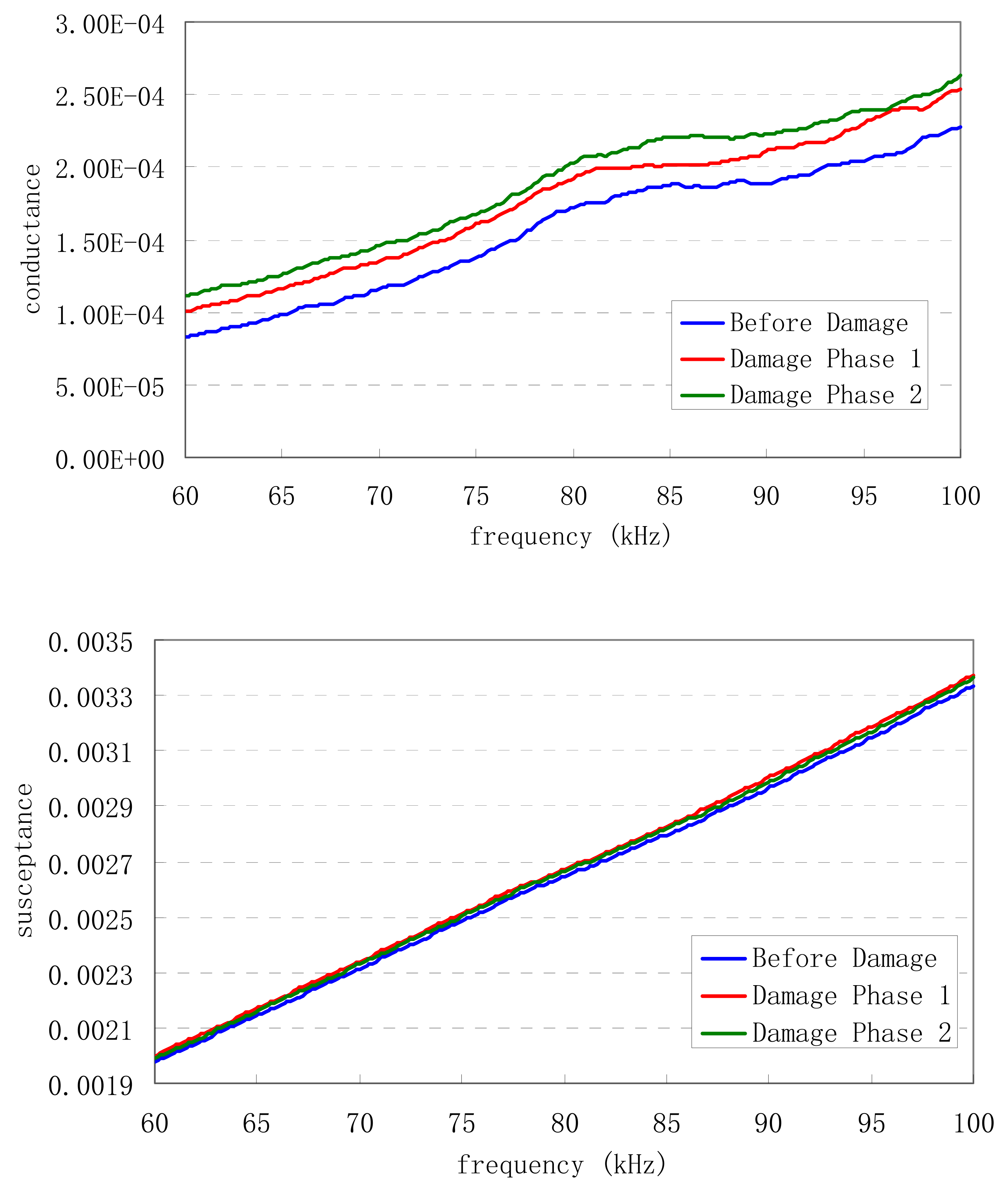
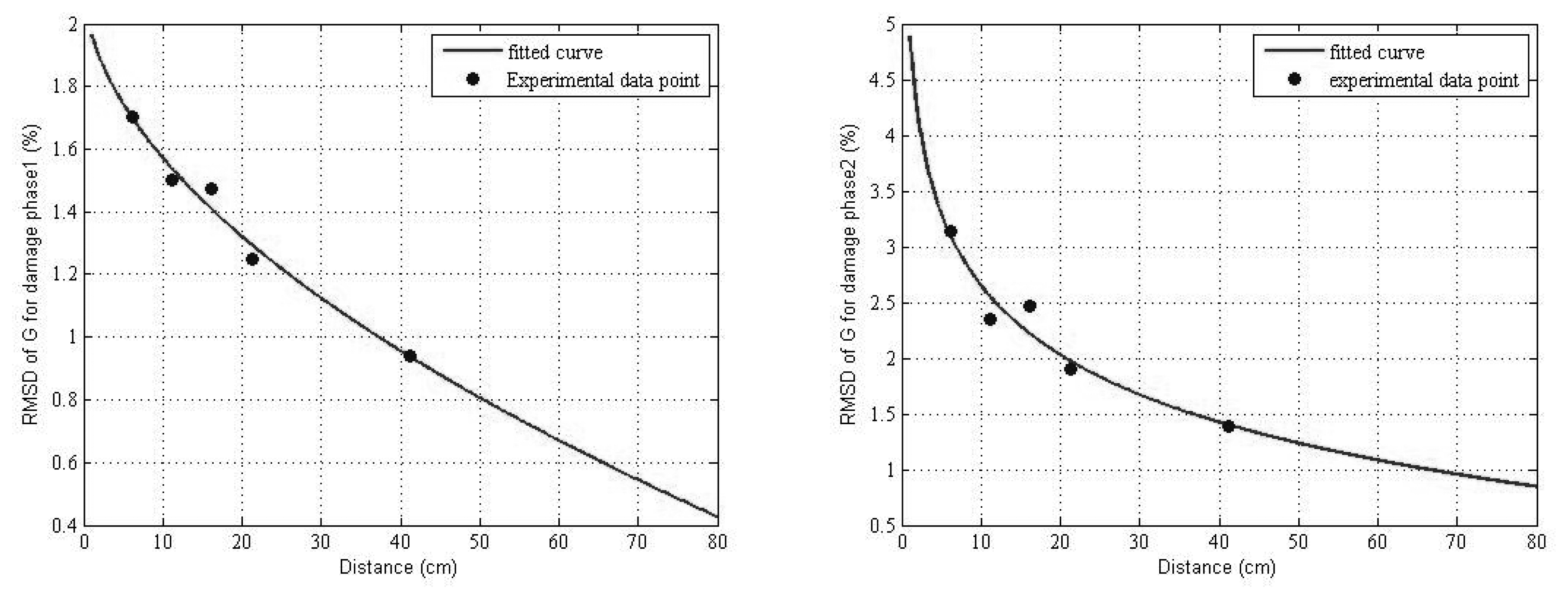
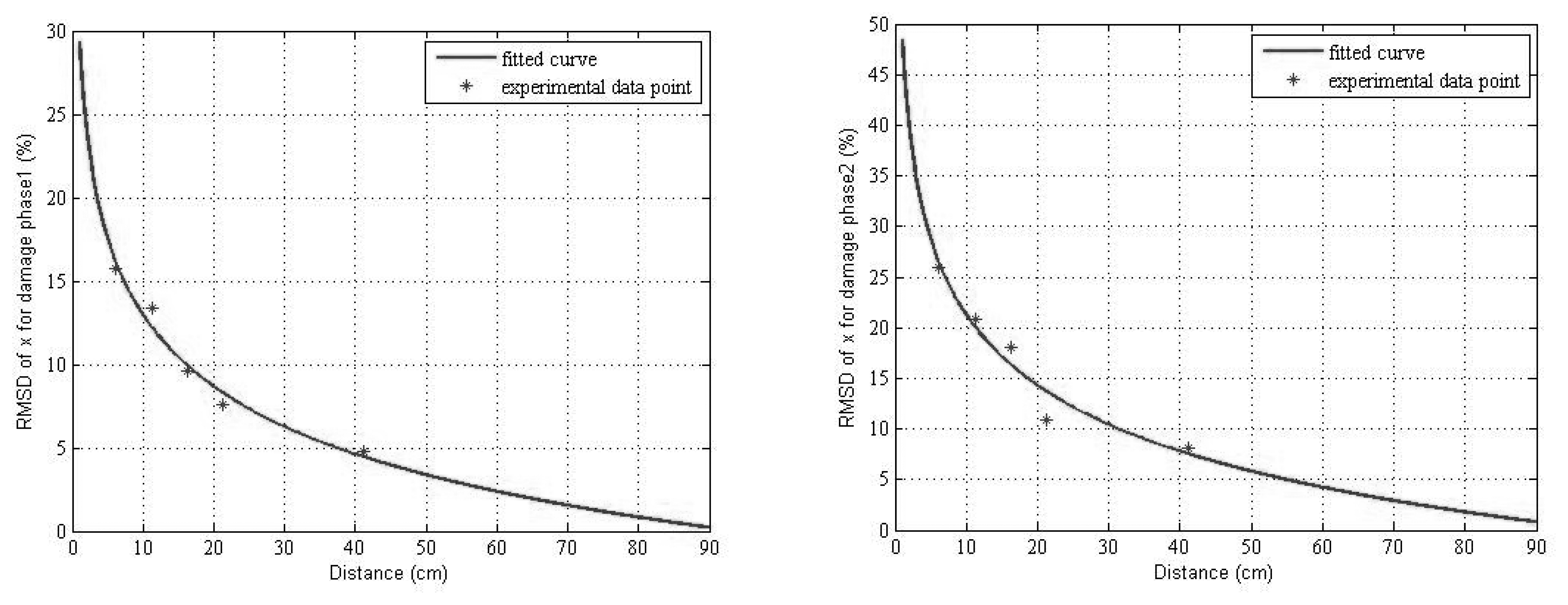
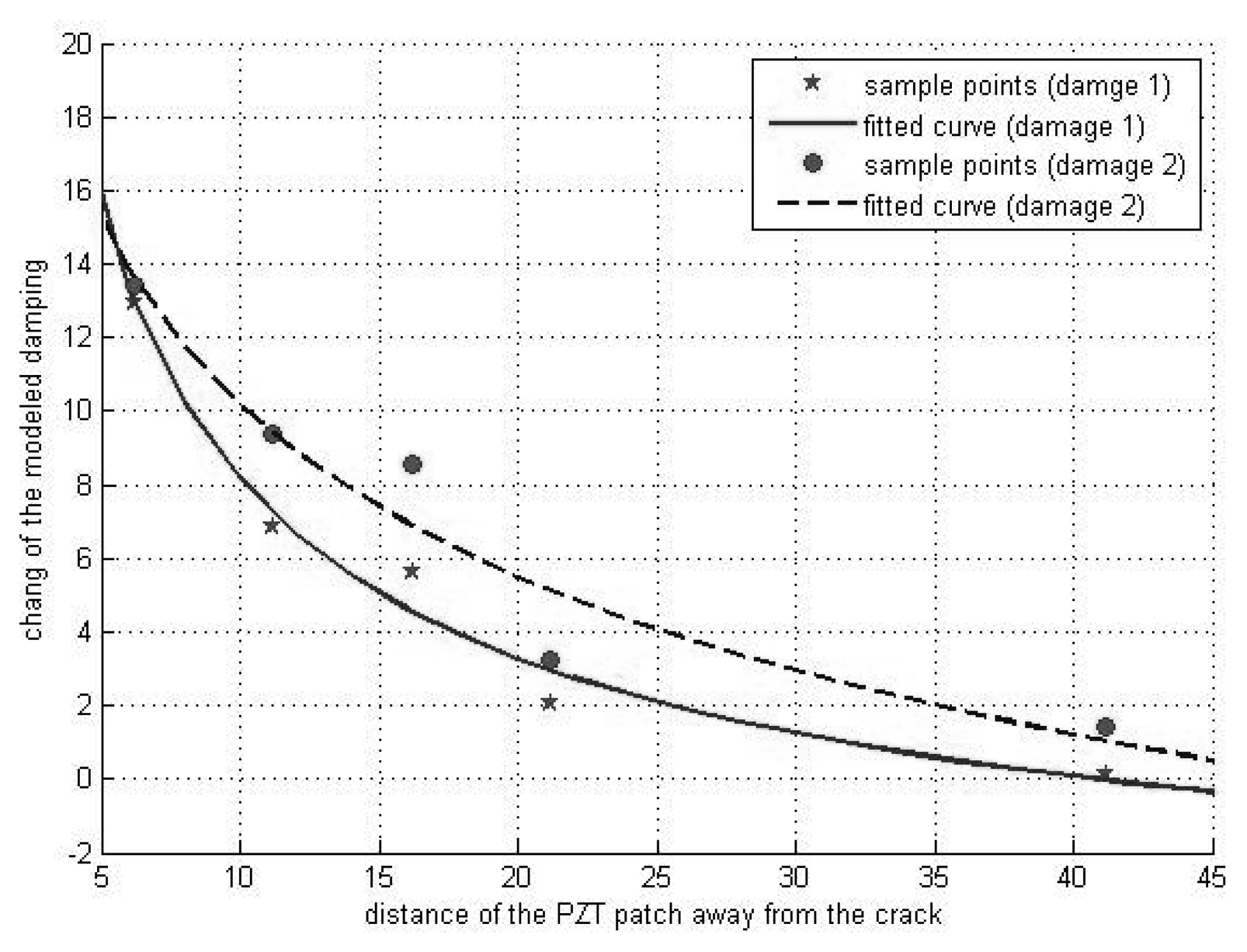
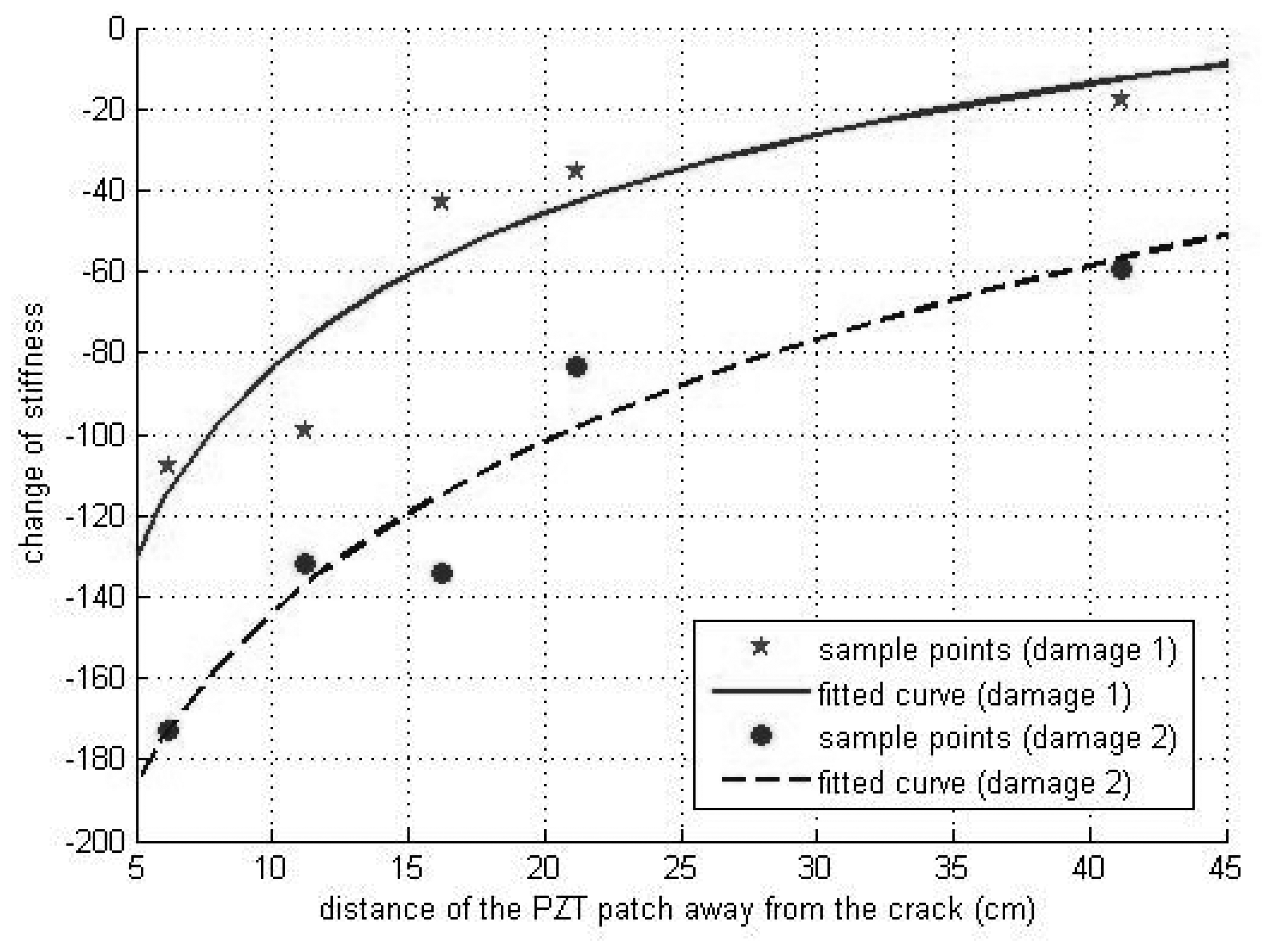
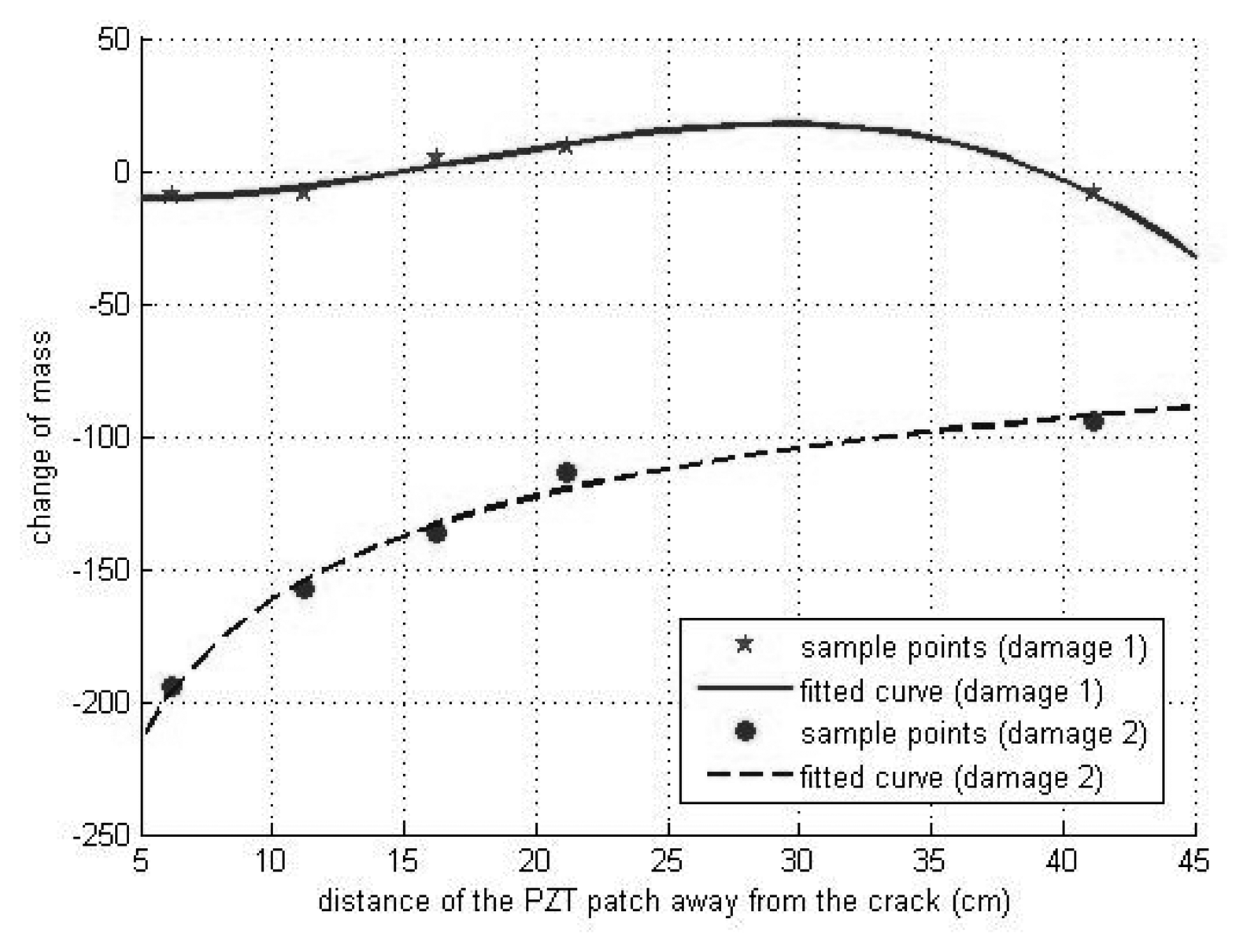
6.2.3 Sensitivity to Damage Detection
7. Conclusion
References and Notes
- Sun, F.; Chaudhry, Z.; Liang, C.; Rogers, C.A. Truss Structure Integrity Identification Using PZT Sensor-Actuator. Journal of Intelligent Material Systems and Structure 1995, 6, 134–139. [Google Scholar]
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled Electromechanical Analysis of Adaptive Material Systems-Determination of the Actuator Power Consumption and System Energy Transfer. Journal of Intelligent Material Systems and Structures 1994, 5, 12–20. [Google Scholar]
- Liang, C.; Sun, F.P.; Rogers, C.A. Electromechanical Impedance Modeling of Active Material Systems. Smart Materials and Structures 1996, 5, 171–186. [Google Scholar]
- Yang, Y.W.; Xu, J.F.; Soh, C.K. Generic Impedance-Based Model for Structure-Piezoceramic Interacting System. J of Aerospace Engineering 2005, 18, 93–101. [Google Scholar]
- Hu, Y.H.; Yang, Y.W. Wave Propagation Modeling of PZT Sensing Region for Structural Health Monitoring. Smart Materials and Structures 2007, 16, 706–716. [Google Scholar]
- Annamdas, V.G.M.; Yang, Y.W.; Soh, C.K. Influence of Loading on Electromechanical Admittance of Piezoceramic Sensors. Smart Materials and Structures 2007, 16, 1888–1897. [Google Scholar]
- Yang, Y.W.; Hu, Y.H. Electromechanical Impedance Modeling of PZT Sensors for Health Monitoring of Cylindrical Shell Structures. Smart Materials and Structures 2008, 17, 015005. [Google Scholar]
- Ayres, J.W.; Lalande, F.; Chaudhry, Z.; Rogers, C.A. Qualitative Impedance-Based Health Monitoring of Civil Infrastructures. Smart Materials and Structures 1998, 7, 599–605. [Google Scholar]
- Park, G.; Cudney, H.; Inman, D.J. Impedance-Based Health Monitoring of Civil Structural Components. Journal of Infrastructure Systems 2000, 6, 153–160. [Google Scholar]
- Park, G.; Cudney, H.; Inman, D.J. An Integrated Health Monitoring Technique Using Structural Impedance Sensors. Journal of Intelligent Material Systems and Structures 2000, 11, 448–455. [Google Scholar]
- Giurgiutiu, V.; Zagrai, A.N.; Bao, J.J. Piezoelectric Wafer Embedded Active Sensors for Aging Aircraft Structural Health Monitoring. Structural Health Monitoring 2002, 1, 41–61. [Google Scholar]
- Xu, J.F.; Yang, Y.W.; Soh, C.K. Electromechanical Impedance-Based Structural Health Monitoring with Evolutionary Programming. Journal of Aerospace Engineering 2004, 17, 182–193. [Google Scholar]
- Yang, Y.W.; Bhalla, S.; Wang, C.; Soh, C.K.; Zhao, J. Monitoring of Rocks Using Smart Sensors. Tunnelling and Underground Space Technology 2007, 22, 206–221. [Google Scholar]
- Yang, Y.W.; Annamdas, V.G.M.; Wang, C.; Zhou, Y.X. Application of multiplexed FBG and PZT impedance sensors for health monitoring of rocks. Sensors 2008, 8, 271–289. [Google Scholar]
- Giurgiutiu, V.; Rogers, C.A. Recent Advancement in the Electromechanical Impedance Method for Structural Health Monitoring and NDE. Proceedings of SPIE 1998, 3329, 536–547. [Google Scholar]
- Tseng, K.K.H.; Naidu, A.S.K. Non-Parametric Damage Detection and Characterization Using Piezoceramic Material. Smart Materials and Structures 2001, 11, 317–329. [Google Scholar]
- Hu, Y.H.; Yang, Y.W. Sensing Region of PZT Transducers Bonded to Concrete. Proceedings of SPIE 2007, 6529. art no. 652907. [Google Scholar]
- Kreyszig, E. Advanced Engineering Mathematics, 8th Ed. ed; Wiley: New York, 1999. [Google Scholar]
- Holland, J. Adaptation in Natural and Artificial Systems; The University of Michigan Press: Ann Arbor, MI, 1975. [Google Scholar]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: New York, 1989. [Google Scholar]
- Grefenstette, J. Genetic Algorithm for Machine Learning; Kluwer Academic: Norwell, MA, 1994. [Google Scholar]
- Soh, C.K.; Yang, Y.W. Genetic Programming Based Approach for Structural Optimization. Journal of Computing in Civil Engineering 2000, 14, 31–37. [Google Scholar]
- Yang, Y.W.; Soh, C.K. Fuzzy Logic Integrated Genetic Programming for Structural Optimization and Design. Journal of Computing in Civil Engineering 2000, 14, 249–254. [Google Scholar]
- Krishnamoorthy, C.S.; Venkatesh, P.P.; Sudarshan, R. Object-Oriented Framework for Genetic Algorithms with Application to Space Truss Optimization. Journal of Computing in Civil Engineering 2002, 16, 66–75. [Google Scholar]
- Fairbairn, E.M.R.; Silvoso, M.M.; Filho, R.D.T.; Alves, J.L.D.; Ebecken, N.F.F. Optimization of Mass Concrete Construction Using Genetic Algorithm. Computers & Structures 2004, 82, 281–299. [Google Scholar]
- Jin, Z.L.; Yang, Y.W.; Soh, C.K. Application of Fuzzy GA for Optimal Vibration Control of Smart Cylindrical Shells. Smart Materials and Structures 2005, 14, 1250–1264. [Google Scholar]
- Yang, Y.W.; Jin, Z.L.; Soh, C.K. Integrated Optimal Design of Vibration Control System for Smart Beams Using Genetic Algorithms. Journal of Sound and Vibration 2005, 282, 1293–1307. [Google Scholar]
- Yang, Y.W.; Jin, Z.L.; Soh, C.K. Integrated Optimization of Control Systems for Smart Cylindrical Shells Using a Modified GA. Journal of Aerospace Engineering 2006, 19, 68–79. [Google Scholar]
- Park, S.; Ahmad, S.; Yun, C.-B.; Roh, Y. Multiple Crack Detection of Concrete Structures Using Impedance-Based Structural Health Monitoring Techniques. Experimental Mechanics 2006, 46, 609–618. [Google Scholar]
- Koo, K.Y.; Park, S.; Lee, J.-J.; Yun, C.-B.; Inman, D.J. Impedance-Based Structural Health Monitoring Considering Temperature Effects. Proceedings of SPIE 2007, 6532, 65320C. [Google Scholar]
- Park, G.; Kabeya, K.; Cudney, H.H.; Inman, D.J. Impedance-Based Structural Health Monitoring for Temperature Varying Applications. JSME International Journal 1999, 42, 249–258. [Google Scholar]


| Symbol | Quantity | Value |
|---|---|---|
| la | length | 10 mm |
| wa | width | 10 mm |
| ha | thickness | 0.2 mm |
| Y | Young's modulus | 66.7 GPa |
| η | loss factor | 0.005 |
| ρ | mass density | 7800 kg/m3 |
| d31 | strain constant | -2.10E-10 m/volt |
| ε33T | permittivity | 1.93E-08 fatad/m |
| δ | dielectric loss factor | 1.50E-02 |
| Patch Number | Distance from joint O along the column as shown in Figure 2 | Distance of the PZT patch from the main crack |
|---|---|---|
| 1 | 100 mm | 62 mm |
| 2 | 150 mm | 112 mm |
| 3 | 200 mm | 162 mm |
| 4 | 250 mm | 212 mm |
| 5 | 450 mm | 412 mm |
| Phase No. | Name | Description | Purpose |
|---|---|---|---|
| 1 | RND-A | Random, PGA=0.02g | Structural identification |
| 2 | CHL- | Chile, PGA=0.23g, | Moderate shaking |
| 3 | RND-B | Random, PGA=0.02g | Structural identification |
| 4 | CHL- | Chile, PGA=0.46g, | Sever shaking |
| 5 | RND-C | Random, PGA=0.02g | Structural identification |
| Damage Phase 1 | ||||
|---|---|---|---|---|
| PZT patch no. | RMSD of G | RMSD of B | RMSD of x | RMSD of y |
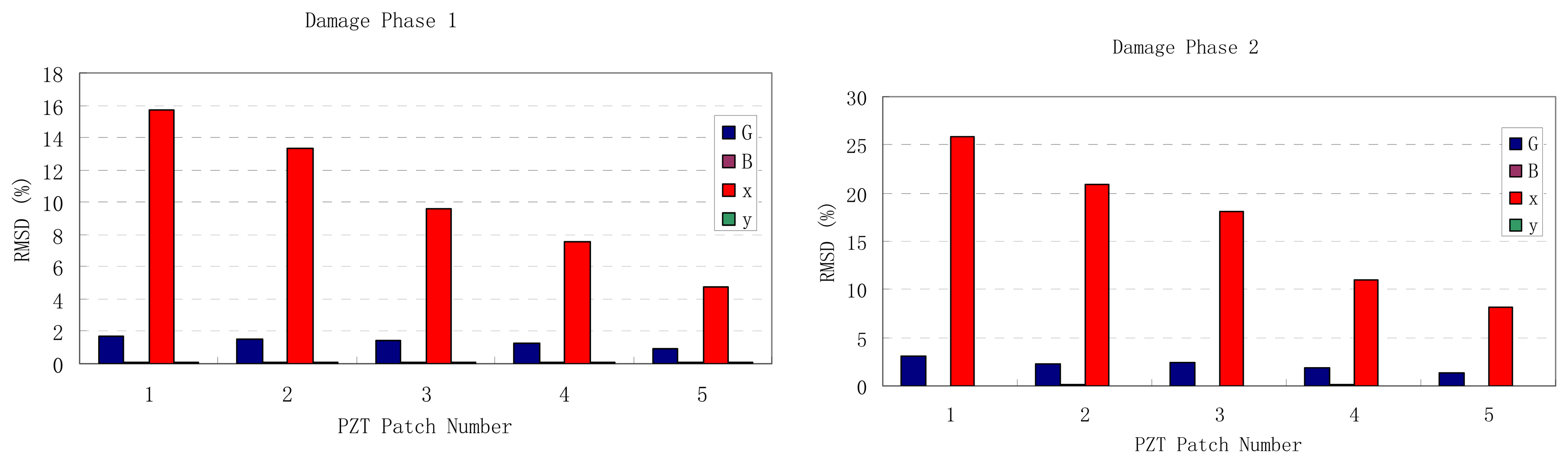
| 1 | 1.700904 | 0.079885 | 15.73118 | 0.077741 |
| 2 | 1.502574 | 0.106806 | 13.34286 | 0.098003 |
| 3 | 1.473301 | 0.086287 | 9.605244 | 0.063772 |
| 4 | 1.25146 | 0.11261 | 7.5918 | 0.095865 |
| 5 | 0.940053 | 0.116923 | 4.747043 | 0.117208 |
| Damage Phase 2 | ||||
| RMSD of G | RMSD of B | RMSD of x | RMSD of y | |
| 1 | 3.139675 | 0.061062 | 25.89481 | 0.049555 |
| 2 | 2.343378 | 0.073566 | 20.84959 | 0.064063 |
| 3 | 2.46278 | 0.058494 | 18.08281 | 0.047549 |
| 4 | 1.898626 | 0.071459 | 10.93107 | 0.054598 |
| 5 | 1.390455 | 0.056117 | 8.161555 | 0.045829 |
© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Yang, Y.; Hu, Y.; Lu, Y. Sensitivity of PZT Impedance Sensors for Damage Detection of Concrete Structures. Sensors 2008, 8, 327-346. https://doi.org/10.3390/s8010327
Yang Y, Hu Y, Lu Y. Sensitivity of PZT Impedance Sensors for Damage Detection of Concrete Structures. Sensors. 2008; 8(1):327-346. https://doi.org/10.3390/s8010327
Chicago/Turabian StyleYang, Yaowen, Yuhang Hu, and Yong Lu. 2008. "Sensitivity of PZT Impedance Sensors for Damage Detection of Concrete Structures" Sensors 8, no. 1: 327-346. https://doi.org/10.3390/s8010327






