Application of Multiplexed FBG and PZT Impedance Sensors for Health Monitoring of Rocks
Abstract
:1. Introduction
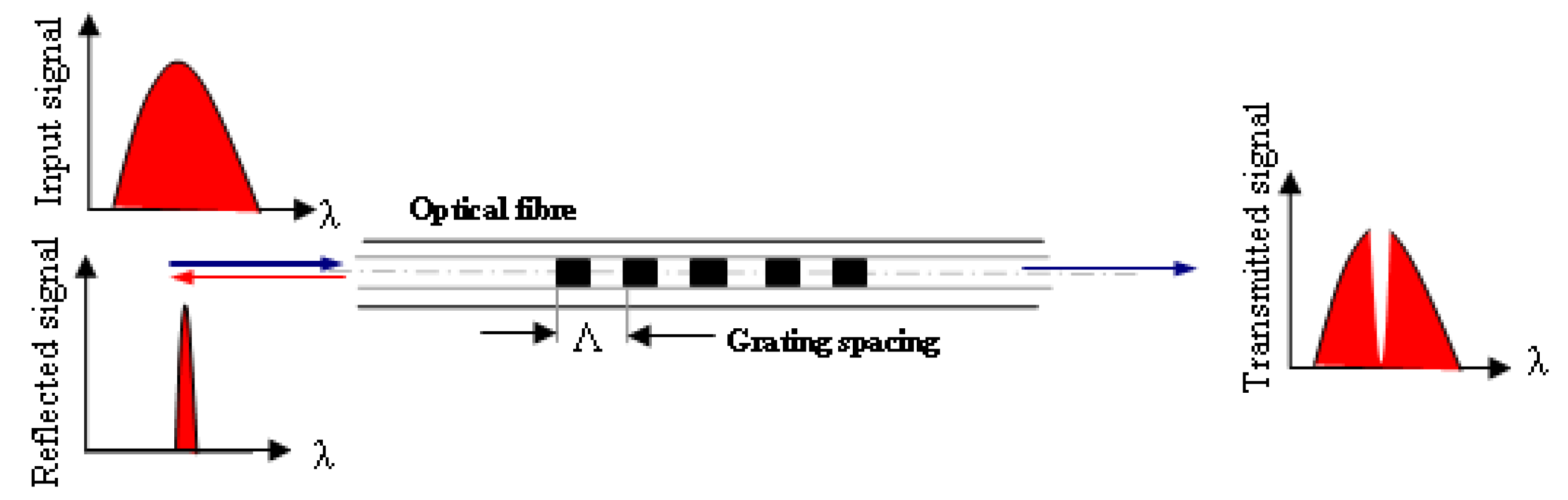
2. FBG Sensors
3. Damage Detection Using PZT Impedance Sensors
4. Health Monitoring of Rocks Using FBG and PZT Sensors
4.1 Strain measurement using FBG and ESG sensors
4.2 Admittance signature measured from PZT patches
4.3 Extraction of structural mechanical impedance from admittance signature
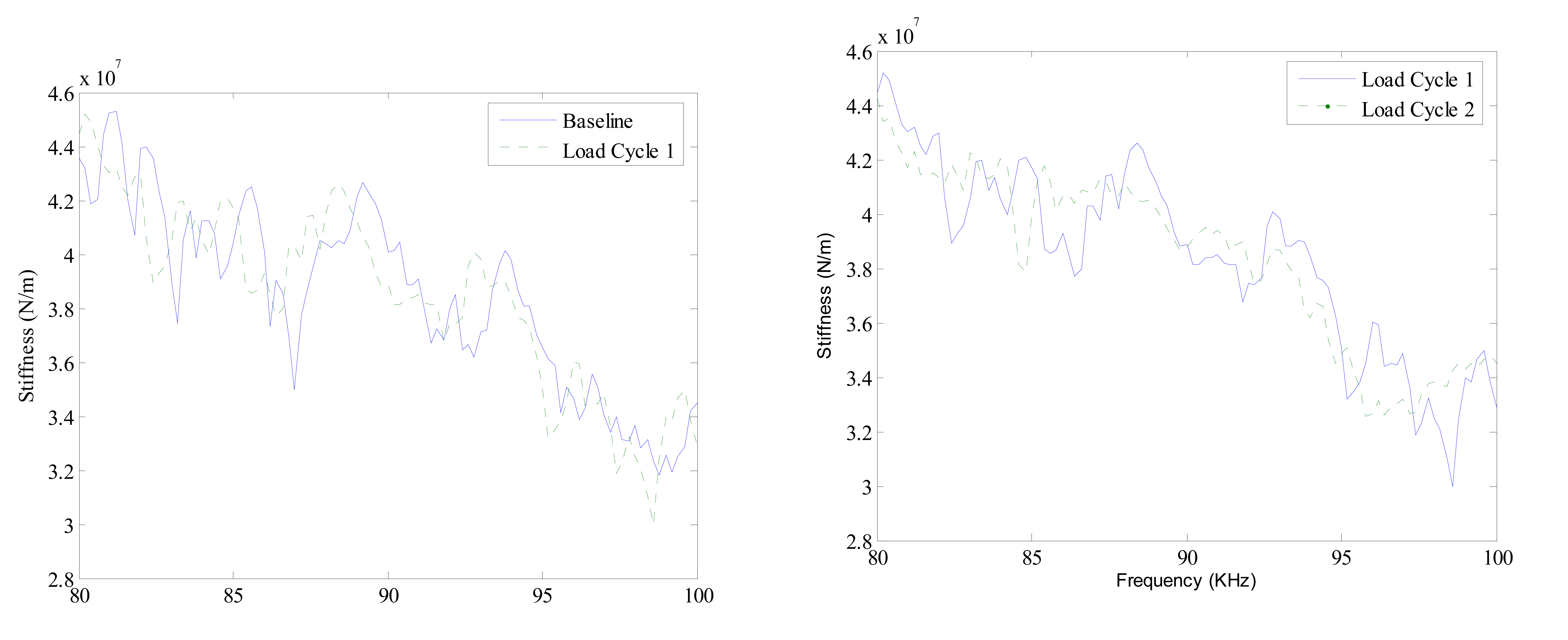
4.4 Calibration of PZT patch for damage assessment
| (1) FFP < 30% | Incipient damage (Micro-cracks) |
| (2) 30% < FFP < 50% | Moderate damage (Cracks opening up) |
| (3) 50% < FFP < 70% | Severe damage (large visible cracks) |
| (4) FFP > 70% | Failure imminent |
5. Conclusion
References and Notes
- Sumitro, S.; Tominaga, M.; Kato, Y. Monitoring Based Maintenance for Long Span Bridges. Presented on First International Conference on Bridge Maintenance, Safety and Management, Barcelona, Spain, 14- 17 July, 2002.
- Bhalla, S.; Yang, Y.W.; Zhao, J.; Soh, C.K. Structural Health Monitoring of Underground Facilities – Technological Issues and Challenges. Tunnelling and Underground Space Technology 2006, 20, 487–500. [Google Scholar]
- Ayres, J.W.; Lalande, F.; Chaudhry, Z.; Rogers, C.A. Qualitative Impedance-Based Health Monitoring of Civil Infrastructures. Smart Materials and Structures 1998, 7, 599–605. [Google Scholar]
- Xu, J.F.; Yang, Y.W.; Soh, C.K. Electromechanical Impedance-Based Structural Health Monitoring with Evolutionary Programming. Journal of Aerospace Engineering 2004, 17, 182–193. [Google Scholar]
- Hill, K.O.; Fujii, Y.; Johnson, D.C.; Kawasaki, B.S. Photosensitivity in Optical Fiber Waveguides: Application to Reflection Filter Fabrication. Applied Physics Letters 1978, 32, 647–649. [Google Scholar]
- Meltz, G.; Morey, W.W.; Glenn, W.H. Formation of Bragg Gratings in Optical Fibers by a Transverse Holographic Method. Optics Letters 1989, 14, 823–825. [Google Scholar]
- Maaskant, R.; Alaie, A.T.; Measures, R.M.; Tadros, G.; Rizkalls, S.H.; Guha-Thakurta, A. Fiber-Optic Bragg Grating Sensors for Bridge Monitoring. Cement and Concrete Composites 1997, 19, 21–33. [Google Scholar]
- Todd, M.D.; Johnson, G.A.; Vohra, S.T. Deployment of Fiber Bragg Grating-Based Measurement System in a Structural Health Monitoring Application. Smart Materials and Structures 2001, 10, 534–539. [Google Scholar]
- Moyo, P.; Brownjohn, J.M.W.; Suresh, R.; Tjin, S.C. Development of Fibre Bragg Grating Sensors for Monitoring Civil Infrastructure. Engineering Structures 2005, 27, 1828–1834. [Google Scholar]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J. Fiber Grating Sensor. Journal of Lightwave Technology 1997, 15, 1442–1461. [Google Scholar]
- Sun, F.P.; Chaudhry, Z.; Rogers, C.A.; Majmundar, M.; Liang, C. Automated Real-Time Structural Health Monitoring via Signature Pattern Recognition. Proceedings of SPIE 1995, 2443, 236–247. [Google Scholar]
- Yang, Y.W.; Xu, J.F.; Soh, C.K. Generic Impedance-Based Model for Structure-Piezoceramic Interacting System. J of Aerospace Engineering 2005, 18, 93–101. [Google Scholar]
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled Electro-Mechanical Analysis of Adaptive Material Systems - Determination of the Actuator Power Consumption and System Energy Transfer. Journal of Intelligent Material Systems and Structures 1994, 5, 12–20. [Google Scholar]
- Zhou, S.; Liang, C.; Rogers, C.A. An Impedance-Based System Modeling Approach for Induced Strain Actuator-Driven Structures. Journal of Vibration and Acoustics 1996, 118, 323–331. [Google Scholar]
- Annamdas, V.G.M.; Yang, Y.W.; Soh, C.K. Influence of Loading on Electromechanical Admittance of Piezoceramic Transducers. Smart Materials and Structures 2007, 16, 1888–1897. [Google Scholar]
- Yang, Y.W.; Hu, Y.H. Electromechanical Impedance Modeling of PZT Transducers for Health Monitoring of Cylindrical Shell Structures. Smart Materials and Structures 2008, 17, 015005. [Google Scholar]
- Hu, Y.H.; Yang, Y.W. Wave Propagation Modeling of PZT Sensing Region for Structural Health Monitoring. Smart Materials and Structures 2007, 16, 706–716. [Google Scholar]
- Yang, Y.W.; Hu, Y.H.; Lu, Y. Sensitivity of PZT Impedance Sensors for Damage Dection of Concrete Structures. Sensors 2008, 8, 327–346. [Google Scholar]
- Park, G.; Cudney, H.H.; Inman, D.J. Impedance-Based Health Monitoring of Civil Structural Components. Journal of Infrastructure Systems 2000, 6, 153–160. [Google Scholar]
- Park, G.; Cudney, H.H.; Inman, D.J. Feasibility of Using Impedance-Based Damage Assessment for Pipeline Structures. Earthquake Engineering and Structural Dynamics 2001, 30, 1463–1474. [Google Scholar]
- Giurgiutiu, V.; Zagrai, A.N. Embedded Self-Sensing Piezoelectric Sensors for On-Line Structural Identification. Journal of Vibration and Acoustics 2002, 124, 116–125. [Google Scholar]
- Micron Optics. http://www.micronoptics.com/.
- Tokyo Sokki Kenkyujo Co. Ltd. TML Products Guide; Tokyo, Japan, 2004. [Google Scholar]
- PI Ceramic. http://www.piceramic.de.
- SiF Universal. http://sif-u.com/.
- RS Components. http://www.rs-componenets.com.
- Huntsman Advanced Materials. http://www.adhesives.vantico.com/.
- Hixon, E.L. Mechanical Impedance. In Shock and Vibration Handbook, 3rd edition; Harris, C.M., Ed.; McGraw Hill: New York, 1988; pp. 10.1–10.46. [Google Scholar]
- Bhalla, S. A Mechanical Impedance Approach for Structural Identification, Health Monitoring and Non-Destructive Evaluation Using Piezo-Impedance Transducer. PhD Thesis, Nanyang Technological University, Singapore, 2004. [Google Scholar]
- Valliappan, S.; Pham, T.D. Fuzzy Finite Element Analysis of a Foundation on an Elastic Medium. International Journal for Numerical and Analytical Methods on Geomechanics 1993, 17, 771–789. [Google Scholar]
- Wu, C.Q.; Hao, H.; Zhou, Y.X. Fuzzy-Random Probabilistic Analysis of Rock Mass Responses to Explosive Loads. Computers and Geotechnics 1999, 25, 205–225. [Google Scholar]











| Load Cycle Number | Maximum Load (KN) | Strain measurement interval (KN) |
|---|---|---|
| 1 | 500 | 100 |
| 2 | 1000 | 200 |
| 3 | 1500 | 300 |
| 4 | 2000 | 300 |
| 5 | 2500 | 300 |
| 6 | 2700 | 300 |
| 7 | 2900 | 300 |
| 8 | 2950 | 300 |
© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Yang, Y.; Annamdas, V.G.M.; Wang, C.; Zhou, Y. Application of Multiplexed FBG and PZT Impedance Sensors for Health Monitoring of Rocks. Sensors 2008, 8, 271-289. https://doi.org/10.3390/s8010271
Yang Y, Annamdas VGM, Wang C, Zhou Y. Application of Multiplexed FBG and PZT Impedance Sensors for Health Monitoring of Rocks. Sensors. 2008; 8(1):271-289. https://doi.org/10.3390/s8010271
Chicago/Turabian StyleYang, Yaowen, Venu Gopal Madhav Annamdas, Chao Wang, and Yingxin Zhou. 2008. "Application of Multiplexed FBG and PZT Impedance Sensors for Health Monitoring of Rocks" Sensors 8, no. 1: 271-289. https://doi.org/10.3390/s8010271




