1. Introduction
In order to design intelligent sensors for measurement systems with improved features a simple reconfiguration process for the main hardware will be required in order to measure different variables by just replacing the sensor element, building reconfigurable systems. Reconfigurable systems, ideally should spend the least possible amount of time in their calibration. An autocalibration algorithm for intelligent sensors should be able to fix major problems such as offset, variation of gain and lack of linearity, all characteristic of degradation, as accurately as possible.
The linearization of output signal sensors and the calibration process are the major items that are involved in defining the features of an intelligent sensor, for example, the capability to be used or applied to different variables, calibration time and accuracy.
The subject of linearization has been considered in different forms and stages, basically from the designs of circuits with MOS technologies [
1]. Cases studied included the use of analog to digital converters to solve nonlinearities at the same time that the conversion is made [
2-
3]. In digital to analog type R-2R converters have also proved to be necessary to improve the linear response [
4]. Other work has focused on improving the nonlinear response of specific sensors, like the thermistor [
5] and the Hall effect current sensors [
6]. Numerical methods have been developed using modern technologies capable of computing linearization algorthms [
7,
8]. Also, ROM memories are used to save data tables and to solve the linearization problem [
9,
10]. Nowadays neural networks have been used for linearization [
11-
14]. Neural networks can be used to identify the transfer function response curve of the sensors [
15]. Recently, neural networks have been used to linearize amplifiers [
16] or specific sensors responses [
17].
The calibration method stage is important for two important aspects: first to define the features of the measurement system and second, the maintenance costs of measurement systems. The costs associated with the maintenance of measurement systems from 70's to now have been discussed [
18-
21], and these documents indicate that the companies have to spend more money applied to pay for quality services due to calibration problems.
A wide application area of neural networks is in recognition of patterns in the analysis of signals from sensors [
22,
23]. The self-calibration concept is approached from different stages, for example in the fabrication of integrated circuits [
24] or in signal transmissions [
25]. In [
26] the improvement of the adaptive network-based fuzzy inference system (ANFIS) technique was shown and in [
27] a radial bases function RBF neural network for pyroelectric sensor array calibration was presented; in both works a complex process training and a PC are required, so they cannot easily be implemented on DSP or small processors. A neural network for electromagnetic flow meter sensor calibration is described in [
28], but only simulated results are presented, the neural network selection is not clear, large quantities of data are used for training and the capability of the method is not evaluated. Back propagation artificial neural networking was used in the data analysis shown in [
29]. A neural network for linearization of the response of a pressure sensor is shown in [
30,
31], but only simulated results are presented and the neural network selection, the training process, the comparison with other methods and the method capability are not clear.
Most of the available literature related to autocalibration methods depends on several experiments to determine its performance. This approach impacts the time and cost of a reconfigurable system. This paper describes a new autocalibration methodology for nonlinear intelligent sensors based on artificial neural networks, ANN. The methodology involves analysis of several network topologies and training algorithms [
32-
34]. The artificial neural network was tested with different levels of nonlinear input signals. The proposed method was compared against the piecewise [
35] and polynomial linearization methods [
36] using simulation software. The comparison was achieved using different numbers of calibration points, and several nonlinear levels of the input signal. The proposed method turned out to have a better overall accuracy than the other two methods.
Besides complete experimental details, results and analysis of the complete study, the paper describes the implementation of the ANN in a microcontroller unit, MCU. In order to illustrate the method capability to build autocalibration and reconfigurable systems a temperature measurement system was designed. The system is based on a thermistor, which presents one of the worst nonlinearity behaviors, and is also found in many real world applications because of its low cost.
One important point that needs clarification before proceeding relates to the meaning of the term calibration. In this paper, calibration is used in the sense of [
3,
8,
9,
15,
22-
25,
28,
30,
35,
36,
40]. In these works, calibration is mainly concerned with the process of removing systematic errors and it is not in accordance with the meaning defined in the Metrology and the International Vocabulary of Basic and General Terms in Metrology (VIM), ISO VIM [
42-
45]. In addition, in this paper the phrase “self-calibration of intelligent sensor” or “autocalibration” has the meaning of “self-adjustment of measurement system” according to VIM [
44].
The paper structure will be as follows: the basic system design considerations are presented in Section 2. The ANN design, training algorithm and simulation are described in Section 3. An ANN of temperature measurement system implementation on MCU is shown in Section 4. The tests and results are described on Section 5. The evaluation results are given in Section 6. Finally, the conclusions are in Section 7.
3. Artificial Neural Network Design to Self-Calibration of Intelligent Sensors
This section describes the ANN design to be used in a Self-Calibration of intelligent sensors. The training algorithm and simulation are also described.
3.1. Artificial Neural Network Design
Several topologies of ANN like a multiplayer perceptron MLP and radial basis function RBF were evaluated. Multilayer perceptron (MLP) neural networks with sufficiently abundant nonlinear units in a single hidden layer have been established as universal function approximators. Some work has been performed to show the relationship between RBF networks and MLPs. since both types of networks are capable of universation approximation capabilities [
37,
38].
Although, it is known that RBF are good function approximation systems, the MLP was selected because is simpler than RBF and furthermore, the RBF network is computationally demanding [
26,
27,
39]. Besides, in other works, the relationship between RBF networks and MLPs has been studied. Mainly, if we assume that an MLP is a universal approximator, then it may approximate an RBF network and vice versa. It has also been showed that in problems with normalized inputs, MLPs work like RBF networks with irregular basis functions [
38].
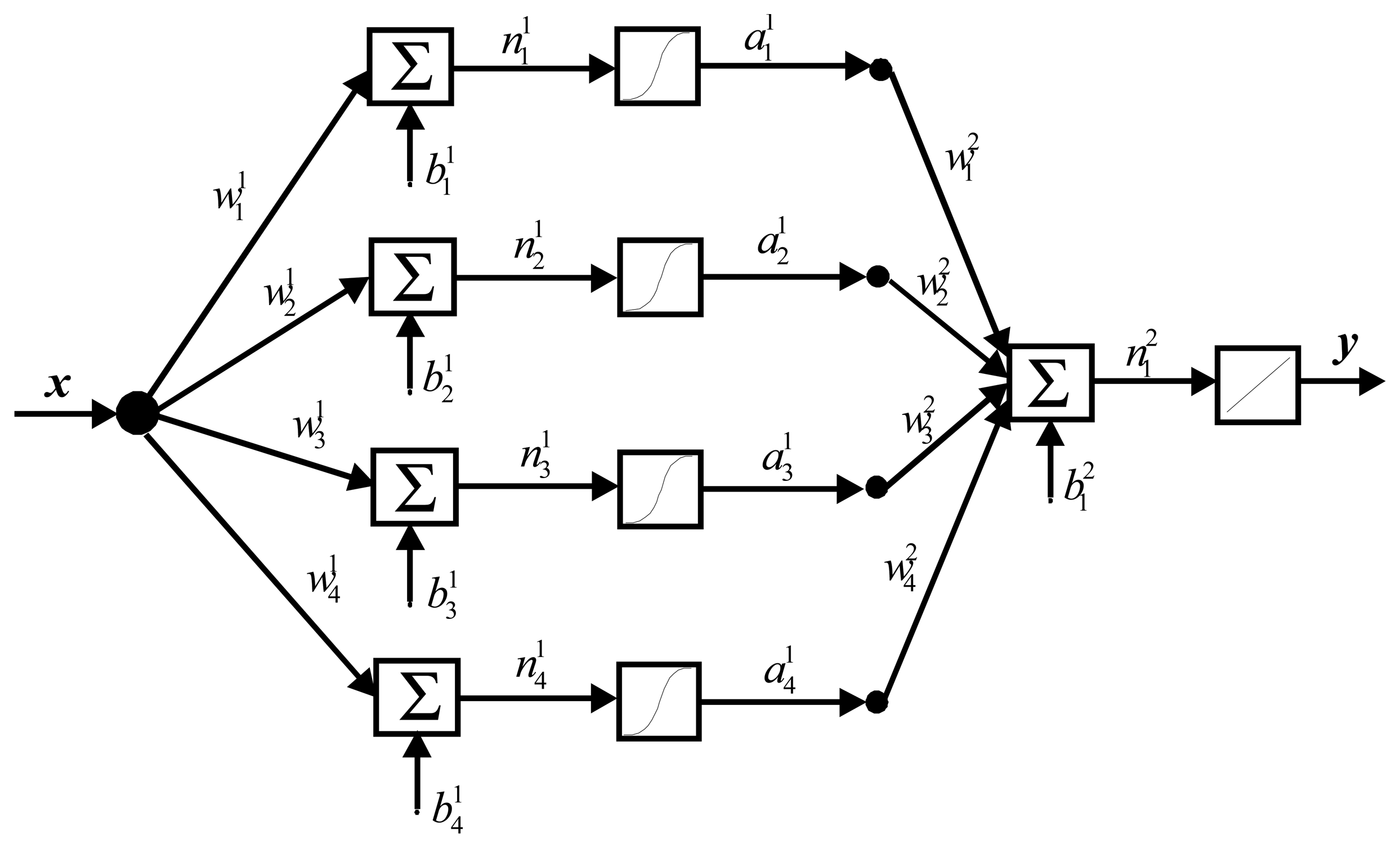
Consequently for our proposal the most appropriate ANN to be implemented was a feed forward MLP with four neurons in the first layer and a logarithmic activation function. The second layer is a single neuron with a linear activation function. The architecture of the ANN is shown in
Figure 1.
The number of neurons, number of layers, activation functions, training algorithm and the computation requirements are the major characteristics considered during the design. These features were determined under the restriction of archiving the least output error and simplest ANN structure to be implemented in a small MCU.
The output of the ANN is defined by:
where
x is the normalized output sensor signal, the weights are represented by the vector
w,
b is the bias and is
y the linearized or autocalibrated signal.
3.2. Training Algorithm
Currently many variations of backpropagation training algorithms are available. The Adaptive Linear Neuron ADALINE and the Least Mean Square LMS were first presented in the late 50′s, they are very frequently used in adaptive filtering applications. Echo cancellers using the LMS algorithm are currently employed on many long distance telephone lines. Backpropagation is an approximate steepest descent algorithm that minimizes mean square error, the difference between LMS and backpropagation is in the manner in which the derivatives is calculated. Backpropagation is a generalization of the LMS algorithm that can be used for multilayer networks. One of major problems with backpropagation has been the long training times needed. The backpropagation process is too slow for most practical applications and it is not feasible to use the basic backpropagation algorithm for real problems, because it can take weeks to train a network, even on a large computer. Since the backpropagation algorithm was first popularized, there has been considerable work on methods to accelerate the convergence. Another important factor in the backpropagation algorithm is the learning rate. Depending on the value of the learning rate the ANN may or may not oscillate. On this item several experiments have been made leading to selection of the appropriate learning rate [
32]. Reducing the probability of oscillation of the ANN is a trade-off with respect to the training speed. Therefore, this situation needs to be faced with faster algorithms. Research on faster algorithms falls roughly into two categories: 1) the development of heuristic techniques. These heuristic techniques include such ideas as varying learning rates, using momentum and rescaling variables; 2) another category of research has focused on standard numerical optimization techniques. The conjugate gradient algorithm and the Levenberg Marquardt algorithm have been very successfully applied to the training of MLP [
32].
The Levenberg Marquardt algorithm is a variation of Newton′s method and uses the backpropagation procedure. Levenberg Marquardt Backpropagation (LMBP) was designed for minimizing functions that are sums of squares of other nonlinear functions. This is very well suited to neural network training where the performance index is the mean squared error. The LMBP is the fastest algorithm that we have tested for training multiplayer networks of moderate size, even though it requires a matrix inversion at each iteration. It is remarkable that the LMBP is always able to reduce the sum of squares at each iteration [
32].
Looking for a training algorithm with the best features of training time, minimum error with practical application we decided to evaluate backpropagation, backpropagation with momentum and the LMBP algorithms.
Table 1 summarizes the results of this evaluation. As can be observed in the table, the Lenvenberg-Marquardt algorithm has a faster convergence time and also the lowest error. Besides, this method works extremely well in practice, and is considered the most efficient algorithm for training median sized ANN [
32,
34].
Next, the Lenvenberg-Marquardt algorithm for our particular application is described. Assuming
N calibration points we define the input sensor signal
vn, the output sensor signal
xn and its desired
tn, with normalized values
equations (2)-
(4) as:
The iterations of the Levemberg Marquardt algorithm to autocalibration of intelligent sensors for
k cycles can be summarized as follows [
32]:
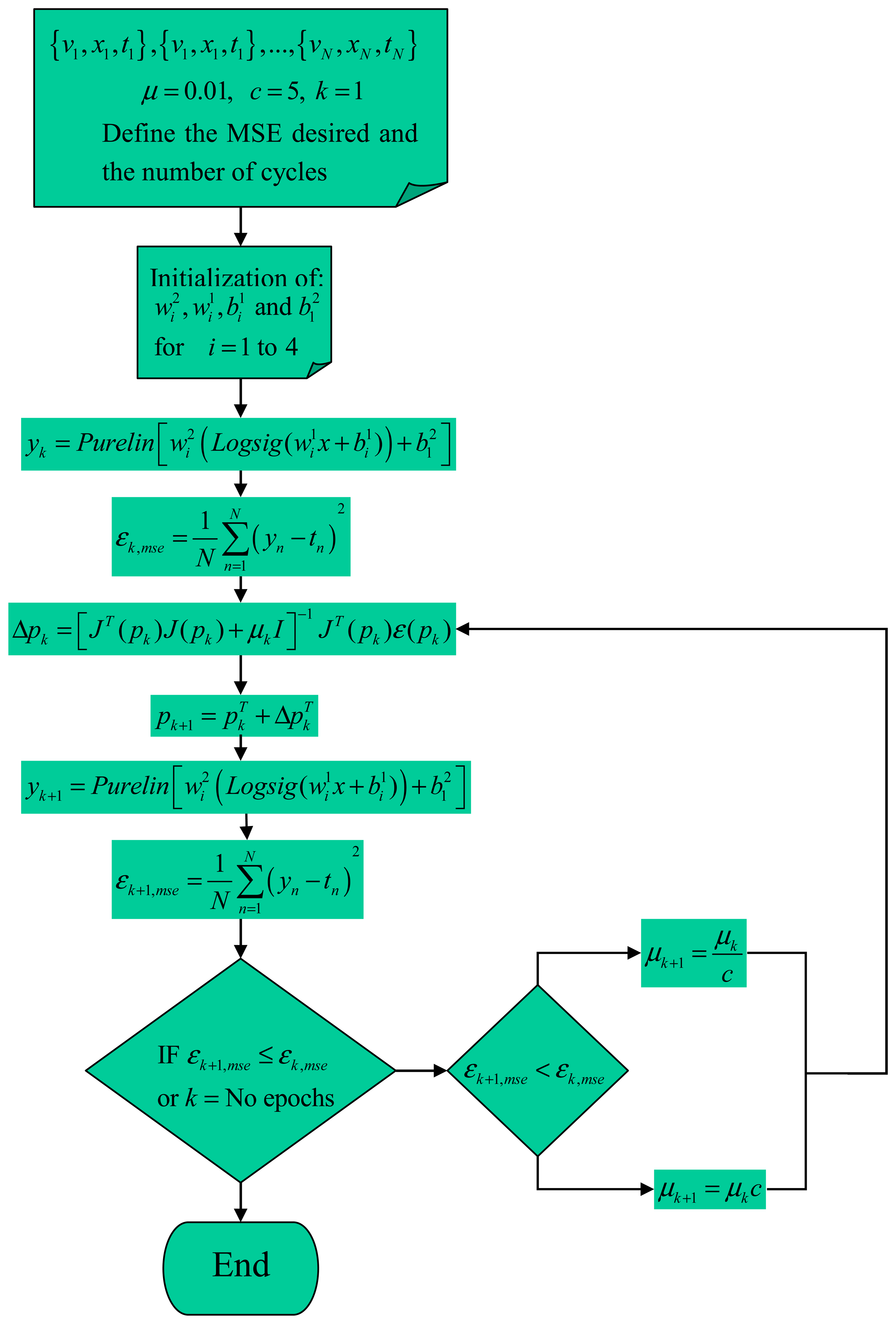
- Step 1:
Present all the
N calibration points and compute the sum of MSE with
equation (6).
- Step 2:
Determine the Jacobian matrix by:
where
ɛ is the error relative for each calibration point computed from the
equation (6)- Step 3:
Now compute the variation or delta of ANN parameters, Δ
pk:
Where the learning factor is represented by
μk,
I is the identity matrix and the
J(
pk) is the Jacobian matrix evaluated with the ANN parameters
pk.
- Step 4:
Recompute the sum of squared errors with the update parameters,
equation (6), step 1 for the update of parameters:
For this case: If the result of MSE is smaller than computed in the step 1,
εk+1,mse <
εk,mse, then evaluate
μk+1 as
,
c is a constant value, and continue with the step 2. If the sum of squares is not reduced,
εk+1,mse >
εk, mse evaluate as
μk+1 =
μkc and go to the step 2. All this will be repeated until the desired error or
k's cycles are reached. Note that the initial values of
μ and
c are the key to the right convergence, the recommend values are
μ =0.01 and
c=5.
Figure 2 shows the flow chart of the LBMP algorithm.
3.3 Simulation to Evaluation and Results Comparison
The ANN training was made with five to eight calibration points using the function
, normalized with the
equations (3) and
(4).
τ represents the percentage of the nolinearity of
x. The artificial neural network was tested with different level of nonlinear input signals. The proposed method was compared against the piecewise [
35] and polynomial linearization methods [
36] using simulation software.
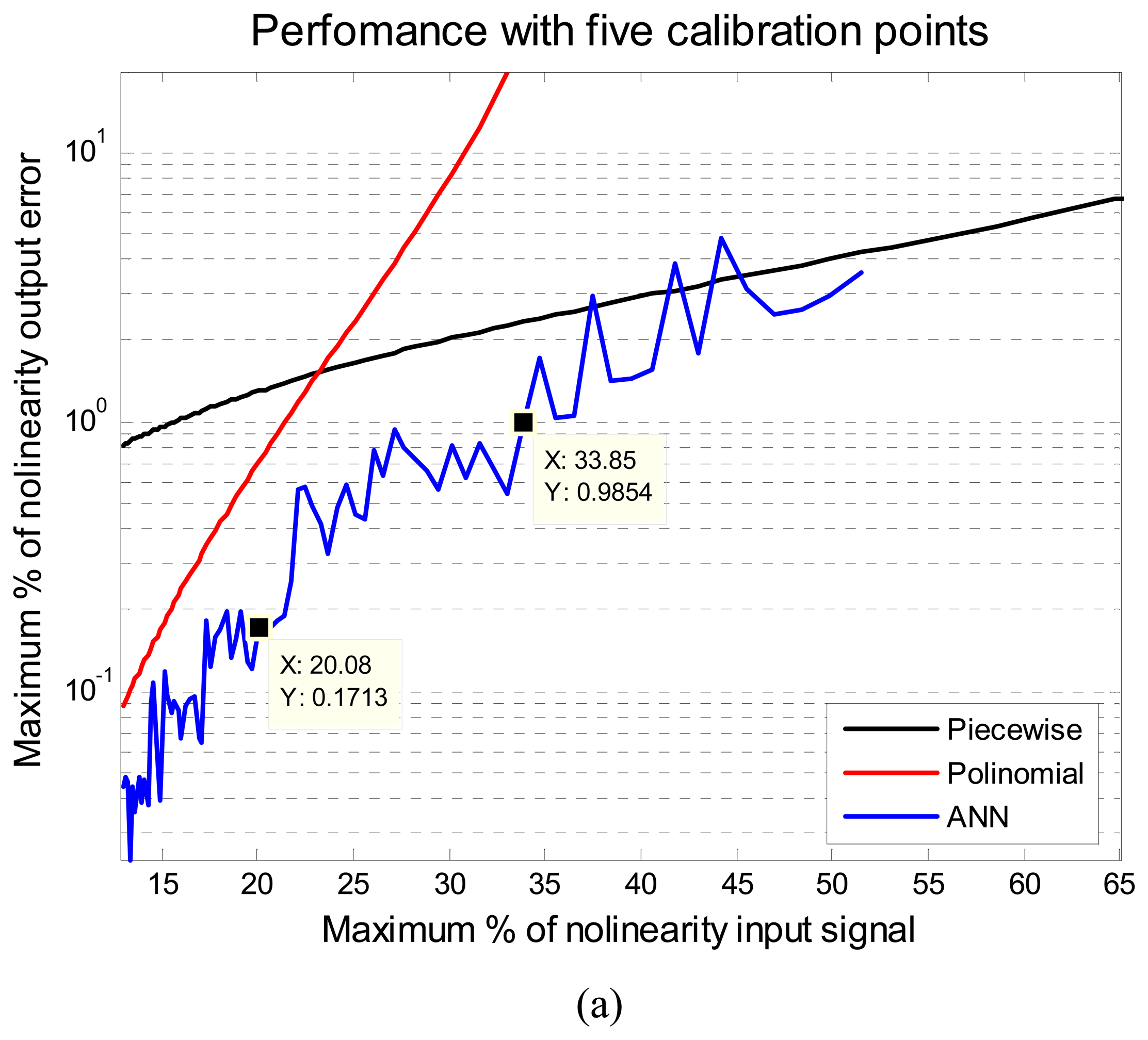
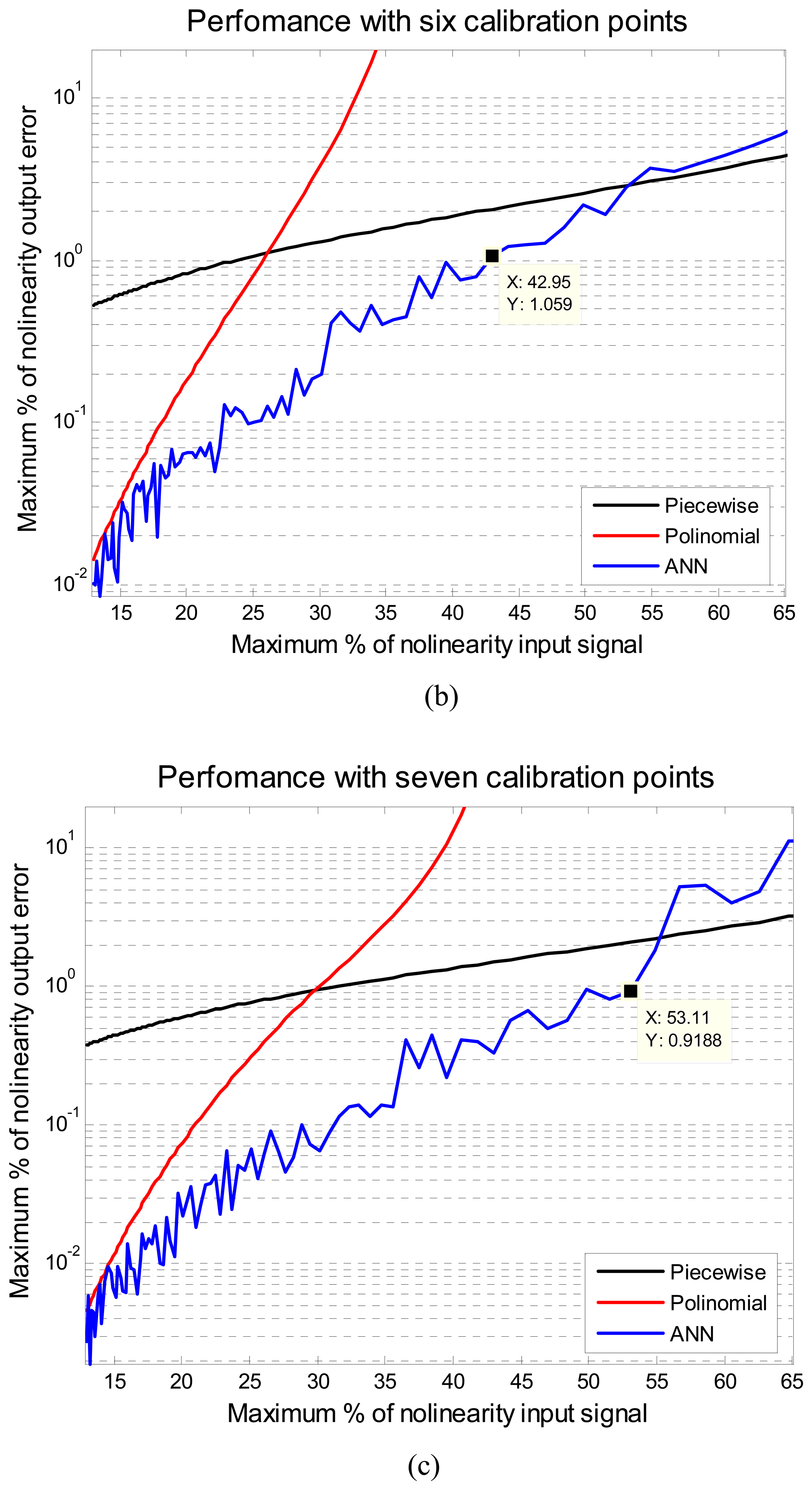
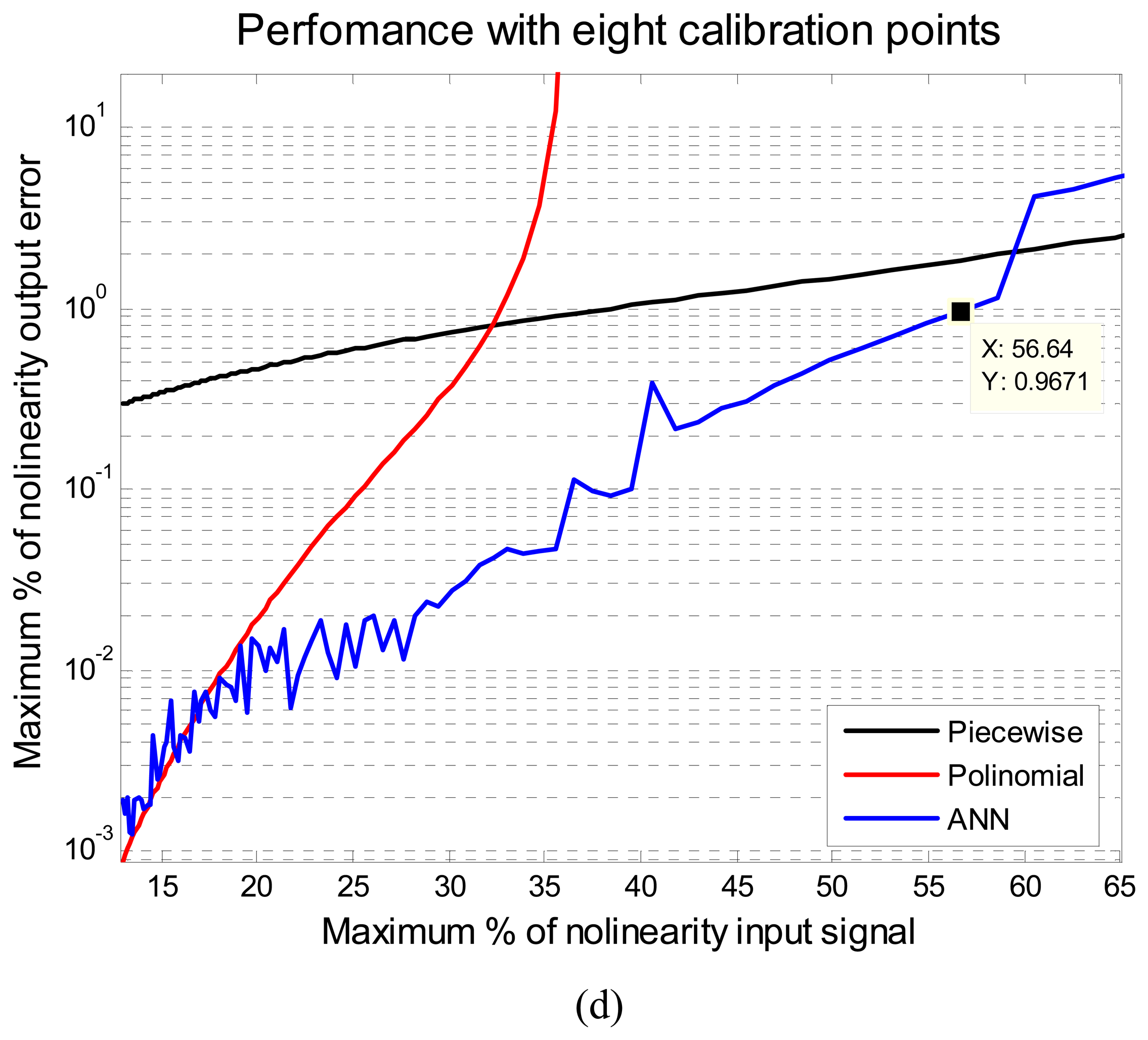
Figure 3 illustrates the results of the comparison of the ANN, piecewise and polynomial methods. Each figure shows the performance of these methods for different calibration points regarding different levels of input nonlinearity, from 10% to 65%.
The performance is given in maximum percentage of nonlinearity output error, MPNOE. In
Figure 3 it can be noted that the proposed method with ANN turned out to have a better overall accuracy than the other two methods. The ANN always presents the minimum MPNOE considering the 1% of MPNOE, maximum acceptable value of practical applications. For example, with five calibration points and supplying a signal of a 20% of relative nonlinearity, the piecewise method has an error above 1%, the polynomial has an error around 0.71% and the proposed method has an error of 0.17 %. The performance of the ANN was obtained using the same initial conditions for all cases. Another advantage of ANN method is that with five calibration points a signal below 33% of the maximum nonlinearity error can be fixed, to yield a performance in the output of less than 1% maximum error of nonlinearity. Using eight calibration points even signals with 56% of maximum error of nonlinearity can be fixed or linearized. The implementation of the ANN method on a MCU using a thermistor will be described in the next section.
4. Temperature Intelligent Sensor Design using ANN on a Small MCU
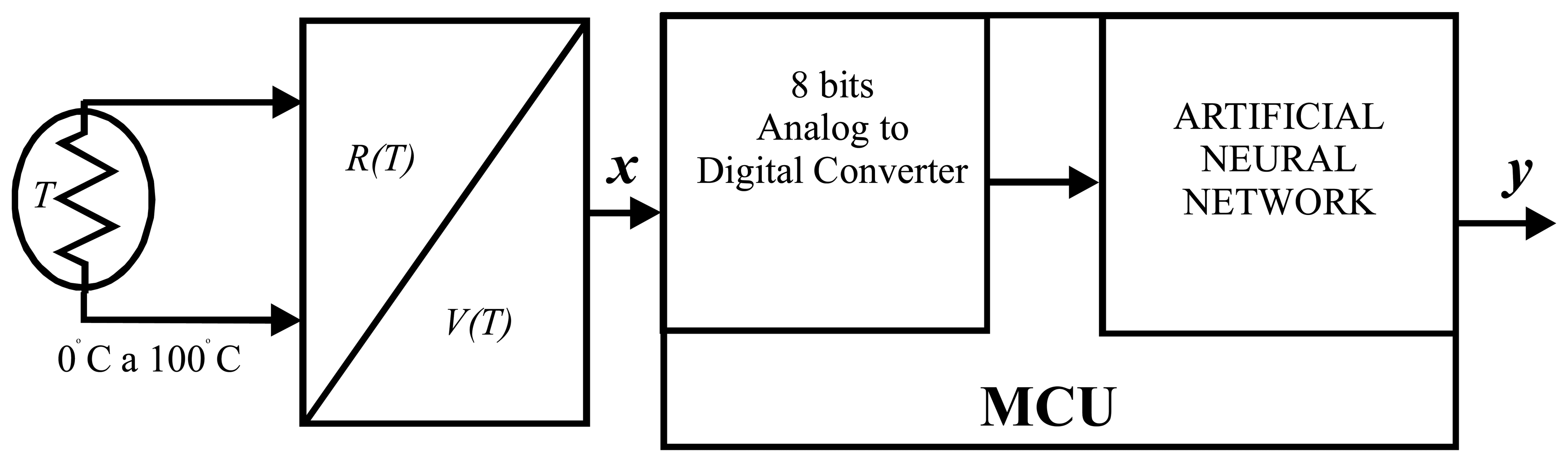
Temperature measurement systems are widely used in almost any process. A thermistor as temperature sensor was selected in the construction of a measurement system,
Figure 4. Thermistors, besides having a diversity of applications, can be found in a great variety of types, sizes and characteristics.
In this case, the major characteristic that will be analyzed is the
β coefficient, a fundamental characteristic used to describe its nonlinearity error. For example, values of
β=
3100 to
β=
4500 generate nonlinearity relative errors ranging from 41.07% to 51.34%. It is clear that in the practical cases, the sensor is incorporated into a circuit to perform the temperature to voltage conversion. For example, it can be found in a voltage divider or a Wheatstone bridge. In our design we used a thermistor with features of
β =4500±10%, R
o=10000 ohms to 25 °C, and assembled on a voltage divider to build a measurement system in the range from 0 to 100 °C as shown in
Figure 4.
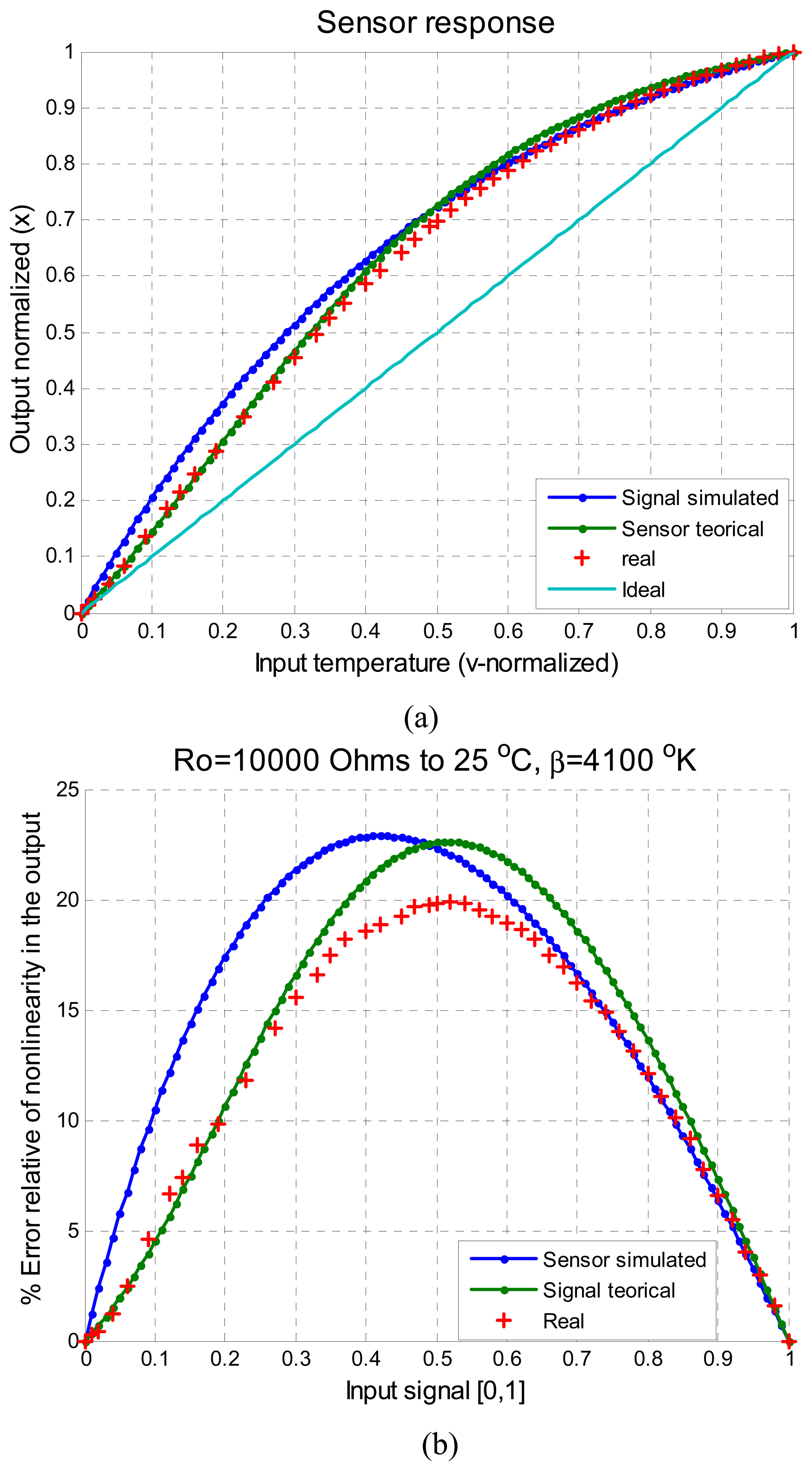
Figure 5 illustrates the characteristics of
x, the input signal to the ANN. This signal is the response the sensor to the temperature and the values are normalized in the ranges of [0,1].
In
Figure 5a the signal simulated as was described in Section 3.3, the signal evaluated with the equation characteristic of a thermistor using nominal values, the response of thermistor real obtained from a practical test and the ideal response
t (a straight line) can be observed.
Figure 5b shows the percentage of nolinearity of this signal
x, evaluated according to
Equation (5). In this figure all the error signals are shown: simulated signal, theorical thermistor response, and the real thermistor response. From
Figure 5b, the similarity of the three signals can be easily appreciated. Taking into consideration just the parameter
β and its ±10% tolerance, the real signal is under this limits and our proposal methodology is acceptable.
The major features of the MCU for the physical implementation are: eight bit words, eight bits analog to digital converter ADC, a 20 MHz clock and 3 Kbytes of RAM.
Equation (7) and the training algorithm described in Section 3.2 were programmed using C language. Next the ANN implementation and its training for autocalibration and to linearize the signal
x in intelligent sensor will be described.
The iterations of the Levemberg Marquardt backpropagation algorithm assuming five calibration points was programmed as follows:
The input calibration signal was
v' = [0,23,50,76,100] temperature in °C. Using the
equation (2)-
(3) the values normalized to the vectors
x,
y and
t were calculated, to obtain the vectors of
equation (8):
The initial values for weights and bias were taken from the simulation described in Section 3.3, with the values of:
- Step 1:
- Step 2:
The Jacobian matrix is computed. In this example the size of the Jacobian matrix according to
equation (17) and five calibration points will be 5 × 13, defined as:
- Step 3:
Solve the
equation (10) to get Δ
pk, for the first iteration for
k=1,
μ1=0.01 and
c=5 the result is:
- Step 4:
Recompute the sum of squared errors with the update parameters,
equation (6), step 1. For this case:
If the result of MSE is smaller than computed in the step 1,
ε2,
mse <
ε1,
mse, than evaluate
μ2 as
, and continue with step 2. If the sum of squares error is not reduced,
ε2,
mse <
ε1,
mse, evaluate as
μ as
μ2 =
μ1c and go to step 2. All this will be repeated until the desired error or k's cycles are reached. The process above described was repeated for
k=500 or 500 cycles and final parameters are:
5. Tests and results
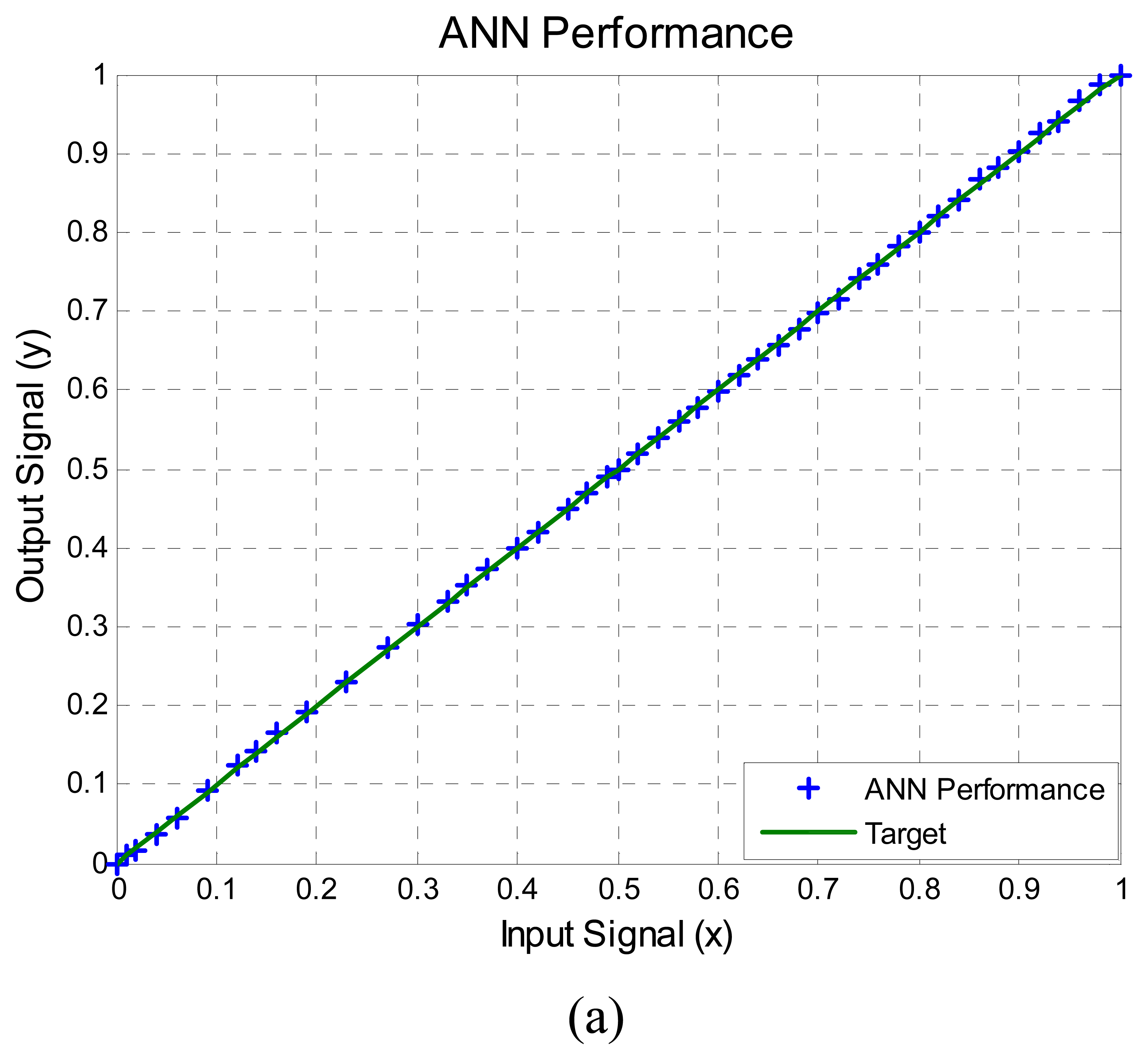
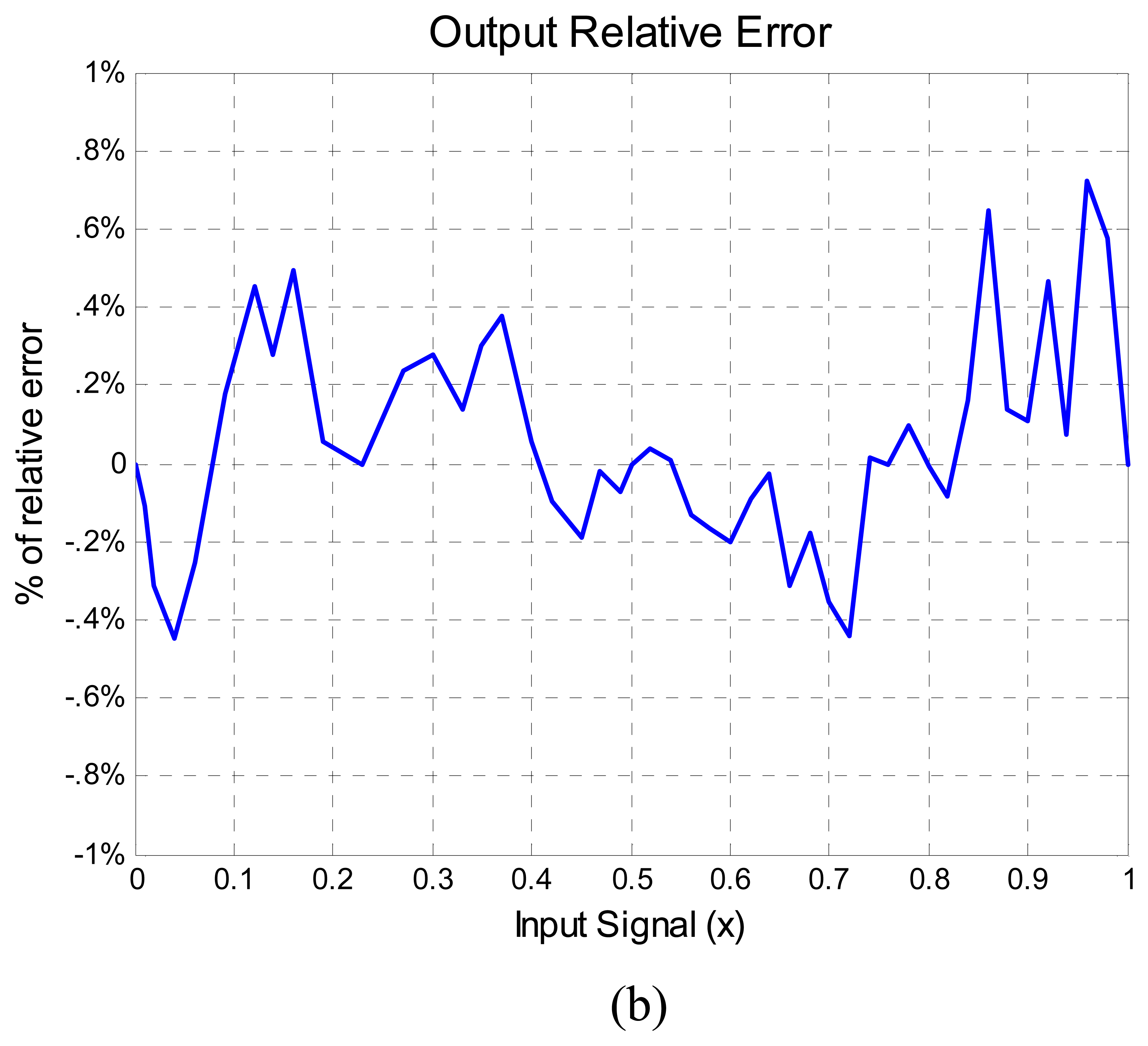
The performance of the ANN was compared against a Honeywell temperature meter number UDC3000 with a type K −29 to 538 °C (–20 to 1000 °F) range thermocouple with an accuracy of ±0.02%, taking 50 measurements from a range of 0 to 100 °C in steps of 2 °C using an oven system to change the temperature. The results are shown in
Figure 6. The ANN output signal
y compared with the target straight line can be seen in
Figure 6a. In order to visualize better the error between the ANN output and the target straight line the percentage of relative error of nolinearity computed with
equation (5) is shown in
Figure 6b. In summary,
Figure 6b shows the difference between the ideal output and the output provided by the ANN. It can also be observed that the maximum percentage of relative nonlinearity error is approximately 0.7%, below 1% as was predicted from simulation and was illustrated in
Figure 3a with five calibration points.
Important evaluations were made considering the computational work that is required in the physical implementation of each method described above. First, the number of operations required for each method using a software tool to program the MCU were counted, as well as the computation time required was predicted This process was made for
N=5, 6, 7 and 8 calibration points, and the results are shown in the
Table 2.
A similar process was carried out to evaluate the computational work and the training time. The computational time for one cycle of the ANN training is showed in
Table 3, considering MCU clocks of 20 Mhz and 40 Mhz.
Besides, it is important to remark about the sensor resolution. The ADC determinates the sensor resolution and this is defined by:
, were EFRS is the full range voltage scale and the number of bits of the ADC is n. In our example EFRS=5 volts, then the sensor resolution is 19.6 mV, that means, the temperature sensor is limited to detect temperature changes of 0.38 °C. In a case where this resolution might represent a problem in an specific application, the MCU can be changed with 10 bits of ADC converter to improve the resolution to 4.9 mV (0.09 °C). Another alternative is the use of an external ADC with more than 10 bits.
6. Evaluation of Results
The performance of the ANN method can be defined if we determine the deviation of the ANN output from a straight line, the ideal response,
equation (5). The performance is obtained by using the collected data from section 5 (
Figure 6) and the linear regression model [
41] to evaluate and quantify the ANN output ŷ as follows:
Ideally, the value of
m should be one and the value of
b should be zero to obtain the best performance of the ANN. The term
b represents the unpredicted or unexplained variation in the response variable; it is conventionally called the “
error” [
41].
The values of
m and
b were computed with the calibration data and using the least squares analysis [
42,
43]. The results where 1.0015 and −0.0281 °C respectively. Then it is clear that the error for
m is 1.5×10
−3, the error for
b is −0.0281 °C.
We made a readjustment in the ANN
equation (7), to the value of
by adding the error value of −0.0281 °C. The experiment of Section 5 was repeated and the new values for
m and
b where computed again. The results where of 1.0015 and −2.15×10
−4 °C, respectively.
The error regarding the best fitting line that was obtained with m=1.0015 and b=0.0281 is acceptable. From the mathematical point of view the readjustment made shows a decrease in the error of the b value, but from the practical point of view the nolinearity error was the same. Therefore, it was shown that with a single training process of the ANN was enough to obtain acceptable results.
7. Conclusions
In this paper a special methodology to design and evaluate an algorithm for autocalibration of intelligent sensors that can be used in the design of a measurement system with any sensor was described.
The major problems such as offset, variation of gain and nonlinearity in sensors can be solved by the ANN method. Most of the available literature related to autocalibration methods depends on several experiments to determine its performance. This process impacts on the time and cost of a reconfigurable system. This paper described a new autocalibration methodology for nonlinear intelligent sensors based on ANN. The artificial neural network was tested with different level of nonlinear input signals. The proposed method was compared against the piecewise and polynomial linearization methods. Method comparison was achieved using different number of calibration points, and several nonlinear levels of the input signal. The proposed method turned out to have a better overall accuracy than the other two methods. For example, for 20% relative nonlinearity the piecewise methods has an error above 1%, the polynomial one has an error around 0.71% and the proposed method has an error of 0.17 % using five calibration points in simulation results, as shown in
Figure 3a.
The ANN method requires fewer operations than the other two methods and the number of operations does not increase if the number of calibration points increases. This can be observed in
Table 2. A training process is required before the ANN method is used, as shown in
Table 3, but this is not a problem because it will be executed each time that the sensor is under calibration or the first time when a new intelligent sensor is designed. The ANN method can be trained in the self MCU but for some cases the required computational time resources in the training process could be a disadvantage but this can be solve using a remote compute system. Thus, if the sensor is on a network, the training can be done using a computer and the ANN parameters sent to the sensor.
Besides the major advantages which are that with a low number of calibration points the ANN method achieves better results than the piecewise and polynomial methods, as a consequence it requires less time and cost for its maintenance than any measurement system.
In conclusion, the proposed method is an improvement over the classic autocalibration methodologies, because it impacts on design process of intelligent sensors, autocalibration methodologies and their associated factors, like time and cost.