Agent Collaborative Target Localization and Classification in Wireless Sensor Networks
Abstract
:1. Introduction
2. Existent Agent Architectures for Wireless Sensor Networks
2.1. Brief overview of multi-agent systems and mobile agents
2.2. Multi-agent and mobile agent architectures for wireless sensor networks
3. Target Localization and Classification Algorithms
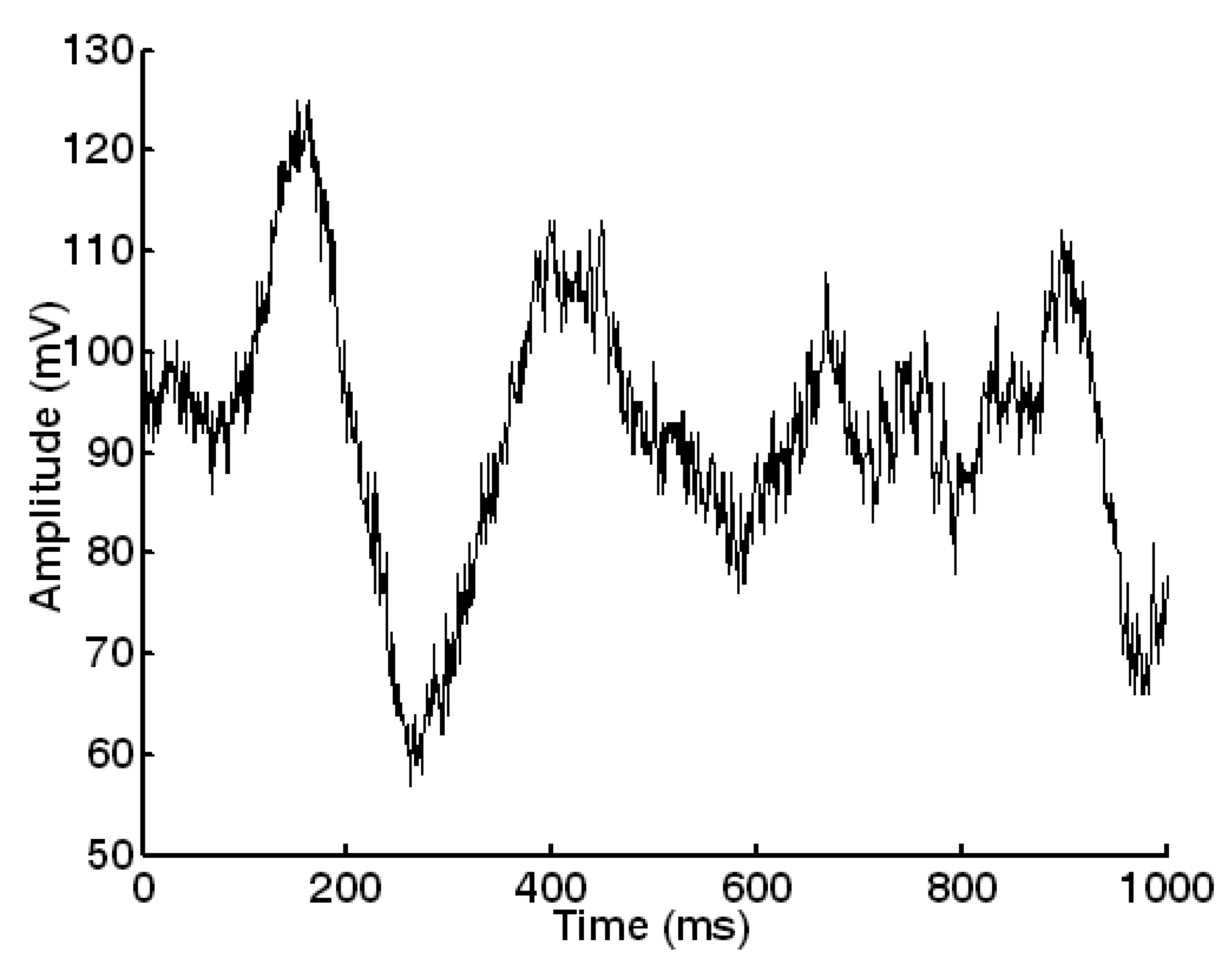
3.1. Target localization with acoustic signatures
3.1.1 Propagation of acoustic signatures
3.1.2 TDOA method
3.1.3 Energy based method
3.2. Target classification with support vector machine
3.2.1 Fundamentals of support vector machine
3.2.2 Simple algorithm for distributed support vector machine learning
3.2.3 Convex hull vector approach for distributed support vector machine learning
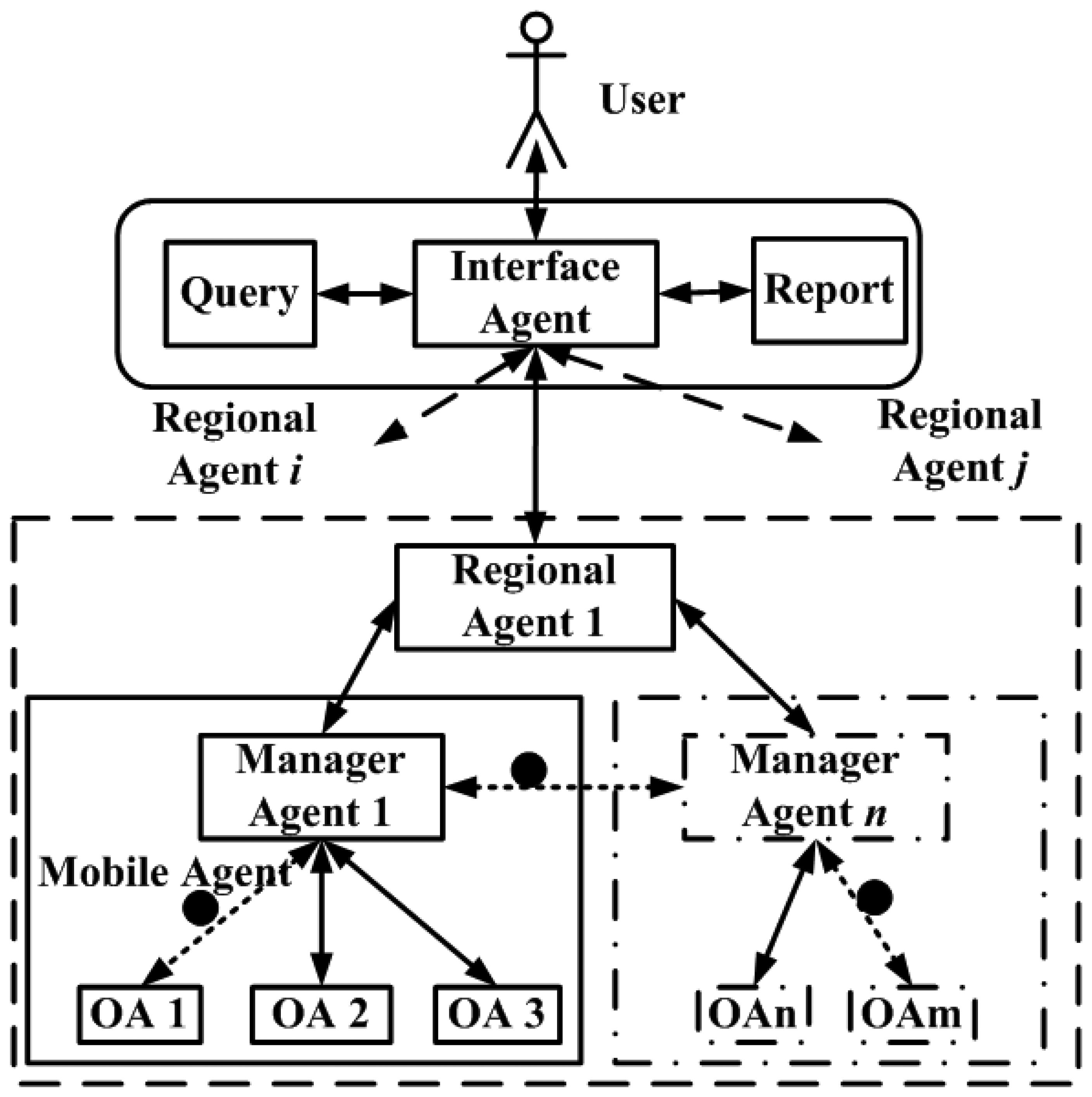
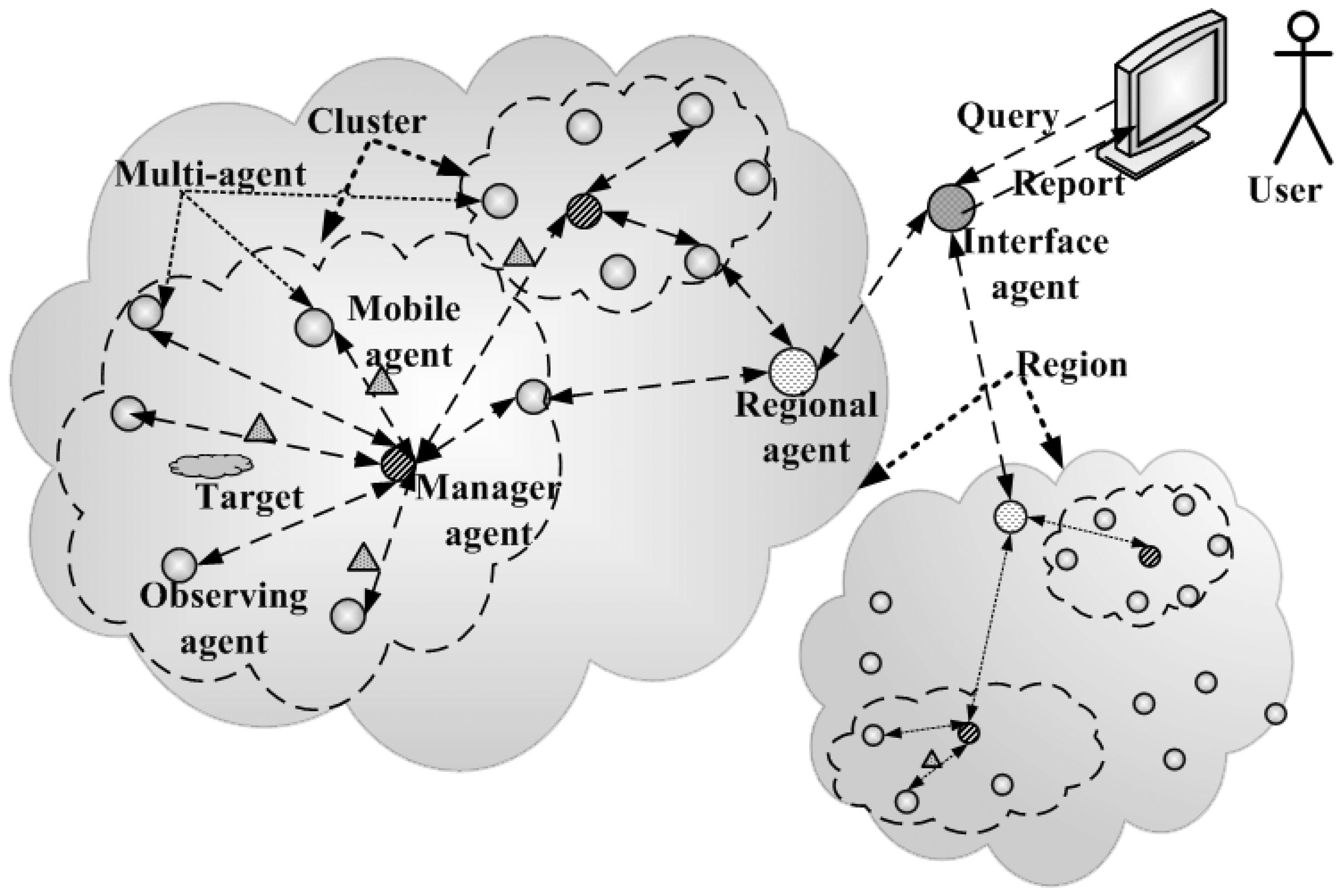
4. Collaborative Localization and Classification with the Heterogeneous Agent Architecture
4.1. Heterogeneous agent architecture for wireless sensor networks
4.2. Agent collaborative acoustic localization
4.3. Agent collaborative support vector machine classification
4.3.1 Distributed support vector machine learning with hull vectors and support vectors
4.3.2 Collaborative support vector machine classification decision
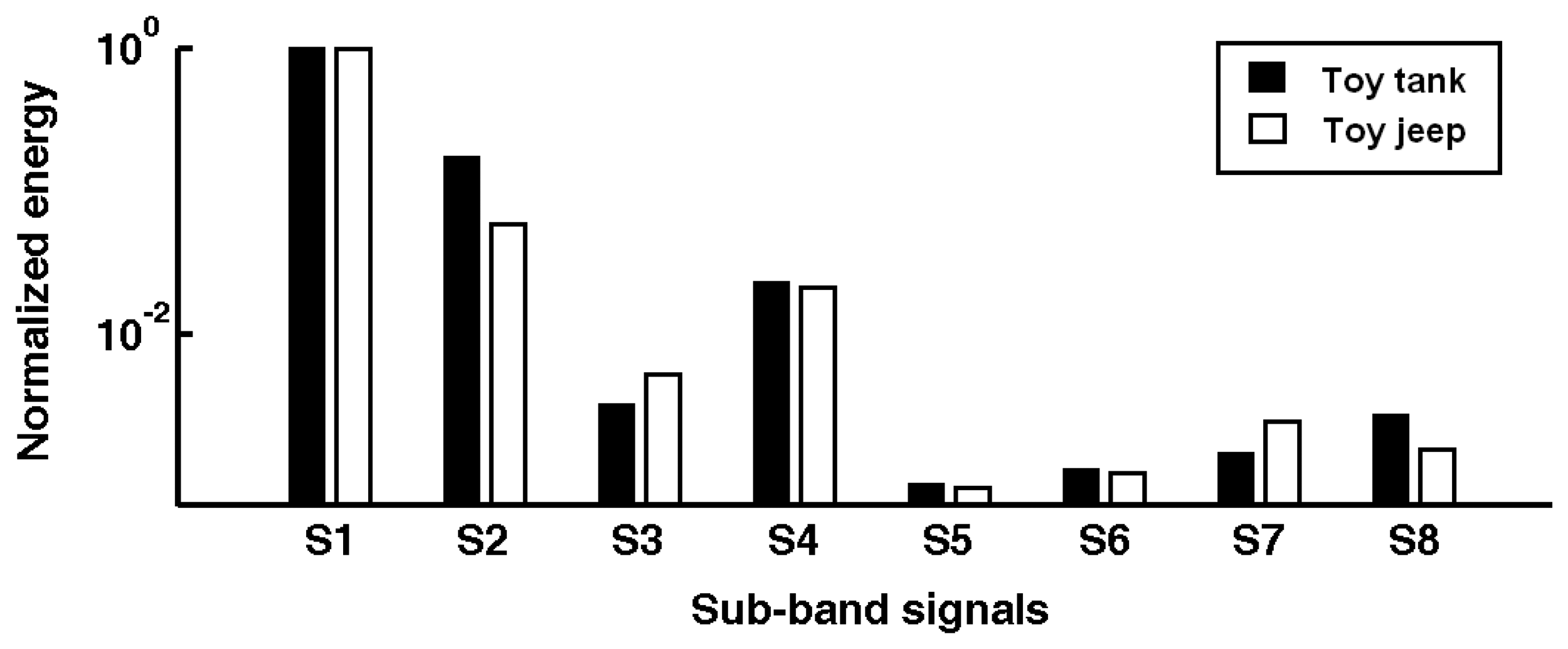
4.3.3 Feature extraction with wavelet packet
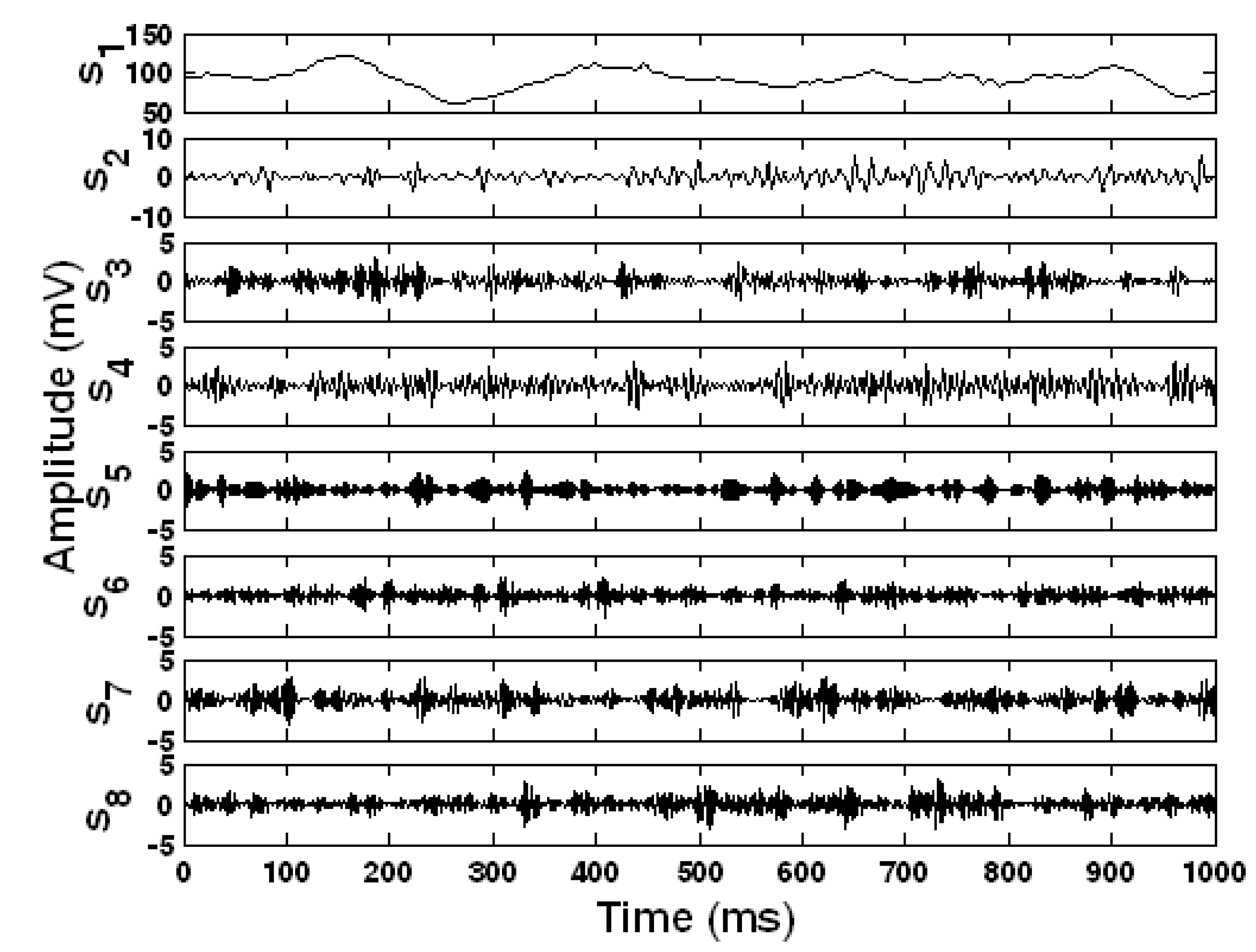
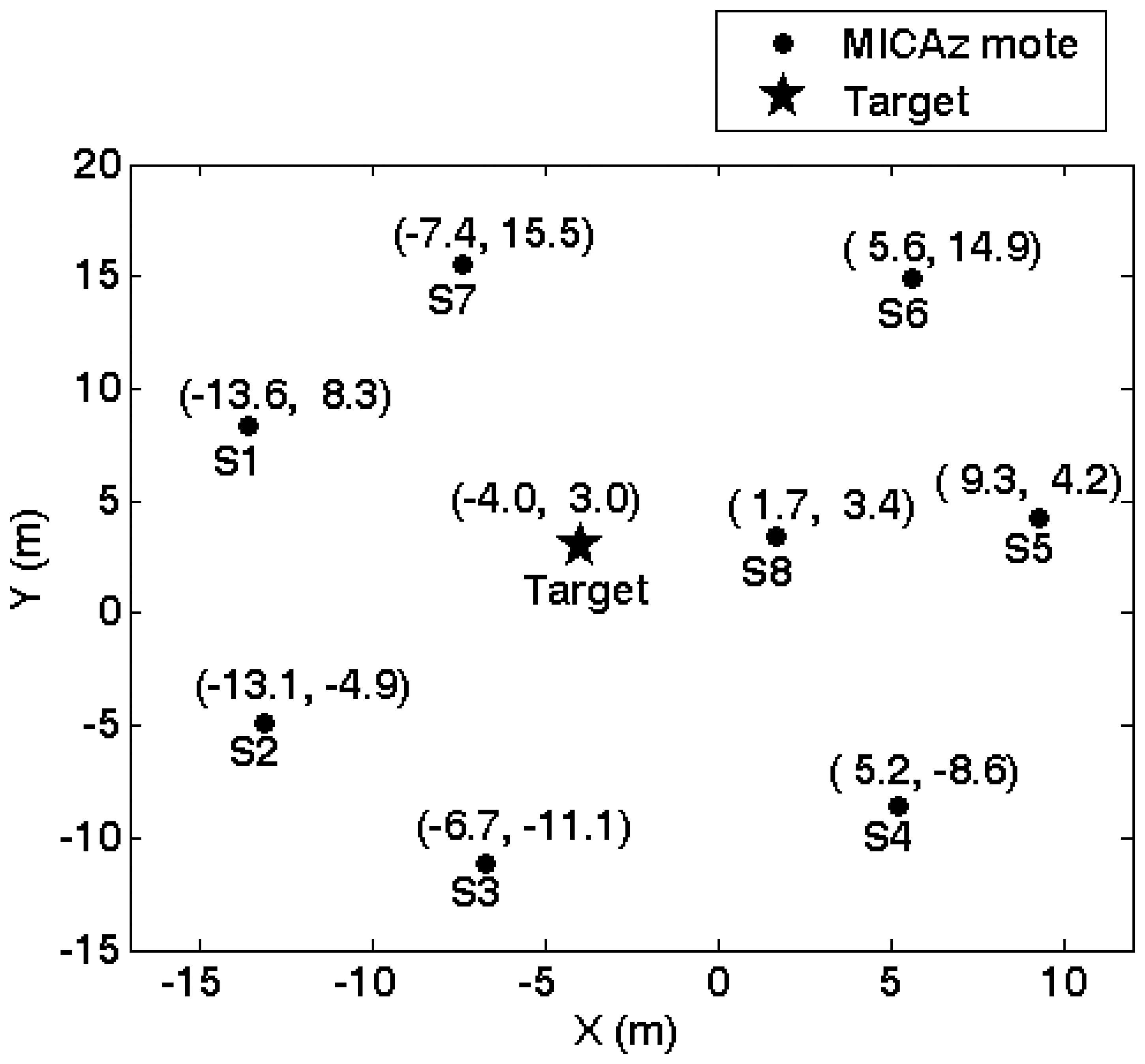
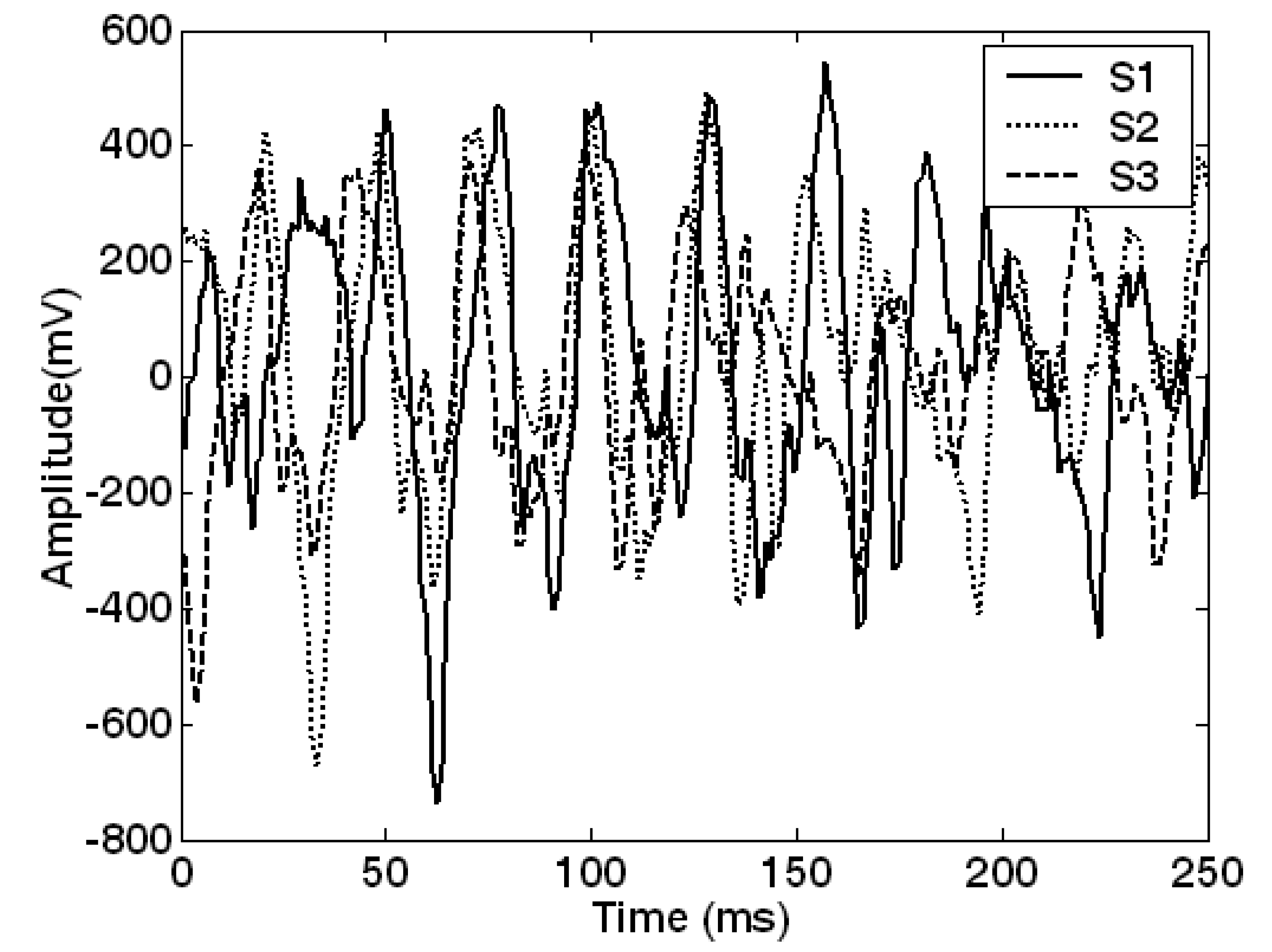
5. Experiments
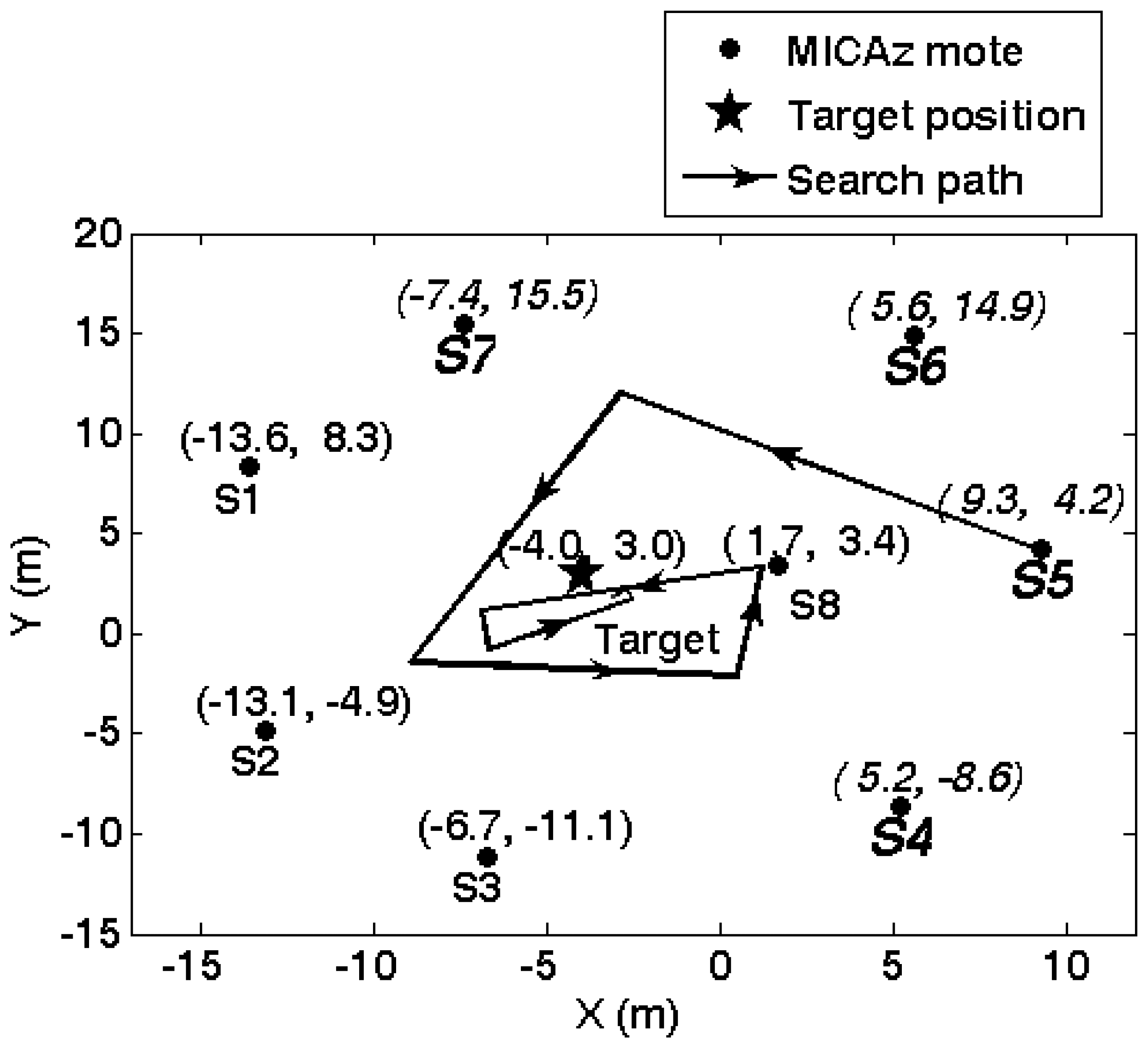
5.1. Experimental setup
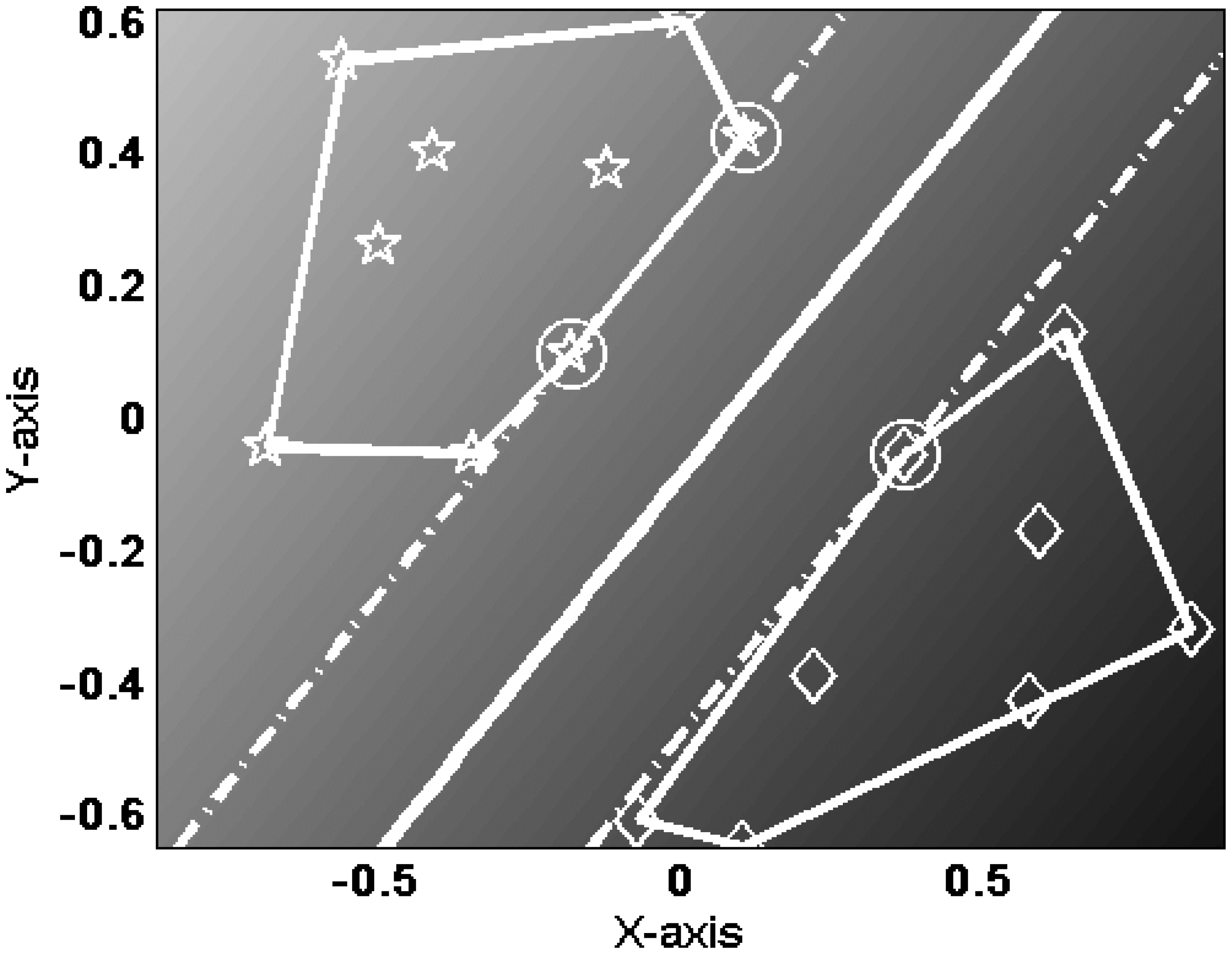
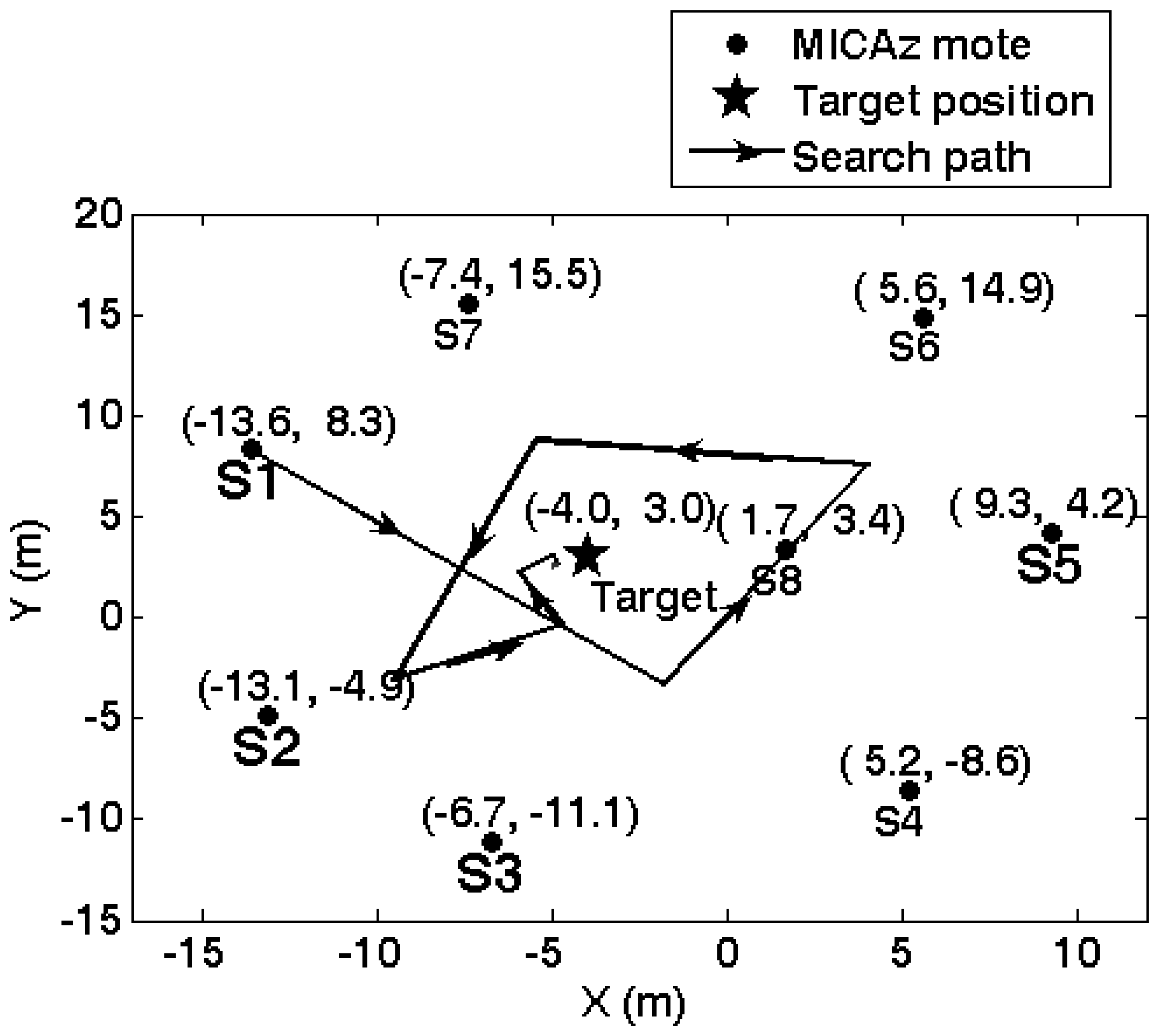
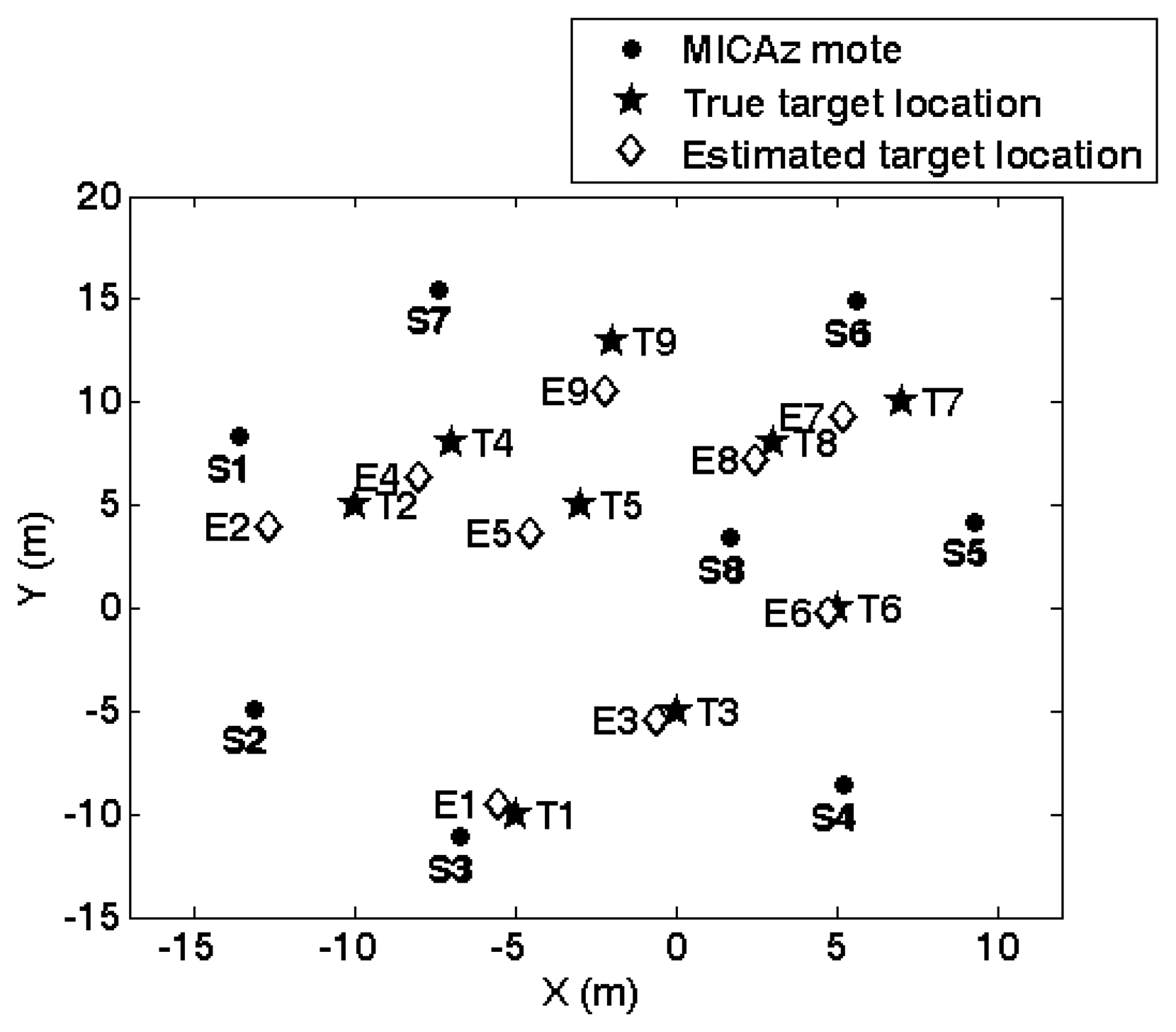
5.2. Agent collaborative vehicle localization experiments
5.3. Agent collaborative vehicle classification experiments
6. Conclusions
Acknowledgments
References and Notes
- Estrin, D.; Girod, L.; Pottie, G.; Srivastava, M. Instrumenting the world with wireless sensor network. Proc. ICASSP'2001 2001, 2675–2678. [Google Scholar]
- Estrin, D.; Culler, D.; Pister, K.; Sukhatme, G. Connecting the physical world with pervasive networks. IEEE Pervasive Computing 2002, 1(1), 59–69. [Google Scholar]
- Li, D.; Wong, K.D.; Hu, Y.H.; Sayeed, A.M. Detection, classification and tracking of targets. IEEE Signal Processing Magazine 2002, 19, 17–29. [Google Scholar]
- Li, D.; Hu, Y.H. Energy based collaborative source localization using acoustic micro-sensor array. EURASIP Journal on Applied Signal Processing 2003, 4, 321–337. [Google Scholar]
- Huang, Y.; Benesty, J.; Elko, G.W.; Mersereau, R.M. Real-time passive source localization: A practical linear-correction least-squares approach. IEEE Trans. Speech Audio Processing 2001, 9(8), 943–956. [Google Scholar]
- Lehmann, E.A.; Ward, D.B.; Williamson, R.C. Experimental comparison of particle filtering algorithms for acoustic source localization in a reverberant room. Proc. 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing; 2003; 5, pp. 375–380. [Google Scholar]
- Marco, F.D.; Yu, H.H. Vehicle classification in distributed sensor networks. Journal of Parallel and Distributed Computing 2004, 64, 826–838. [Google Scholar]
- Wang, X.; Wang, S. Collaborative signal processing for target tracking in distributed wireless sensor networks. Journal of Parallel and Distributed Computing 2007, 67(5), 501–515. [Google Scholar]
- Liu, J.; Reich, J.; Zhao, F. Collaborative in-network processing for target tracking. EURASIP Journal on Applied Signal Processing 2003, 4, 378–391. [Google Scholar]
- Xu, Y. Distributed computing paradigms for collaborative signal and information processing in sensor networks. Journal of Parallel and Distributed Computing 2004, 64(8), 945–959. [Google Scholar]
- Qi, H.; Wang, X.; Iyengar, S.S.; Chakrabarty, K. Multisensor data fusion in distributed sensor networks using mobile agents. Proceedings of International Conference on Information Fusion 2001, 11–16. [Google Scholar]
- Panait, L.; Luke, S. Cooperative multi-agent learning: the state of the art. Autonomous Agents and Multi-Agent Systems 2005, 11(3), 387–434. [Google Scholar]
- Shakshuki, E.; Ghenniwa, H.; Kamel, M. Agent-based system architecture for dynamic and open environments. Journal of Information Technology and Decision Making 2003, 2(1), 105–133. [Google Scholar]
- Hussain, S.; Shakshuki, E.; Matin, A.W. Agent-based system architecture for wireless sensor networks. 2006 Proc. 20th International Conference on Advanced Information Networking and Applications 2006, 2, 18–20. [Google Scholar]
- Wang, X.; Wang, S. An improved particle filter for target tracking in sensor system. Sensors 2007, 7(1), 144–156. [Google Scholar]
- Knapp, C.H.; Carter, G.C. The generalized correlation method of estimation of time delay. IEEE Trans. on Acoustics, Speech, and Signal Processing 1976, 24(4), 320–327. [Google Scholar]
- Vapnik, V. the Nature of Statistical Learning Theory; New York; Springer, 1998. [Google Scholar]
- Burges, C.J.C. A tutorial on support vector machines for pattern recognition. Data Mining and Knowledge Discovery 1998, 2, 21–167. [Google Scholar]
- Caragea, C.; Caragea, D.; Honavar, V. Learning support vector machine classifiers from distributed data sources. Proc. of the Twentieth National Conference on Artificial Intelligence; 2005; pp. 1602–1603. [Google Scholar]
- Syed, N.; Liu, H.; Sung, K. Incremental learning with support vector machines. Proc. of Workshop on Support Vector Machines at the International Joint Conference on Artificial Intelligence; 1999; pp. 272–276. [Google Scholar]
- Osuna, E.; Castro, O.D. Convex hull in feature space for support vector machines. Lecture Notes in Computer Science 2002, 2527/2002, 411–419. [Google Scholar]
- Rawlins, G.J.E.; Wood, D. Ortho-convexity and its generalizations. Computational Morphology 1988, 137–152. [Google Scholar]
- Moses, R.L.; Krishnamurthy, D.; Patterson, R. A self-localization method for wireless sensor networks. EURASIP Journal on Applied Signal Processing 2003, 4, 348–358. [Google Scholar]
- Polak, E. Optimization: Algorithms and Consistent Approximations.; Springer-Verlag, 1997. [Google Scholar]
- Averbuch, A.; Hulata, E.; Zheludev, V. Wavelet packet algorithm for classification and detection of moving vehicles. Multidimensional Systems and Signal Processing 2001, 12(1), 9–31. [Google Scholar]
- MICAz Datasheet; Crossbow Technology Inc.: San Jose, California, 2006.




| Observing Agents | Training# | Testing# | Accuracy | |||
|---|---|---|---|---|---|---|
| T | J | T | J | |||
| Acoustic | s1 | 40 | 38 | 42 | 36 | 92.31% |
| s3 | 41 | 37 | 41 | 37 | 89.74% | |
| s5 | 42 | 36 | 40 | 39 | 83.33% | |
| Seismic | s2 | 39 | 36 | 43 | 35 | 82.05% |
| s4 | 40 | 35 | 38 | 40 | 76.92% | |
| s6 | 38 | 37 | 39 | 39 | 78.21% | |
| Observing Agents | SV# | HV# | HSV# | ||||
|---|---|---|---|---|---|---|---|
| T | J | T | J | T | J | ||
| Acoustic | s1 | 29 | 13 | 26 | 22 | 36 | 26 |
| s3 | 35 | 9 | 30 | 26 | 38 | 26 | |
| s5 | 29 | 13 | 26 | 22 | 36 | 26 | |
| Seismic | s2 | 17 | 17 | 28 | 19 | 32 | 25 |
| s4 | 19 | 19 | 24 | 25 | 32 | 32 | |
| s6 | 18 | 18 | 24 | 24 | 32 | 30 | |
| Learning Algorithm | Training# | Testing# | SV# | Accuracy | |
|---|---|---|---|---|---|
| Acoustic | SV only | 126 | 234 | 41 | 88.46% |
| HV and SV | 188 | 234 | 35 | 93.59% | |
| Centralized | 156 | 312 | 64 | 95.19% | |
| Seismic | SV only | 108 | 234 | 108 | 74.79% |
| HV and SV | 183 | 234 | 93 | 83.33% | |
| Centralized | 156 | 312 | 64 | 84.29% | |
| Modality | Modality Weight | Agent | Homogeneous Fusion | Hetero- geneous Decision | ||
|---|---|---|---|---|---|---|
| Decision | Weight | Fusion | ||||
| Acoustic | 0.529 | s1 | 1.6405 | 0.2459 | 1.1692 | 1.0638 |
| s3 | 2.2360 | 0.5344 | ||||
| s5 | -1.9544 | 0.2196 | ||||
| Seismic | 0.471 | s2 | 0.9673 | 0.4894 | 0.9455 | |
| s4 | 1.8766 | 0.3373 | ||||
| s6 | -0.9279 | 0.1733 | ||||
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Wang, X.; Bi, D.-w.; Ding, L.; Wang, S. Agent Collaborative Target Localization and Classification in Wireless Sensor Networks. Sensors 2007, 7, 1359-1386. https://doi.org/10.3390/s7081359
Wang X, Bi D-w, Ding L, Wang S. Agent Collaborative Target Localization and Classification in Wireless Sensor Networks. Sensors. 2007; 7(8):1359-1386. https://doi.org/10.3390/s7081359
Chicago/Turabian StyleWang, Xue, Dao-wei Bi, Liang Ding, and Sheng Wang. 2007. "Agent Collaborative Target Localization and Classification in Wireless Sensor Networks" Sensors 7, no. 8: 1359-1386. https://doi.org/10.3390/s7081359
APA StyleWang, X., Bi, D.-w., Ding, L., & Wang, S. (2007). Agent Collaborative Target Localization and Classification in Wireless Sensor Networks. Sensors, 7(8), 1359-1386. https://doi.org/10.3390/s7081359





