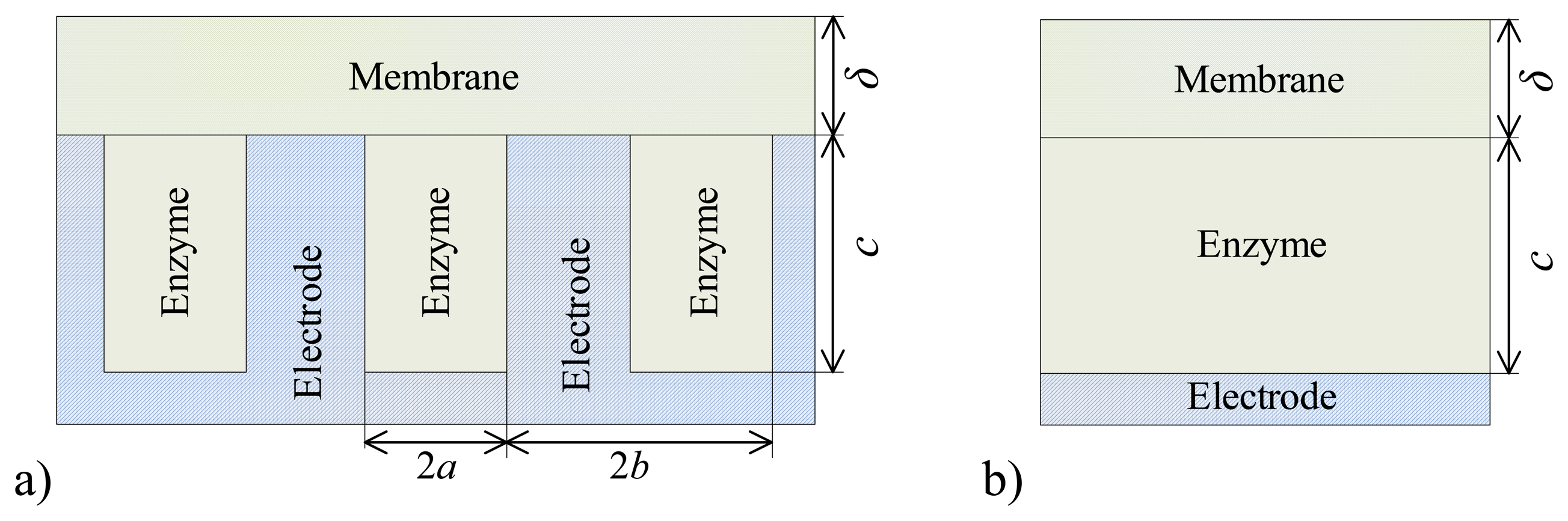
5.1. The Effect of the Outer Membrane on the Biosensor Response
To investigate the effect of the thickness
δ of the outer membrane on the biosensor response we calculate the steady state current changing the thickness
δ at different values of the maximal enzymatic rate
Vmax and substrate concentration
S0. The steady state biosensor current is very sensitive to changes of
Vmax and
S0 [
2,
3,
17]. Changing values of these two parameters, the steady state current varies even in orders of magnitude. To evaluate the effect of the membrane thickness on the biosensor response we normalize the biosensor current. Let
If(
δ) and
Ig(
δ) be the steady state currents of the flat and the plate–gap biosensors, respectively, both having the outer membrane of the thickness
δ. Thus,
If(0) and
Ig(0) correspond to the steady state currents of the biosensors having no outer membrane, i.e.
δ =
d –
c = 0. We express the normalized steady state biosensor currents
Iδf and
Iδg as the steady state currents of the biosensors, having outer membrane divided by the steady state currents of the corresponding biosensors having no outer membrane,
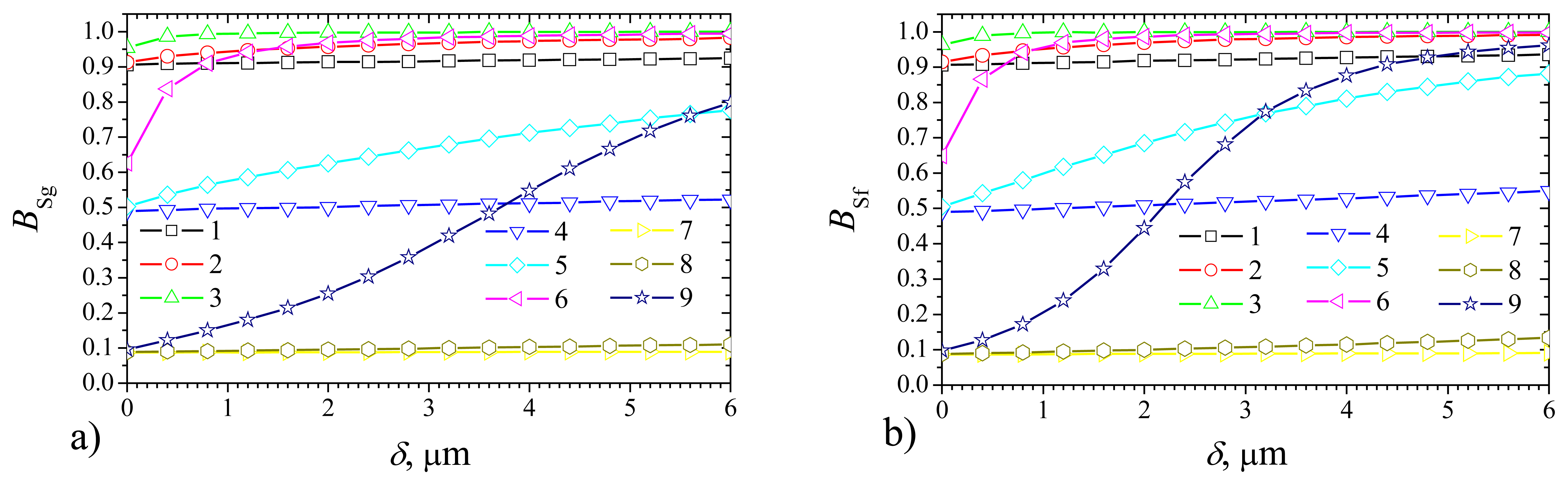
Fig. 3 shows the dependence of the steady state biosensor current on the thickness
δ of outer membrane in the cases of the plate–gap (
Fig. 3a) biosensor and the flat one (
Fig. 3b) at the membrane diffusivity
Dm = 0.1μm
2/s = 0.1
De and the following values of the domain geometry:
b = 2
a = 4μm,
c = 4μm,
d =
c +
δ. In the case of the plate–gap biosensor the geometry parameter
c stands for the depth of the gaps while in the case of the flat biosensor it stands for the thickness of the enzyme layer. Of course,
a and
b are vacuous for the flat biosensors.
Fig. 4 shows the effect of the membrane thickness
δ on the biosensor sensitivity at the same values of the parameters as in
Fig. 3.
One can see in
Fig. 3, that the shape of the normalized steady state currents
Iδg and
Iδf (as well as of the non–normalized ones
Ig and
If) is very sensitive to changes of the maximal enzymatic rate
Vmax and substrate concentration
S0.
Iδg and
Iδf are monotonous decreasing functions of the outer membrane thickness
δ at a high value of
Vmax (10 mM/s) and relatively low values of
S0 (0.1 and 1 mM) (curves 3 and 6).
Iδg and
Iδf are monotonous increasing functions of
δ at low enough values of
Vmax (0.1 and 1.0 mM/s) and a high value of
S0 (10 mM) (curves 7 and 8).
Very similar behavior of the biosensor response was observed when modeling one–layer biosensors acting in a non–stirred analyte [
24]. Then the steady state biosensor current was found to be a monotonous decreasing function of the thickness of the external diffusion layer if the biosensor response is distinctly under diffusion control (
σ2 > 1). In the cases when the enzyme kinetics controls the biosensor response (
σ2 < 1), the steady state current increases with increase of the thickness of the diffusion layer. Thus the steady state current varied up to several times. When
σ2 ≈ 1, the variation of the steady state current is rather small. Let us notice that in the cases presented in
Fig. 3,
σ2 = 0.16 at
Vmax = 0.1 mM/s and
σ2 = 1.6 at
Vmax = 10 mM/s.
When comparing simulation results of biosensors of different types, we can see in
Fig. 3 that the response of the flat biosensor may increase by a factor of about 1.9 times when changing
δ, while the corresponding factor for the plate–gap biosensor equals only about 1.15. Consequently, at low maximal enzymatic rates and high substrate concentrations (
S0 >
KM) the response of the plate–gap biosensor is more stable to changes of the thickness
δ of the outer membrane than the response of the flat one.
As one can see in
Fig. 4, the effect of the thickness
δ of the outer membrane on the sensitivity of the plate–gap biosensor is very similar to that of the flat one.
Fig. 4 shows well known feature of biosensors, that the biosensor sensitivity is higher at lower substrate concentrations rather than at higher ones. However, in the cases of high enough enzymatic activity, the sensitivity can be notably increased by increasing the thickness
δ of the outer membrane even at high substrate concentrations (curves 5, 6, 9 in
Fig. 4). Thus, the advantage of the outer membranes to prolong the region of the application of the biosensor is applicable also to gap–plate biosensors not only to flat ones [
10–
12].
On the other hand, at high values of
Vmax and
S0 (curve 9), the sensitivity of the plate–gap biosensor (
Fig. 4a) is slightly more stable than of the flat one (
Fig. 4b) to changes in the thickness
δ. This feature increases the reliability of a bioanalytical system which is one of the most important parameters of biosensors. This feature is very important in the biosensors implanted into systems with unstable pressure (body blood system, or reactor with peristaltic pumping of the probe). Fluctuations of the outer membrane of the biosensor induced by fluctuations of the pressure can influence distance of the diffusion way, thereby influence response of the biosensor.
The main physical reason of the superior behavior of the plate–gap biosensors vs. the flat ones is that the product of the enzymatic reaction is better (more completely) converted into the biosensor current. The product, which is electro–active substance, is better captured, i.e. it has less time to diffuse away before it is electro–oxidized or – reduced, in the plate–gap model rather than in flat one.
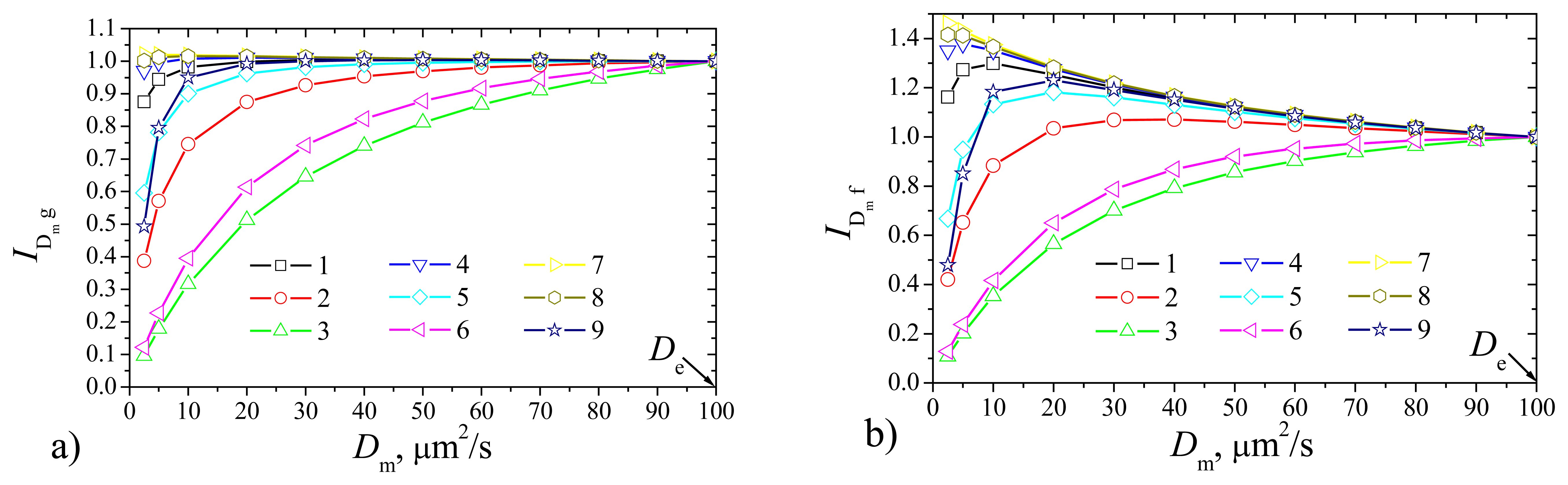
To investigate the dependence of the biosensor response on the diffusivity
Dm =
DSm =
DPm of the outer membrane the biosensor responses were calculated at constant thickness
δ = 2 μm of the outer membrane changing the diffusion coefficient
Dm from 1 to 0.025 μm
2/s, i.e. from
De to 1/50
De. In this case the current was normalized with respect to the maximal value
De of the diffusivity the outer membrane to be analyzed,
where
If(
Dm) and
Ig(
Dm) are the steady state currents calculated at the diffusivity
Dm the outer membrane for the flat and plate–gap biosensors, respectively. Results of the calculations are depicted in
Fig. 5, where one can see, that the effect of the diffusivity
Dm notably depends on the maximal enzymatic rate
Vmax and substrate concentration
S0. Although the shapes of curves in
Fig. 5 notable differ from those in
Fig. 3, the effect of the diffusivity
Dm of the membrane is very similar to that of the membrane thickness
δ. A decrease in diffusivity influences the steady state current similarly to the increase in thickness of the membrane. The plate–gap biosensor is notably less sensitive to changes of the permeability of the outer membrane than the corresponding flat biosensor. However, this peculiarity is valid only in the cases when the biosensor operates at low maximal enzymatic rates and high substrate concentrations (
S0 >
KM) conditions.
The similarity between the effects of the outer membrane thickness
δ on the biosensor response and that of the diffusivity
Dm is also notable when comparing
Figs. 4 and
6. Particularly, in the cases of high enough enzymatic activity and high substrate concentrations the sensitivity can be significantly increased by decreasing the diffusivity
Dm of the outer membrane (curves 5, 6, 9 in
Fig. 6).
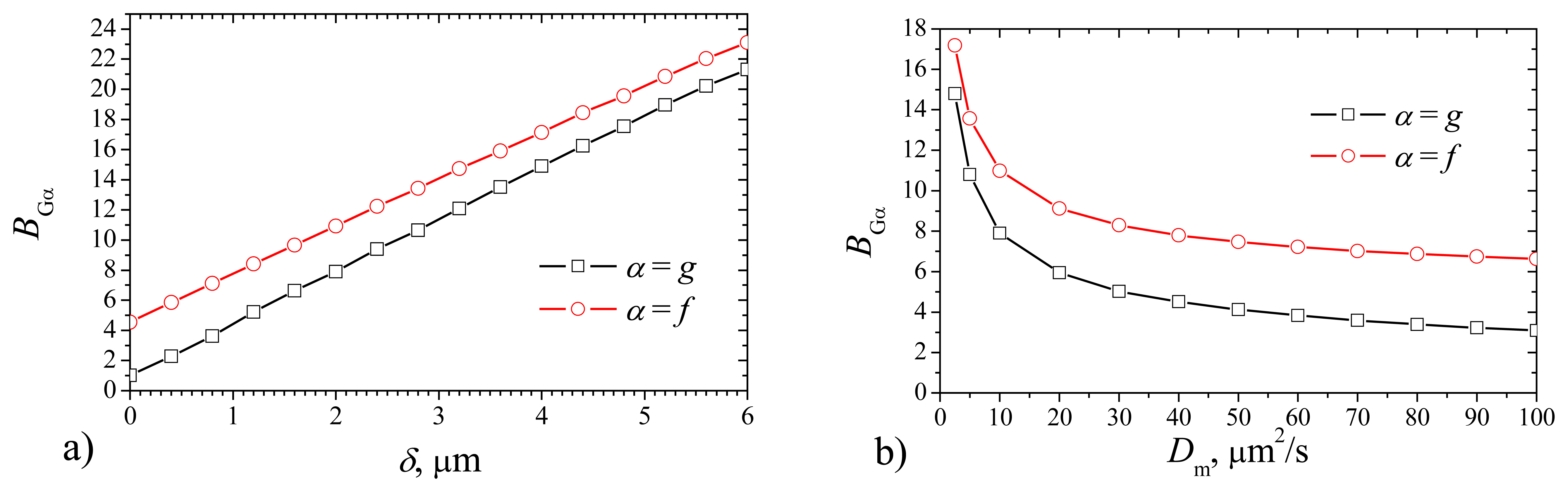
When calculating the maximal gradients
BGg and
BGf of the biosensor responses, no notable difference was found changing the substrate concentration
S0 and maximal enzymatic rate
Vmax. Changing
S0 and
Vmax in several orders of magnitude, values of the gradients
BGg and
BGf varied less than 1%. However, the effect of the thickness
δ as well as of the diffusivity
Dm of the outer membrane on the biosensor response was substantial. As one can see in
Fig. 7, the maximal gradient increases with increase of the thickness
δ as well as with decrease of the diffusivity
Dm. However, the shape of curves differs. The maximal gradient is practically linear function of
δ, while it is highly non linear monotonously decreasing function of
Dm. The maximal gradient method of evaluation of biosensor response usually is used in bioanalytical instruments, when the time of the measurement cycle is necessary to reduce, thereby, to increase the speed of the analysis. Another feature – after the biosensor response passes maximal gradient, probe can be removed or replaced by buffer, and thereby the biosensor operates at lower concentrations of the substrate inside of the membrane and products as well. In some cases it is important for the stability of the biosensor, because the product of the enzymatic reaction can be chemically active and destroy the membrane (for example, a number of biosensors, containing oxidases and producing hydrogen peroxide;. This positive feature compensates the worse stability of biosensor concerning the sensitivity to the fluctuations of the membrane thickness.
Fig. 7 shows that the absolute difference between the gradients of different biosensors varies slightly, 1.8 <
BGf –
BGg < 3.6. The maximal gradient of the response of plate–gap biosensor is lower than that of the corresponding flat one. Additional numerical experiments at other values of the parameters approved this feature. This can be explained by difference in the geometry of the electrodes. When the enzyme reaction starts, the gradient of the current gains the maximum immediately after some product touches the electrode surface, i.e. at the very beginning of the biosensor operation. The delay time depends mainly on the rate of the diffusion through the enzyme. In the case of the flat biosensor the touch occurs in one time at entire surface of the electrode, while in the case of the plate–gap biosensor, the current arises very gradually: firstly on the sides of gaps (from outside to inside the biosensor) and only then on the bottom of gaps. The current gradient is greater when the current arises like avalanche, i.e. in the case of the flat biosensor.
5.2. The Effect of the Geometry of Gaps on the Biosensor Response
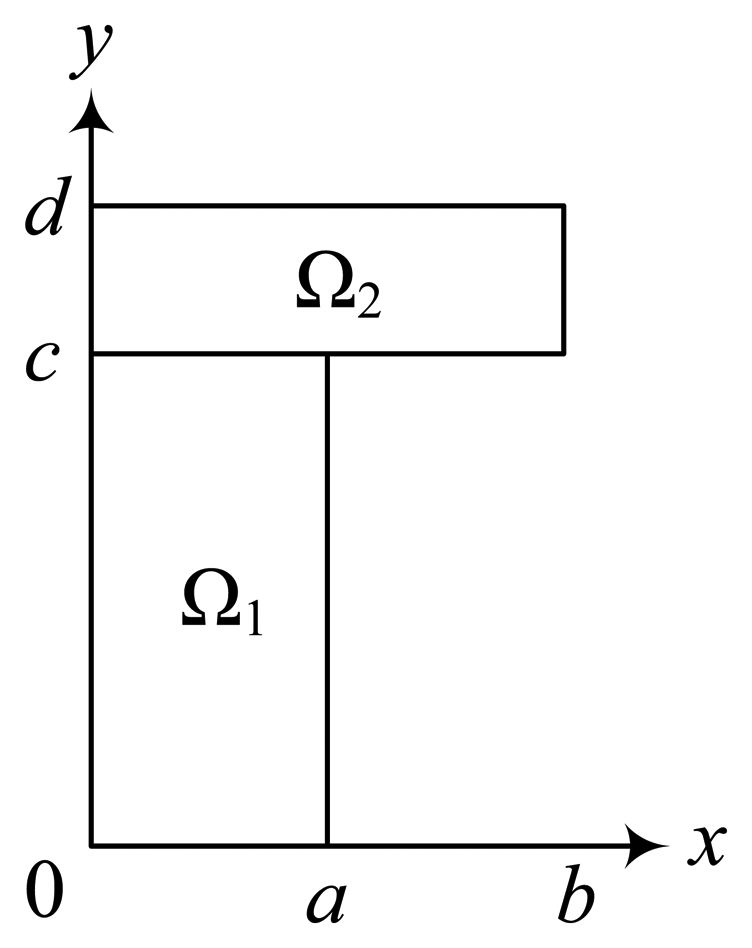
For the plate–gap biosensors the model parameter
c (
Fig. 1a) stands for the depth of the gaps in the electrode. In the case of the corresponding flat biosensors (
Fig. 1b)
c is the thickness of the enzyme layer.
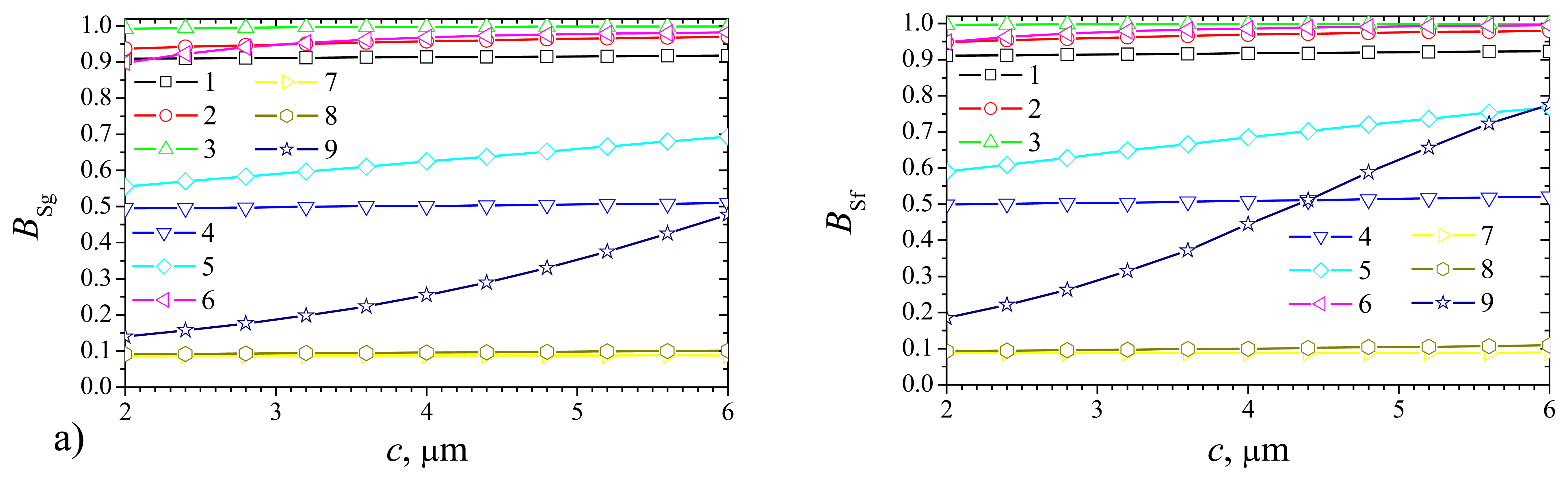
Fig. 8 shows the dependence of the steady state biosensor current on the parameter
c, while
Fig. 9 shows the dependence of the biosensor sensitivity on that parameter. The biosensors responses were calculated at constant thickness
δ = 2μm and constant diffusivity
Dm = 0.1μm
2/s of the outer membrane changing
c from 2 to 6 μm. In this case the steady state currents were normalized with respect to the minimal value
c0 of
c to be analyzed,
where
If(
c) and
Ig(
c) are the steady state currents calculated at a value
c,
c0 = 2 μm.
As it is possible to notice in
Fig. 8, the effect of the depth of the gaps on the steady state current (
Fig. 8a) is very similar to that of the thickness of the enzyme layer (
Fig. 8b). The steady state current of the plate–gap biosensor as well as of the flat one are monotonous increasing functions of
c. However,
Icg and
Icf are practically constant functions of
c at high maximal enzymatic rate
Vmax (10 mM/s) and relatively low values of
S0 (0.1 and 1 mM) (curves 3 and 6).
Let us notice, that these properties are valid at values of
c specific to the plate–gap biosensors, i.e. when the depth of gaps is of a few micrometers. At wide range of
c it may not be true, e.g. in the case of biosensors with a mono–enzyme layer, the steady state current is a non–monotonous function of the thickness of the enzyme layer [
17].
Fig. 9 shows that the effect of the gap depth on the sensitivity of the plate–gap biosensor is very similar to that of the thickness of the enzyme layer of the flat biosensor. However, it is possible to notice, that the sensitivity of the plate–gap biosensor (
Fig. 9a) is slightly more stable than of the flat one (
Fig. 9b) to changes in
c only at very high values of
Vmax and
S0 (curve 9).
To investigate the dependence of the biosensor response on the width of the gaps we calculated the biosensor response at a constant distance 2(
b–
a) between two adjacent gaps changing the half width
a from to 0.5μm to 5 μm. As it was mentioned above, increasing the half width
a of the gaps the current density of the plate–gap biosensor approaches the current density of the corresponding flat one, i.e.
Ig →
If when
a → ∞. Because of this the steady state currents of the plate–gap biosensor were normalized with the steady state current of the corresponding flat biosensor,
where
Ig(
a) is the steady state current calculated assuming the width
a of the gaps, and
If is the steady state current of the corresponding flat biosensor.
Fig. 10a shows the dependence of the steady state current of the plat–gap biosensor on the width
a of the gaps at different values of
Vmax and
S0. As one can see in
Fig 10a, the
Iag(
a) approaches to unit rather quickly. At
a = 1.5
b = 3μm the relative difference between
Ig(
a) and
If does not exceed 20% (
Iag≥0.8). At very high maximal enzymatic rate
Vmax (10 mM/s) and low values of the concentration
S0 (0.1 and 1 mM) (curves 3 and 6)
Ig(
a) approaches
If notable faster than at other values of
Vmax and
S0.
An increase in the width as well as in the depth of the gaps increases the volume of the enzyme used in plate–gap biosensors. Summarizing the results presented in
Figs. 8,
9 and
10a, we can notice, that the biosensors of two considered types: plate–gap and flat, both with the outer membrane, are more resistant to changes in volume of the enzyme at lower values of
Vmax rather than at higher ones and at higher values of
S0 rather than at lower ones.
Fig. 10b shows the dependence of the sensitivity
BSg of the plate–gap biosensor on the width of the gaps. As it is possible to notice in
Fig. 10b the sensitivity
BSg is practically constant function of the width
a of the gaps when
a varies from 0.5 to 5μm.
Fig. 10b shows also an important influence of the substrate concentration
S0 upon the biosensor sensitivity
BSg. At all the values of
a the lower concentration
S0 corresponds to the higher sensitivity
BSg. This feature of the biosensor is very well known [
1–
3,
17]. The effect of the maximal enzymatic rate
Vmax on the biosensor sensitivity is more or less notable only in the cases when the substrate concentration
S0 varies about the Michaelis constant
KM, i.e. when the enzyme kinetics changes from zero order to the first order across the enzyme region,
S0 ≈
KM.
5.3. The Dependence of the Biosensor Response on the Substrate Concentration
To investigate the dependence of the biosensor response on the substrate concentration the response was simulated at wide range of the concentrations
S0.
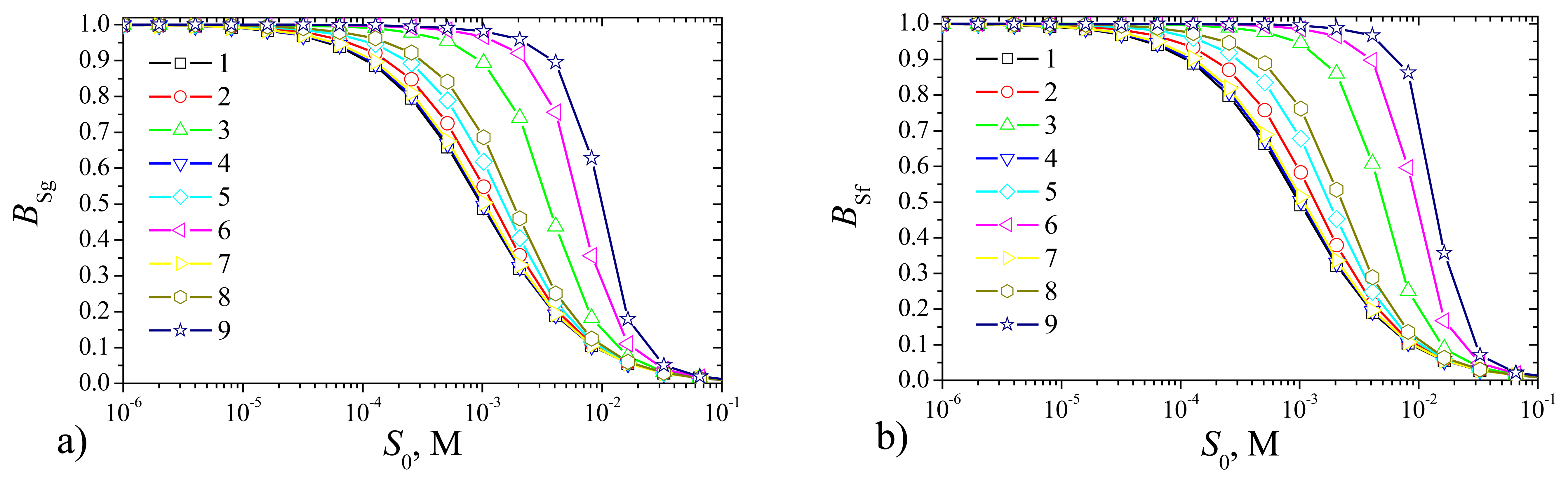
Fig. 11 shows the steady state currents,
Fig. 12 shows the sensitivities, and
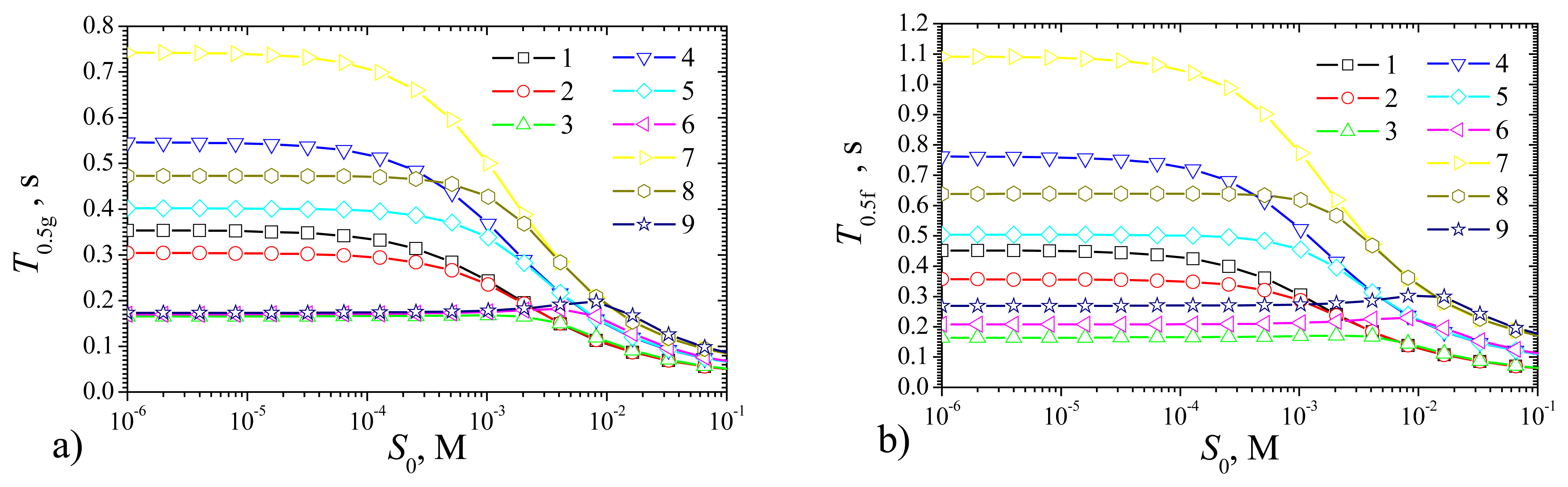
Fig. 13 shows the half times of the steady state for both types of biosensors: the plate–gap and the flat.
As one can see in
Fig. 11 the density
Ig of the steady state current of the plate–gap biosensor is slightly less than that of the flat one. However, when comparing the simulation results of the biosensors of different types one can see very similar shape of all curves. Very similar shapes of all curves we can see also in
Fig. 12 presenting the sensitivity of the biosensors at the same values of the parameters as in
Fig. 11. Thus, the recognition capability of the novel plat–gap biosensors is very similar to the corresponding flat biosensors both with the outer membranes.
As it is possible to notice in
Fig. 13,
T0.5g and
T0.5f are monotonous decreasing functions of
S0 at the maximal enzymatic rate
Vmax of 10 as well as of 100 mM/s. At
S0 being between 0.1 and 10 mM (between
KM and 100
KM) shoulders on the curves appears for
Vmax = 1 mM/s. It seems possible that the shoulders on the curves arise because of high maximal enzymatic rate
Vmax at the substrate concentrations at which the kinetics changes from zero order to first order across the enzyme region. At substrate concentration
S0 ≫
KM the reaction kinetics for
S is zero order throughout the enzyme region whereas for
S0 ≪
KM the kinetics is first order throughout. At intermediate values of
S0 the kinetics changes from zero order to first order across the membrane. Similar effect of the substrate concentration on the response time was noticed in the cases of an amperometric biosensor based on an array of enzyme microreactors [
21] and of the oxidation of β-nicotinamide adenine dinucleotide (NADH) at poly(aniline;-coated electrodes [
30].
Fig. 13 shows that at high substrate concentration
S0 = 100 mM (
S0 = 100
KM), the catalytic reaction makes no notable effect on the biosensors response time.