Characterizing Clutter in the Context of Detecting Weak Gaseous Plumes in Hyperspectral Imagery
Abstract
:1. Introduction
2. Background
3. Data Models and Associated GLS-based Plume Detection Methods
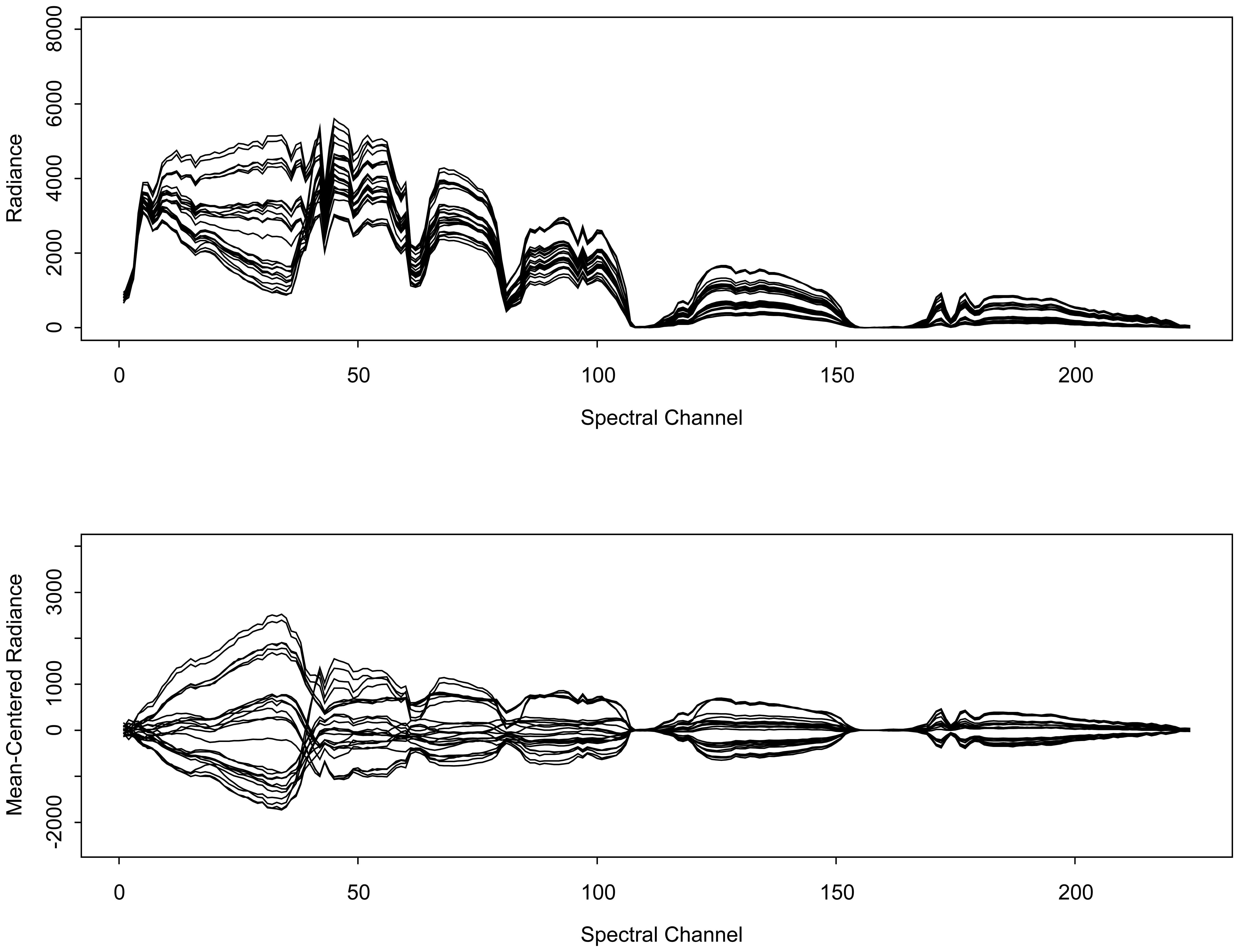
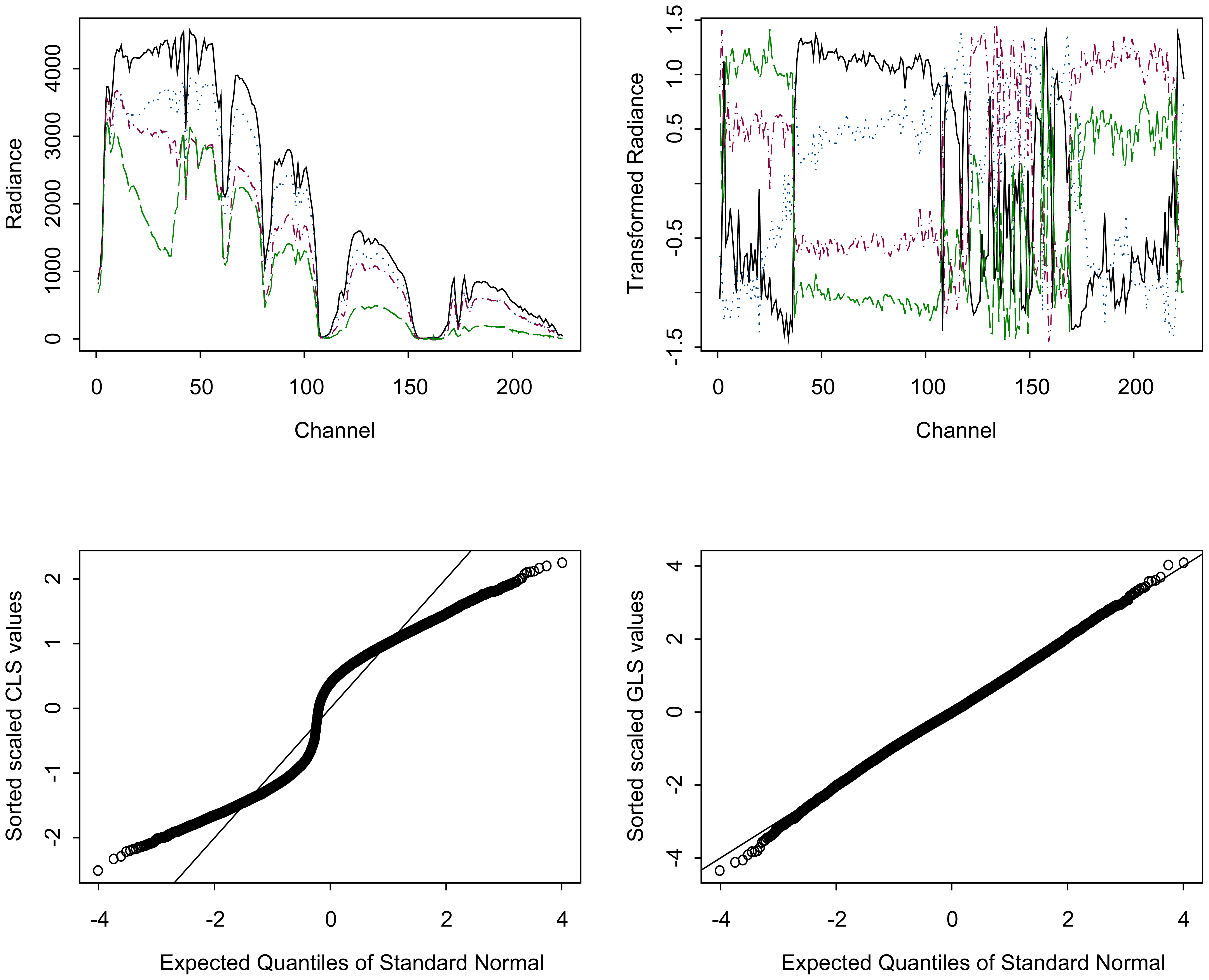
3.1. AVIRIS signals
3.2. GLS
3.3. BMA
4. Evaluation of the multivariate Gaussian assumption
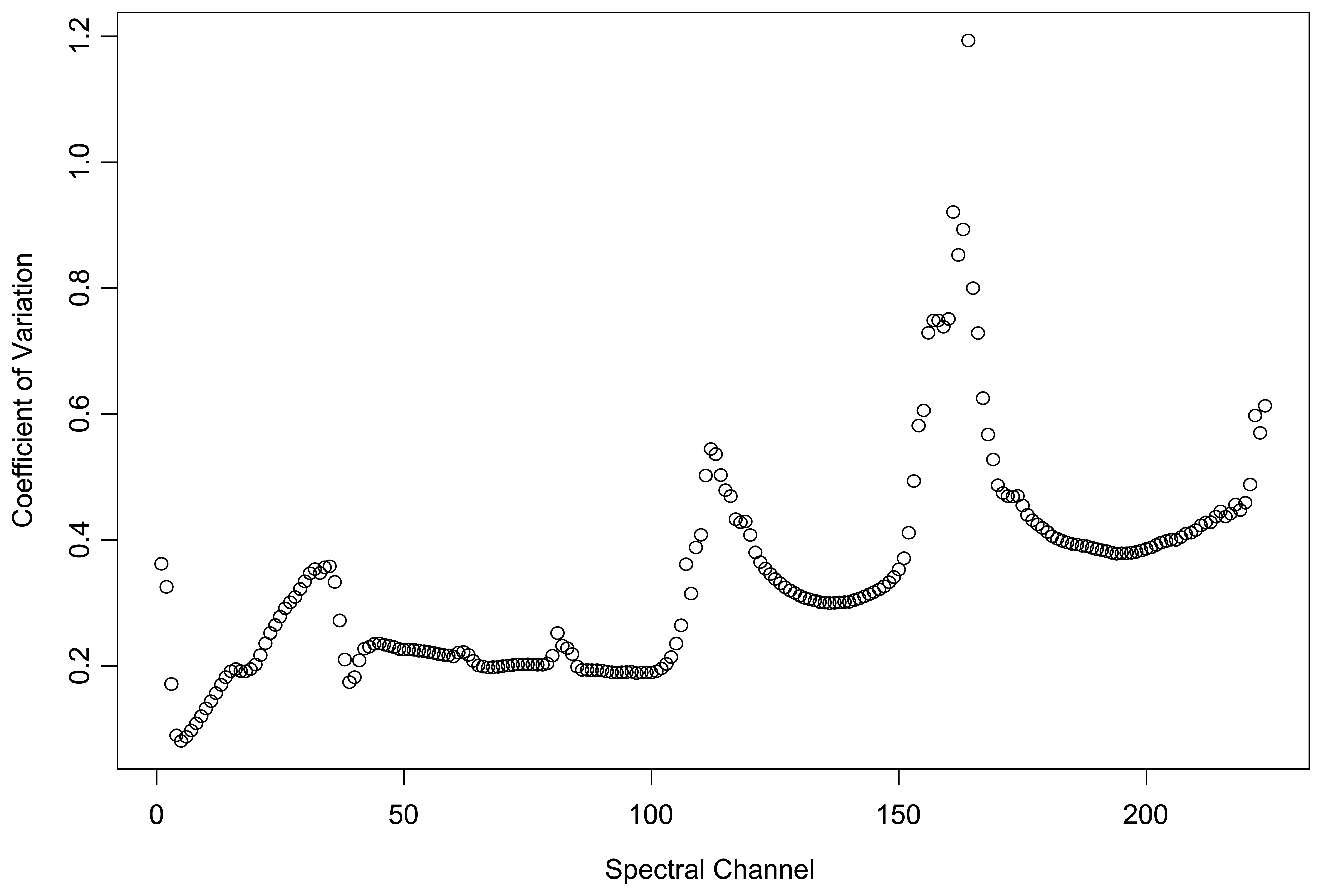
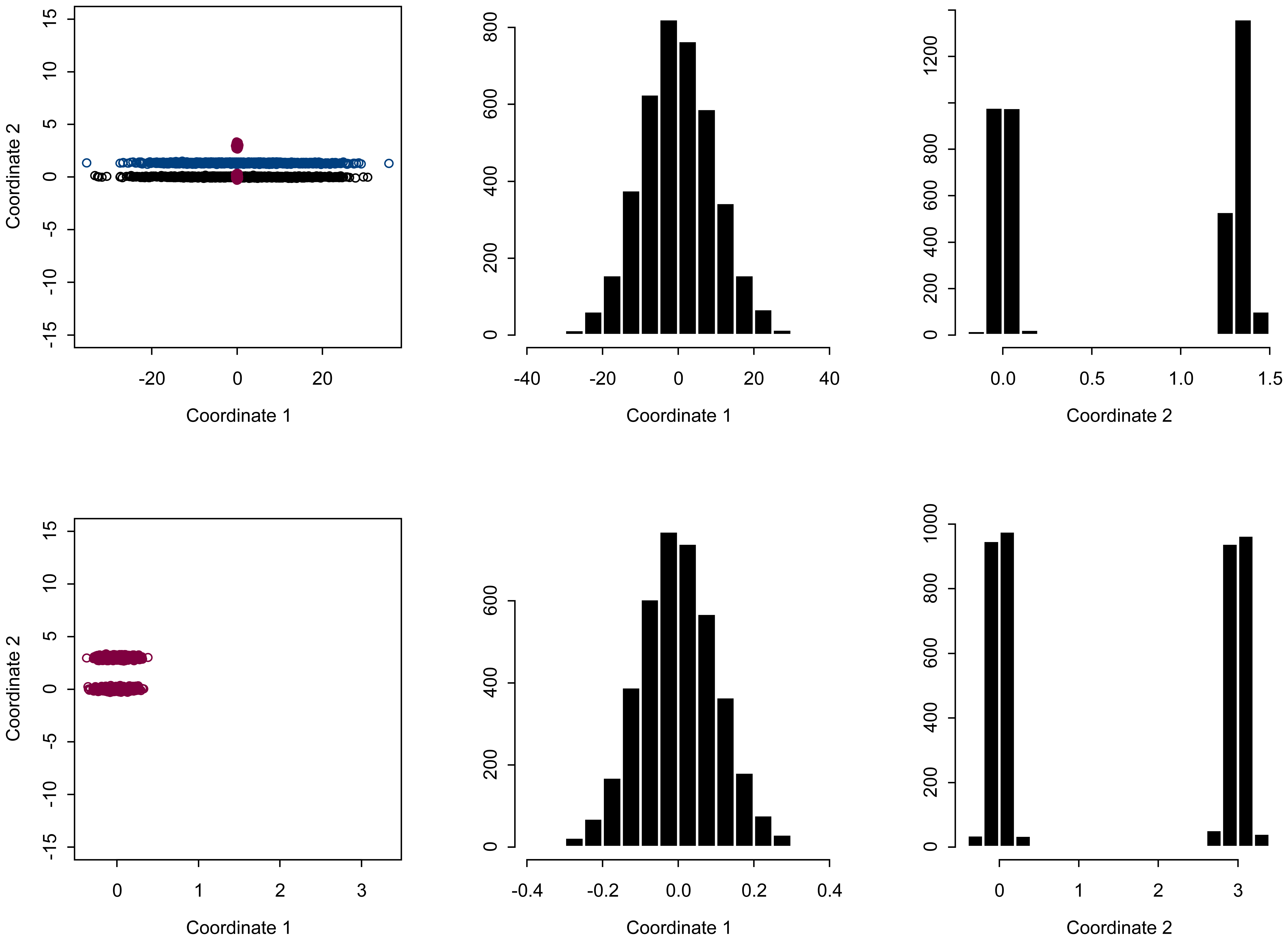
4.1. Kurtosis and Skewness
4.2. Mixtures of Scalar-valued Gaussian Variables
4.3. Simulated scenes to compare to SCMG scenes
4.4. Scalar-valued β̂ for each pixel
4.4.1 Searching for a plume containing one particular chemical
4.4.2 Searching for a plume containing one chemical from a library of L chemicals
4.5. Vector-valued β̂ for each pixel
4.6. BMA-based estimates of the probability that a given chemical from the library is present
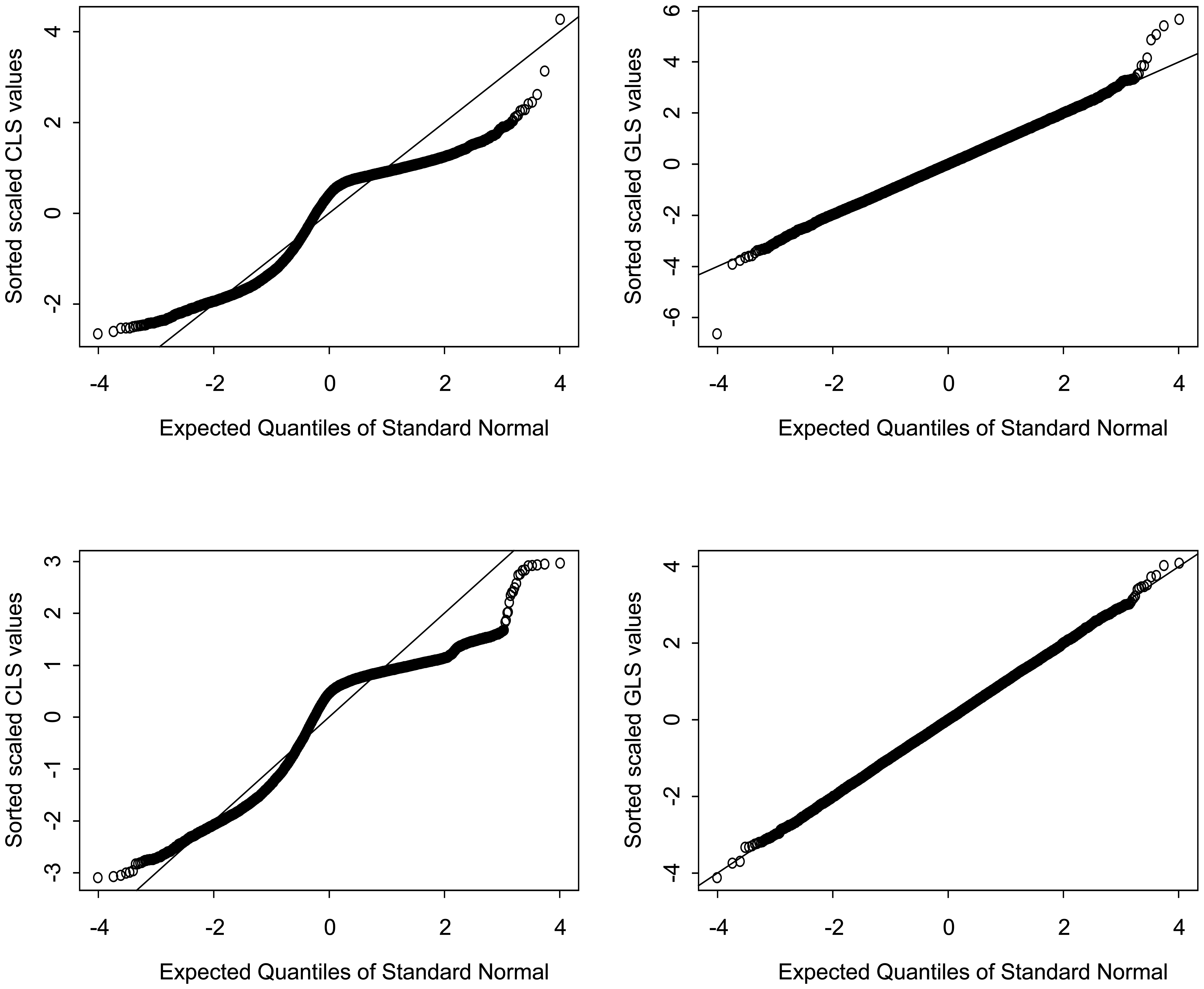
5. Exploring why the GLS values are closer than CLS values to Gaussian
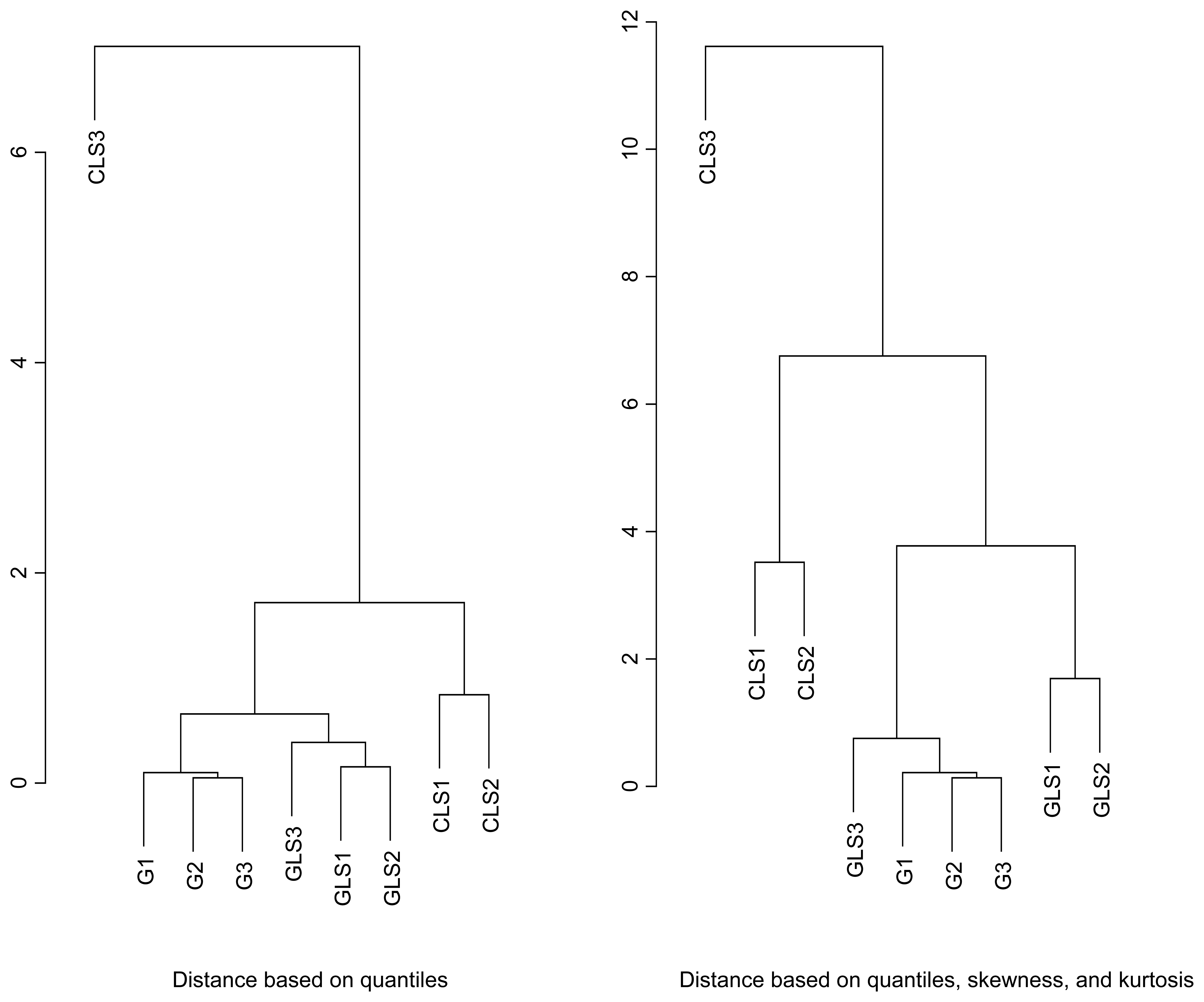
6. Scene-specific reference distribution
7. Summary
Acknowledgments
References and Notes
- AVIRIS Free Standard Data Products, Jet Propulsion Laboratory (JPL), National Aeronautics and Space Administration (NASA). http://aviris.jpl.nasa.gov/html/aviris.freedata.html.
- Vane, G.; Green, R.; Chrien, T.; Enmark, H.; Hansen, E.; Porter, W. The Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote Sensing of the Environment 1993, 44, 127–143. [Google Scholar]
- Theiler, J.; Foy, B.; Fraser, A. Characterizing non-Gaussian Clutter and Detecting Weak Gaseous Plumes in Hyperspectral Imagery. Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI; In Proc. SPIE; 2005; Volume 5806, pp. 182–193. [Google Scholar]
- McVey, B.; Burr, T.; Fry, H. Distribution of Chemical False Positives for Hyperspectral Image Data; Los Alamos National Laboratory Restricted Release; Technical Report LA-CP-02-521; 2003. [Google Scholar]
- Bernhardt, M.; Heather, J.; Smith, M. New Models for Hyperspectral Anomaly Detection and Un-Mixing. Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XII; Shen, Sylvia S., Lewis, Paul E., Eds.; In Proc. SPIE.; 2005; Volume 5806, pp. 720–730. [Google Scholar]
- Villeneuve, P.; Fry, H.; Theiler, J.; Smith, B.; Stocker, A. Improved Matched-Filter Detection Techniques. Proc. SPIE. 1999, 3753, 278–285. [Google Scholar]
- Manolakis, D.; Marden, D.; Kerekes, J.; Shaw, G. On the Statistics of Hyperspectral Imaging Data. Proc. SPIE. 2001, 4381, 308–316. [Google Scholar]
- Harsanyi, J.; Chang, C. Hyperspectral Image Classification and Dimensionality Reduction: an Orthogonal Subspace Projection Approach. IEEE Trans. Geoscience and Remote Sensing 1994, 32, 779–785. [Google Scholar]
- Marden, D.; Manolakis, D. Modeling Hyperspectral Imaging Data. Proc. SPIE. 2003, 5093, 253–262. [Google Scholar]
- Marden, D.; Manolakis, D. Using Elliptically Contoured Distributions to Model Hyperspectral Imaging Data and Generate Statistically Similar Synthetic Data. Proc. SPIE. 2004, 5425, 558–572. [Google Scholar]
- Funk, C.; Theiler, J.; Roberts, D.; Borel, C. Clustering to Improve Matched Filter Detection of Weak Gas Plumes in Hyperspectral Thermal Imagery. IEEE Trans. Geoscience and Remote Sensing 2001, 39, 1410–1420. [Google Scholar]
- Manolakis, D.; Siracusa, C.; Marden, D.; Shaw, G. Hyperspectral Adaptive Matched Filter Detectors: Practical Performance Comparison. Proc. SPIE. 2001, 4381, 18–33. [Google Scholar]
- Manolakis, D.; Shaw, G. Detection Algorithms for Hyperspectral Imaging Applications. IEEE Signal Processing Magazine 2002, 19(1), 29–43. [Google Scholar]
- Bajorski, P. Analytical Comparison of the Matched Filter and Orthogonal Subspace Projection Detectors in Structured Models for Hyperspectral Images. Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XII; Shen, Sylvia S., Lewis, Paul E., Eds.; In Proc. SPIE.; 2006; Volume 6233, pp. 1–12. [Google Scholar]
- Gallagher, N.; Sheen, D.; Shaver, J.; Wise, B.; Shultz, J. Estimation of Trace Vapor Concentration-Pathlength in Plumes for Remote Sensing Applications From Hyperspectral Images. Proc. SPIE. 2003, 5093, 184–194. [Google Scholar]
- Foy, B.; Theiler, J.; Fraser, A. Unreasonable Effectiveness of the Adaptive Matched Filter, to appear. 2006. private communication. [Google Scholar]
- Young, S.; Johnson, B.; Hackwell, J. An In-scene Method for Atmospheric Compensation of Thermal Hyperspectral Data. J. Geophys. Res. Atm. 2002, 107, 4774–4774. [Google Scholar]
- FASCODE for atmospheric transmission calculations. see http://www.vs.afrl.af.mil/ProductLines/IR-Clutter/fascode.aspx.
- Foy, B.; Petrin, R.; Quick, R.; Shimada, T.; Tiee, J. Comparisons Between Hyperspectral Passive and Multispectral Active Sensor Measurements. Proc. SPIE. 2002, 4722, 98–109. [Google Scholar]
- Carroll, R.; Ruppert, D.; Stefanski, L. Measurement Error in Nonlinear Models; Chapman and Hall: London, 1996; pp. 1–78. [Google Scholar]
- Burr, T.; Fry, H.; McVey, B.; Sander, E. Chemical Identification using Bayesian Model Selection. Proc. of the American Statistical Association, Section on Physical and Engineering Sciences; [CD-ROM]. American Statistical Association LA-UR 02 7281. : Ann Arbor, Michigan, 2002. [Google Scholar]
- Heasler, P.; Hylden, J. Technical Letter Report for Non-Linear methods Task: Fits of Nonlinear Bayesian Regression (NBLR) to Tanasi and Polecat Images; Pacific Northwest National Laboratory Official Use Only Report; 2005. [Google Scholar]
- McVey, B. Official use only internal presentation cited with permission. 2004.
- Montgomery, D.; Peck, E. Introduction to Linear Regression Analysis, 2nd edition; Wiley: New York, 1992. [Google Scholar]
- Burr, T.; Fry, H.; McVey, B.; Sander, E.; Cavenaugh, J.; Neath, A. Performance of Variable Selection Methods in Regression using Variations of the Bayesian Information Criterion. LAUR-05-6324 submitted for publication. 2005. [Google Scholar]
- Raftery, A.; Madigan, D.; Hoeting, J. Bayesian Model Averaging for Linear Regression Models. Journal of the American Statistical Association 1997, 92, 179–191. [Google Scholar]
- DiCiccio, T.; Kass, R.; Raftery, A.; Wasserman, L. Computing Bayes Factors by Combining Simulation and Asymptotic Approximations. Journal of the American Statistical Association 1997, 92, 903–915. [Google Scholar]
- Kass, R.; Raftery, A. Bayes Factors. Journal of the American Statistical Association 1995, 90, 773–795. [Google Scholar]
- Neath, A.; Cavanaugh, J. Regression and Time Series Model Selection Using Variants of the Schwarz Information Criterion. Communications in Statistics-Theory and Methods 1997, 26, 559–580. [Google Scholar]
- Mardia, K. Tests of Univariate and Multivariate Normality. In Handbook of Statistics; vol. 1, North-Holland Publishing Co, 1980; pp. 279–320. [Google Scholar]
- Splus 7 for Windows; Insightful Corp., 2005.
- Burr, T.; Foy, B.; Fry, F.; McVey, B. Characterizing Clutter in the Context of Detecting Weak Gaseous Plumes using the SEBASS Sensor.; Los Alamos National Laboratory Restricted Release Report; LA-CP-06-0982; 2006; private communication. [Google Scholar]
- Chung, K. A Course in Probability Theory; Academic Press: Orlando, 1974; pp. 196–249. [Google Scholar]

| Case | P(Z>2) | P(Z>3) | P(Z>4) | P(Z>5) | kurtosis | skewness | Correlation in the normal probability plot |
|---|---|---|---|---|---|---|---|
| Gauss. Mix 1 | 2,2 | 0.08,0.1 | 0.01,3e-3 | 0,6e-5 | -0.13,-04e-3 | -0.07,-0.01 | 0.999,1 |
| 2,2 | 0.1,0.1 | 3e-3,3e-3 | 4e-5,0 | 0.004,-2e-3 | 0.1e-3,-2e-3 | 1,1 | |
| Gauss. Mix 2 | 4,3 | 4,1 | 1,1 | 0.03,0.3 | 6.7,18.2 | 2.48,-0.12 | 0.78,0.86 |
| 2,2 | 0.09,0.01 | 8e-5,3e-3 | 0,2e-5 | -0.07,-3e-3 | 2e-3,3e-4 | 1,1 | |
| Gauss.Mix 3 | 3,2 | 0.2,0,3 | 0.02,0.4 | 0,0.01 | -0.25,1.05 | 0.33,-0.16 | 0.984,0.991 |
| 2,2 | 0.2,0.1 | 3e-3,3e-3 | 2e-5,4e-5 | -0.017,0.01 | -5e-35,7e-3 | 1,1 | |
| Multi-t with 5 df. | 2,2 | 0.1,0.4 | 4e-3,0.1 | 2e-4,2e-4 | 0.02,2.25 | -0.02,0.02 | 1, 0.990 |
| 2,2 | 0.1,0.1 | 2e-3,2e-3 | 0,4e-5 | 0.02,2e-3 | -0.01,-0.01 | 1,1 | |
| Scene A: | 3,2 | 0.4,0.2 | 0.05,0.02 | 0.02,6e-3 | 1.81,0.47 | 0.41,4e-3 | 0.987,0.989 |
| Pixelsubset 1 | 2,2 | 0.2,0.1 | 0.01,4e-3 | 0,6e-5 | 0.01,2e-3 | 0.02,-0.002 | 1,1 |
| Scene A: | 2,2 | 0.3,0.2 | 0.2,0.02 | 0.1,4e-3 | 16.1,0.43 | 1.26,7e-3 | 0.95,0.999 |
| Pixelsubset 2 | 2,2 | 0.1,0.1 | 1e-3,e3-3 | 0,0 | -0.04,2e-3 | 9e-4,-4e-3 | 1,1 |
| Scene A: | 0.5,2 | 0.1,0.2 | 0.03,0.02 | 0.01,5e-3 | 4.4,0.49 | -0.14,7e-3 | 0.91,0.99 |
| Pixelsubset 3 | 2,2 | 0.2,0.1 | 4e-3,3e-3 | 0,2e-5 | -6e-3,-4e-3 | 0.03,2e-3 | 1,1 |
| Case | P(Z>2) | P(Z>3) | P(Z>4) | P(Z>5) | kurtosis |
|---|---|---|---|---|---|
| Gauss. Mixture 1 | 78,75 | 11,14 | 0.3,0.5 | 0,0.01 | -0.16,-4e-3 |
| 74,76 | 14,15 | 0.6,0.6 | 0.01,0 | 0.01,0.03 | |
| Gauss. Mixture 2 | 12,24 | 5,22 | 4,16 | 3,6 | -0.76,-0.57 |
| 7,88 | 0.5,17 | 0.02,0.6 | 0,6e-3 | -0.14,-1e-3 | |
| Gauss. | 89,89 | 40,36 | 4,10 | 0,4 | -0.46,1.33 |
| Mixture 3 | 72,69 | 12,11 | 0.4,0.5 | 6e-3,0.01 | -0.02,0.02 |
| Multi-t with 5 df. | 18,66 | 3,27 | 0.4,10 | 0.05,4 | 0.19,2.14 |
| 15,81 | 1,4 | 0.04,0.5 | 0,0.01 | 0.18,0.01 | |
| Scene A: | 14,92 | 3,22 | 0.5,2 | 0,3,0.5 | 1.59,0.24 |
| pixel subset 1 | 14,94 | 1,21 | 0.05,0.7 | 0,6e-3 | -6e-3,-1e-3 |
| Scene A: | 11,91 | 1,22 | 0.5,2 | 0.4,0.5 | 21.6,0.54 |
| pixel subset 2 | 14,94 | 1,20 | 0.04,0.8 | 0,0 | -0.05,2e-3 |
| Scene A: | 4,89 | 1,23 | 0.4,2 | 0.3,0.6 | 4.46,0.37 |
| pixel subset 3 | 10,94 | 0.9,21 | 0.03,0.7 | 0,6e-3 | -5e-3,7e-3 |
| Direction | P(Z>2) x 100 | P(Z>3) x 100 | P(Z>4) x 100 | kurtosis | skewness |
|---|---|---|---|---|---|
| Chemical* | 1.9,2.3,2.2 | 0.3,0.2,0.1 | 0.09,0,03,2e-3 | 1.82,0.77,-5e-3 | 0.46,4e-3,5e-3 |
| Chemical | 2.2,2.3,2.3 | 0.3,0.2,0.2 | 0.1,0.03,0.03 | 14.7,0.47,0.47 | 1.0,0.02,0.02 |
| Random | 2.8,2.3,2.3 | 0.5,0.2,0.1 | 0.1,5e-3,3e-3 | 17.3,4e-3,-1e-3 | 1.46,0.02,2e-3 |
| Data Source | Agreement Measure | Chemical | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| Real Data: 10 random subsets of 16,384 pixels from scene A | Avg Abs Diff | 0.50, 0.07 | 0.20, 0.08 | 0.19, 0.08 | 0.43, 0.07 |
| R2 | 0.09, 0.80 | 0.60, 0.78 | 0.46, 0.78 | 0.54, 0.79 | |
| Reference Gaussian Data having same Σ as Scene A | Avg Abs Diff | 0.46, 0.07 | 0.20, 0.07 | 0.20, 0.07 | 0.43, 0.07 |
| R2 | 0.06, 0.78 | 0.57, 0.78 | 0.45, 0.78 | 0.57, 0.77 | |
| Reference Gaussian Data having Diagonal Σ | Avg Abs Diff | 0.11, 0.04 | 0.04, 0.04 | 0.04, 0.04 | 0.06, 0.04 |
| R2 | 0.91, 0.93 | 0.96, 0.94 | 0.92, 0.94 | 0.79, 0.94 | |
© 2006 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Burr, T.; Foy, B.; Fry, H.; McVey, B. Characterizing Clutter in the Context of Detecting Weak Gaseous Plumes in Hyperspectral Imagery. Sensors 2006, 6, 1587-1615. https://doi.org/10.3390/s6111587
Burr T, Foy B, Fry H, McVey B. Characterizing Clutter in the Context of Detecting Weak Gaseous Plumes in Hyperspectral Imagery. Sensors. 2006; 6(11):1587-1615. https://doi.org/10.3390/s6111587
Chicago/Turabian StyleBurr, Tom, Bernie Foy, Herb Fry, and Brian McVey. 2006. "Characterizing Clutter in the Context of Detecting Weak Gaseous Plumes in Hyperspectral Imagery" Sensors 6, no. 11: 1587-1615. https://doi.org/10.3390/s6111587





