Robot Navigation in Complex Workspaces Employing Harmonic Maps and Adaptive Artificial Potential Fields
Abstract
:1. Introduction
1.1. Contributions
1.2. Preliminaries
2. Problem Formulation
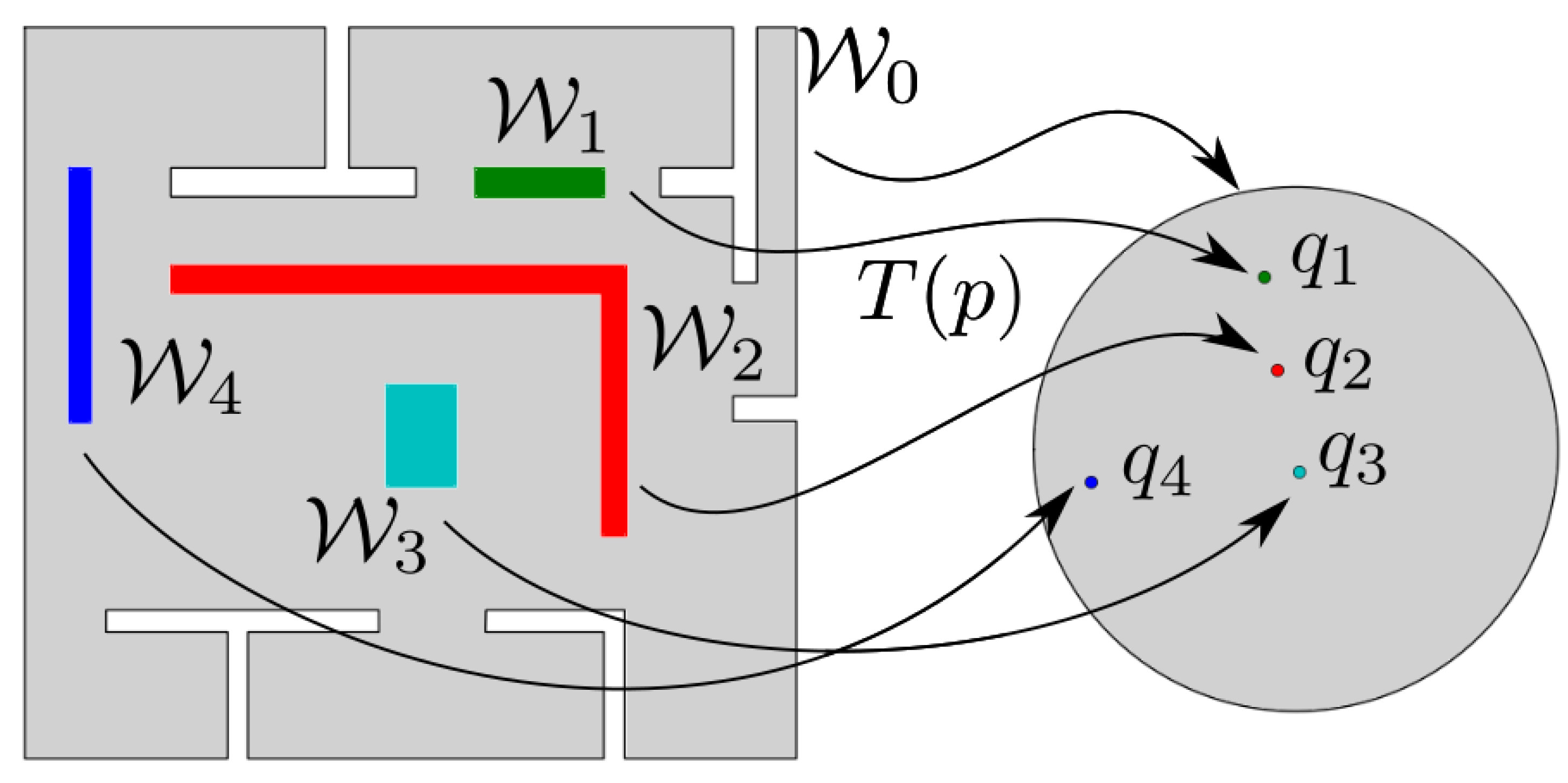
3. Harmonic Maps for Planar Navigation
- maps the outer boundary to the unit circle ;
- maps the boundary of each obstacle to a distinct point ;
- is a diffeomorphism for all .
4. Control Design
4.1. Artificial Harmonic Potential Fields
4.2. Adaptive Laws
4.3. Stability Analysis
5. Extensions
5.1. Unicycle Robot Kinematics
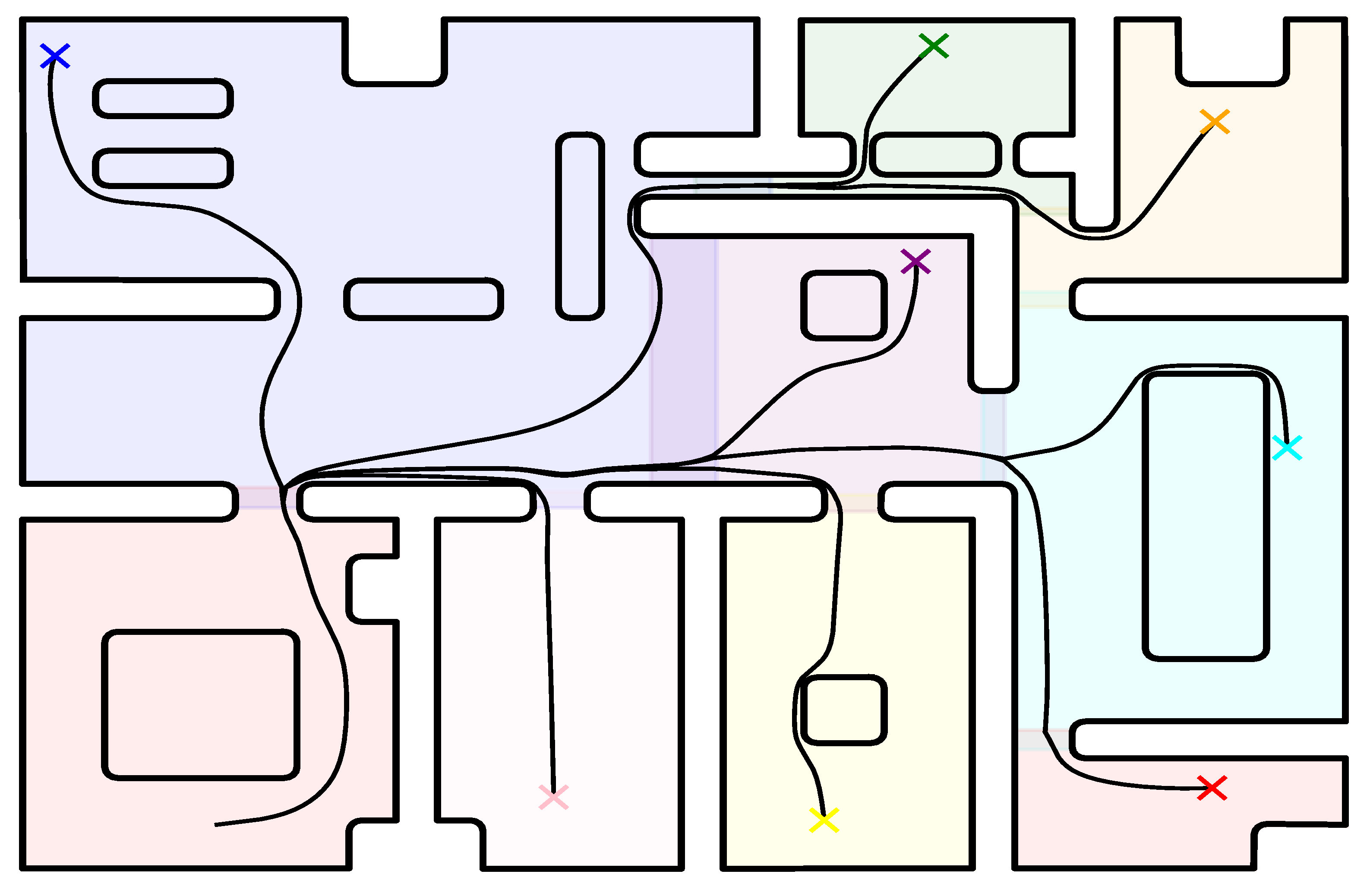
5.2. Atlas of Harmonic Maps
| Algorithm 1 Altas-based motion planning scheme for a holonomic robot |
| Require: , , |
6. Simulations and Experimental Results
6.1. Simulations—Full Workspace Transformation
6.2. Simulations—Atlas of Harmonic Maps
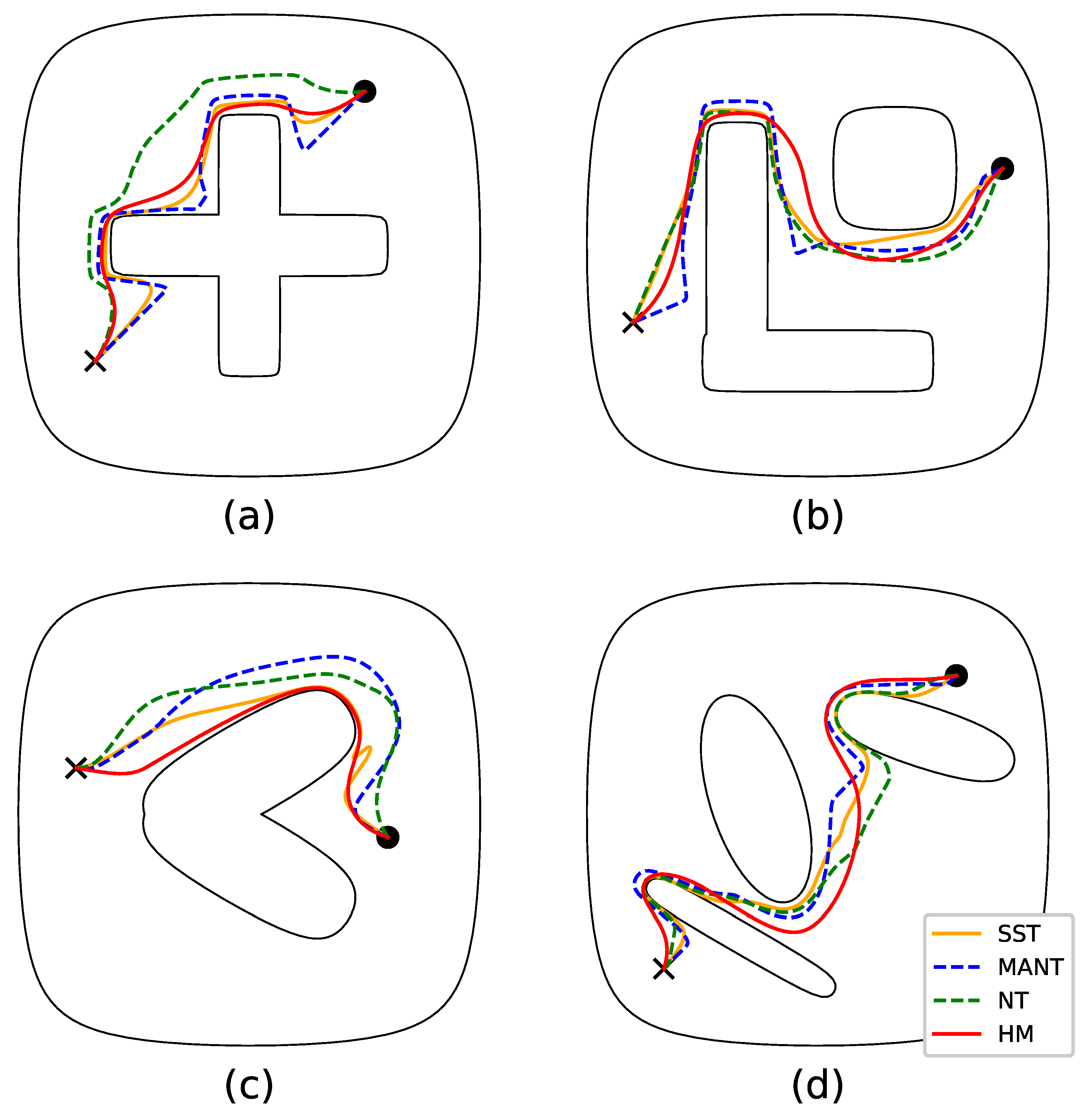
6.3. Comparative Study—Workspace Transformation
6.4. Comparative Study—Control Law
6.4.1. APF-Based Schemes
6.4.2. Sampling-Based Scheme
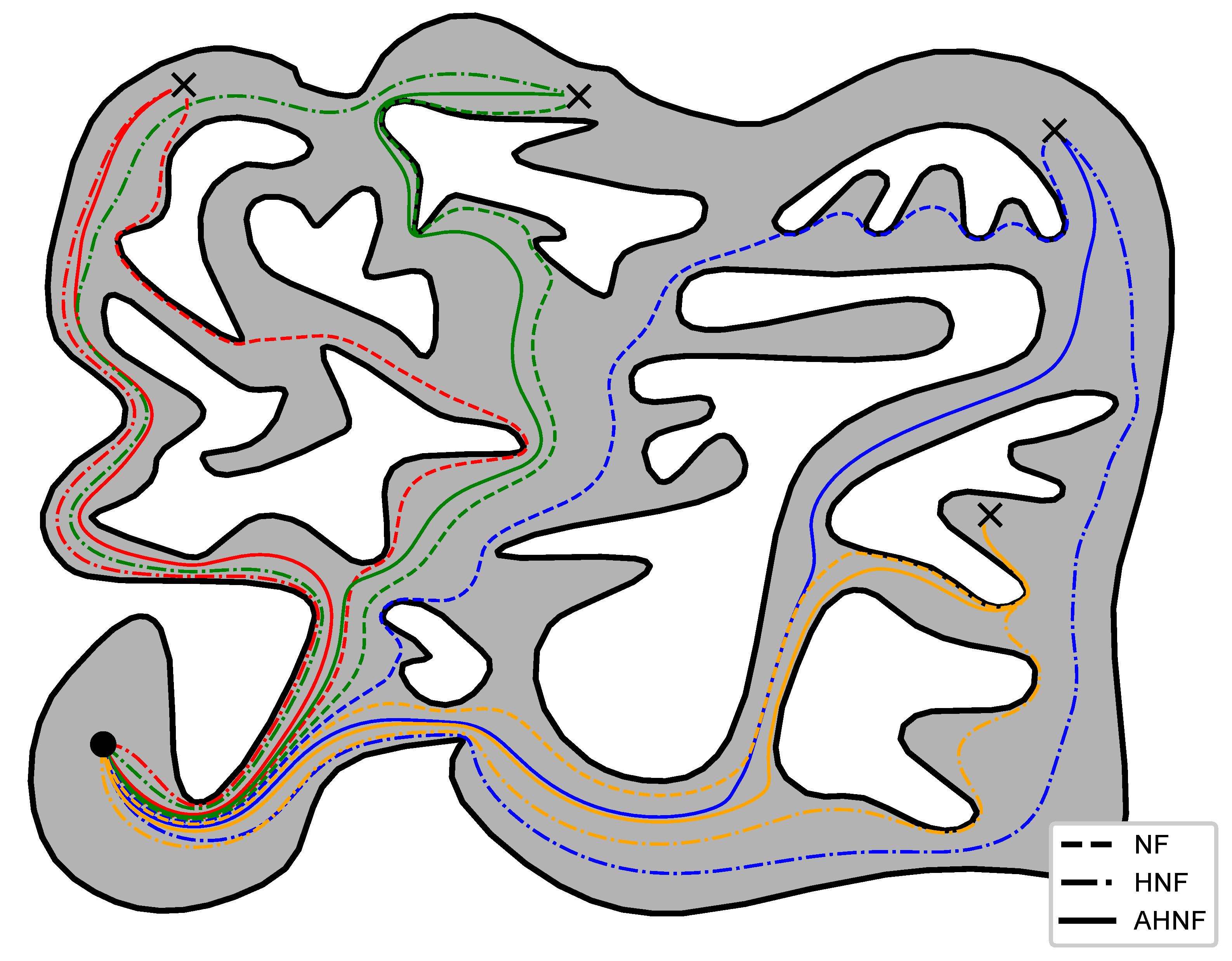
6.5. Experiments
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Proposition 2
Appendix A.3. Proof of Proposition 3
Appendix A.4. Proof of Proposition 4
Appendix A.5. Proof of Proposition 5
Appendix A.6. Proof of Theorem 1
Appendix A.7. Proof of Theorem 2
Appendix A.8. Proof of Theorem 3
References
- Canny, J. The Complexity of Robot Motion Planning; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Mesesan, G.; Roa, M.A.; Icer, E.; Althoff, M. Hierarchical Path Planner Using Workspace Decomposition and Parallel Task-Space RRTs. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 6524–6531. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Chi, W.; Wang, C.; Wang, J.; Meng, M.Q. Risk-DTRRT-Based Optimal Motion Planning Algorithm for Mobile Robots. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1271–1288. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Svestka, P.; Latombe, J.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Chen, G.; Luo, N.; Liu, D.; Zhao, Z.; Liang, C. Path planning for manipulators based on an improved probabilistic roadmap method. Robot. Comput.-Integr. Manuf. 2021, 72, 102196. [Google Scholar] [CrossRef]
- Salzman, O.; Hemmer, M.; Halperin, D. On the Power of Manifold Samples in Exploring Configuration Spaces and the Dimensionality of Narrow Passages. IEEE Trans. Autom. Sci. Eng. 2015, 12, 529–538. [Google Scholar] [CrossRef]
- Kingston, Z.; Moll, M.; Kavraki, L.E. Sampling-Based Methods for Motion Planning with Constraints. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 159–185. [Google Scholar] [CrossRef]
- Ogren, P.; Leonard, N.E. A convergent dynamic window approach to obstacle avoidance. IEEE Trans. Robot. 2005, 21, 188–195. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, X.; Gao, H.; Yuan, J.; Fang, Y. E3MoP: Efficient Motion Planning Based on Heuristic-Guided Motion Primitives Pruning and Path Optimization With Sparse-Banded Structure. IEEE Trans. Autom. Sci. Eng. 2021, 19, 2762–2775. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Ghrist, R. Path Homotopy Invariants and their Application to Optimal Trajectory Planning. Ann. Math. Artif. Intell. 2018, 84, 139–160. [Google Scholar] [CrossRef]
- Diaz-Arango, G.; Vázquez-Leal, H.; Hernandez-Martinez, L.; Pascual, M.T.S.; Sandoval-Hernandez, M. Homotopy Path Planning for Terrestrial Robots Using Spherical Algorithm. IEEE Trans. Autom. Sci. Eng. 2018, 15, 567–585. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; pp. 500–505. [Google Scholar]
- Koditschek, D. Exact robot navigation by means of potential functions: Some topological considerations. In Proceedings of the IEEE International Conference on Robotics and Automation, Raleigh, NC, USA, 31 March–3 April 1987; pp. 1–6. [Google Scholar]
- Rimon, E.; Koditschek, D. Exact Robot Navigation Using Artificial Potential Functions. IEEE Trans. Robot. Autom. 1992, 8, 501–518. [Google Scholar] [CrossRef]
- Loizou, S.G.; Jadbabaie, A. Density Functions for Navigation-Function-Based Systems. IEEE Trans. Autom. Control 2008, 53, 612–617. [Google Scholar] [CrossRef]
- Filippidis, I.; Kyriakopoulos, K.J. Adjustable navigation functions for unknown sphere worlds. In Proceedings of the IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 4276–4281. [Google Scholar]
- Filippidis, I.F.; Kyriakopoulos, K.J. Navigation Functions for everywhere partially sufficiently curved worlds. In Proceedings of the IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 2115–2120. [Google Scholar]
- Paternain, S.; Koditschek, D.E.; Ribeiro, A. Navigation Functions for Convex Potentials in a Space With Convex Obstacles. IEEE Trans. Autom. Control 2018, 63, 2944–2959. [Google Scholar] [CrossRef]
- Arslan, O.; Koditschek, D.E. Sensor-based reactive navigation in unknown convex sphere worlds. Int. J. Robot. Res. 2019, 38, 196–223. [Google Scholar] [CrossRef]
- Connolly, C.; B Burns, J.; Weiss, R. Path Planning Using Laplace’s Equation. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 2102–2106. [Google Scholar]
- Mantegh, I.; Jenkin, M.R.M.; Goldenberg, A.A. Path Planning for Autonomous Mobile Robots Using the Boundary Integral Equation Method. J. Intell. Robot. Syst. 2010, 59, 191–220. [Google Scholar] [CrossRef]
- Golan, Y.; Edelman, S.; Shapiro, A.; Rimon, E. Online Robot Navigation Using Continuously Updated Artificial Temperature Gradients. IEEE Robot. Autom. Lett. 2017, 2, 1280–1287. [Google Scholar] [CrossRef]
- Kim, J.O.; Khosla, P.K. Real-time obstacle avoidance using harmonic potential functions. IEEE Trans. Robot. Autom. 1992, 8, 338–349. [Google Scholar] [CrossRef]
- Merheb, A.; Gazi, V.; Sezer-Uzol, N. Implementation Studies of Robot Swarm Navigation Using Potential Functions and Panel Methods. IEEE/ASME Trans. Mechatron. 2016, 21, 2556–2567. [Google Scholar] [CrossRef]
- Velagić, J.; Vuković, L.; Ibrahimović, B. Mobile Robot Motion Framework Based on Enhanced Robust Panel Method. Int. J. Control Autom. Syst. 2020, 18, 1264–1276. [Google Scholar] [CrossRef]
- Feder, H.J.S.; Slotine, J.J.E. Real-time path planning using harmonic potentials in dynamic environments. In Proceedings of the IEEE International Conference on Robotics and Automation, Albuquerque, NM, USA, 20–25 April 1997; pp. 874–881. [Google Scholar]
- Marchidan, A.; Bakolas, E. A local reactive steering law for 2D collision avoidance with curvature constraints and constant speed. Robot. Auton. Syst. 2022, 155, 104156. [Google Scholar] [CrossRef]
- e Silva, E.P.; Engel, P.M.; Trevisan, M.; Idiart, M.A. Exploration Method Using Harmonic Functions. Robot. Auton. Syst. 2002, 40, 25–42. [Google Scholar] [CrossRef]
- Maffei, R.; Souza, M.P.; Mantelli, M.; Pittol, D.; Kolberg, M.; Jorge, V.A.M. Exploration of 3D terrains using potential fields with elevation-based local distortions. In Proceedings of the IEEE International Conference on Robotics and Automation, Paris, France, 31 May–31 August 2020; pp. 4239–4244. [Google Scholar]
- Voruganti, H.; Dasgupta, B.; Hommel, U. A novel potential field based domain mapping method. In Proceedings of the 10th WSEAS Conference on Computers (ICCOMPP06), Athens, Greece, 13 July 2006; pp. 655–661. [Google Scholar]
- Gautam Pradeepkumar, B.; Gondegaon, S.; Voruganti, H.K. Domain Mapping for Path Planning and Mesh Generation. In Proceedings of the International Conference on Theoretical, Applied, Computational and Experimental Mechanics, Kharagpur, India, 29–31 December 2014. [Google Scholar]
- Loizou, S.G. Closed form Navigation Functions based on harmonic potentials. In Proceedings of the IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 6361–6366. [Google Scholar]
- Loizou, S.G. The Navigation Transformation. IEEE Trans. Robot. 2017, 33, 1516–1523. [Google Scholar] [CrossRef]
- Loizou, S.G. Navigation functions in topologically complex 3-D workspaces. In Proceedings of the American Control Conference, Montreal, QC, Canada, 27–29 June 2012; pp. 4861–4866. [Google Scholar]
- Loizou, S.G. The Multi-Agent Navigation Transformation: Tuning-Free Multi-Robot Navigation. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 14–16 July 2014; pp. 1–9. [Google Scholar]
- Vlantis, P.; Vrohidis, C.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Robot Navigation in Complex Workspaces Using Harmonic Maps. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 1726–1731. [Google Scholar]
- Duren, P.; Hengartner, W. Harmonic mappings of multiply connected domains. Pac. J. Math. 1997, 180, 201–220. [Google Scholar] [CrossRef]
- Biringen, S.; Chow, C.Y. An Introduction to Computational Fluid Mechanics by Example; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Kuethe, A.M.; Chow, C.Y.; Fung, Y.C. Foundations of Aerodynamics: Bases of Aerodynamics Design, 5th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1997. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice-Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- Panageas, I.; Piliouras, G. Gradient Descent Only Converges to Minimizers: Non-Isolated Critical Points and Invariant Regions. arXiv 2016, arXiv:1605.00405. [Google Scholar]







| Geometry Representation | Global | Analytic | |
|---|---|---|---|
| HM | Points on the boundary | Yes | Yes |
| SST | Trees of Stars | Yes | Yes |
| NT | -manifolds | No | No |
| MANT | Trees of -manifolds | No | No |
| Convergence | Collision Avoidance | Computational Cost | |
|---|---|---|---|
| AHPF | By design | By design | Cheap |
| HPF | By design | By design | Expensive |
| RKNF | Requires tuning | By design | Cheap |
| HNF | By design | Requires tuning | Cheap |
| a | b | c | d | |
|---|---|---|---|---|
| SST | 3.63 | 4.18 | 2.12 | 4.09 |
| MANT | 4.26 | 4.69 | 2.34 | 4.45 |
| NT | 3.35 | 4.30 | 2.18 | 4.22 |
| HM | 3.19 | 4.21 | 2.05 | 4.32 |
| a | b | c | d | |
|---|---|---|---|---|
| SST | 4.22 | 5.43 | 86.93 | 2.16 |
| MANT | 1.23 | 1.47 | 13.56 | 2.06 |
| NT | 66.97 | 25.23 | 14.89 | 6.92 |
| HM | 2.47 | 2.49 | 14.76 | 2.77 |
| a | b | c | d | |
|---|---|---|---|---|
| SST | 0.0303 | 0.0283 | 0.0159 | 0.0063 |
| MANT | 0.0644 | 0.1253 | 0.1870 | 0.0648 |
| NT | 0.1386 | 0.0506 | 0.0915 | 0.0058 |
| HM | 0.0335 | 0.0377 | 0.0103 | 0.0181 |
| Red | Green | Blue | Yellow | |
|---|---|---|---|---|
| NF | 19.781 | 20.427 | 22.090 | 18.397 |
| HNF | 18.224 | 22.538 | 26.959 | 20.062 |
| AHNF | 17.874 | 19.419 | 23.364 | 18.595 |
| Red | Green | Blue | Yellow | |
|---|---|---|---|---|
| NF | 0.1158 | 0.0102 | 0.1210 | 0.1103 |
| HNF | 0.3347 | 0.2135 | 0.2591 | 0.2166 |
| AHPF | 0.1310 | 0.0352 | 0.2043 | 0.1854 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlantis, P.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Robot Navigation in Complex Workspaces Employing Harmonic Maps and Adaptive Artificial Potential Fields. Sensors 2023, 23, 4464. https://doi.org/10.3390/s23094464
Vlantis P, Bechlioulis CP, Kyriakopoulos KJ. Robot Navigation in Complex Workspaces Employing Harmonic Maps and Adaptive Artificial Potential Fields. Sensors. 2023; 23(9):4464. https://doi.org/10.3390/s23094464
Chicago/Turabian StyleVlantis, Panagiotis, Charalampos P. Bechlioulis, and Kostas J. Kyriakopoulos. 2023. "Robot Navigation in Complex Workspaces Employing Harmonic Maps and Adaptive Artificial Potential Fields" Sensors 23, no. 9: 4464. https://doi.org/10.3390/s23094464
APA StyleVlantis, P., Bechlioulis, C. P., & Kyriakopoulos, K. J. (2023). Robot Navigation in Complex Workspaces Employing Harmonic Maps and Adaptive Artificial Potential Fields. Sensors, 23(9), 4464. https://doi.org/10.3390/s23094464









