Self Calibration of a Sonar–Vision System for Underwater Vehicles: A New Method and a Dataset
Abstract
:1. Introduction
2. Problem Statement, Notations and Models
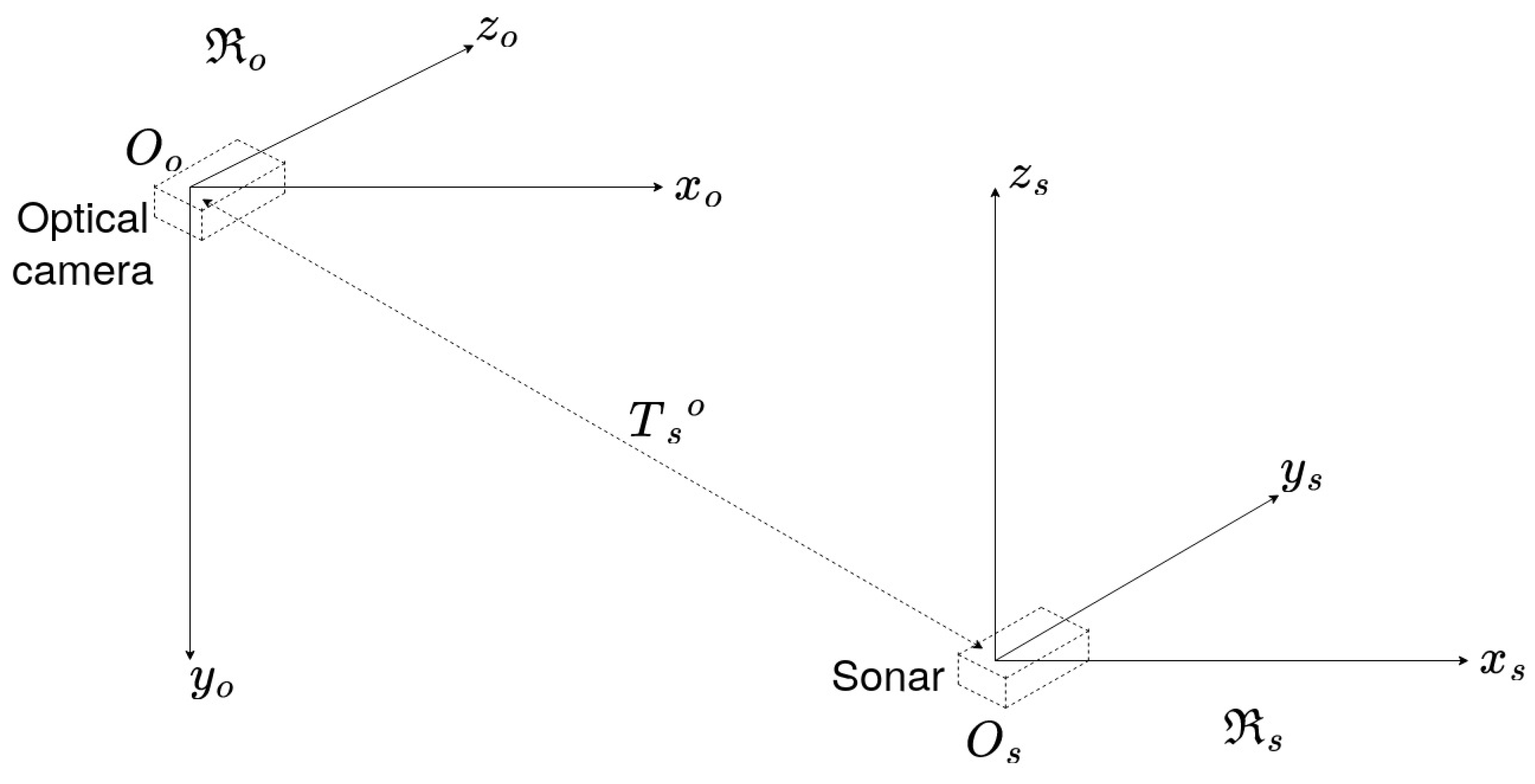
2.1. Problem Statement
2.2. Monocular Camera’s Model
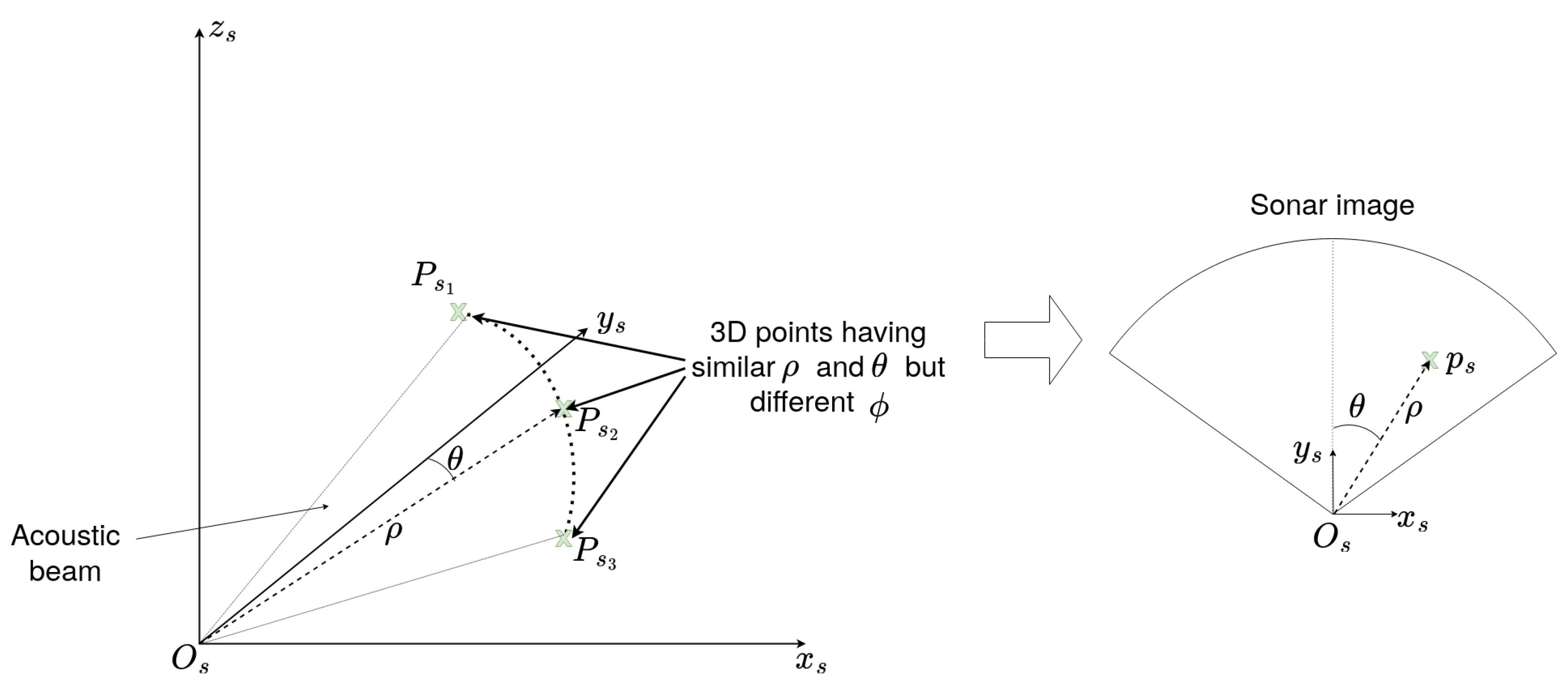
2.3. Sonar’s Projection Model
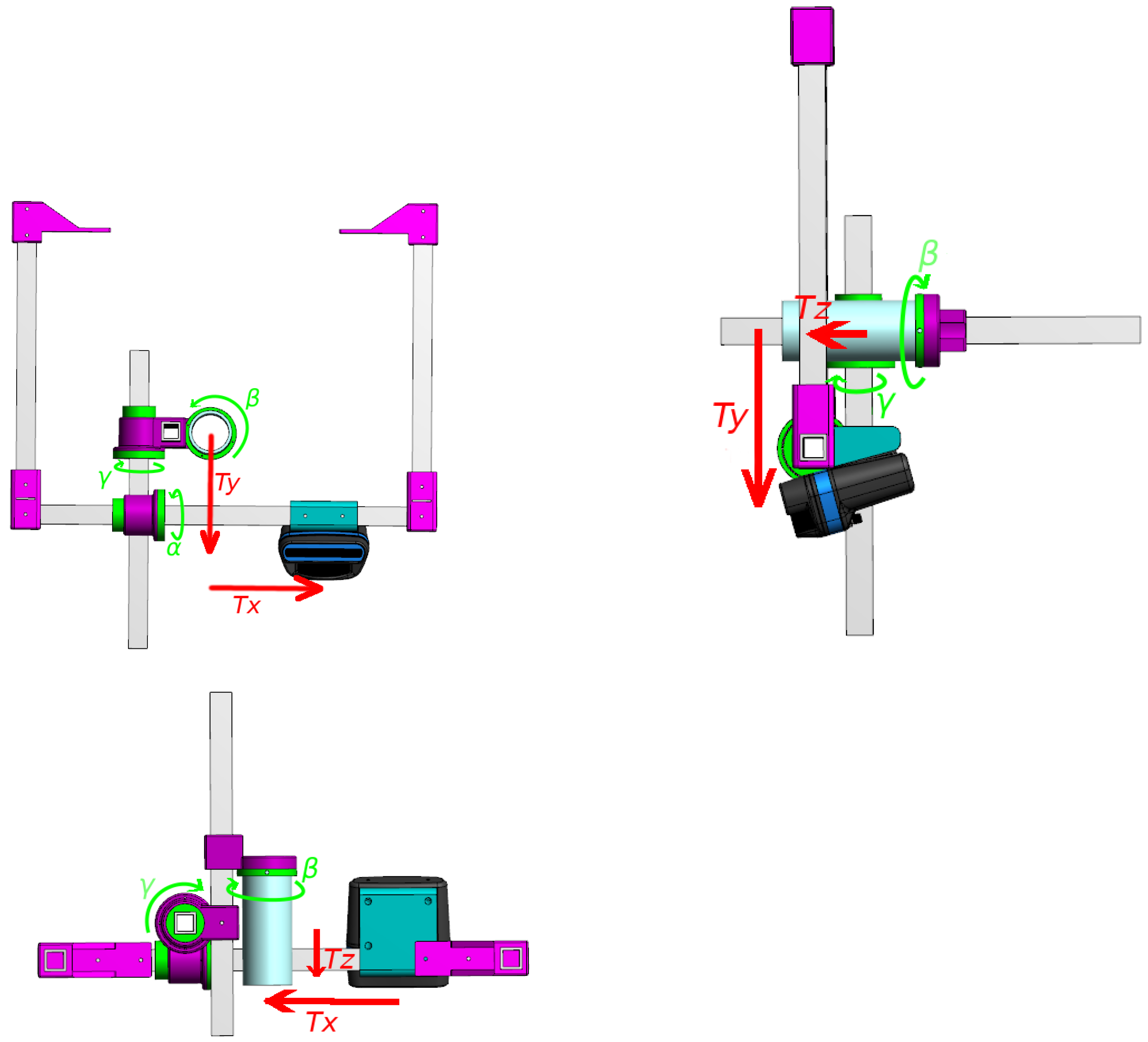
2.4. Frame Transformation
3. Calibration Method
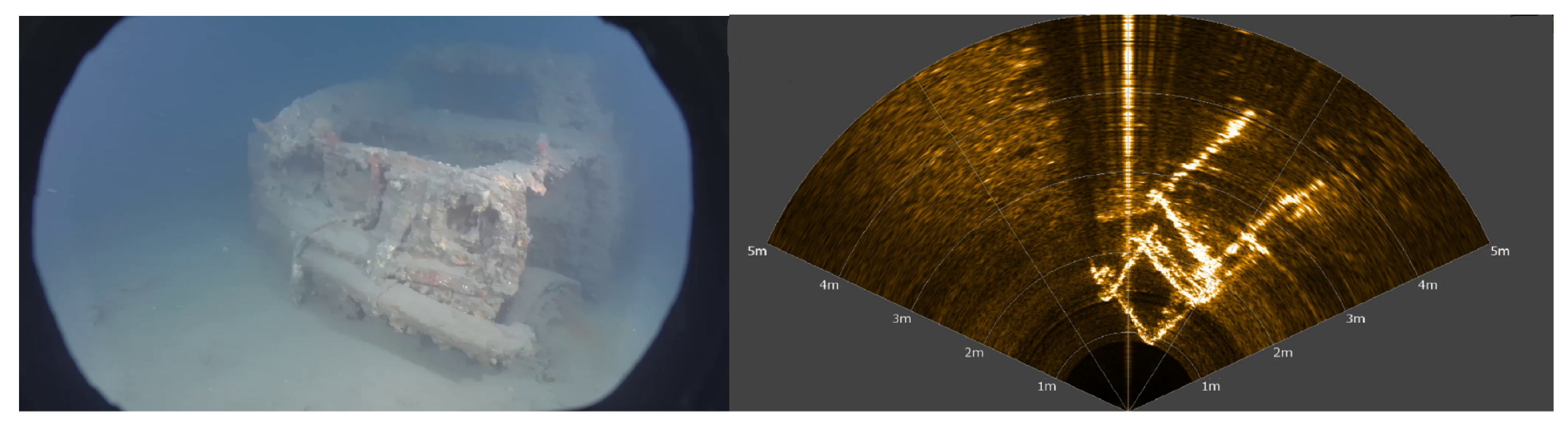
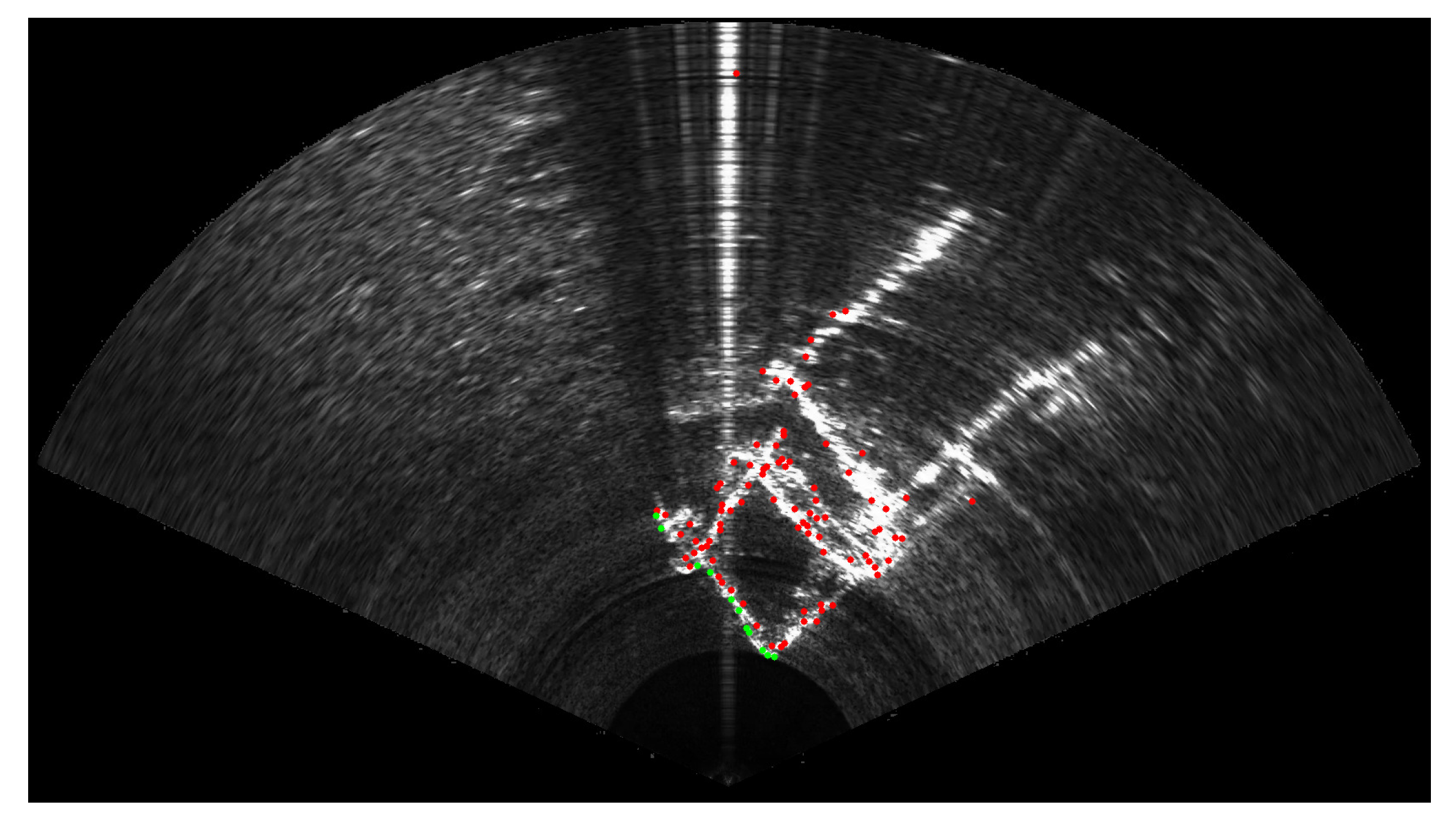
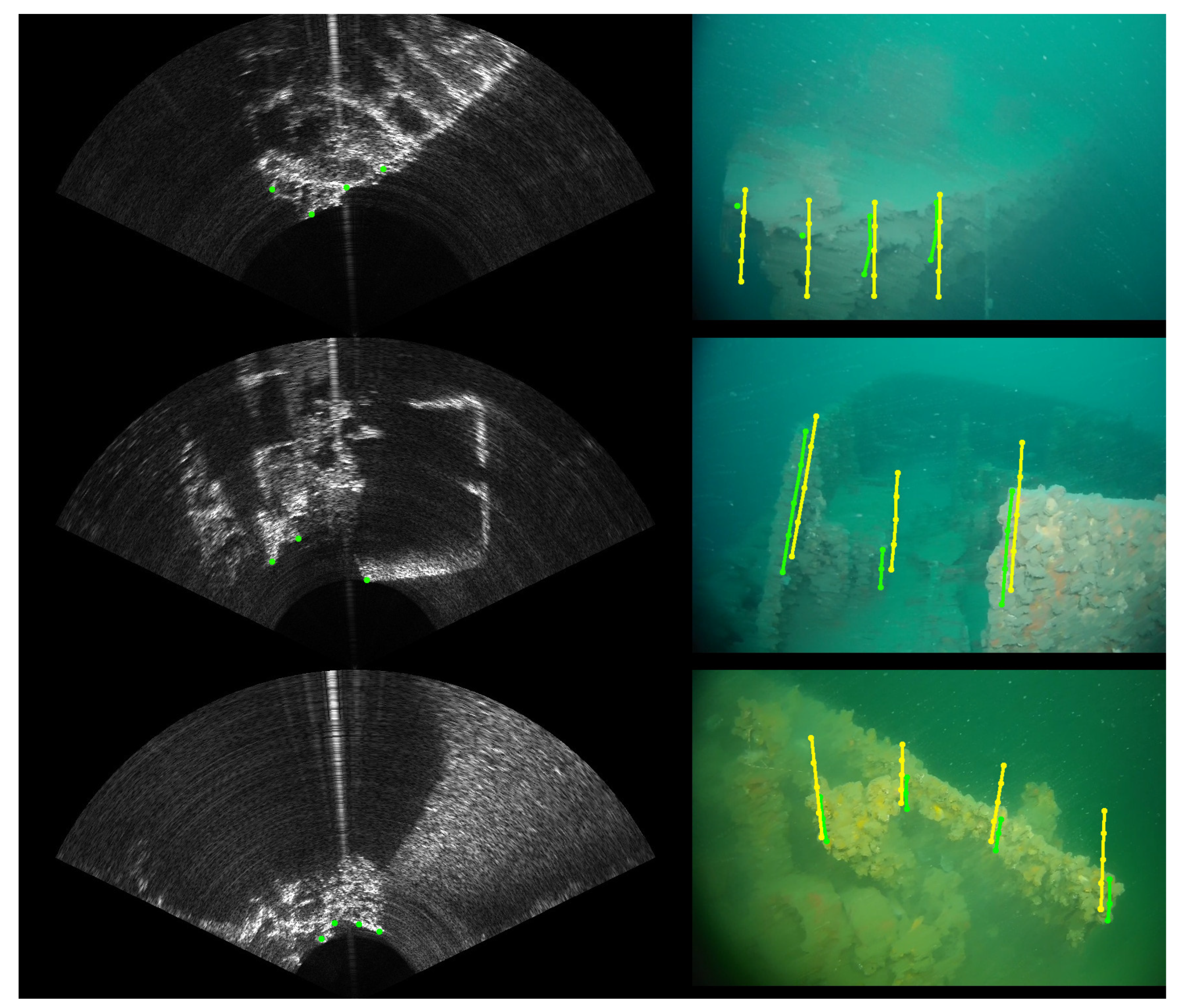
3.1. Selection of a Set of Feature Points in the Sonar Images
3.2. Projection and Evaluation
3.3. Estimation of the Calibration Parameters
| Algorithm 1 Research of the calibration algorithm on one set of camera and sonar image pairs. |
|
4. Experimental Validation and Dataset
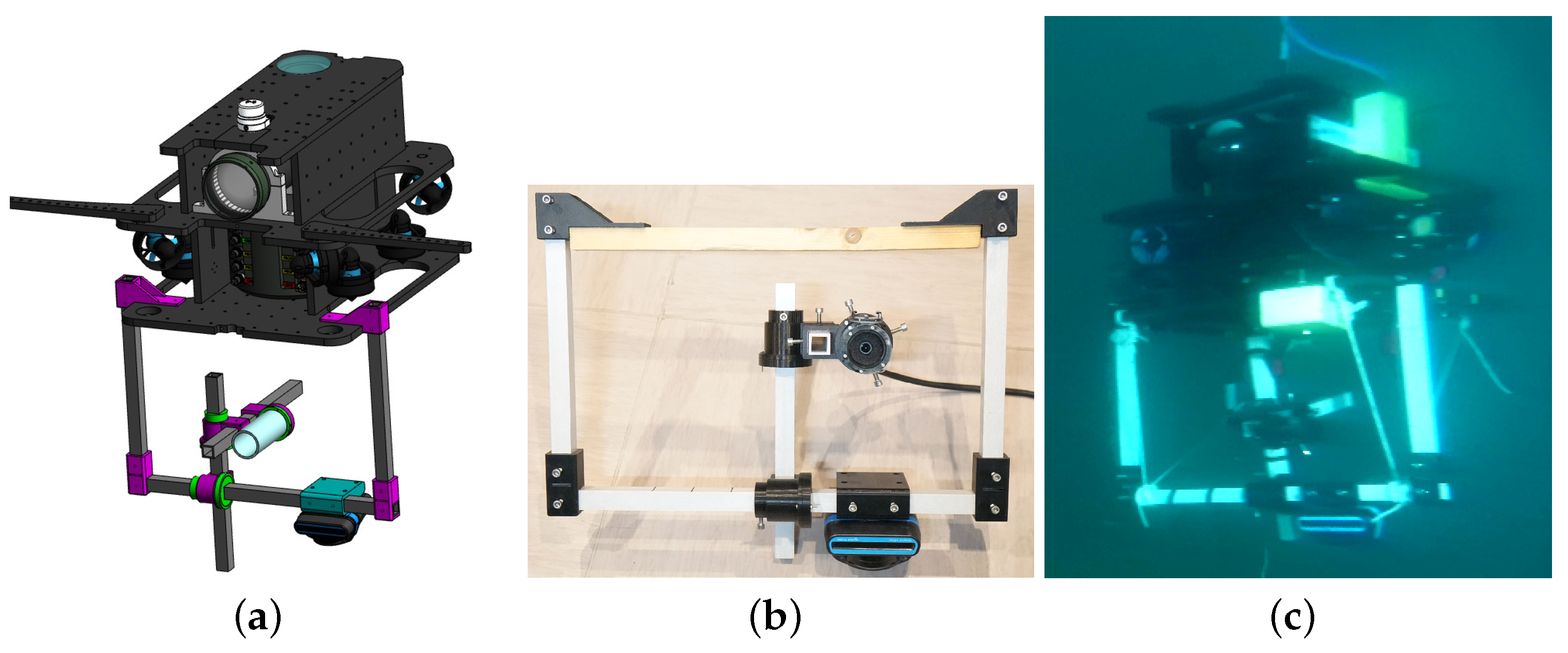
4.1. Experimental Setup
4.2. Dataset
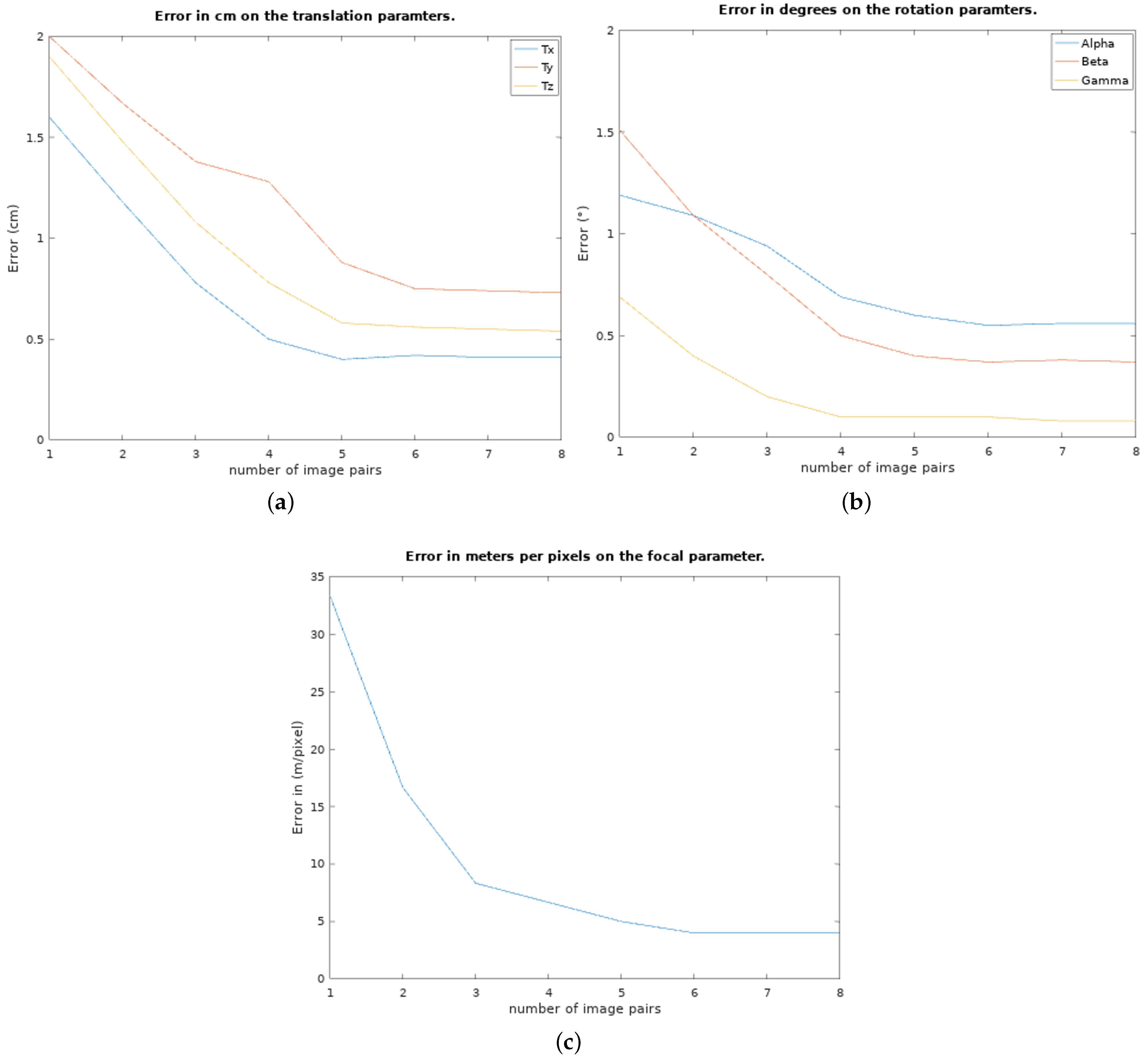
4.3. Experimental Evaluation of the Calibration Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nguyen, L.H.; Hua, M.D.; Allibert, G.; Hamel, T. A Homography-Based Dynamic Control Approach Applied to Station Keeping of Autonomous Underwater Vehicles Without Linear Velocity Measurements. IEEE Trans. Control. Syst. Technol. 2021, 29, 2065–2078. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Bu, Y.; Dai, F.; Fan, T.; Wang, H. Underwater object segmentation based on optical features. Sensors 2018, 18, 196. [Google Scholar] [CrossRef] [PubMed]
- Moghimi, M.K.; Mohanna, F. Real-time underwater image enhancement: A systematic review. J. -Real-Time Image Process. 2021, 18, 1509–1525. [Google Scholar] [CrossRef]
- Zhuang, P.; Li, C.; Wu, J. Bayesian retinex underwater image enhancement. Eng. Appl. Artif. Intell. 2021, 101, 104171. [Google Scholar] [CrossRef]
- Li, C.; Lian, S.; Niu, J.; Wang, C.; Zhou, X. Research on Underwater Image Denoising Based on Wavelet Threshold Method. In Proceedings of the 2022 7th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 15–17 April 2022; pp. 1941–1947. [Google Scholar]
- Kis, A.; Balta, H.; Ancuti, C. Underwater Image Enhancement on Low-Cost Hardware Platform. In Proceedings of the 2021 International Symposium ELMAR, Zadar, Croatia, 13–15 September 2021; pp. 97–100. [Google Scholar]
- Pyo, J.; Cho, H.; Yu, S.C. Beam slice-based recognition method for acoustic landmark with multi-beam forward looking sonar. IEEE Sens. J. 2017, 17, 7074–7085. [Google Scholar] [CrossRef]
- Cotter, E.; Polagye, B. Automatic classification of biological targets in a tidal channel using a multibeam sonar. J. Atmos. Ocean. Technol. 2020, 37, 1437–1455. [Google Scholar] [CrossRef]
- Palomeras, N.; Furfaro, T.; Williams, D.P.; Carreras, M.; Dugelay, S. Automatic Target Recognition for Mine Countermeasure Missions Using Forward-Looking Sonar Data. IEEE J. Ocean. Eng. 2021, 47, 141–161. [Google Scholar] [CrossRef]
- Tulsook, S.; Kasetkasem, T.; Tipsuwan, Y.; Sugino, N.; Chanwimaluang, T.; Hoonsuwan, P. A Pipeline Extraction on Forward-Looking Sonar Images Using the Self-Organizing Map. In Proceedings of the 2018 15th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Rai, Thailand, 18–21 July 2018; pp. 584–587. [Google Scholar] [CrossRef]
- Negahdaripour, S. Calibration of DIDSON forward-scan acoustic video camera. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005; pp. 1287–1294. [Google Scholar]
- Negahdaripour, S.; Sekkati, H.; Pirsiavash, H. Opti-acoustic stereo imaging: On system calibration and 3-D target reconstruction. IEEE Trans. Image Process. 2009, 18, 1203–1214. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; He, B.; Zhu, M.; Liu, J. An extrinsic calibration method with closed-form solution for underwater opti-acoustic imaging system. IEEE Trans. Instrum. Meas. 2020, 69, 6828–6842. [Google Scholar] [CrossRef]
- Lindzey, L.; Marburg, A. Extrinsic Calibration between an Optical Camera and an Imaging Sonar. In Proceedings of the OCEANS 2021: San Diego–Porto, San Diego, CA, USA, 20–23 September 2021; pp. 1–8. [Google Scholar]
- Hurtos, N.; Cufi, X.; Salvi, J. Calibration of optical camera coupled to acoustic multibeam for underwater 3D scene reconstruction. In Proceedings of the OCEANS’10 IEEE SYDNEY, Sydney, NSW, Australia, 24–27 May 2010; pp. 1–7. [Google Scholar]
- Lagudi, A.; Bianco, G.; Muzzupappa, M.; Bruno, F. An alignment method for the integration of underwater 3D data captured by a stereovision system and an acoustic camera. Sensors 2016, 16, 536. [Google Scholar] [CrossRef] [PubMed]
- Roznere, M.; Li, A.Q. Underwater monocular image depth estimation using single-beam echosounder. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 1785–1790. [Google Scholar]
- Legg, M.; Bradley, S. A combined microphone and camera calibration technique with application to acoustic imaging. IEEE Trans. Image Process. 2013, 22, 4028–4039. [Google Scholar] [CrossRef] [PubMed]
- Barat, C.; Rendas, M.J. Exploiting natural contours for automatic sonar-to-video calibration. In Proceedings of the Europe Oceans 2005, Brest, France, 20–23 June 2005; Volume 1, pp. 271–275. [Google Scholar]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer Nature: Berlin/Heidelberg, Germany, 2022; p. 46. [Google Scholar]
- McConnell, J.; Martin, J.D.; Englot, B. Fusing Concurrent Orthogonal Wide-aperture Sonar Images for Dense Underwater 3D Reconstruction. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 1653–1660. [Google Scholar]
- Ji, Y.; Kwak, S.; Yamashita, A.; Asama, H. Acoustic camera-based 3D measurement of underwater objects through automated extraction and association of feature points. In Proceedings of the 2016 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Baden, Germany, 19–21 September 2016; pp. 224–230. [Google Scholar]
- Aykin, M.; Negahdaripour, S. On feature extraction and region matching for forward scan sonar imaging. In Proceedings of the 2012 Oceans, Hampton Roads, VA, USA, 14–19 October 2012; pp. 1–9. [Google Scholar]
- Cho, H.; Kim, B.; Yu, S.C. AUV-based underwater 3-D point cloud generation using acoustic lens-based multibeam sonar. IEEE J. Ocean. Eng. 2017, 43, 856–872. [Google Scholar] [CrossRef]
- Jang, H.; Kim, G.; Lee, Y.; Kim, A. CNN-based approach for opti-acoustic reciprocal feature matching. In Proceedings of the IEEE International Conference on Robotics and Automation Workshop, Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Jang, H.; Yoon, S.; Kim, A. Multi-session underwater pose-graph slam using inter-session opti-acoustic two-view factor. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 11668–11674. [Google Scholar]
- Gwon, D.H.; Shin, Y.S.; Kim, Y.; Kim, A.; Lee, Y.; Choi, H.T. Nontemporal relative pose estimation for opti-acoustic bundle adjustment. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–5. [Google Scholar]
- Bouguet, J.Y. Pyramidal implementation of the affine lucas kanade feature tracker description of the algorithm. Intel Corp. 2001, 5, 4. [Google Scholar]







| Monocular Video Camera | |
|---|---|
| Camera model | Optovision HD mini IP camera |
| Image size | 720 × 480 pixels |
| Frame rate | 30 fps |
| Sonar | |
| Sonar model | Oculus 1200 M |
| Image size | 1024 × 507 pixels |
| Frame rate | 10 fps |
| Horizontal aperture | 130 |
| Vertical aperture | 20 |
| Angular resolution | 0.5 |
| IMU data frequency | 20 Hz |
| (cm) | (cm) | (cm) | (°) | (°) | (°) | f (pixel/m) | |
|---|---|---|---|---|---|---|---|
| Configuration I | 0 | 5 | 0 | 0 | 0 | 0 | 600 |
| Configuration II | 0 | 15 | 0 | 0 | 0 | 0 | 600 |
| Configuration III | 10 | 5 | 0 | 0 | 0 | 0 | 600 |
| (cm) | (cm) | (cm) | (°) | (°) | (°) | Focal | |
|---|---|---|---|---|---|---|---|
| Configuration I ground truth | 0 | 5 | 0 | 0 | 0 | 0 | 600 |
| Configuration I estimated | 1.2 | 3.8 | 0.9 | 0.7 | 1.0 | 0.1 | 570 |
| Configuration II ground truth | 0 | 15 | 0 | 0 | 0 | 0 | 600 |
| Configuration II estimated | 0.5 | 14.2 | 0.8 | 0.3 | 1.1 | 0.4 | 610 |
| Configuration III ground truth | 10 | 5 | 0 | 0 | 0 | 0 | 600 |
| Configuration III estimated | 8.7 | 4.0 | 0.8 | 0.7 | 1.0 | 0.1 | 570 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pecheux, N.; Creuze, V.; Comby, F.; Tempier, O. Self Calibration of a Sonar–Vision System for Underwater Vehicles: A New Method and a Dataset. Sensors 2023, 23, 1700. https://doi.org/10.3390/s23031700
Pecheux N, Creuze V, Comby F, Tempier O. Self Calibration of a Sonar–Vision System for Underwater Vehicles: A New Method and a Dataset. Sensors. 2023; 23(3):1700. https://doi.org/10.3390/s23031700
Chicago/Turabian StylePecheux, Nicolas, Vincent Creuze, Frédéric Comby, and Olivier Tempier. 2023. "Self Calibration of a Sonar–Vision System for Underwater Vehicles: A New Method and a Dataset" Sensors 23, no. 3: 1700. https://doi.org/10.3390/s23031700
APA StylePecheux, N., Creuze, V., Comby, F., & Tempier, O. (2023). Self Calibration of a Sonar–Vision System for Underwater Vehicles: A New Method and a Dataset. Sensors, 23(3), 1700. https://doi.org/10.3390/s23031700







