A Novel Ionospheric Disturbance Index to Evaluate the Global Effect on BeiDou Navigation Satellite System Signal Caused by the Moderate Geomagnetic Storm on May 12, 2021
Abstract
:1. Introduction
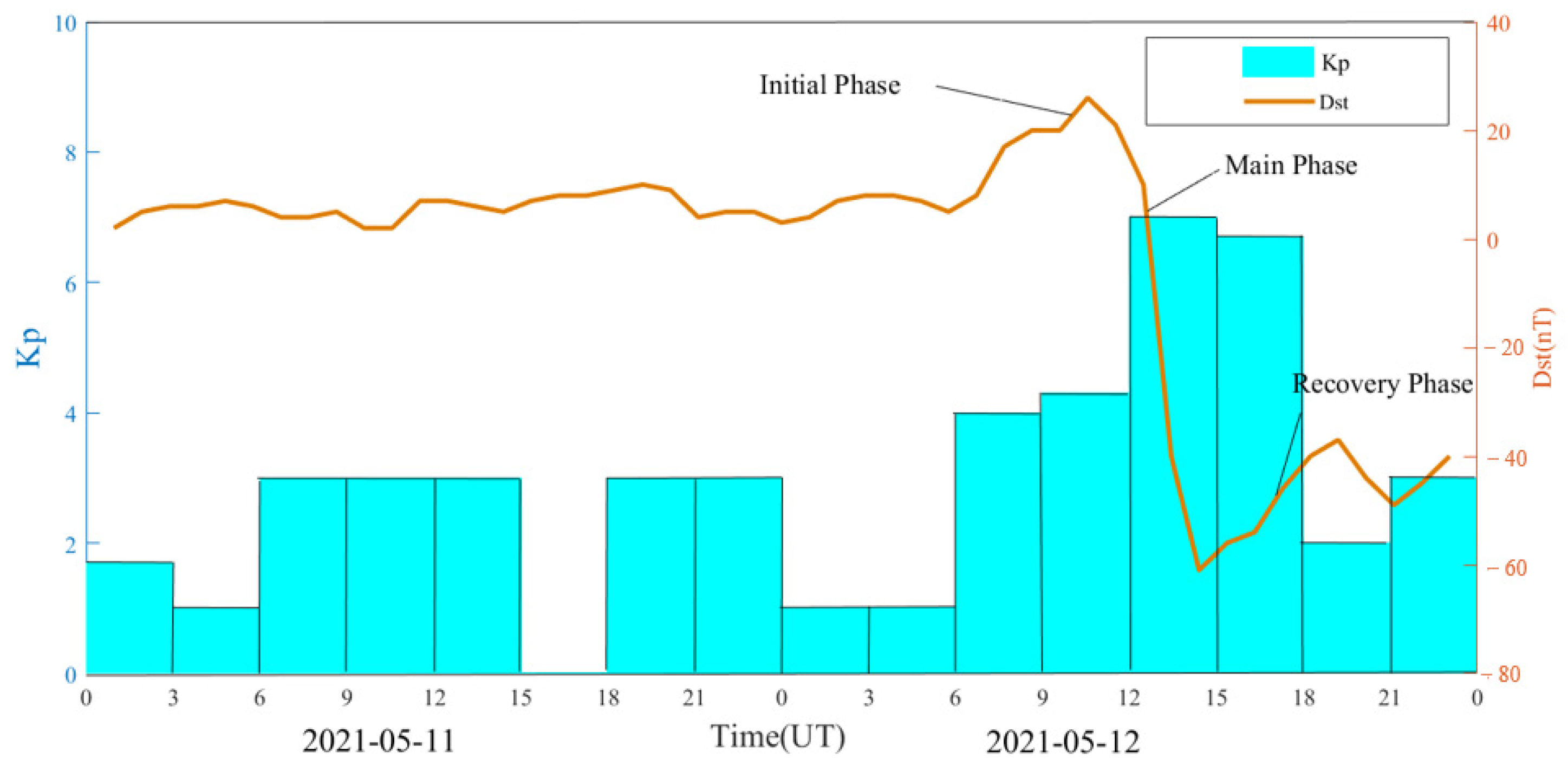
2. Geomagnetic Storm Event and Data Source
3. Definition of GNSS Observation Signal Quality Evaluation Index
3.1. Index Definition
3.2. Data Processing
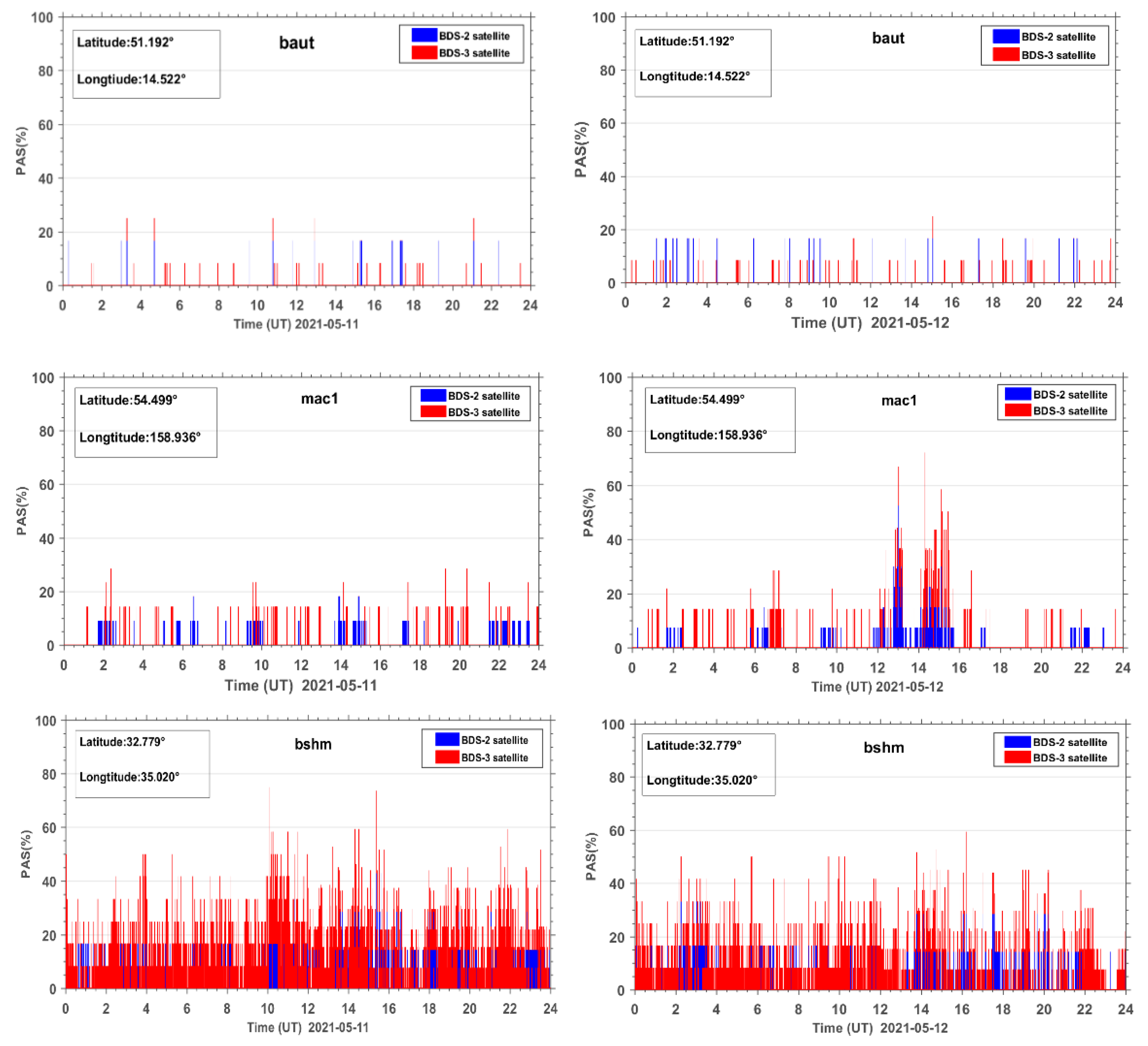
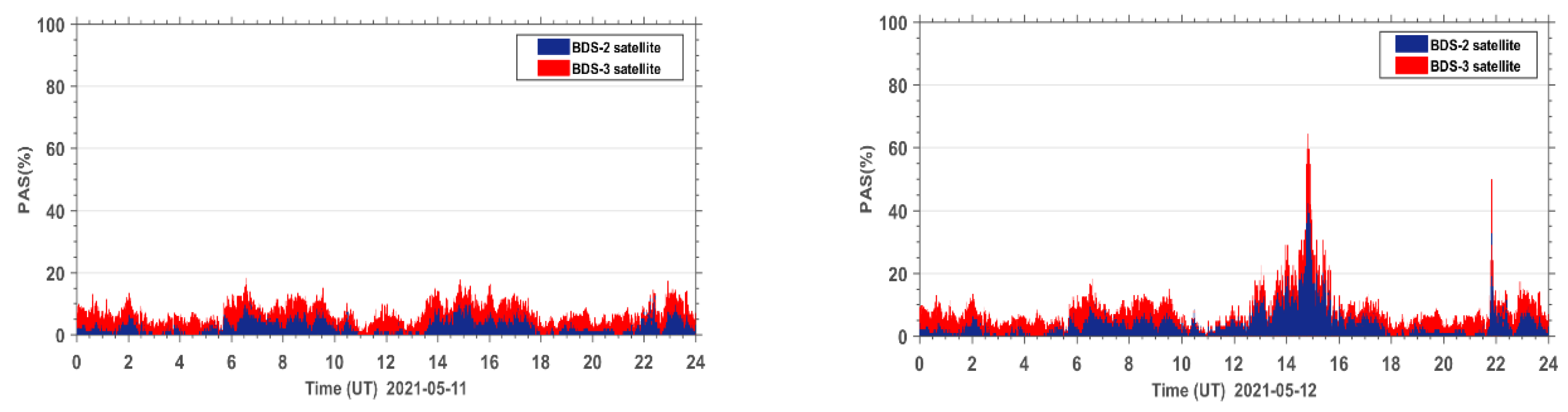
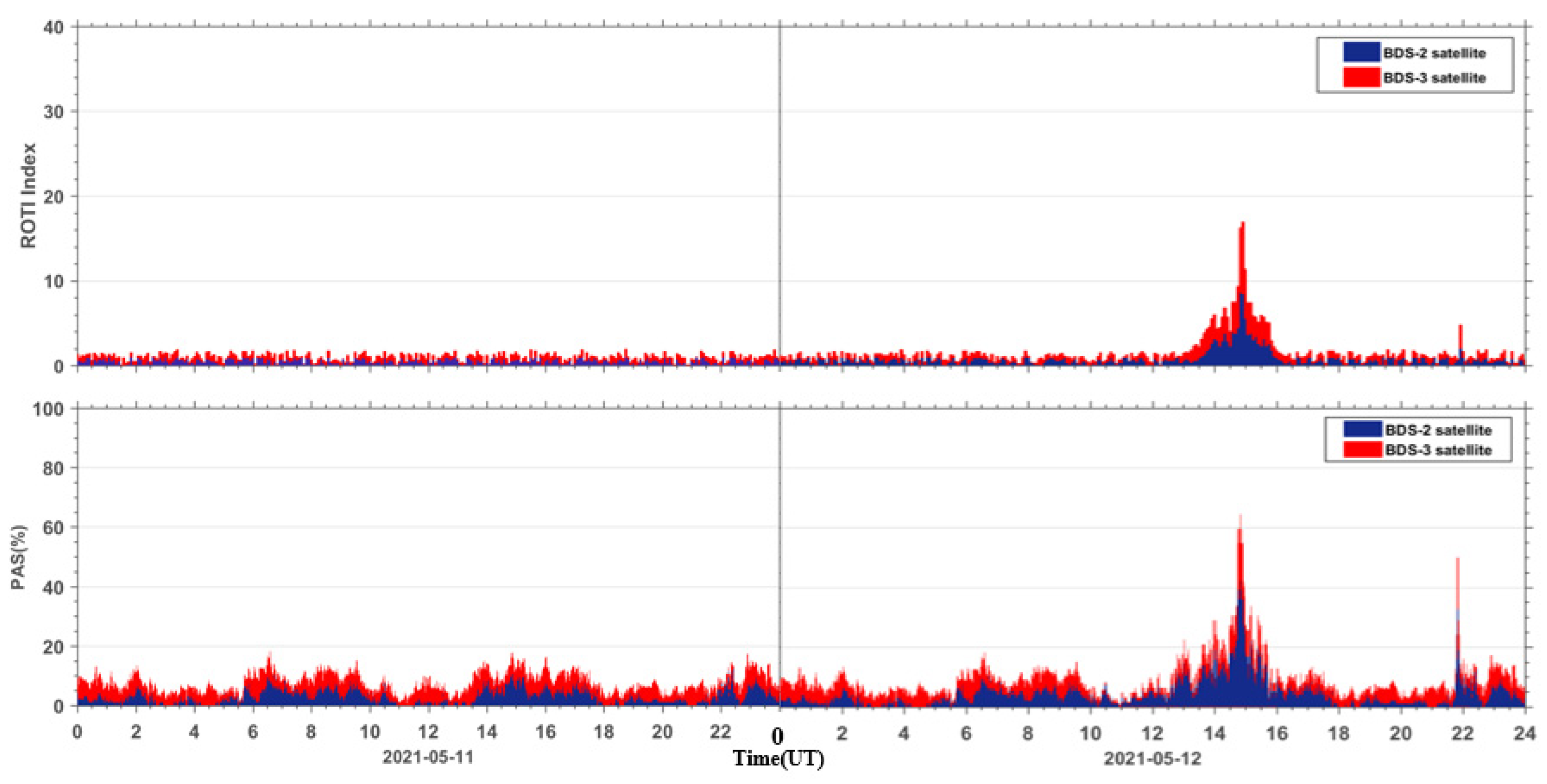
4. Results
5. Discussion
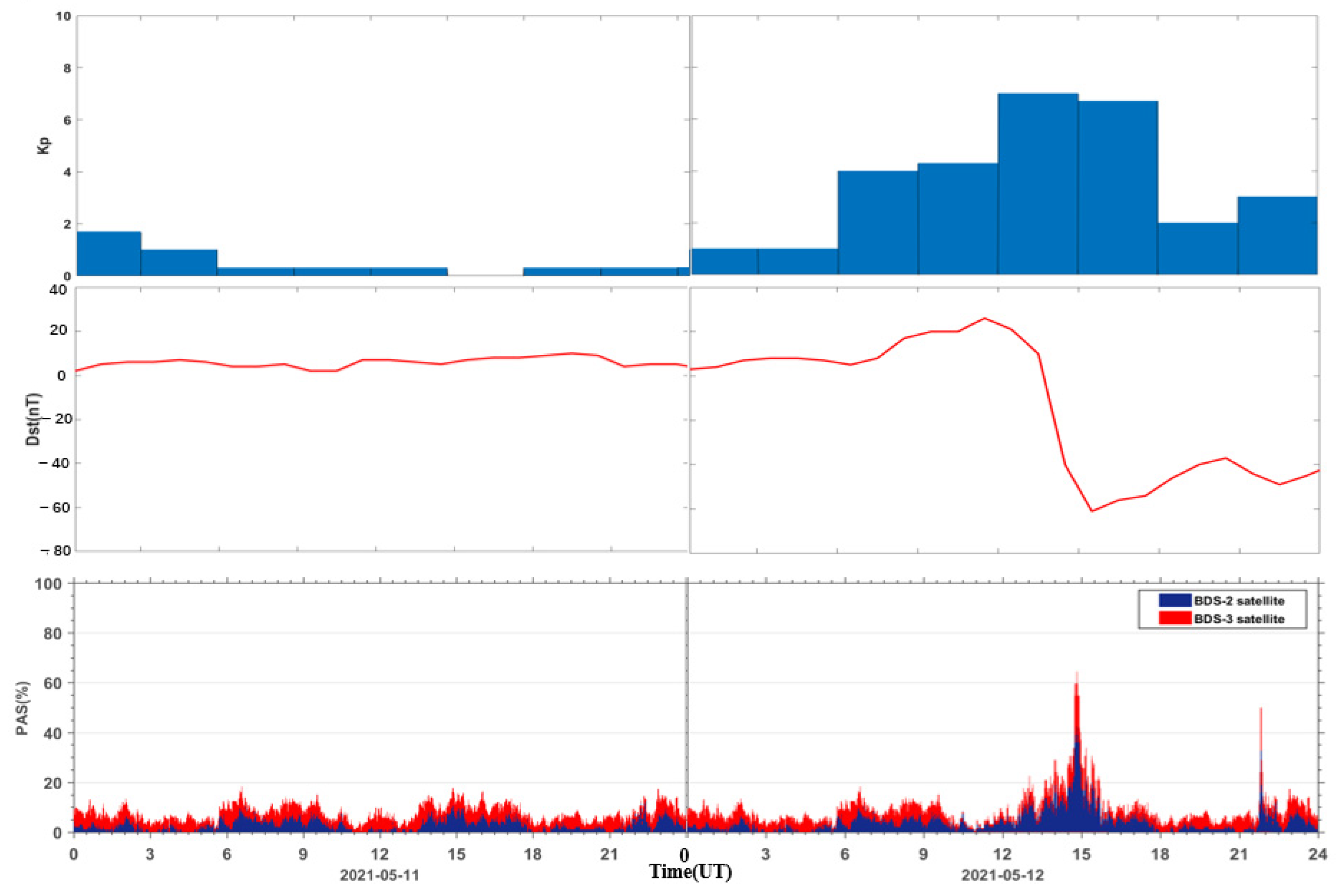
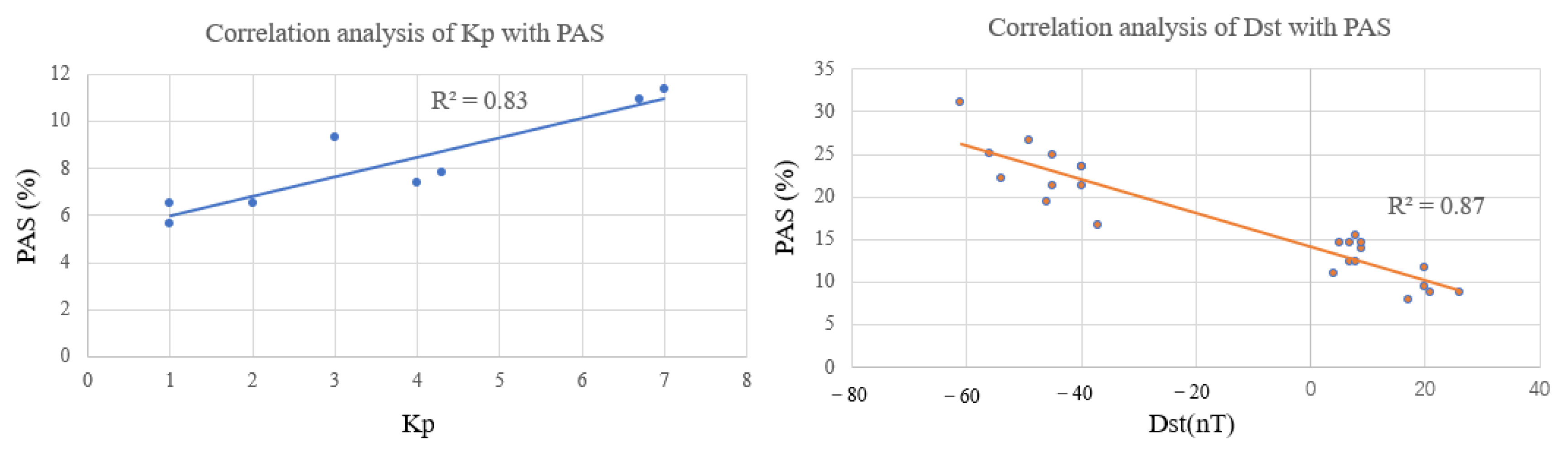
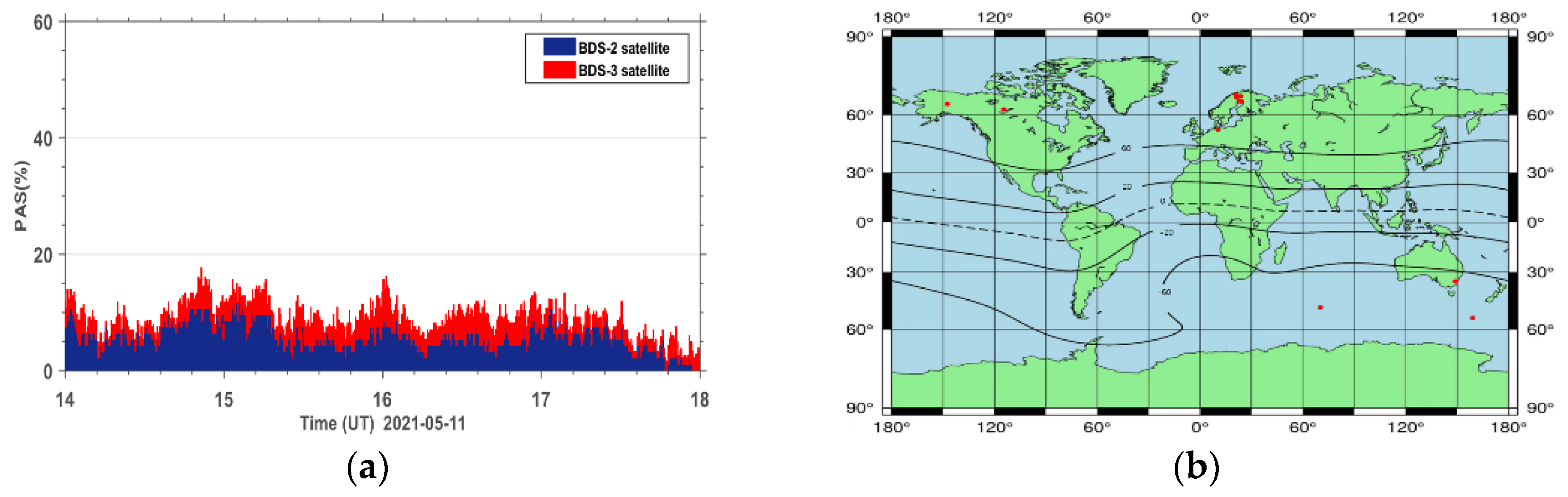
5.1. Temporal Correlation between the Geomagnetic Storm Index and the PAS Index
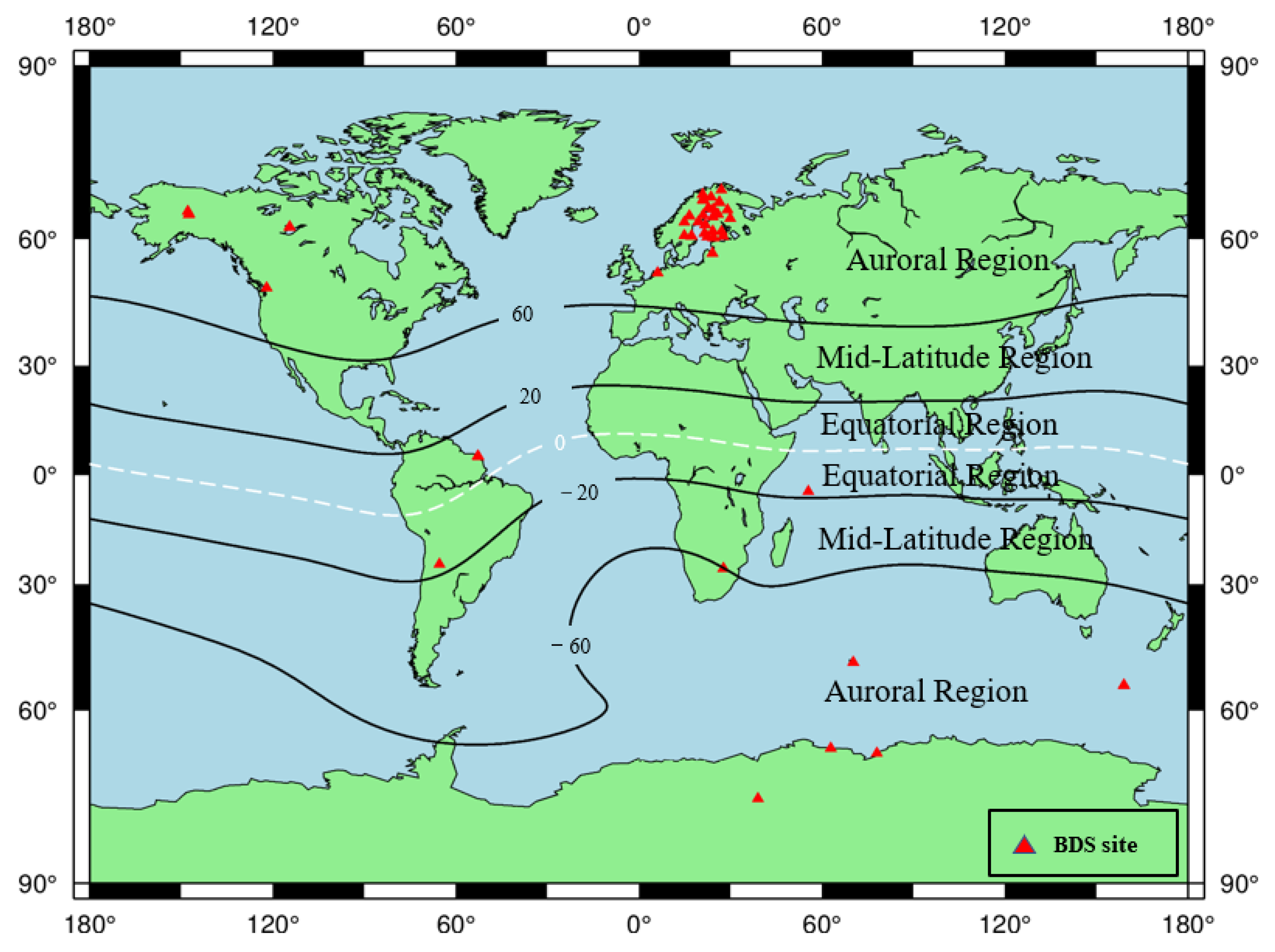
5.2. Spatial Distribution of the Affected BDS Sites during the Geomagnetic Storm
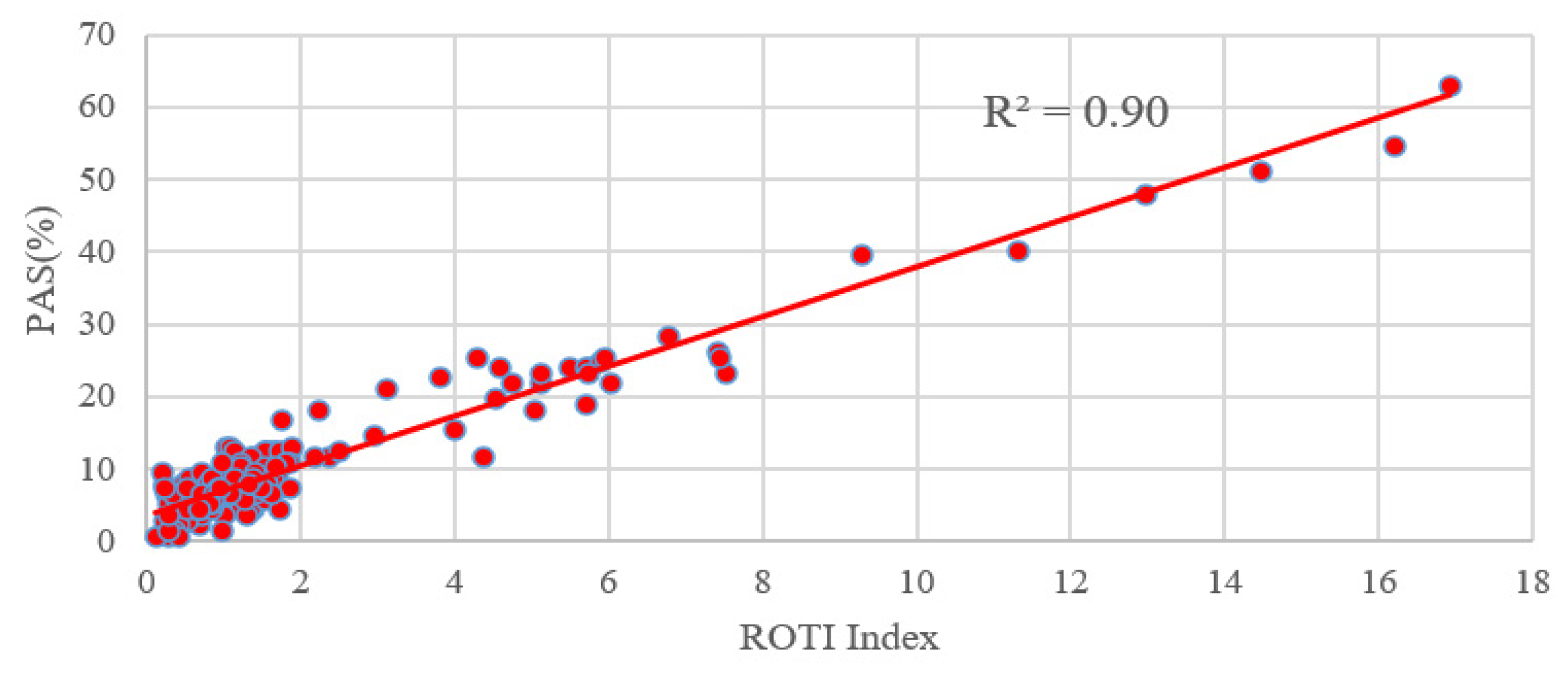
5.3. Comparison between the PAS Index and the ROTI Index
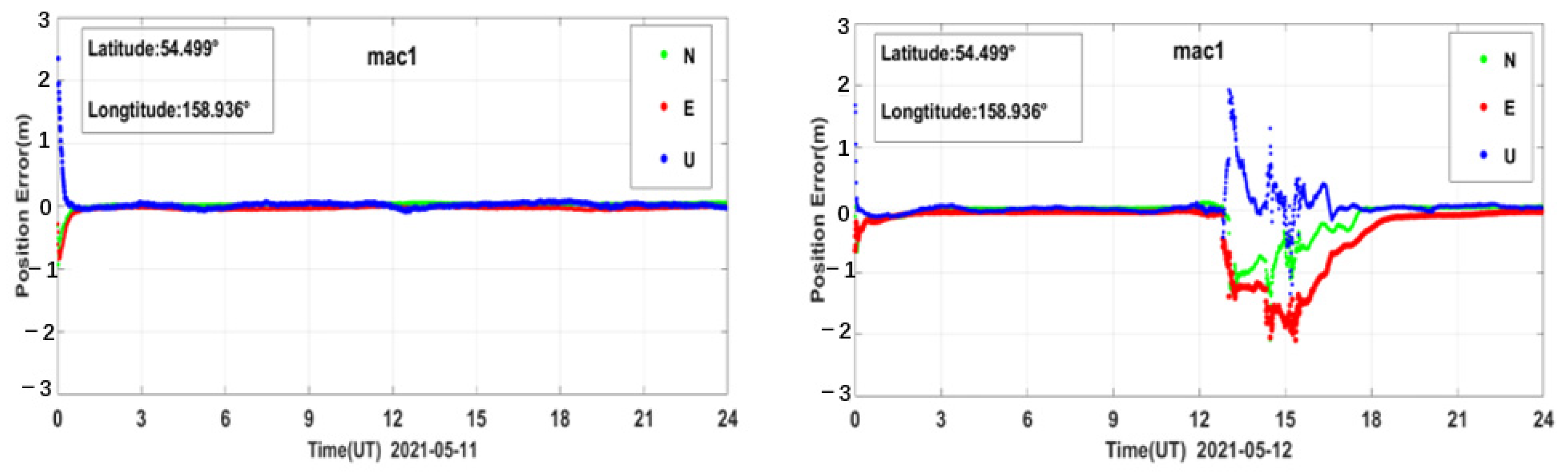
5.4. Effect of the Geomagnetic Storm on Precision Point Positioning (PPP)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aa, E.; Huang, W.; Liu, S.; Ridley, A.; Zou, S.; Shi, L.; Chen, Y.; Shen, H.; Yuan, T.; Li, J. Midlatitude plasma bubbles over China and adjacent areas during a magnetic storm on 8 September 2017. Space Weather 2018, 16, 321–331. [Google Scholar] [CrossRef]
- Szuszczewicz, E.; Lester, M.; Wilkinson, P.; Blanchard, P.; Abdu, M.; Hanbaba, R.; Igarashi, K.; Pulinets, S.; Reddy, B. A comparative study of global ionospheric responses to intense magnetic storm conditions. J. Geophys. Res. Space Phys. 1998, 103, 11665–11684. [Google Scholar] [CrossRef]
- Song, Q.; Ding, F.; Wan, W.; Ning, B.; Zhao, B. Monitoring traveling ionospheric disturbances using the GPS network around China during the geomagnetic storm on 28 May 2011. Sci. China Earth Sci. 2013, 56, 718–726. [Google Scholar] [CrossRef]
- Jiao, Y.; Morton, Y.T. Comparison of the effect of high-latitude and equatorial ionospheric scintillation on GPS signals during the maximum of solar cycle 24. Radio Sci. 2015, 50, 886–903. [Google Scholar] [CrossRef]
- Zhao, D.; Li, W.; Li, C.; Hancock, C.M.; Roberts, G.W.; Wang, Q. Analysis on the ionospheric scintillation monitoring performance of ROTI extracted from GNSS observations in high-latitude regions. Adv. Space Res. 2022, 69, 142–158. [Google Scholar] [CrossRef]
- DasGupta, A.; Ray, S.; Paul, A.; Banerjee, P.; Bose, A. Errors in position-fixing by GPS in an environment of strong equatorial scintillations in the Indian zone. Radio Sci. 2004, 39, 1–8. [Google Scholar] [CrossRef]
- Jacobsen, K.S.; Andalsvik, Y.L. Overview of the 2015 St. Patrick’s day storm and its consequences for RTK and PPP positioning in Norway. J. Space Weather Space Clim. 2016, 6, A9. [Google Scholar] [CrossRef]
- Paziewski, J.; Sieradzki, R.; Baryla, R. Multi-GNSS high-rate RTK, PPP and novel direct phase observation processing method: Application to precise dynamic displacement detection. Meas. Sci. Technol. 2018, 29, 035002. [Google Scholar] [CrossRef]
- Gao, Z.; Ge, M.; Li, Y.; Shen, W.; Zhang, H.; Schuh, H. Railway irregularity measuring using Rauch-Tung-Striebel smoothed multi-sensors fusion system: Quad-GNSS PPP, IMU, odometer, and track gauge. GPS Solut. 2018, 22, 36. [Google Scholar] [CrossRef]
- Specht, M.; Specht, C.; Dąbrowski, P.; Czaplewski, K.; Smolarek, L.; Lewicka, O. Road Tests of the Positioning Accuracy of INS/GNSS Systems Based on MEMS Technology for Navigating Railway Vehicles. Energies 2020, 13, 4463. [Google Scholar] [CrossRef]
- Yeh, K.; Liu, C. Radio Wave Scintillations in the Ionosphere. Proc. IEEE 1982, 70, 324–360. [Google Scholar]
- Pi, X.; Mannucci, A.; Lindqwister, U.; Ho, C. Monitoring of global ionospheric irregularities using the worldwide GPS network. Geophys. Res. Lett. 1997, 24, 2283–2286. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Lesyuta, O.S.; Ushakov, I.I.; Voeykov, S.V. Geomagnetic storms and the occurrence of phase slips in the reception of GPS signals. Ann. Geophys. 2002, 45, 55–71. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Demyanov, V.V.; Kondakova, T.N. Degradation of performance of the navigation GPS system in geomagnetically disturbed conditions. GPS Solut. 2003, 7, 109–119. [Google Scholar] [CrossRef] [Green Version]
- Sanz, J.; Juan, J.M.; González-Casado, G.; Prieto-Cerdeira, R.; Schlueter, S.; Orús, R. Novel ionospheric activity indicator specifically tailored for GNSS users. In Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS + 2014), Tampa, FL, USA, 8–12 September 2014; pp. 1173–1182. [Google Scholar]
- Juan, J.M.; Aragon-Angel, A.; Sanz, J.; González-Casado, G.; Rovira-Garcia, A. A method for scintillation characterization using geodetic receivers operating at 1 Hz. J. Geod. 2017, 91, 1383–1397. [Google Scholar] [CrossRef] [Green Version]
- Wilken, V.; Kriegel, M.; Jakowski, N.; Berdermann, J. An ionospheric index suitable for estimating the degree of ionospheric perturbations. J. Space Weather Space Clim. 2018, 8, A19. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Gu, S.; Lou, Y.; Cai, L.; Liu, Z. Amplitude scintillation index derived from C/N0 measurements released by common geodetic GNSS receivers operating at 1 Hz. J. Geod. 2020, 94, 27. [Google Scholar] [CrossRef]
- Yue, X.; Schreiner, W.S.; Pedatella, N.M.; Kuo, Y.H. Characterizing GPS radio occultation loss of lock due to ionospheric weather. Space Weather 2016, 14, 285–299. [Google Scholar] [CrossRef] [Green Version]
- Kun, D.; Yonghui, M.; Minbo, L.; Zhixiong, G.; Shu, W. Observations of TEC depletion, periodic structure of TEC, ROTI and scintillation associated with ESF irregularities over South China. Chin. J. Space Sci. 2020, 40, 331–340. [Google Scholar]
- Xu, F.; Zishen, L.; Zhang, K.; Ningbo, W.; Wu, S.; Andong, H.; Holden, L. An investigation of optimal machine learning methods for the prediction of ROTI. J. Geod. Geoinf. Sci. 2020, 3, 1. [Google Scholar]
- Ge, W.; Ningbo, W.; Zishen, L.; Kai, Z.; Ang, L. Impact of Geomagnetic Storms on Ionosphere Variability and Precise Point Positioning Application in High Latitudes of the Northern Hemisphereormalsize. Chin. J. Space Sci. 2021, 41, 261–272. [Google Scholar]
- Jiayan, W.; Weimin, Z.; Ming, O.; Xiao, Y.; Longjiang, C. A Characterization Method of Global Ionospheric Irregularities Activities Based on GNSS Data. Chin. J. Space Sci. 2022, 42, 82–90. [Google Scholar]
- He, L.-M.; Zhang, S.-X.; Wu, L.-X. Influence of Strong Geomagnetic Storms on Global GNSS Observation Signals. J. Northeast. Univ. (Nat. Sci.) 2019, 40, 1480. [Google Scholar]
- Zhang, S.; He, L.; Wu, L. Statistical study of loss of GPS signals caused by severe and great geomagnetic storms. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027749. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Wang, E.; Chen, J.; Feng, S.; Wang, D.; Dai, L. Advances in BeiDou Navigation Satellite System (BDS) and satellite navigation augmentation technologies. Satell. Navig. 2020, 1, 12. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, Q.; Li, M.; Tang, W.; Hu, Z.; Lou, Y.; Zhang, H.; Niu, X.; Liu, J. Precise orbit determination of Beidou Satellites with precise positioning. Sci. China Earth Sci. 2012, 55, 1079–1086. [Google Scholar] [CrossRef]
- Loewe, C.; Prölss, G. Classification and mean behavior of magnetic storms. J. Geophys. Res. Space Phys. 1997, 102, 14209–14213. [Google Scholar] [CrossRef]
- Zhu, S.; Yue, D.; He, L.; Chen, J.; Liu, Z. Modeling and performance assessment of BDS-2/BDS-3 triple-frequency ionosphere-free and uncombined precise point positioning. Measurement 2021, 180, 109564. [Google Scholar] [CrossRef]
- Luo, X.; Du, J.; Lou, Y.; Gu, S.; Yue, X.; Liu, J.; Chen, B. A method to mitigate the effects of strong geomagnetic storm on GNSS precise point positioning. Space Weather 2022, 20, e2021SW002908. [Google Scholar] [CrossRef]
- Blewitt, G. An automatic editing algorithm for GPS data. Geophys. Res. Lett. 1990, 17, 199–202. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Wang, S. Effect of selection of combined observations on cycle-slip repair success rate for BDS triple-frequency signals. Adv. Space Res. 2020, 66, 2914–2925. [Google Scholar] [CrossRef]
- Luo, X.; Lou, Y.; Gu, S.; Song, W. A strategy to mitigate the ionospheric scintillation effects on BDS precise point positioning: Cycle-slip threshold model. Remote Sens. 2019, 11, 2551. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Mi, J.; Cheng, P.; Yuan, Y.; Gan, X. A cycle slip repair method against ionospheric effects and observational noises for BDS triple-frequency undifferenced phases. Sensors 2020, 20, 2819. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Jin, X.; Wu, M.; Hu, J.; Wu, Y. A new real-time cycle slip detection and repair method under high ionospheric activity for a triple-frequency GPS/BDS receiver. Sensors 2018, 18, 427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Q.; Wang, G.; Liu, Z.; Hu, Z.; Dai, Z.; Liu, J. Analysis of BeiDou Satellite Measurements with Code Multipath and Geometry-Free Ionosphere-Free Combinations. Sensors 2016, 16, 123. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Ning, B.; Ren, Z.; Hu, L. Statistics of GPS ionospheric scintillation and irregularities over polar regions at solar minimum. GPS Solut. 2010, 14, 331–341. [Google Scholar] [CrossRef]
- Jin, Y.; Moen, J.I.; Miloch, W.J. On the colocation of the cusp aurora and the GPS phase scintillation: A statistical study. J. Geophys. Res. Space Phys. 2015, 120, 9176–9191. [Google Scholar] [CrossRef]
- van der Meeren, C.; Oksavik, K.; Lorentzen, D.A.; Paxton, L.J.; Clausen, L.B. Scintillation and irregularities from the nightside part of a Sun-aligned polar cap arc. J. Geophys. Res. 2016, 121, 5723–5736. [Google Scholar] [CrossRef] [Green Version]
- Cherniak, I.; Zakharenkova, I.; Sokolovsky, S. Multi-instrumental observation of storm-induced ionospheric plasma bubbles at equatorial and middle latitudes. J. Geophys. Res. Space Phys. 2019, 124, 1491–1508. [Google Scholar] [CrossRef]
- Chen, H.; Liu, X.; Jiang, W.; Yuan, P.; Ju, B.; Chen, Y. Preliminary analysis and evaluation of BDS-2/BDS-3 precise point positioning. Adv. Space Res. 2021, 68, 4113–4128. [Google Scholar] [CrossRef]
- Su, K.; Jin, S.; Hoque, M.M. Evaluation of ionospheric delay effects on multi-GNSS positioning performance. Remote Sens. 2019, 11, 171. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Li, X.; Yu, W.; Dai, W.; Kuang, C.; Chen, J.; Chen, F.; Xia, P. Performance evaluation of real-time precise point positioning with both BDS-3 and BDS-2 observations. Sensors 2020, 20, 6027. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Xia, L.; Wu, D.; Xia, J.; Li, Q. Study on Multi-GNSS Precise Point Positioning Performance with Adverse Effects of Satellite Signals on Android Smartphone. Sensors 2020, 20, 6447. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Zhang, Y.; Yang, S.; Chen, Q.; Gong, X. Modeling and assessment of GPS/BDS combined precise point positioning. Sensors 2016, 16, 1151. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Kubo, N.; Chen, J.; Wang, J.; Wang, H. Initial Positioning Assessment of BDS New Satellites and New Signals. Remote Sens. 2019, 11, 1320. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Wang, Z.; Ji, S.; Chen, W. Assessing the positioning performance under the effects of strong ionospheric anomalies with multi-GNSS in Hong Kong. Radio Sci. 2020, 55, 1–18. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, H.; He, C.; Wang, Z.; Shao, W.; Zhang, Y.; Wang, J. Initial performance evaluation of precise point positioning with triple-frequency observations from BDS-2 and BDS-3 satellites. J. Navig. 2020, 73, 763–775. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, X.; Liu, C.; Zhu, S.; Liu, Z.; Yue, D. Evaluating the latest performance of precise point positioning in multi-GNSS/RNSS: GPS, GLONASS, BDS, Galileo and QZSS. J. Navig. 2021, 74, 247–267. [Google Scholar] [CrossRef]







| Satellite Signal Status | Coefficients | |||
|---|---|---|---|---|
| k1 | k2 | k3 | ||
| Satellite signal loss | 1 | 0 | 0 | |
| Satellite signal exists | LLI = 1~7 | 0 | 1 | 0 |
| LLI = 0 or Blank | 0 | 0 | 1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Guo, C.; Yue, Q.; Zhang, S.; Qin, Z.; Zhang, J. A Novel Ionospheric Disturbance Index to Evaluate the Global Effect on BeiDou Navigation Satellite System Signal Caused by the Moderate Geomagnetic Storm on May 12, 2021. Sensors 2023, 23, 1183. https://doi.org/10.3390/s23031183
He L, Guo C, Yue Q, Zhang S, Qin Z, Zhang J. A Novel Ionospheric Disturbance Index to Evaluate the Global Effect on BeiDou Navigation Satellite System Signal Caused by the Moderate Geomagnetic Storm on May 12, 2021. Sensors. 2023; 23(3):1183. https://doi.org/10.3390/s23031183
Chicago/Turabian StyleHe, Liming, Cong Guo, Quanyou Yue, Shixuan Zhang, Zenghui Qin, and Junfei Zhang. 2023. "A Novel Ionospheric Disturbance Index to Evaluate the Global Effect on BeiDou Navigation Satellite System Signal Caused by the Moderate Geomagnetic Storm on May 12, 2021" Sensors 23, no. 3: 1183. https://doi.org/10.3390/s23031183







