Liquid Level Sensor with Two FBGs Embedded in a PDMS Diaphragm: Analysis of the Linearity and Sensitivity
Abstract
:1. Introduction
2. Operating Principle and Experimental Configuration
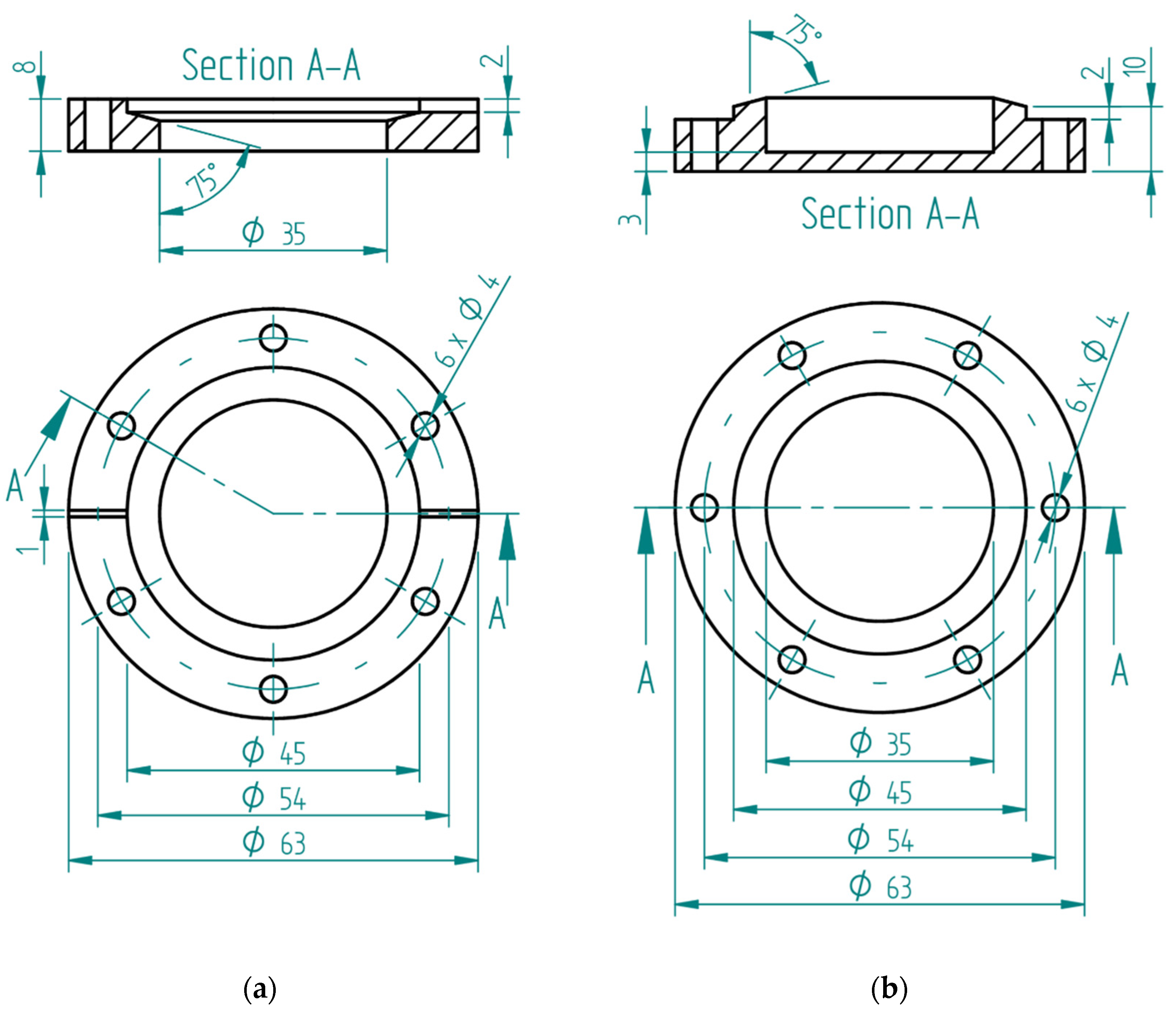
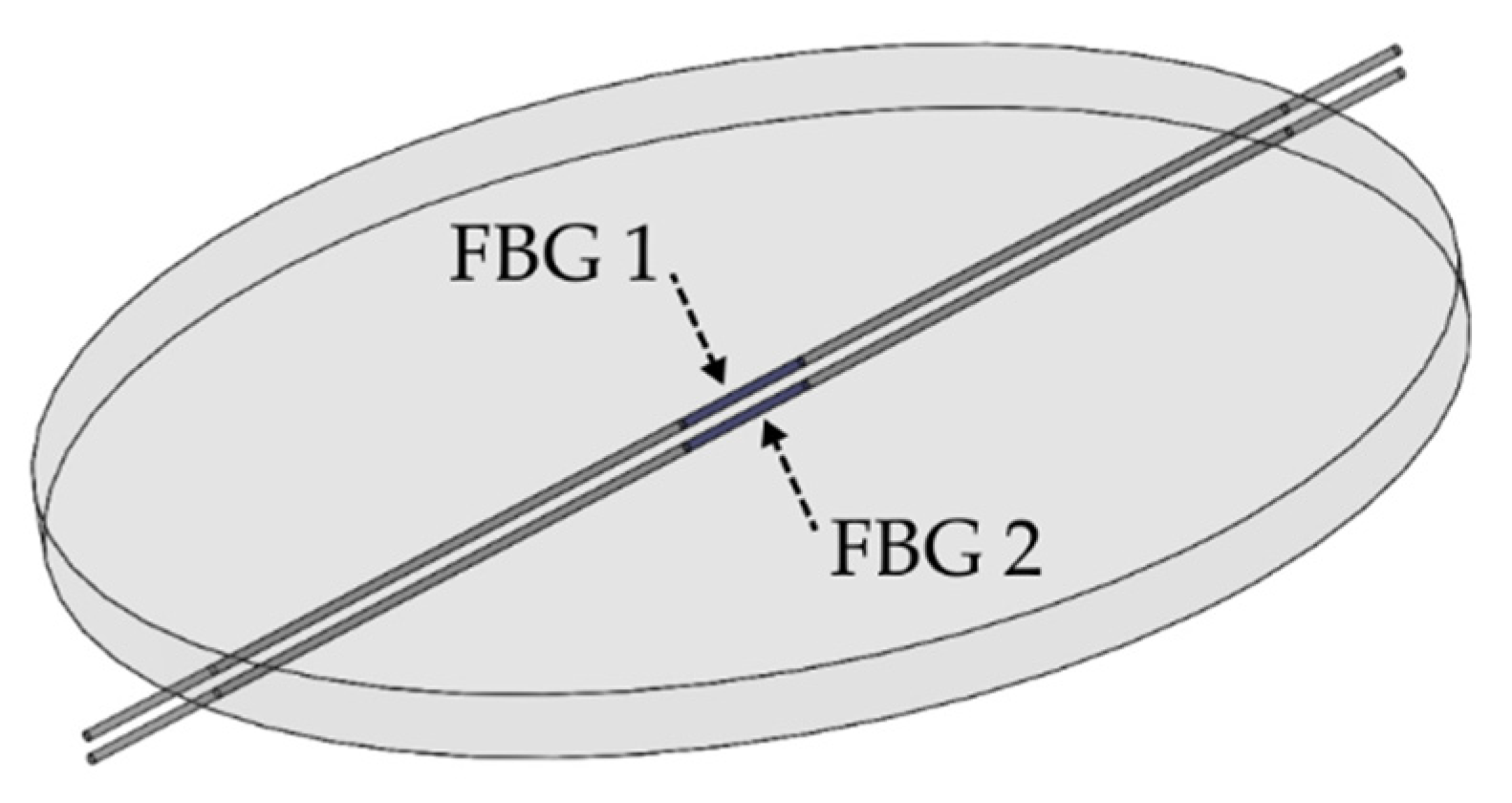
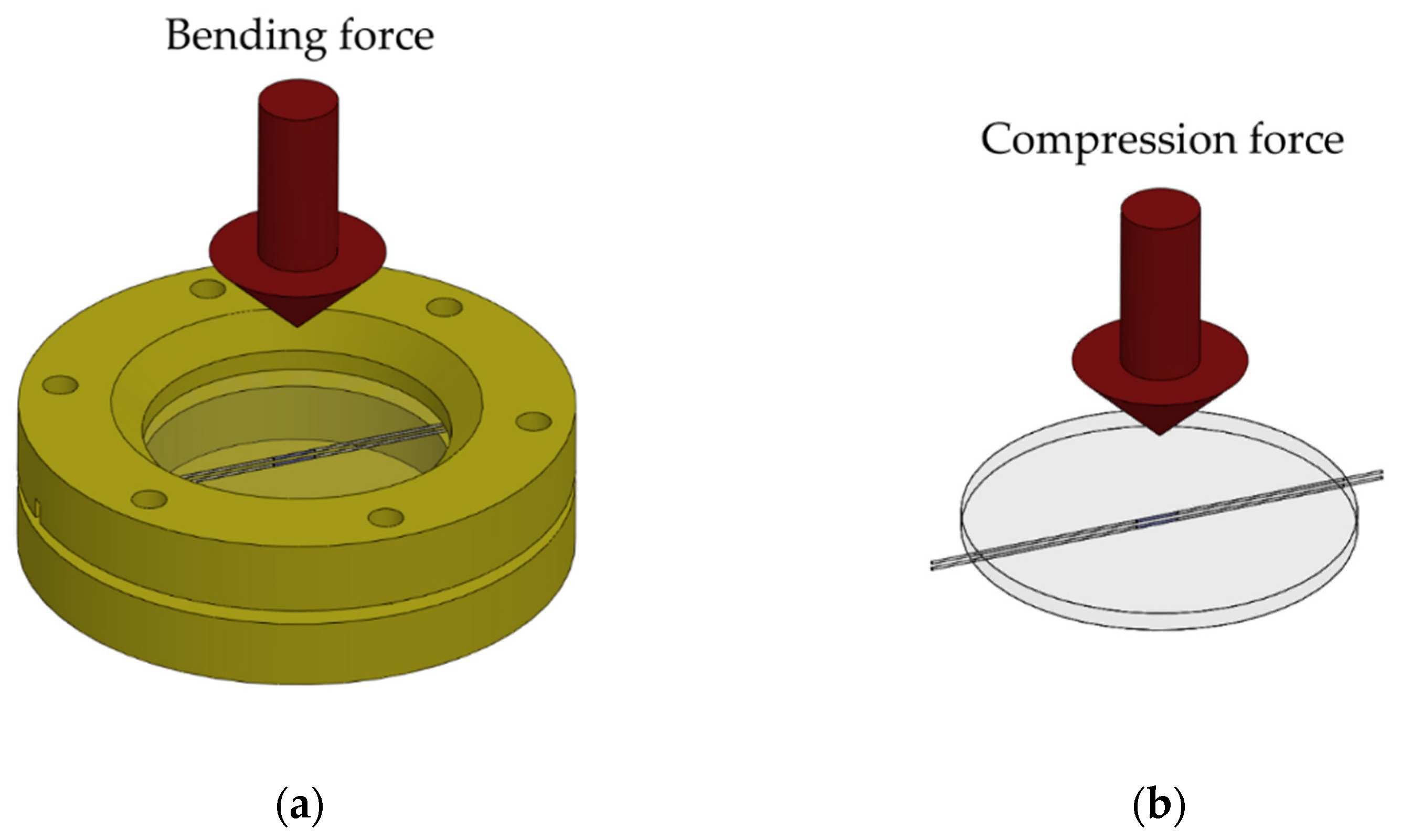
2.1. Operating Principle
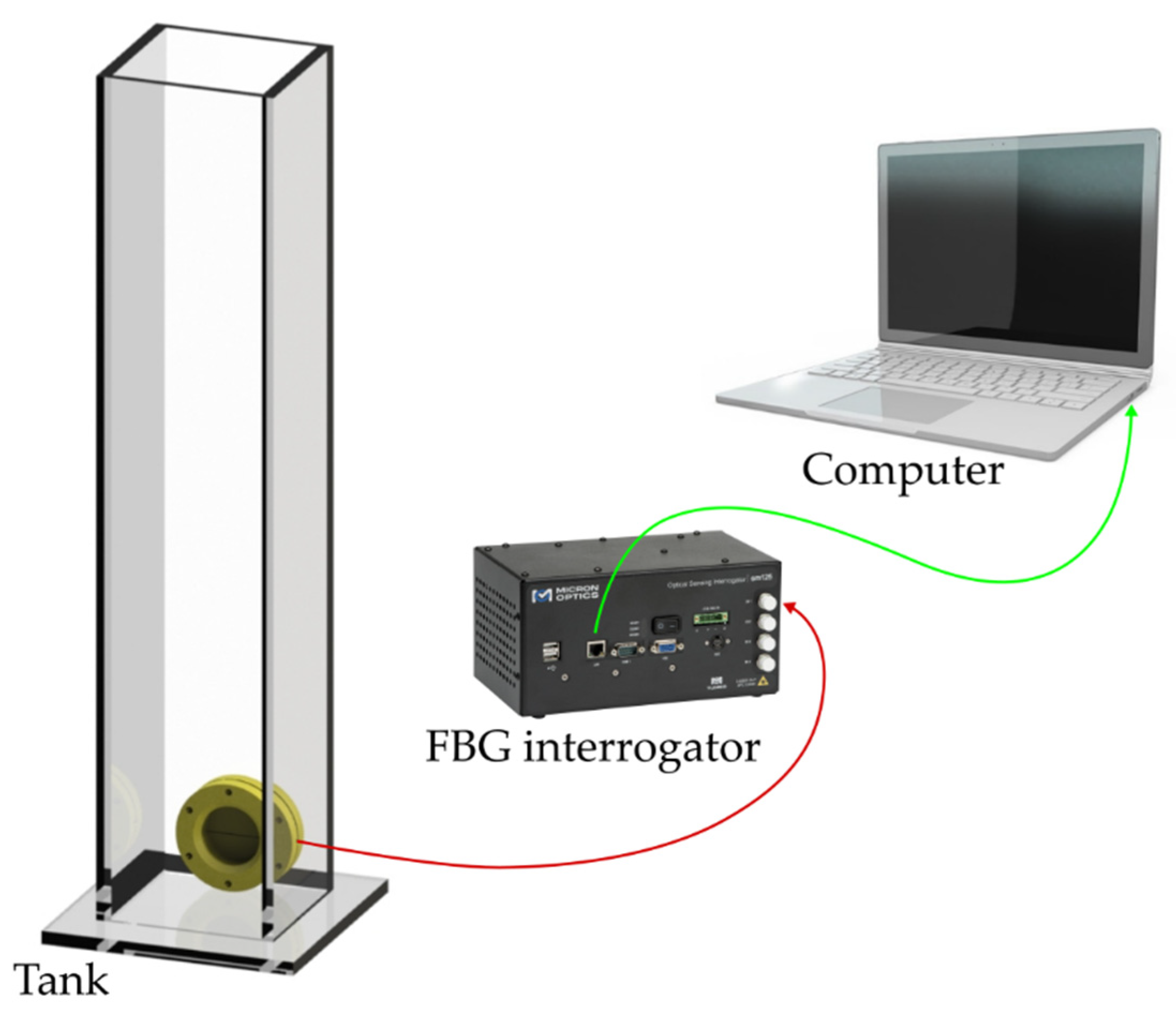
2.2. Experimental Configuration
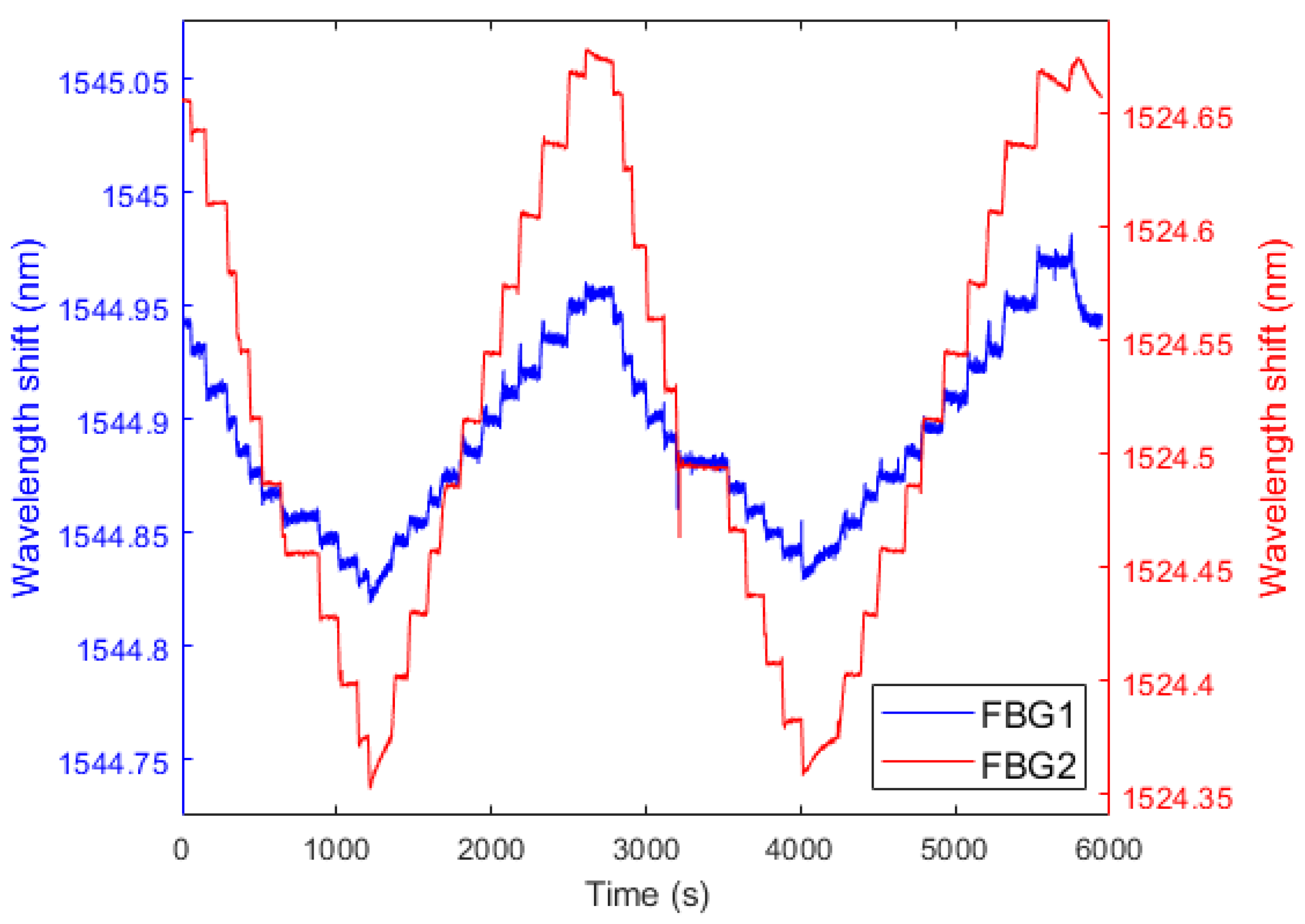
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
References
- Alwis, L.; Sun, T.; Grattan, K.T.V. Developments in optical fibre sensors for industrial applications. Opt. Laser Technol. 2016, 78, 62–66. [Google Scholar] [CrossRef]
- Roriz, P.; Frazão, O.; Lobo-Ribeiro, A.B.; Santos, J.L.; Simões, J.A. Review of fiber-optic pressure sensors for biomedical and biomechanical applications. J. Biomed. Opt. 2013, 18, 050903. [Google Scholar] [CrossRef] [PubMed]
- Broadway, C.; Kinet, D.; Theodosiou, A.; Kalli, K.; Gusarov, A.; Caucheteur, C.; Mégret, P. CYTOP fibre Bragg grating sensors for harsh radiation environments. Sensors 2019, 19, 2853. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, B.; Chen, Z.; Zhang, Y.; Gao, S.; He, S. Active fiber gas sensor for methane detecting based on a laser heated fiber Bragg grating. IEEE Photonics Technol. Lett. 2014, 26, 1069–1072. [Google Scholar] [CrossRef]
- Yazdizadeh, Z.; Marzouk, H.; Hadianfard, M.A. Monitoring of concrete shrinkage and creep using Fiber Bragg Grating sensors. Constr. Build. Mater. 2017, 137, 505–512. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Rocha, H.R.O.; Theodosiou, A.; Frizera, A.; Marques, C.; Kalli, K.; Ribeiro, M.R.N. Optimizing linearity and sensitivity of 3D-printed diaphragms with chirped FBGs in CYTOP fibers. IEEE Access 2020, 8, 31983–31991. [Google Scholar] [CrossRef]
- Díaz, C.A.R.; Leal-Junior, A.; Marques, C.; Frizera, A.; Pontes, M.J.; Antunes, P.F.C.; André, P.S.B.; Ribeiro, M.R.N. Optical fiber sensing for sub-millimeter liquid-level monitoring: A review. IEEE Sens. J. 2019, 19, 7179–7191. [Google Scholar] [CrossRef]
- Sun, C.; Dong, Y.; Wang, M.; Jian, S. Liquid level and temperature sensing by using dual-wavelength fiber laser based on multimode interferometer and FBG in parallel. Opt. Fiber Technol. 2018, 41, 212–216. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera, A.; Marques, C. A fiber Bragg gratings pair embedded in a polyurethane diaphragm: Towards a temperature-insensitive pressure sensor. Opt. Laser Technol. 2020, 131, 106440. [Google Scholar] [CrossRef]
- Marques, C.A.F.; Pospori, A.; Sáez-Rodríguez, D.; Nielsen, K.; Bang, O.; Webb, D.J. Fibre optic liquid level monitoring system using microstructured polymer fibre Bragg grating array sensors: Performance analysis. In Proceedings of the 24th International Conference on Optical Fibre Sensors, Curitiba, Brazil, 28 September–2 October 2015. [Google Scholar]
- Lee, B.H.; Kim, Y.H.; Park, K.S.; Eom, J.B.; Kim, M.J.; Rho, B.S.; Choi, H.Y. Interferometric fiber optic sensors. Sensors 2012, 12, 2467–2486. [Google Scholar] [CrossRef] [Green Version]
- Hill, K.O.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Light. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef] [Green Version]
- Liang, M.F.; Fang, X.Q.; Wu, G.; Xue, G.Z.; Li, H.W. A fiber Bragg grating pressure sensor with temperature compensation based on diaphragm-cantilever structure. Optik 2017, 145, 503–512. [Google Scholar] [CrossRef]
- Liang, M.; Fang, X.; Ning, Y. Temperature compensation fiber Bragg grating pressure sensor based on plane diaphragm. Photonic Sens. 2018, 8, 157–167. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Zhou, Z.; Wen, X.; Zhang, D. A diaphragm-type fiber Bragg grating pressure sensor with temperature compensation. Measurement 2013, 46, 1041–1046. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Frizera, A.; Marques, C. Thermal and mechanical analyses of fiber Bragg gratings-embedded polymer diaphragms. IEEE Photonics Technol. Lett. 2020, 32, 623–626. [Google Scholar] [CrossRef]
- Kinet, D.; Mégret, P.; Goossen, K.W.; Qiu, L.; Heider, D.; Caucheteur, C. Fiber Bragg grating sensors toward structural health monitoring in composite materials: Challenges and solutions. Sensors 2014, 14, 7394–7419. [Google Scholar] [CrossRef]
- Ahmad, H.; Harun, S.W.; Chong, W.Y.; Zulkifli, M.Z.; Thant, M.M.M.; Yusof, Z.; Poopalan, P. High-sensitivity pressure sensor using a polymer-embedded FBG. Microw. Opt. Technol. Lett. 2008, 50, 60–61. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, H.; Zhao, Q.; Liu, Y.; Li, F. Temperature-independent FBG pressure sensor with high sensitivity. Opt. Fiber Technol. 2007, 13, 78–80. [Google Scholar] [CrossRef]
- Vilarinho, D.; Theodosiou, A.; Leitão, C.; Leal-Junior, A.G.; Domingues, M.D.F.; Kalli, K.; André, P.; Antunes, P.; Marques, C. POFBG-embedded cork insole for plantar pressure monitoring. Sensors 2017, 17, 2924. [Google Scholar] [CrossRef] [Green Version]
- Grandal, T.; Zornoza, A.; López, A.; Fraga, S.; Sun, T.; Grattan, K.T. Analysis of fiber optic sensor embedded in metals by automatic and manual TIG welding. IEEE Sens. J. 2019, 19, 7425–7433. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, H.K.; Lv, R.Q.; Yang, Y. A practical FBG pressure sensor based on diaphragm-cantilever. Sens. Actuators A Phys. 2018, 279, 101–106. [Google Scholar] [CrossRef]
- Srimannarayana, K.; Rao, P.V.; Shankar, M.S.; Kishore, P. FBG sensor for temperature-independent high sensitive pressure measurement with aid of a Bourdon tube. Proc. SPIE 2014, 9141, 91412E. [Google Scholar]
- Song, D.; Zou, J.; Wei, Z.; Chen, Z.; Cui, H. Liquid-level sensor using a fiber Bragg grating and carbon fiber composite diaphragm. Opt. Eng. 2011, 50, 014401. [Google Scholar] [CrossRef]
- Al-Fakih, E.A.; Osman, N.A.A.; Adikan, F.R.M.; Eshraghi, A.; Jahanshahi, P. Development and validation of fiber Bragg grating sensing pad for interface pressure measurements within prosthetic sockets. IEEE Sens. J. 2015, 16, 965–974. [Google Scholar] [CrossRef]
- Li, T.; Shi, C.; Tan, Y.; Li, R.; Zhou, Z.; Ren, H. A diaphragm type fiber Bragg grating vibration sensor based on transverse property of optical fiber with temperature compensation. IEEE Sens. J. 2016, 17, 1021–1029. [Google Scholar] [CrossRef]
- Marques, C.A.F.; Peng, G.D.; Webb, D.J. Highly sensitive liquid level monitoring system utilizing polymer fiber Bragg gratings. Opt. Express 2015, 23, 6058–6072. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, H.; Qian, X.; Zhang, Y.; An, G.; Zhao, Y. Recent advancements in optical fiber hydrogen sensors. Sens. Actuators B Chem. 2017, 244, 393–416. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Tan, Y.; Han, X.; Zheng, K.; Zhou, Z. Diaphragm based fiber Bragg grating acceleration sensor with temperature compensation. Sensors 2017, 17, 218. [Google Scholar] [CrossRef] [Green Version]
- Li, R.Y.; Tan, Y.G.; Bing, J.Y.; Li, T.L.; Hong, L.; Yan, J.W.; Hu, J.; Zhou, Z.D. A diaphragm-type highly sensitive fiber Bragg grating force transducer with temperature compensation. IEEE Sens. J. 2017, 18, 1073–1080. [Google Scholar] [CrossRef]
- Díaz, C.A.R.; Leal-Junior, A.G.; André, P.S.B.; da Costa Antunes, P.F.; Pontes, M.J.; Frizera-Neto, A.; Ribeiro, M.R.N. Liquid level measurement based on FBG-embedded diaphragms with temperature compensation. IEEE Sens. J. 2018, 18, 193–200. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera, A.; Díaz, C.; Marques, C.; Ribeiro, M.; Pontes, M.J. Material features based compensation technique for the temperature effects in a polymer diaphragm-based FBG pressure sensor. Opt. Express 2018, 26, 20590–20602. [Google Scholar] [CrossRef]
- Ameen, O.F.; Younus, M.H.; Aziz, M.S.; Azmi, A.I.; Ibrahim, R.K.R.; Ghoshal, S.K. Graphene diaphragm integrated FBG sensors for simultaneous measurement of water level and temperature. Sens. Actuators A Phys. 2016, 252, 225–232. [Google Scholar] [CrossRef]
- Vorathin, E.; Hafizi, Z.M.; Aizzuddin, A.M.; Lim, K.S. A natural rubber diaphragm based transducer for simultaneous pressure and temperature measurement by using a single FBG. Opt. Fiber Technol. 2018, 45, 8–13. [Google Scholar] [CrossRef]
- Her, S.C.; Weng, S.Z. Fiber Bragg Grating Pressure Sensor Integrated with Epoxy Diaphragm. Sensors 2021, 21, 3199. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Frizera, A.; Díaz, C.R.; Ribeiro, M.R.; Pontes, M.J. FBG-embedded oblong diaphragms with extended dynamic range. IEEE Sens. Lett. 2018, 2, 5000404. [Google Scholar] [CrossRef]
- Vaddadi, V.S.C.S.; Parne, S.R.; Afzulpurkar, S.; Desai, S.P.; Parambil, V.V. Design and development of pressure sensor based on Fiber Bragg Grating (FBG) for ocean applications. Eur. Phys. J. Appl. Phys. 2020, 90, 30501. [Google Scholar] [CrossRef]
- Sengupta, D.; Kishore, P. Continuous liquid level monitoring sensor system using fiber Bragg grating. Opt. Eng. 2014, 53, 017102. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Díaz, C.A.; Frizera, A.; Marques, C.; Ribeiro, M.R.; Pontes, M.J. Simultaneous measurement of pressure and temperature with a single FBG embedded in a polymer diaphragm. Opt. Laser Technol. 2019, 112, 77–84. [Google Scholar] [CrossRef]





| Reference | Temperature | Force/Pressure | Liquid Level | |||
|---|---|---|---|---|---|---|
| Sensitivity | Linearity | Sensitivity | Linearity | Sensitivity | Linearity | |
| This work | 11.73 pm/°C | 0.996 | 6.99 pm/N | 0.983 | −0.29 pm/mm | 0.992 |
| [35] | Not reported | Not reported | 175.5 pm/kPa | 0.999 | 1.62 pm/mm | 0.999 |
| [31] | 43.2 pm/°C | 0.999 | Not reported | Not reported | 2.74 pm/mm | 0.999 |
| [34] | 79.7 pm/°C | 0.955 | 100.7 pm/kPa | 0.997 | Not reported | Not reported |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morais, E.; Pontes, M.J.; Marques, C.; Leal-Junior, A. Liquid Level Sensor with Two FBGs Embedded in a PDMS Diaphragm: Analysis of the Linearity and Sensitivity. Sensors 2022, 22, 1268. https://doi.org/10.3390/s22031268
Morais E, Pontes MJ, Marques C, Leal-Junior A. Liquid Level Sensor with Two FBGs Embedded in a PDMS Diaphragm: Analysis of the Linearity and Sensitivity. Sensors. 2022; 22(3):1268. https://doi.org/10.3390/s22031268
Chicago/Turabian StyleMorais, Eliton, Maria José Pontes, Carlos Marques, and Arnaldo Leal-Junior. 2022. "Liquid Level Sensor with Two FBGs Embedded in a PDMS Diaphragm: Analysis of the Linearity and Sensitivity" Sensors 22, no. 3: 1268. https://doi.org/10.3390/s22031268






