Design and 3D FEM Analysis of a Flexible Piezoelectric Micromechanical Ultrasonic Transducer Based on Sc-Doped AlN Film
Abstract
:1. Introduction
2. Materials and Methods
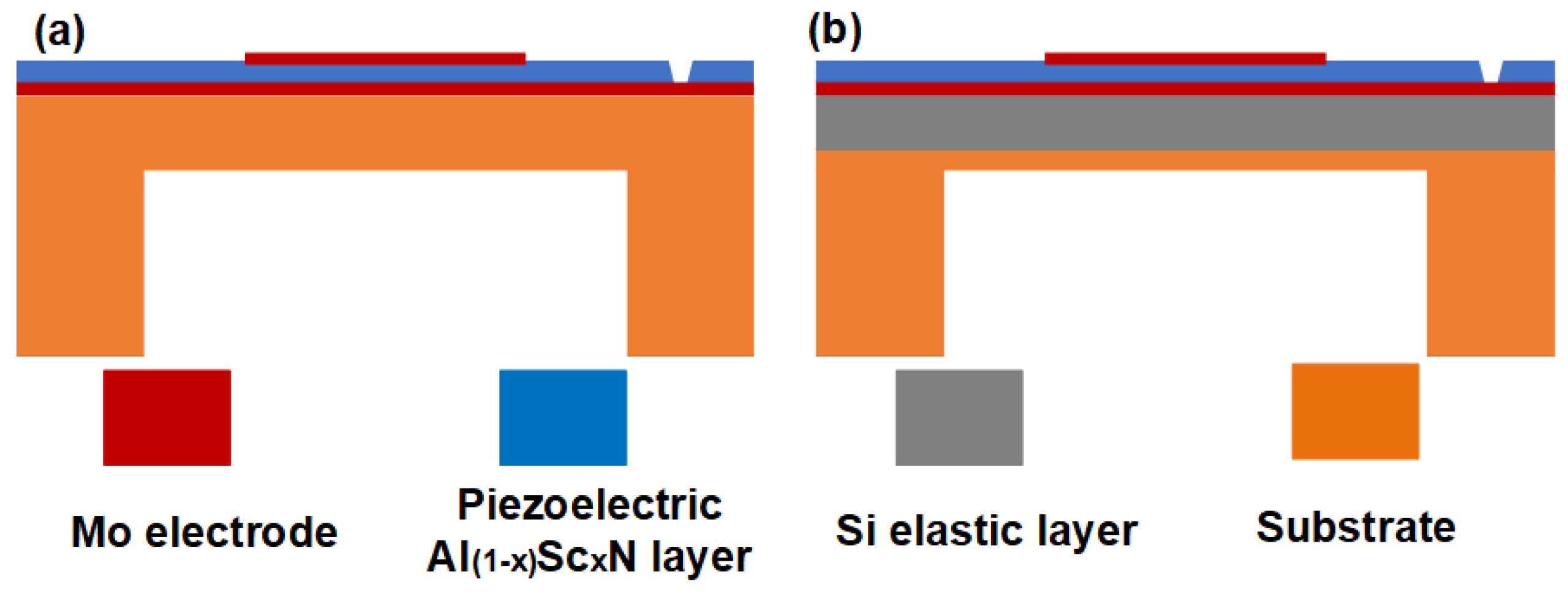
2.1. Device Structure
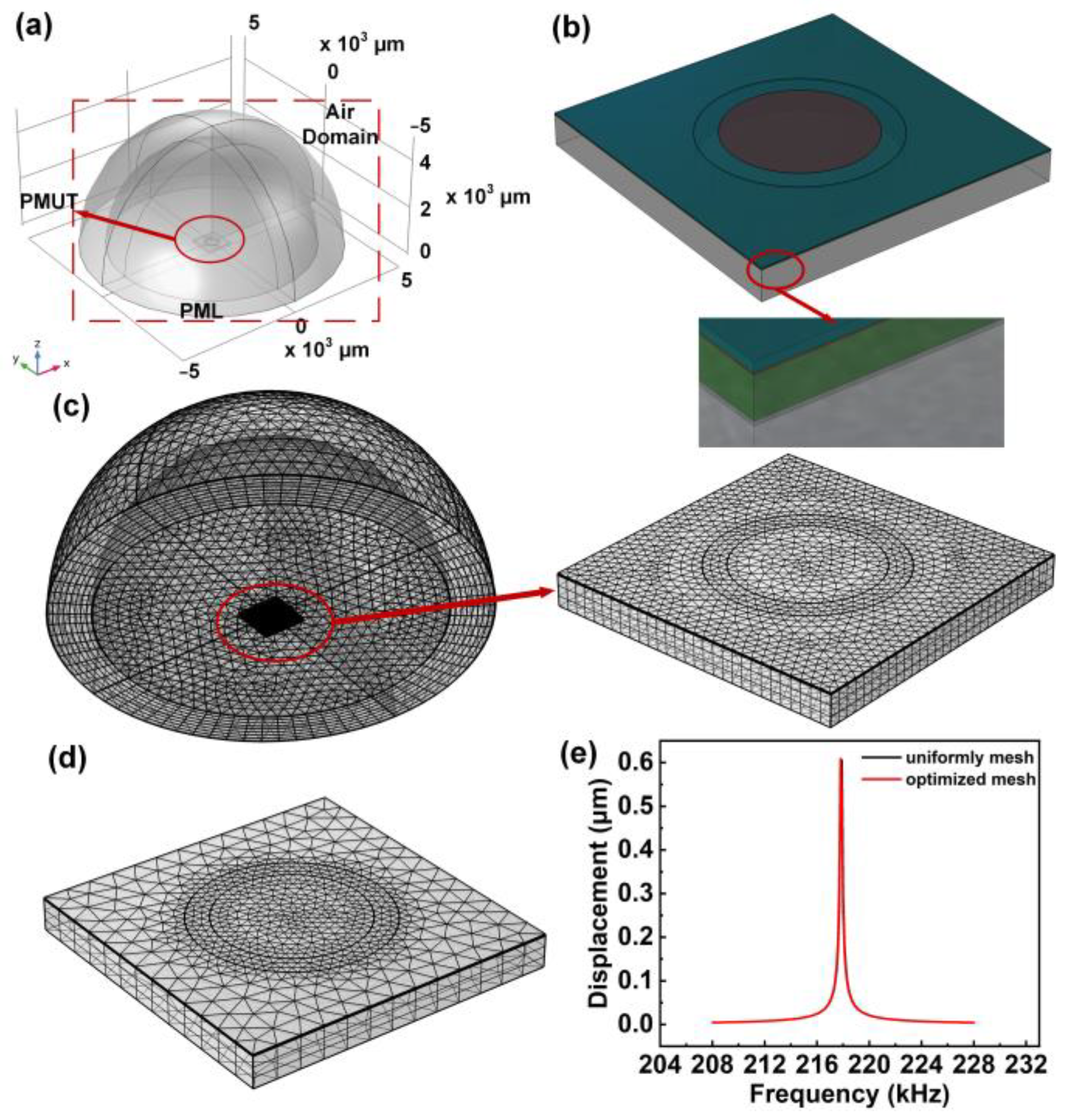
2.2. 3D-FEM Model and Mesh-Dependency Analysis
2.3. Mode Shape Selection
2.4. Evaluation of PMUT Properties
3. Results and Discussions
3.1. Basic Characteristics of PMUT
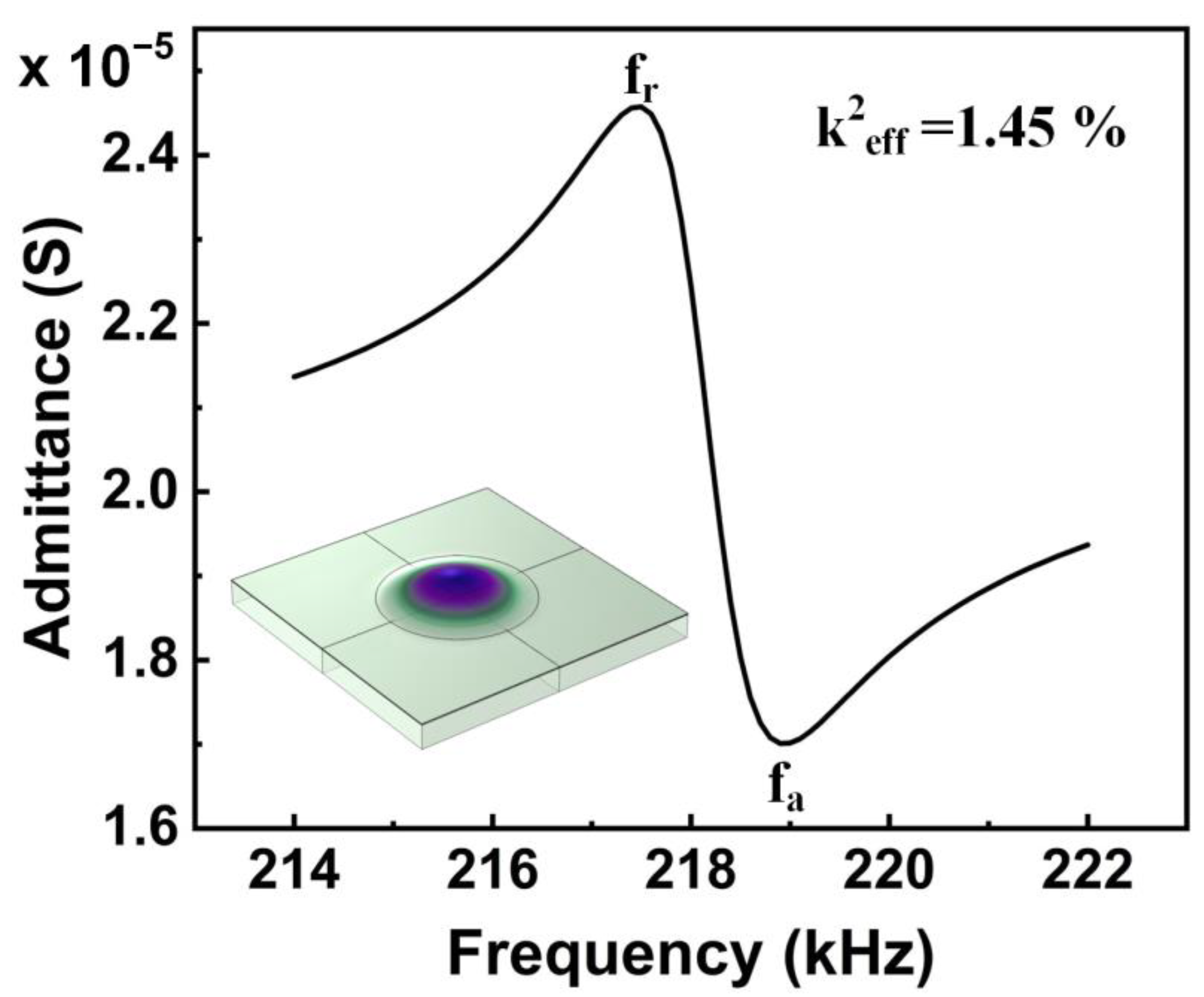
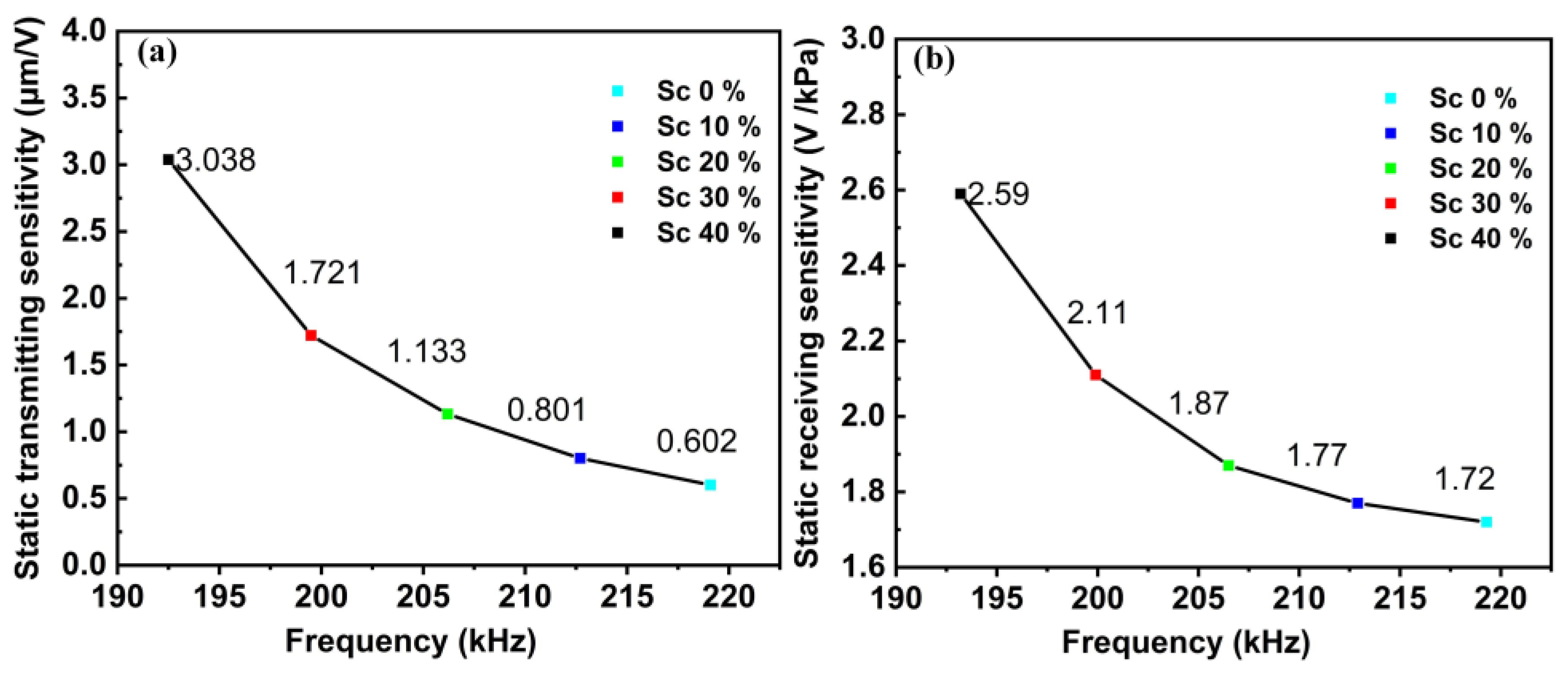
3.2. Piezoelectric Characteristics of PMUT with Different Sc Doping Concentrations in Al1-xScxN Piezoelectric Materials
3.3. Mechanical Properties
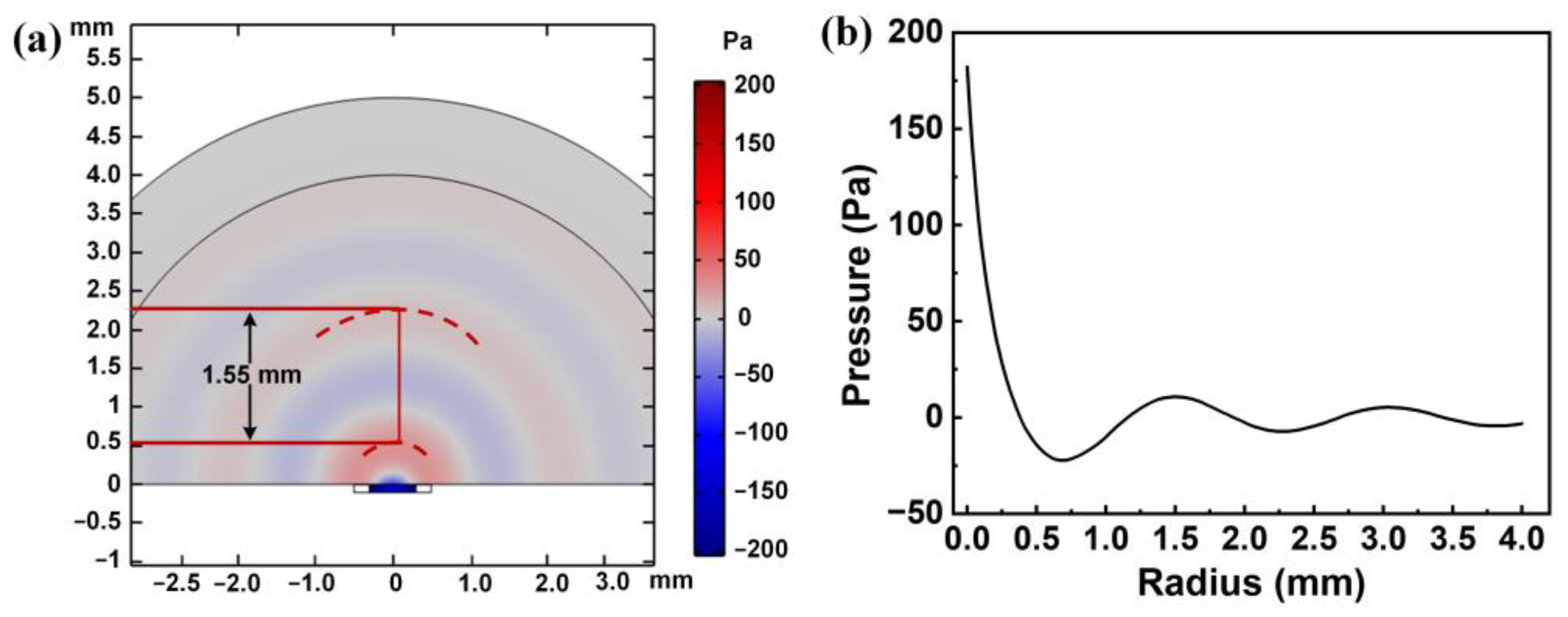
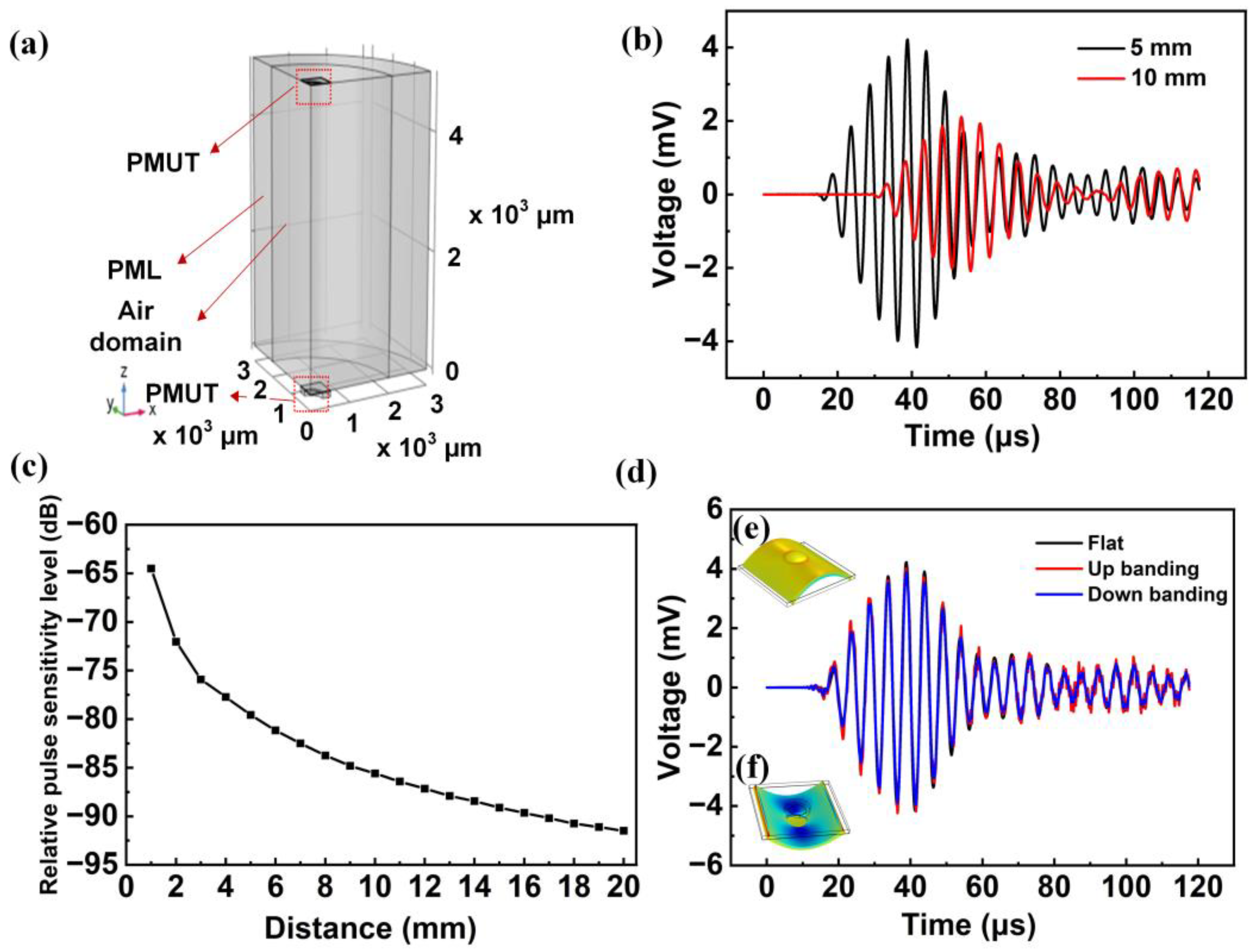
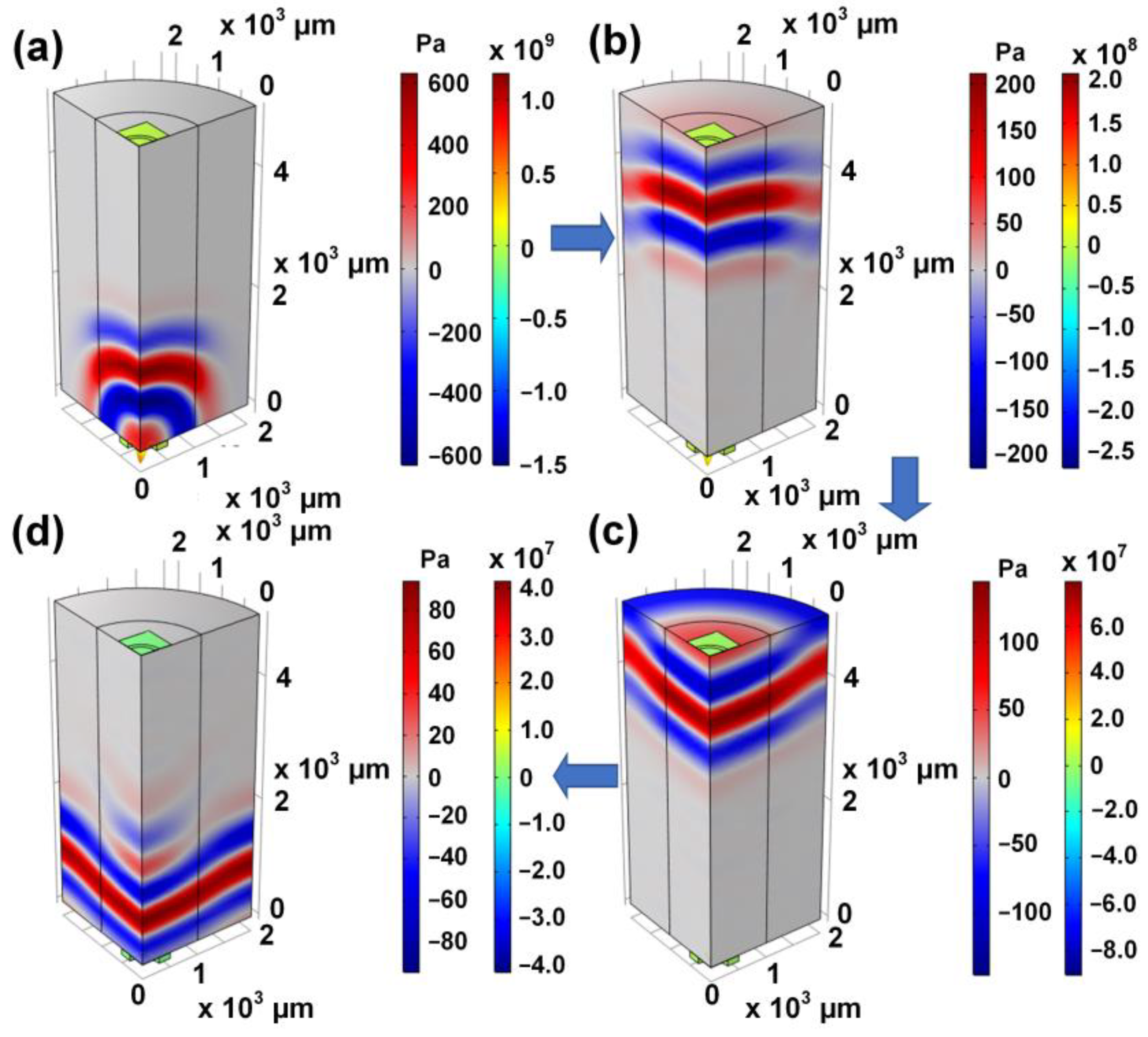
3.4. Dynamic Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, T.; Kobayashi, T.; Lee, C. Micromachined piezoelectric ultrasonic transducer with ultra-wide frequency bandwidth. Appl. Phys. Lett. 2015, 106, 1. [Google Scholar] [CrossRef] [Green Version]
- Dangi, A.; Cheng, C.Y.; Agrawal, S.; Tiwari, S.; Datta, G.R.; Benoit, R.R.; Pratap, R.; Trolier-Mckinstry, S.; Kothapalli, S.-R. A Photoacoustic Imaging Device Using Piezoelectric Micromachined Ultrasound Transducers (PMUTs). IEEE Trans. Ultra. Ferro. Freq. Control. 2020, 67, 801–809. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Tang, H.; Fung, S.; Wang, Q.; Tsai, J.M.; Daneman, M.; Boser, B.E.; Horsley, D.A. Ultrasonic fingerprint sensor using a piezoelectric micromachined ultrasonic transducer array integrated with complementary metal oxide semiconductor electronics. Appl. Phys. Lett. 2015, 106, 26. [Google Scholar] [CrossRef] [Green Version]
- Emadi, T.A.; Buchanan, D.A. Design and Characterization of a Capacitive Micromachined Transducer With a Deflectable Bottom Electrode. IEEE Electron Device Lett. 2015, 36, 612–614. [Google Scholar] [CrossRef]
- Joontaek, J.; Wonjun, L.; Woojin, K.; Eunjung, S.; Jungho, R.; Hongsoo, C. Review of piezoelectric micromachined ultrasonic transducers and their applications. Micromech. Microeng. 2017, 27, 0960–1317. [Google Scholar]
- Lu, Y.; Horsley, D.A. Modeling, Fabrication, and Characterization of Piezoelectric Micromachined Ultrasonic Transducer Arrays Based on Cavity SOI Wafers. J. Microelectromech. Syst. 2015, 24, 1142–1149. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Yang, H.; Jiang, H.; Xie, H. A Ceramic PZT-Based PMUT Array for Endoscopic Photoacoustic Imaging. J. Microelectromech. Syst. 2020, 29, 1038–1043. [Google Scholar] [CrossRef]
- Gong, D.; Ma, S.; Chiu, Y.; Lee, H.; Jin, Y. Study of the Properties of AlN PMUT used as a Wireless Power Receiver. In Proceedings of the 2019 IEEE 69th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 28–31 May 2019; pp. 1503–1508. [Google Scholar]
- Herrera, B.; Pop, F.; Cassella, C.; Rinaldi, M. AlN PMUT-based Ultrasonic Power Transfer Links for Implantable Electronics. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 861–864. [Google Scholar]
- Liu, W.; Wu, D. Low Temperature Adhesive Bonding-Based Fabrication of an Air-Borne Flexible Piezoelectric Micromachined Ultrasonic Transducer. Sensors 2020, 20, 3333. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, H.; Yan, B.; Sun, H.; Wu, C.; Shu, Y.; Ren, T.L. A flexible piezoelectric micromachined ultrasound transducer. Rsc Adv. 2013, 3, 24900–24905. [Google Scholar] [CrossRef]
- Zhe, W.; Xue, Q.T.; Chen, Y.Q.; Shu, Y.; Tian, H.; Yang, Y.; Xie, D.; Luo, J.W.; Ren, T.L. A Flexible Ultrasound Transducer Array with Micro-Machined Bulk PZT. Sensors 2015, 15, 2538–2547. [Google Scholar]
- Sadeghpour, S.; Lips, B.; Kraft, M.; Puers, R. Flexible Soi-Based Piezoelectric Micromachined Ultrasound Transducer (PMUT) Arrays. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 250–253. [Google Scholar]
- Liu, W.; Zhu, C.; Wu, D.; Yu, T. Flexible Piezoelectric Micro Ultrasonic Transducer Based on a Laser Processed Substrate. In Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7–11 September 2020; pp. 1–4. [Google Scholar]
- Liu, H.; Geng, J.; Zhu, Q.; Zhang, L.; Wang, F.; Chen, T.; Sun, L. Flexible Ultrasonic Transducer Array with Bulk PZT for Adjuvant Treatment of Bone Injury. Sensors 2020, 20, 86. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gijsenbergh, P.; Halbach, A.; Jeong, Y.; Cheyns, D.; Rottenberg, X.; Rochus, V. Polymer PMUT array for high-bandwidth underwater communications. In Proceedings of the 2020 IEEE SENSORS, Rotterdam, The Netherlands, 25–28 October 2020; pp. 1–4. [Google Scholar]
- Gao, H.; Rottenberg, X.; Rochus, V.; Gijsenbergh, P.; Halbach, A.; Serrahima, C.P.; Torri, G.B.; Jeong, Y.; Billen, M.; Cheyns, D.; et al. Design of polymer-based PMUT array for multi-frequency ultrasound imaging. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 6–9 October 2019; pp. 1092–1095. [Google Scholar]
- Joseph, J.; Singh, S.G.; Vanjari, S.R.K. Piezoelectric Micromachined Ultrasonic Transducer Using Silk Piezoelectric Thin Film. IEEE Electron Device Lett. 2018, 39, 749–752. [Google Scholar] [CrossRef]
- Zhao, M.H.; Wang, Z.L.; Mao, S.X. Piezoelectric characterization of individual zinc oxide nanobelt probed by piezoresponse force microscope. Nano Lett. 2004, 4, 587–590. [Google Scholar] [CrossRef]
- Guy, I.L.; Muensit, S.; Goldys, E.M. Extensional piezoelectric coefficients of gallium nitride and aluminum nitride. Appl. Phys. Lett. 1999, 75, 4133–4135. [Google Scholar] [CrossRef]
- Mastronardi, V.M.; Guido, F.; Amato, M.; Vittorio, M.D.; Petroni, S. Piezoelectric ultrasonic transducer based on flexible AlN. Microelectron. Eng. 2014, 121, 59–63. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, M.; Gao, C.; Liu, B.; Pang, W. Flexible Piezoelectric Micromachined Ultrasonic Transducers Towards New Applications. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018; pp. 1–4. [Google Scholar]
- Liu, W.; Li, X.; Wu, D.; Yu, T. Design and Fabrication of Flexible and Transparent Piezoelectric Micromachined Ultrasonic Transducer Based on Mica Substrates. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 6–9 October 2019; pp. 785–787. [Google Scholar]
- Liu, W.; He, L.; Wang, X.; Zhou, J.; Xu, W.; Smagin, N.; Toubal, M.; Yu, H.; Gu, Y.; Xu, J.; et al. 3D FEM Analysis of High-Frequency AlN-Based PMUT Arrays on Cavity SOI. Sensors 2019, 19, 4450. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, M.-Z.; Zhang, Q.-Z.; Zhao, X.-Y.; Wang, F.-F. Modeling and Simulation of Aluminium Nitride-Based Piezoelectric Micromachined Ultrasonic Transducer for Ultrasound Imaging. In Proceedings of the 2019 14th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Shijiazhuang, China, 1–4 November 2019; pp. 1–5. [Google Scholar]
- Meeker, T.R. Publication and Proposed Revision of ANSI/IEEE Standard 176-1987. ANSI/IEEE Standard on Piezoelectricity. IEEE Trans. Ultras. Ferroe., Freq. Control. 1996, 43, 717. [Google Scholar]
- Kim, J.; Lee, M.; Shim, H.J.; Ghaffari, R.; Cho, H.R.; Son, D.; Jung, Y.H.; Soh, M.; Choi, C.; Jung, S.; et al. Stretchable silicon nanoribbon electronics for skin prosthesis. Nat. Commun. 2014, 5, 5747. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Tang, H.-Y.; Fung, S.; Boser, B.E.; Horsley, D.A. Pulse-Echo Ultrasound Imaging Using an AlN Piezoelectric Micromachined Ultrasonic Transducer Array With Transmit Beam-Forming. J. Microelectromechanical Syst. 2016, 25, 179–187. [Google Scholar] [CrossRef]
- Chen, M.Z.; Zhang, Q.Z.; Zhao, X.Y.; Wang, F.F.; Liu, H.L.; Li, B.C.; Zhang, X.F.; Luo, H.S. Design and analysis of piezoelectric micromachined ultrasonic transducer using high coupling PMN-PT single crystal thin film for ultrasound imaging. Smart Mater. Struct. 2021, 964–1726. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, C.; Wu, D. Flexible piezoelectric micro ultrasonic transducer array integrated on various flexible substrates. Sensors Actuators A Phys. 2021, 317, 112476. [Google Scholar] [CrossRef]
- Sandu, C.S.; Parsapour, F.; Mertin, S.; Pashchenko, V.; Matloub, R.; LaGrange, T.; Heinz, B.; Muralt, P. Abnormal Grain Growth in AlScN Thin Films Induced by Complexion Formation at Crystallite Interfaces. Phys. Status Solidi (A) 2019, 216, 1862–6300. [Google Scholar] [CrossRef]
- Daniel, F.U.; Oliver, A.; Christian, E. First-principles calculation of electroacoustic properties of wurtzite (Al, Sc)N. Phys. Rev. B 2021, 103, 115204. [Google Scholar]
- Kurz, N.; Ding, A.; Urban, D.F.; Lu, Y.; Kirste, L.; Feil, N.M.; Žukauskaitė, A.; Ambacher, O. Experimental determination of the electro-acoustic properties of thin film AlScN using surface acoustic wave resonators. J. Appl. Phys. 2019, 126, 075106. [Google Scholar] [CrossRef]
- Guo, J.; Liu, C.; Han, T.; Miao, J. Model of scandium doped aluminum nitride based PMUT with high transmitting performance. In Proceedings of the 2017 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Chengdu, China, 27–30 October 2017; pp. 211–216. [Google Scholar]
- Li, D.S.; Yang, D.R.; Que, D.L. Progress in Study of Crystal Silicon Mechanical Properties. Mater. Sci. Eng. 2000, 18, 3. [Google Scholar]


| Parameter | Value |
|---|---|
| The thickness of top Mo | 0.2 μm |
| The thickness of AlN/Al1-xScxN | 1 μm |
| The thickness of bottom Mo | 0.2 μm |
| Thickness of Si | 3.5 μm |
| The depth of the cavity | 100 μm |
| Radius of cavity | 300 μm |
| Radius of Si | 500 μm |
| The radius of bottom Mo | 500 μm |
| The radius of top Mo | 230 μm |
| Property | Symbol | AlN | Si | Mo | PI |
|---|---|---|---|---|---|
| Density (kg/m3) | 𝜌 | 3300 | 2329 | 10,200 | 1300 |
| Poisson ratio | 𝜐 | 0.3 | 0.064 | 0.3 | 0.37 |
| Young’s modulus (GPa) | 𝛶 | 330 | 170 | 312 | 3.1 |
| Elastic stiffness constants cEij (×1011 N m−1) | c11 c12 c13 c33 c44 c66 | 4.1 1.49 0.99 3.89 1.25 1.305 | - | - | - |
| Piezoelectric constants eij (C m−2) | e31 e33 e15 | −0.58 1.55 −0.48 | - | - | - |
| Dielectric permittivity | ε/ε0 | 10 | - | - | - |
| Substrate Types | Si | PI with a Thin Layer of Si | PI |
|---|---|---|---|
| Resonant frequency f (kHz) | 226.5 | 218.1 | 203.9 |
| Effective electromechanical coupling k2eff (%) | 1.31 | 1.45 | 1.07 |
| Static transmitting sensitivity (μm/V) | 0.547 | 0.602 | 0.247 |
| Static receiving sensitivity (V/kPa) | 1.70 | 1.72 | 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Q.; Chen, J.; Liu, X.; Zhang, S.; Gu, Y. Design and 3D FEM Analysis of a Flexible Piezoelectric Micromechanical Ultrasonic Transducer Based on Sc-Doped AlN Film. Sensors 2022, 22, 8100. https://doi.org/10.3390/s22218100
Ren Q, Chen J, Liu X, Zhang S, Gu Y. Design and 3D FEM Analysis of a Flexible Piezoelectric Micromechanical Ultrasonic Transducer Based on Sc-Doped AlN Film. Sensors. 2022; 22(21):8100. https://doi.org/10.3390/s22218100
Chicago/Turabian StyleRen, Qinghua, Junhong Chen, Xin Liu, Songsong Zhang, and Yuandong Gu. 2022. "Design and 3D FEM Analysis of a Flexible Piezoelectric Micromechanical Ultrasonic Transducer Based on Sc-Doped AlN Film" Sensors 22, no. 21: 8100. https://doi.org/10.3390/s22218100







