Specific Resonant Properties of Non-Symmetrical Microwave Antennas
Abstract
:1. Introduction
2. Materials and Method
2.1. Material for Measuring the Properties of Microwave Antennas
2.2. Method for Evaluating Resonant Properties of Microwave Antennas
3. Results and Discussion
3.1. Resonance Properties of Measured Classical Cylindrical Antennas
3.2. Resonance Properties of Measured Flat Microwave Antennas
- (1)
- Set of antennas w = 5 mm Figure 12a 0.231–0.204 = 0.027
- (2)
- Set of antennas w = 10 mm Figure 12b 0.24–0.171 = 0.069
- (3)
- Set of antennas w = 30 mm Figure 12c 0.247–0.139 = 0.108
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, J.; Wang, H.; Lv, Z.; Wang, H. Design of miniaturized dual-band microstrip antenna for WLAN application. Sensors 2016, 16, 983. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arias, M.; Jost, T.; Gonzalez-Valdes, B.; Wang, W.; Zhang, S.; Ulmschneider, M.; Gentner, C. Statistical analysis of the radiation pattern of an antenna mounted on an aircraft. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Su, D.; Yang, Z.; Wu, Q. Characteristic Mode Assisted Placement of Antennas for the Isolation Enhancement. IEEE Antennas Wirel. Propag. 2018, 17, 251–254. [Google Scholar] [CrossRef]
- Thite, V.; Kazi, A.Y. Wideband VHF/UHF antennas for UAV platform with RCS approach. In Proceedings of the 2012 1st International Conference on Emerging Technology Trends in Electronics, Communication & Networking, Gujarat, India, 19–21 December 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Cheng, Y.J.; Guo, Y.X.; Liu, Z.G. W-Band large-scale high-gain planar integrated antenna array. IEEE Trans. Antennas Propag. 2014, 62, 3370–3373. [Google Scholar] [CrossRef]
- Kasyanov, A.O.; Obukhovets, V.A. Flat microwave antennas for telecommunication systems. In Proceedings of the 7th International Seminar/Workshop on Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory, Tbilisi, Georgia, 13 October 2002; pp. 74–79. [Google Scholar] [CrossRef]
- Arias-Acuña, M.; García-Pino, A.; Rubiños-López, O. Fast far field computation of single and dual reflector antennas. J. Eng. 2013, 2013, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wilson, P.F. Radiation patterns of unintentional antennas: Estimates, simulations, and measurements. In Proceedings of the 2010 Asia-Pacific International Symposium on Electromagnetic Compatibility, Beijing, China, 12–16 April 2010; pp. 985–989. [Google Scholar] [CrossRef] [Green Version]
- Yeon, K.; Lee, D.; Kim, B. Efficiency Improvement of Vehicular Antenna Systems for Ubiquitous Intelligent Systems. Information 2014, 5, 602–611. [Google Scholar] [CrossRef] [Green Version]
- Tusă, L.; Nicolaescu, I.; Moni, M.; Banciu, M.G. Time-Frequency domain radar cross section evaluation of an IAR 99 scaled model aircraft. In Proceedings of the 2015 7th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Bucharest, Romania, 25–27 June 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Rao, B.R.; Rosario, E.N.; Davis, R.J. Radiation pattern analysis of aircraft mounted GPS antennas and verification through scale model testing. In Proceedings of the 2006 IEEE/ION Position, Location, and Navigation Symposium, Coronado, CA, USA, 25–27 April 2006; pp. 306–318. [Google Scholar] [CrossRef]
- Zbojovský, J.; Pavlík, M. Measuring and simulation of the shielding effectiveness of electromagnetic field of brick wall in the frequency range from 0.9 GHz to 5 GHz. In Proceedings of the 2017 18th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 17–19 May 2017; pp. 1–4. [Google Scholar] [CrossRef]
- López-Yela, A.; Albarracín-Vargas, F.; Segovia-Vargas, D. An electrically small antenna for potential aircraft applications. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 1993–1994. [Google Scholar] [CrossRef]
- Ullah, S.; Ruan, C.; Sadiq, M.S.; Haq, T.U.; He, W. High Efficient and Ultra Wide Band Monopole Antenna for Microwave Imaging and Communication Applications. Sensors 2020, 20, 115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gevorkyan, A.V. The wideband patch antenna with low level of the VSWR. In Proceedings of the 2017 Radiation and Scattering of Electromagnetic Waves (RSEMW), Divnomorskoe, Russia, 26–30 June 2017; pp. 309–310. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Virdee, B.S.; See, C.H.; Abd-Alhameed, R.A.; Falcone, F.; Limiti, E. Super-wide impedance bandwidth planar antenna for microwave and millimeter-wave applications. Sensors 2019, 19, 2306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karwowski, A.; Hoga, A. On the interpolation of the frequency variations of the MoM-PO impedance matrix over a wide bandwidth. Microw. Opt. Technol. Lett. 2008, 50, 738–741. [Google Scholar] [CrossRef]
- Nguyen, T.K.; Park, I. Resonant antennas on semi-infinite and lens substrates at terahertz frequency. In Convergence of Terahertz Sciences in Biomedical Systems; Park, G.S., Ed.; Springer: Dordrecht, The Netherlands, 2012; pp. 181–193. [Google Scholar] [CrossRef]
- Balanis, C.A. Modern Antenna Handbook; John Wiley & Sons: New York, NY, USA, 2011; p. 1712. ISBN 9781118209752. [Google Scholar]
- Stutzman, W.L.; Thiele, G.A. Antenna Theory and Design; John Wiley & Sons: New York, NY, USA, 2012; p. 848. ISBN 978-0-470-57664-9. [Google Scholar]
- Sabaawi, A.M.A.; Tsimenidis, C.C.; Sharif, B.S. Analysis and modeling of infrared solar rectennas. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 9000208. [Google Scholar] [CrossRef]


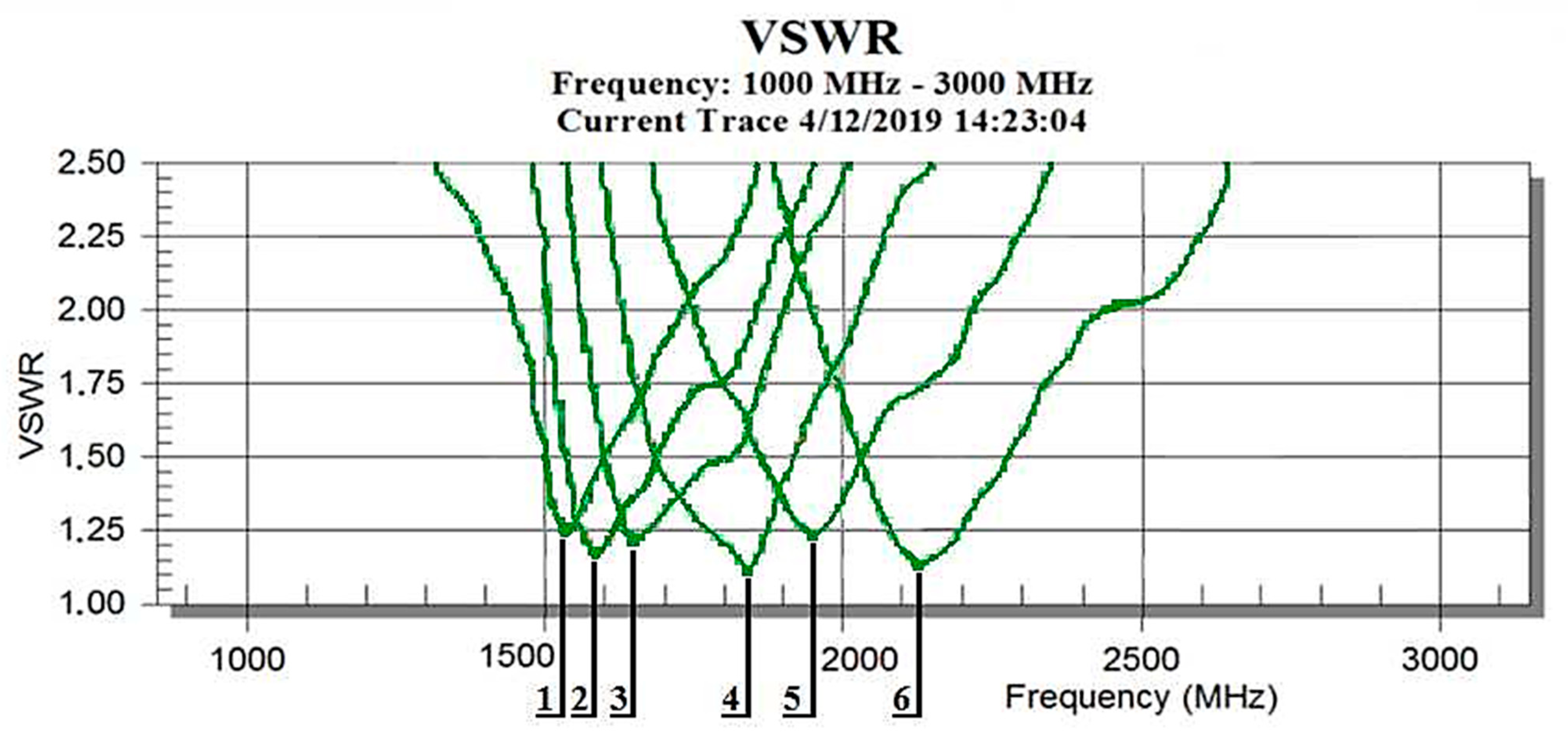
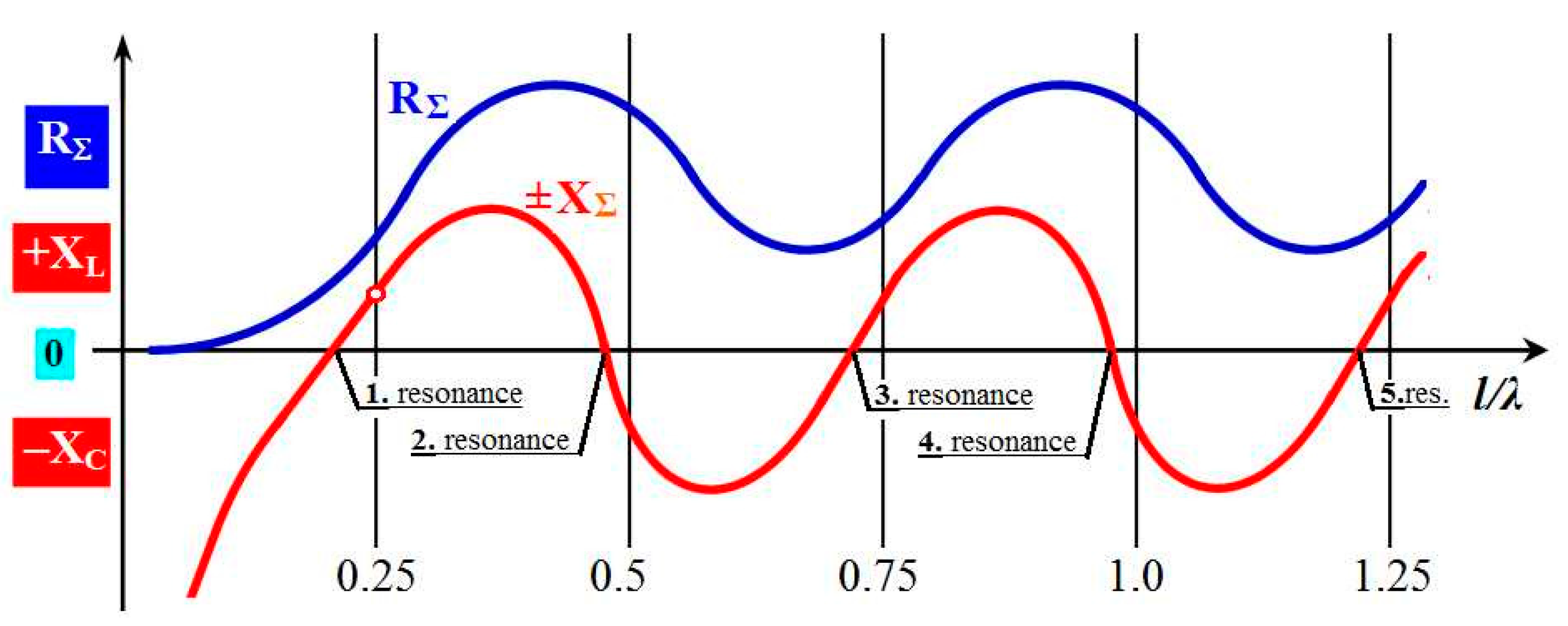
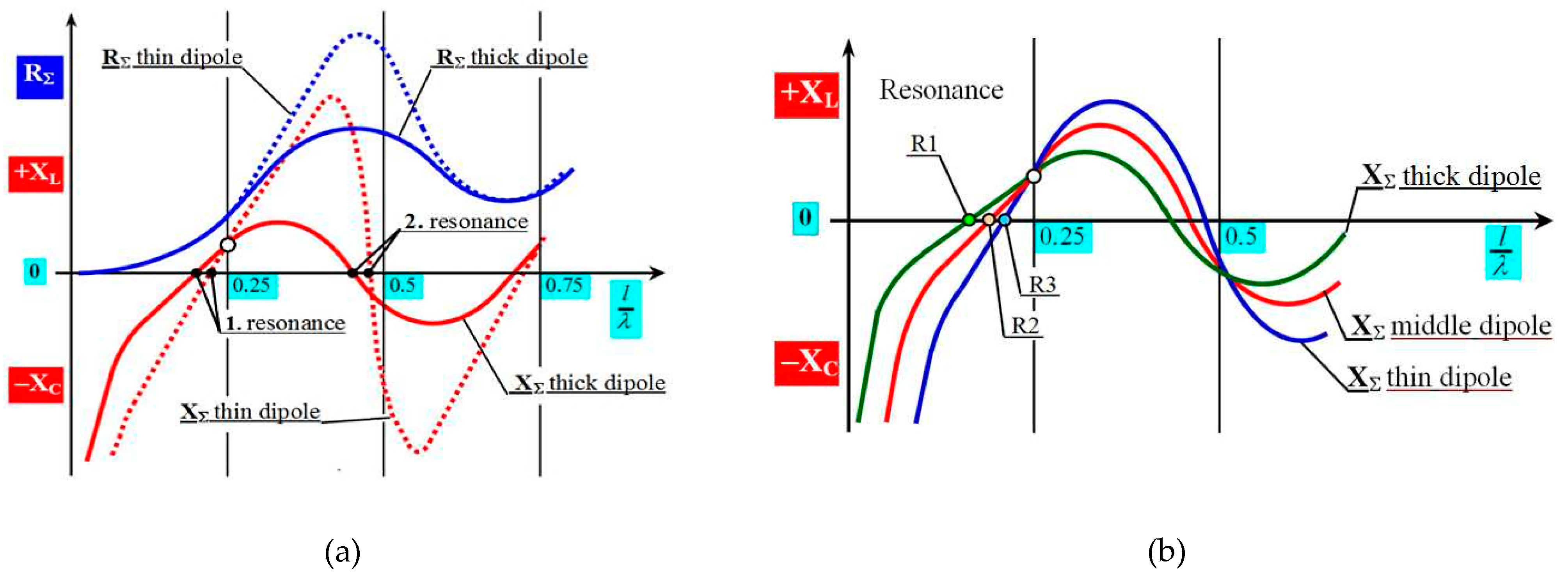
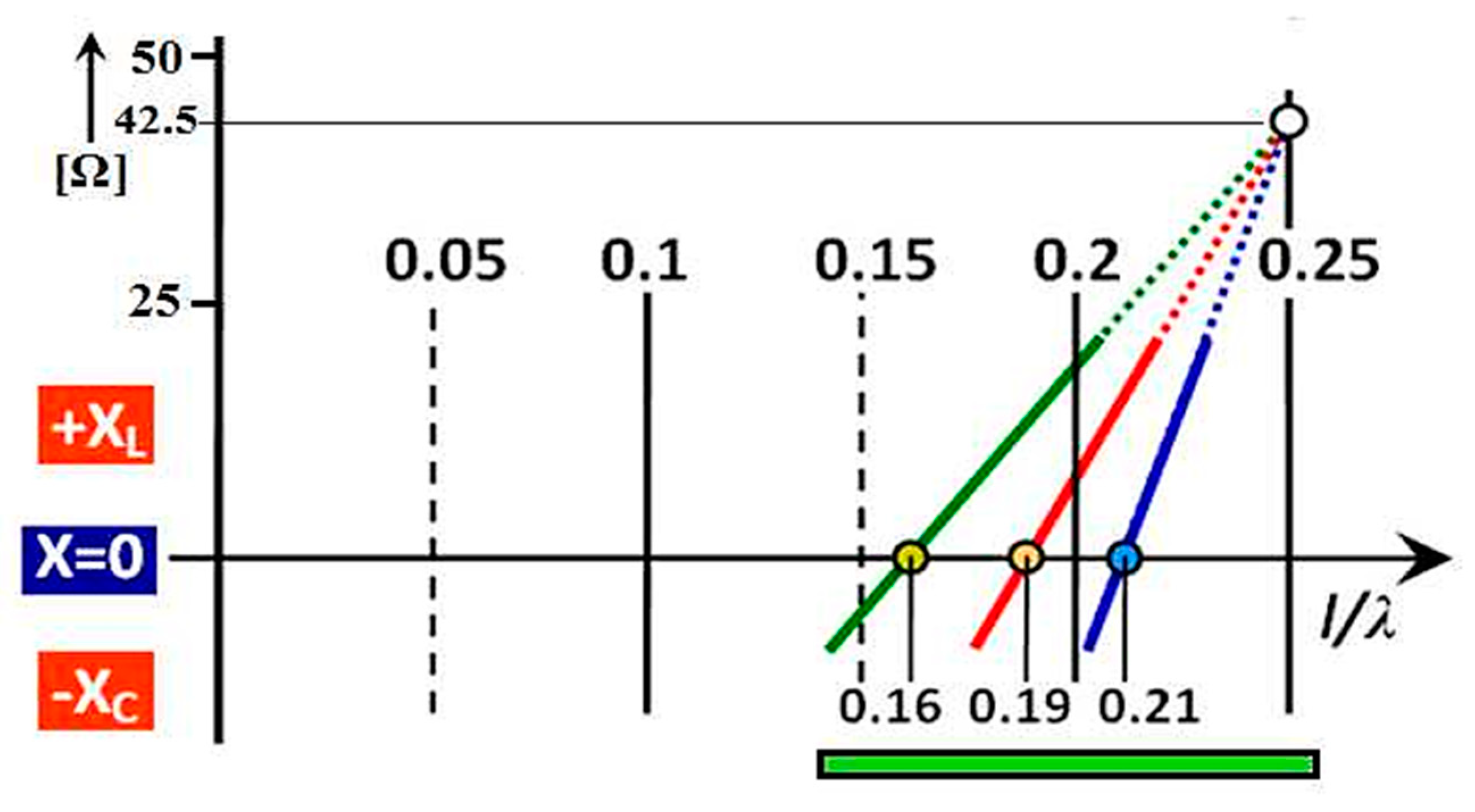
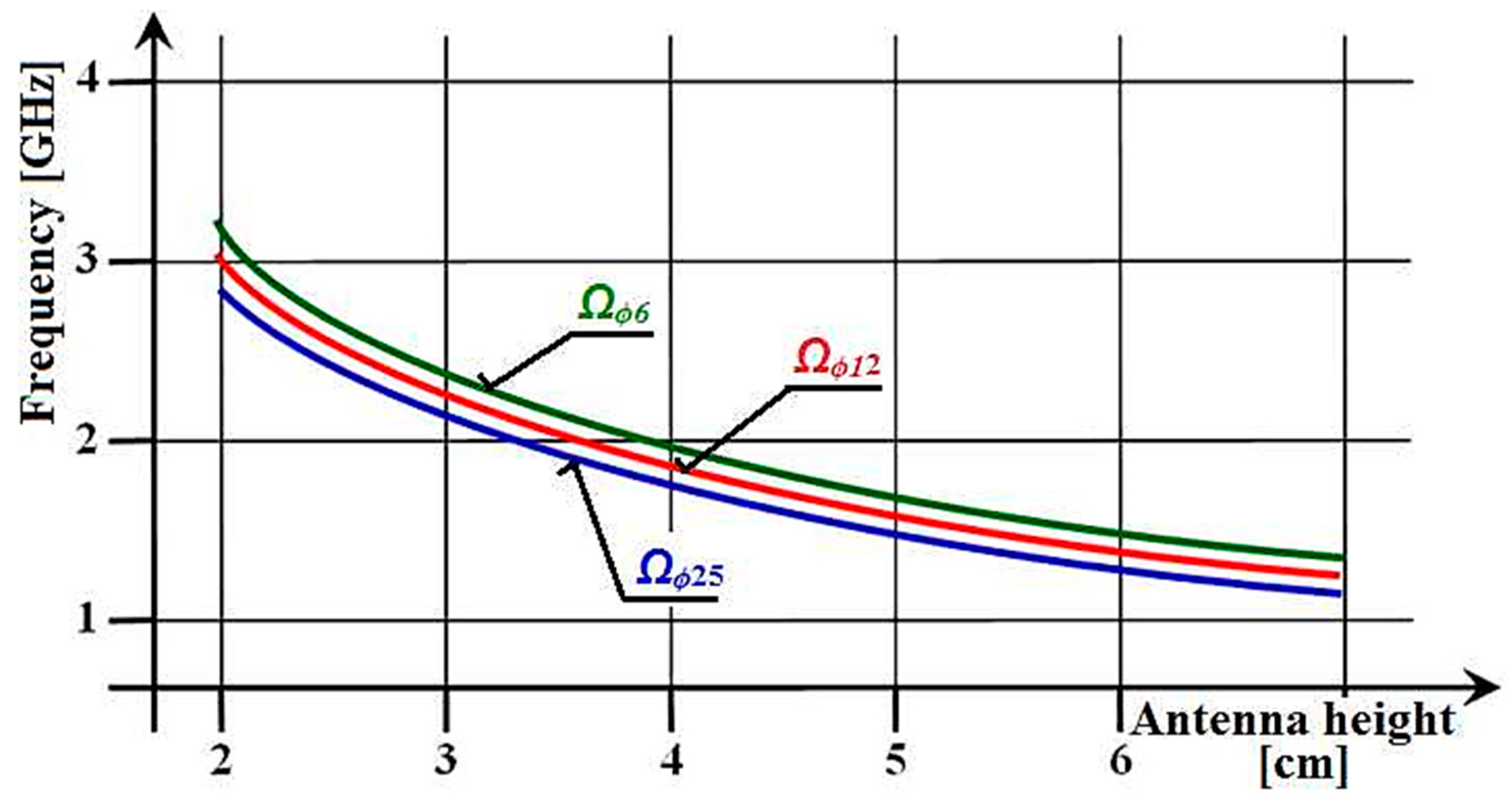

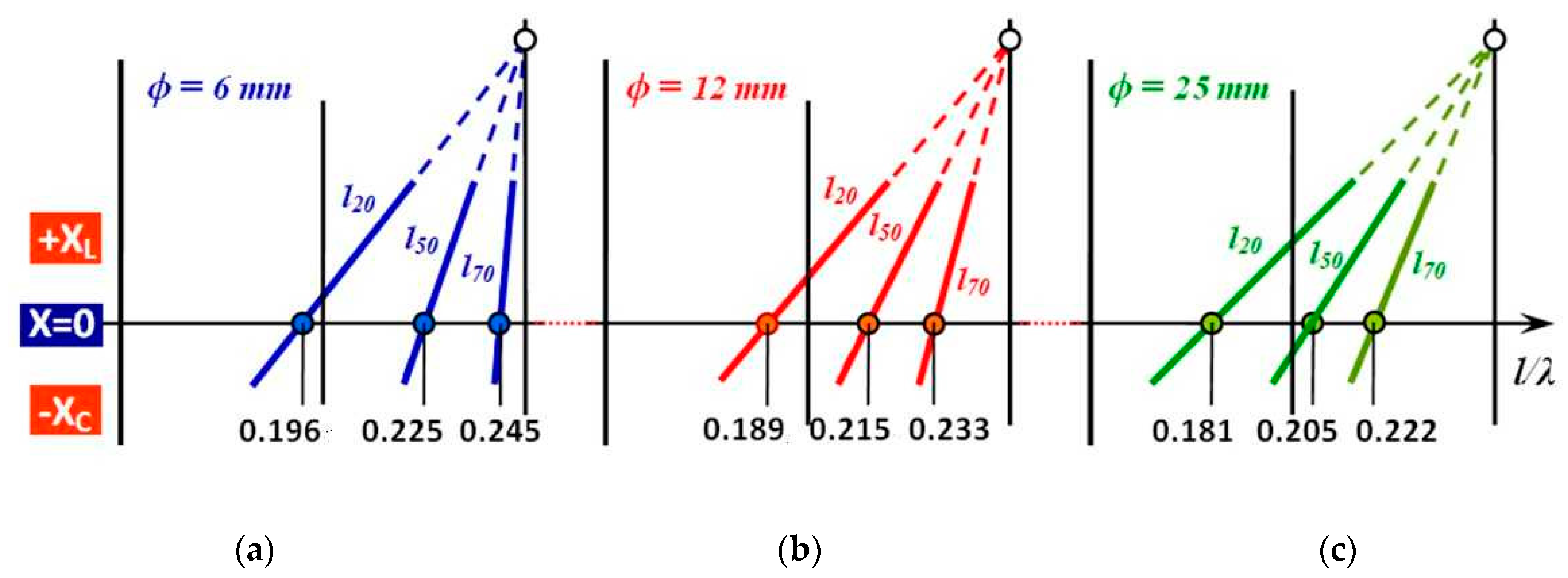



| 20 | 30 | 40 | 50 | 60 | 70 | l [mm] |
|---|---|---|---|---|---|---|
| 0.196 | 0.200 | 0.209 | 0.225 | 0.237 | 0.245 | (ϕ = 6 mm) |
| 0.189 | 0.194 | 0.202 | 0.215 | 0.225 | 0.234 | (ϕ = 12 mm) |
| 0.181 | 0.187 | 0.193 | 0.205 | 0.213 | 0.223 | (ϕ = 25 mm) |
| Ωϕ6l20 > Ωϕ12 l20 > Ωϕ25 l20 | Ωϕ6l20 < Ωϕ6 l50 < Ωϕ6 l70 |
| 0.196 0.189 0.181 | 0.1960 0.225 0.245 |
| Ωϕ6l50 > Ωϕ12 l50 > Ωϕ25 l50 | Ωϕ12l20 < Ωϕ12 l50 < Ωϕ12 l70 |
| 0.225 0.215 0.205 | 0.189 0.215 0.233 |
| Ωϕ6l70, > Ωϕ12 l70 > Ωϕ25 l70 | Ωϕ25l20 < Ωϕ25 l50 < Ωϕ25 l70 |
| 0.245 0.233 0.222 | 0.181 0.205 0.222 |
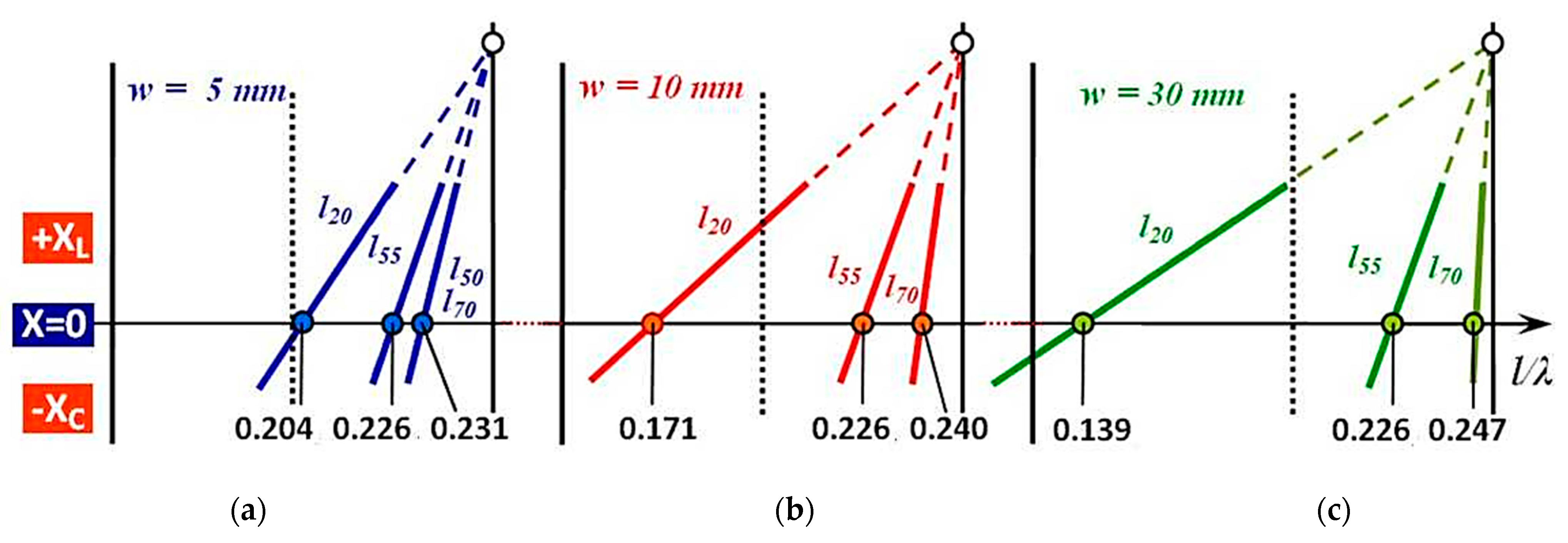
| 20 | 30 | 40 | 50 | 55 | 60 | 70 | l [mm] |
|---|---|---|---|---|---|---|---|
| 0.204 | 0.215 | 0.224 | 0.231 | 0.226 | 0.224 | 0.231 | l/λ (w = 5 mm) |
| 0.171 | 0.190 | 0.203 | 0.222 | 0.226 | 0.229 | 0.240 | l/λ (w = 10mm) |
| 0.139 | 0.170 | 0.188 | 0.212 | 0.226 | 0.236 | 0.247 | l/λ (w = 30 mm) |
| Influence of the change Ω of the flat antenna on the change of the ratio l/λres due to changing w at the same l. | Influence of the change Ω of the flat antenna on the change of the ratio l/λres due to changing l at the same w. |
|---|---|
| Ωw5 l20 > Ωw10 l20 > Ωw30 l20 | Ω w5 l20 < Ω w5 l55 < Ω w5 l70 |
| 0.204 0.171 0.139 | 0.204 0.226 0.231 |
| Ωw5 l55 = Ωw10 l55 = Ωw30 l55 | Ω w10 l20 < Ω w10 l55 < Ω w10 l70 |
| 0.226 0.226 0.226 | 0.171 0.226 0.240 |
| Ωw5 l70 < Ωw10 l70 < Ωw30 l70 | Ω w30 l20 < Ω w30 l55 < Ω w30 l70 |
| 0.231 0.240 0.247 | 0.139 0.226 0.247 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Labun, J.; Kurdel, P.; Nekrasov, A.; Gamcová, M.; Češkovič, M.; Fidge, C. Specific Resonant Properties of Non-Symmetrical Microwave Antennas. Sensors 2021, 21, 939. https://doi.org/10.3390/s21030939
Labun J, Kurdel P, Nekrasov A, Gamcová M, Češkovič M, Fidge C. Specific Resonant Properties of Non-Symmetrical Microwave Antennas. Sensors. 2021; 21(3):939. https://doi.org/10.3390/s21030939
Chicago/Turabian StyleLabun, Ján, Pavol Kurdel, Alexey Nekrasov, Mária Gamcová, Marek Češkovič, and Colin Fidge. 2021. "Specific Resonant Properties of Non-Symmetrical Microwave Antennas" Sensors 21, no. 3: 939. https://doi.org/10.3390/s21030939











