Wearable Inertial Gait Algorithms: Impact of Wear Location and Environment in Healthy and Parkinson’s Populations
Abstract
:1. Introduction
- (i)
- Investigate agreement between algorithms across different groups (YA-OA-PD),
- (ii)
- Investigate impact of walking environment (treadmill-indoor-outdoor) on agreement between algorithms,
- (iii)
- Provide recommendations when deciding optimal IMU location and gait algorithms.
2. Materials and Methods
2.1. Datasets
2.1.1. Datasets-1 (DS1)
2.1.2. Datasets-2 (DS2)
2.2. Methodology
2.2.1. Algorithm S1 (A1): Lower Back
2.2.2. Algorithm S2 (A2): Shanks (Right and Left)
2.2.3. Temporal Parameter and Statistical Calculations
3. Results
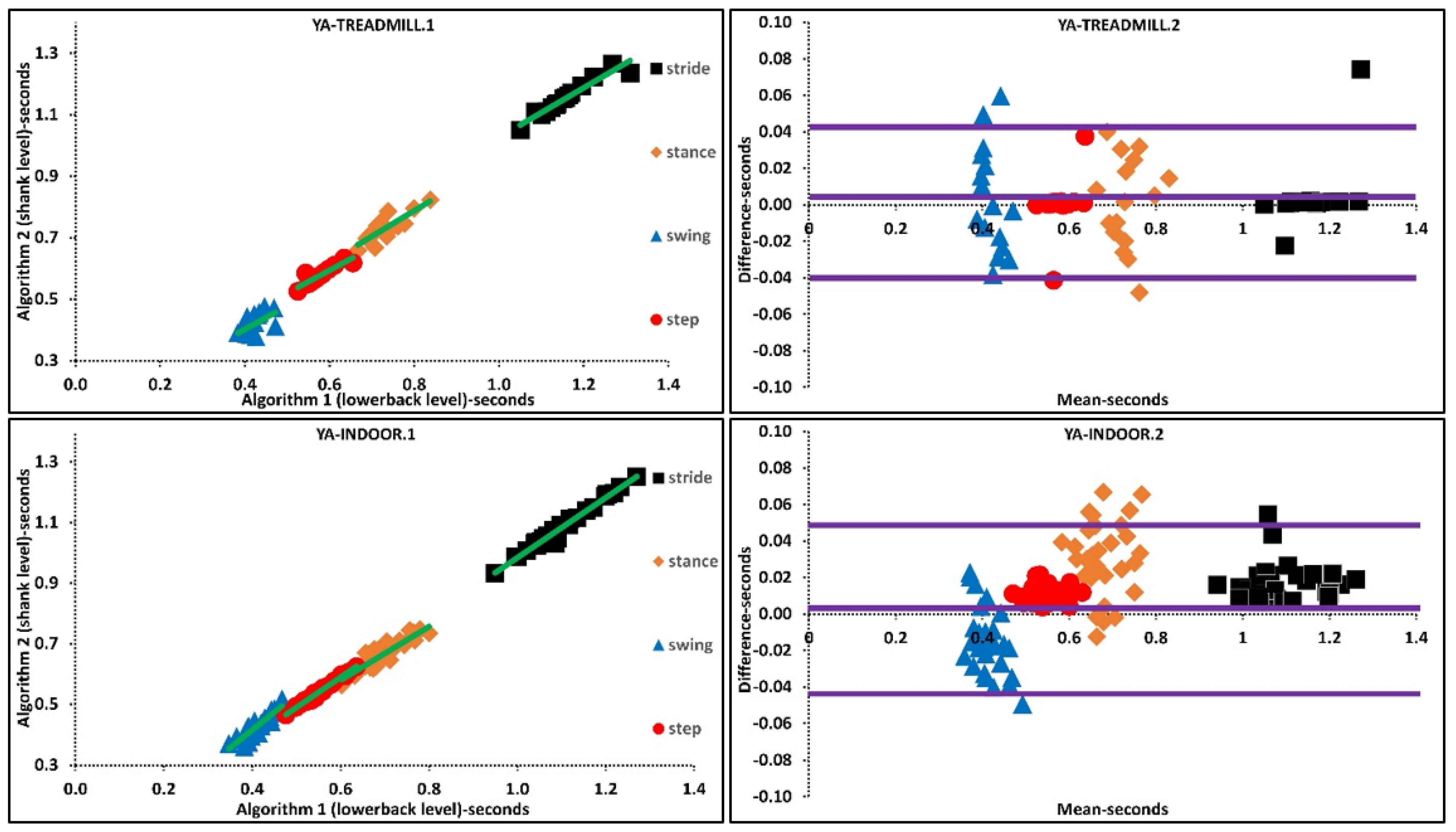
3.1. A1 vs. A2: Treadmill
3.2. A1 vs. A2: Indoor
3.3. A1 vs. A2: Outdoor
4. Discussion
4.1. Impact of Pathology and Age
4.2. Impact of Environment
4.3. Considerations: Sensor Location and Algorithms
- The first factor needing consideration for IMU gait algorithms is the preferred pre-processing and post-processing methodologies as it has an impact on the extracted mean, variability, and asymmetry of temporal characteristics. For example, using algorithms like A1 [23] requires strict filtering and may affect variability of extracted characteristics as the signal is much smoother compared to less strict filters (e.g., A2).
- Sensor location and sensor signal are other important factors affecting accuracy. Research suggests the shank angular velocity signals provide more accurate and repeatable results for IC-FC detection compared to algorithms that use waist acceleration [9,10]. However, this has not been fully investigated in neurological cohorts. Here we also found that correlation/agreement of lower back and shank algorithms change when applied in various walking environments and decrease when applied to those with PD.
- Although findings show that the threshold/rule-based inertial algorithms for ICs-FCs detection provide highly correlated mean results, the fact that performances are sensitive to target cohort and environment limits widespread use.
4.4. Limitations and Future Works
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pirker, W.; Katzenschlager, R. Gait disorders in adults and the elderly. Wien. Klin. Wochenschr. 2017, 129, 81–95. [Google Scholar] [CrossRef] [Green Version]
- Morris, R.; Hickey, A.; Del Din, S.; Godfrey, A.; Lord, S.; Rochester, L. A model of free-living gait: A factor analysis in Parkinson’s disease. Gait Posture 2017, 52, 68–71. [Google Scholar] [CrossRef] [Green Version]
- Del Din, S.; Godfrey, A.; Mazzà, C.; Lord, S.; Rochester, L. Free-living monitoring of Parkinson’s disease: Lessons from the field. Mov. Disord. 2016, 31, 1293–1313. [Google Scholar] [CrossRef]
- Navarro-Flores, E.; Jiménez-Cebrián, A.M.; Becerro-de-Bengoa-Vallejo, R.; Calvo-Lobo, C.; Losa-Iglesias, M.E.; Romero-Morales, C.; López-López, D.; Palomo-López, P. Effect of foot health and quality of life in patients with Parkinson disease: A prospective case-control investigation. J. Tissue Viability 2021. [Google Scholar] [CrossRef]
- Jiménez-Cebrián, A.M.; Becerro-de-Bengoa-Vallejo, R.; Losa-Iglesias, M.E.; López-López, D.; Calvo-Lobo, C.; Palomo-López, P.; Romero-Morales, C.; Navarro-Flores, E. The Impact of Depression Symptoms in Patients with Parkinson’s Disease: A Novel Case-Control Investigation. Int. J. Environ. Res. Public Health 2021, 18, 2369. [Google Scholar] [CrossRef]
- Celik, Y.; Stuart, S.; Woo, W.L.; Godfrey, A. Gait analysis in neurological populations: Progression in the use of wearables. Med. Eng. Phys. 2020, 87, 9–29. [Google Scholar] [CrossRef]
- Morris, R.; Stuart, S.; McBarron, G.; Fino, P.C.; Mancini, M.; Curtze, C. Validity of Mobility Lab (version 2) for gait assessment in young adults, older adults and Parkinson’s disease. Physiol. Meas. 2019, 40, 095003. [Google Scholar] [CrossRef] [PubMed]
- Bravi, M.; Massaroni, C.; Santacaterina, F.; Di Tocco, J.; Schena, E.; Sterzi, S.; Bressi, F.; Miccinilli, S. Validity Analysis of WalkerViewTM Instrumented Treadmill for Measuring Spatiotemporal and Kinematic Gait Parameters. Sensors 2021, 21, 4795. [Google Scholar] [CrossRef] [PubMed]
- Panebianco, G.P.; Bisi, M.C.; Stagni, R.; Fantozzi, S. Analysis of the performance of 17 algorithms from a systematic review: Influence of sensor position, analysed variable and computational approach in gait timing estimation from IMU measurements. Gait Posture 2018, 66, 76–82. [Google Scholar] [CrossRef]
- Mansour, K.B.; Rezzoug, N.; Gorce, P. Analysis of several methods and inertial sensors locations to assess gait parameters in able-bodied subjects. Gait Posture 2015, 42, 409–414. [Google Scholar] [CrossRef] [PubMed]
- Storm, F.A.; Buckley, C.J.; Mazzà, C. Gait event detection in laboratory and real life settings: Accuracy of ankle and waist sensor based methods. Gait Posture 2016, 50, 42–46. [Google Scholar] [CrossRef] [Green Version]
- Catalfamo, P.; Ghoussayni, S.; Ewins, D. Gait event detection on level ground and incline walking using a rate gyroscope. Sensors 2010, 10, 5683–5702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- González, R.C.; López, A.M.; Rodriguez-Uría, J.; Alvarez, D.; Alvarez, J.C. Real-time gait event detection for normal subjects from lower trunk accelerations. Gait Posture 2010, 31, 322–325. [Google Scholar] [CrossRef]
- Shin, S.H.; Park, C.G. Adaptive step length estimation algorithm using optimal parameters and movement status awareness. Med. Eng. Phys. 2011, 33, 1064–1071. [Google Scholar] [CrossRef] [PubMed]
- Bugané, F.; Benedetti, M.; Casadio, G.; Attala, S.; Biagi, F.; Manca, M.; Leardini, A. Estimation of spatial-temporal gait parameters in level walking based on a single accelerometer: Validation on normal subjects by standard gait analysis. Comput. Methods Programs Biomed. 2012, 108, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Trojaniello, D.; Cereatti, A.; Pelosin, E.; Avanzino, L.; Mirelman, A.; Hausdorff, J.M.; Della Croce, U. Estimation of step-by-step spatio-temporal parameters of normal and impaired gait using shank-mounted magneto-inertial sensors: Application to elderly, hemiparetic, parkinsonian and choreic gait. J. Neuroeng. Rehabil. 2014, 11, 152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salarian, A.; Russmann, H.; Vingerhoets, F.J.; Dehollain, C.; Blanc, Y.; Burkhard, P.R.; Aminian, K. Gait assessment in Parkinson’s disease: Toward an ambulatory system for long-term monitoring. IEEE Trans. Biomed. Eng. 2004, 51, 1434–1443. [Google Scholar] [CrossRef]
- Khandelwal, S.; Wickström, N. Identification of gait events using expert knowledge and continuous wavelet transform analysis. In Proceedings of the 7th International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS 2014), Angers, France, 3–6 March 2014; pp. 197–204. [Google Scholar]
- Jasiewicz, J.M.; Allum, J.H.; Middleton, J.W.; Barriskill, A.; Condie, P.; Purcell, B.; Li, R.C.T. Gait event detection using linear accelerometers or angular velocity transducers in able-bodied and spinal-cord injured individuals. Gait Posture 2006, 24, 502–509. [Google Scholar] [CrossRef] [Green Version]
- Muthukrishnan, N.; Abbas, J.J.; Krishnamurthi, N. A wearable sensor system to measure step-based gait parameters for parkinson’s disease rehabilitation. Sensors 2020, 20, 6417. [Google Scholar] [CrossRef]
- Yeo, S.S.; Park, G.Y. Accuracy verification of spatio-temporal and kinematic parameters for gait using inertial measurement unit system. Sensors 2020, 20, 1343. [Google Scholar] [CrossRef] [Green Version]
- Trojaniello, D.; Cereatti, A.; Della Croce, U. Accuracy, sensitivity and robustness of five different methods for the estimation of gait temporal parameters using a single inertial sensor mounted on the lower trunk. Gait Posture 2014, 40, 487–492. [Google Scholar] [CrossRef]
- McCamley, J.; Donati, M.; Grimpampi, E.; Mazza, C. An enhanced estimate of initial contact and final contact instants of time using lower trunk inertial sensor data. Gait Posture 2012, 36, 316–318. [Google Scholar] [CrossRef] [PubMed]
- Trojaniello, D.; Ravaschio, A.; Hausdorff, J.M.; Cereatti, A. Comparative assessment of different methods for the estimation of gait temporal parameters using a single inertial sensor: Application to elderly, post-stroke, Parkinson’s disease and Huntington’s disease subjects. Gait Posture 2015, 42, 310–316. [Google Scholar] [CrossRef]
- Khandelwal, S.; Wickström, N. Evaluation of the performance of accelerometer-based gait event detection algorithms in different real-world scenarios using the MAREA gait database. Gait Posture 2017, 51, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Del Din, S.; Galna, B.; Godfrey, A.; Bekkers, E.M.; Pelosin, E.; Nieuwhof, F.; Mirelman, A.; Hausdorff, J.M.; Rochester, L. Analysis of free-living gait in older adults with and without Parkinson’s disease and with and without a history of falls: Identifying generic and disease-specific characteristics. J. Gerontol. Ser. A 2019, 74, 500–506. [Google Scholar] [CrossRef]
- Hickey, A.; Del Din, S.; Rochester, L.; Godfrey, A. Detecting free-living steps and walking bouts: Validating an algorithm for macro gait analysis. Physiol. Meas. 2016, 38, N1. [Google Scholar] [CrossRef]
- Del Din, S.; Godfrey, A.; Galna, B.; Lord, S.; Rochester, L. Free-living gait characteristics in ageing and Parkinson’s disease: Impact of environment and ambulatory bout length. J. Neuroeng. Rehabil. 2016, 13, 46. [Google Scholar] [CrossRef] [Green Version]
- Warmerdam, E.; Hausdorff, J.M.; Atrsaei, A.; Zhou, Y.; Mirelman, A.; Aminian, K.; Espay, A.J.; Hansen, C.; Evers, L.J.; Keller, A. Long-term unsupervised mobility assessment in movement disorders. Lancet Neurol. 2020, 19, 462–470. [Google Scholar] [CrossRef]
- Loose, H.; Bolmgren, J.L. GaitAnalysisDataBase–Short Overview. Tech. Hochsch. Brandenbg. 2019, 1–6. [Google Scholar]
- Mancini, M.; Curtze, C.; Stuart, S.; El-Gohary, M.; McNames, J.; Nutt, J.G.; Horak, F.B. The impact of freezing of gait on balance perception and mobility in community-living with Parkinson’s disease. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 3040–3043. [Google Scholar]
- Aminian, K.; Najafi, B.; Büla, C.; Leyvraz, P.-F.; Robert, P. Spatio-temporal parameters of gait measured by an ambulatory system using miniature gyroscopes. J. Biomech. 2002, 35, 689–699. [Google Scholar] [CrossRef]
- Moe-Nilssen, R. A new method for evaluating motor control in gait under real-life environmental conditions. Part 1: The instrument. Clin. Biomech. 1998, 13, 320–327. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [Green Version]
- Shrout, P.E.; Fleiss, J.L. Intraclass correlations: Uses in assessing rater reliability. Psychol. Bull. 1979, 86, 420–428. [Google Scholar] [CrossRef]
- Coulby, G.; Clear, A.K.; Jones, O.; Godfrey, A. Low-cost, multimodal environmental monitoring based on the Internet of Things. Build. Environ. 2021, 203, 108014. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Del Din, S.; Hickey, A.; Hurwitz, N.; Mathers, J.C.; Rochester, L.; Godfrey, A. Measuring gait with an accelerometer-based wearable: Influence of device location, testing protocol and age. Physiol. Meas. 2016, 37, 1785. [Google Scholar] [CrossRef]
- Beijer, T.R.; Lord, S.R.; Brodie, M.A. Comparison of Handheld Video Camera and GAITRite® Measurement of Gait Impairment in People with Early Stage Parkinson’s Disease: A Pilot Study. J. Parkinson’s Dis. 2013, 3, 199–203. [Google Scholar] [CrossRef]
- Brodie, M.A.; Coppens, M.J.; Lord, S.R.; Lovell, N.H.; Gschwind, Y.J.; Redmond, S.J.; Del Rosario, M.B.; Wang, K.; Sturnieks, D.L.; Persiani, M. Wearable pendant device monitoring using new wavelet-based methods shows daily life and laboratory gaits are different. Med. Biol. Eng. Compu. 2016, 54, 663–674. [Google Scholar] [CrossRef]
- Toda, H.; Maruyama, T.; Tada, M. Indoor versus outdoor walking: Does it make any difference in joint angle depending on road surface? Front. Sports Act. Living 2020, 2, 119. [Google Scholar] [CrossRef] [PubMed]
- Agostini, V.; Ghislieri, M.; Rosati, S.; Balestra, G.; Knaflitz, M. Surface electromyography applied to gait analysis: How to improve its impact in clinics? Front. Neurol. 2020, 11, 994. [Google Scholar] [CrossRef]
- Zurales, K.; DeMott, T.K.; Kim, H.; Allet, L.; Ashton-Miller, J.A.; Richardson, J.K. Gait efficiency on an uneven surface is associated with falls and injury in older subjects with a spectrum of lower limb neuromuscular function: A prospective study. Am. J. Phys. Med. Rehabil./Assoc. Acad. Phys. 2016, 95, 83. [Google Scholar] [CrossRef] [Green Version]
- Aqueveque, P.; Germany, E.; Osorio, R.; Pastene, F. Gait Segmentation Method Using a Plantar Pressure Measurement System with Custom-Made Capacitive Sensors. Sensors 2020, 20, 656. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Del Din, S.; Godfrey, A.; Rochester, L. Validation of an accelerometer to quantify a comprehensive battery of gait characteristics in healthy older adults and Parkinson’s disease: Toward clinical and at home use. IEEE J. Biomed. Health Inform. 2015, 20, 838–847. [Google Scholar] [CrossRef] [PubMed]
- Moore, S.A.; Hickey, A.; Lord, S.; Del Din, S.; Godfrey, A.; Rochester, L. Comprehensive measurement of stroke gait characteristics with a single accelerometer in the laboratory and community: A feasibility, validity and reliability study. J. Neuroeng. Rehabil. 2017, 14, 130. [Google Scholar] [CrossRef] [PubMed]
- Rast, F.M.; Labruyère, R. Systematic review on the application of wearable inertial sensors to quantify everyday life motor activity in people with mobility impairments. J. NeuroEng. Rehabil. 2020, 17, 1–19. [Google Scholar] [CrossRef]
- Zhou, Y.; Romijnders, R.; Hansen, C.; van Campen, J.; Maetzler, W.; Hortobágyi, T.; Lamoth, C.J. The detection of age groups by dynamic gait outcomes using machine learning approaches. Sci. Rep. 2020, 10, 4426. [Google Scholar] [CrossRef]
- Phinyomark, A.; Petri, G.; Ibáñez-Marcelo, E.; Osis, S.T.; Ferber, R. Analysis of big data in gait biomechanics: Current trends and future directions. J. Med. Biol. Eng. 2018, 38, 244–260. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mirelman, A.; Ben Or Frank, M.; Melamed, M.; Granovsky, L.; Nieuwboer, A.; Rochester, L.; Del Din, S.; Avanzino, L.; Pelosin, E.; Bloem, B.R. Detecting Sensitive Mobility Features for Parkinson’s Disease Stages Via Machine Learning. Mov. Disord. 2021, 36, 2144–2155. [Google Scholar] [CrossRef]


| DS1 | DS2 | ||||
|---|---|---|---|---|---|
| Environment Cohort-Number | Treadmill (YA-16) | Indoor (YA-31) | Outdoor (YA-25) | Indoor (OA-20) | Indoor (PD-36) |
| Male/Female (n) | 10/6 | 22/9 | 16/9 | 10/10 | 18/18 |
| Age(years) Mean ± SD | 32.6 ± 11.9 | 26.6 ± 11.0 | 26.28 ± 12.2 | 69.76 ± 7.82 | 69.20 ± 6.64 |
| Sampling Frequency | 60 Hz | 60 Hz | 75–100 Hz | 128 Hz | 128 Hz |
| Disease Duration (years) | -- | -- | -- | -- | 7.82 ± 5.62 |
| UPDRS III | -- | -- | -- | -- | 32.51 ± 4.12 |
| NFOGQ | -- | -- | -- | -- | 7.44 ± 8.62 |
| LEDD | -- | -- | -- | -- | 786.68 ± 416.88 |
| (YA) Treadmill DS1 n= 16 | A1-Lower Back | A2-Shank | Pearson’s R | Spearman’s Rho | 95% CI Bounds | ||||||
| Mean Time (s) | Average | SD | Average | SD | ICC2,1 | Lower | Upper | p | |||
| Stride | 1.156 | 0.065 | 1.152 | 0.054 | 0.965 ** | 0.988 ** | 0.975 | 0.929 | 0.991 | 0.000 | |
| Stance | 0.733 | 0.042 | 0.732 | 0.042 | 0.832 ** | 0.753 ** | 0.914 | 0.750 | 0.970 | 0.000 | |
| Swing | 0.423 | 0.023 | 0.420 | 0.033 | 0.537 * | 0.547 * | 0.684 | 0.073 | 0.890 | 0.019 | |
| Step | 0.578 | 0.033 | 0.578 | 0.027 | 0.907 ** | 0.865 ** | 0.945 | 0.841 | 0.981 | 0.000 | |
| Variability Time (s) | |||||||||||
| Stride | 0.068 | 0.029 | 0.075 | 0.028 | 0.918 ** | 0.956 ** | 0.946 | 0.814 | 0.982 | 0.000 | |
| Stance | 0.045 | 0.018 | 0.084 | 0.021 | 0.630 ** | 0.632 ** | 0.441 | −0,228 | 0.804 | 0.005 | |
| Swing | 0.026 | 0.010 | 0.027 | 0.006 | 0.116 | −0.300 | 0.132 | −1.666 | 0.704 | 0.398 | |
| Step | 0.036 | 0.014 | 0.040 | 0.017 | 0.885 ** | 0.886 ** | 0.915 | 0.735 | 0.971 | 0.000 | |
| Asymmetry Time (s) | |||||||||||
| Stride | 0.000 | 0.000 | 0.003 | 0.010 | 0.436 | 0.455 | 0.564 | −0.150 | 0.847 | 0.049 | |
| Stance | 0.004 | 0.004 | 0.016 | 0.013 | 0.019 | 0.176 | 0.019 | −0.633 | 0.552 | 0.476 | |
| Swing | 0.004 | 0.004 | 0.013 | 0.008 | −0.050 | 0.037 | −0.050 | −0.698 | 0.408 | 0.563 | |
| Step | 0.005 | 0.005 | 0.019 | 0.009 | −0.085 | 0.046 | −0.069 | −0.509 | 0.428 | 0.612 | |
| (YA) Indoor DS1 n= 31 | A1-Lower Back | A2-Shank | Pearson’s R | Spearman’s Rho | 95% CI Bounds | ||||||
| Mean Time (s) | Average | SD | Average | SD | ICC2,1 | Lower | Upper | p | |||
| Stride | 1.096 | 0.138 | 1.079 | 0.138 | 0.982 ** | 0.974 ** | 0.987 | 0.965 | 0.994 | 0.000 | |
| Stance | 0.692 | 0.084 | 0.663 | 0.092 | 0.931 ** | 0.892 ** | 0.936 | 0.716 | 0.974 | 0.000 | |
| Swing | 0.402 | 0.052 | 0.416 | 0.058 | 0.863 ** | 0.797 ** | 0.909 | 0.842 | 0.942 | 0.000 | |
| Step | 0.548 | 0.069 | 0.537 | 0.070 | 0.989 ** | 0.984 ** | 0.989 | 0.916 | 0.996 | 0.000 | |
| Variability Time (s) | |||||||||||
| Stride | 0.040 | 0.037 | 0.032 | 0.018 | 0.040 | 0.221 ** | 0.600 | −0.176 | 0.251 | 0.294 | |
| Stance | 0.026 | 0.020 | 0.024 | 0.015 | 0.025 | 0.122 * | 0.047 | −0.204 | 0.246 | 0.343 | |
| Swing | 0.019 | 0.020 | 0.032 | 0.011 | 0.054 | 0.301 ** | 0.070 | −0.116 | 0.231 | 0.217 | |
| Step | 0.024 | 0.021 | 0.023 | 0.016 | −0.025 | −0.016 | −0.049 | −0.325 | 0.169 | 0.656 | |
| Asymmetry Time (s) | |||||||||||
| Stride | 0.005 | 0.006 | 0.007 | 0.010 | −0.034 | 0.000 | −0.060 | −0.338 | 0.159 | 0.690 | |
| Stance | 0.009 | 0.008 | 0.016 | 0.019 | 0.013 | 0.800 | 0.017 | −0.214 | 0.207 | 0.437 | |
| Swing | 0.009 | 0.009 | 0.017 | 0.015 | 0.130 * | 0.155 ** | 0.184 | −0.011 | 0.344 | 0.025 | |
| Step | 0.011 | 0.010 | 0.032 | 0.036 | 0.081 | 0.097 | 0.062 | −0.122 | 0.223 | 0.241 | |
|
(OA)
Indoor DS2 n= 20 | Mean Time (s) | ||||||||||
| Stride | 1.162 | 0.077 | 1.164 | 0.0866 | 0.962 ** | 0.974 ** | 0.979 | 0.947 | 0.992 | 0.000 | |
| Stance | 0.707 | 0.0404 | 0.716 | 0.0630 | 0.816 ** | 0.811 ** | 0.851 | 0.631 | 0.941 | 0.000 | |
| Swing | 0.447 | 0.05 | 0.444 | 0.0442 | 0.699 ** | 0.657 ** | 0.824 | 0.551 | 0.930 | 0.000 | |
| Step | 0.579 | 0.043 | 0.570 | 0.0452 | 0.989 ** | 0.991 ** | 0.985 | 0.766 | 0.996 | 0.000 | |
| Variability Time (s) | |||||||||||
| Stride | 0.086 | 0.034 | 0.162 | 0.106 | 0.130 | 0.316 | 0.124 | −0.639 | 0.603 | 0.356 | |
| Stance | 0.041 | 0.008 | 0.151 | 0.108 | −0.153 | −0.041 | −0.025 | −0.494 | 0.428 | 0.542 | |
| Swing | 0.046 | 0.012 | 0.043 | 0.004 | −0.109 | −0.039 | −0.155 | −1.991 | 0.547 | 0.621 | |
| Step | 0.042 | 0.010 | 0.033 | 0.009 | 0.061 | 0.108 | 0.083 | −0.609 | 0.561 | 0.396 | |
| Asymmetry Time (s) | |||||||||||
| Stride | 0.001 | 0.002 | 0.016 | 0.012 | 0.147 | 0.278 | 0.042 | −0.319 | 0.441 | 0.418 | |
| Stance | 0.000 | 0.000 | 0.020 | 0.016 | 0.226 | 0.199 | 0.013 | −0.338 | 0.406 | 0.475 | |
| Swing | 0.001 | 0.002 | 0.012 | 0.011 | −0.028 | −0.017 | −0.011 | −0.549 | 0.462 | 0.516 | |
| Step | 0.000 | 0.000 | 0.016 | 0.011 | 0.050 | 0.068 | 0.004 | −0.177 | 0.308 | 0.488 | |
|
(PD)
Indoor DS2 n= 36 | Mean Time (s) | ||||||||||
| Stride | 1.168 | 0.096 | 1.183 | 0.106 | 0.973 ** | 0.960 ** | 0.979 | 0.940 | 0.991 | 0.000 | |
| Stance | 0.704 | 0.051 | 0.727 | 0.087 | 0.804 ** | 0.750 ** | 0.806 | 0.608 | 0.903 | 0.000 | |
| Swing | 0.458 | 0.052 | 0.454 | 0.052 | 0.570 ** | 0.545 ** | 0.730 | 0.469 | 0.863 | 0.000 | |
| Step | 0.584 | 0.049 | 0.574 | 0.049 | 0.979 ** | 0.949 ** | 0.980 | 0.849 | 0.993 | 0.000 | |
| Variability Time (s) | |||||||||||
| Stride | 0.083 | 0.044 | 0.237 | 0.161 | 0.033 | 0.082 | 0.018 | −0.350 | 0.360 | 0.461 | |
| Stance | 0.058 | 0.038 | 0.231 | 0.163 | 0.057 | 0.315 | 0.025 | −0.295 | 0.343 | 0.441 | |
| Swing | 0.054 | 0.023 | 0.045 | 0.007 | 0.316 | 0.361 * | 0.284 | −0.299 | 0.620 | 0.140 | |
| Step | 0.059 | 0.038 | 0.038 | 0.023 | 0.069 | 0.525 ** | 0.097 | 0.528 | 0.499 | 0.359 | |
| Asymmetry Time (s) | |||||||||||
| Stride | 0.002 | 0.006 | 0.023 | 0.021 | −0.161 | 0.136 | −0.158 | −0.699 | 0.777 | 0.760 | |
| Stance | 0.001 | 0.005 | 0.032 | 0.024 | −0.165 | −0.075 | −0.062 | −0.354 | 0.256 | 0.664 | |
| Swing | 0.002 | 0.003 | 0.026 | 0.018 | −0.309 | −0.211 | −0.076 | −0.343 | 0.236 | 0.723 | |
| Step | 0.002 | 0.005 | 0.033 | 0.026 | −0.200 | −0.021 | −0.073 | −0.391 | 0.262 | 0.682 | |
|
(YA)
Outdoor DS1 n= 25 | A1-Lower Back | A2-Shank | Pearson’s R | Spearman’s Rho | 95% CI Bounds | ||||||
| Mean Time (s) | Average | SD | Average | SD | ICC2,1 | Lower | Upper | p | |||
| Stride | 1.084 | 0.152 | 1.084 | 0.153 | 0.996 ** | 0.997 ** | 0.998 | 0.997 | 0.998 | 0.000 | |
| Stance | 0.680 | 0.085 | 0.668 | 0.111 | 0.924 ** | 0.936 ** | 0.940 | 0.913 | 0.958 | 0.000 | |
| Swing | 0.403 | 0.068 | 0.416 | 0.055 | 0.779 ** | 0.835 ** | 0.856 | 0.790 | 0.900 | 0.000 | |
| Step | 0.541 | 0.076 | 0.539 | 0.076 | 0.996 ** | 0.993 ** | 0.998 | 0.997 | 0.999 | 0.000 | |
| Variability Time (s) | |||||||||||
| Stride | 0.025 | 0.018 | 0.040 | 0.030 | 0.563 ** | 0.434 ** | 0.605 | 0.314 | 0.757 | 0.000 | |
| Stance | 0.018 | 0.011 | 0.033 | 0.026 | 0.445 ** | 0.346 ** | 0.413 | 0.102 | 0.607 | 0.000 | |
| Swing | 0.016 | 0.014 | 0.035 | 0.011 | 0.226 ** | 0.257 ** | 0.195 | −0.123 | 0.436 | 0.004 | |
| Step | 0.017 | 0.011 | 0.025 | 0.018 | 0.044 | 0.025 | 0.068 | −0.234 | 0.305 | 0.314 | |
| Asymmetry Time (s) | |||||||||||
| Stride | 0.003 | 0.003 | 0.006 | 0.010 | 0.104 | 0.202 * | 0.109 | −0.2013 | 0.350 | 0.234 | |
| Stance | 0.014 | 0.014 | 0.022 | 0.028 | 0.079 | 0.066 | 0.113 | −0.210 | 0.353 | 0.226 | |
| Swing | 0.014 | 0.014 | 0.023 | 0.024 | 0.008 | −0.026 | 0.013 | −0.337 | 0.277 | 0.466 | |
| Step | 0.014 | 0.014 | 0.040 | 0.054 | 0.030 | −0.013 | 0.025 | −0.271 | 0.264 | 0.429 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Celik, Y.; Stuart, S.; Woo, W.L.; Godfrey, A. Wearable Inertial Gait Algorithms: Impact of Wear Location and Environment in Healthy and Parkinson’s Populations. Sensors 2021, 21, 6476. https://doi.org/10.3390/s21196476
Celik Y, Stuart S, Woo WL, Godfrey A. Wearable Inertial Gait Algorithms: Impact of Wear Location and Environment in Healthy and Parkinson’s Populations. Sensors. 2021; 21(19):6476. https://doi.org/10.3390/s21196476
Chicago/Turabian StyleCelik, Yunus, Sam Stuart, Wai Lok Woo, and Alan Godfrey. 2021. "Wearable Inertial Gait Algorithms: Impact of Wear Location and Environment in Healthy and Parkinson’s Populations" Sensors 21, no. 19: 6476. https://doi.org/10.3390/s21196476
APA StyleCelik, Y., Stuart, S., Woo, W. L., & Godfrey, A. (2021). Wearable Inertial Gait Algorithms: Impact of Wear Location and Environment in Healthy and Parkinson’s Populations. Sensors, 21(19), 6476. https://doi.org/10.3390/s21196476









