pH Colorimetric Sensor Arrays: Role of the Color Space Adopted for the Calculation of the Prediction Error
Abstract
1. Introduction
2. Materials and Methods
2.1. Reagents and Instrumentation
2.2. Preparation of the CSA
3. Theoretical Considerations
3.1. Main Error Contributions Affecting a Generic X Color Coordinate
- β is the background level due to the lighting conditions and to the CSA support (associated with the spot);
- δ is the error due to the image acquisition conditions (associated with the spot);
- ε is the instrumental error of the camera (associated with the detected color).
3.2. Linearization of the Sigmoidal Calibration Model
4. Results and Discussion
4.1. Experimental Analytical Performance of Various Color Spaces
4.2. Quantification of the Error Contributions on pH Discrimination
4.3. Calculation of the Discriminated pH Precision for a CSA
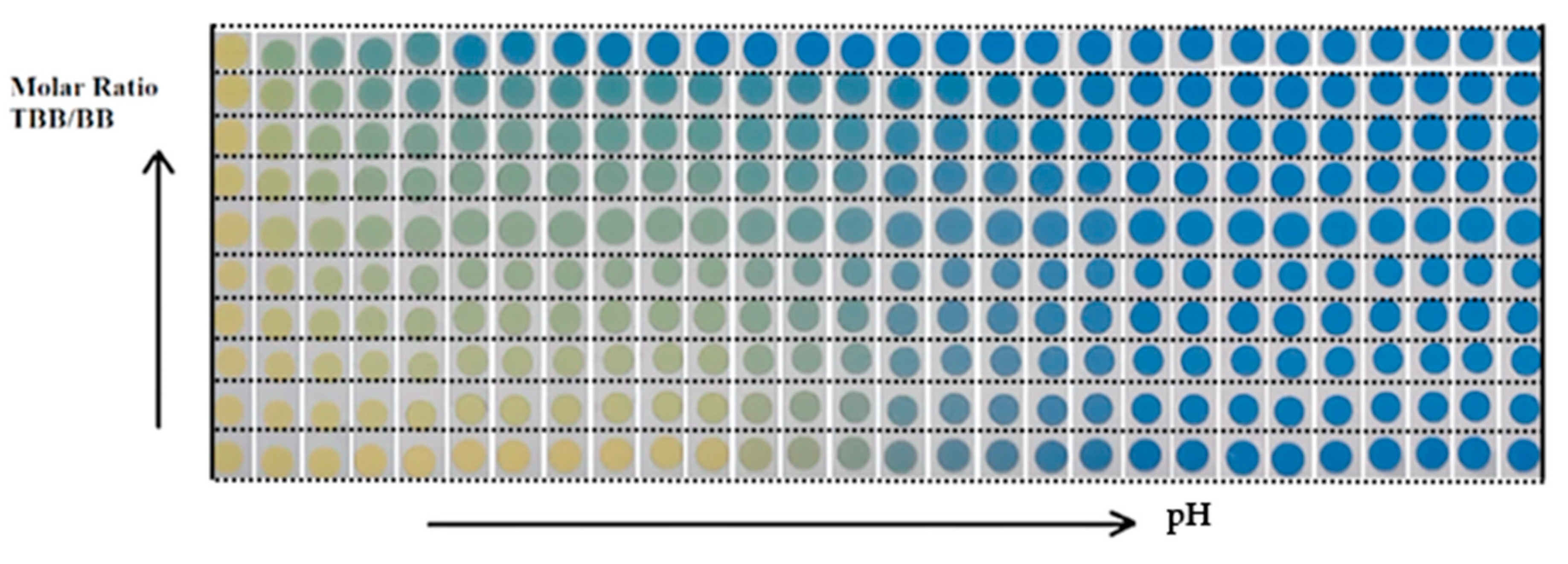
4.4. The Behavior of the Mixture TBB/BB in the CSA
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lim, S.H.; Musto, C.J.; Park, E.; Zhong, W.; Suslick, K.S. A colorimetric sensor array for detection and identification of sugars. Org. Lett. 2008, 10, 4405–4408. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Suslick, K.S. Colorimetric Sensor Array for Monitoring CO and Ethylene. Anal. Chem. 2019, 91, 797–802. [Google Scholar] [CrossRef] [PubMed]
- Janzen, M.C.; Ponder, J.B.; Bailey, D.P.; Ingison, C.K.; Suslick, K.S. Colorimetric sensor arrays for volatile organic compounds. Anal. Chem. 2006, 78, 3591–3600. [Google Scholar] [CrossRef]
- Pastore, A.; Badocco, D.; Pastore, P. Kinetic response of pH colorimetric sensors: Role of the cationic surfactant concentration and amount and type of solvent used in the preparation of the sensing spot. Microchem. J. 2020, 157, 104891. [Google Scholar] [CrossRef]
- Boukhriss, A.; El Messoudi, M.; Roblin, J.-P.; Aaboub, T.; Boyer, D.; Gmouh, S. Luminescent hybrid coatings prepared by a sol-gel process for a textile-based pH sensor. Mater. Adv. 2020, 1, 918–925. [Google Scholar] [CrossRef]
- Abdolla, N.S.Y.; Davies, D.L.; Lowe, M.P.; Singh, K. Bis-cyclometallated Ir(III) complexes containing 2-(1H-pyrazol-3-yl)pyridine ligands; influence of substituents and cyclometallating ligands on response to changes in pH. Dalton Trans. 2020, 49, 12025–12036. [Google Scholar] [CrossRef] [PubMed]
- Aich, K.; Das, S.; Goswami, S.; Quah, C.K.; Sarkar, D.; Mondal, T.K.; Fun, H.K. Carbazole-benzimidazole based dyes for acid responsive ratiometric emissive switches. New J. Chem. 2016, 40, 6907–6915. [Google Scholar] [CrossRef]
- Das, S.; Goswami, S.; Aich, K.; Ghoshal, K.; Quah, C.K.; Bhattacharyya, M.; Fun, H.K. ESIPT and CHEF based highly sensitive and selective ratiometric sensor for Al3+ with imaging in human blood cells. New J. Chem. 2015, 39, 8582–8587. [Google Scholar] [CrossRef]
- Goswami, S.; Das, S.; Aich, K.; Sarkar, D.; Mondal, T.K.; Quah, C.K.; Fun, H.K. CHEF induced highly selective and sensitive turn-on fluorogenic and colorimetric sensor for Fe3+. Dalt. Trans. 2013, 42, 15113–15119. [Google Scholar] [CrossRef]
- Safavi, A.; Maleki, N.; Rostamzadeh, A.; Maesum, S. CCD camera full range pH sensor array. Talanta 2007, 71, 498–501. [Google Scholar] [CrossRef]
- Sun, W.; Li, H.; Wang, H.; Xiao, S.; Wang, J.; Feng, L. Sensitivity enhancement of pH indicator and its application in the evaluation of fish freshness. Talanta 2015, 143, 127–131. [Google Scholar] [CrossRef] [PubMed]
- Ragain, J.C. A Review of Color Science in Dentistry: Colorimetry and Color Space. J. Dent. Oral Disord. Ther. 2016, 4, 1–5. [Google Scholar] [CrossRef]
- Capel-Cuevas, S.; Cuéllar, M.P.; de Orbe-Payá, I.; Pegalajar, M.C.; Capitán-Vallvey, L.F. Full-range optical pH sensor array based on neural networks. Microchem. J. 2011, 97, 225–233. [Google Scholar] [CrossRef]
- Chang, B.Y. Smartphone-based chemistry instrumentation: Digitization of colorimetric measurements. Bull. Korean Chem. Soc. 2012, 33, 549–552. [Google Scholar] [CrossRef]
- Cantrell, K.; Erenas, M.M.; De Orbe-Payá, I.; Capitán-Vallvey, L.F. Use of the hue parameter of the hue, saturation, value color space as a quantitative analytical parameter for bitonal optical sensors. Anal. Chem. 2010, 82, 531–542. [Google Scholar] [CrossRef] [PubMed]
- Chavolla, E.; Zaldivar, D.; Cuevas, E.; Perez, M.A. Color Spaces Advantages and Disadvantages in Image Color Clustering Segmentation. In Advances in Soft Computing and Machine Learning in Image Processing; Hassanien, A.E., Oliva, D.A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–22. ISBN 978-3-319-63754-9. [Google Scholar]
- Mohr, G.J.; Müller, H. Tailoring colour changes of optical sensor materials by combining indicator and inert dyes and their use in sensor layers, textiles and non-wovens. Sens. Actuators B Chem. 2015, 206, 788–793. [Google Scholar] [CrossRef]
- Bosch, E.; Casassas, E.; Izquierdo, A.; Rosés, M. Color Changes in Screened Indicators. Anal. Chem. 1984, 56, 1422–1428. [Google Scholar] [CrossRef]
- Pastore, A.; Badocco, D.; Cappellin, L.; Pastore, P. Enhancement of the pH Measurement of a PVDF-Supported Colorimetric Sensor by Tailoring Hue Changes with the Addition of a Second Dye. Microchem. J. 2020, 154, 104552. [Google Scholar] [CrossRef]
- Pastore, A.; Badocco, D.; Bogialli, S.; Cappellin, L.; Pastore, P. Behavior of Sulfonephthalein and Azo Dyes as Effective pH Sensors in Hybrid Materials. Microchem. J. 2020, 105605. [Google Scholar] [CrossRef]
- Jurmanović, S.; Kordić, Š.; Steinberg, M.D.; Steinberg, I.M. Organically modified silicate thin films doped with colourimetric pH indicators methyl red and bromocresol green as pH responsive sol-gel hybrid materials. Thin Solid Films 2010, 518, 2234–2240. [Google Scholar] [CrossRef]
- Pastore, A.; Badocco, D.; Pastore, P. Reversible and high accuracy pH colorimetric sensor array based on a single acid-base indicator working in a wide pH interval. Talanta 2020, 219, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Butler, T.M.; MacCraith, B.D.; McDonagh, C. Leaching in sol-gel-derived silica films for optical pH sensing. J. Non. Cryst. Solids 1998, 224, 249–258. [Google Scholar] [CrossRef]
- El-Nahhal, I.M.; Zourab, S.M.; Kodeh, F.S.; Abdelsalam, F.H. Sol-gel encapsulation of bromothymol blue pH indicator in presence of Gemini 12-2-12 surfactant. J. Sol-Gel Sci. Technol. 2014, 71, 16–23. [Google Scholar] [CrossRef]
- Rottman, C.; Grader, G.; De Hazan, Y.; Melchior, S.; Avnir, D. Surfactant-induced modification of dopants reactivity in sol-gel matrixes. J. Am. Chem. Soc. 1999, 121, 8533–8543. [Google Scholar] [CrossRef]
- Pastore, A.; Badocco, D.; Pastore, P. Influence of surfactant chain length, counterion and OrMoSil precursors on reversibility and working interval of pH colorimetric sensors. Talanta 2020, 212, 120739. [Google Scholar] [CrossRef]
- Capel-Cuevas, S.; Cuéllar, M.P.; de Orbe-Payá, I.; Pegalajar, M.C.; Capitán-Vallvey, L.F. Full-range optical pH sensor based on imaging techniques. Anal. Chim. Acta 2010, 681, 71–81. [Google Scholar] [CrossRef]
- Martinez-Olmos, A.; Capel-Cuevas, S.; López-Ruiz, N.; Palma, A.J.; De Orbe, I.; Capitán-Vallvey, L.F. Sensor array-based optical portable instrument for determination of pH. Sens. Actuators B Chem. 2011, 156, 840–848. [Google Scholar] [CrossRef]
- Pathak, A.; Borana, J.; Adhikari, J.V.; Gorthi, S.S. Indicator-impregnated agarose films for colorimetric measurement of pH. SLAS Technol. 2017, 22, 81–88. [Google Scholar] [CrossRef]
- Pastore, A.; Badocco, D.; Pastore, P. High accuracy OrMoSil (Polyvinylidene Fluoride)-supported colorimetric sensor: Novel approach for the calculation of the pH prediction error. Talanta 2020, 213, 120840. [Google Scholar] [CrossRef]
- Mathematics, A. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 2019, 11, 431–441. [Google Scholar]


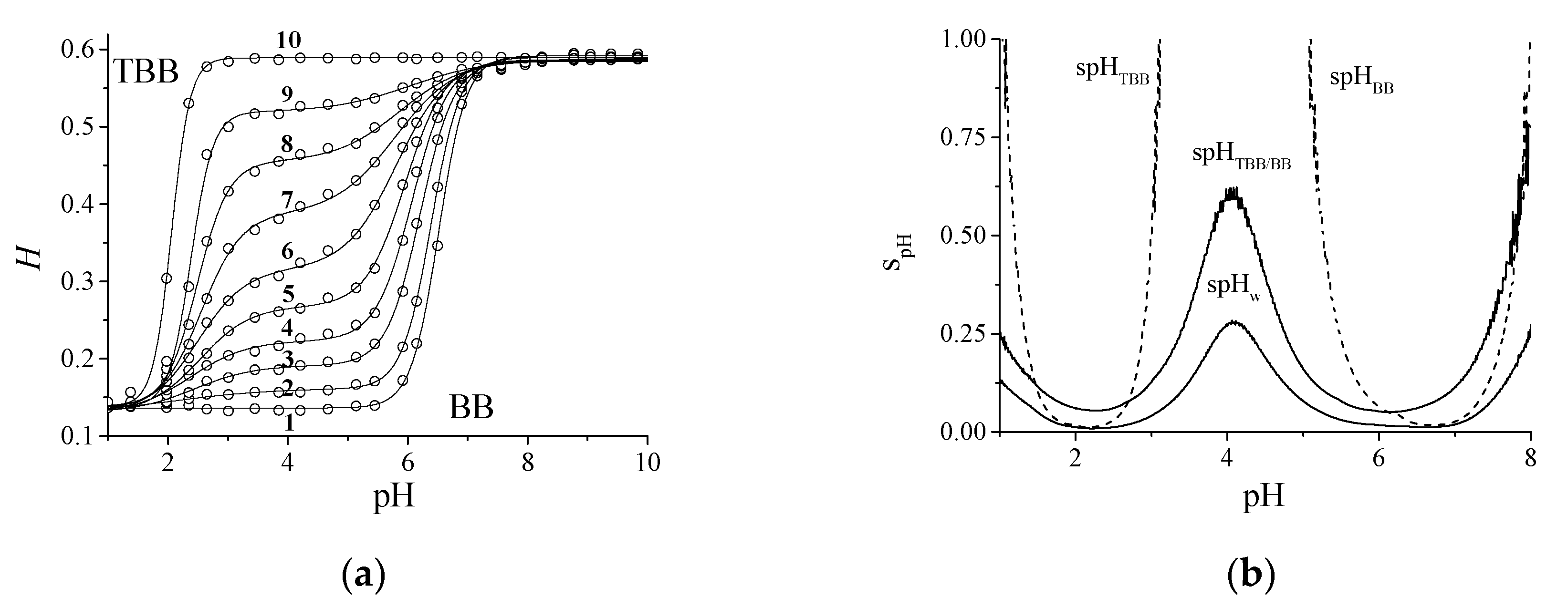
| X | Spot # | R2 | X | Spot # | R2 | ||||
|---|---|---|---|---|---|---|---|---|---|
| H | 5 | 0.9 | 0.999 | 0.016 | x | 3 | 2.2 | 0.996 | 0.080 |
| H | 3 | 0.9 | 0.999 | 0.017 | L | 2 | 2.2 | 0.996 | 0.081 |
| H | 2 | 1.0 | 0.999 | 0.017 | y | 2 | 2.1 | 0.995 | 0.084 |
| H | 4 | 0.9 | 0.999 | 0.020 | R | 2 | 2.3 | 0.996 | 0.085 |
| H | 1 | 1.1 | 0.999 | 0.021 | G | 2 | 2.1 | 0.994 | 0.090 |
| X | 1 | 2.0 | 0.997 | 0.064 | G | 4 | 2.2 | 0.994 | 0.096 |
| Y | 1 | 2.0 | 0.996 | 0.070 | B | 4 | 2.6 | 0.995 | 0.097 |
| L | 1 | 2.1 | 0.996 | 0.070 | R | 3 | 2.4 | 0.995 | 0.097 |
| R | 1 | 2.2 | 0.996 | 0.073 | L | 4 | 2.4 | 0.994 | 0.100 |
| G | 1 | 2.0 | 0.996 | 0.074 | y | 4 | 2.3 | 0.994 | 0.101 |
| G | 3 | 2.1 | 0.996 | 0.075 | B | 1 | 2.6 | 0.995 | 0.101 |
| L | 3 | 2.2 | 0.996 | 0.076 | B | 2 | 2.6 | 0.995 | 0.104 |
| X | 2 | 2.1 | 0.996 | 0.076 | B | 3 | 2.5 | 0.994 | 0.109 |
| Y | 3 | 2.2 | 0.996 | 0.077 | x | 4 | 2.4 | 0.993 | 0.109 |
| r | H0 | p | pH1 | pH2 | R2 | pH1 | ∆pH2 | |
|---|---|---|---|---|---|---|---|---|
| BB | 0.136 | 0.456 | 0.000 | 2.58 | 6.52 | 0.9996 | 2.38 | 0.92 |
| 0.024 | 0.130 | 0.460 | 0.068 | 2.14 | 6.39 | 0.9999 | 2.18 | 0.97 |
| 0.061 | 0.130 | 0.456 | 0.135 | 2.44 | 6.21 | 0.9995 | 2.00 | 1.13 |
| 0.098 | 0.130 | 0.457 | 0.205 | 2.39 | 6.08 | 0.9991 | 1.87 | 1.20 |
| 0.147 | 0.132 | 0.453 | 0.300 | 2.55 | 5.96 | 0.9987 | 1.65 | 1.31 |
| 0.184 | 0.130 | 0.456 | 0.407 | 2.50 | 5.81 | 0.9993 | 1.59 | 1.70 |
| 0.233 | 0.135 | 0.452 | 0.556 | 2.56 | 5.80 | 0.9992 | 1.34 | 2.02 |
| 0.331 | 0.139 | 0.447 | 0.706 | 2.49 | 5.87 | 0.9990 | 1.04 | 2.13 |
| 0.478 | 0.138 | 0.450 | 0.845 | 2.38 | 6.06 | 0.9987 | 0.74 | 2.05 |
| TBB | 0.139 | 0.450 | 1.000 | 2.06 | 6.00 | 0.9994 | 0.62 | 1.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pastore, A.; Badocco, D.; Bogialli, S.; Cappellin, L.; Pastore, P. pH Colorimetric Sensor Arrays: Role of the Color Space Adopted for the Calculation of the Prediction Error. Sensors 2020, 20, 6036. https://doi.org/10.3390/s20216036
Pastore A, Badocco D, Bogialli S, Cappellin L, Pastore P. pH Colorimetric Sensor Arrays: Role of the Color Space Adopted for the Calculation of the Prediction Error. Sensors. 2020; 20(21):6036. https://doi.org/10.3390/s20216036
Chicago/Turabian StylePastore, Andrea, Denis Badocco, Sara Bogialli, Luca Cappellin, and Paolo Pastore. 2020. "pH Colorimetric Sensor Arrays: Role of the Color Space Adopted for the Calculation of the Prediction Error" Sensors 20, no. 21: 6036. https://doi.org/10.3390/s20216036
APA StylePastore, A., Badocco, D., Bogialli, S., Cappellin, L., & Pastore, P. (2020). pH Colorimetric Sensor Arrays: Role of the Color Space Adopted for the Calculation of the Prediction Error. Sensors, 20(21), 6036. https://doi.org/10.3390/s20216036







