Damage Identification in Various Types of Composite Plates Using Guided Waves Excited by a Piezoelectric Transducer and Measured by a Laser Vibrometer
Abstract
:1. Introduction
2. Method for Detection of Anomalies in Guided Wave Propagation
2.1. Median Filtering
2.2. Energy Function
2.3. Attenuation Compensation
2.4. Two-Dimensional Discrete Fourier Transform
2.5. Spectral Wavefield Pattern
2.6. Filter Mask
2.7. Smoothing Filter Mask
2.8. Filtering
2.9. Inverse Two-Dimensional Discrete Fourier Transform
2.10. Root Mean Squared
3. Experimental Verification
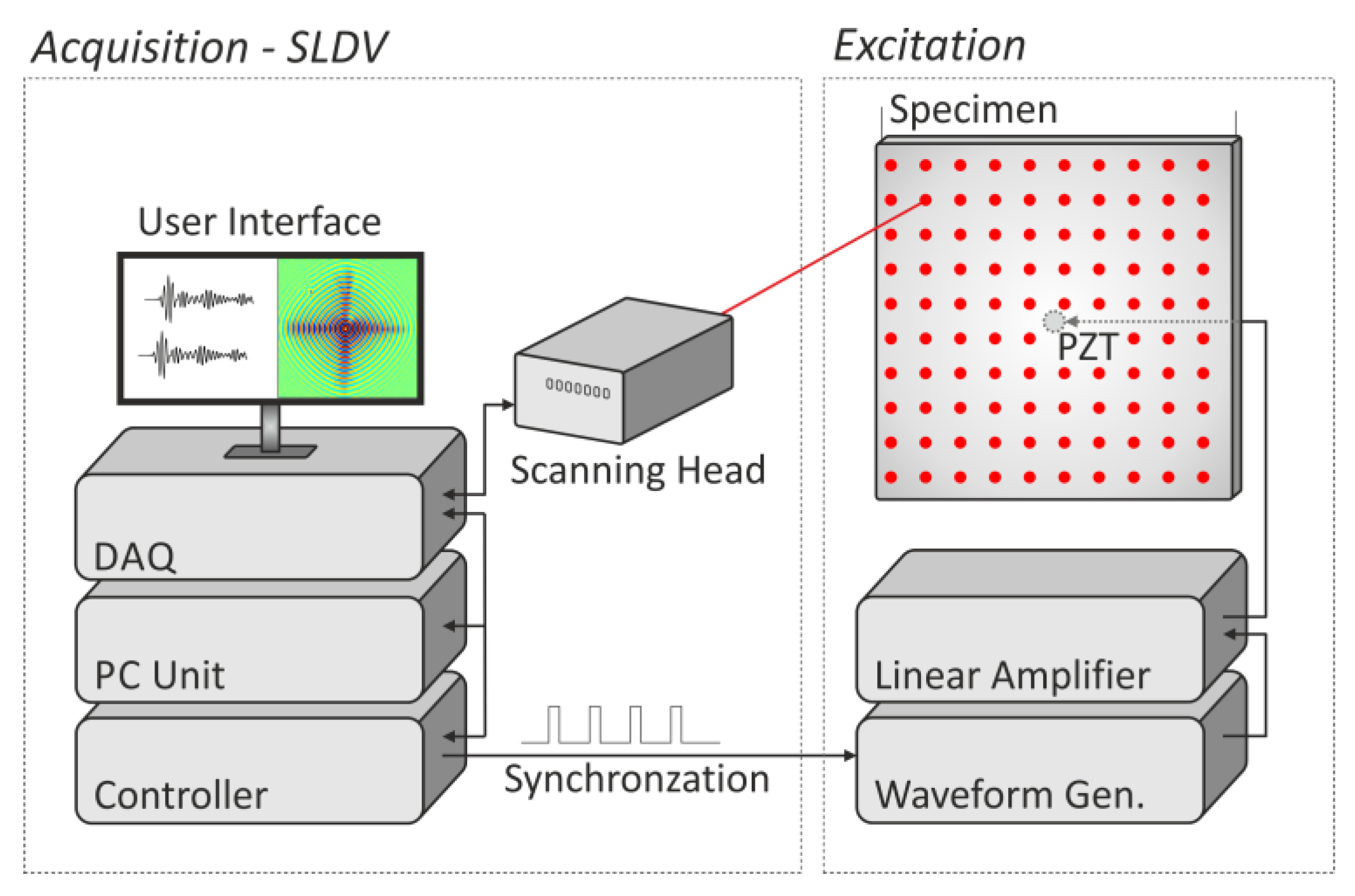
3.1. Experimental Set-Up
3.2. Specimens
3.2.1. CFRP
3.2.2. GFRP
3.2.3. SFRP
3.2.4. HCSP
3.3. Results
3.3.1. Wavefield Images
3.3.2. Spectral Wavefield Patterns
3.3.3. Wavefield Irregularities Maps
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Wandowski, T.; Malinowski, P.H.; Ostachowicz, W.M. Circular sensing networks for guided waves based structural health monitoring. Mech. Syst. Signal Process. 2016, 66, 248–267. [Google Scholar] [CrossRef]
- Malinowski, P.; Wandowski, T.; Ostachowicz, W. Damage detection potential of a triangular piezoelectric configuration. Mech. Syst. Signal Process. 2011, 25, 2722–2732. [Google Scholar] [CrossRef]
- Wandowski, T.; Malinowski, P.; Ostachowicz, W.M. Damage detection with concentrated configurations of piezoelectric transducers. Smart Mater. Struct. 2011, 20, 025002. [Google Scholar] [CrossRef]
- Wandowski, T.; Malinowski, P.; Ostachowicz, W. Diagnostics using different configurations of sensing networks. J. Phys. Conf. Ser. 2011, 305, 012007. [Google Scholar] [CrossRef] [Green Version]
- Kudela, P.; Radzienski, M.; Ostachowicz, W.; Yang, Z. Structural Health Monitoring system based on a concept of Lamb wave focusing by the piezoelectric array. Mech. Syst. Signal Process. 2018, 108, 21–32. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Piezoelectric Wafer Active Sensors for Structural Health Monitoring of Composite Structures Using Tuned Guided Waves. J. Eng. Mater. Technol. 2011, 133, 041012. [Google Scholar] [CrossRef]
- Michaels, J.E.; Michaels, T.E. Guided wave signal processing and image fusion for in situ damage localization in plates. Wave Motion 2007, 44, 482–492. [Google Scholar] [CrossRef]
- Rao, J.; Ratassepp, M.; Lisevych, D.; Hamzah Caffoor, M.; Fan, Z. On-Line Corrosion Monitoring of Plate Structures Based on Guided Wave Tomography Using Piezoelectric Sensors. Sensors 2017, 17, 2882. [Google Scholar] [CrossRef]
- Bijudas, C.R.; Mitra, M.; Mujumdar, P.M. Time reversed Lamb wave for damage detection in a stiffened aluminum plate. Smart Mater. Struct. 2013, 22, 105026. [Google Scholar] [CrossRef]
- Wang, C.H.; Rose, J.T.; Chang, F.-K. A synthetic time-reversal imaging method for structural health monitoring. Smart Mater. Struct. 2004, 13, 415–423. [Google Scholar] [CrossRef]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 053001. [Google Scholar] [CrossRef]
- Wandowski, T.; Kudela, P.; Malinowski, P.; Ostachowicz, W. Lamb Waves for Damage Localisation in Panels. Strain 2011, 47, 449–457. [Google Scholar] [CrossRef]
- Zhao, J.; Li, F.; Cao, X.; Li, H. Wave Propagation in Aluminum Honeycomb Plate and Debonding Detection Using Scanning Laser Vibrometer. Sensors 2018, 18, 1669. [Google Scholar] [CrossRef]
- Ruzzene, M. Frequency–wavenumber domain filtering for improved damage visualization. Smart Mater. Struct. 2007, 16, 2116–2129. [Google Scholar] [CrossRef] [Green Version]
- Park, B.; An, Y.-K.; Sohn, H. Visualization of hidden delamination and debonding in composites through noncontact laser ultrasonic scanning. Compos. Sci. Technol. 2014, 100, 10–18. [Google Scholar] [CrossRef]
- Tian, Z.; Leckey, C.; Rogge, M.; Yu, L. Crack detection with Lamb wave wavenumber analysis. In Proceedings of the International Society for Optics and Photonics, San Diego, CA, USA, 11–14 March 2013; p. 86952Z. [Google Scholar]
- Ruzzene, M. Simulation and Measurement of Ultrasonic Waves in Elastic Plates Using Laser Vibrometry. AIP Conf. Proc. 2005, 760, 172–179. [Google Scholar] [CrossRef] [Green Version]
- Radzieński, M.; Doliński, Ł.; Krawczuk, M.; Żak, A.; Ostachowicz, W. Application of RMS for damage detection by guided elastic waves. J. Phys. Conf. Ser. 2011, 305, 012085. [Google Scholar] [CrossRef] [Green Version]
- Staszewski, W.J.; Lee, B.C.; Traynor, R. Fatigue crack detection in metallic structures with Lamb waves and 3D laser vibrometry. Meas. Sci. Technol. 2007, 18, 727–739. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Radzieński, M.; Kudela, P. 50th Anniversary Article: Comparison Studies of Full Wavefield Signal Processing for Crack Detection. Strain 2014, 50, 275–291. [Google Scholar] [CrossRef]
- An, Y.-K.; Park, B.; Sohn, H. Complete noncontact laser ultrasonic imaging for automated crack visualization in a plate. Smart Mater. Struct. 2013, 22, 025022. [Google Scholar] [CrossRef]
- Kudela, P.; Radzieński, M.; Ostachowicz, W. Identification of cracks in thin-walled structures by means of wavenumber filtering. Mech. Syst. Signal Process. 2015, 50–51, 456–466. [Google Scholar] [CrossRef]
- Kudela, P.; Radzienski, M.; Ostachowicz, W. Impact induced damage assessment by means of Lamb wave image processing. Mech. Syst. Signal Process. 2018, 102, 23–36. [Google Scholar] [CrossRef]











| Designation | Position in Thickness | Size |
|---|---|---|
| D1 | between 10th and 9th layer | d = 20 mm |
| D2 | between 8th and 7th layer | d = 20 mm |
| D3 | between 6th and 5th layer | d = 20 mm |
| D4 | between 4th and 3rd layer | d = 20 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radzieński, M.; Kudela, P.; Marzani, A.; De Marchi, L.; Ostachowicz, W. Damage Identification in Various Types of Composite Plates Using Guided Waves Excited by a Piezoelectric Transducer and Measured by a Laser Vibrometer. Sensors 2019, 19, 1958. https://doi.org/10.3390/s19091958
Radzieński M, Kudela P, Marzani A, De Marchi L, Ostachowicz W. Damage Identification in Various Types of Composite Plates Using Guided Waves Excited by a Piezoelectric Transducer and Measured by a Laser Vibrometer. Sensors. 2019; 19(9):1958. https://doi.org/10.3390/s19091958
Chicago/Turabian StyleRadzieński, Maciej, Paweł Kudela, Alessandro Marzani, Luca De Marchi, and Wiesław Ostachowicz. 2019. "Damage Identification in Various Types of Composite Plates Using Guided Waves Excited by a Piezoelectric Transducer and Measured by a Laser Vibrometer" Sensors 19, no. 9: 1958. https://doi.org/10.3390/s19091958






