M-Bonacci Zone Plates for Ultrasound Focusing
Abstract
:1. Introduction
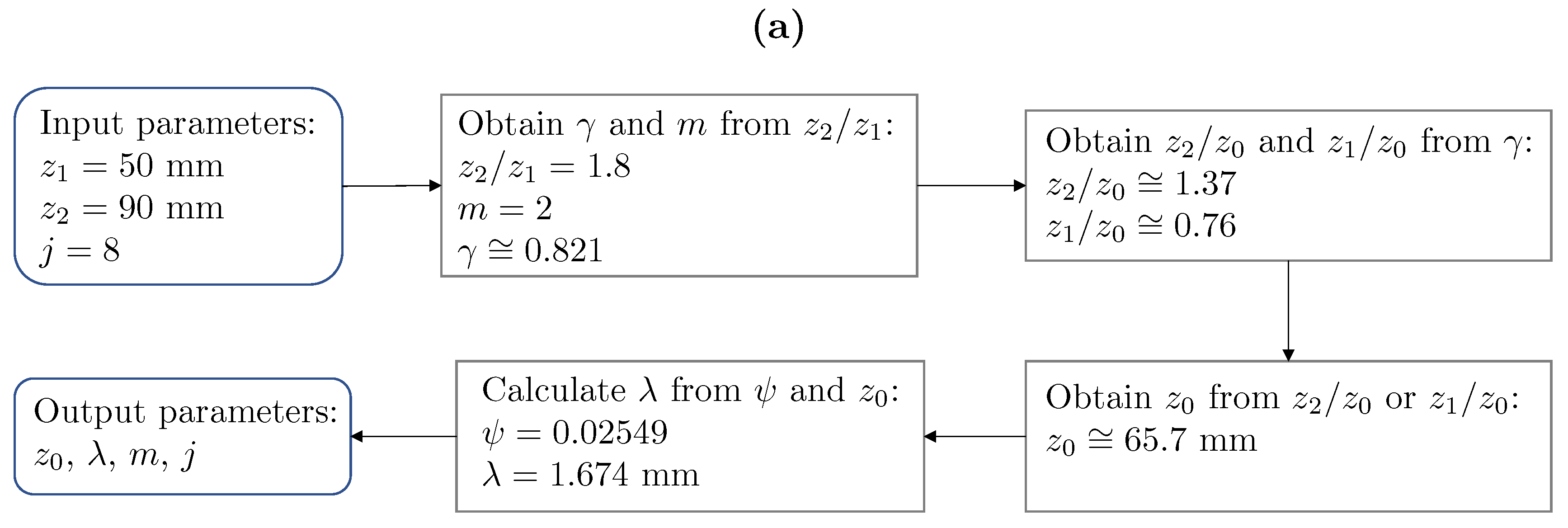
2. M-Bonacci Zone Plates
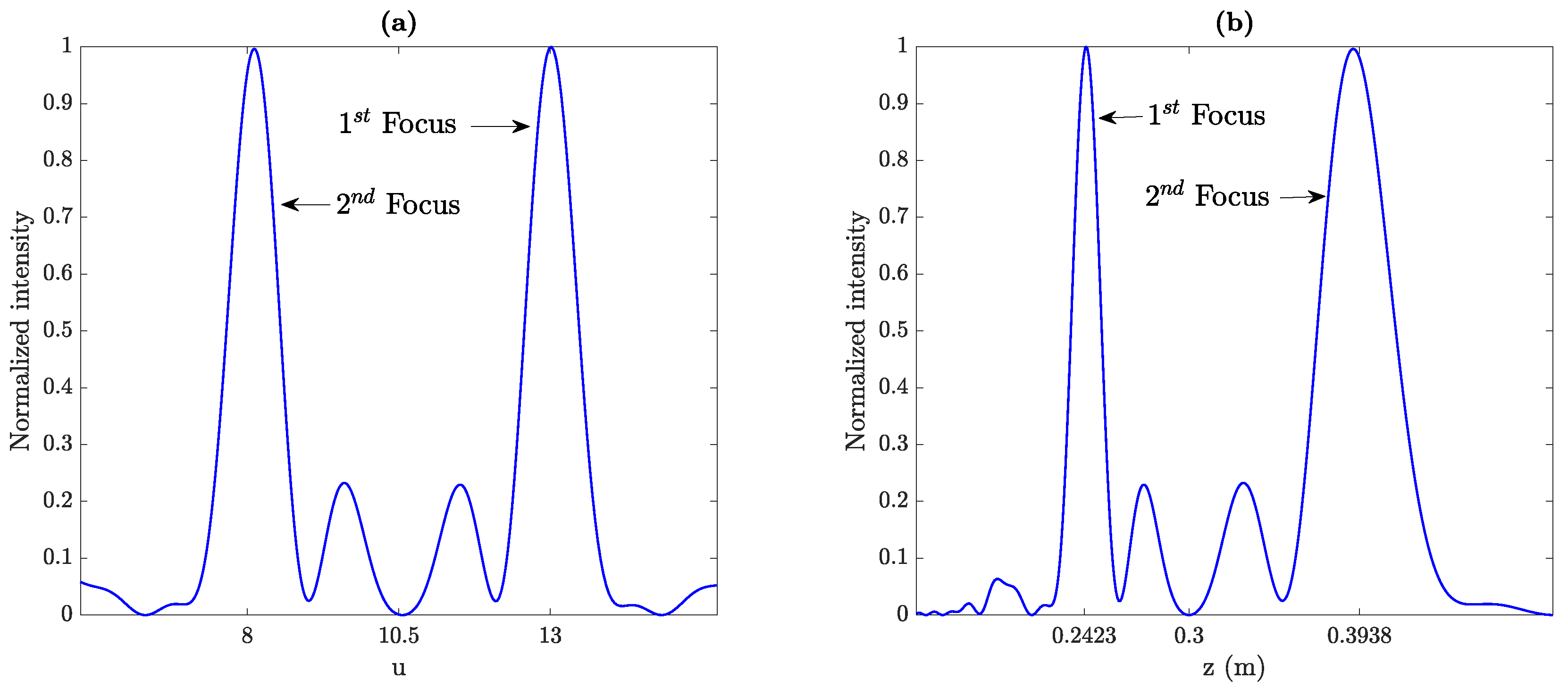
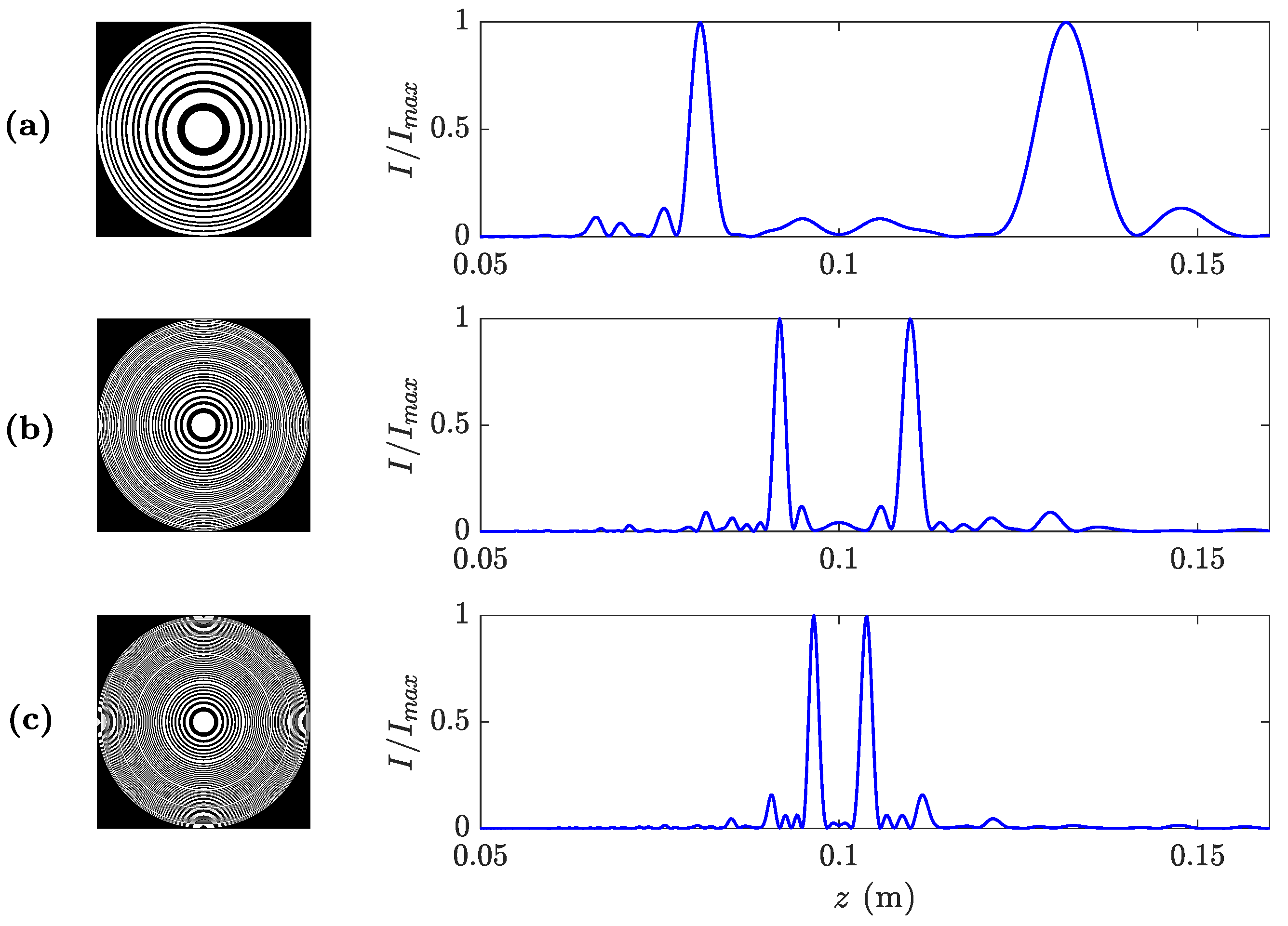
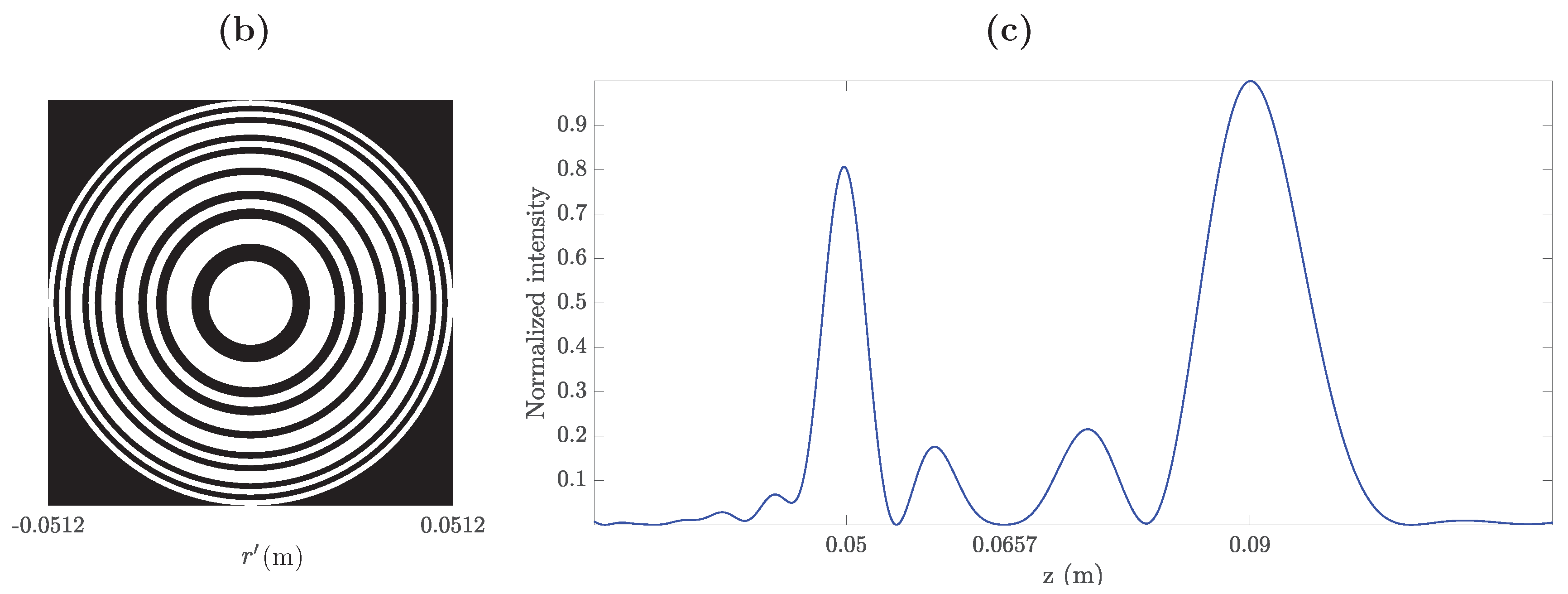
2.1. Design and Focusing Properties
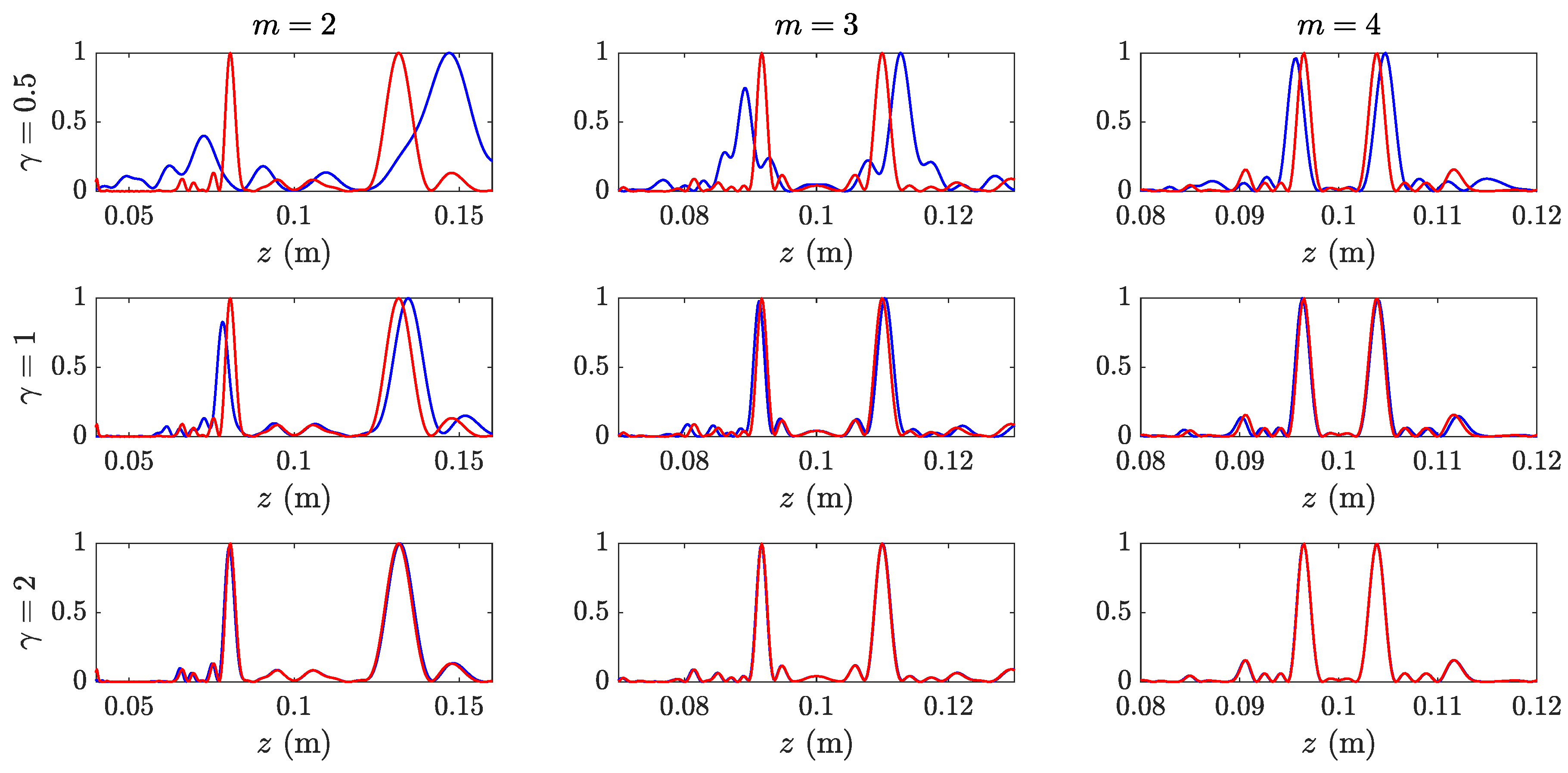
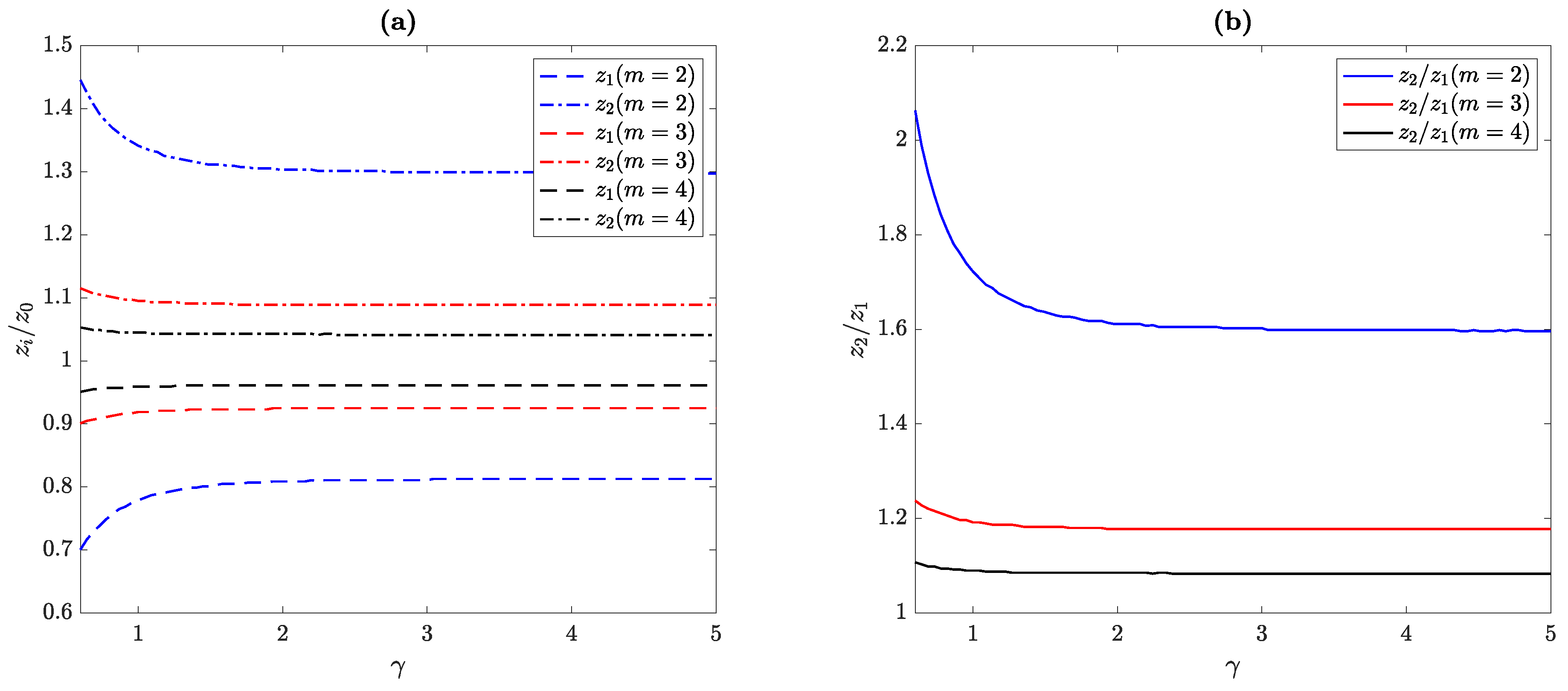
2.2. -Parameter
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, J.; Xiao, J.; Lisevych, D.; Shakouri, A.; Fan, Z. Deep-subwavelength control of acoustic waves in an ultra-compact metasurface lens. Nat. Commun. 2018, 9, 4920. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liang, B.; Tao, X.; Zhu, X.F.; Zou, X.Y.; Cheng, J.C. Acoustic focusing by coiling up space. Appl. Phys. Lett. 2012, 101, 233508. [Google Scholar] [CrossRef]
- Molerón, M.; Serra-Garcia, M.; Daraio, C. Acoustic Fresnel lenses with extraordinary transmission. Appl. Phys. Lett. 2014, 105, 114109. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Yu, G.; Liang, B.; Zou, X.; Li, G.; Cheng, S.; Cheng, J. Three-dimensional Ultrathin Planar Lenses by Acoustic Metamaterials. Sci. Rep. 2015, 4, 6830. [Google Scholar] [CrossRef] [PubMed]
- Lan, J.; Li, Y.; Xu, Y.; Liu, X. Manipulation of acoustic wavefront by gradient metasurface based on Helmholtz Resonators. Sci. Rep. 2017, 7, 10587. [Google Scholar] [CrossRef] [Green Version]
- Jiménez-Gambín, S.; Jiménez, N.; Benlloch, J.M.; Camarena, F. Holograms to Focus Arbitrary Ultrasonic Fields through the Skull. Phys. Rev. Appl. 2019, 12, 014016. [Google Scholar] [CrossRef]
- Pérez-López, S.; Fuster, J.M.; Minin, I.V.; Minin, O.V.; Candelas, P. Tunable subwavelength ultrasound focusing in mesoscale spherical lenses using liquid mixtures. Sci. Rep. 2019, 9, 13363. [Google Scholar] [CrossRef]
- Veira Canle, D.; Kekkonen, T.; Mäkinen, J.; Puranen, T.; Nieminen, H.J.; Kuronen, A.; Franssila, S.; Kotiaho, T.; Salmi, A.; Hæggström, E. Practical realization of a sub-λ/2 acoustic jet. Sci. Rep. 2019, 9, 5189. [Google Scholar] [CrossRef]
- Calvo, D.C.; Thangawng, A.L.; Nicholas, M.; Layman, C.N. Thin Fresnel zone plate lenses for focusing underwater sound. Appl. Phys. Lett. 2015, 107, 014103. [Google Scholar] [CrossRef]
- Pérez-López, S.; Fuster, J.M.; Candelas, P.; Rubio, C.; Belmar, F. On the use of phase correction rings on Fresnel zone plates with ultrasound piston emitters. Appl. Phys. Lett. 2018, 112, 264102. [Google Scholar] [CrossRef]
- Tarrazó-Serrano, D.; Pérez-López, S.; Candelas, P.; Uris, A.; Rubio, C. Acoustic Focusing Enhancement in Fresnel Zone Plate Lenses. Sci. Rep. 2019, 9, 7067. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues Ribeiro, R.S.; Dahal, P.; Guerreiro, A.; Jorge, P.A.S.; Viegas, J. Fabrication of Fresnel plates on optical fibres by FIB milling for optical trapping, manipulation and detection of single cells. Sci. Rep. 2017, 7, 4485. [Google Scholar] [CrossRef] [PubMed]
- Hristov, H.D.; Rodriguez, J.M. Design Equation for Multidielectric Fresnel Zone Plate Lens. IEEE Microw. Wirel. Compone. Lett. 2012, 22, 574–576. [Google Scholar] [CrossRef]
- Clement, G.; Nomura, H.; Kamakura, T. Ultrasound field measurement using a binary lens. IEEE Trans. Ultrason. Ferroelectr. Freq. Cont. 2015, 62, 350–359. [Google Scholar] [CrossRef] [PubMed]
- Pérez-López, S.; Fuster, J.M.; Candelas, P.; Rubio, C. On the focusing enhancement of Soret zone plates with ultrasound directional transducers. Appl. Phys. Lett. 2019, 114, 224101. [Google Scholar] [CrossRef] [Green Version]
- Monsoriu, J.A.; Calatayud, A.; Remon, L.; Furlan, W.D.; Saavedra, G.; Andres, P. Bifocal Fibonacci Diffractive Lenses. IEEE Photon. J. 2013, 5, 3400106. [Google Scholar] [CrossRef]
- Machado, F.; Ferrando, V.; Furlan, W.D.; Monsoriu, J.A. Diffractive m-bonacci lenses. Opt. Expr. 2017, 25, 8267. [Google Scholar] [CrossRef]
- Saavedra, G.; Furlan, W.D.; Monsoriu, J.A. Fractal zone plates. Opt. Lett. 2003, 28, 971. [Google Scholar] [CrossRef]
- Furlan, W.D.; Saavedra, G.; Monsoriu, J.A. White-light imaging with fractal zone plates. Opt. Lett. 2007, 32, 2109. [Google Scholar] [CrossRef]
- Mendoza-Yero, O.; Fernández-Alonso, M.; Mínguez-Vega, G.; Lancis, J.; Climent, V.; Monsoriu, J.A. Fractal generalized zone plates. Opt. Soc. Am. A 2009, 26, 1161. [Google Scholar] [CrossRef]
- Ferrando, V.; Giménez, F.; Furlan, W.D.; Monsoriu, J.A. Bifractal focusing and imaging properties of Thue–Morse Zone Plates. Opt. Expr. 2015, 23, 19846. [Google Scholar] [CrossRef] [PubMed]
- Xia, T.; Cheng, S.; Tao, S. Generation of three equal-intensity foci based on a modified composite zone plate. Optik 2018, 159, 150–156. [Google Scholar] [CrossRef]
- Fuster, J.; Pérez-López, S.; Candelas, P.; Rubio, C. Design of Binary-Sequence Zone Plates in High Wavelength Domains. Sensors 2018, 18, 2604. [Google Scholar] [CrossRef]
- Nie, L.; Cai, X.; Maslov, K.; Garcia-Uribe, A.; Anastasio, M.A.; Wang, L.V. Photoacoustic tomography through a whole adult human skull with a photon recycler. J. Biomed. Opt. 2012, 17, 110506. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Knox, H.J.; Tang, Y.; Liu, W.; Nie, L.; Chan, J.; Yao, J. Simultaneous photoacoustic imaging of intravascular and tissue oxygenation. Opt. Lett. 2019, 44, 3773. [Google Scholar] [CrossRef]
- ter Haar, G.; Coussios, C. High intensity focused ultrasound: Physical principles and devices. Int. J. Hyperth. 2007, 23, 89–104. [Google Scholar] [CrossRef] [Green Version]
- Suo, D.; Jin, Z.; Jiang, X.; Dayton, P.A.; Jing, Y. Microbubble mediated dual-frequency high intensity focused ultrasound thrombolysis: An In vitro study. Appl. Phys. Lett. 2017, 110, 023703. [Google Scholar] [CrossRef]
- GyP, S.; DY, L.; G, H. What is on the Horizon for Hyperthermic Cancer Therapy? J. Tradit. Med. Clin. Naturop. 2017, 6. [Google Scholar] [CrossRef]
- Simon, J.C.; Sapozhnikov, O.A.; Khokhlova, V.A.; Wang, Y.N.; Crum, L.A.; Bailey, M.R. Ultrasonic atomization of tissue and its role in tissue fractionation by high intensity focused ultrasound. Phys. Med. Biol. 2012, 57, 8061–8078. [Google Scholar] [CrossRef] [Green Version]
- Jeong, J.S.; Cannata, J.M.; Shung, K.K. Dual-Focus Therapeutic Ultrasound Transducer for Production of Broad Tissue Lesions. Ultr. Med. Biol. 2010, 36, 1836–1848. [Google Scholar] [CrossRef] [Green Version]
- Jeong, J. Dual concentric-sectored HIFU transducer with phase-shifted ultrasound excitation for expanded necrotic region: A simulation study. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 924–931. [Google Scholar] [CrossRef] [PubMed]




| m | |
|---|---|
| 2 | |
| 3 | |
| 4 |
| j | |||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-López, S.; Fuster, J.M.; Candelas, P. M-Bonacci Zone Plates for Ultrasound Focusing. Sensors 2019, 19, 4313. https://doi.org/10.3390/s19194313
Pérez-López S, Fuster JM, Candelas P. M-Bonacci Zone Plates for Ultrasound Focusing. Sensors. 2019; 19(19):4313. https://doi.org/10.3390/s19194313
Chicago/Turabian StylePérez-López, Sergio, José Miguel Fuster, and Pilar Candelas. 2019. "M-Bonacci Zone Plates for Ultrasound Focusing" Sensors 19, no. 19: 4313. https://doi.org/10.3390/s19194313





