Aspect-Aware Target Detection and Localization by Wireless Sensor Networks
Abstract
1. Introduction
- A GLRT detector based on one-bit quantized data is developed. If the target is detected, the MLE of the target location is given as a by-product of the GLRT detector. The differential evolution (DE) algorithm is introduced to solve the MLE. It is shown that the GLRT detector with one-bit quantization outperforms the existing detection scheme based on scan statistic [20].
- A GLRT detector based on adaptive multi-bit quantization is proposed to further improve the detection and localization performance. The proposed adaptive quantizer achieves higher quantization precision; meanwhile, its yielding data has a greatly reduced communication burden compared with the typical multi-bit quantization scheme. The Cramer–Rao lower bound (CRLB) of the MLE is also derived.
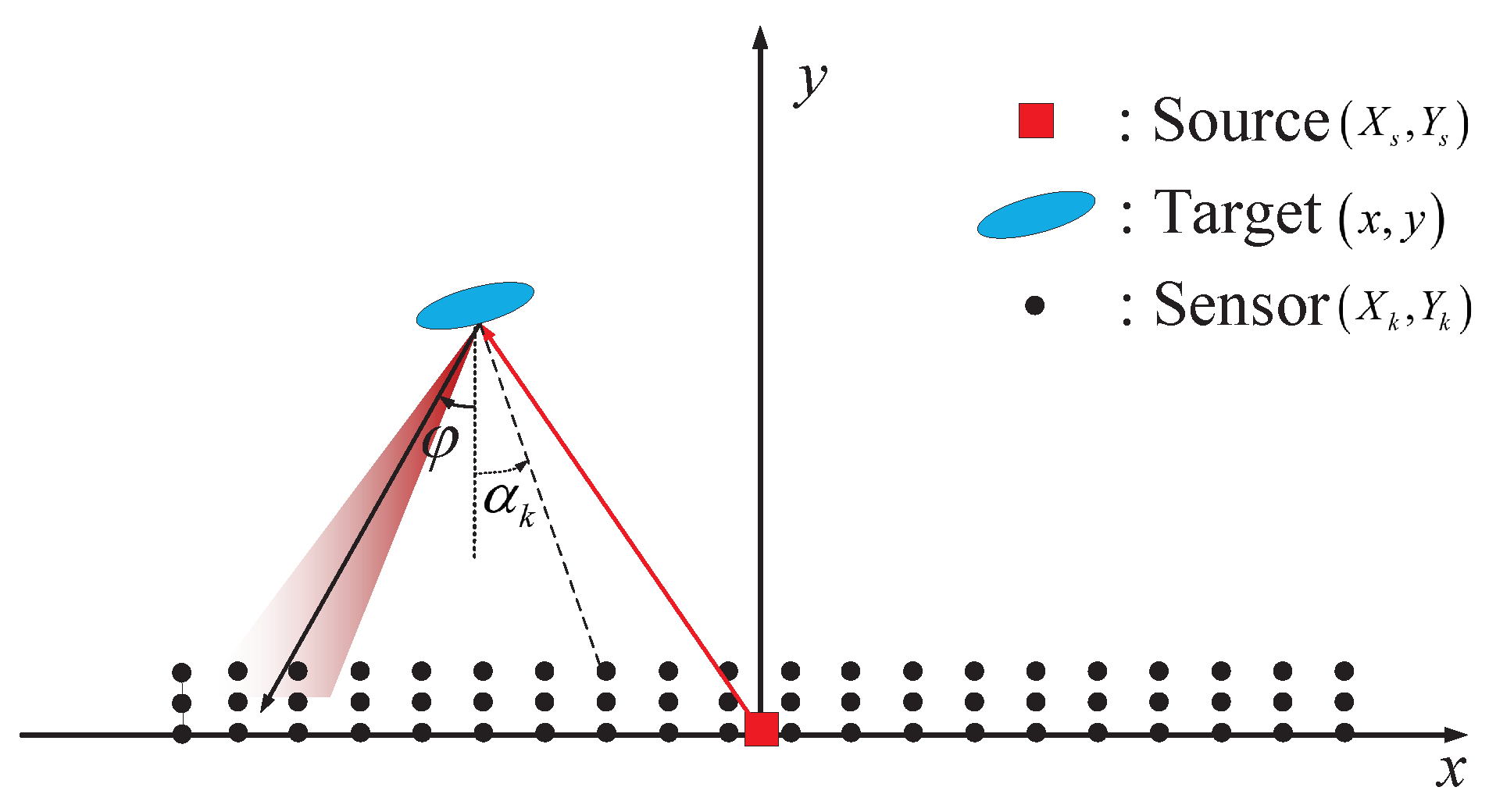
2. Problem Statement
2.1. Observing the Reflected Signal at Sensors
2.2. Data Transmission and Global Decision Making
3. Target Detection and Localization by GLRT Utilizing One-Bit Quantized Data
3.1. Derivation of GLRT Detector
3.2. Solve the MLE with the Differential Evolution Algorithm
- Initialization. The generation number was set to and individuals were randomly initialized with their goal vectors () uniformly drawn from the search space , where .
- Generation Evolution. While the current generation count () was occurring, Steps 2.1–2.3 were performed for each individual i, and then was set.Step 2.1: Mutation. Create a donor vector for the i-th goal vector following the differential mutation scheme:The indices , , and are different integers randomly chosen from , which are also different from the current goal vector index (i).Step 2.2: Crossover. On the basis of goal vector and donor vector , generate a trial vector by performing the following crossover operation on each of the three components:where is a uniformly distributed random number within , and is a randomly chosen index ensuring that gets at least one component from .Step 2.3: Selection. Determine whether the goal vector or the trial vector survives to the next generation by comparing their objective function values, which are respectively calculated by substituting and into (17), i.e.,
- Termination. The iteration in Step 2 stops at the -th generation. Among the goal vectors of the -th generation, the goal vector that yields the largest objective function value is chosen as the final solution.
3.3. Discussion
4. Target Detection and Localization by GLRT Employing an Adaptive Multi-Bit Quantizer
4.1. Adaptive Multi-Bit Quantization
4.2. Derivation of GLRT Detector
4.3. Discussion and Derivation of the Cramer–Rao Lower Bound
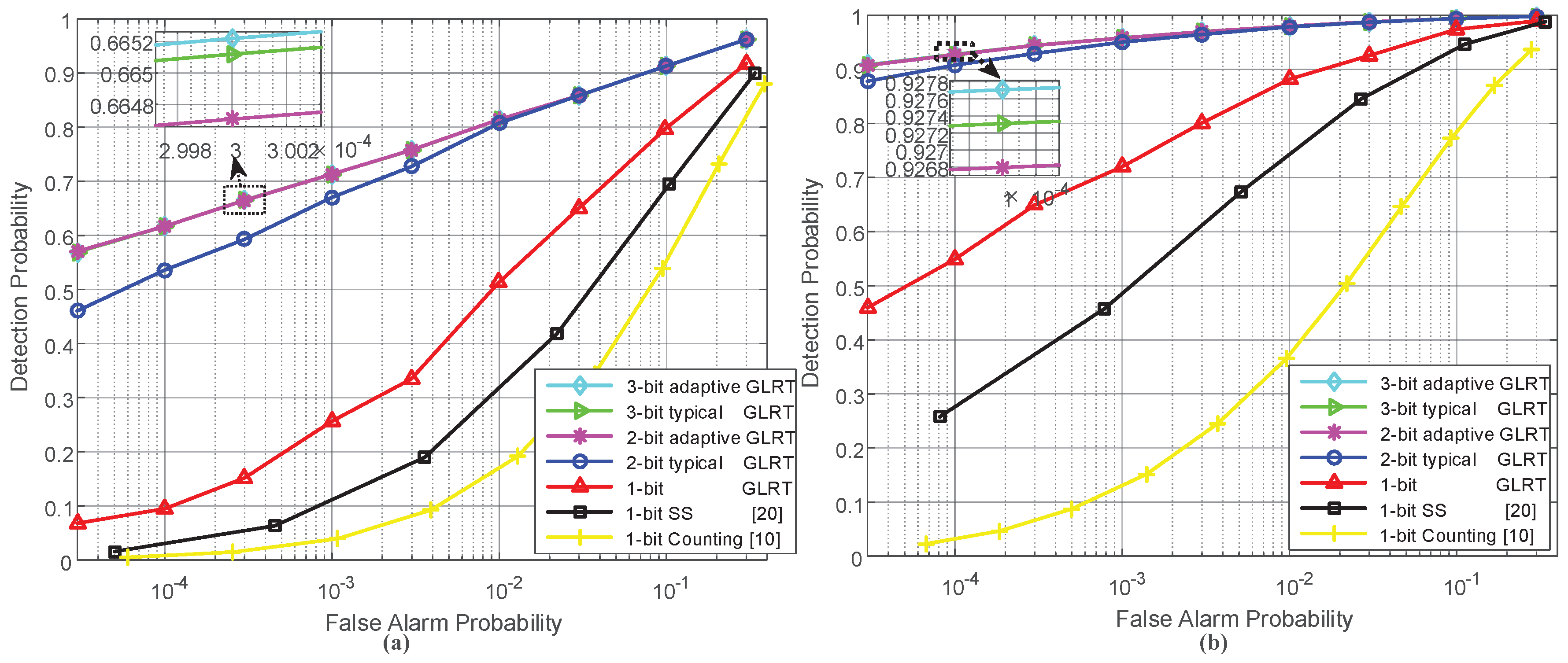
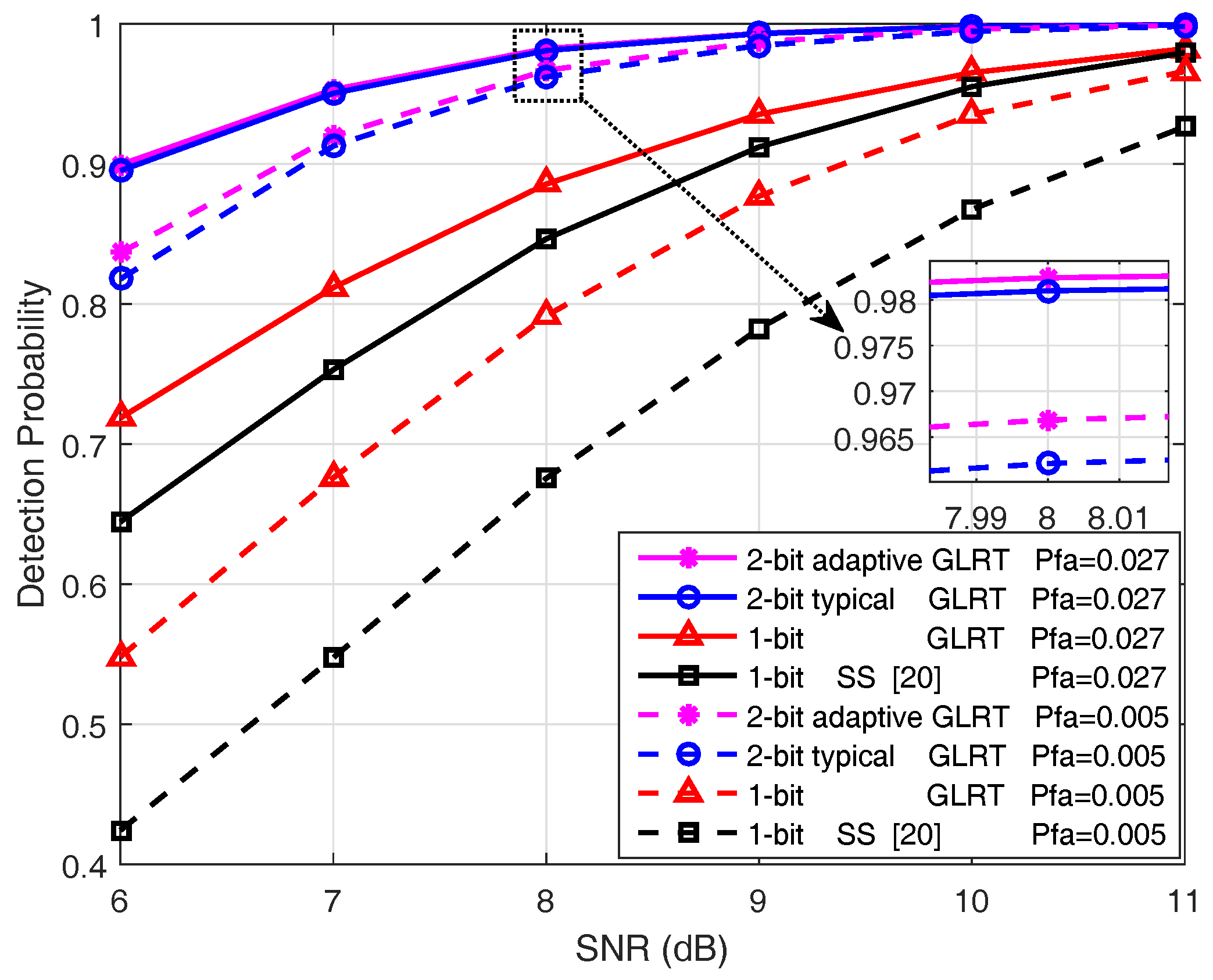
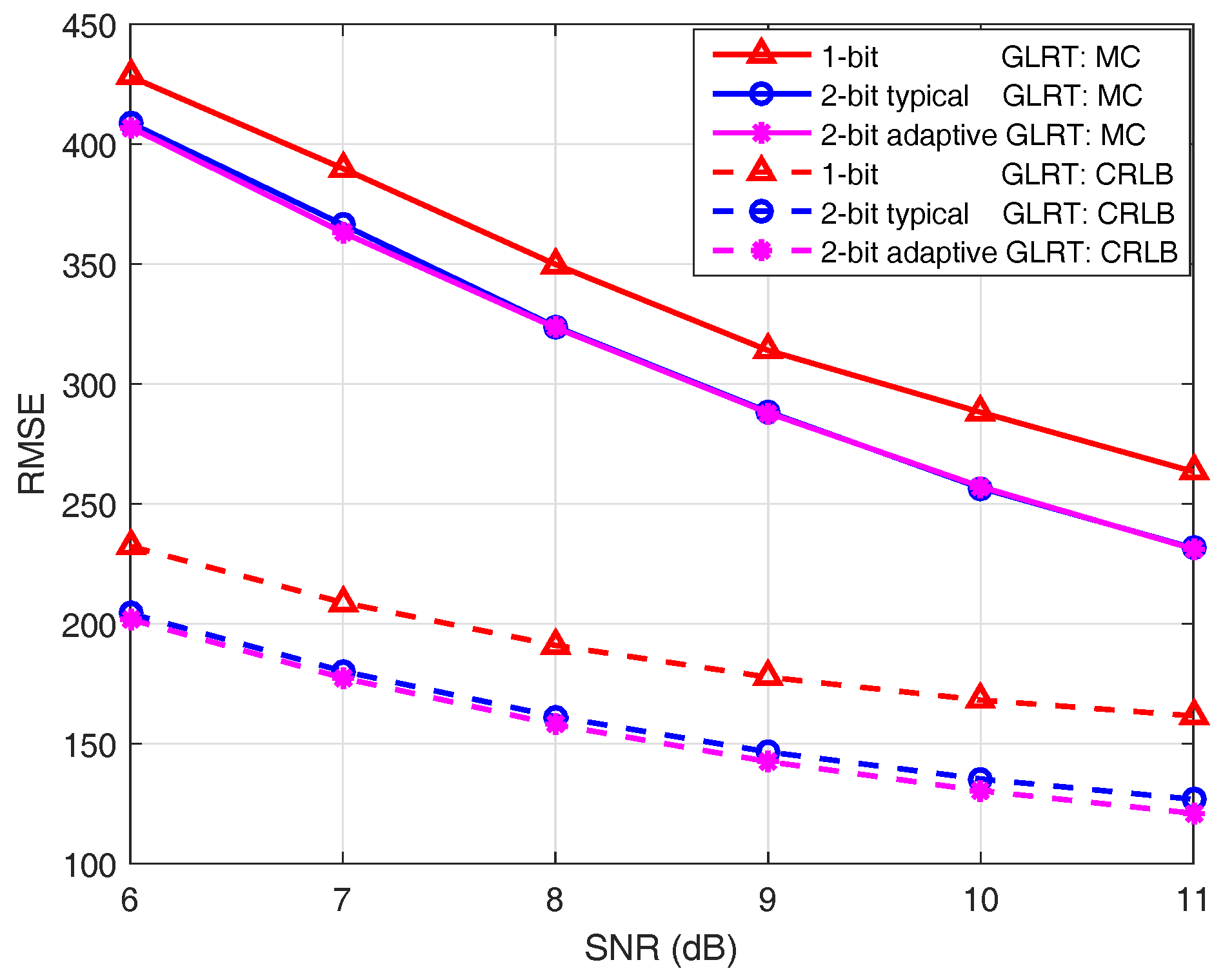
5. Simulation Results
5.1. Detection Performance Evaluation
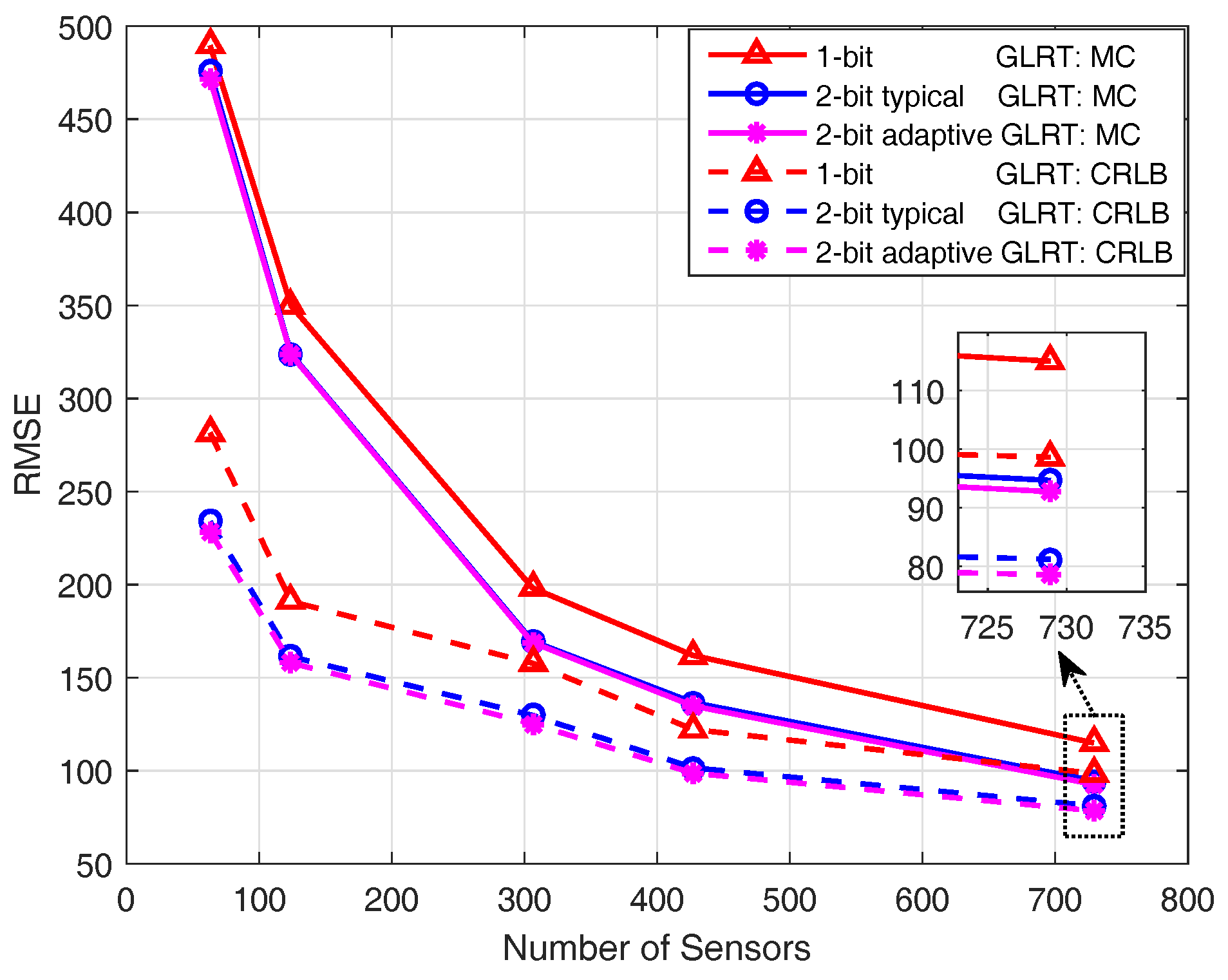
5.2. Localization Performance Evaluation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chong, C.Y.; Kumar, S.P. Sensor networks: evolution, opportunities, and challenges. Proc. IEEE 2003, 91, 1247–1256. [Google Scholar] [CrossRef]
- Veeravalli, V.V.; Varshney, P.K. Distributed inference in wireless sensor networks. Philos. Trans. R. Soc. A 2012, 370, 100–117. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.; Li, X.; Li, H.; Huang, L. Precoding for decentralized detection of unknown deterministic signals. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2116–2128. [Google Scholar] [CrossRef]
- Javadi, S.H. Detection over sensor networks: A tutorial. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 2–18. [Google Scholar] [CrossRef]
- Viswanathan, R.; Varshney, P.K. Distributed detection with multiple sensors I. fundamentals. Proc. IEEE 1997, 85, 54–63. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Wang, X.; Liu, J. Decentralized sequential composite hypothesis test based on one-bit communication. IEEE Trans. Inf. Theory 2017, 63, 3405–3424. [Google Scholar] [CrossRef]
- Fang, J.; Liu, Y.; Li, H.; Li, S. One-bit quantizer design for multisensor GLRT fusion. IEEE Signal Process. Lett. 2013, 20, 257–260. [Google Scholar] [CrossRef]
- Aziz, A.M. A simple and efficient suboptimal multilevel quantization approach in geographically distributed sensor systems. Signal Process. 2008, 88, 1698–1714. [Google Scholar] [CrossRef]
- Gao, F.; Guo, L.; Li, H.; Liu, J.; Fang, J. Quantizer design for distributed GLRT detection of weak signal in wireless sensor networks. IEEE Trans. Wireless Commun. 2015, 14, 2032–2042. [Google Scholar] [CrossRef]
- Niu, R.; Varshney, P.K.; Cheng, Q. Distributed detection in a large wireless sensor network. Inform. Fusion 2006, 7, 380–394. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing, Volume II: Detection Theory; Prentice-Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Gao, F.; Guo, L.; Li, H.; Fang, J. One-bit quantization and distributed detection with an unknown scale parameter. Algorithms 2015, 8, 621–631. [Google Scholar] [CrossRef]
- Niu, R.; Varshney, P.K. Joint detection and location in sensor networks based on local decisions. In Proceedings of the Fortieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 29 October–1 November 2006; pp. 525–529. [Google Scholar]
- Shoari, A.; Seyedi, A. Detection of a non-cooperative transmitter in Rayleigh fading with binary observations. In Proceedings of the IEEE Military Communications Conference (MILCOM), Orlando, FL, USA, 29 October–1 November 2012; pp. 1–5. [Google Scholar]
- Ciuonzo, D.; Rossi, P.S.; Willett, P. Generalized Rao test for decentralized detection of an uncooperative target. IEEE Signal Process. Lett. 2017, 24, 678–682. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Rossi, P.S. Distributed detection of a non-cooperative target via generalized locally-optimum approaches. Inform. Fusion 2017, 36, 261–274. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Rossi, P.S. Quantizer design for generalized locally-optimum detectors in wireless sensor networks. IEEE Wireless Commun. Lett. 2018, 7, 162–165. [Google Scholar] [CrossRef]
- Zhou, S.; Willett, P. Submarine location estimation via a network of detection-only sensors. IEEE Trans. Signal Process. 2007, 55, 3104–3115. [Google Scholar] [CrossRef]
- Berger, C.R.; Zhou, S.; Willett, P. Aspect aware UAV localization. In Proceedings of the 2008 Defense and Security Symposium, Orlando, FL, USA, 16–21 March 2008; pp. 1–10. [Google Scholar]
- Song, X.; Willett, P.; Glaz, J.; Zhou, S. Active detection with a barrier sensor network using a scan statistic. IEEE J. Ocean. Eng. 2012, 37, 66–74. [Google Scholar] [CrossRef]
- Rago, C.; Willett, P.; Bar-Shalom, Y. Detection-tracking performance with combined waveforms. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 612–624. [Google Scholar] [CrossRef]
- Erol-Kantarci, M.; Mouftah, H.T.; Oktug, S. Localization techniques for underwater acoustic sensor networks. IEEE Commun. Mag. 2010, 48, 152–158. [Google Scholar] [CrossRef]
- Luo, H.; Wu, K.; Gong, Y.; Ni, L. Localization for drifting restricted floating ocean sensor networks. IEEE Trans. Veh. Technol. 2016, 65, 9968–9981. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: a survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Tang, C.; Jiang, M.; Zhao, C.; Shen, H. Design of protograph-based LDPC codes with limited decoding complexity. IEEE Commun. Lett. 2017, 21, 2570–2573. [Google Scholar] [CrossRef]
- Mason, S.F.; Berger, C.R.; Zhou, S.; Willett, P. Detection, synchronization, and doppler scale estimation with multicarrier waveforms in underwater acoustic communication. IEEE J. Sel. Areas Commun. 2008, 26, 1638–1649. [Google Scholar] [CrossRef]
| 0 | 1 | 2 | 3 | 4 | 5 | ⋯ | ⋯ | ||||
| 1 | 2 | ⋯ | Q | ||||||||
| 0 | 1 | 00 | 01 | 10 | 11 | ⋯ | ⋯ | ||||
| Sensor Field | Field (a): | Field (b): | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Schemes | 1-bit GLRT/ SS/Counting | 2-bit Adaptive | 2-bit Typical | 3-bit Adaptive | 3-bit Typical | 1-bit GLRT/ SS/Counting | 2-bit Adaptive | 2-bit Typical | 3-bit Adaptive | 3-bit Typical |
| Overhead under | 63 | 64.78 | 126 | 65.05 | 189 | 124 | 127.77 | 248 | 128.35 | 372 |
| Overhead under | 63 | 63.16 | 126 | 63.16 | 189 | 124 | 124.31 | 248 | 124.31 | 372 |
| Counting | SS | 1-bit GLRT | 2-bit Adaptive | 2-bit Typical | 3-bit Adaptive | 3-bit Typical | |
|---|---|---|---|---|---|---|---|
| Field (a): | 1728.6 | 1746.7 | 79,581 | 87,643 | 86,887 | 87,632 | 89,267 |
| Field (b): | 1752.8 | 2574.1 | 126,189 | 136,617 | 136,390 | 136,146 | 134,108 |
| SNR (dB) | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|
| 2-bit adaptive: | 126.58 | 127.15 | 127.77 | 128.42 | 129.08 | 129.74 |
| 2-bit adaptive: | 124.31 | |||||
| 1-bit GLRT/Scan statistic: & | 124 | |||||
| 2-bit typical: & | 248 | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Wang, S.; Zhang, E. Aspect-Aware Target Detection and Localization by Wireless Sensor Networks. Sensors 2018, 18, 2810. https://doi.org/10.3390/s18092810
Hu L, Wang S, Zhang E. Aspect-Aware Target Detection and Localization by Wireless Sensor Networks. Sensors. 2018; 18(9):2810. https://doi.org/10.3390/s18092810
Chicago/Turabian StyleHu, Li, Shilian Wang, and Eryang Zhang. 2018. "Aspect-Aware Target Detection and Localization by Wireless Sensor Networks" Sensors 18, no. 9: 2810. https://doi.org/10.3390/s18092810
APA StyleHu, L., Wang, S., & Zhang, E. (2018). Aspect-Aware Target Detection and Localization by Wireless Sensor Networks. Sensors, 18(9), 2810. https://doi.org/10.3390/s18092810





