Analysis and Improvement of a Dual-Core Photonic Crystal Fiber Sensor
Abstract
:1. Introduction
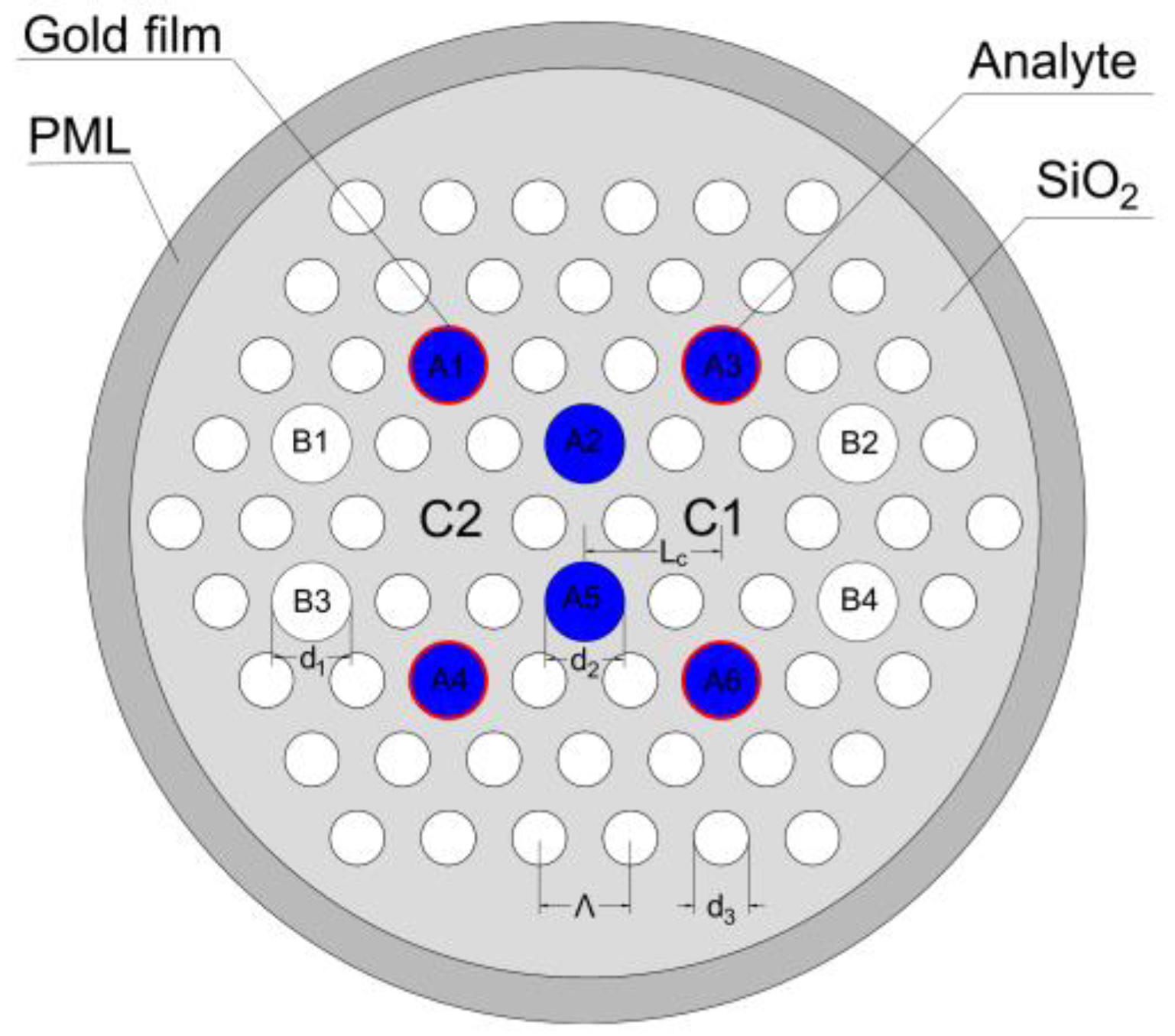
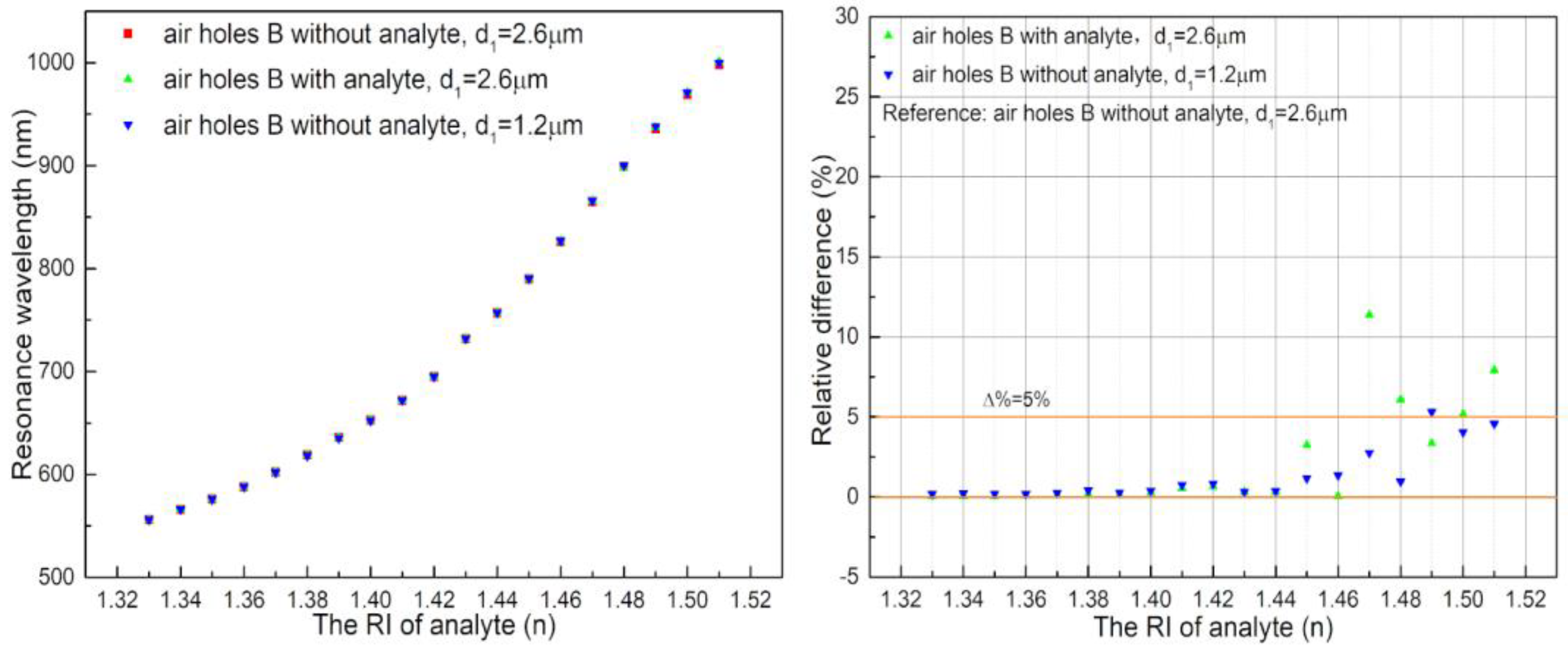
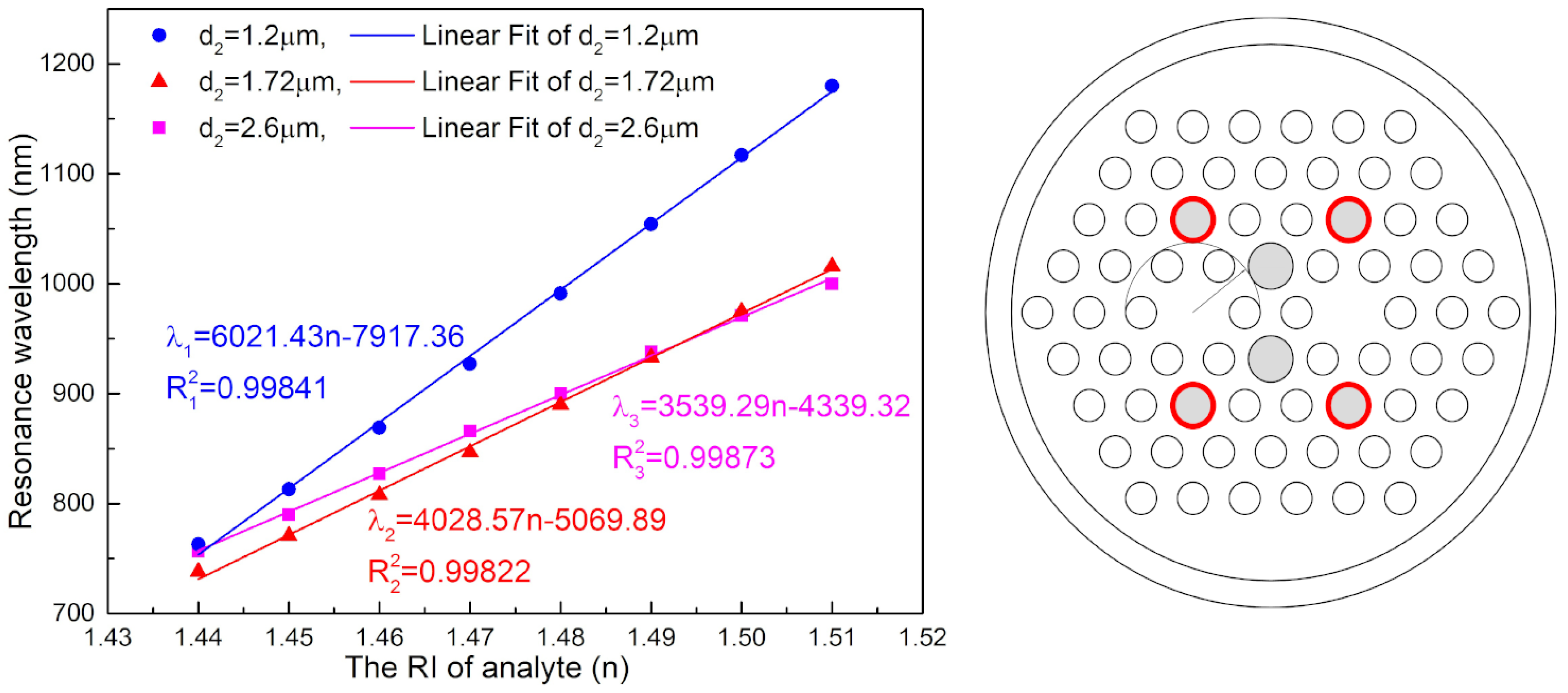
2. Design and Analysis
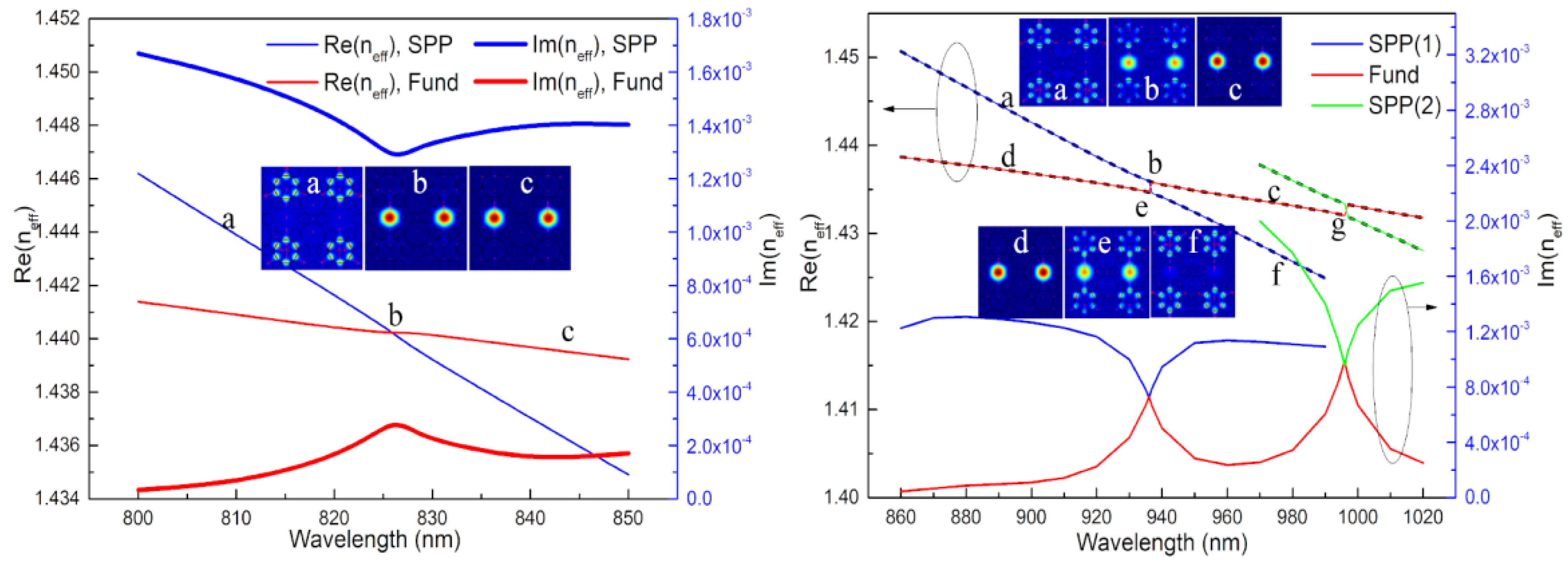
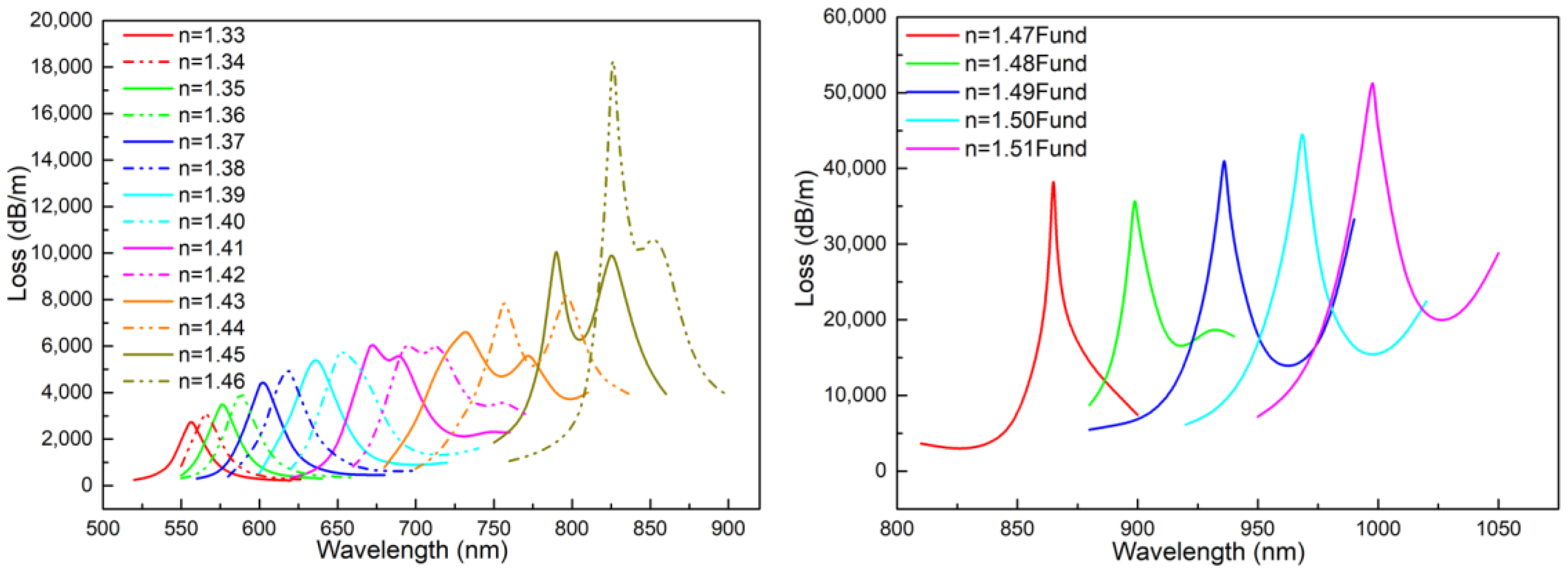
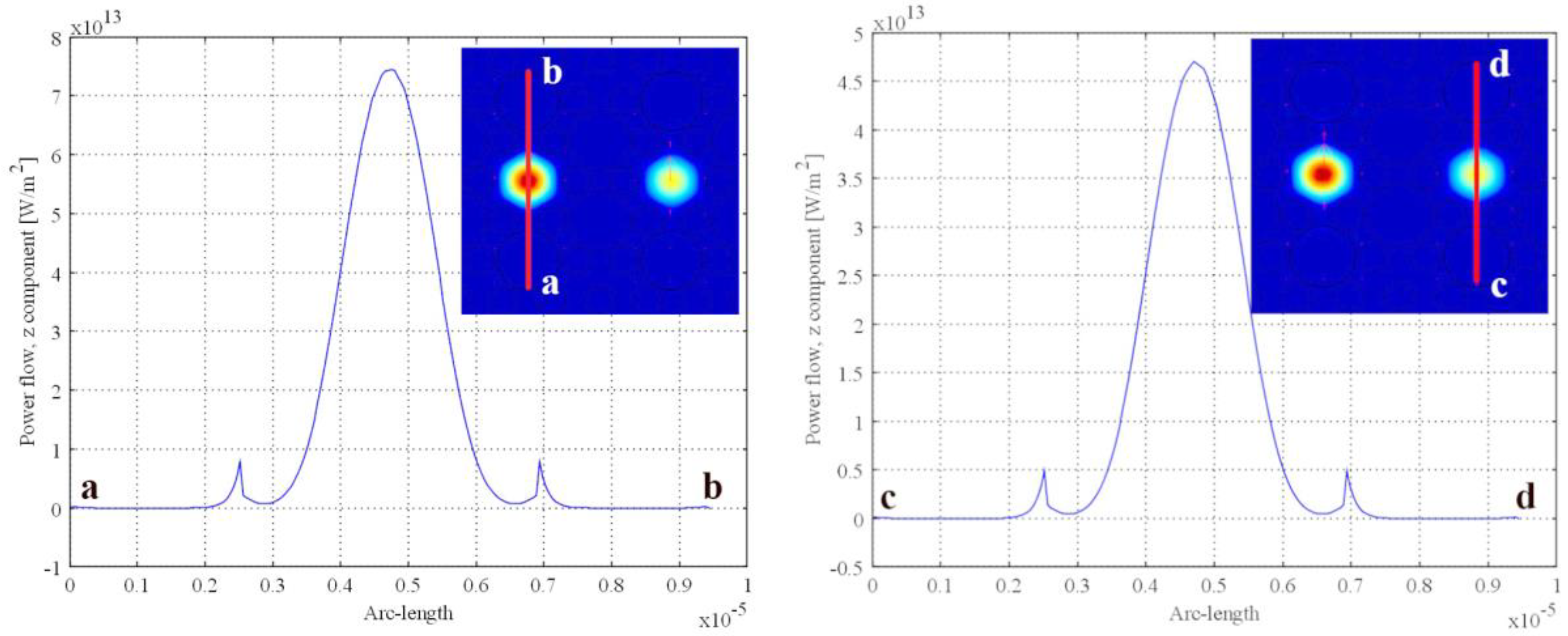
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hassani, A.; Skorobogatiy, M. Design criteria for microstructured optical fiber based surface-plasmon-resonance sensors. J. Opt. Soc. Am. B 2007, 24, 1423–1429. [Google Scholar] [CrossRef]
- Yang, X.; Lu, Y.; Wang, M.; Yao, J. An Exposed-Core Grapefruit Fibers Based Surface Plasmon Resonance Sensor. Sensors 2015, 15, 17106–17114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, X.; Lu, Y.; Wang, M.; Yao, J. SPR Sensor Based on Exposed-Core Grapefruit Fiber With Bimetallic Structure. IEEE Photonics Technol. Lett. 2016, 28, 649–652. [Google Scholar] [CrossRef]
- Tian, M.; Lu, P.; Chen, L.; Lv, C.; Liu, D. All-solid D-shaped photonic fiber sensor based on surface plasmon resonance. Opt. Commun. 2012, 285, 1550–1554. [Google Scholar] [CrossRef]
- Gangwar, R.K.; Singh, V.K. Highly sensitive surface plasmon resonance based D-shaped photonic crystal fiber refractive index sensor. Plasmonics 2017, 12, 1367–1372. [Google Scholar] [CrossRef]
- An, G.; Li, S.; Qin, W.; Zhang, W.; Fan, Z.; Bao, Y. High-Sensitivity Refractive Index Sensor Based on D-Shaped Photonic Crystal Fiber with Rectangular Lattice and Nanoscale Gold Film. Plasmonics 2014, 9, 1355–1360. [Google Scholar] [CrossRef]
- Tan, Z.; Li, X.; Chen, Y.; Fan, P. Improving the Sensitivity of Fiber Surface Plasmon Resonance Sensor by Filling Liquid in a Hollow Core Photonic Crystal Fiber. Plasmonics 2014, 9, 167–173. [Google Scholar] [CrossRef]
- Dash, J.N.; Jha, R. Highly sensitive D shaped PCF sensor based on SPR for near IR. Opt. Quant. Electron. 2016, 48, 137. [Google Scholar] [CrossRef]
- Huang, T. Highly Sensitive SPR Sensor Based on D-shaped Photonic Crystal Fiber Coated with Indium Tin Oxide at Near-Infrared Wavelength. Plasmonics 2017, 12, 583–588. [Google Scholar] [CrossRef]
- Qazi, H.H.; Mohammad, A.B.B.; Ahmad, H.; Zulkifli, M.Z.; Harun, S.W. Single-mode D-shaped optical fiber sensor for the refractive index monitoring of liquid. J. Mod. Opt. 2016, 63, 750–755. [Google Scholar] [CrossRef]
- Yang, X.; Lu, Y.; Liu, B.; Yao, J. Analysis of Graphene-Based Photonic Crystal Fiber Sensor Using Birefringence and Surface Plasmon Resonance. Plasmonics 2017, 12, 489–496. [Google Scholar] [CrossRef]
- Wang, F.; Sun, Z.; Liu, C.; Sun, T.; Chu, P.K. A Highly Sensitive Dual-Core Photonic Crystal Fiber Based on a Surface Plasmon Resonance Biosensor with Silver-Graphene Layer. Plasmonics 2017, 12, 1847–1853. [Google Scholar] [CrossRef]
- Momota, M.R.; Hasan, M.R. Hollow-core silver coated photonic crystal fiber plasmonic sensor. Opt. Mater. 2018, 76, 287–294. [Google Scholar] [CrossRef]
- Chakma, S.; Khalek, M.A.; Paul, B.K.; Ahmed, K.; Hasan, M.R.; Bahar, A.N. Gold-coated photonic crystal fiber biosensor based on surface plasmon resonance: Design and analysis. Sens. Bio-Sens. Res. 2018, 18, 7–12. [Google Scholar] [CrossRef]
- Bing, P.; Li, L.; Yao, J.; Lu, Y. Effects of heterogeneity on the surface plasmon resonance biosensor based on three-hole photonic crystal fiber. Opt. Eng. 2013, 52, 4401. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, Y.; Xia, L.; Liu, D. Photonic crystal fiber sensor based on hybrid mechanisms: Plasmonic and directional resonance coupling. Opt. Commun. 2012, 285, 2466–2471. [Google Scholar] [CrossRef]
- Shuai, B.; Xia, L.; Zhang, Y.; Liu, D. A multi-core holey fiber based plasmonic sensor with large detection range and high linearity. Opt. Express 2012, 20, 5974–5986. [Google Scholar] [CrossRef] [PubMed]
- Popescu, V.A.; Puscas, N.N.; Perrone, G. Simulation of the Sensing Performance of a Plasmonic Biosensor Based on Birefringent Solid-Core Microstructured Optical Fiber. Plasmonics 2017, 12, 905–911. [Google Scholar] [CrossRef]
- Chen, X.; Xia, L.; Li, C. Surface Plasmon Resonance Sensor Based on a Novel D-Shaped Photonic Crystal Fiber for Low Refractive Index Detection. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Yu, Y.; Sun, B. Ultra-Wide-Bandwidth Tunable Magnetic Fluid-Filled Hybrid Connected Dual-Core Photonic Crystal Fiber Mode Converter. Crystals 2018, 8, 95. [Google Scholar]
- Wang, H.; Yan, X.; Li, S.; An, G.; Zhang, X. High Sensitivity Refractive Index Sensor Based on Dual-Core Photonic Crystal Fiber with Hexagonal Lattice. Sensors 2016, 16, 1655. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Yan, X.; Li, S.; Zhang, X. Tunable surface plasmon resonance polarization beam splitter based on dual-core photonic crystal fiber with magnetic fluid. Opt. Quant. Electron. 2017, 49, 368. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, S.; Liu, Q.; Feng, X.; Zhang, S.; Wang, Y.; Wu, J. Groove micro-structure optical fiber refractive index sensor with nanoscale gold film based on surface plasmon resonance. Opt. Fiber Technol. 2018, 43, 45–48. [Google Scholar] [CrossRef]
- An, G.; Li, S.; Yan, X.; Zhang, X.; Yuan, Z.; Wang, H.; Zhang, Y.; Hao, X.; Shao, Y.; Han, Z. Extra-broad Photonic Crystal Fiber Refractive Index Sensor Based on Surface Plasmon Resonance. Plasmonics 2017, 12, 465–471. [Google Scholar] [CrossRef]
- Malka, D.; Zalevsky, Z. Multicore Photonic Crystal Fiber Based 1 × 8 Two-Dimensional Intensity Splitters/Couplers. Electromagnetics 2013, 33, 413–420. [Google Scholar] [CrossRef]
- Malka, D.; Peled, A. Power splitting of 1 × 16 in multicore photonic crystal fibers. Appl. Surf. Sci. 2017, 417, 34–39. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Li, S.; Liu, Q.; Liu, Y.; Zhang, Z.; Wang, Y. A tunable single-polarization photonic crystal fber flter based on surface plasmon resonance. Appl. Phys. B 2018, 124, 112. [Google Scholar] [CrossRef]
- Zhou, X.; Li, S.; Cheng, T.; An, G. Design of offset core photonic crystal fiber filter based on surface plasmon resonance. Opt. Quant. Electron. 2018, 50, 157. [Google Scholar] [CrossRef]
- Malka, D.; Cohen, E.; Zalevsky, Z. Design of 4 × 1 Power Beam Combiner Based on MultiCore Photonic Crystal Fiber. Appl. Sci. 2017, 7, 695. [Google Scholar] [CrossRef]
- Liu, C.; Su, W.; Liu, Q.; Lu, X.; Wang, F.; Sun, T.; Chu, P.K. Symmetrical dual D-shape photonic crystal fibers for surface plasmon resonance sensing. Opt. Express 2018, 26, 9039. [Google Scholar] [CrossRef] [PubMed]


| Sensor | Refractive Index Range | Wavelength Sensitivity (nm/RIU) | R2 | Structure of the Photonic Crystal Fiber (PCF) |
|---|---|---|---|---|
| Ref. [3] | 1.33–1.42 | 16,400 (maximum) | (Nonlinearity) | Exposed-core grapefruit PCF |
| Ref. [8] | 1.33–1.37 | 5200 | (Not given) | D-shaped PCF |
| Ref. [12] | 1.39–1.42 1.43–1.46 | 4350 9200 | 0.99698 0.99864 | Dual-core PCF |
| Ref. [14] | 1.34–1.37 | 4400 | 0.9584 | Circular lattice PCF |
| Ref. [30] | 1.36–1.41 | 14,660 (average) | (Not given) | Dual D-shaped PCF |
| This work (d2 = 1.2 μm) | 1.44–1.51 | 6021 | 0.99841 | Dual-core PCF |
| This work (d2 = 1.72 μm) | 1.44–1.51 | 4028 | 0.99822 | Dual-core PCF |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bing, P.; Huang, S.; Sui, J.; Wang, H.; Wang, Z. Analysis and Improvement of a Dual-Core Photonic Crystal Fiber Sensor. Sensors 2018, 18, 2051. https://doi.org/10.3390/s18072051
Bing P, Huang S, Sui J, Wang H, Wang Z. Analysis and Improvement of a Dual-Core Photonic Crystal Fiber Sensor. Sensors. 2018; 18(7):2051. https://doi.org/10.3390/s18072051
Chicago/Turabian StyleBing, Pibin, Shichao Huang, Jialei Sui, Hua Wang, and Zhiyong Wang. 2018. "Analysis and Improvement of a Dual-Core Photonic Crystal Fiber Sensor" Sensors 18, no. 7: 2051. https://doi.org/10.3390/s18072051





