An Improved Strong Tracking Cubature Kalman Filter for GPS/INS Integrated Navigation Systems
Abstract
:1. Introduction
2. The Strong Tracking Filter and Cubature Kalman Filter
2.1. Strong Tracking Filter
2.2. Cubature Kalman Filter
2.2.1. Prediction
- (1)
- Factorize the covariance and evaluate the cubature points ():
- (2)
- Evaluate the propagated cubature points through the process model:
- (3)
- Estimate the predicted state and the corresponding error covariance:
2.2.2. Update
- (1)
- Factorize the covariance and evaluate the cubature points ():
- (2)
- Evaluate the propagated cubature points through the observation model:
- (3)
- Estimate the predicted measurement:
- (4)
- Estimate the covariance and Kalman gain:
- (5)
- Estimate the updated state and the corresponding error covariance:
3. An Improved Strong Tracking 7thSSRCKF Algorithm
3.1. The Improvement of Strong Tracking Kalman Filter
3.1.1. Process Uncertainty Identification
3.1.2. Improved Strategy for Fading Factor
3.2. The Seventh-Degree Spherical Simplex-Radial Cubature Rule for Cubature Kalman Filter
3.2.1. Seventh-Degree Spherical Simplex Rule
3.2.2. Seven-Degree Radial Rule
3.2.3. Seventh-Degree Spherical Simplex-Radial Rule
3.3. Steps of the IST-7thSSRCKF
- Step 1. State prediction
- Step 2. Process uncertainty identification and calculation of the improved fading factor
- (a)
- If , , the strong tracking cubature Kalman filter therefore reduces to the standard cubature Kalman filter.
- (b)
- If , perform the improved strong tracking cubature Kalman filter. The improved multiple fading factor used in the IST-7thSSRCKF is calculated as follows:
- Step 3. Covariance prediction using the improved strong tracking technique
- Step 4. Measurement update
4. Performance Evaluation
4.1. Design of SINS/GPS Filtering Model
4.2. Simulation for SINS/GPS Integration
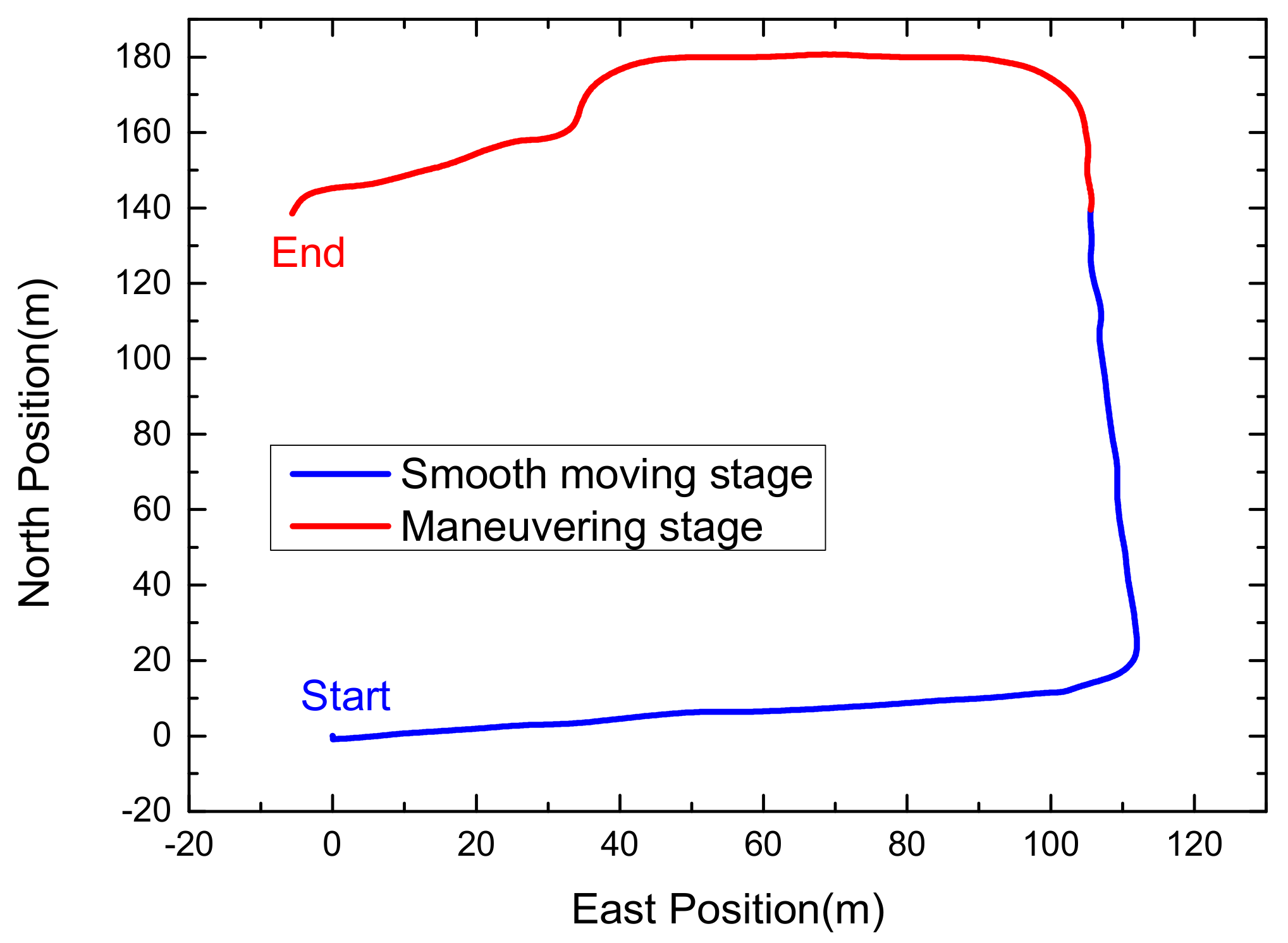
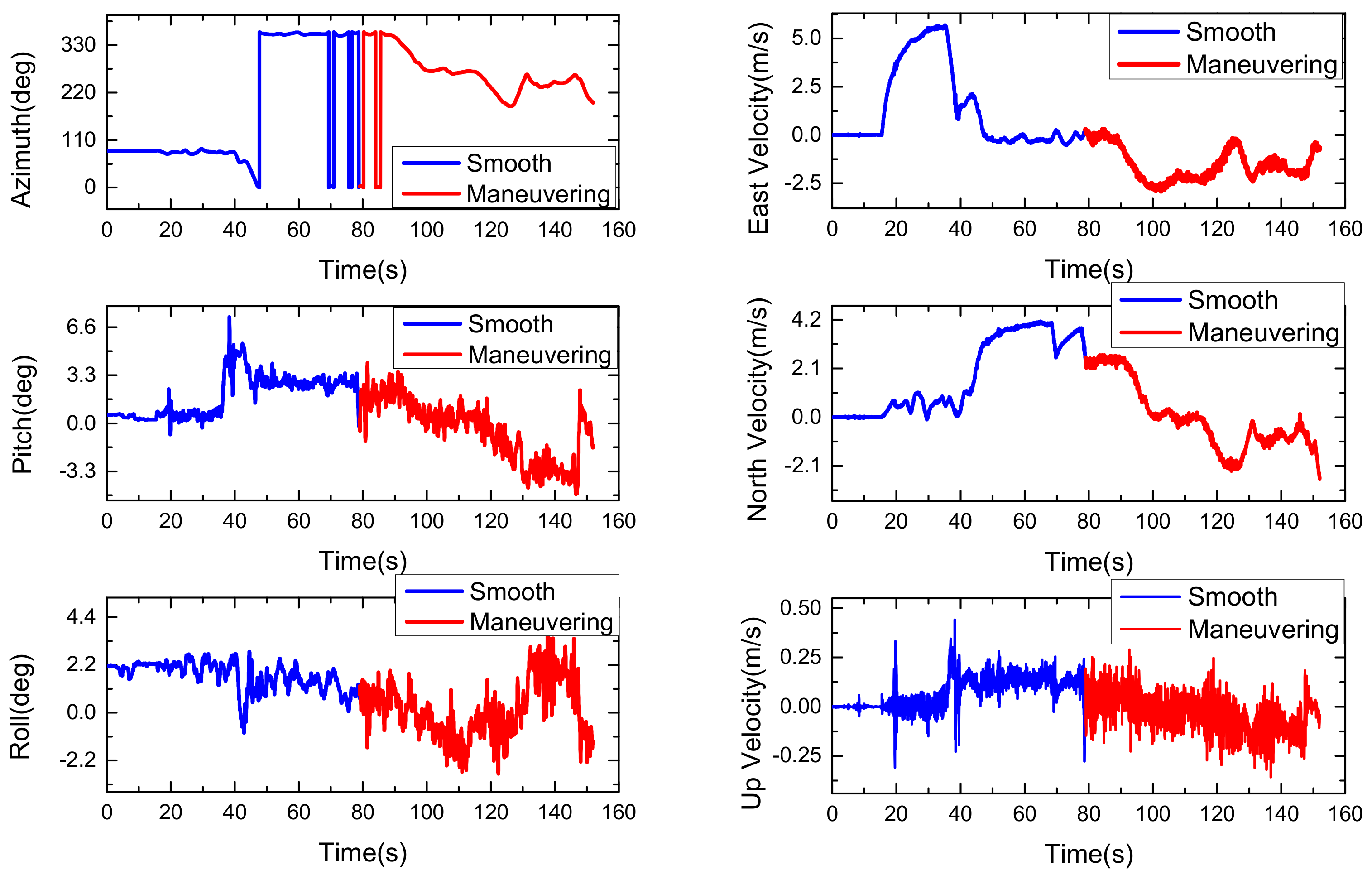
4.3. Car-Mounted Experiment for SINS/GPS Integration
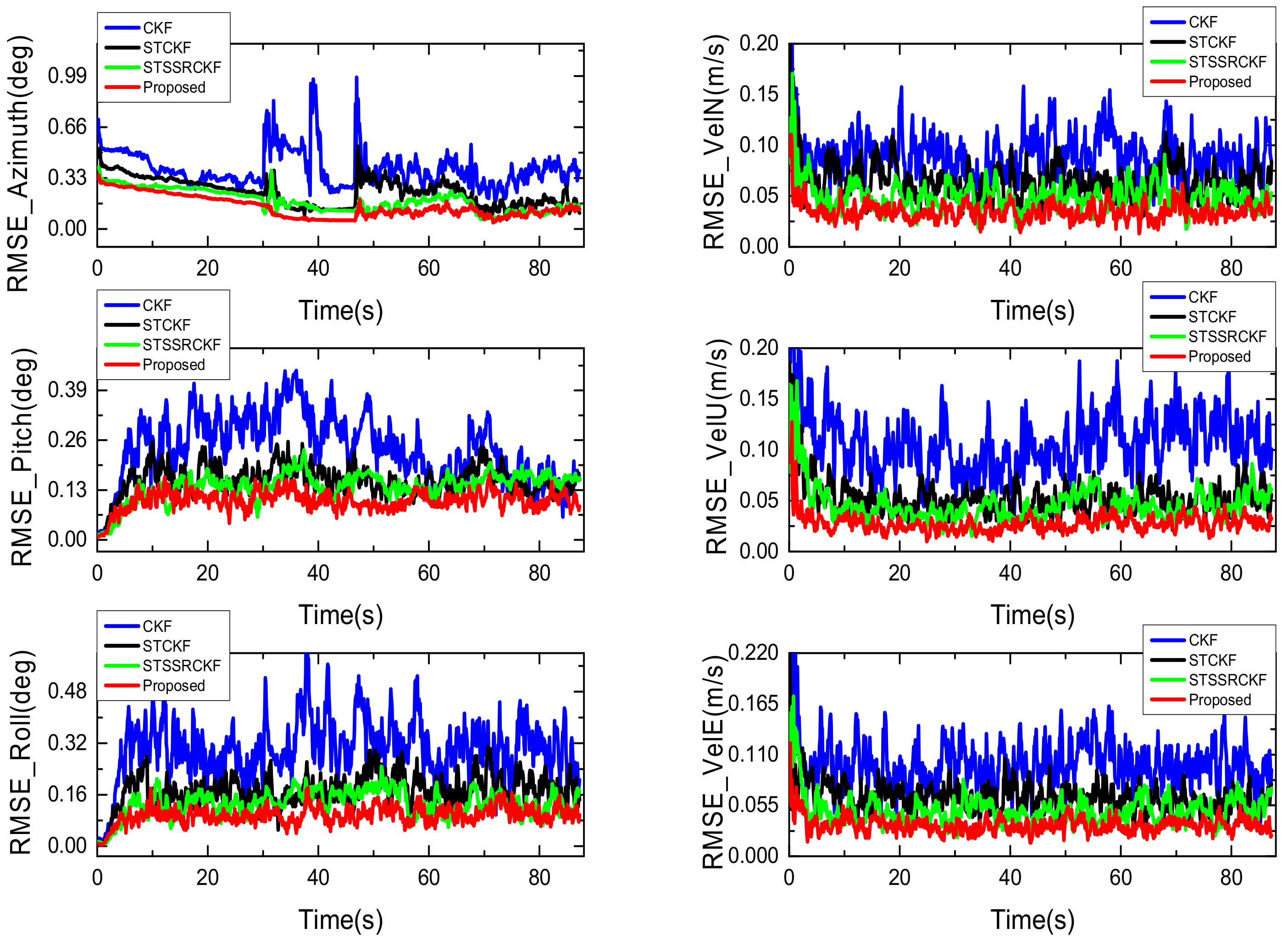
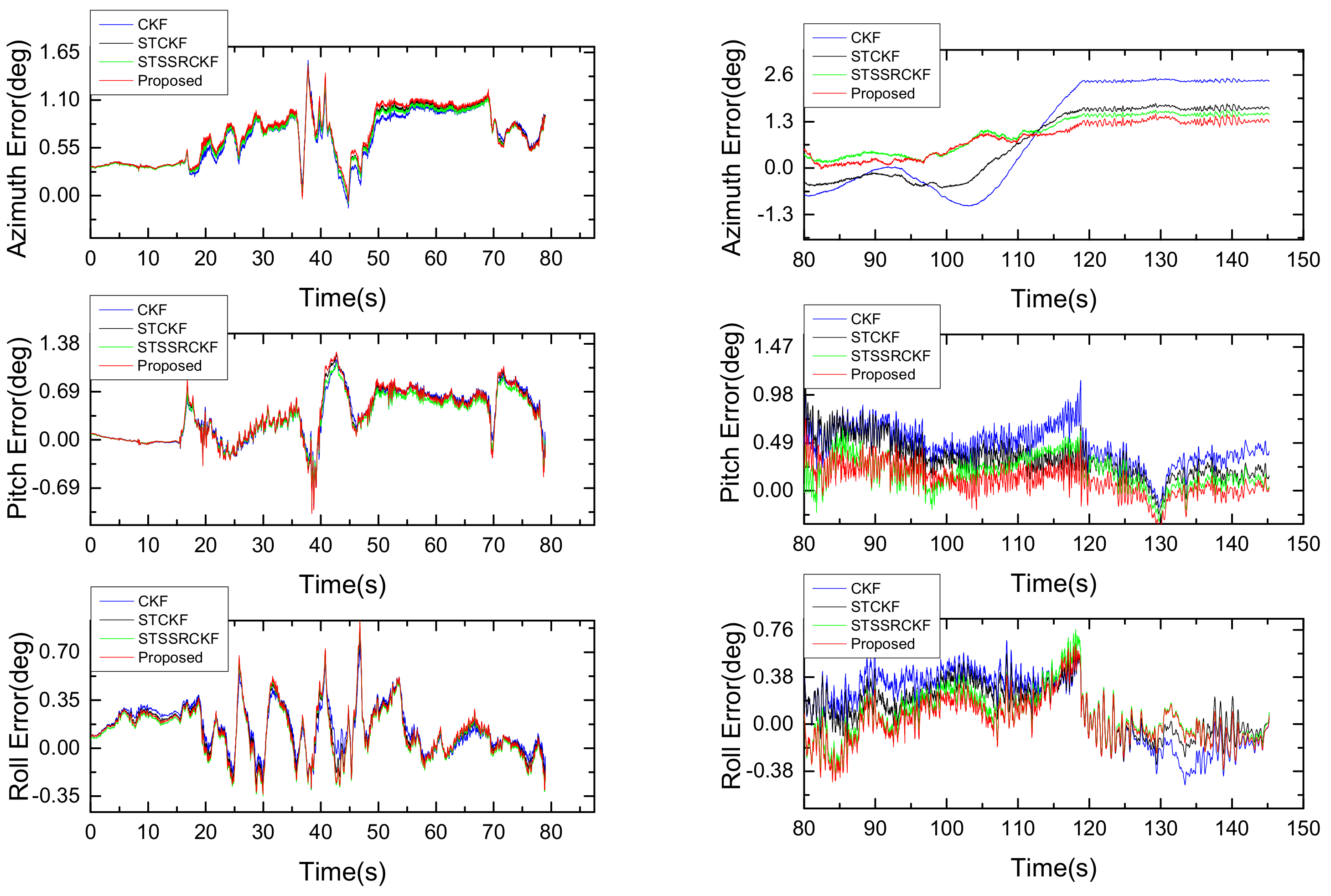
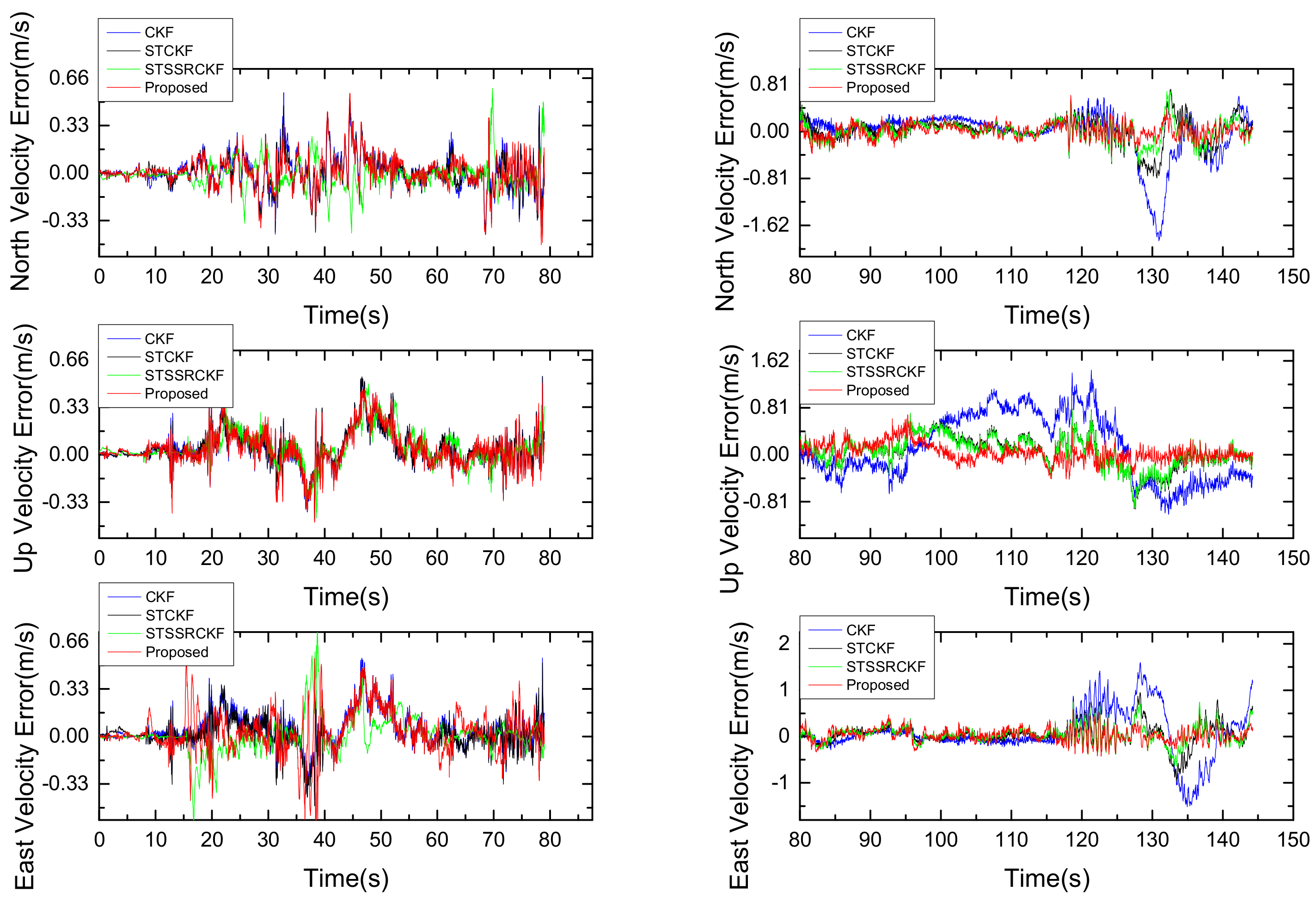
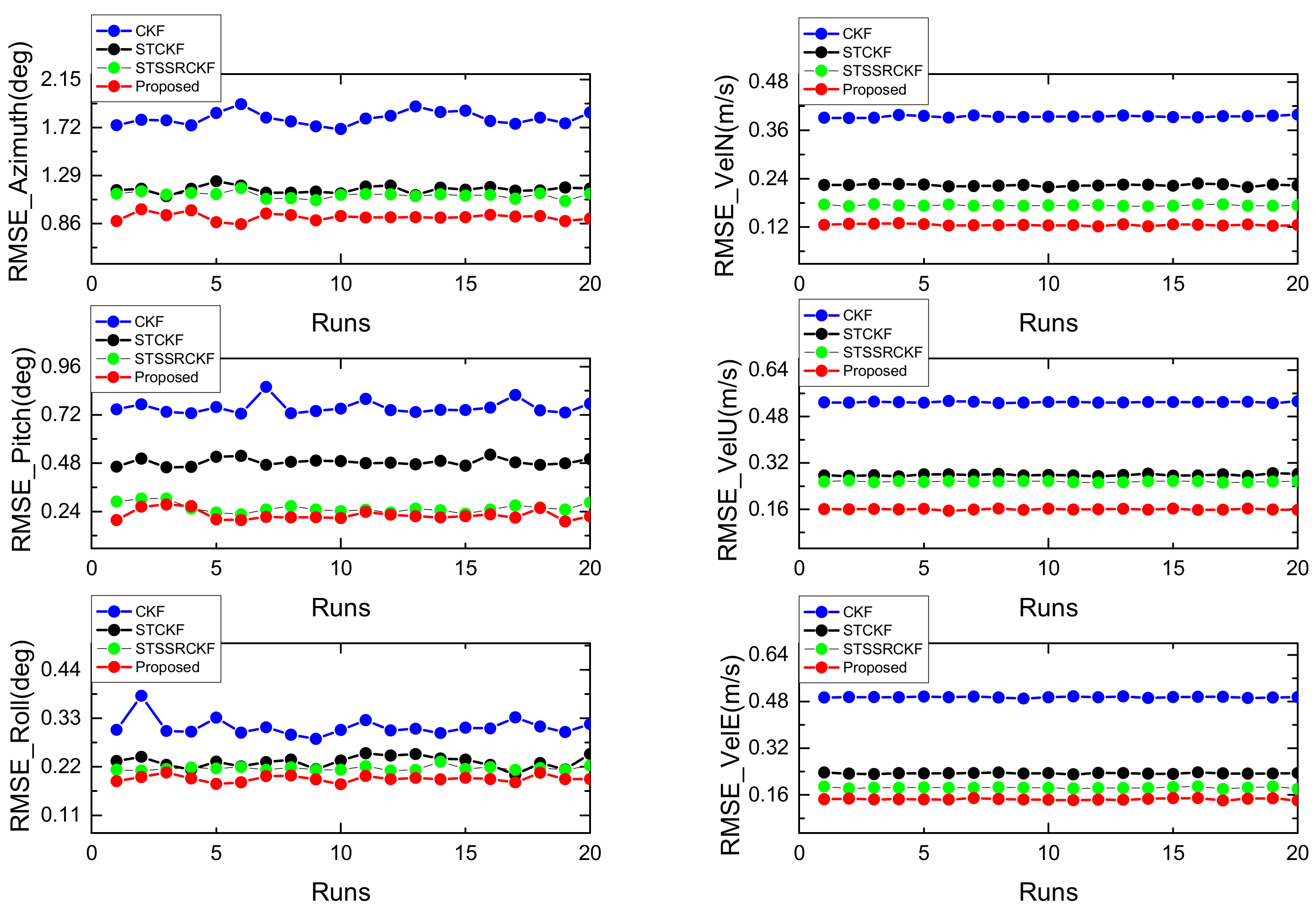
4.4. Performance Comparison with Different Filtering Algorithms
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, Z.; Yao, M.; Ma, H.; Jia, W.; Tian, F. Low-cost antenna attitude estimation by fusing inertial sensing and two-antenna GPS for vehicle-mounted satcom-on-the-move. IEEE Trans. Veh. Technol. 2013, 62, 1084–1096. [Google Scholar] [CrossRef]
- Sun, D.; Petovello, M.G.; Cannon, M.E. Ultratight GPS/reduced-imu integration for land vehicle navigation. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1781–1791. [Google Scholar] [CrossRef]
- Crassidis, J.L. Sigma-point Kalman filtering for integrated GPS and inertial navigation. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 750–756. [Google Scholar] [CrossRef]
- Zhao, L.; Qiu, H.; Feng, Y. Analysis of a robust Kalman filter in loosely coupled GPS/INS navigation system. Measurement 2016, 80, 138–147. [Google Scholar] [CrossRef]
- Falco, G.; Pini, M.; Marucco, G. Loose and tight GNSS/INS integrations: Comparison of performance assessed in real urban scenarios. Sensors 2017, 17, 255. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.H.; Hwang, D.-H. Low-cost and high performance ultra-tightly coupled GPS/INS integrated navigation method. Adv. Space Res. 2017, 60, 2691–2706. [Google Scholar] [CrossRef]
- Dan, S. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Chang, L.; Li, K.; Hu, B. Huber’s m-estimation-based process uncertainty robust filter for integrated INS/GPS. IEEE Sens. J. 2015, 15, 3367–3374. [Google Scholar] [CrossRef]
- Zhong, M.; Guo, J.; Cao, Q. On designing PMI Kalman filter for INS/GPS integrated systems with unknown sensor errors. IEEE Sens. J. 2015, 15, 535–544. [Google Scholar] [CrossRef]
- Chorin, A.J.; Tu, X. A tutorial on particle filters for online nonlinear/nongaussian bayesia tracking. Esaim Math. Model. Numer. Anal. 2012, 46, 535–543. [Google Scholar] [CrossRef]
- Sarkka, S.; Nummenmaa, A. Recursive noise adaptive Kalman filtering by variational bayesian approximations. IEEE Trans. Autom. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Dong, P.; Jing, Z.; Leung, H.; Shen, K. Variational bayesian adaptive cubature information filter based on wishart distribution. IEEE Trans. Autom. Control 2017, 62, 6051–6057. [Google Scholar] [CrossRef]
- Li, K.; Chang, L.; Hu, B. A variational bayesian-based unscented Kalman filter with both adaptivity and robustness. IEEE Sens. J. 2016, 16, 6966–6976. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Yin, C.; Duan, S.-K.; Wang, L.-D. A modified variational bayesian noise adaptive Kalman filter. Circuits Syst. Signal Process. 2017, 36, 4260–4277. [Google Scholar] [CrossRef]
- Chen, B.; Principe, J.C. Maximum correntropy estimation is a smoothed map estimation. IEEE Signal Process. Lett. 2012, 19, 491–494. [Google Scholar] [CrossRef]
- Chen, B.; Liu, X.; Zhao, H.; Principe, J.C. Maximum correntropy Kalman filter. Automatica 2017, 76, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Kulikova, M.V. Square-root algorithms for maximum correntropy estimation of linear discrete-time systems in presence of non-gaussian noise. Syst. Control Lett. 2017, 108, 8–15. [Google Scholar] [CrossRef]
- Liu, X.; Chen, B.; Xu, B.; Wu, Z.; Honeine, P. Maximum correntropy unscented filter. Int. J. Syst. Sci. 2017, 48, 1607–1615. [Google Scholar] [CrossRef]
- Wang, G.; Li, N.; Zhang, Y. Maximum correntropy unscented Kalman and information filters for non-gaussian measurement noise. J. Frankl. Inst. 2017, 354, 8659–8677. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y. A new process uncertainty robust student’s t based Kalman filter for SINS/GPS integration. IEEE Access 2017, 5, 14391–14404. [Google Scholar] [CrossRef]
- Hide, C.; Moore, T.; Smith, M. Adaptive Kalman filtering for low-cost INS/GPS. J. Navig. 2003, 56, 143–152. [Google Scholar] [CrossRef]
- Karasalo, M.; Hu, X. An optimization approach to adaptive Kalman filtering. In Proceedings of the 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference, Shanghai, China, 16–18 December 2011; pp. 2333–2338. [Google Scholar]
- Bilik, I.; Tabrikian, J. Mmse-based filtering in presence of non-gaussian system and measurement noise. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1153–1170. [Google Scholar] [CrossRef]
- Hu, G.; Gao, S.; Zhong, Y.; Gao, B.; Aleksandar, S. Modified strong tracking unscented Kalman filter for nonlinear state estimation with process model uncertainty. Int. J. Adapt. Control Signal Process. 2015, 29, 1561–1577. [Google Scholar] [CrossRef]
- Huang, W.; Xie, H.; Shen, C.; Li, J. A robust strong tracking cubature Kalman filter for spacecraft attitude estimation with quaternion constraint. Acta Astronaut. 2016, 121, 153–163. [Google Scholar] [CrossRef]
- Liu, H.; Wu, W. Strong tracking spherical simplex-radial cubature Kalman filter for maneuvering target tracking. Sensors 2017, 17, 741. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.H.; Frank, P.M. Strong tracking filtering of nonlinear time-varying stochastic systems with coloured noise: Application to parameter estimation and empirical robustness analysis. Int. J. Control 1996, 65, 295–307. [Google Scholar] [CrossRef]
- Jwo, D.J.; Wang, S.H. Adaptive fuzzy strong tracking extended Kalman filtering for GPS navigation. IEEE Sens. J. 2007, 7, 778–789. [Google Scholar] [CrossRef]
- Lin, C.L.; Chang, Y.M.; Hung, C.C.; Tu, C.D.; Chuang, C.Y. Position estimation and smooth tracking with a fuzzy-logic-based adaptive strong tracking Kalman filter for capacitive touch panels. IEEE Trans. Ind. Electron. 2015, 62, 5097–5108. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Xiong, H.; Tang, J.; Xu, H.; Zhang, W.; Du, Z. A robust single GPS navigation and positioning algorithm based on strong tracking filtering. IEEE Sens. J. 2018, 18, 290–298. [Google Scholar] [CrossRef]
- Chang, G. Robust Kalman filtering based on mahalanobis distance as outlier judging criterion. J. Geod. 2014, 88, 391–401. [Google Scholar] [CrossRef]
- Jia, B.; Xin, M.; Cheng, Y. High-degree cubature Kalman filter. Automatica 2013, 49, 510–518. [Google Scholar] [CrossRef]
- Lu, J.; Darmofal, D.L. Higher-dimensional integration with gaussian weight for applications in probabilistic design. SIAM J. Sci. Comput. 2008, 26, 613–624. [Google Scholar] [CrossRef]
- Genz, A.; Monahan, J. Stochastic integration rules for infinite regions. SIAM J. Sci. Comput. 1998, 19, 426–439. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Li, N.; Chambers, J. A robust gaussian approximate fixed-interval smoother for nonlinear systems with heavy-tailed process and measurement noises. IEEE Signal Process. Lett. 2016, 23, 468–472. [Google Scholar] [CrossRef]
- Feng, K.; Li, J.; Zhang, X.; Shen, C.; Bi, Y.; Zheng, T.; Liu, J. A new quaternion-based Kalman filter for real-time attitude estimation using the two-step geometrically-intuitive correction algorithm. Sensors 2017, 17, 2146. [Google Scholar] [CrossRef] [PubMed]
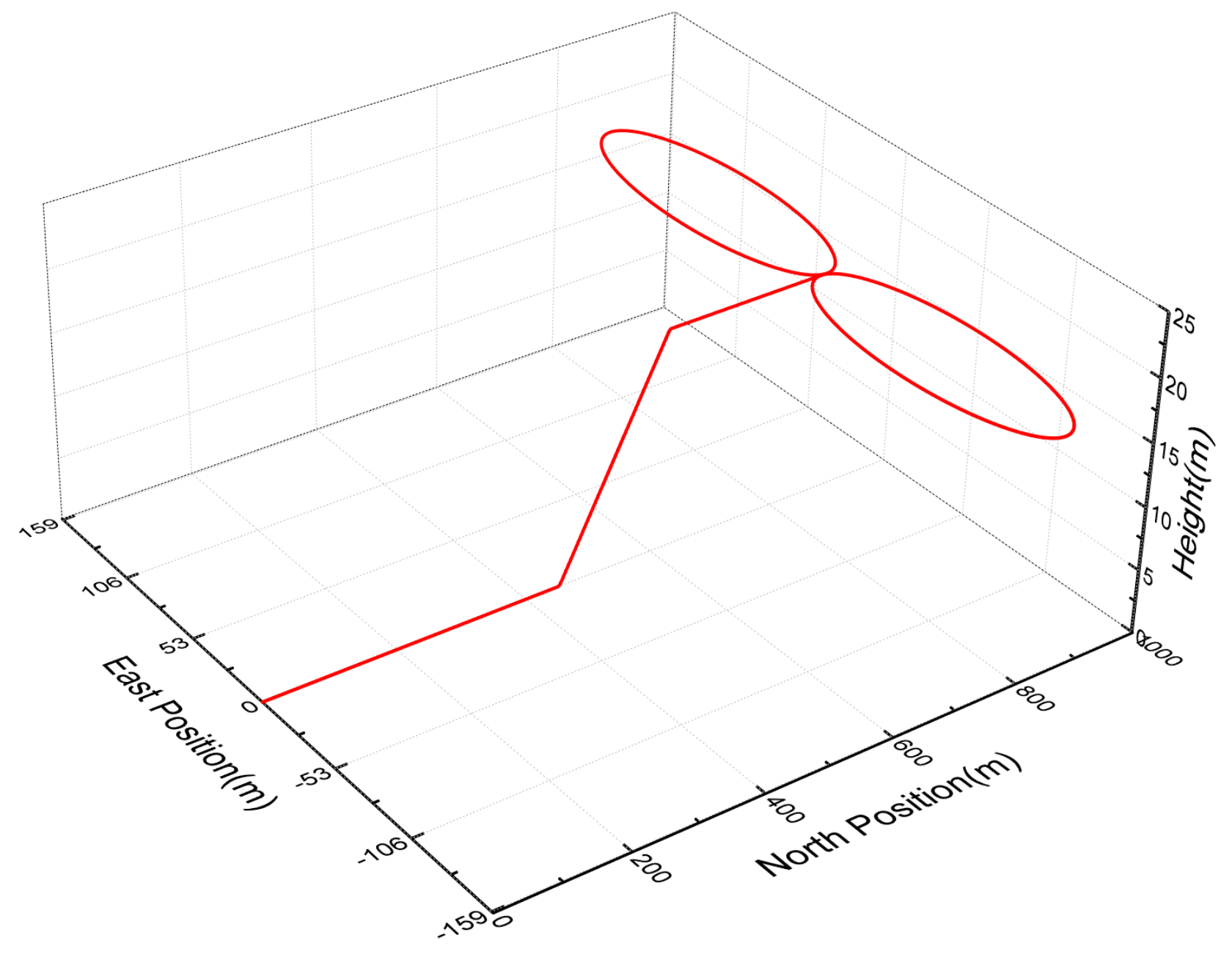

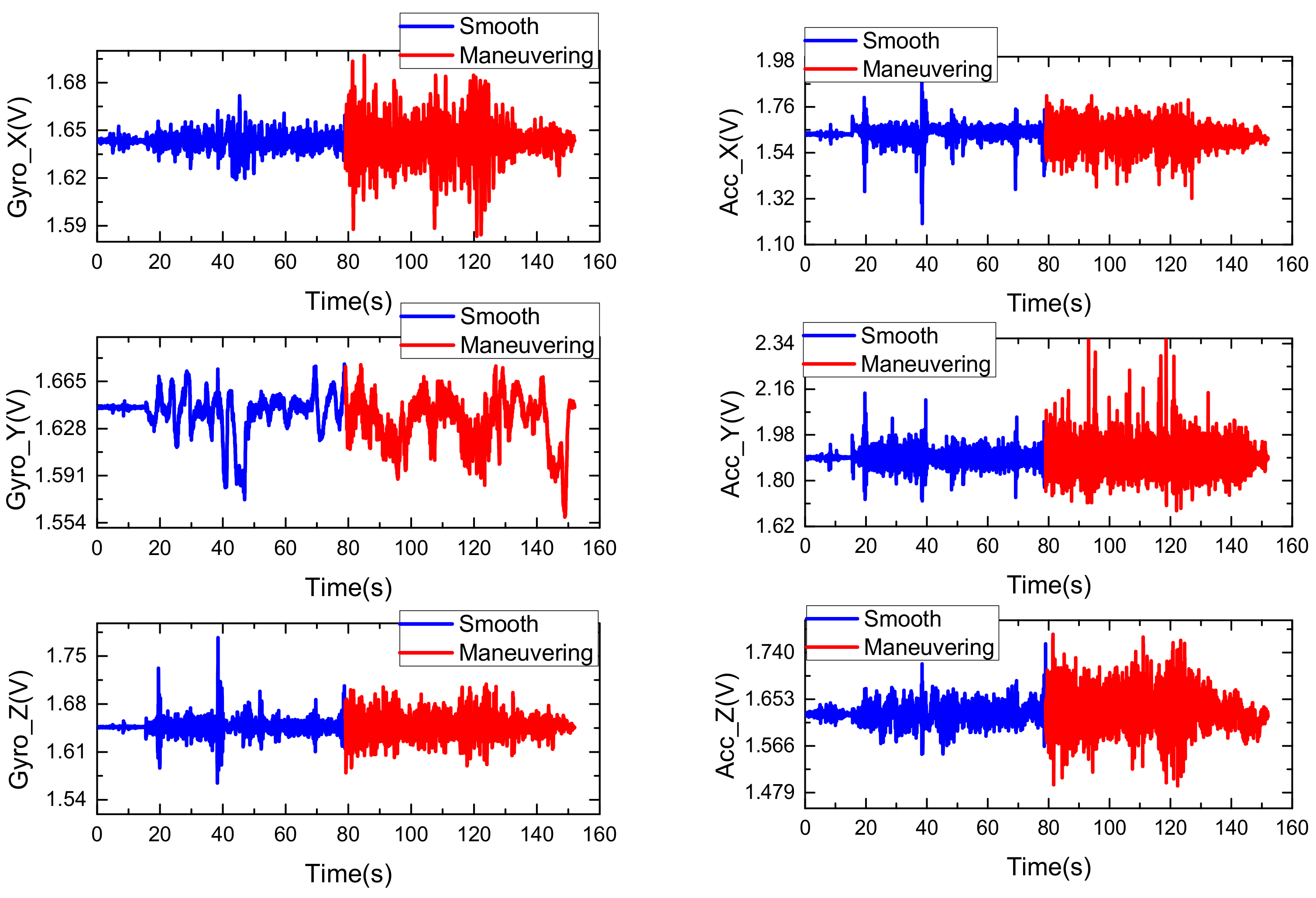
| Time (s) | Motion |
|---|---|
| 0–30 | Accelerate |
| 30–36 | Head up and decelerate |
| 37–47 | Uniform |
| 48–87 | 8-driving |
| Quantity | Gyroscope | Accelerometer |
|---|---|---|
| Range | ±300°/s | ±10 g |
| Bias | 12°/h | 5 mg |
| Random walk | 0.28 | 90 |
| Filers | Points Number | Time (s) |
|---|---|---|
| CKF | 42 | 0.011 |
| ST-CKF | 42 | 0.016 |
| ST-SSRCKF | 44 | 0.018 |
| IST-7thSSRCKF | 4510 | 0.968 |
| Filers | CKF | ST-CKF | ST-SSRCKF | IST-7thSSRCKF |
|---|---|---|---|---|
| Azimuth (deg) | 1.70 | 1.19 | 1.11 | 0.96 |
| Pitch (deg) | 0.74 | 0.49 | 0.24 | 0.19 |
| Roll (deg) | 0.30 | 0.22 | 0.21 | 0.18 |
| North Velocity (m/s) | 0.39 | 0.22 | 0.17 | 0.12 |
| Up Velocity (m/s) | 0.50 | 0.27 | 0.25 | 0.16 |
| East Velocity (m/s) | 0.49 | 0.23 | 0.18 | 0.14 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, K.; Li, J.; Zhang, X.; Zhang, X.; Shen, C.; Cao, H.; Yang, Y.; Liu, J. An Improved Strong Tracking Cubature Kalman Filter for GPS/INS Integrated Navigation Systems. Sensors 2018, 18, 1919. https://doi.org/10.3390/s18061919
Feng K, Li J, Zhang X, Zhang X, Shen C, Cao H, Yang Y, Liu J. An Improved Strong Tracking Cubature Kalman Filter for GPS/INS Integrated Navigation Systems. Sensors. 2018; 18(6):1919. https://doi.org/10.3390/s18061919
Chicago/Turabian StyleFeng, Kaiqiang, Jie Li, Xi Zhang, Xiaoming Zhang, Chong Shen, Huiliang Cao, Yanyu Yang, and Jun Liu. 2018. "An Improved Strong Tracking Cubature Kalman Filter for GPS/INS Integrated Navigation Systems" Sensors 18, no. 6: 1919. https://doi.org/10.3390/s18061919





