Study on Misalignment Angle Compensation during Scale Factor Matching for Two Pairs of Accelerometers in a Gravity Gradient Instrument
Abstract
:1. Introduction
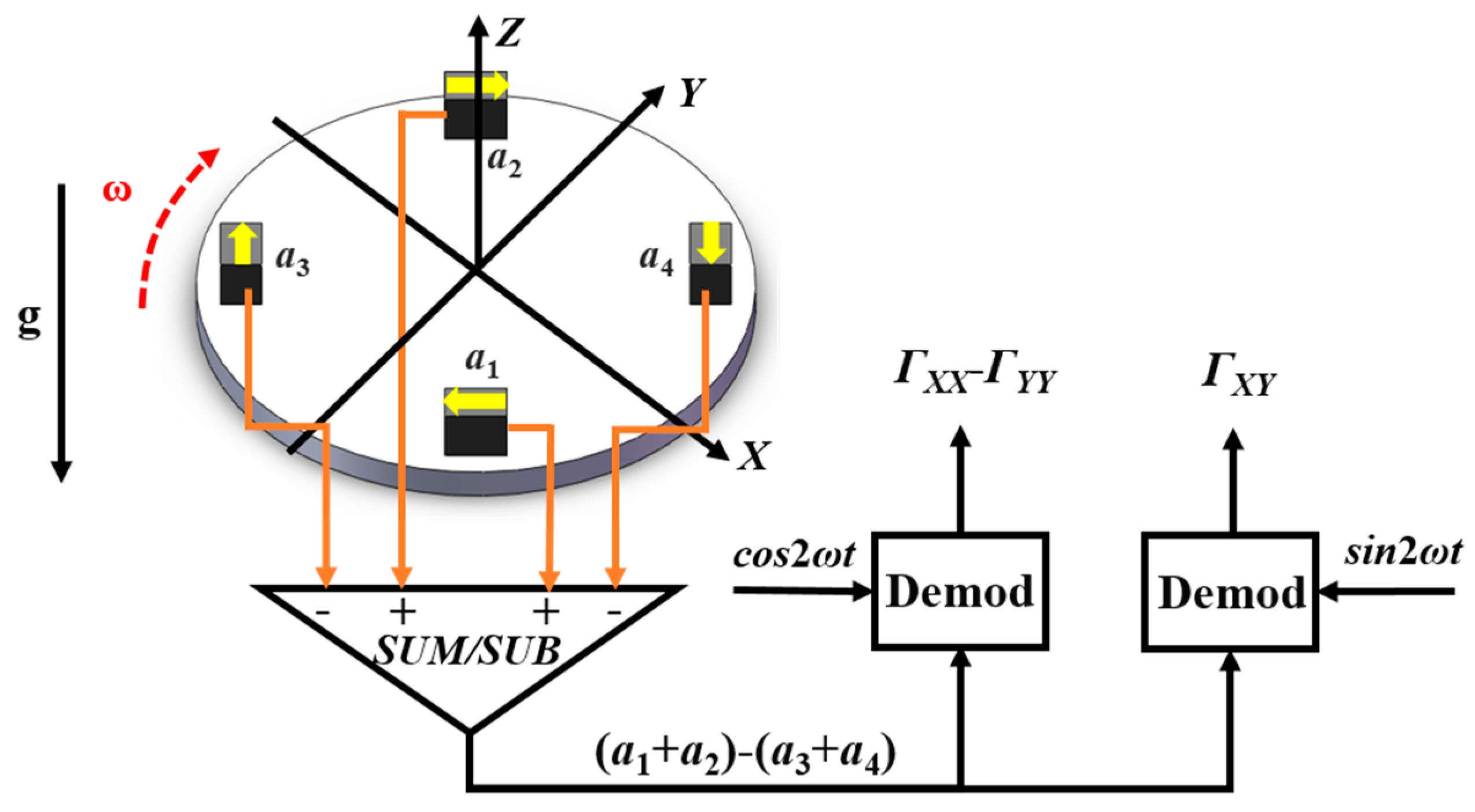
2. Principle of the Misalignment Angle Compensation in Scale Factor Balance for a Pair of Accelerometers
2.1. The noise effect of the misalignment angle
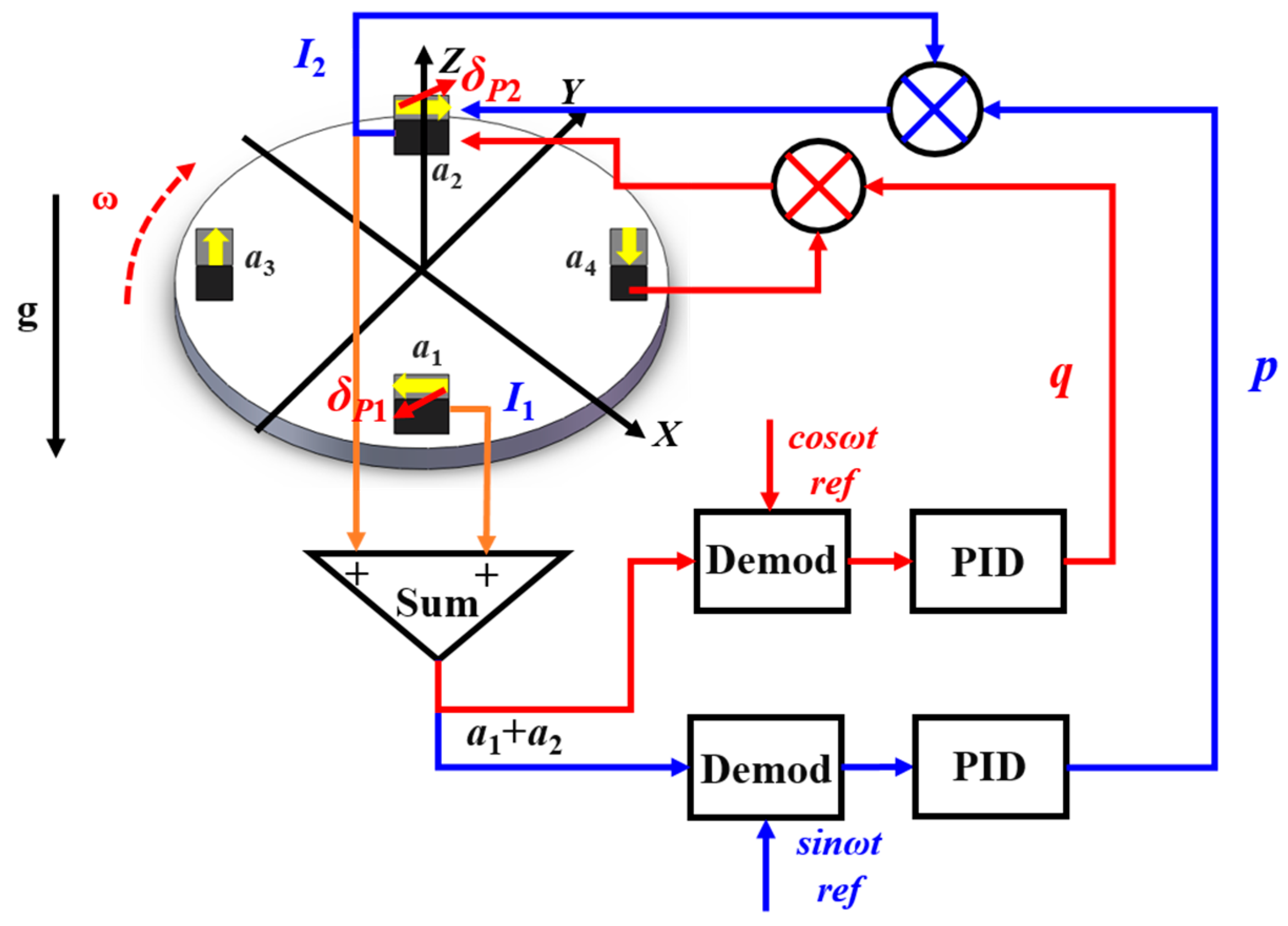
2.2. The principle of the misalignment angle compensation
3. Experimental Results
4. Conclusions and Prospects
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lane, R.J.L. (Ed.) Airborne Gravity 2010—Abstracts from the ASEG-PESA Airborne Gravity 2010 Workshop: Published Jointly by Geoscience Australia and the Geological Survey of New South Wales. 2010. Geoscience Australia Record 2010/23 and GSNSW File GS2010/0457. Available online: https://d28rz98at9flks.cloudfront.net/70673/Rec2010_023.pdf (accessed on 23 August 2010).
- Chapin, D. Gravity instruments; past, present, future. Lead. Edge 1998, 17, 100–112. [Google Scholar] [CrossRef]
- DiFrancesco, D.; Grierson, A.; Kaputa, D.; Meyer, T. Gravity gradiometer systems-advances and challenges. Geophys. Prospect. 2009, 57, 615–623. [Google Scholar] [CrossRef]
- Bell, R.E.; Anderson, R.; Pratson, L.F. Gravity gradiometry resurfaces. Lead. Edge 1997, 16, 55–59. [Google Scholar] [CrossRef]
- Dransfield, M.H.; Christensen, A.N. Performance of airborne gravity gradiometers. Lead. Edge 2013, 32, 908–922. [Google Scholar] [CrossRef]
- Lane, R.J.L. (Ed.) Airborne Gravity 2004—Abstracts from the ASEG-PESA Airborne Gravity 2004 Workshop: Geoscience Australia Record 2004/18. 2004. Available online: https://d28rz98at9flks.cloudfront.net/61129/Rec2004_018.pdf (accessed on 15 August 2004).
- Braga, M.A.; Endo, I.; Galbiatti, H.F.; Carlos, D.U. 3D full tensor gradiometry and Falcon Systems data analysis for iron ore exploration: Bau Mine, Quadrilatero Ferrifero, Minas Gerais, Brazil. Geophysics 2014, 79, B213–B220. [Google Scholar] [CrossRef]
- Lee, J.; Kwon, J.H.; Yu, M. Performance evaluation and requirements assessment for gravity gradient referenced navigation. Sensors 2015, 15, 16833–16847. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.B. FALCON gravity gradiometer technology. Exp. Geophys. 2001, 32, 247–250. [Google Scholar] [CrossRef]
- Metzger, E.H. Recent Gravity Gradiometer Developments. In Proceedings of the Guidance and Control Conference, Hollywood, FL, USA, 8–10 August 1977. [Google Scholar]
- Metzger, E.H. Development experience of gravity gradiometer system. IEEE PLANS 1982, 82, 323–332. [Google Scholar]
- Jekeli, C. Airborne gradiometry error analysis. Surv. Geophys. 2006, 27, 257–275. [Google Scholar] [CrossRef]
- Difrancesco, D. (Ed.) Advances and Challenges in the Development and Deployment of Gravity Gradiometer Systems. In Proceedings of the EGM 2007 International Workshop, Capri, Italy, 15–18 April 2007. [Google Scholar]
- Moody, M.V. A superconducting gravity gradiometer for measurements from a moving vehicle. Rev. Sci. Instrum. 2011, 82. [Google Scholar] [CrossRef] [PubMed]
- Snadden, M.J.; Mcguirk, J.M.; Bouyer, P.; Haritos, K.G.; Kasevich, M.A. Measurement of the Earth’s gravity gradient with an atom interferometer-based gravity gradiometer. Phys. Rev. Lett. 1998, 81, 971–974. [Google Scholar] [CrossRef]
- Liu, H.F.; Pike, W.T.; Dou, G.B. A seesaw-lever force-balancing suspension design for space and terrestrial gravity-gradient sensing. J. Appl. Phys. 2016, 119, 615–623. [Google Scholar] [CrossRef]
- Wei, H.W.; Wu, M.P.; Cao, J.L. New matching method for accelerometers in gravity gradiometer. Sensors 2017, 17, 1710. [Google Scholar] [CrossRef] [PubMed]
- Tu, L.C.; Wang, Z.W.; Liu, J.Q.; Huang, X.Q.; Li, Z.; Xie, Y.F.; Luo, J. Implementation of the scale factor balance on two pairs of quartz-flexure capacitive accelerometers by trimming bias voltage. Rev. Sci. Instrum. 2014, 85, 095108. [Google Scholar] [CrossRef] [PubMed]
- IEEE Aerospace and Electronic Systems Society. IEEE recommended practice for precision centrifuge testing of linear accelerometers. IEEE Std 2009, 836, 33–34. [Google Scholar] [CrossRef]
- O’keefe, G.J.; Lee, J.B.; Turner, R.J.; Adams, G.J.; Goodwin, G.C. Gravity Gradiometer. U.S. Patent 5922951, 13 July 1999. [Google Scholar]
- Brett, J.; Brewster, J. Accelerometer and Rate Sensor Pakage for Gravity Gradiometer Instruments. U.S. Patent 7788975 B2, 7 September 2010. [Google Scholar]
- Huang, X.Q.; Deng, Z.G.; Xie, Y.F.; Li, Z.; Fan, J.; Tu, L.C. A new scale factor adjustment method for magnetic force feedback accelerometer. Sensors 2017, 17, 2471. [Google Scholar] [CrossRef] [PubMed]
- Guan, W.; Meng, X.F.; Dong, X.M. Testing accelerometer rectification error caused by multidimensional composite inputs with double turntable centrifuge. Rev. Sci. Instrum. 2014, 85, 125003. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.T.; Xie, Y.F.; Zhang, M.Q.; Deng, Z.G.; Tu, L.C. A subnano-g electrostatic force-rebalanced flexure accelerometer for gravity gradient instruments. Sensors 2017, 17, 2669. [Google Scholar] [CrossRef] [PubMed]


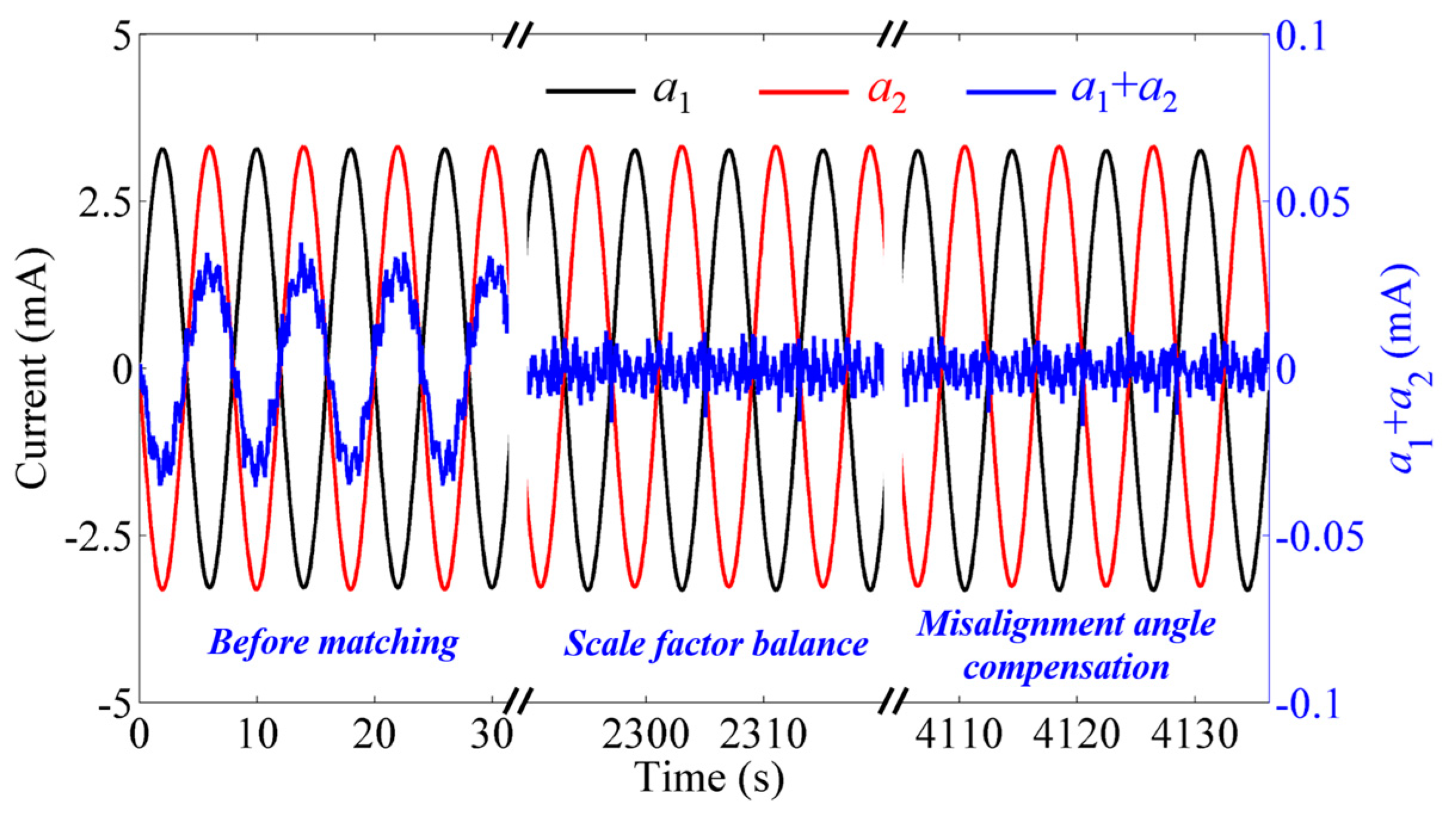
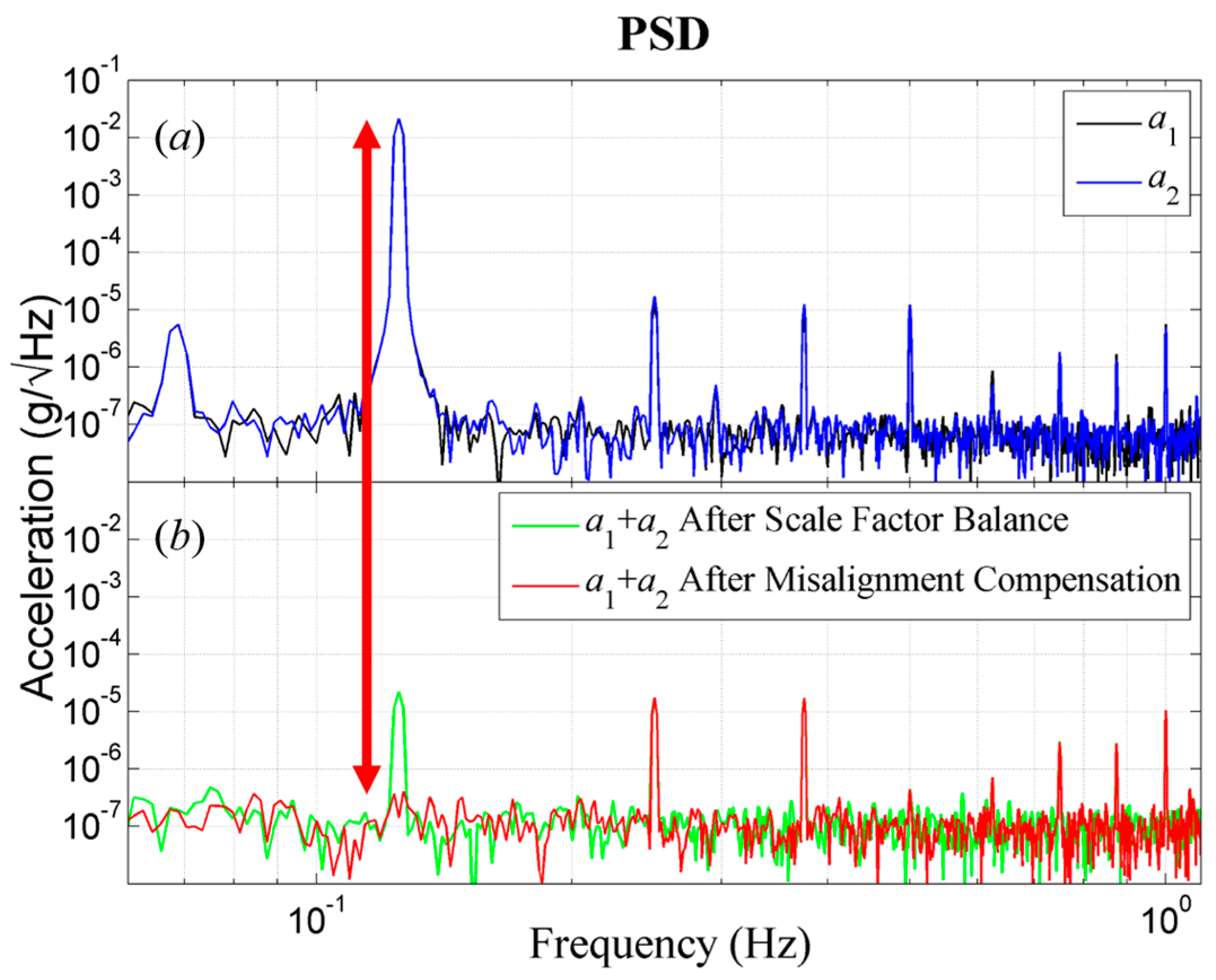
| Output Current (mA) | Before Matching | After Scale Factor Balance | After Misalignment Angle Compensation | |||
|---|---|---|---|---|---|---|
| sinωt | cosωt | sinωt | cosωt | sinωt | cosωt | |
| a1 | 3.3830(3) | −0.0747(3) | 3.3953(3) | −0.0763(3) | 3.3963(3) | −0.0060(3) |
| a2 | −3.4150(3) | 0.0753(3) | −3.3957(3) | 0.0750(3) | −3.3963(3) | 0.0060(3) |
| a1 + a2 | −0.0322(2) | 0.0006(2) | −0.0001(2) | −0.0013(2) | −0.0000(2) | −0.0000(2) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Deng, Z.; Xie, Y.; Fan, J.; Hu, C.; Tu, L. Study on Misalignment Angle Compensation during Scale Factor Matching for Two Pairs of Accelerometers in a Gravity Gradient Instrument. Sensors 2018, 18, 1247. https://doi.org/10.3390/s18041247
Huang X, Deng Z, Xie Y, Fan J, Hu C, Tu L. Study on Misalignment Angle Compensation during Scale Factor Matching for Two Pairs of Accelerometers in a Gravity Gradient Instrument. Sensors. 2018; 18(4):1247. https://doi.org/10.3390/s18041247
Chicago/Turabian StyleHuang, Xiangqing, Zhongguang Deng, Yafei Xie, Ji Fan, Chenyuan Hu, and Liangcheng Tu. 2018. "Study on Misalignment Angle Compensation during Scale Factor Matching for Two Pairs of Accelerometers in a Gravity Gradient Instrument" Sensors 18, no. 4: 1247. https://doi.org/10.3390/s18041247
APA StyleHuang, X., Deng, Z., Xie, Y., Fan, J., Hu, C., & Tu, L. (2018). Study on Misalignment Angle Compensation during Scale Factor Matching for Two Pairs of Accelerometers in a Gravity Gradient Instrument. Sensors, 18(4), 1247. https://doi.org/10.3390/s18041247





