1. Introduction
Lameness in horses can be defined as an alteration of the normal gait due to a functional or structural disorder of the loco-motor system, and can commonly be attributed to orthopedic pain [
1]. It is by far the most expensive health issue in the equine field, with economic costs estimated between
$680 million and
$1 billion in the USA alone [
2]. It has been demonstrated that equine veterinarians spend up to 40% of their working time assessing lameness [
3]. Currently, most veterinarians rely on subjective visual examination of gait to detect movement asymmetries that are the common clinical sign of lameness. However, subjective lameness assessment has been shown to have some substantial drawbacks, most due to the limitations of human visual symmetry perception [
4] and the bias effect [
5], which ultimately leads to a poor agreement between veterinarians [
6,
7,
8,
9].
Objective quantification of lameness has been a topic of investigation in the field of equine research for several years now [
10]. The solutions that were devised can be broadly divided into two categories: kinetic methods and kinematic methods. Kinetic methods analyze the forces resulting from movement, whereas kinematic methods analyze movement of internal and external body segments during locomotion.
Force platforms were among the first instruments used for objective lameness assessment [
11], and are still described today as the “gold standard” for kinetic gait analysis. Force platforms measure the ground reaction force (GRF), as exerted on a limb during the stance phase, in three dimensions [
12]. Force platforms are very precise and accurate instruments, but the data collection process is laborious and time-consuming: since only very few strides are captured as the horse moves over the limited surface of the force platform, several runs are necessary to collect the necessary number of strides. To address this problem, force-measuring horse shoes [
13,
14] and a force-measuring treadmill [
15] were developed. However, these are not yet widely available as a practical tool for daily gait analysis.
For kinematic analysis, optical motion capture (OMC) systems [
16,
17] have been applied successfully [
18,
19]. These systems use reflective markers attached to the body of the subject and several (infra-red) cameras distributed across the room that track the 3D position of the markers. These systems are highly accurate and precise: the average position error is usually better than a few millimeters [
17,
20]. Generic motion parameters that can reveal early signs of lameness have been defined and validated [
19,
21,
22]. Therefore, OMC systems are considered the “gold standard” for kinematic analysis [
23]. However, for a full-body capture of a horse moving through a large volume, a significant number of OMC cameras and supporting infrastructure is needed, which incurs significant cost. Due to the scale, size, and complexity of the system, it is difficult to relocate it to other venues [
23,
24]; e.g., each time it is relocated, a calibration procedure needs to be followed by an expert in order to ensure data quality [
17]. Therefore, the application of OMC systems is mostly limited to a fixed laboratory environment [
23], and in some exceptional cases, large clinics.
Inertial measurement units (IMUs) [
25] have been considered as a promising cost-effective alternative to OMC systems [
8,
26,
27,
28,
29,
30,
31,
32,
33]. By rigidly attaching an IMU to a body segment, the orientation and (less reliably) the displacement of that body segment can be determined, making a set of these devices applicable as a kinematic measurement system [
34]. Recent technological progress in microelectromechanical (MEMS) inertial sensors, combined with the abrupt drop of sensor prices thanks to the smartphone market, made small, low-cost, low-power, yet accurate IMUs available. Moreover, the development of low-power wireless technologies has made it possible to explore a new paradigm: wireless networked IMUs, which avoids the need to draw cables between the sensor locations.
This is what the EquiMoves system described in the present study provides: a wireless IMU-based solution that operates as a network capturing relevant horse motion variables at a high sample rate, at eight bodily positions, in real time and accurately synchronized.
In this article, we compare the EquiMoves system to a well-established OMC system for a set of well-defined kinematic horse locomotion parameters that both systems can produce. Since the EquiMoves system is designed for everyday use by a veterinarian, we performed experiments that best match that scenario. This precludes the use of a treadmill, for example, since that may influence the horse’s gait [
35,
36].
Although we use the OMC system as a source of an accurate ground truth, we do not consider it the gold standard per se; we are interested mainly in the level of agreement between the two systems and what may cause the observed differences. Both IMU-based and OMC-based systems have limitations; e.g., IMU systems suffer from drift errors that accumulate in the underlying integration calculations [
25], while OMC measurements are influenced by the number of cameras that have each marker in view and the distance between each camera and each marker [
17,
20]. We chose to focus on differences caused by errors in the displacement and orientation measurements of both systems. Therefore, timing-related differences are eliminated by choosing one of the two systems as the timing reference for both.
Our contributions are as follows:
We present a system that provides real-time wireless data acquisition with the potential for real-time feedback to the user. The system can handle various equine gaits (e.g., walk and trot). It registers and analyzes movements for all individual limbs, rather than only upper-body movement, for example, which is what the previously described systems [
21,
37] do. Most existing systems only work for a horse trotting along a straight line, and involve only sensors to measure asymmetry on the vertical displacement of head and/or pelvis [
34,
37]. In contrast, the EquiMoves system can be used for walking and trotting horses, for arbitrary paths, and can also measure limb motion.
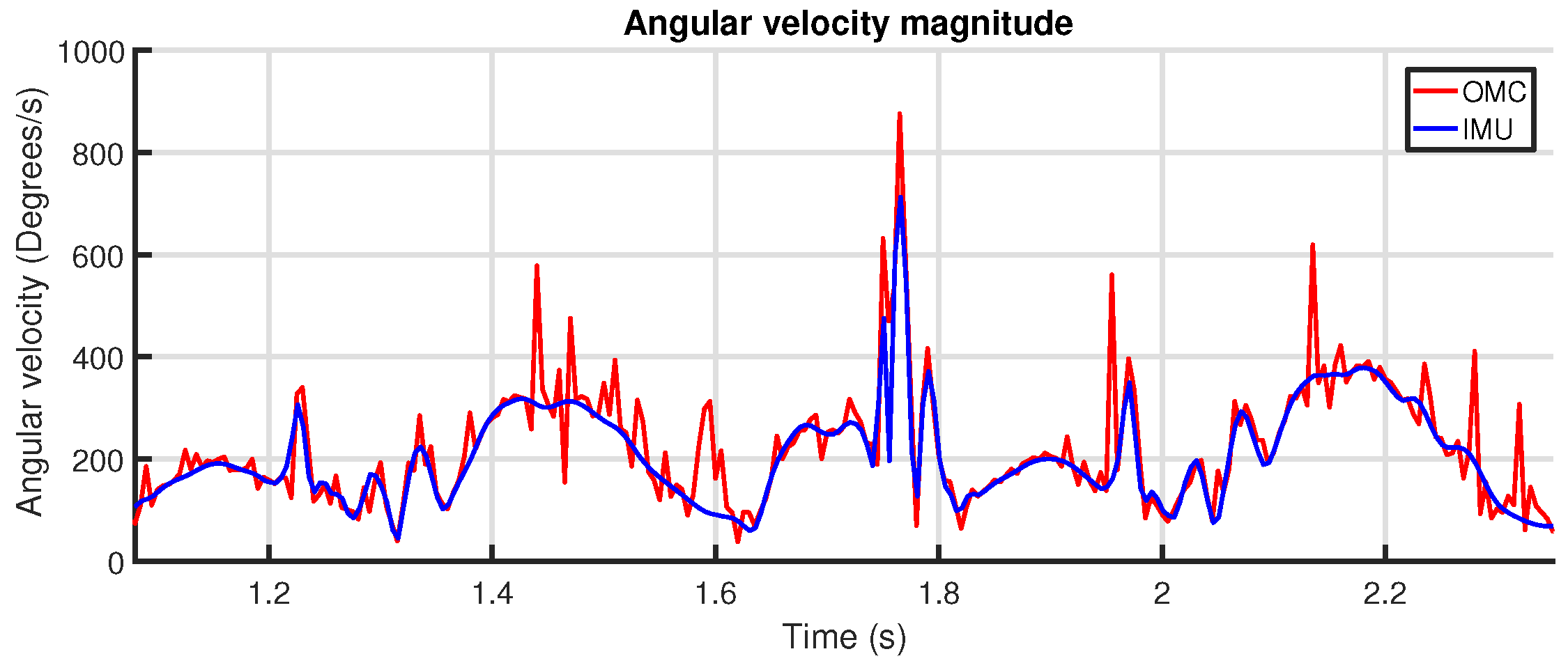
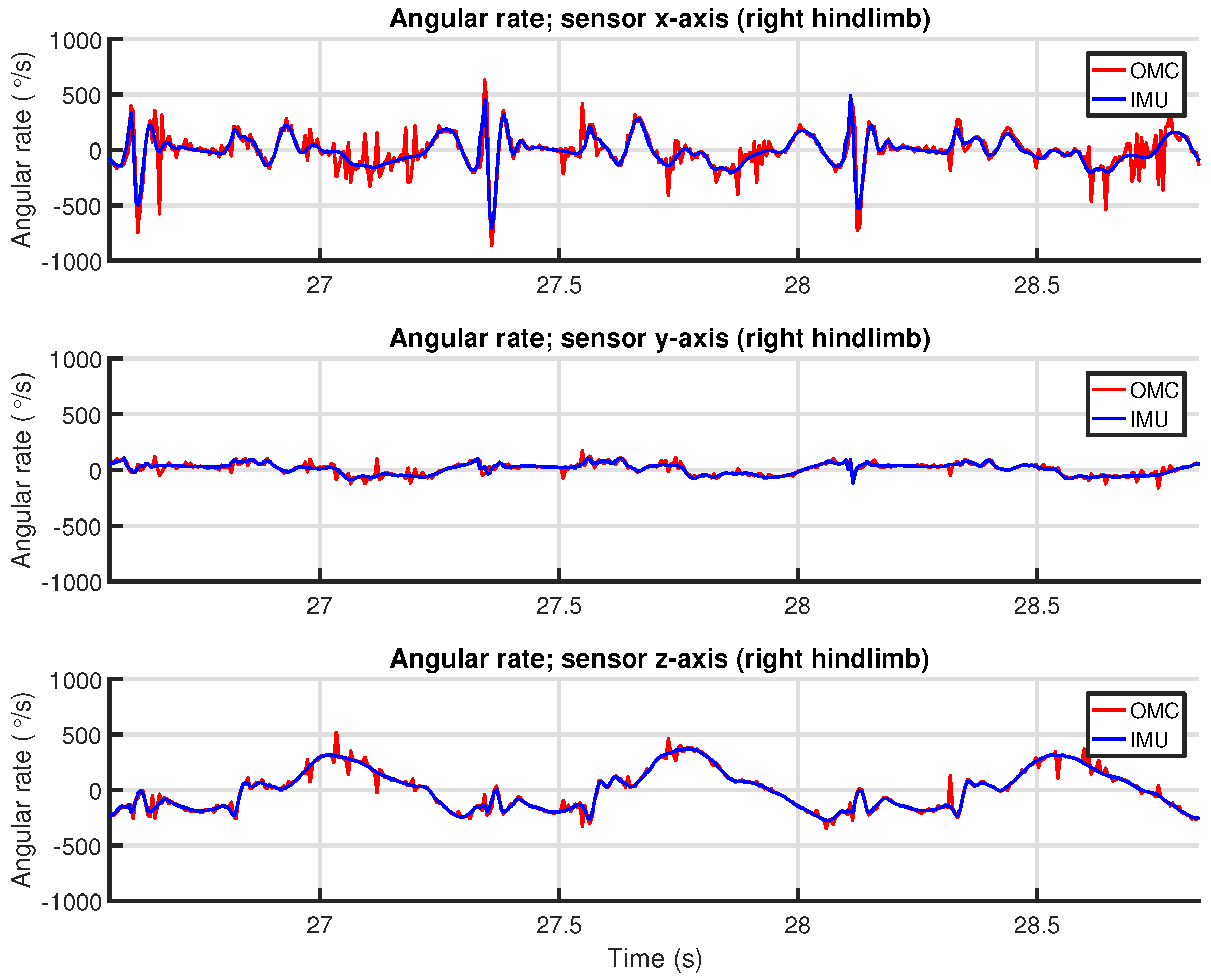
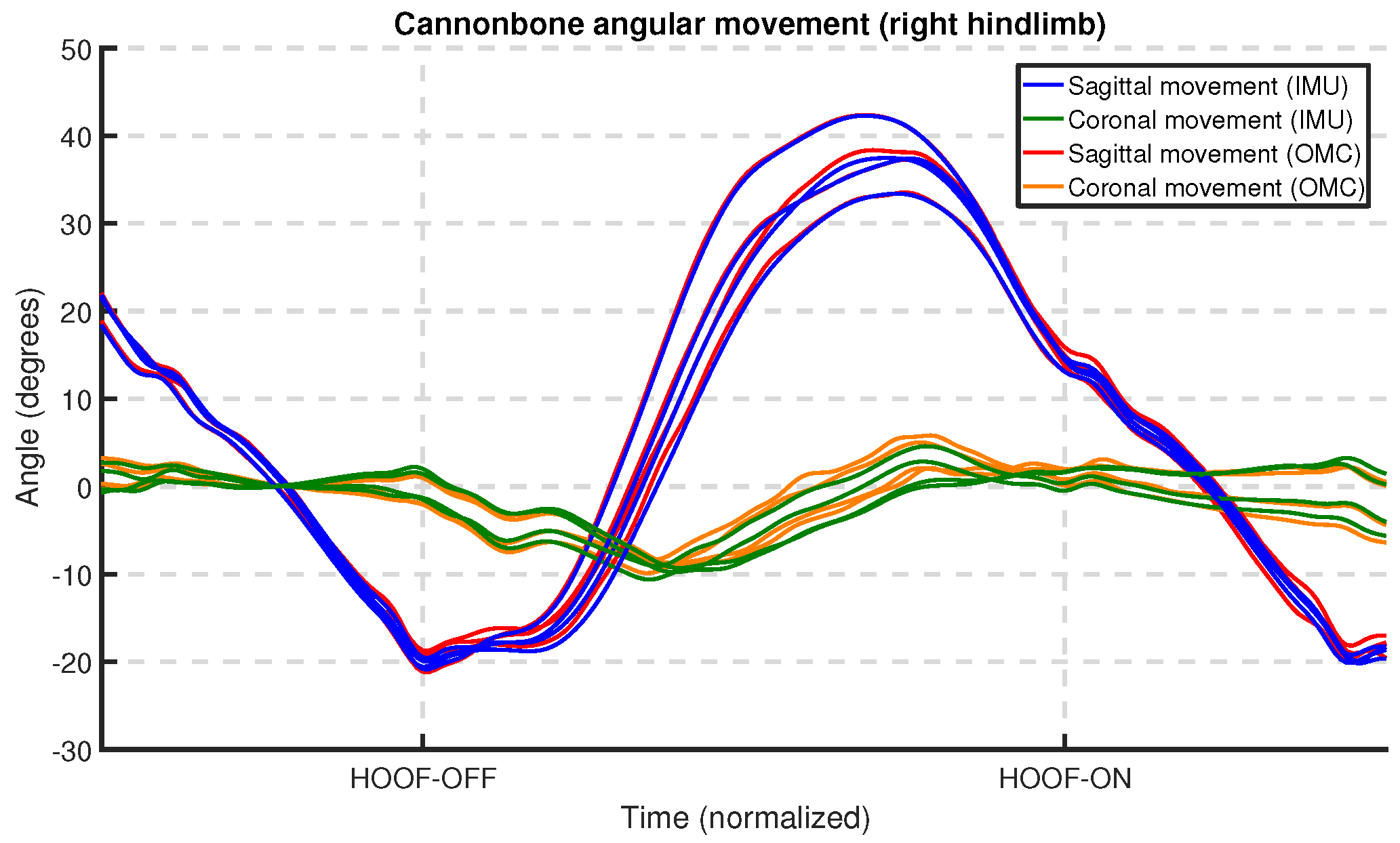
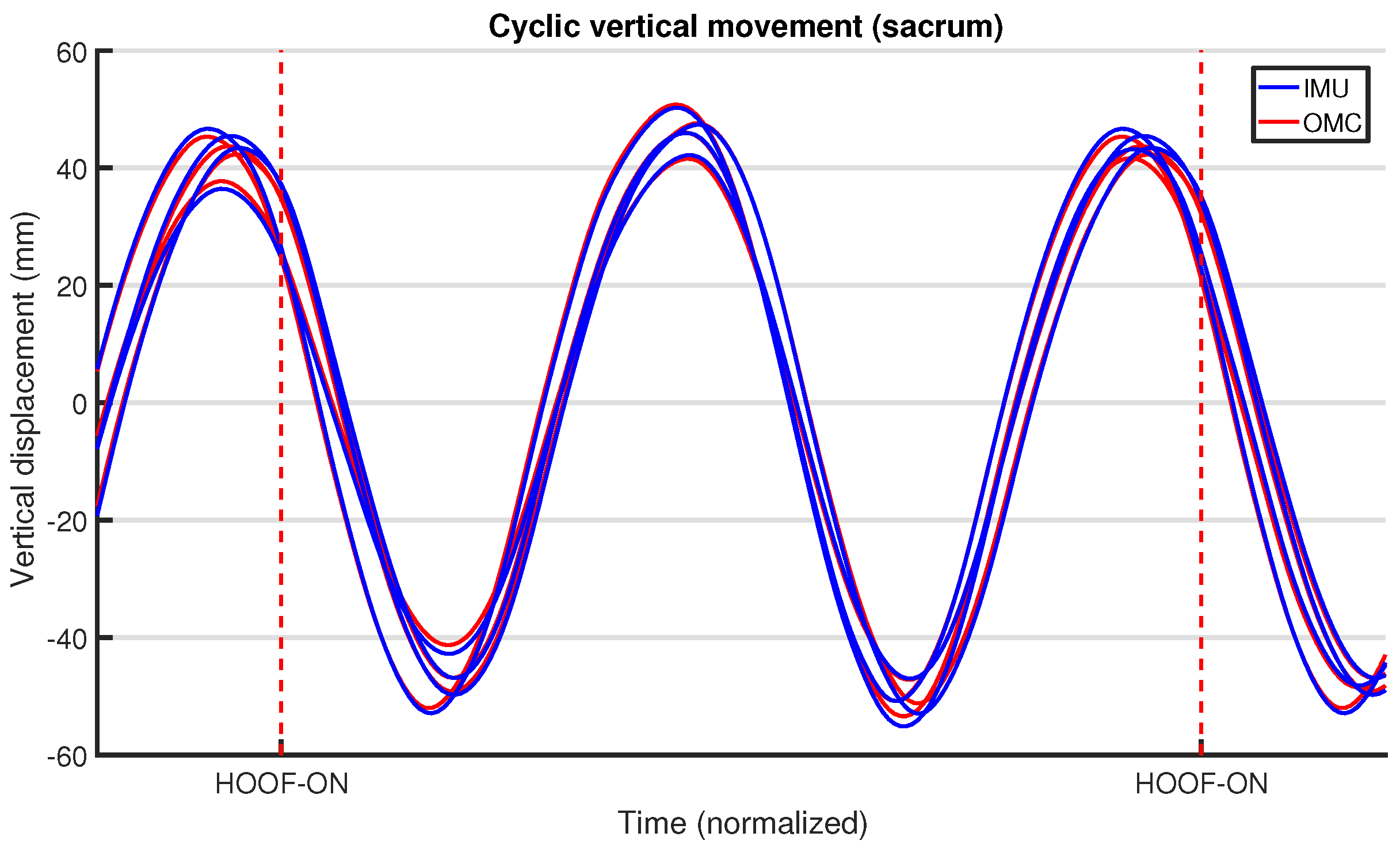
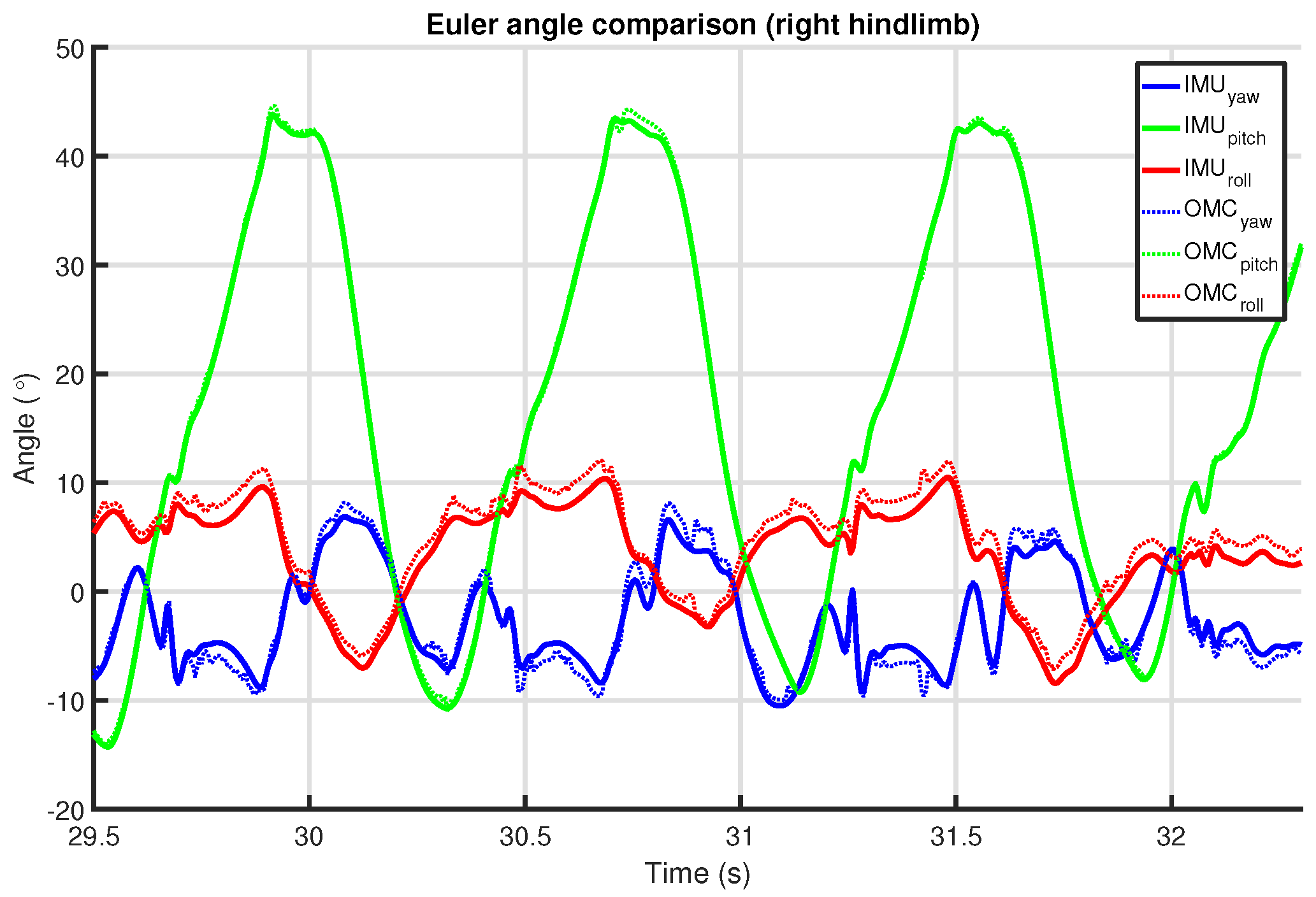
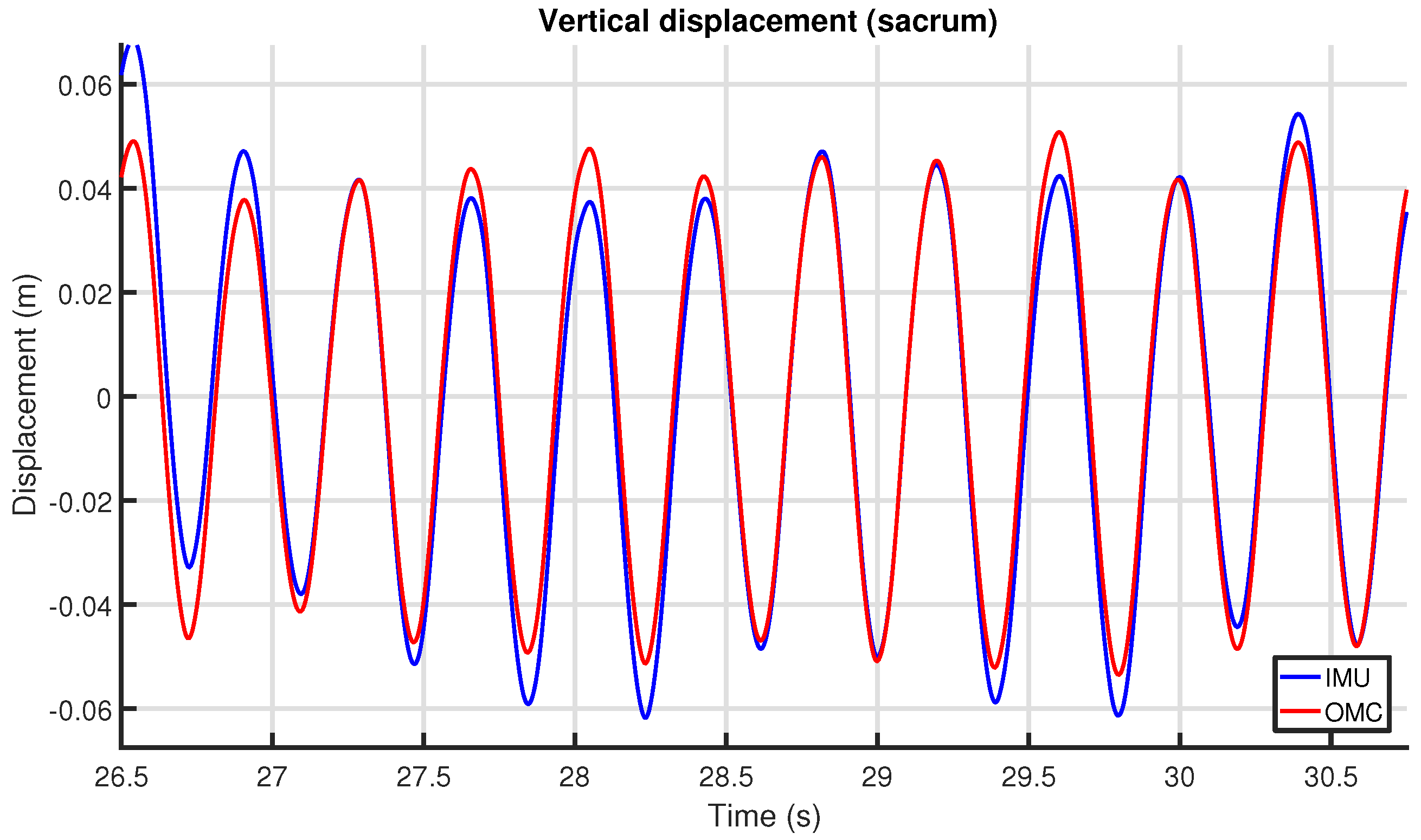
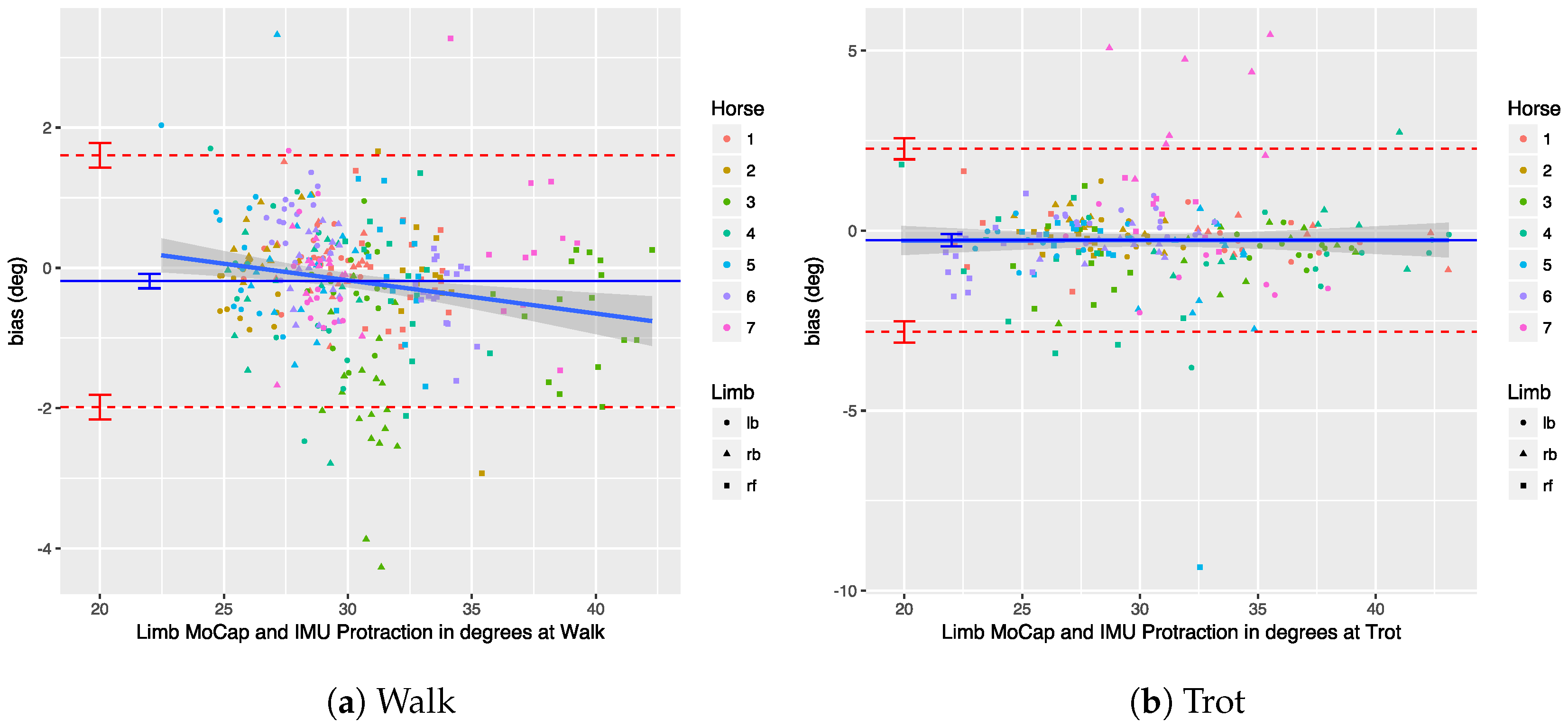
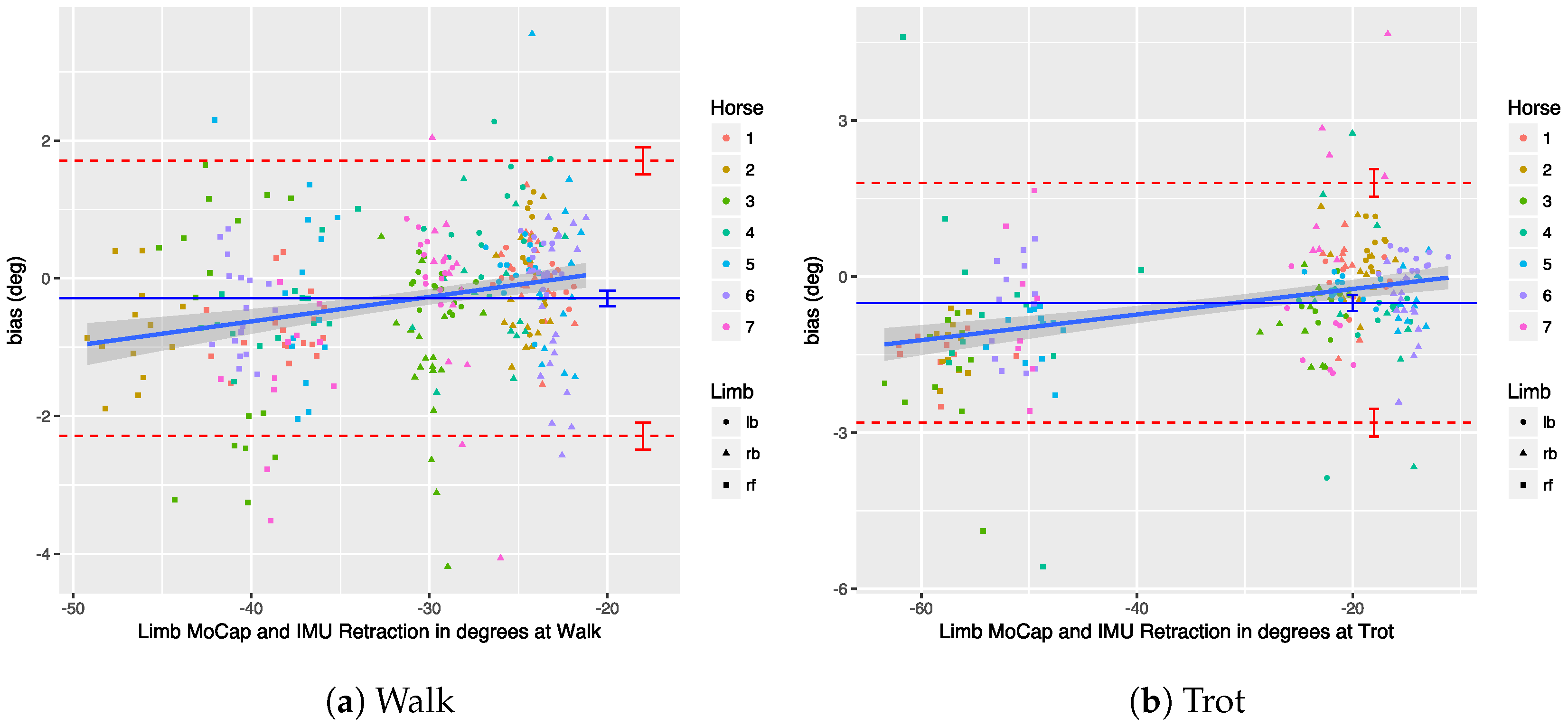
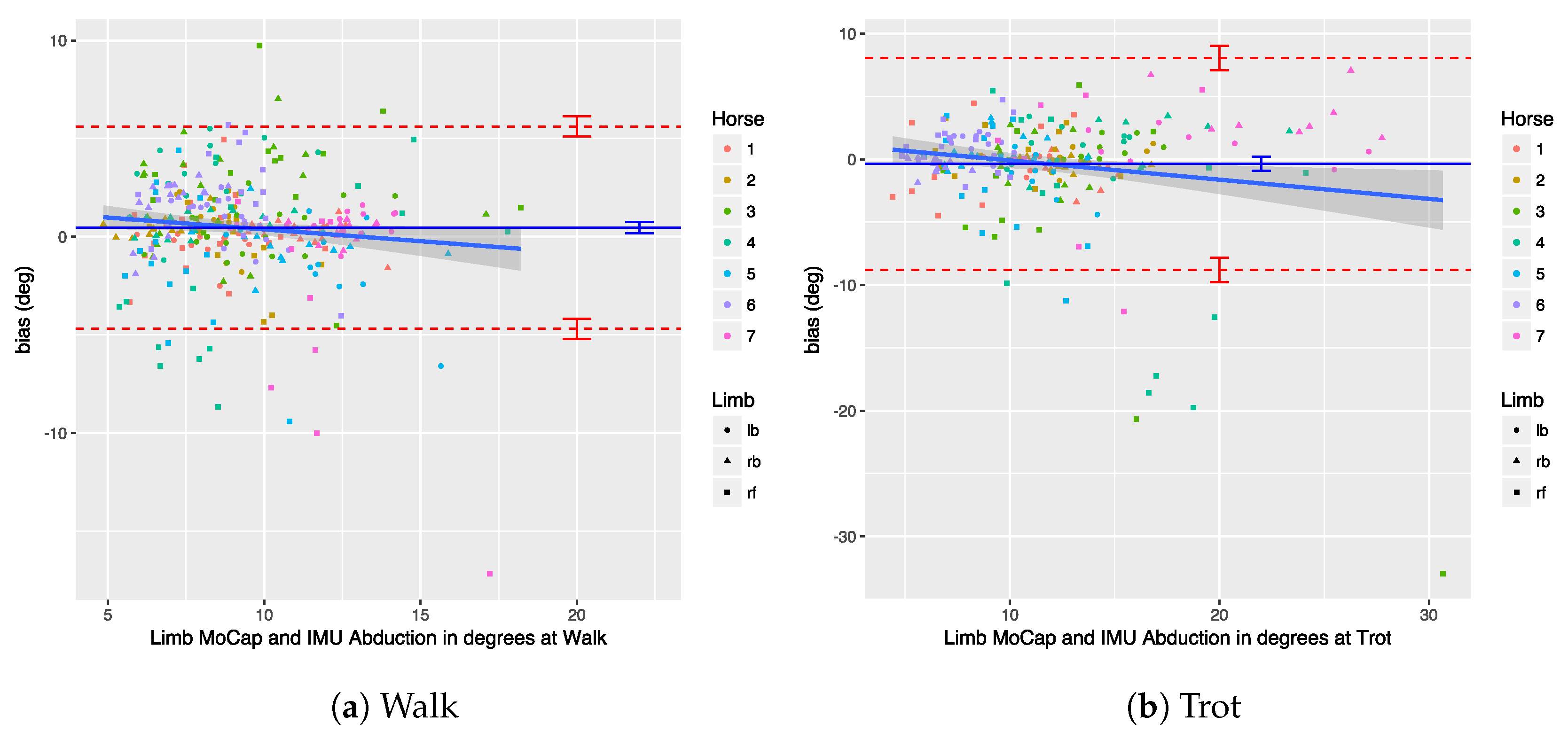
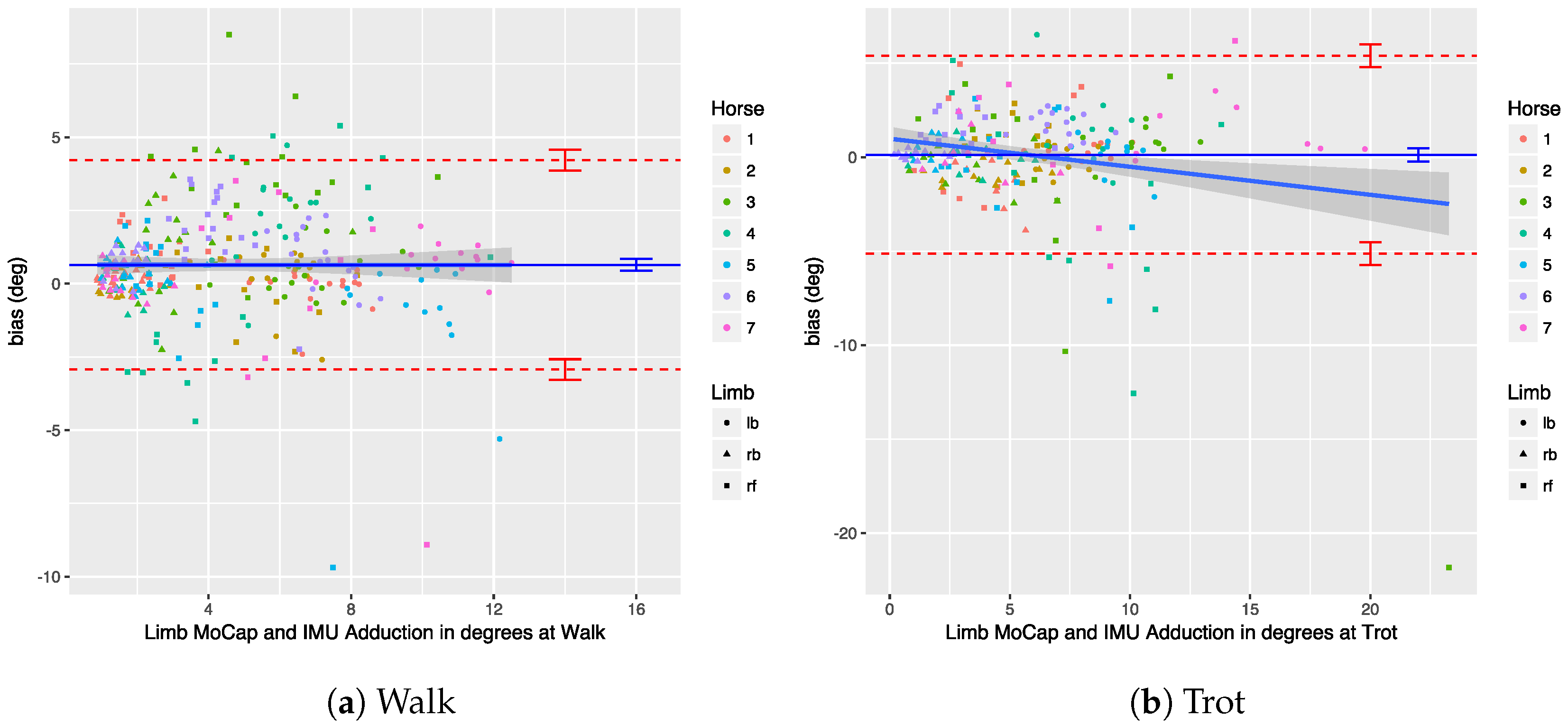
We provide an in-depth analysis of the agreement of the measurements of our system with an OMC system, looking at both upper-body and limb-related parameters.
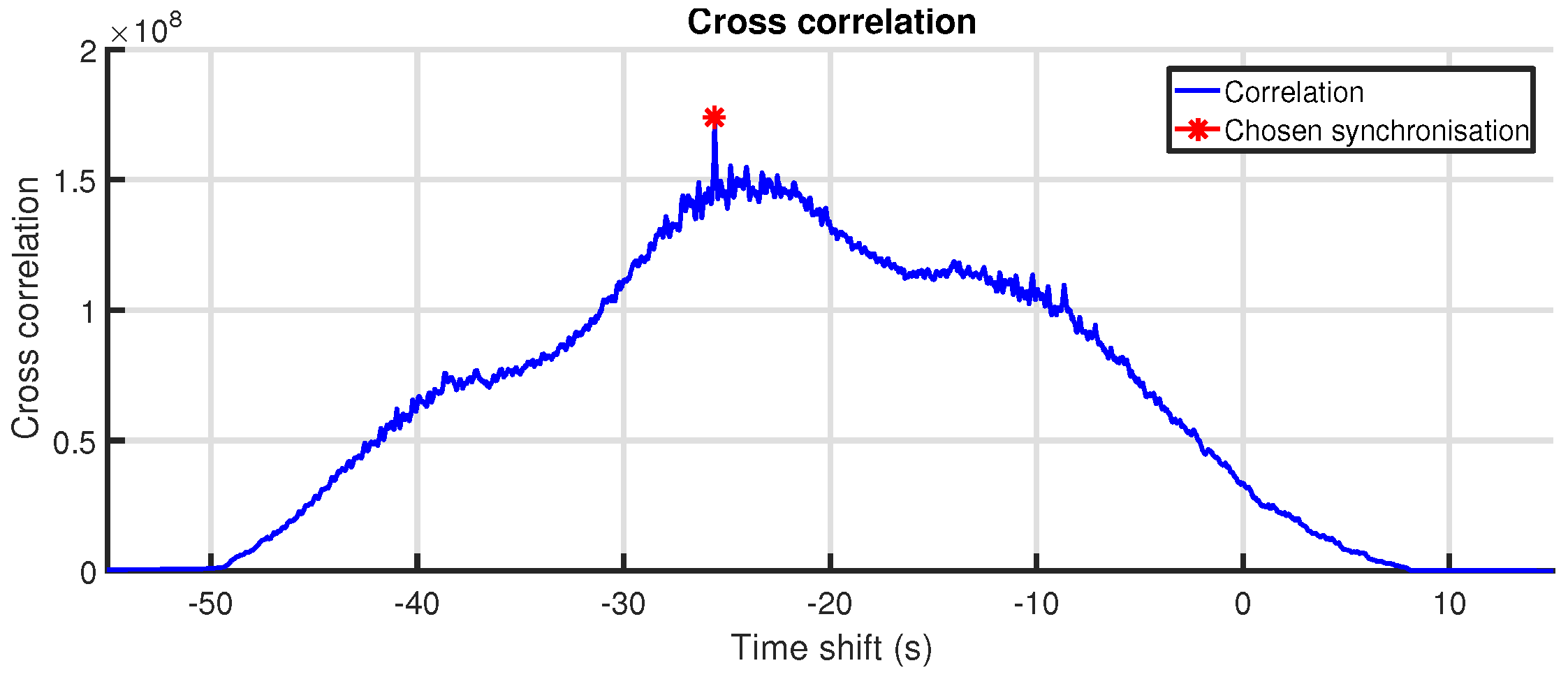
We provide a detailed description of a data-based algorithm for time synchronization and the alignment of position and orientation between the IMU and OMC data sets.
In the following sections, we describe the EquiMoves system in detail. We start by positioning it with respect to related work; then, we present background information on horse gait analysis. Subsequently, the main system components and methods are described. Next, we discuss the practical trials and results obtained for validating the system. We conclude with a discussion of the results, current limitations, and points of improvement as future work.
2. Related Work
The most widely-used method for equine gait analysis is currently visual examination, which is prone to the subjectivity and limited accuracy of the human eye [
4]. This has been suggested as one of the reasons why agreement between equine vets evaluating lameness in horses is often low [
8]. There is also a susceptibility to bias during the orthopedic exam [
5]. Particularly in cases of mild lameness, studies showed that vets agreed whether a limb was lame or not in only 62% of the cases with mild lameness (i.e., having a mean score of less than 1.5 on the AAEP lameness scale [
6,
38]). When given the task of deciding whether the horse was lame and choosing the limb, vets agreed in less than 52% of the cases [
6].
As discussed previously in
Section 1, optical motion capture (OMC) systems have been applied successfully for kinematic gait analysis [
18,
19]. Generic motion parameters that can be used to assess the soundness of the horse objectively have been defined and validated for data produced by such systems [
21,
22]. Some of the disadvantages of these OMC systems are that they are quite expensive and mostly confined to a laboratory [
23,
24,
28].
Those limitations can pose problems for practitioners who wish to make these assessments in the field, which includes outdoor locations. Apart from practical considerations, it can also be very important in general to perform such experiments in the horse’s familiar environment [
39]. Another disadvantage is that an OMC system is limited to a specific motion capture volume, constrained by space and equipment [
23]. Thus, unless that volume is large, only a small number of strides can be recorded for gait analysis [
23,
28,
40]. Additionally, OMC systems use reflective markers that need to stay in view of a sufficient number of the OMC system’s cameras: it is not always possible to prevent occlusions (particularly self-occlusions), which results in missing or less-reliable data [
24,
41].
An alternative to OMC systems is the use of inertial measurement units (IMUs) [
42,
43]. These devices can be attached at key locations on the body of the subject and measure acceleration and angular velocity using accelerometers and gyroscopes, respectively (both are inertial sensors). Using these measurements, the kinematic variables like displacement and orientation of the body at these locations can be determined [
34].
IMUs have been applied extensively and successfully for human motion capture applications, particularly in healthcare [
23,
40,
42,
44,
45] and sports [
46,
47,
48,
49,
50,
51]. In equine research, inertial sensor systems are also quickly gaining popularity [
34,
52,
53], particularly for objective lameness assessment [
8,
26,
27,
28,
29,
30,
31,
32,
33]. Some older systems only used a single-axis accelerometer and/or gyroscope, which means that those systems rely only on one-dimensional data. Therefore, for those systems, the rotation of the sensors during movement and variation in sensor attachment influence the signals and their quality [
26]. More recent works use full IMUs on several locations of the body [
26,
31,
54,
55].
For human motion capture applications, IMU technology has been validated using OMC systems [
23,
49,
50,
56,
57,
58,
59] and normal video recordings [
60]. So far, the IMU-based horse gait analysis systems have only been sparsely evaluated: there is work comparing IMU-based systems with subjective assessment [
7,
8,
61,
62,
63], there is work comparing IMU-based systems with force platform systems [
62,
64,
65], and there are studies comparing between IMU-based kinematic systems [
30,
66,
67]. However, the agreement of IMU-based and OMC-based kinematic horse gait analysis systems is barely explored: earlier work is either limited to stride timing or frequency [
28], limited to upper-body [
32,
34], limited to limb measurements [
68,
69], or performs no agreement analysis [
34,
70,
71]. In this work, we perform an extensive comparison of our IMU-based system with a well-established OMC system, for both limb and upper-body parameters.
There are three known initiatives in the market to provide portable sensor-based systems for assisting equine veterinarians with gait analysis, which are related to the EquiMoves system presented here. A well-known commercial system is the Lameness Locator from the company Equinosis (Columbia, MO, USA) [
27,
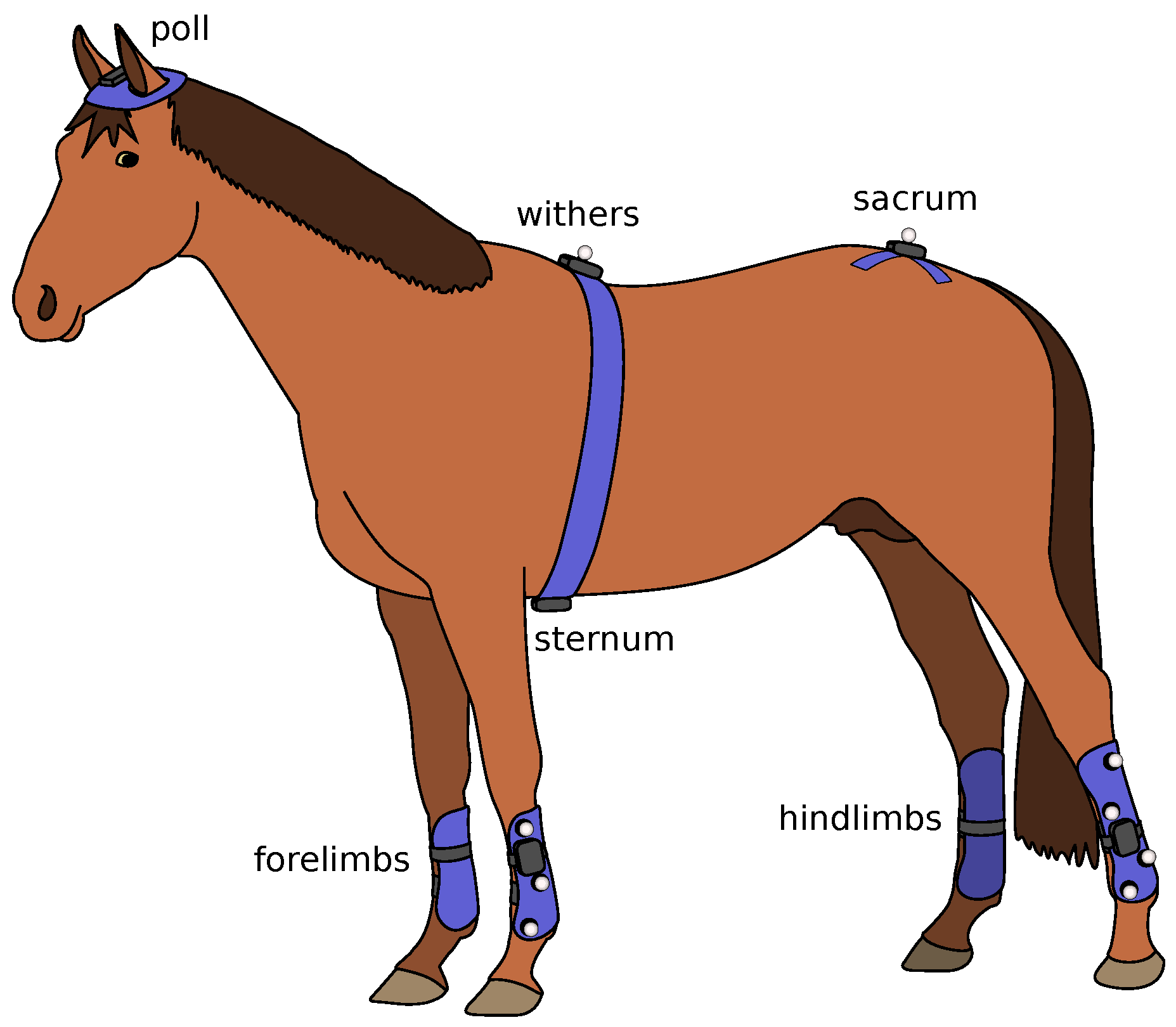
72]. The Lameness Locator is based on three sensors: two single-axis accelerometers on the head and sacrum (see
Section 3.1), and one single-axis gyroscope on the right forelimb, for determining the stance or swing phase of the diagonal pair of limbs in trot. The measured vertical acceleration of the torso is used to determine asymmetries in head and pelvic position between left and right halves of stride in trot. Due to the limited number and type of sensors, the Lameness Locator is usable only in trot, and the produced results relate only to the upper body of the horse.
Another commercial system is GaitSmart Pegasus (Codicote, Hitchin, Hertfordshire, UK) [
73], which mainly uses the gyroscope in two directions attached to the limbs, so it focuses on limb-related parameters. Some of the main outputs of Pegasus are the temporal phase-lag between limb cycles and the (angular) range of motion. However, none of these parameters are fully validated with respect to the gold-standard laboratory equipment [
69], and their biological significance still needs to be investigated with respect to their correlation with lameness. For the Pegasus system, the angular range of motion was compared with an OMC system similar to ours in an earlier study by Roepstorff et al. [
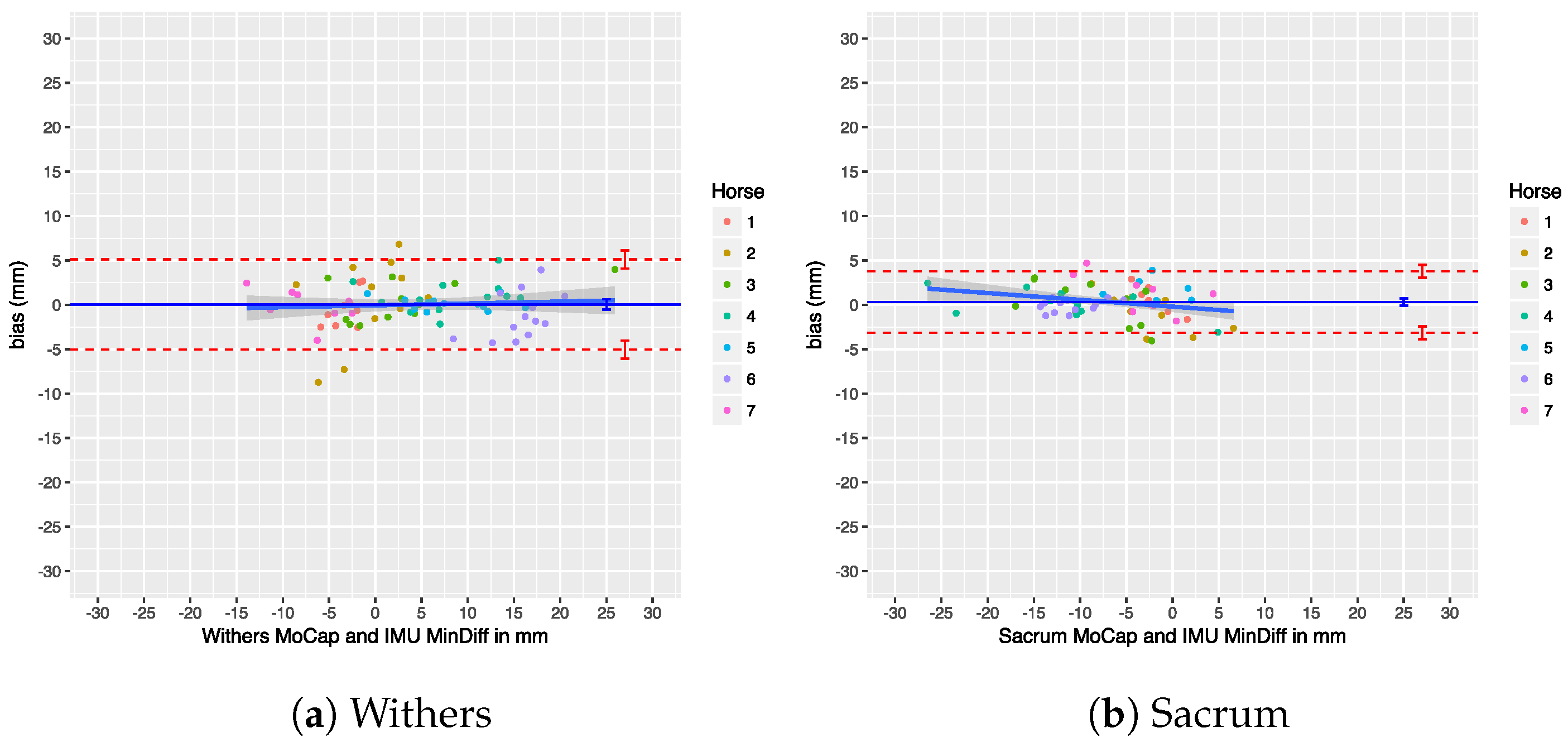
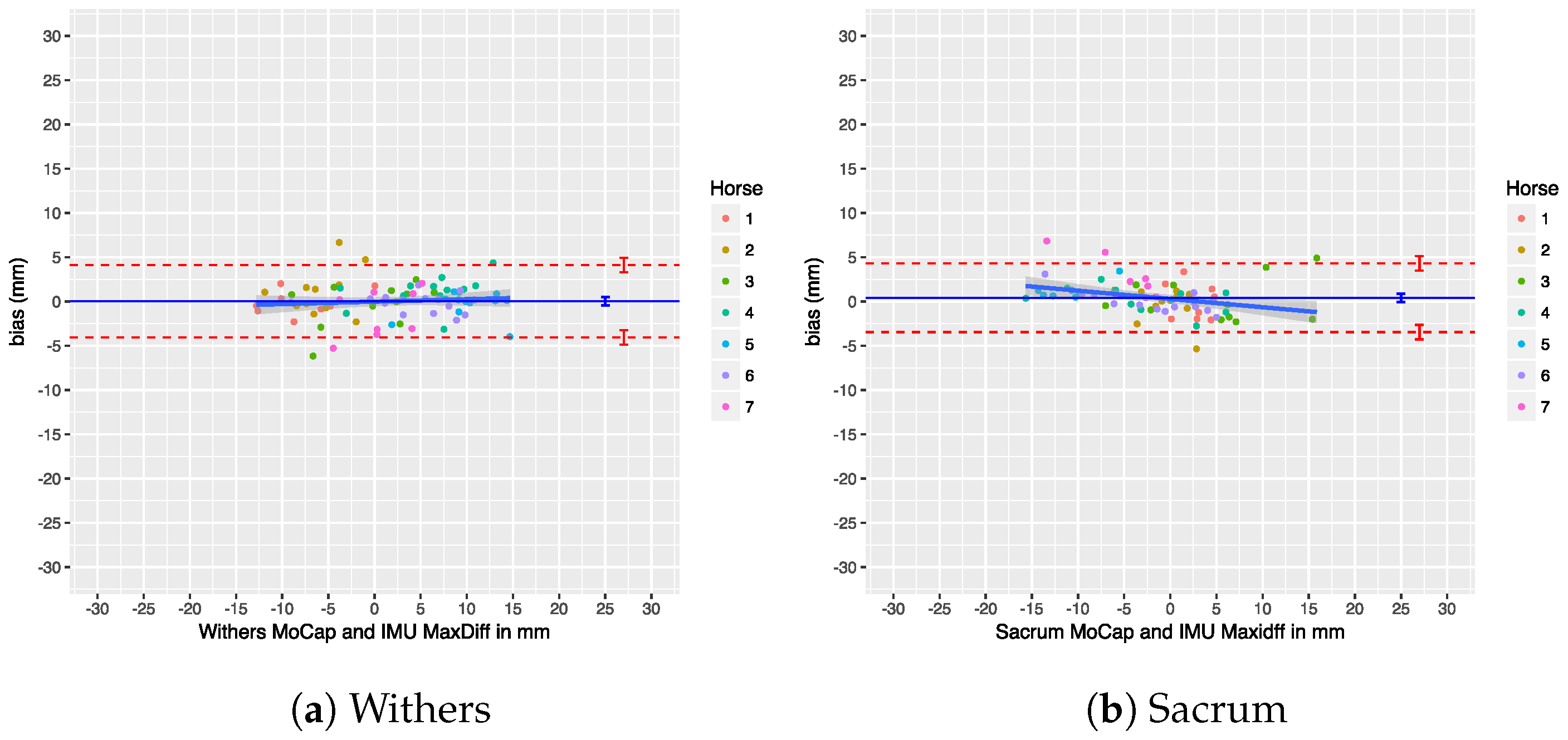
69]. Their results show a rather large bias between the two systems, yet the agreement between the two systems looks quite good. However, as we demonstrate in the discussion of our own results in
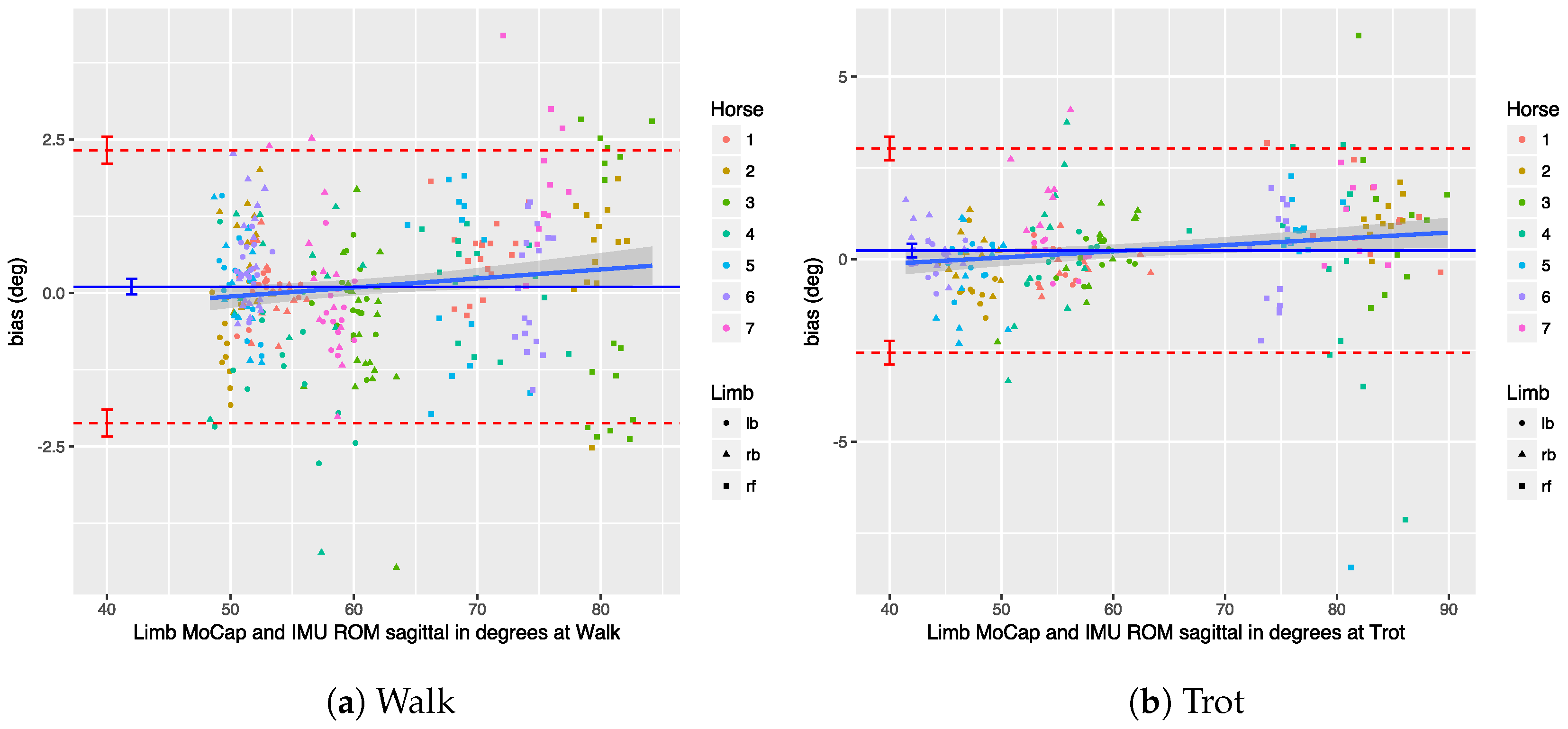
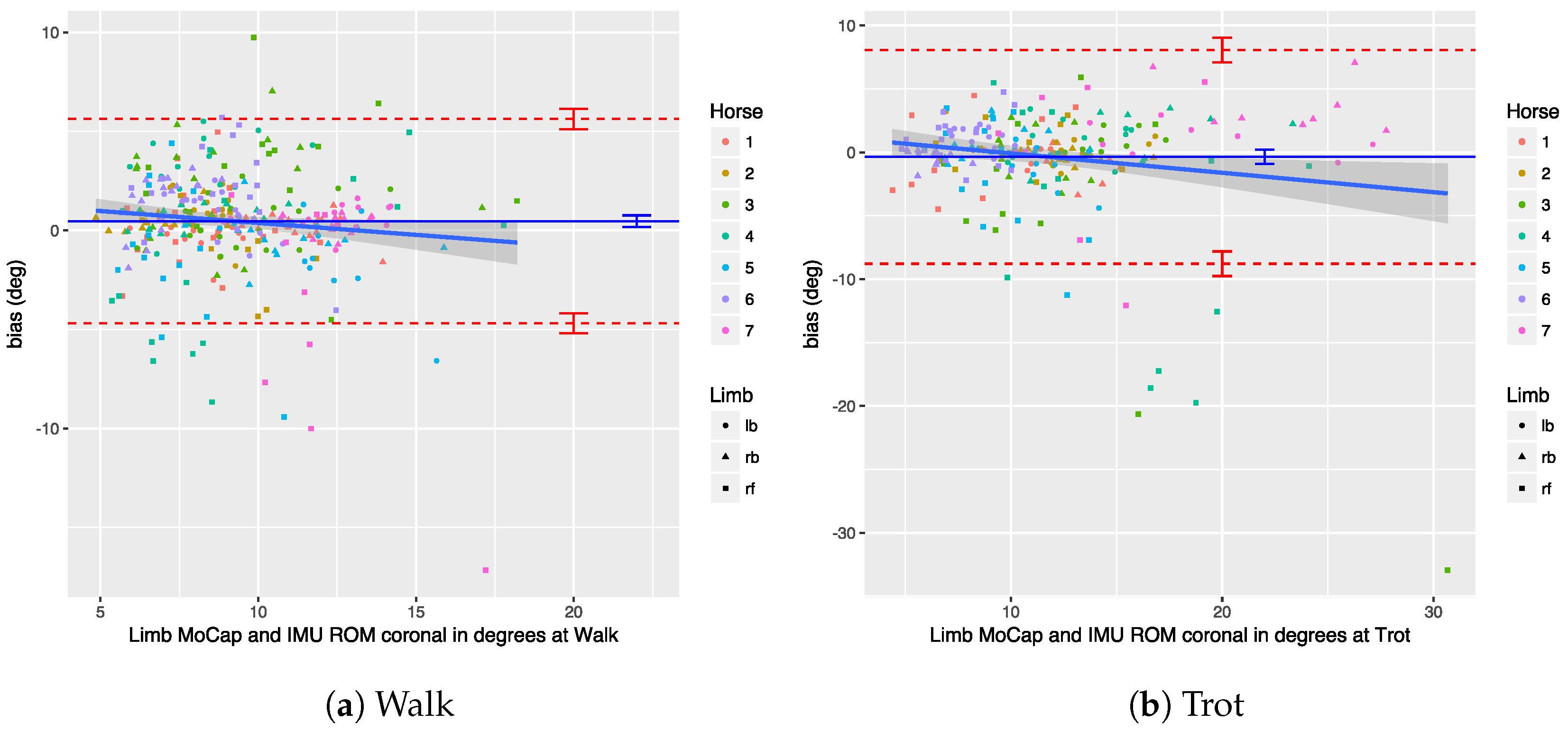
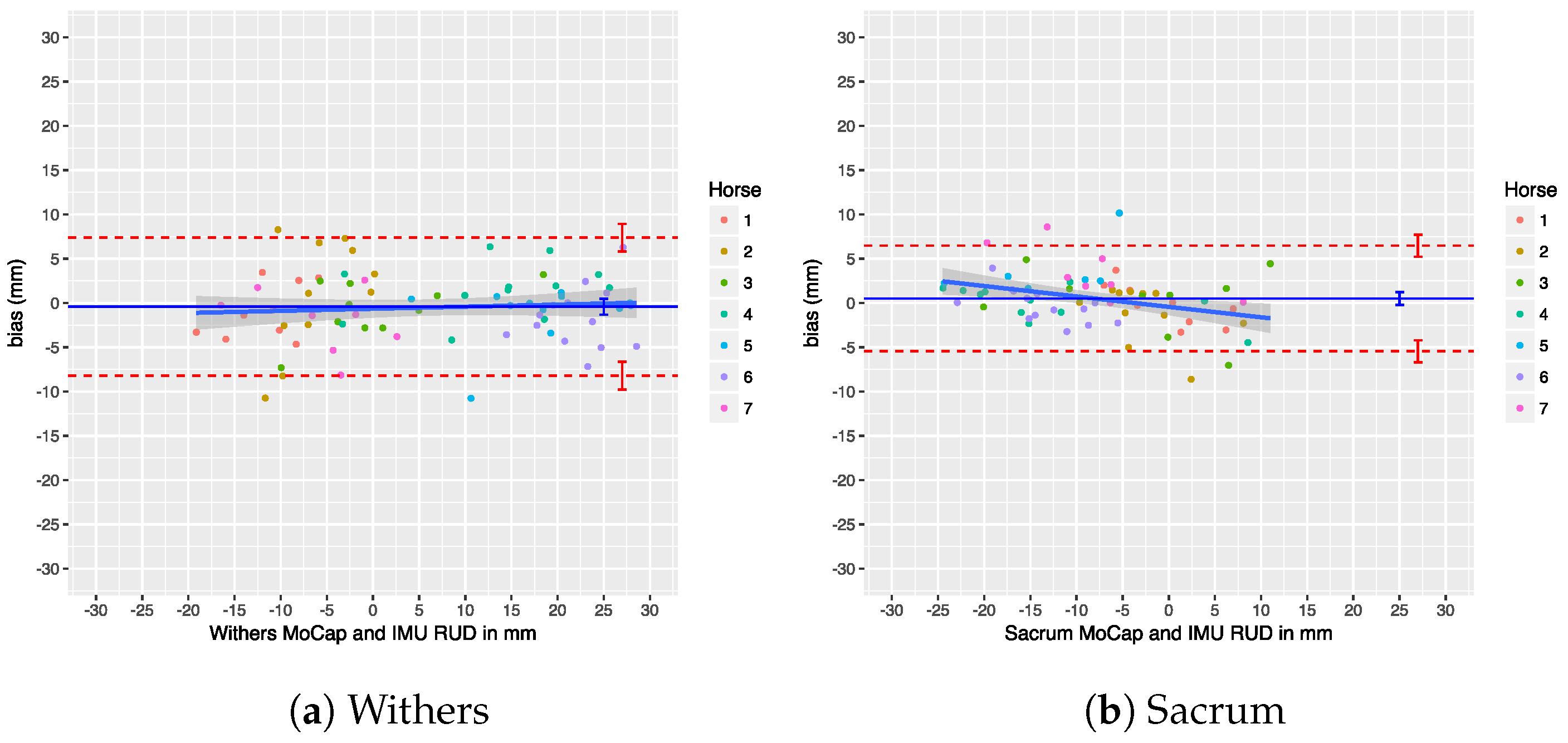
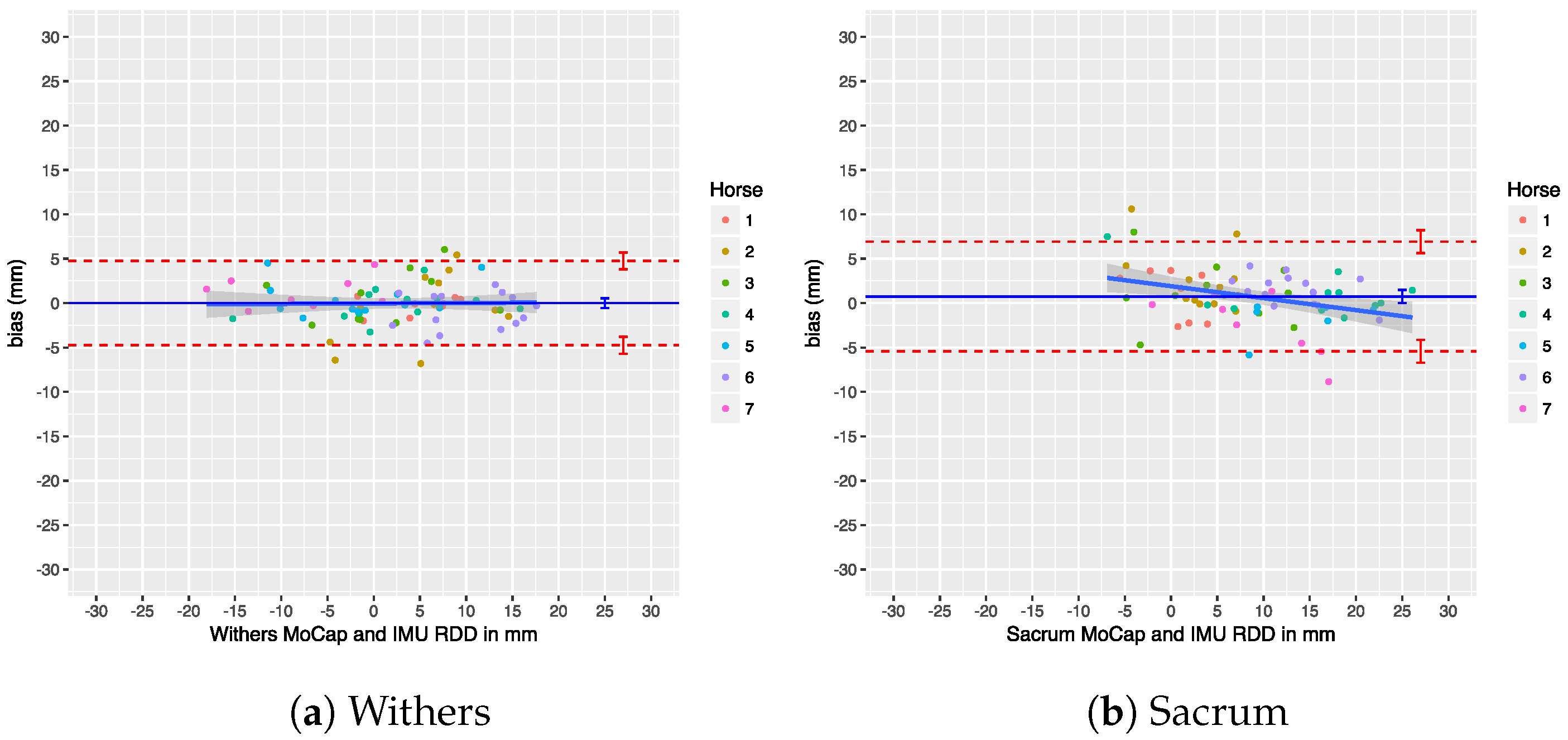
Section 7.3, Roepstorff et al. analyzed the agreement on a trial level, rather than on a per stride basis, which means that their agreement results are somewhat diluted, potentially painting an unrealistic picture of the true error. Additionally, the agreement was calculated on a mixed data set of walk and trot trials, thereby diluting the effect of gait.
Finally, the EquiGait system [
74] (Brickendon, Hertford, Hertfordshire, UK) uses IMUs on the upper body to measure either gait symmetry, back movement, or horse–rider interaction (with one IMU on the rider). Alternatively, a mobile phone can be used over the pelvic area. Although the EquiGait system is validated [
34] for the upper-body parameters that it can produce, it is currently not used to assess limb-related parameters (to the best of our knowledge).
8. Future Work
Based on experience gained from these experiments, the experimental setup should be adjusted in a few points for future experiments. Firstly, the handler needs to be farther away from the horse to prevent OMC marker occlusion on the forelimbs. Additionally, the placement of the markers on the forelimbs is too linear—the markers need to be spread more. The OMC system company provides special rigid marker clusters now, which should be used instead of placing markers individually. Furthermore, the IMU and/or OMC markers at the poll should be moved such that a reliable comparison between the systems is possible for that location. Finally, it is better to also have cameras closer to the ground to capture limb motion reliably. However, expanding the OMC system is costly.
In future experiments, we aim to calculate more horse locomotion parameters. For the limbs, we currently only measure angles, but it is also useful to determine limb displacement parameters such as stride length, average stride speed, and the maximum hoof elevation [
91]. Conversely, for the upper body, we currently rely solely on parameters based on vertical displacement. However, for example, the pelvis roll angle, which is the coronal attitude of the pelvis relative to the horizontal, has merit as well [
92].
The scope of future experiments will be extended. In the present study, we performed an agreement analysis involving only horses that have no known locomotion issues. To perform actual lameness detection, we will perform a proof-of-concept study with induced lameness. Furthermore, it is important to evaluate our system and algorithms with gaits other than walk and trot, and trials with horses moving in a nonlinear path; e.g., circular (lungeing) [
9,
33,
93].