Robust Angle Estimation for MIMO Radar with the Coexistence of Mutual Coupling and Colored Noise
Abstract
:1. Introduction
2. Tensor Preliminaries and Signal Model
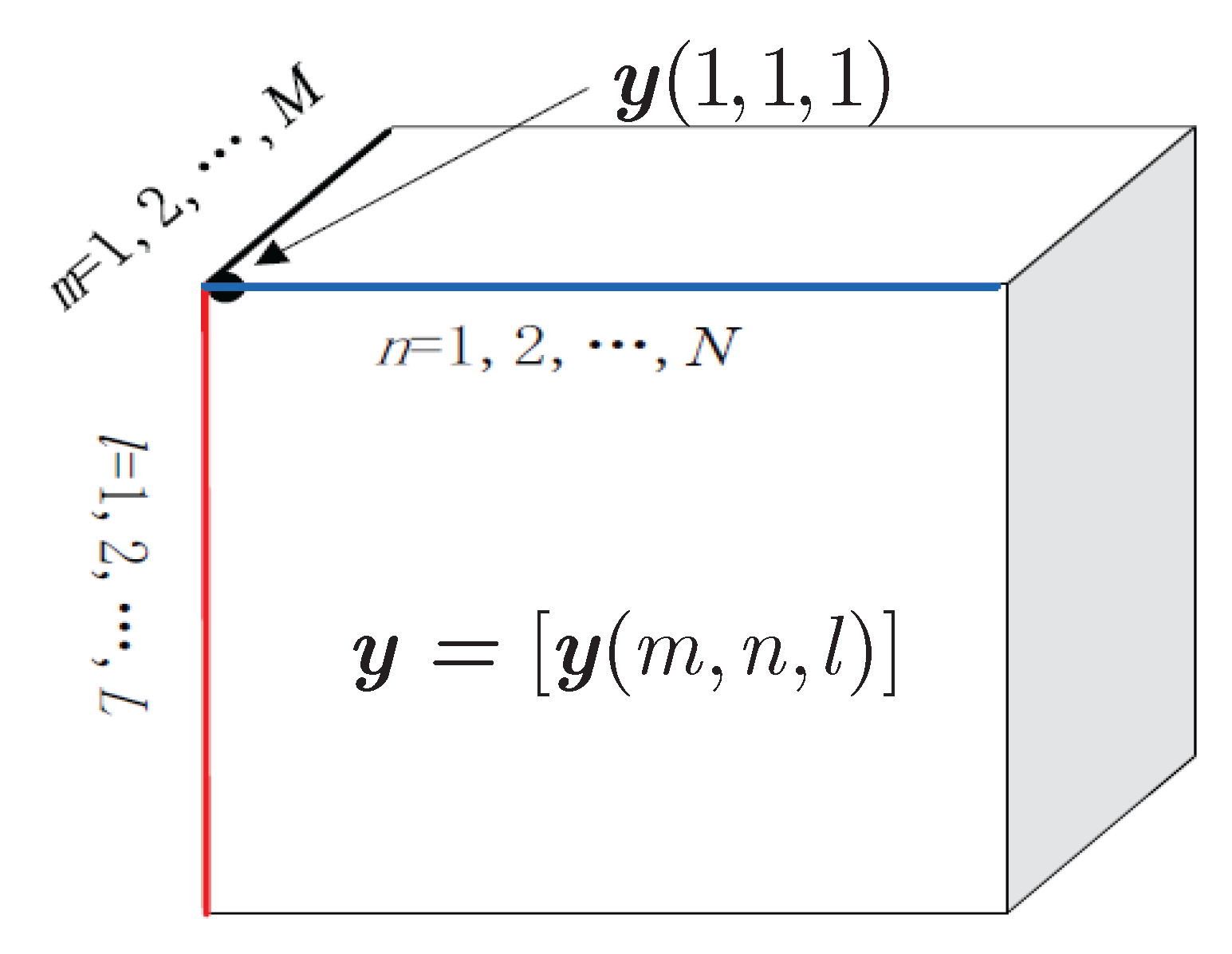
2.1. Tensor Preliminaries
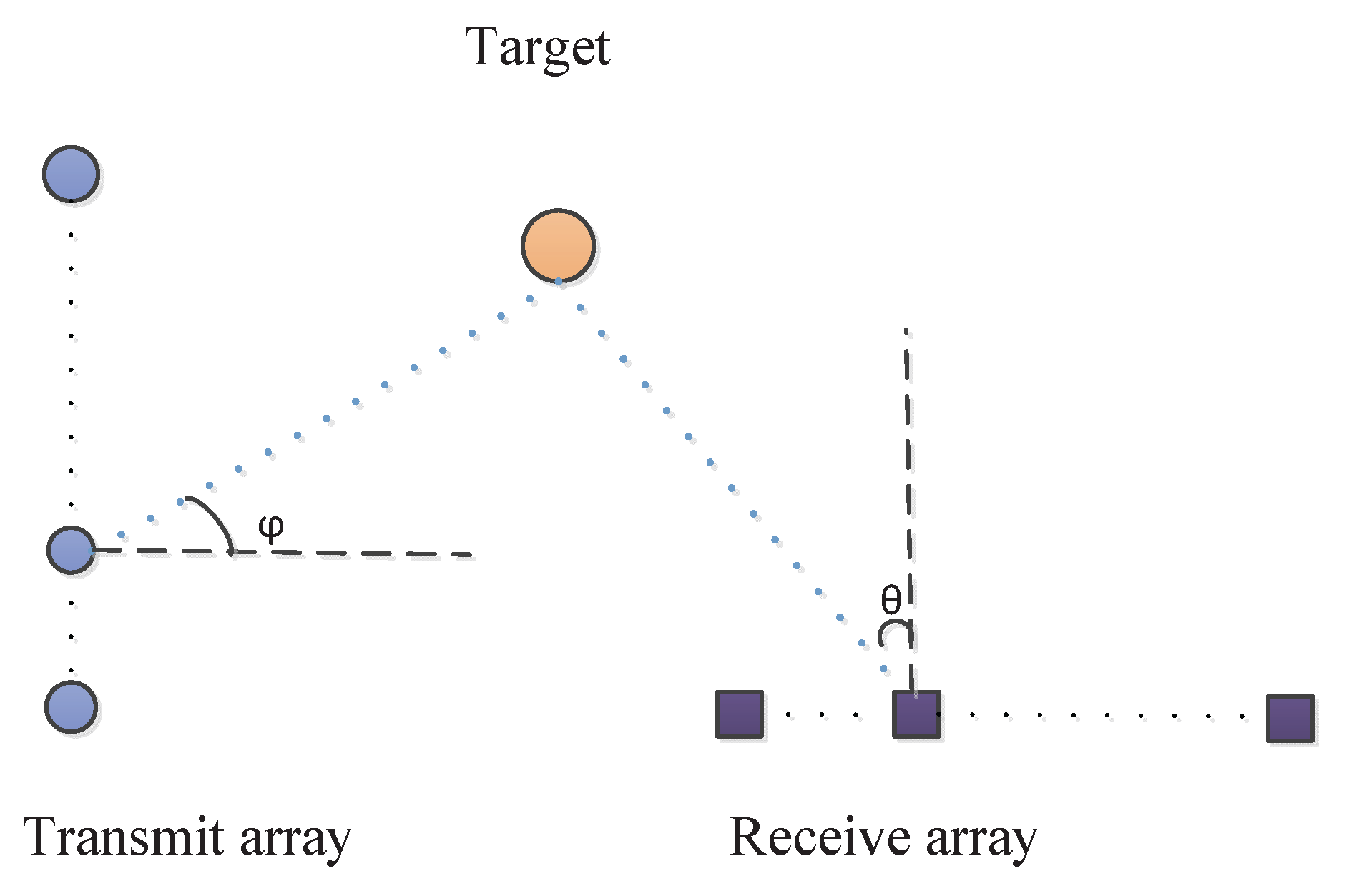
2.2. Signal Model
3. Robust Covariance Tensor-based Angle Estimation Method
3.1. Spatial Colored Noise Suppression and Mutual Coupling Elimination
3.2. Tensor-Based Signal Subspace Estimation and Angle Estimation
3.3. Joint DOD and DOA Estimation
- Step.1
- Stack the matched data into a third-order tensor as Equation (9);
- Step.2
- Step.3
- Perform HOSVD of to get , (), and get via Equation (22);
- Step.4
- Perform EVD of to get , obtain and via Equation (27), and compute EVD of to get and .
- Step.5
- Calculate via and finally get the DODs and DOAs via Equation (28).
4. Remarks and Algorithm Analysis
4.1. Related Remarks
4.2. Computation Complexity
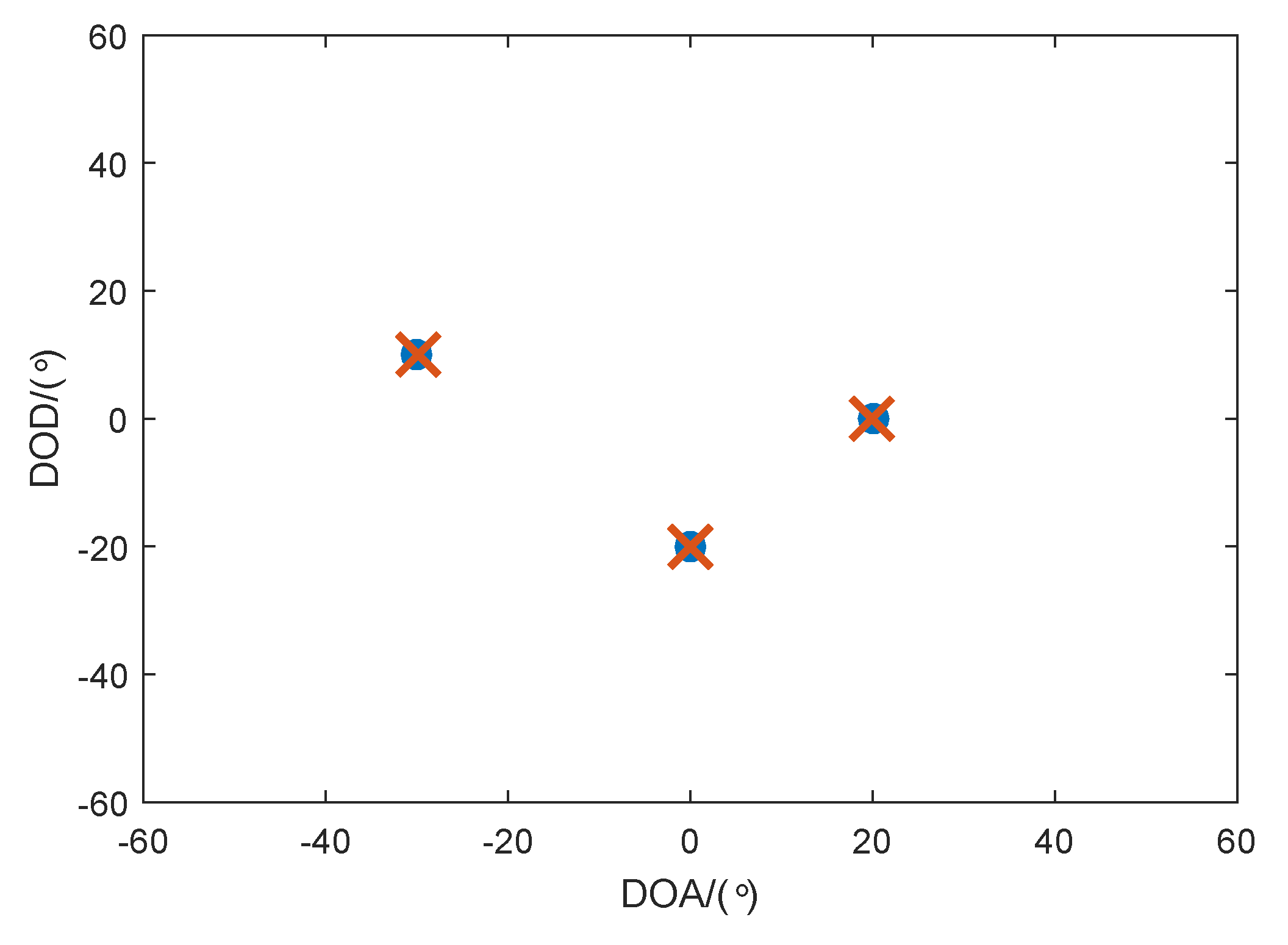
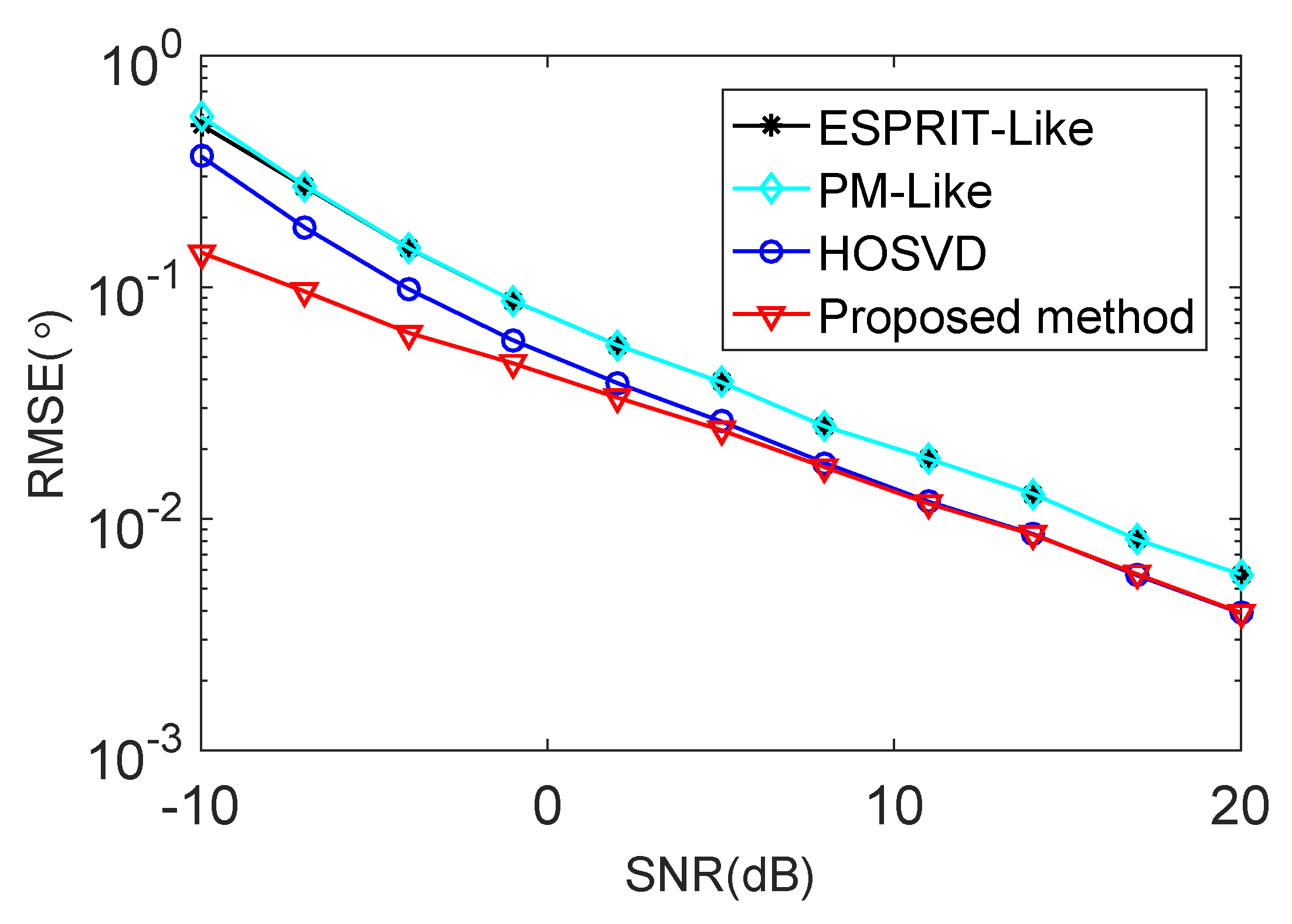
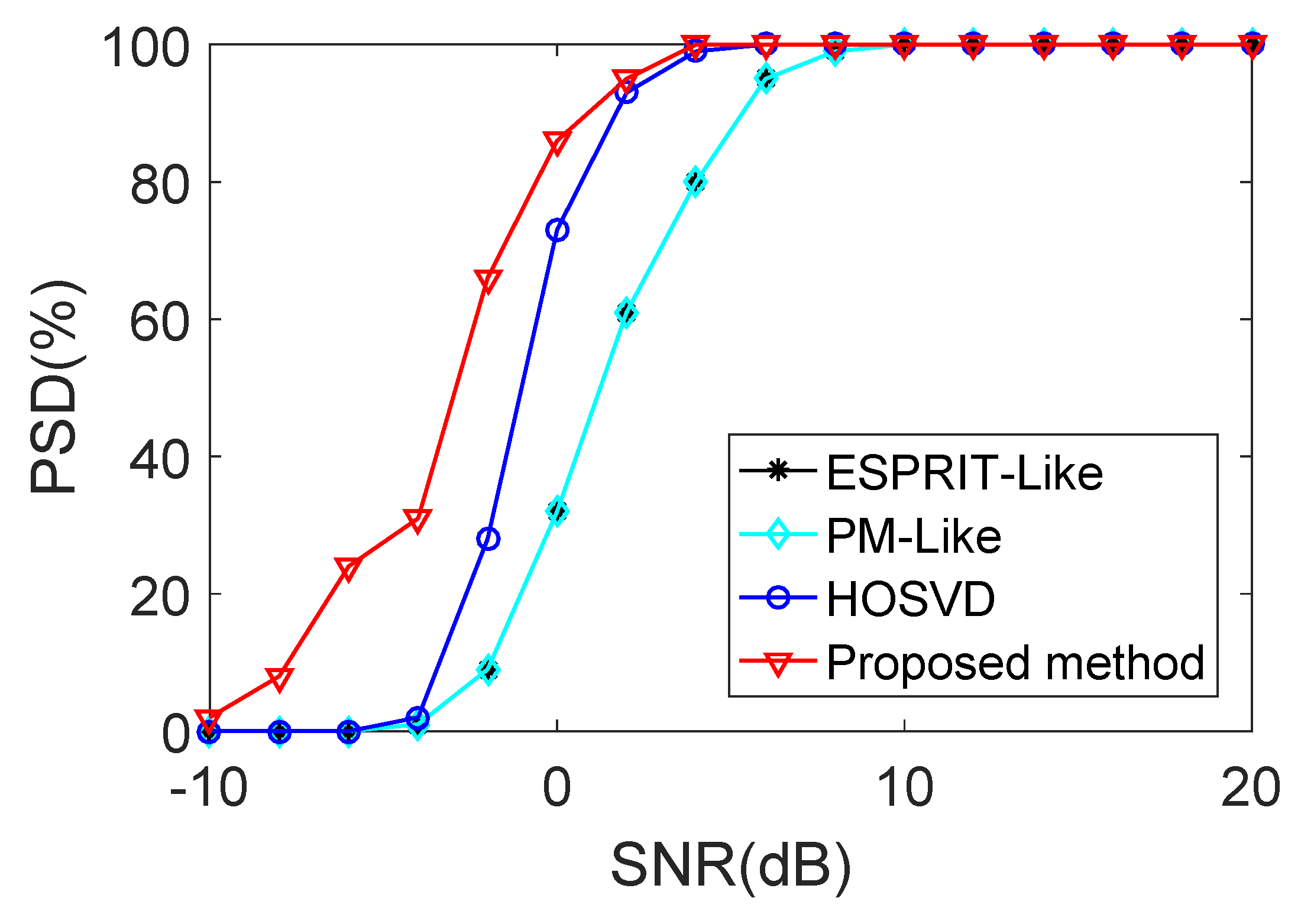
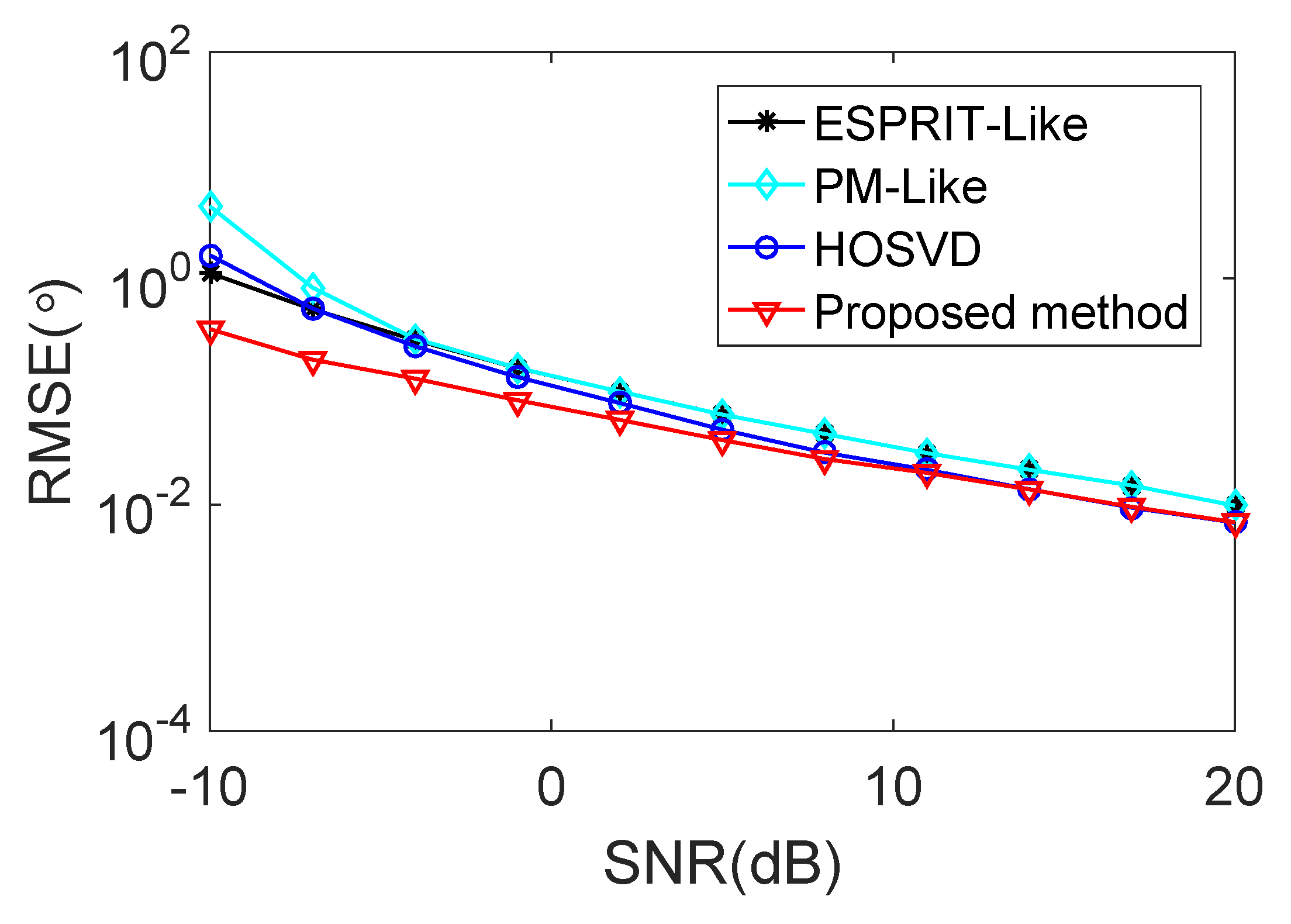
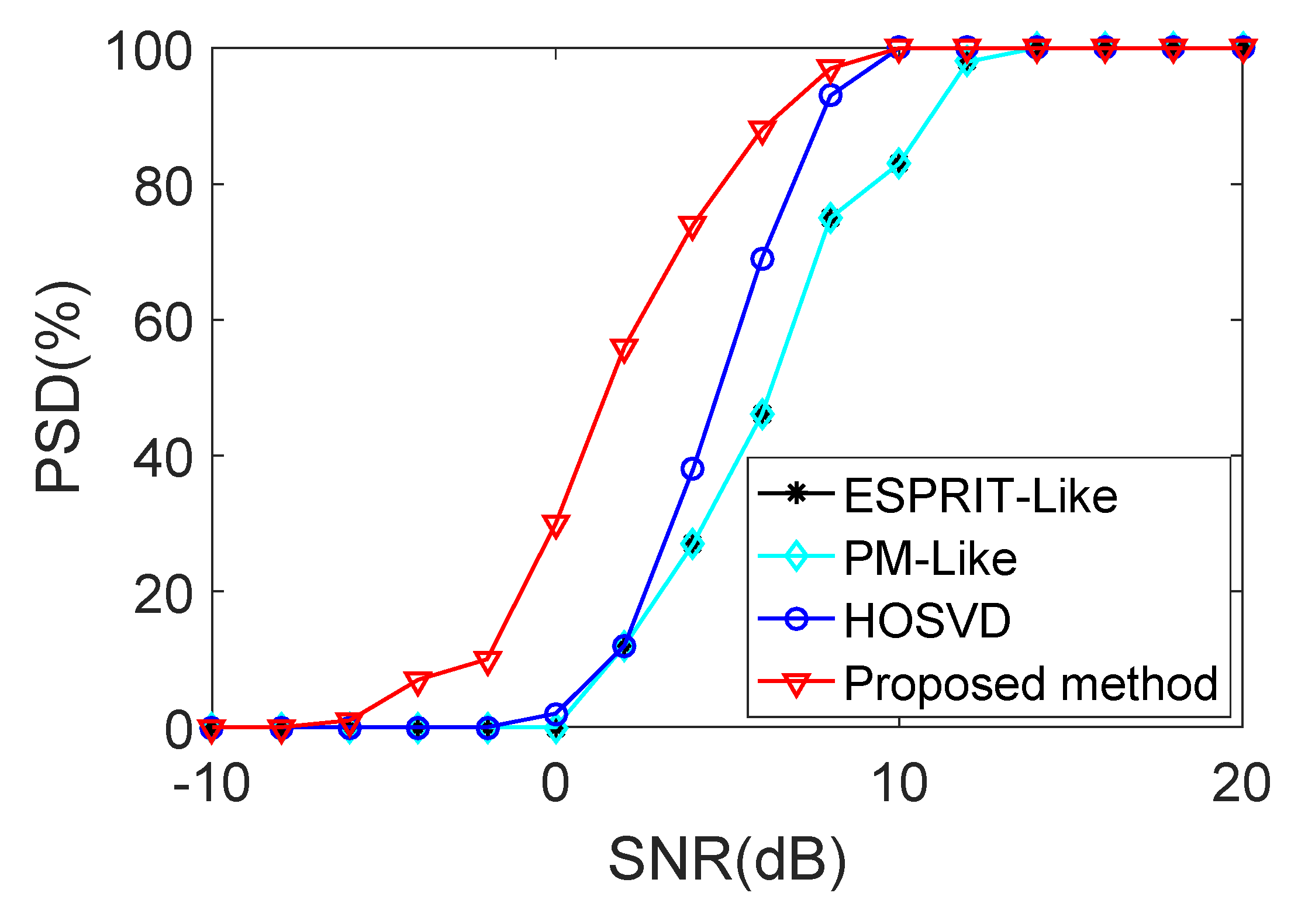
5. Simulation Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO radar: An idea whose time has come. In Proceedings of the IEEE Radar Conference, Philadelphia, PA, USA, 29 April 2004; pp. 71–78. [Google Scholar]
- Haimovich, A.; Blum, R.; Cimini, L. MIMO Radar with Widely Separated Antennas. IEEE Signal Process. Mag. 2008, 25, 116–129. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO Radar with Colocated Antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Yan, H.; Li, J.; Liao, G. Multitarget identification and localization using bistatic MIMO radar systems. EURASIP J. Adv. Signal Process. 2008, 2008, 48. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Xu, L.; Xu, D. Direction of departure (DOD) and direction of arrival (DOA) estimation in MIMO radar with reduced-dimension MUSIC. IEEE Commun. Lett. 2010, 14, 1161–1163. [Google Scholar] [CrossRef]
- Duofang, C.; Baixiao, C.; Guodong, Q. Angle estimation using ESPRIT in MIMO radar. Electron. Lett. 2008, 44, 770–771. [Google Scholar] [CrossRef]
- Chen, J.L.; Gu, H.; Su, W.M. Angle estimation using ESPRIT without pairing in MIMO radar. Electron. Lett. 2008, 44, 1422–1423. [Google Scholar]
- Zheng, Z.D.; Zhang, J.Y. Fast method for multi-target localisation in bistatic MIMO radar. Electron. Lett. 2011, 47, 138–139. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, H.; Li, J.; Xu, D. Computationally efficient DOD and DOA estimation for bistatic MIMO radar with propagator method. Int. J. Electron. 2012, 99, 1207–1221. [Google Scholar] [CrossRef]
- Xu, L.Y.; Wen, F.Q. Fast Noncircular 2D-DOA Estimation for Rectangular Planar Array. Sensors 2017, 17, 840. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, W.; Liu, J.; Li, X.; Wang, J. A sparse representation scheme for angle estimation in monostatic MIMO radar. Signal Process. 2014, 104, 258–263. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Li, X.; Bi, G. Nuclear Norm Minimization Framework for DOA Estimation in MIMO Radar. Signal Process. 2017, 135, 147–152. [Google Scholar] [CrossRef]
- Cheng, Y.; Yu, R.; Gu, H.; Su, W. Multi-SVD based subspace estimation to improve angle estimation accuracy in bistatic MIMO radar. Signal Process. 2013, 93, 2003–2009. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.; Xu, L.; Xu, D. Trilinear decomposition-based transmit angle and receive angle estimation for multiple-input multiple-output radar. Radar Sonar Navig. IET 2011, 5, 626–631. [Google Scholar] [CrossRef]
- Xu, B.; Zhao, Y.; Cheng, Z.; Li, H. A novel unitary PARAFAC method for DOD and DOA estimation in bistatic MIMO radar. Signal Process. 2017, 138, 273–279. [Google Scholar] [CrossRef]
- Boudaher, E.; Ahmad, F.; Amin, M.G.; Hoorfar, A. Mutual coupling effect and compensation in non-uniform arrays for direction-of-arrival estimation. Digit. Signal Process. 2017, 61, 3–14. [Google Scholar] [CrossRef]
- Liao, B.; Chan, S.C. A cumulant-based method for direction finding in uniform linear arrays with mutual coupling. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1717–1720. [Google Scholar] [CrossRef]
- Liao, B.; Chan, S. A cumulant-based approach for direction finding in the presence of mutual coupling. Signal Process. 2014, 104, 197–202. [Google Scholar] [CrossRef]
- Liao, B.; Zhang, Z.G.; Chan, S.C. DOA estimation and tracking of ULAs with mutual coupling. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 891–905. [Google Scholar] [CrossRef] [Green Version]
- Liao, B.; Huang, L.; Chan, S.C. DOA estimation under the coexistence of nonuniform noise and mutual coupling. In Proceedings of the 2015 IEEE China Summit and International Conference on Signal and Information Processing (ChinaSIP), Chengdu, China, 12–15 July 2015; pp. 731–735. [Google Scholar]
- Li, J.; Zhang, X. Joint angles and mutual coupling estimation algorithm for bistatic MIMO radar. Int. J. Antennas Propag. 2012, 2012, 921878. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, H.; Liao, B. Direction finding in MIMO radar with unknown mutual coupling. IEEE Access 2017, 5, 4439–4447. [Google Scholar] [CrossRef]
- Liu, X.; Liao, G. Direction finding and mutual coupling estimation for bistatic MIMO radar. Signal Process. 2012, 92, 517–522. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, J.; Zhang, J. Joint DOD and DOA estimation of bistatic MIMO radar in the presence of unknown mutual coupling. Signal Process. 2012, 92, 3039–3048. [Google Scholar] [CrossRef]
- Li, J.F.; Chen, W.Y.; Zhang, X.F. Angle Estimation for Bistatic MIMO Radar with Unknown Mutual Coupling Based on Improved Propagator Method. Appl. Mech. Mater. 2014, 513-517, 3029–3033. [Google Scholar] [CrossRef]
- Wang, X.; Wang, W.; Liu, J.; Liu, Q.; Wang, B. Tensor-based real-valued subspace approach for angle estimation in bistatic MIMO radar with unknown mutual coupling. Signal Process. 2015, 116, 152–158. [Google Scholar] [CrossRef]
- Wen, F.; Xiong, X.; Zhang, Z. Angle and mutual coupling estimation in bistatic MIMO radar based on PARAFAC decomposition. Digit. Signal Process. 2017, 65, 1–10. [Google Scholar] [CrossRef]
- Jin, M.; Liao, G.; Li, J. Joint DOD and DOA estimation for bistatic MIMO radar. Signal Process. 2009, 89, 244–251. [Google Scholar] [CrossRef]
- Chen, J.; Gu, H.; Su, W. A new method for joint DOD and DOA estimation in bistatic MIMO radar. Signal Process. 2010, 90, 714–718. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, J.K.; Wong, K.M. Joint DOD and DOA Estimation for Bistatic MIMO Radar in Unknown Correlated Noise. IEEE Trans. Veh. Technol. 2015, 64, 5113–5125. [Google Scholar] [CrossRef]
- Wang, X.; Wang, W.; Li, X.; Wang, J. A tensor-based subspace approach for bistatic MIMO radar in spatial colored noise. Sensors 2014, 14, 3897–3907. [Google Scholar] [CrossRef] [PubMed]
- Fu, W.; Su, T.; Zhao, Y.; He, X. Joint Estimation of Angle and Doppler Frequency for Bistatic MIMO Radar in Spatial Colored Noise Based on Temporal-spatial Structure. J. Electron. Inf. Technol. 2011, 33, 1649–1654. [Google Scholar] [CrossRef]
- Wen, F.; Xiong, X.; Su, J.; Zhang, Z. Angle estimation for bistatic MIMO radar in the presence of spatial colored noise. Signal Process. 2017, 134, 261–267. [Google Scholar] [CrossRef]
- Wen, F.; Zhang, Z.J.; Wang, K.; Sheng, G. A covariance differencing-based angle estimation method for bistatic MIMO radar in unknown colored noise. J. Eng. 2017, 1. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
| Method | Computational Complexity |
|---|---|
| ESPRIT-Like | |
| PM-Like | |
| HOSVD | |
| Proposed |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, X.; Xu, D.; Bi, G. Robust Angle Estimation for MIMO Radar with the Coexistence of Mutual Coupling and Colored Noise. Sensors 2018, 18, 832. https://doi.org/10.3390/s18030832
Wang J, Wang X, Xu D, Bi G. Robust Angle Estimation for MIMO Radar with the Coexistence of Mutual Coupling and Colored Noise. Sensors. 2018; 18(3):832. https://doi.org/10.3390/s18030832
Chicago/Turabian StyleWang, Junxiang, Xianpeng Wang, Dingjie Xu, and Guoan Bi. 2018. "Robust Angle Estimation for MIMO Radar with the Coexistence of Mutual Coupling and Colored Noise" Sensors 18, no. 3: 832. https://doi.org/10.3390/s18030832




