EDDA: An Efficient Distributed Data Replication Algorithm in VANETs
Abstract
:1. Introduction
1.1. Our Goal
1.2. Main Contributions
- (1)
- We apply graph theory to different scenarios in VANETs and divide the network into arbitrary graph, linear graph and complete graph. The cases of arbitrary graph and linear graph are discussed in this study. We propose a general system model for disseminating a bounded number of message copies in the network. Under this model, we develop EDDA, an efficient data replication algorithm that can be applied to both arbitrary graph and linear graph, in which the number of messages that can be replicated is limited and a network balanced status will be achieved.
- (2)
- We derive the theoretical analysis to obtain the approximate number of nodes that would receive the message when the system achieves an -balanced status. The convergence speed of the algorithm is also presented. As a special case of arbitrary graph, detailed analysis of the upper bound and lower bound for linear graph is provided, to show the efficiency of the proposed algorithm. The effectiveness of our algorithm has been validated by extensive simulations.
1.3. Paper Organization
2. Related Work
2.1. Data Dissemination Algorithms
2.2. Average Consensus Problem
3. Bounded Number of Data Replication in Message Passing
3.1. An Example
3.2. Definitions and Model
- In urban areas, due to fast speed of the vehicles, the network topology changes from time to time, so do the communication links. We can formalize this type of network topology as arbitrary graph.
- In the scenario of a highway, assume vehicles move at a constant velocity along the road and every vehicle has full knowledge of its neighbors right next to it. In this situation, the network topology can be seen as a special case of arbitrary graph, that is linear graph.
- Each node of G with satisfies .
- For every two nodes with , , and
- There is no edge between nodes of values and in G, respectively, such that and .
- A real average function is a mapping , such that for two numbers , if , or if .
- An integer average function is a mapping such that for two numbers , if , if , or if .
- For a list of numbers, define the potential of L to be .
- For an average function , define , where . Number b is considered a bar of length b. can be considered a small piece of length from the bar of length b to go down by . Function gives the potential change after an average operation (See Lemma 1).
- Let be an average function. Assume that is a list of numbers. It is transformed into another list by a series of average operations. Define its sum of the product to be (see Lemma 1), where H is the set of tuples that take average operations to transform the first list into the second list. It is considered as the change of the potential after taking a series of average operations.
3.3. Algorithm
- (1)
- First, EDDA constructs the graph and initializes the value of every vertex of graph G. In the initialization procedure (see algorithm 2), the vehicle node that carries the message will be assigned a value of n. All other nodes will be assigned a value of zero, which means they do not have the message.
- (2)
- Second, select independent edges from G so different pairs of nodes can communicate with each other in parallel. After the selection, replace the values of nodes with their new values by taking the average of the current values. Each stage should update the values of the nodes in the graph one time. Then, go to the next stage, and stop the average operations until the system is -balanced.
- (3)
- Third, EDDA outputs graph , with the final values of all nodes updated. If new nodes enter into the network and break the balance, the procedures will be executed again to achieve network balance.
3.4. Approximation
| Algorithm 1 Data replication algorithm. |
| Input: bounded message graph G (see Definition 2); parameter Output: Bounded message graph ; number of stages a 1: Call Algorithm 2; 2: Let ; 3: repeat 4: Select independent edges (disjoint pairs of G) with for ; 5: for to k do 6: ; 7: ; 8: ; 9: let and be the maximum and minimum value of G, respectively; 10: until ) 11: return a and graph with updated values; |
| Algorithm 2 Initialization. |
| Input: Graph G; parameter n Output: Weighted graph G with values 1: Let denote the nodes in graph G; 2: Let () denote the node that carries message M; 3: Let denote the assigned value of node ; 4: ; 5: for to m do 6: ; |
4. Speed of Convergence on Arbitrary Graph and Linear Graph
4.1. Arbitrary Graph
- 1.
- A node with a weight of at least can take the average with a node with weight zero, and
- 2.
- two nodes with a weight of at least w can take the average.
4.2. Upper Bound for Linear Graph
4.3. Lower Bound for Linear Graph
- Either or ,
- Integer j is the least, and ( or ).
5. Performance Evaluation
5.1. Simulation Setup
5.2. Performance Metrics
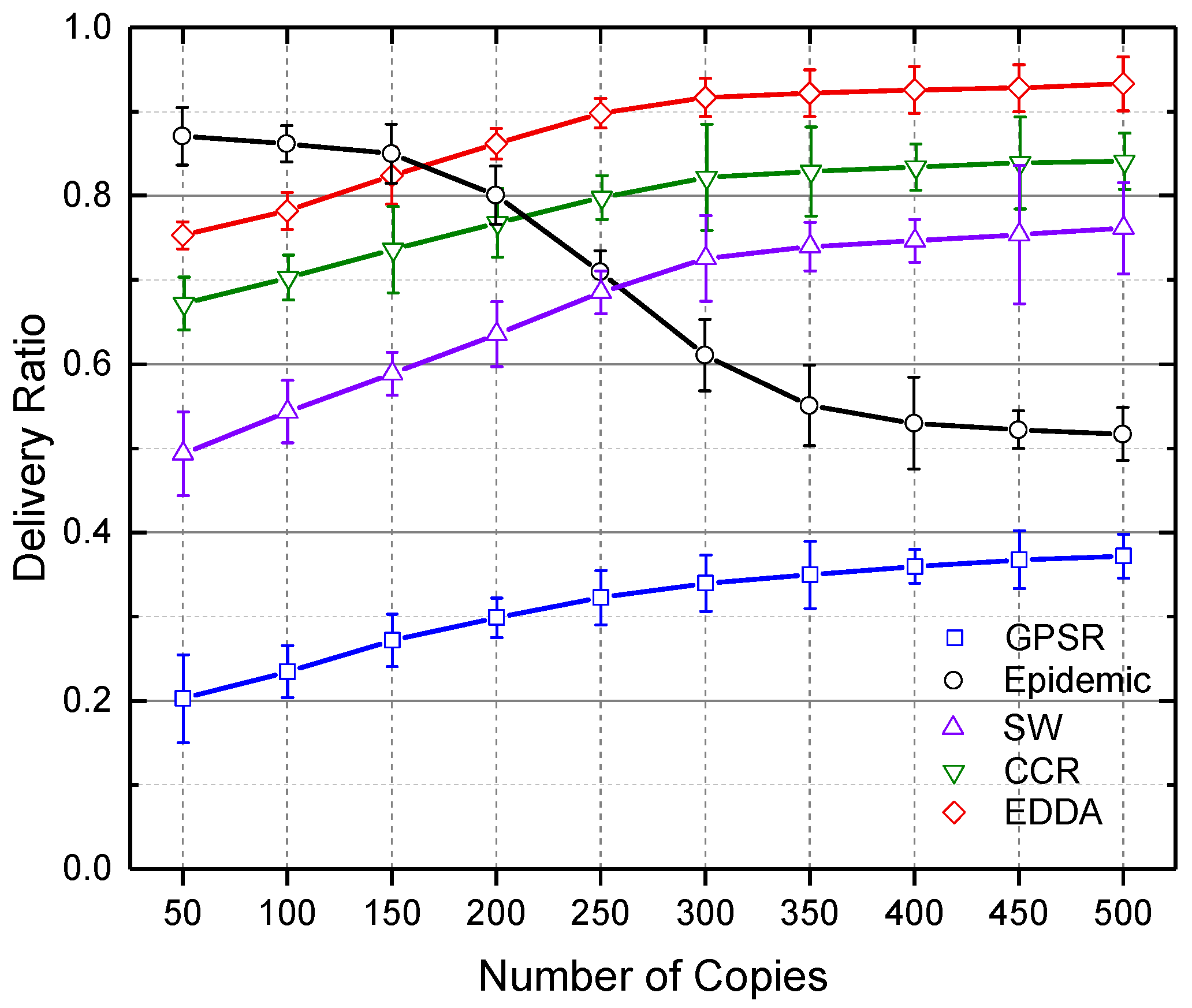
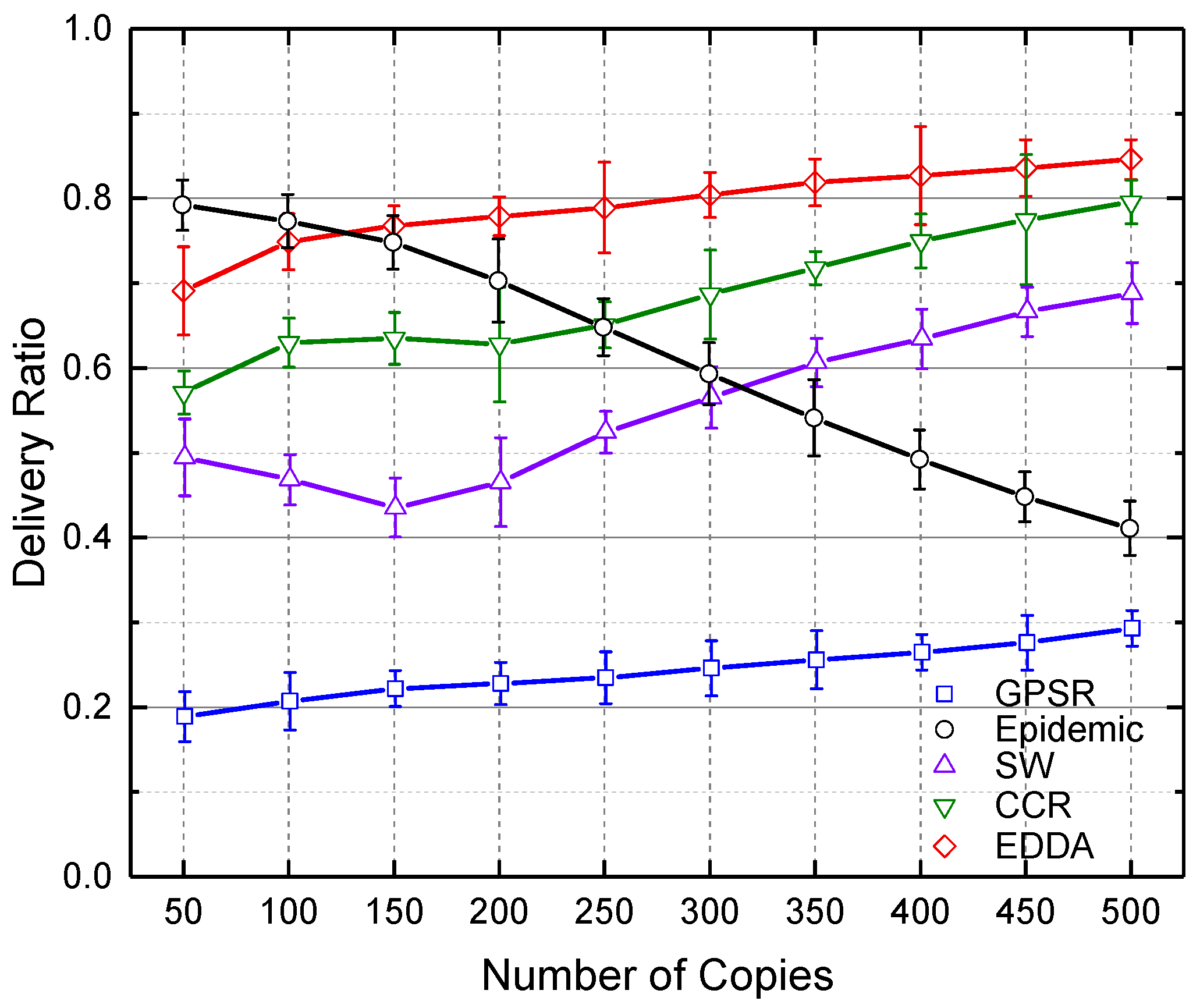
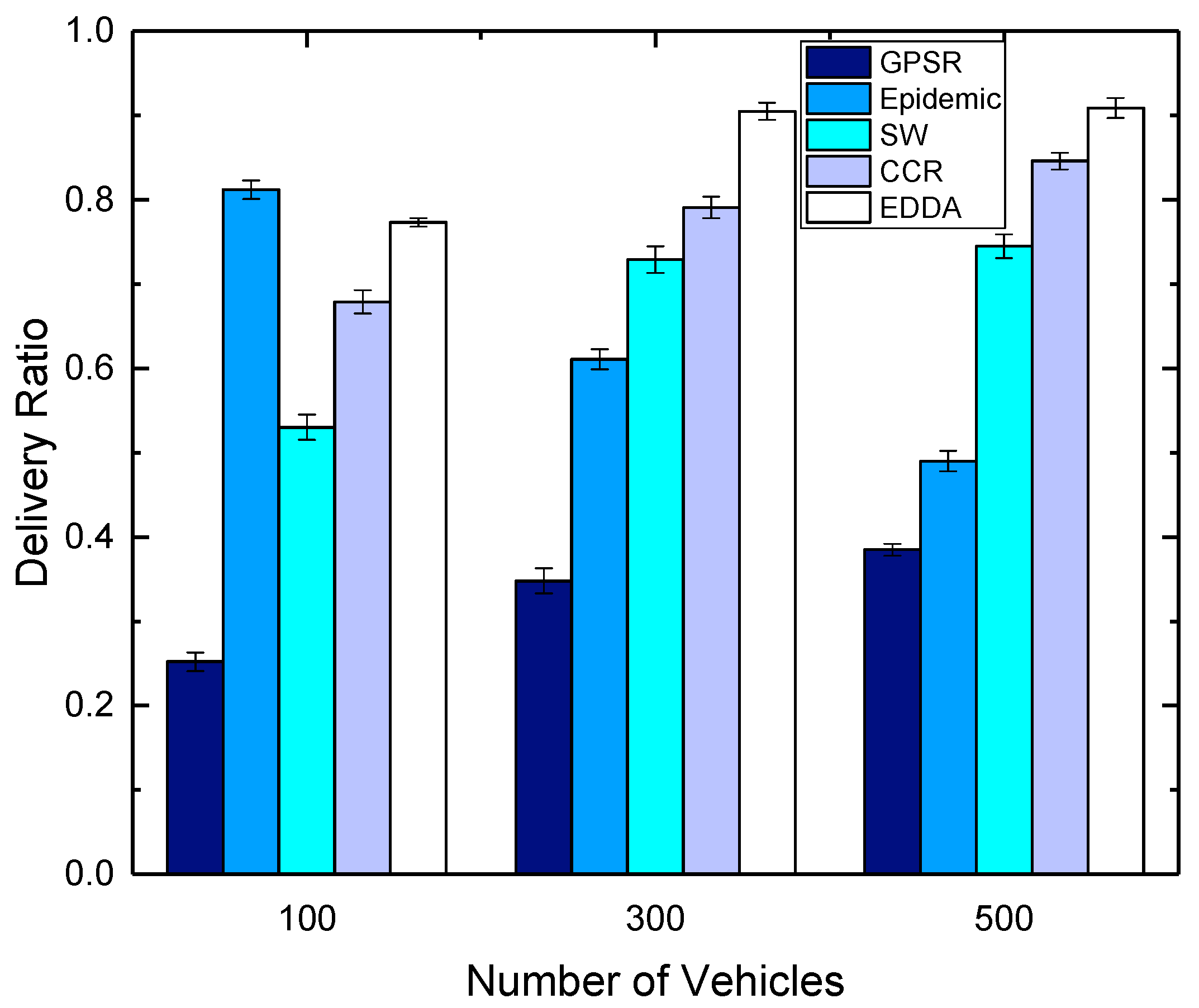
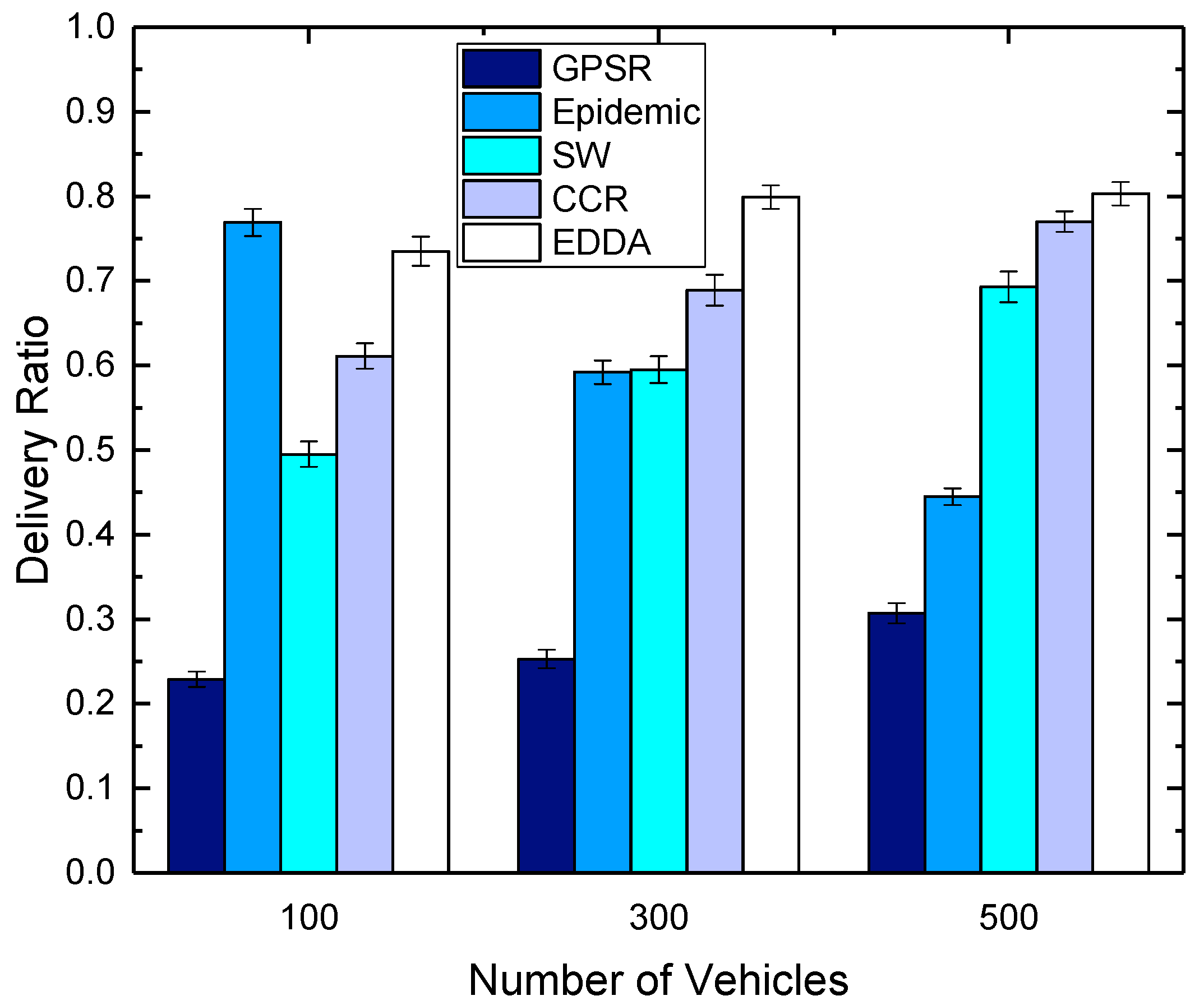
5.3. Data Delivery Ratio
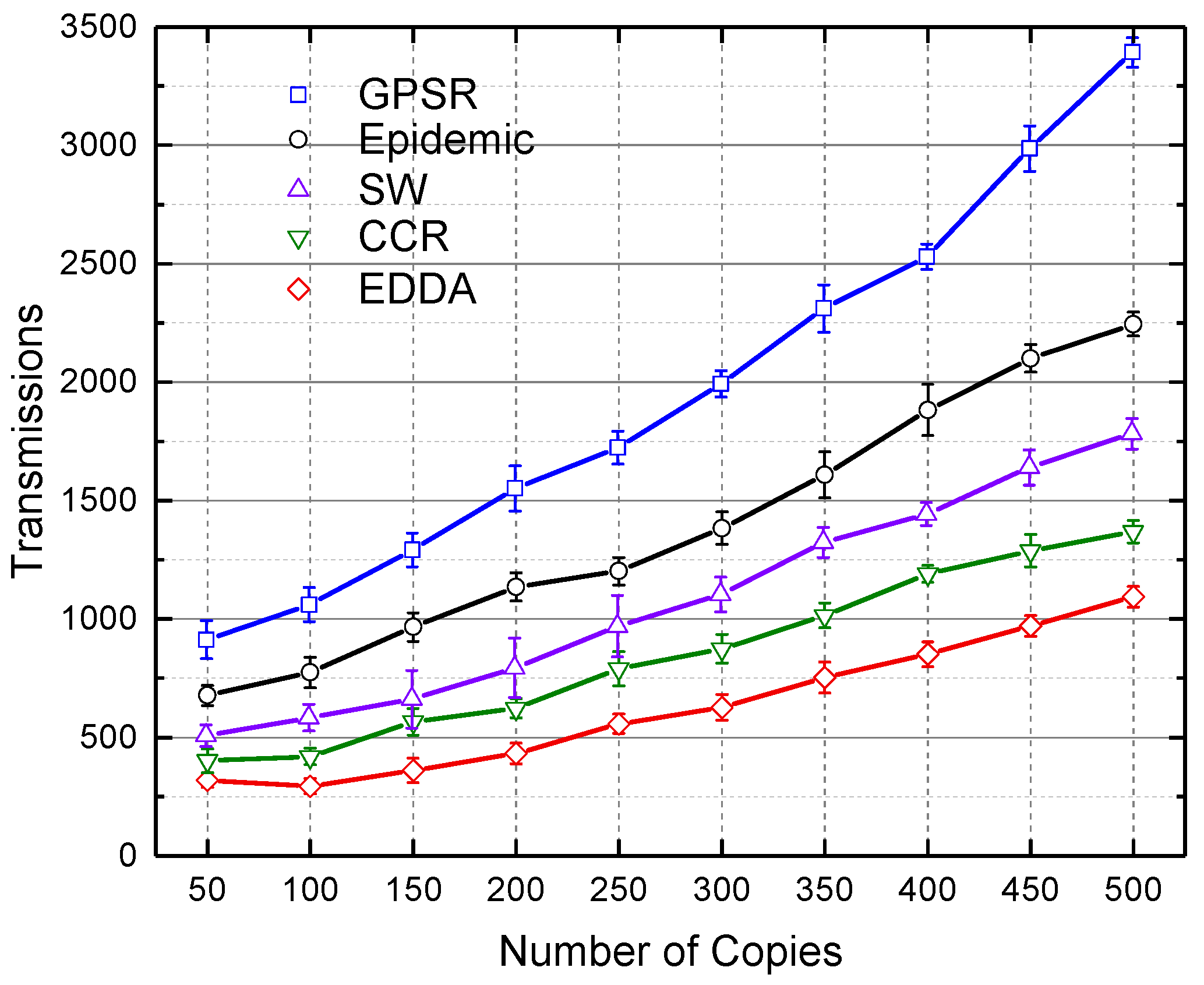
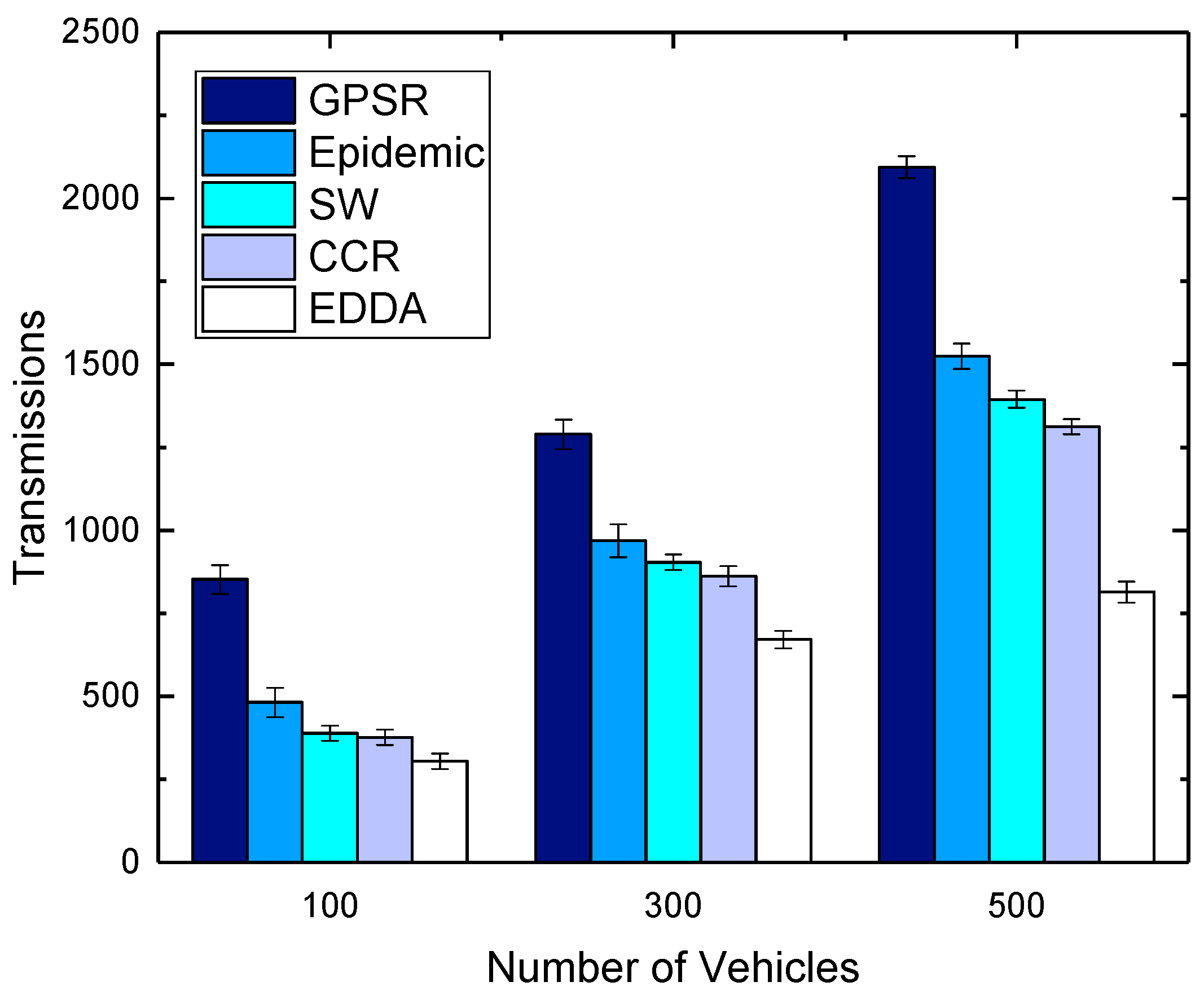
5.4. Transmissions
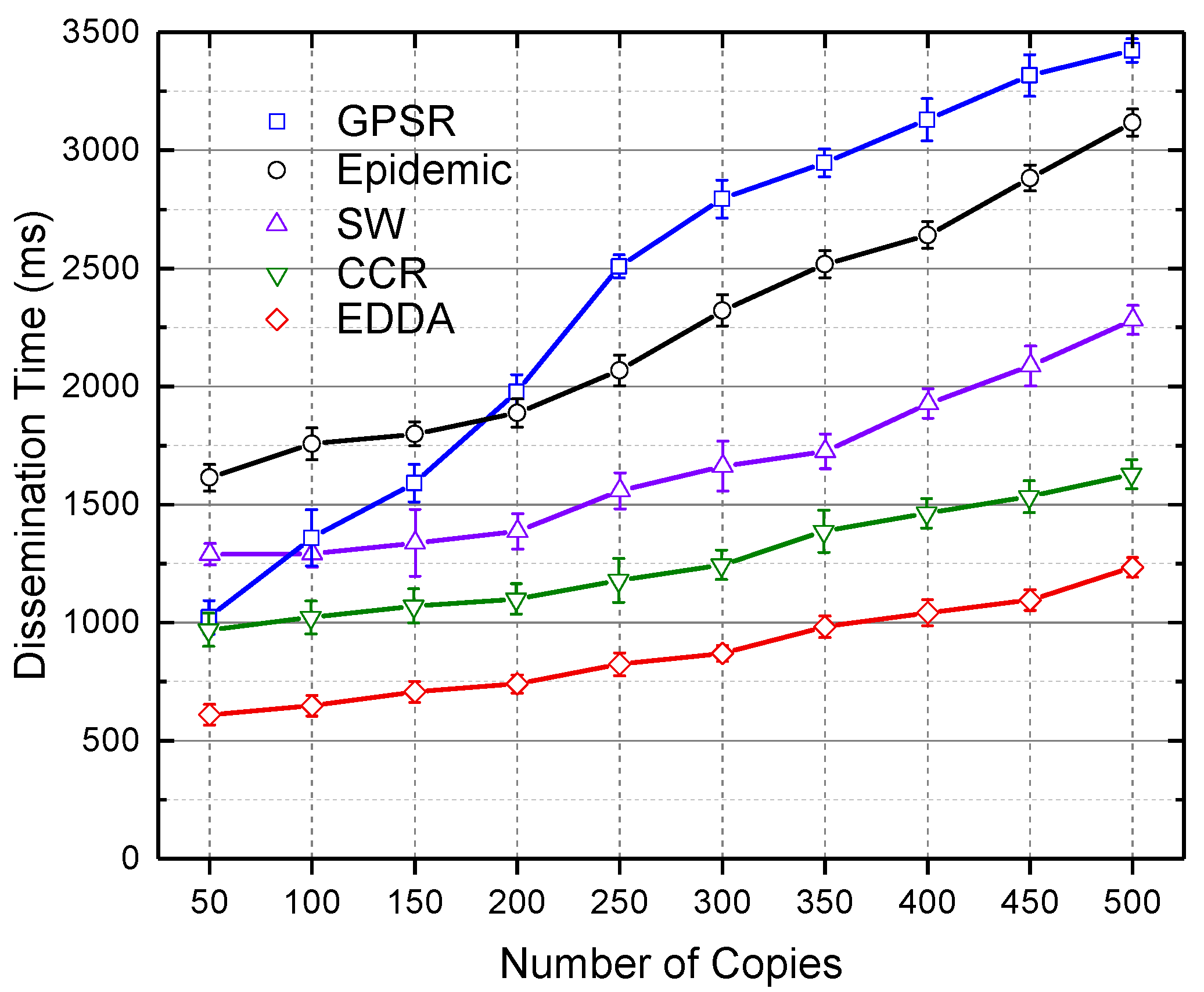
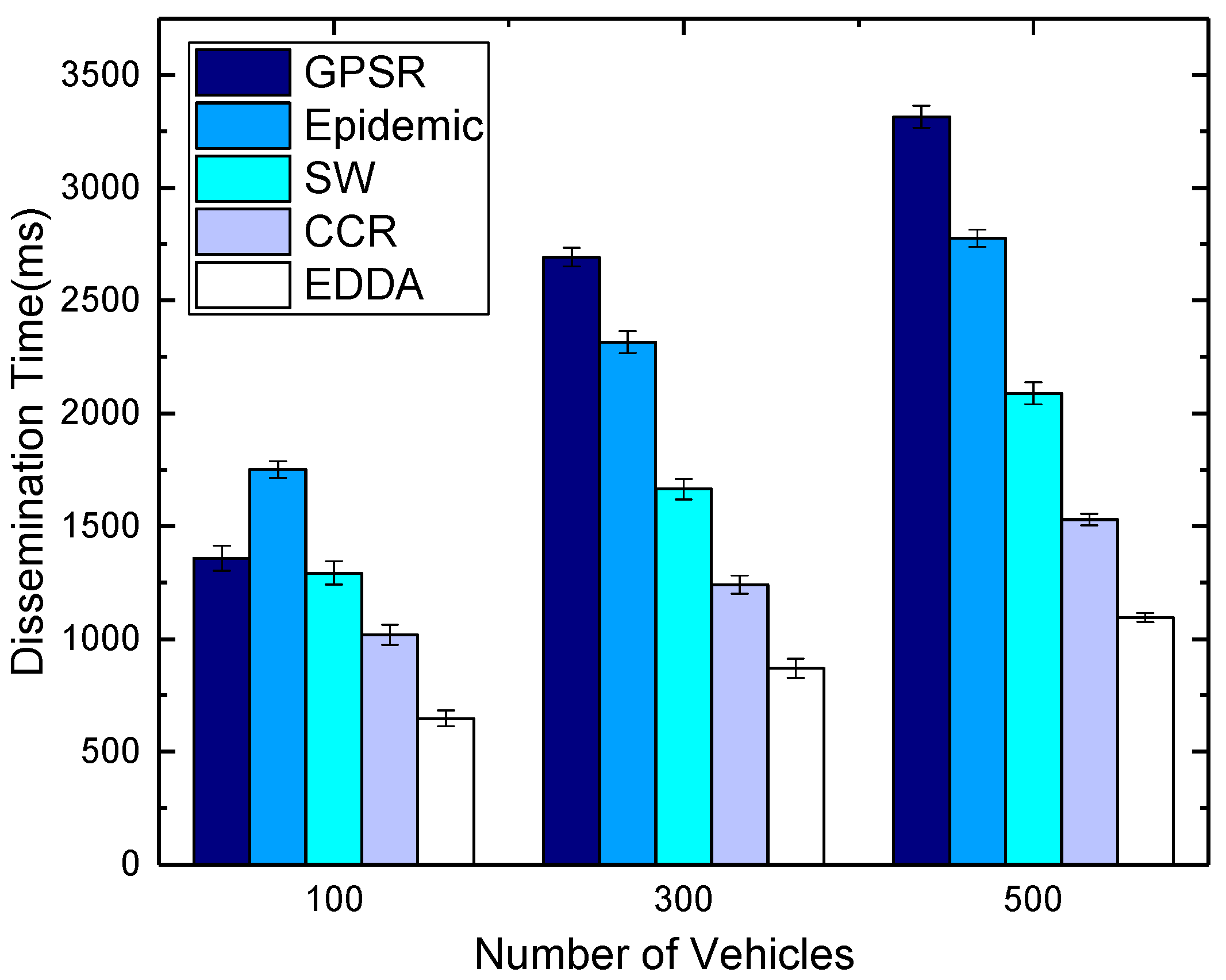
5.5. Data Dissemination Delay
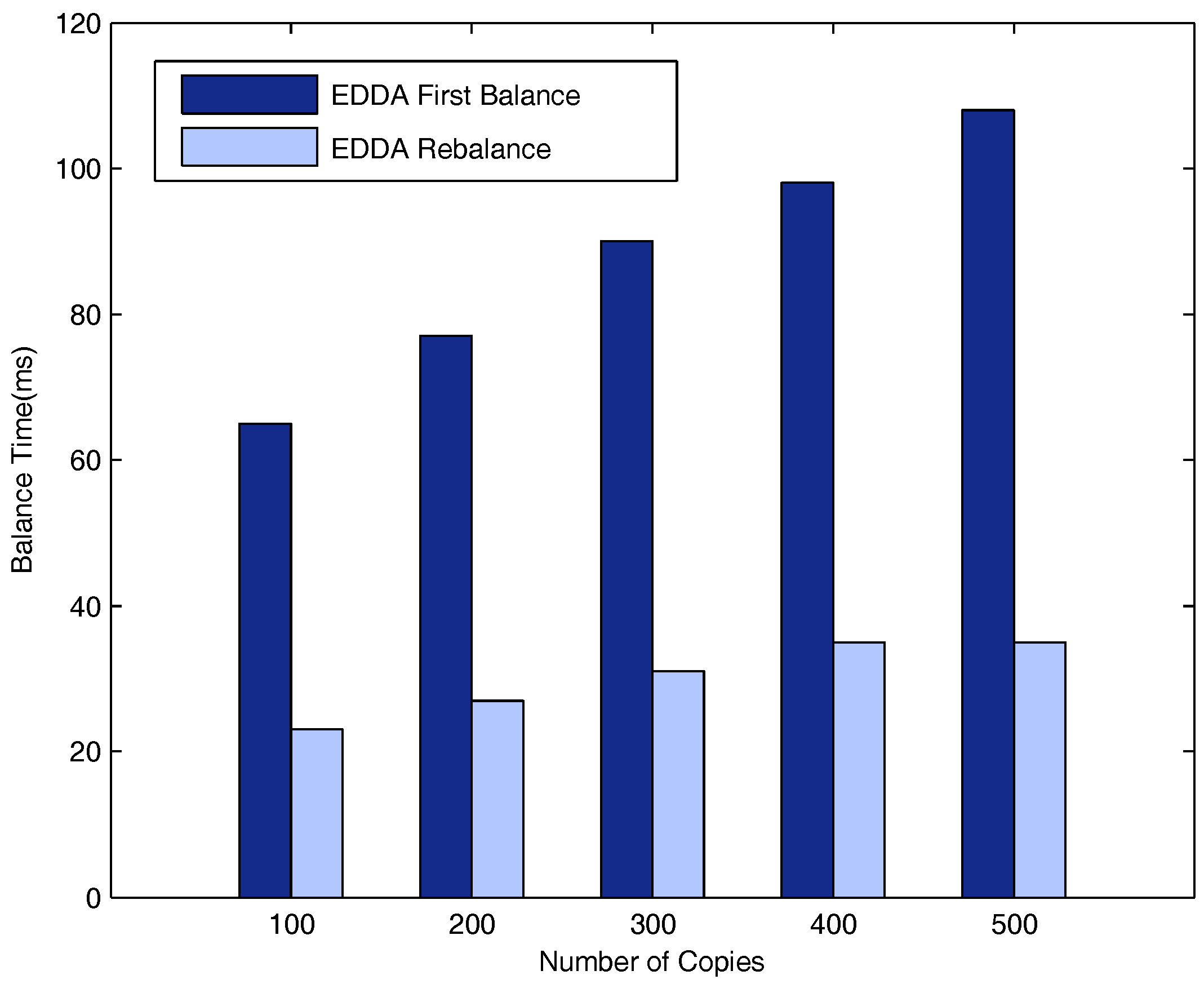
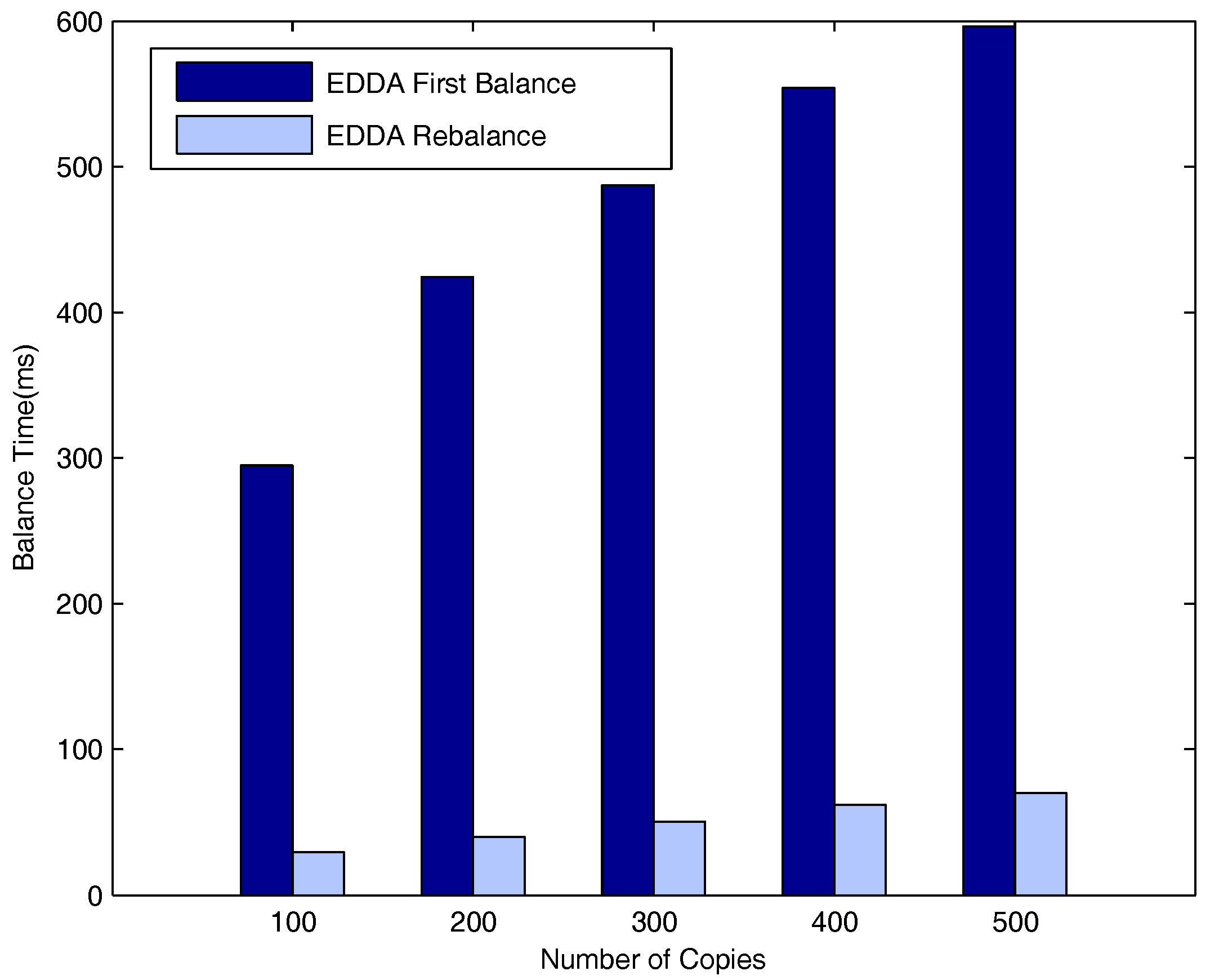
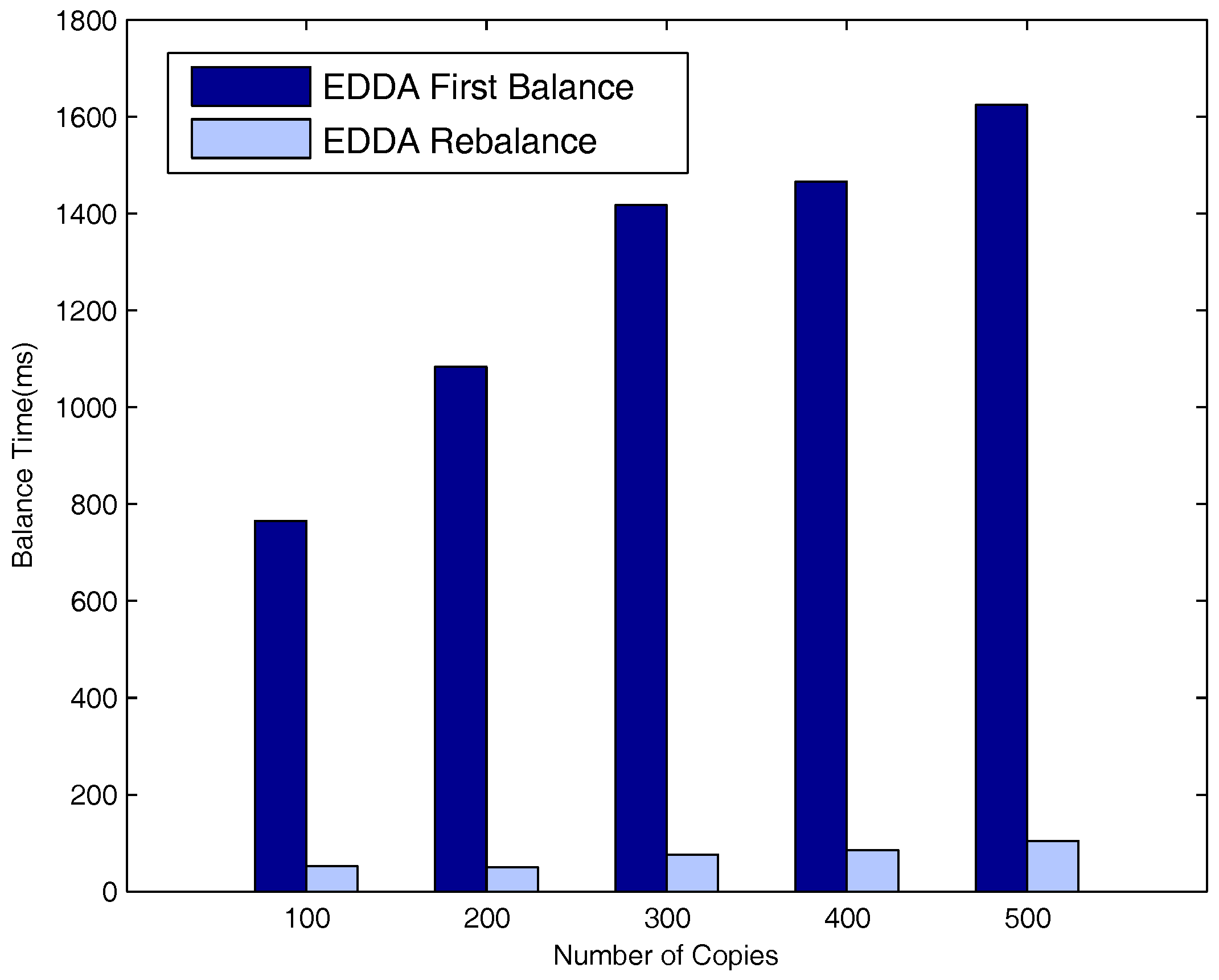
5.6. Evaluation of Network Balance on the Highway
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| VANETs | Vehicular ad-hoc networks |
| V2V | Vehicle-to-vehicle |
| RSU | Road side unit |
| EDDA | Efficient distributed data replication algorithm |
References
- Cunha, F.; Villas, L.; Boukerche, A.; Maia, G.; Viana, A.; Mini, R.A.F.; Loureiro, A.A.F. Data communication in VANETs: Protocols, applications and challenges. Ad Hoc Netw. 2016, 44, 104–117. [Google Scholar] [CrossRef]
- Mukherjee, J.C.; Gupta, A.; Sreenivas, R.C. Event Notification in VANET With Capacitated Roadside Units. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1867–1879. [Google Scholar] [CrossRef]
- Said, A.M.; Marot, M.; Ibrahim, A.W.; Afifi, H. Modeling interactive real-time applications in VANETs with performance evaluation. Comput. Netw. 2016, 104, 66–78. [Google Scholar] [CrossRef]
- Hu, M.; Zhong, Z.; Ni, M.; Wang, Z.; Xie, W.; Qiao, X. Integrity-oriented Content Offloading in Vehicular Sensor Network. IEEE Access. 2017, 5, 4140–4153. [Google Scholar] [CrossRef]
- Kosch, T. Local danger warning based on vehicle ad-hoc networks: Prototype and simulation. In Proceedings of the First International Workshop on Intelligent Transportation (WIT), Paderborn, Germany, 5–8 July 2016. [Google Scholar]
- Nandan, A.; Das, S.; Zhou, B.; Pau, G.; Gerla, M. Adtorrent: Digital billboards for vehicular networks. In Proceedings of the IEEE/ACM International Workshop on Vehicle-to-Vehicle Communications(V2VCOM), San Diego, CA, USA, July 2005; pp. 286–294. [Google Scholar]
- Kangasharju, J.; Heinemann, A. Incentives for electronic coupon systems. In Proceedings of the International Workshop on Decentralized Resource Sharing in Mobile Computing and Networking, Los Angeles, CA, USA, 25 July 2006; pp. 60–62. [Google Scholar] [CrossRef]
- Lee, U.; Park, J.S.; Amir, E.; Gerla, M. FleaNet: A Virtual Market Place on Vehicular Networks. IEEE Trans. Veh. Technol. 2010, 59, 344–355. [Google Scholar] [CrossRef]
- Liu, F.; Chen, Z.; Xia, B. Data Dissemination With Network Coding in Two-Way Vehicle-to-Vehicle Networks. IEEE Trans. Veh. Technol. 2016, 65, 2445–2456. [Google Scholar] [CrossRef]
- He, J.; Cai, L.; Cheng, P.; Pan, J. Delay Minimization for Data Dissemination in Large-Scale VANETs with Buses and Taxis. IEEE Trans. Mob. Comput. 2016, 15, 1939–1950. [Google Scholar] [CrossRef]
- Wu, Y.C.; Zhu, Y.; Zhu, H.; Li, B. CCR: Capacity-constrained replication for data delivery in vehicular networks. In Proceedings of the 2013 IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2580–2588. [Google Scholar]
- Janech, J.; Lieskovsky, A.; Krsak, E. Comparation of strategies for data replication in VANET environment. In Proceedings of the International Conference on Advanced Information Networking and Applications Workshops, Fukuoka, Japan, 26–29 March 2012; Volume 26, pp. 575–580. [Google Scholar] [CrossRef]
- Rajagopalan, S.; Shah, D. Distributed averaging in dynamic networks. IEEE J. Sel. Top. Signal Process. 2011, 5, 845–854. [Google Scholar] [CrossRef]
- Hadjicostis, C.N.; Vaidya, N.H.; Domínguez-García, A.D. Robust distributed average consensus via exchange of running sums. IEEE Trans. Autom. Control. 2016, 61, 1492–1507. [Google Scholar] [CrossRef]
- Dimakis, A.G.; Sarwate, A.D.; Wainwright, M.J. Geographic gossip: Efficient aggregation for sensor networks. In Proceedings of the ACM International Conference on Information Processing in Sensor Networks, Nashville, TN, USA, 19–21 April 2006; pp. 69–76. [Google Scholar] [CrossRef]
- Xing, M.; He, J.; Cai, L. Utility Maximization for Multimedia Data Dissemination in Large-Scale VANETs. IEEE Trans. Mob. Comput. 2017, 16, 1188–1198. [Google Scholar] [CrossRef]
- Hajlaoui, R.; Guyennet, H.; Moulahi, T. A Survey on Heuristic-Based Routing Methods in Vehicular Ad-Hoc Network: Technical Challenges and Future Trends. IEEE Sens. J. 2016, 16, 6782–6792. [Google Scholar] [CrossRef]
- Ye, F.; Roy, S.; Wang, H. Efficient Data Dissemination in Vehicular Ad Hoc Networks. IEEE J. Sel. Areas Commun. 2012, 30, 769–779. [Google Scholar] [CrossRef]
- Wu, C.; Chen, X.; Ji, Y.; Ohzahata, S.; Ji, Y. Efficient Broadcasting in VANETs Using Dynamic Backbone and Network Coding. IEEE Trans Wirel. Commun. 2015, 14, 6057–6071. [Google Scholar] [CrossRef]
- Torres, A.; Calafate, C.T.; Cano, J.C.; Manzoni, P.; Ji, Y. Evaluation of flooding schemes for real-time video transmission in VANETs. Ad Hoc Netw. 2015, 24, 3–20. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, C.; Yao, S.; Zhang, W.X.; Ge, X.H.; Mao, G.Q. Delay Performance of Network-Coding-Based Epidemic Routing. IEEE Trans. Veh. Technol. 2016, 65, 3676–3684. [Google Scholar] [CrossRef]
- Taherkhani, N.; Pierre, S. Prioritizing and scheduling messages for congestion control in vehicular ad hoc networks. Comput. Netw. 2016, 108, 15–28. [Google Scholar] [CrossRef]
- Goonewardene, R.T.; Ali, F.H.; Stipidis, E. Robust mobility adaptive clustering scheme with support for geographic routing for vehicular ad hoc networks. IET Intell. Transp. Syst. 2009, 3, 148–158. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.Y.; Zhang, W.; Hu, Y.Q. A New Cluster Based Routing Protocol for VANET. In Proceedings of the Second International Conference on Networks Security, Wireless Communications and Trusted Computing, Wuhan, China, 24–25 April 2010; pp. 176–180. [Google Scholar] [CrossRef]
- Ohta, Y.; Ohta, T.; Kakuda, Y. An autonomous clustering based data transfer scheme using positions and moving direction of vehicles for VANETs. In Proceedings of the 2012 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 1–4 April 2012; pp. 2900–2904. [Google Scholar] [CrossRef]
- Lin, D.; Kang, J.; Squicciarini, A.; Wu, Y.J.; Gurung, S.; Tonguz, O. MoZo: A Moving Zone Based Routing Protocol Using Pure V2V Communication in VANETs. IEEE Trans. Mob. Comput. 2017, 16, 1357–1370. [Google Scholar] [CrossRef]
- Kumer, N.; Rodrigues, J.; Lloret, J. Replication-aware data dissemination for vehicular ad hoc networks using location determine. Mob. Netw. Appl. 2015, 20, 251–267. [Google Scholar] [CrossRef]
- Bi, Y.G.; Shan, H.G.; Shen, X.M.; Wang, N.; Zhao, H. A multi-hop broadcast protocol for emergency message dissemination in urban vehicular ad hoc networks. IEEE Trans. Intell. Transport. Syst. 2016, 17, 736–750. [Google Scholar] [CrossRef]
- Rivoirard, L.; Wahl, M.; Sondi, P.; Berbineau, M.; Gruyer, D. Chain-Branch-Leaf: A Clustering Scheme for Vehicular Networks Using Only V2V Communications. Ad Hoc Netw. 2017, 68, 70–84. [Google Scholar] [CrossRef]
- Nilsson, M.; Gustafson, C.; Abbas, T.; Tufvesson, F. A Measurement-Based Multilink Shadowing Model for V2V Network Simulations of Highway Scenarios. IEEE Trans. Veh. Techonol. 2017, 66, 8632–8643. [Google Scholar] [CrossRef]
- Basheer, H.S.; Bassil, C. A review of broadcasting safety data in V2V: Weaknesses and requirements. Ad Hoc Netw. 2017, 65, 13–25. [Google Scholar] [CrossRef]
- Vahdat, A.; Becker, D. Epidemic routing for partially connected ad hoc networks. Master’s Thesis, University of Kansas, Lawrence, KS, USA, 2000; pp. 1–14. [Google Scholar]
- Lindgren, A.; Doria, A.; Scheln, O. Probabilistic routing in intermittently connected networks. In Proceedings of the Fourth ACM International Symposium on Mobile Ad Hoc Networking and Computing, New York, NY, USA, 2003; Volume 7, pp. 19–20. [Google Scholar] [CrossRef]
- Burgess, J.; Gallagher, B.; Jensen, D.; Levine, N.B. MaxProp: Routing for vehicle-based disruption-tolerant networks. In Proceedings of the 25TH IEEE International Conference on Computer Communications, IEEE INFOCOM 2006, Barcelona, Spain, 23–29 April 2006. [Google Scholar] [CrossRef]
- Spyropoulos, T.; Psounis, K.; Raghavendra, C.S. Efficient routing in intermittently connected mobile networks: The multiple-copy case. IEEE/ACM Trans. Netw. 2008, 16, 77–90. [Google Scholar] [CrossRef]
- Balasubramanian, A.; Levine, B.N.; Venkataramani, A. Replication routing in DTNs: A resource allocation approach. IEEE/ACM Trans. Netw. 2010, 18, 596–609. [Google Scholar] [CrossRef]
- Akabane, A.T.; Villas, L.A.; Madeira, E.R.M. An adaptive solution for data dissemination under diverse road traffic conditions in urban scenarios. In Proceedings of the IEEE Wireless Communications and Networking Conference, New Orleans, LA, USA, 9–12 March 2015; pp. 1654–1659. [Google Scholar] [CrossRef]
- Yan, T.; Zhang, W.S.; Wang, G.L. DOVE: Data dissemination to a desired number of receivers in VANET. IEEE Trans. Veh. Technol. 2014, 63, 1903–1916. [Google Scholar] [CrossRef]
- Takahashi, A.; Nishiyama, H.; Kato, N.; Nakahira, K.; Sugiyama, T. Replication control for ensuring reliability of convergecast message delivery in infrastructure-aided dtns. IEEE Trans. Veh. Technol. 2014, 63, 3223–3231. [Google Scholar] [CrossRef]
- Li, W.F.; Ma, X.M.; Wu, J.; Trivedi, K.S.; Huang, X.L.; Liu, Q.W. Analytical Model and Performance evaluation of Long Term Evolution for vehicle Safety Services. IEEE Trans. Veh. Technol. 2017, 66, 1926–1939. [Google Scholar] [CrossRef]
- Li, P.; Huang, C.; Liu, Q. BCDP: Budget constrained and delay-bounded placement for hybrid roadside units in vehicular ad hoc networks. Sensors 2014, 14, 22564–22594. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Mao, G.; Li, C.; Liang, W.; Zhang, D. Capacity of Cooperative Vehicular Networks with Infrastructure Support: Multi-user Case. IEEE Trans. Veh. Technol. 2017. [Google Scholar] [CrossRef]
- Li, G.; Boukhatem, L.; Wu, J. Adaptive Quality-of-Service-Based Routing for Vehicular Ad Hoc Networks With Ant Colony Optimization. IEEE Trans. Veh. Technol. 2016, 66, 3249–3264. [Google Scholar] [CrossRef]
- Tsitsiklis, J.N. Problems in decentralized decision making and computation. Ph.D. Thesis, Massachusetts Institute of Technology, Boston, MA, USA, 1984. [Google Scholar]
- Carlia, R.; Fagnanib, F. Communication constraints in the average consensus problem. Automatica 2008, 44, 671–684. [Google Scholar] [CrossRef]
- Hadjicostis, C.N.; Charalambous, T. Average consensus in the presence of delays in directed graph topologies. IEEE Trans. Autom. Control. 2014, 59, 763–768. [Google Scholar] [CrossRef]
- Nedic, A.; Olshevsky, A.; Ozdaglar, A.; Tsitsiklis, J.N. On Distributed Averaging Algorithms and Quantization Effects. IEEE Trans. Autom. Control. 2009, 54, 2506–2517. [Google Scholar] [CrossRef]
- Khosravi, A.; Kavian, Y.S. Broadcast Gossip Ratio Consensus: Asynchronous Distributed Averaging in Strongly Connected Networks. IEEE Trans. Signal Process. 2017, 65, 119–129. [Google Scholar] [CrossRef]
- Nedić, A.; Ozdaglar, A. Convergence rate for consensus with delays. J. Glob. Optim. 2010, 47, 437–456. [Google Scholar] [CrossRef]
- Fagnani, F.; Zampieri, S. Randomized consensus algorithms over large scale networks. IEEE J. Sel. Areas Commun. 2008, 26, 634–649. [Google Scholar] [CrossRef]
- Aysal, T.C.; Yildiz, M.E.; Sarwate, A.D.; Scaglione, A. Broadcast Gossip Algorithms for Consensus. IEEE Trans. Signal Process. 2009, 57, 2748–2761. [Google Scholar] [CrossRef]
- Boyd, S.; Ghosh, A.; Prabhakar, B.; Shah, D. Randomized gossip algorithms. IEEE Trans. Inf. Theory 2006, 52, 2508–2530. [Google Scholar] [CrossRef]
- Wu, S.C.; Rabbat, M.G. Broadcast Gossip Algorithms for Consensus on Strongly Connected Digraphs. IEEE Trans. Signal Process. 2013, 61, 3959–3971. [Google Scholar] [CrossRef]
- Nedić, A.; Ozdaglar, A.; Parrilo, P.A. Constrained Consensus and Optimization in Multi-Agent Networks. IEEE Trans. Autom. Control. 2010, 55, 922–938. [Google Scholar] [CrossRef]
- Nedić, A.; Liu, J. On Convergence Rate of Weighted-Averaging Dynamics for Consensus Problems. IEEE Trans. Autom. Control. 2017, 62, 766–781. [Google Scholar] [CrossRef]
- Shi, G.D.; Li, B.; Johansson, M.; Johansson, K.H. Finite-Time Convergent Gossiping. IEEE/ACM Trans. Netw. 2016, 24, 2782–2794. [Google Scholar] [CrossRef]
- Haklay, M.; Weber, P. OpenStreetMap: User-Generated Street Maps. IEEE Pervasive Comput. 2008, 7, 12–18. [Google Scholar] [CrossRef]
- SUMO-Simulation of Urban Mobility. Available online: http://sumo.sourceforge.net (accessed on 1 January 2001).





| Parameter | Value |
|---|---|
| Simulation area | 2000 m × 2000 m |
| Simulation time | 1 h |
| Vehicle communication range | 300 m |
| Vehicle velocity | [30, 120] km/h |
| Number of Vehicles | 100, 300, 500 |
| Number of message copies | [50, 500] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Huang, C.; Fan, X.; Guo, S.; Fu, B. EDDA: An Efficient Distributed Data Replication Algorithm in VANETs. Sensors 2018, 18, 547. https://doi.org/10.3390/s18020547
Zhu J, Huang C, Fan X, Guo S, Fu B. EDDA: An Efficient Distributed Data Replication Algorithm in VANETs. Sensors. 2018; 18(2):547. https://doi.org/10.3390/s18020547
Chicago/Turabian StyleZhu, Junyu, Chuanhe Huang, Xiying Fan, Sipei Guo, and Bin Fu. 2018. "EDDA: An Efficient Distributed Data Replication Algorithm in VANETs" Sensors 18, no. 2: 547. https://doi.org/10.3390/s18020547
APA StyleZhu, J., Huang, C., Fan, X., Guo, S., & Fu, B. (2018). EDDA: An Efficient Distributed Data Replication Algorithm in VANETs. Sensors, 18(2), 547. https://doi.org/10.3390/s18020547




