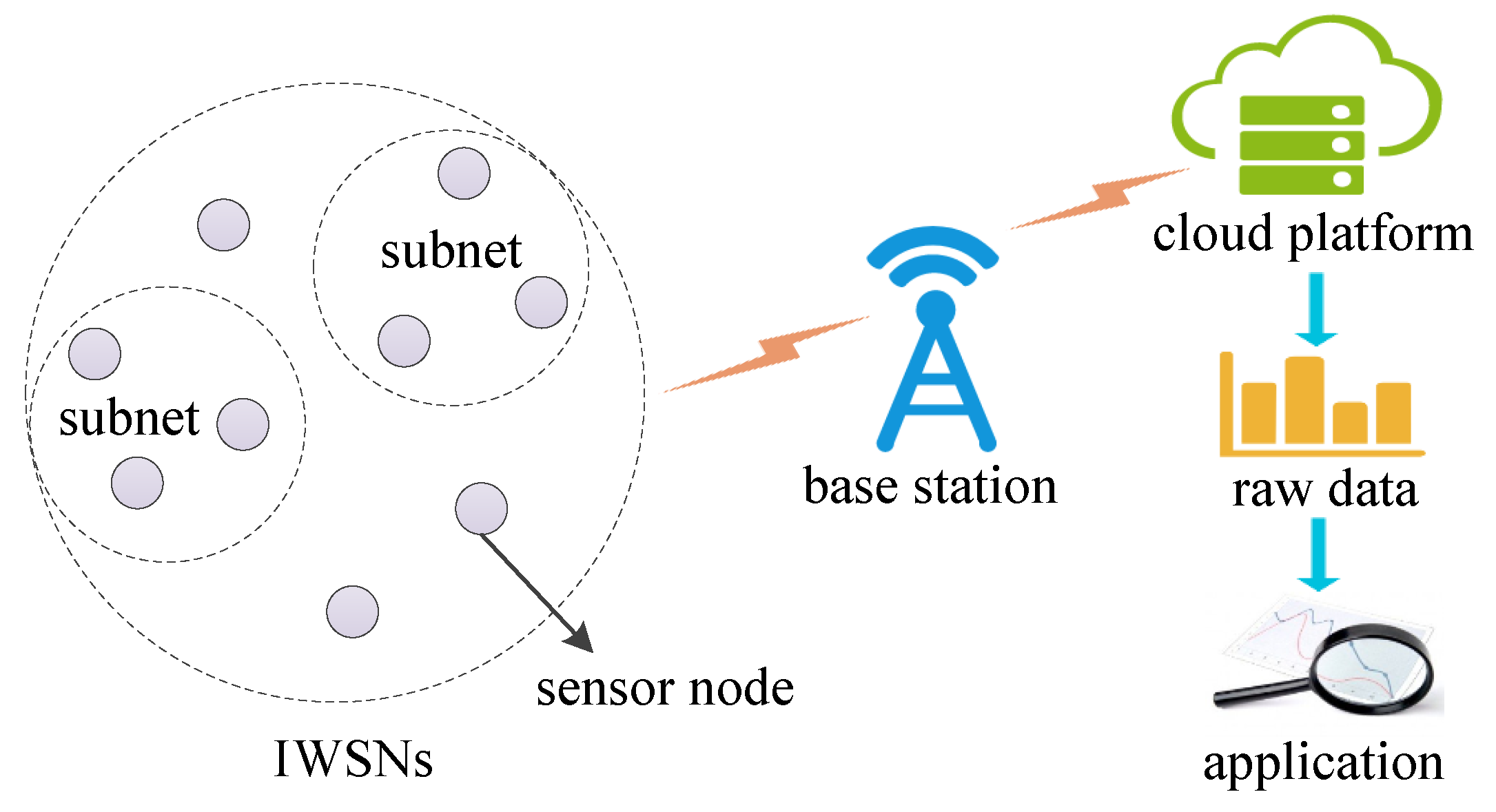
Node Location Privacy Protection Based on Differentially Private Grids in Industrial Wireless Sensor Networks
Abstract
:1. Introduction
- We propose a novel granularity partitioning model of data domain, which is effective to balance the noise error and the non-uniformity error. The partition granularity is proportional to the area of data domain, privacy budget and coefficient k.
- We adopt a cells merging strategy based on bucket sort, which groups all the similar cells of data domain into a partition, in order to decrease the noise added to each cell. This merging strategy further raises the accuracy of query.
- We conduct evaluations using two real-world datasets to verify the effectiveness of the granularity partitioning model and the similar cells merging strategy, and results show that the proposed approach has better query accuracy and enhances the utility of released data.
2. Related Work
3. Preliminaries
3.1. Differential Privacy
3.2. Problem Definition
4. Sanitized Data Release Based on Grid Partition
4.1. Uniform Grid Release Approach
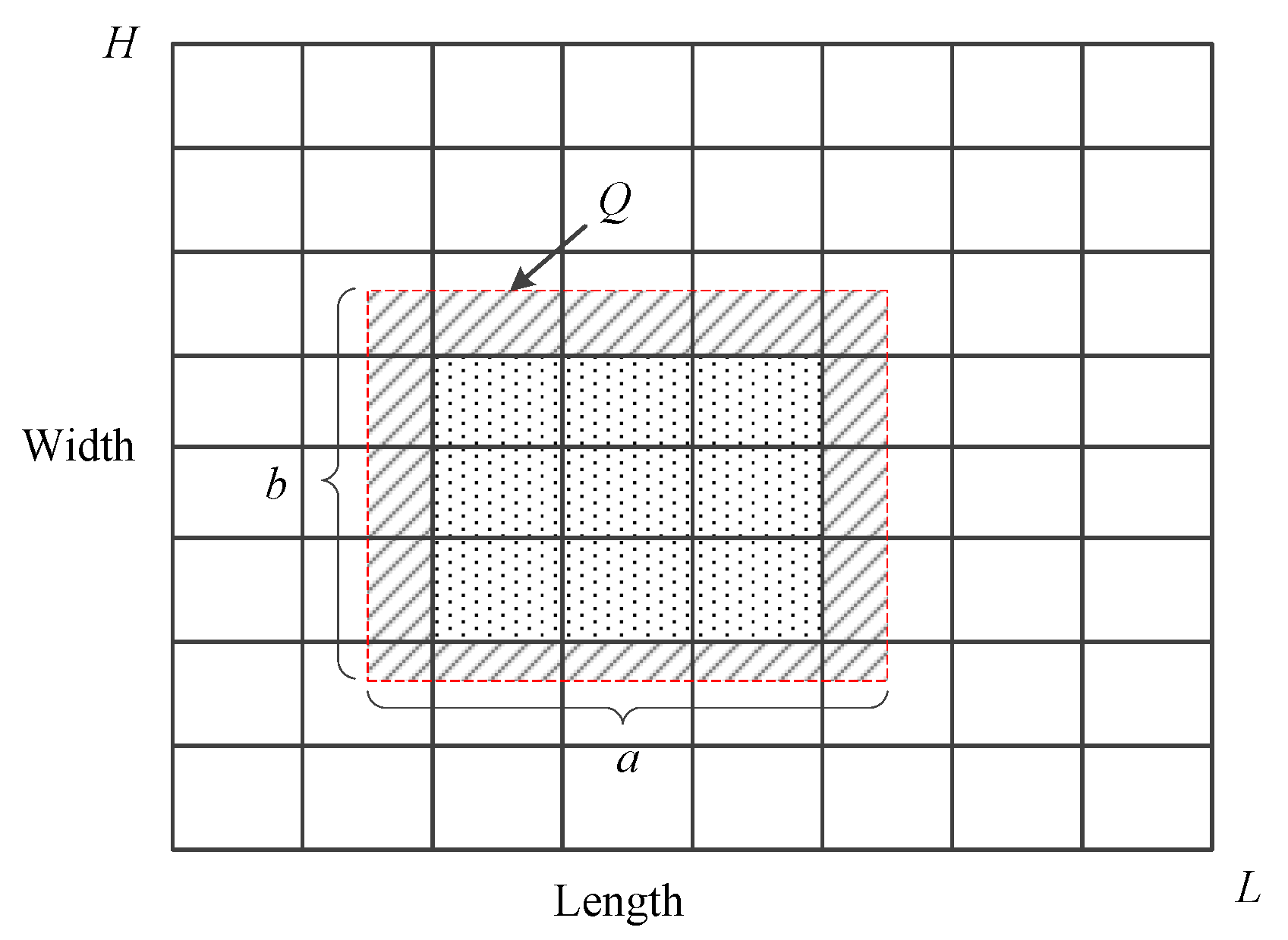
4.1.1. Granularity Partitioning Model of Data Domain
4.1.2. Ugrid Method
| Algorithm 1 Ugrid |
| Input: geospatial dataset D, privacy budget , partition granularity m |
| Output: sanitized dataset |
|
4.2. Merging Grids Release Approach
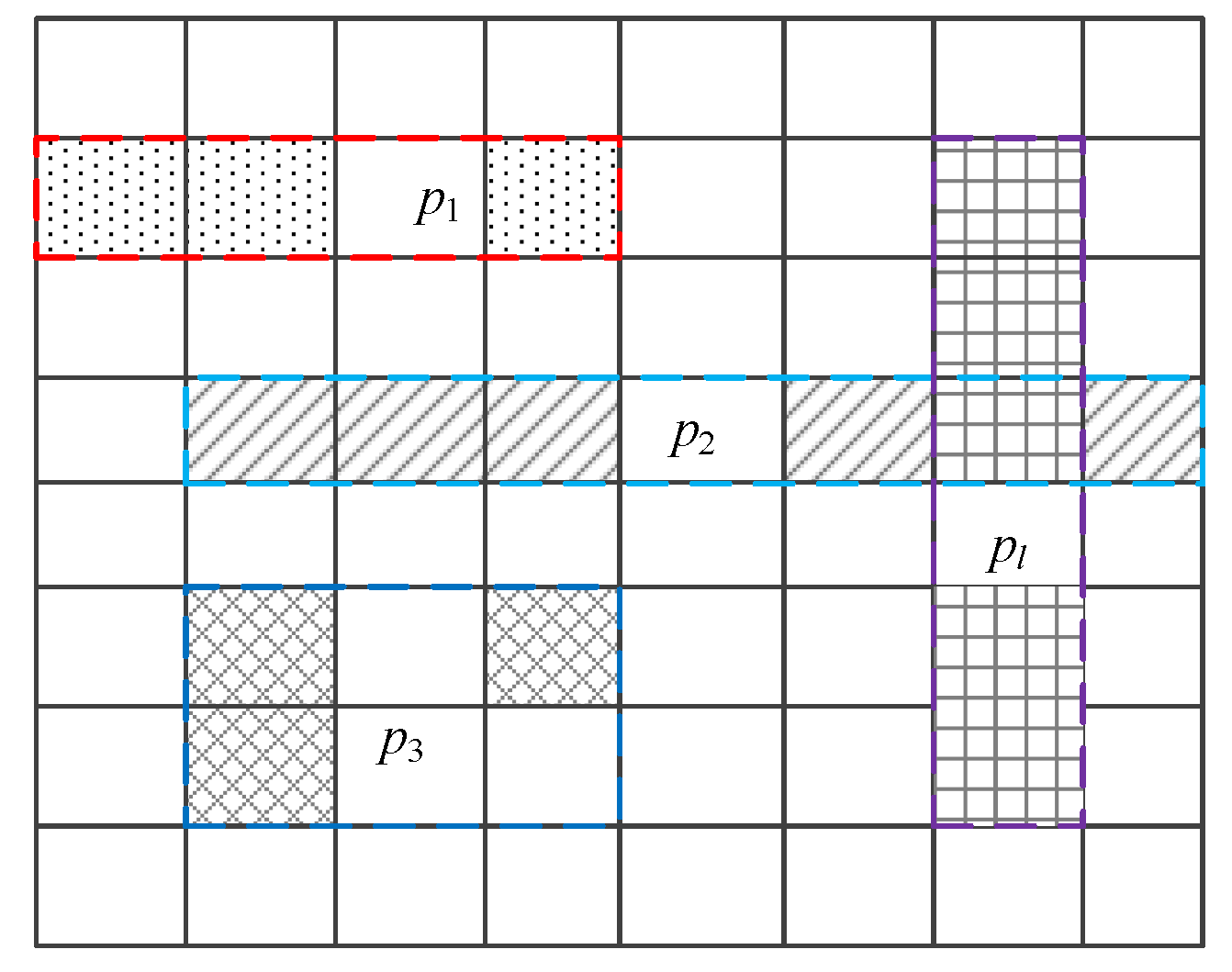
4.2.1. Merging of Similar Cells
4.2.2. Mgrid Method
| Algorithm 2 Mgrid |
| Input: geospatial dataset D, privacy budget , partition granularity m, threshold c |
| Output: sanitized dataset |
|
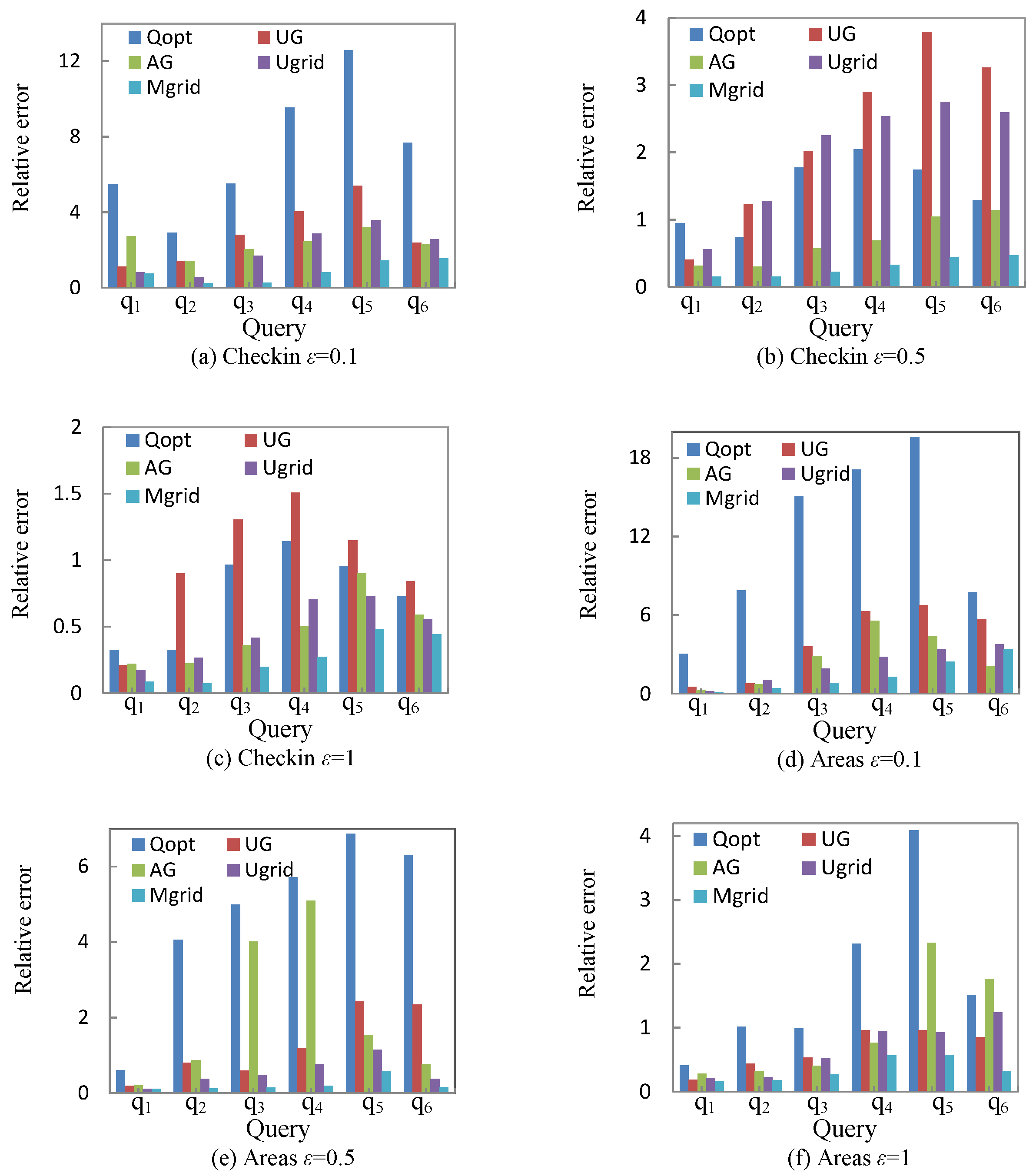
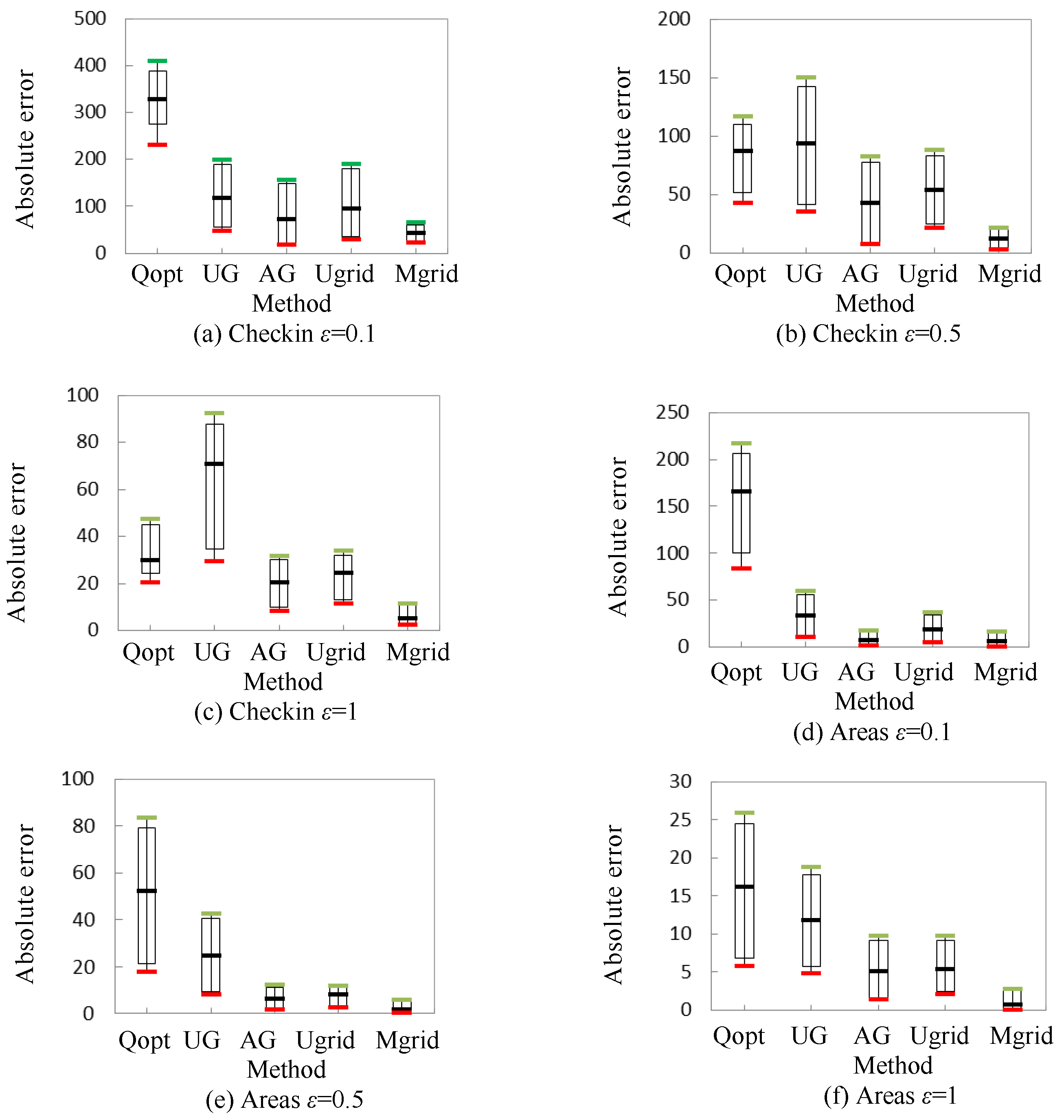
5. Experimental Results and Analysis
5.1. Utility Metric
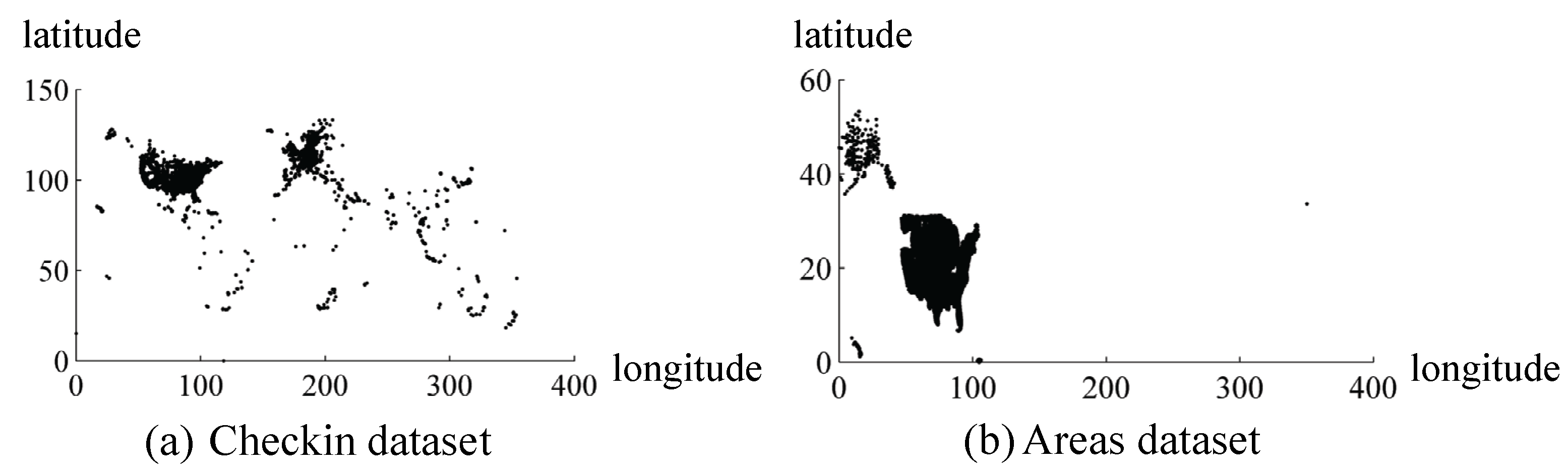
5.2. Experimental Datasets
5.3. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| IWSNs | Industrial Wireless Sensor Networks |
| WSNs | Wireless Sensor Networks |
| PSD | Privacy Spatial Decomposition |
References
- Posada, J.; Toro, C.; Barandiaran, I.; Oyarzun, D.; Stricker, D.; de Amicis, R.; Pinto, E.B.; Eisert, P.; Döllner, J.; Vallarino, I., Jr. Visual computing as a key enabling technology for Industrie 4.0 and Industrial Internet. IEEE Comput. Graph. Appl. 2015, 35, 26–40. [Google Scholar] [CrossRef] [PubMed]
- Chu, W.C.; Ssu, K.F. Location-free boundary detection in mobile wireless sensor networks with a distributed approach. Comput. Netw. 2014, 70, 96–112. [Google Scholar] [CrossRef]
- Li, X.; Li, D.; Wan, J.; Vasilakos, A.; Lai, C.; Wang, S. A review of industrial wireless networks in the context of Industry 4.0. Wirel. Netw. 2017, 23, 23–41. [Google Scholar] [CrossRef]
- Salam, H.A.; Khan, B.M. IWSN—Standards, challenges and future. IEEE Potentials 2016, 35, 9–16. [Google Scholar] [CrossRef]
- Francis, T.; Madiajagan, M.; Kumar, V. Privacy issues and techniques in E-health systems. In Proceedings of the ACM SIGMIS Conference on Computers and People Research, Newport Beach, CA, USA, 4–6 June 2015; pp. 113–115. [Google Scholar]
- Dwork, C. Differential privacy. In Proceedings of the 33rd International Colloquium on Automata, Languages and Programming, Venice, Italy, 10–14 July 2006; pp. 1–12. [Google Scholar]
- Qardaji, W.; Yang, W.N.; Li, N.H. Differentially private grids for geospatial data. In Proceedings of the IEEE 29th International Conference on data Engineering, Brisbane, Australia, 8–12 April 2013; pp. 757–768. [Google Scholar]
- Abiola, S.O.; Portman, E.; Kautz, H.; Dorsey, E.R. Node view: A mHealth real-time infectious disease interface disease interface. In Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing and 2015 ACM International Symposium on Wearable Computers, Osaka, Japan, 7–11 September 2015; pp. 297–300. [Google Scholar]
- De Montjoye, Y.A.; Radaelli, L.; Singh, V.K.; Pentland, A.S. Unique in the shopping mall: On the reidentifiability of credit card metadata. Science 2015, 347, 536–539. [Google Scholar] [CrossRef] [PubMed]
- Xue, A.Y.; Zhang, R.; Zheng, Y.; Xie, X.; Yu, J.H.; Tang, Y. DesTeller: A System for Destination Prediction Based on Trajectories with Privacy Protection. Proc. VLDB Endow. 2013, 6, 1198–1201. [Google Scholar] [CrossRef]
- Oualha, N.; Olivereau, A. Sensor and data privacy in industrial wireless sensor networks. In Proceedings of the Network and Information Systems Security, La Rochelle, France, 18–21 May 2011; pp. 1–8. [Google Scholar]
- Anas, B.; Abdelshakour, A.; Ausif, M. Source anonymity in WSNs against global adversary utilizing low transmission rates with delay constraints. Sensor 2016, 16, 957. [Google Scholar]
- Huang, C.; Ma, M.; Liu, Y.; Liu, A. Preserving source location privacy for energy harvesting WSNs. Sensor 2017, 17, 724. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, M.; Matam, R.; Shu, L.; Maglaras, L.; Ferrag, M.A.; Choudhry, N.; Kumar, V. Security and privacy in fog computing: Challenges. IEEE Access 2017, 5, 19293–19304. [Google Scholar] [CrossRef]
- Cicek, A.E.; Nergiz, M.E.; Saygin, Y. Ensuring location diversity in privacy-preserving spatio-temporal data publishing. Int. J. Large Data Bases 2014, 23, 609–625. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Xiong, L. Protecting location with dynamic differential privacy under temporal correlations. In Proceedings of the 22nd ACM Audit and Control Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 1298–1309. [Google Scholar]
- Machanavajjhala, A.; Kifer, D.; Gehrke, J. L-diversity: Privacy beyond k-anonymity. ACM Trans. Knowl. Discov. Data 2007, 1, 1–52. [Google Scholar] [CrossRef]
- Li, N.H.; Li, T.C.; Venkatasubramanian, S. T-closeness: Privacy beyond k-anonymity and l-diversity. In Proceedings of the IEEE 23rd International Conference on Data Engineering, Istanbul, Turkey, 15–20 April 2007; pp. 106–115. [Google Scholar]
- Fabienne, E.; Aniket, K.; Matteo, M.; Francesca, P.; Ivan, P. Differentially private data aggregation with optimal utility. In Proceedings of the 30th Annual Computer Security Applications Conference, New Orleans, LA, USA, 8–12 December 2014; pp. 316–325. [Google Scholar]
- Ebadi, H.; Sands, D.; Schneider, G. Differential privacy: Now it’s getting personal. In Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, Mumbai, India, 15–17 January 2015; pp. 69–81. [Google Scholar]
- Fan, L.Y.; Bonomi, L.; Xiong, L.; Sunderam, V. Monitoring web browsing behavior with differential privacy. In Proceedings of the 23rd International Conference on World Wide Web, Seoul, Korea, 7–11 April 2014; pp. 177–188. [Google Scholar]
- Dwork, C. A firm foundation for private data analysis. Commun. ACM 2011, 54, 86–95. [Google Scholar] [CrossRef]
- Soria-Comas, J.; Domingo-Ferrer, J.; Sánchez, D.; Martínez, S. Enhancing data utility in differential privacy via microaggregation-based k-anonymity. VLDB J. 2014, 23, 771–794. [Google Scholar] [CrossRef]
- Shu, L.; Chen, Y.; Huo, Z.; Bergmann, N.; Wang, L. When mobile crowd sensing meets traditional industry. IEEE Access 2017, 5, 15300–15307. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.B.; Li, Y.K. A review of differential privacy in individual data release. Int. J. Distrib. Sens. Netw. 2015, 11, 259682. [Google Scholar] [CrossRef]
- Cormode, G.; Procopiuc, C.; Srivastava, D.; Shen, E.; Yu, T. Differentially private spatial decompositions. In Proceedings of the IEEE 28th International Conference on Data Engineering, Washington, DC, USA, 1–5 April 2012; pp. 20–31. [Google Scholar]
- Xiao, Y.H.; Xiong, L.; Yuan, C. Differentially private data release through multidimensional partitioning. In Proceedings of the 7th Very Large Data Base Workshop on Secure Date Management, Lecture Notes in Computer Science, Singapore, 17 September 2010; pp. 150–168. [Google Scholar]
- Xiao, Y.H.; Gardner, J.; Xiong, L. Dpcube: Releasing differentially private data cubes for health information. In Proceedings of the IEEE 28th International Conference on Data Engineering, Washington, DC, USA, 1–5 April 2012; pp. 1305–1308. [Google Scholar]
- Fan, L.Y.; Xiong, L.; Sunderam, V. Differentially private multi-dimensional time series release for traffic monitoring. In Proceedings of the 27th Annual IFIP WG 11.3 Conference, Newark, NJ, USA, 15–17 July 2013; pp. 33–48. [Google Scholar]
- Shu, L.; Wang, L.; Niu, J.; Zhu, C.; Mukherjee, M. Releasing network isolation problem in group-based industrial wireless sensor networks. IEEE Syst. J. 2017, 11, 1340–1350. [Google Scholar] [CrossRef]
- Shu, L.; Chen, Y.; Sun, Z.; Tong, F.; Mukherjee, M. Detecting the dangerous area of toxic gases with wireless sensor networks. IEEE Trans. Emerg. Top. Comput. 2017, 1. [Google Scholar] [CrossRef]
- Hay, M.; Rastogi, V.; Miklau, G. Boosting the accuracy of differentially private histograms through consistency. Proc. Large Data Base Endow. 2010, 3, 1021–1032. [Google Scholar] [CrossRef]
- To, H.; Ghinita, G.; Shahabi, C. A framework for protecting worker location privacy in spatial crowdsourcing. Proc. Large Data Base Endow. 2014, 7, 919–930. [Google Scholar] [CrossRef]
- McSherry, F.; Liu, S.B.; Li, Y.K. Privacy integrated queries: An extensible platform for privacy-preserving data analysis. Commun. ACM 2010, 53, 89–97. [Google Scholar] [CrossRef]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating noise to sensitivity in private data analysis. In Proceedings of the 3rd Conference on Theory of Cryptography, New York, NY, USA, 4–7 March 2006; pp. 265–284. [Google Scholar]
- Mcsherry, F.; Talwar, K. Mechanism design via differential privacy. In Proceedings of the 48th Annual IEEE Symposium on Foundations of Computer Science, Providence, RI, USA, 21–23 October 2007; pp. 94–103. [Google Scholar]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Q.; Chen, R.; Tan, K.L. Differentially private network data release via structural inference. In Proceedings of the 20th ACM Knowledge Discovery and Data Mining International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 911–920. [Google Scholar]
- Leskovec, J. Govalla. Available online: http://snap.stanford.edu/data/loc-gowalla.html (accessed on 28 January 2018).
- Geodatabases. Available online: https://www.census.gov/geo/maps-data/data/tiger-geodatabases.html (accessed on 19 July 2015).
| Symbol | Description |
|---|---|
| D | two-dimensional geospatial dataset |
| sanitized dataset | |
| cell | |
| count of data points in cell | |
| k | proportionality coefficient |
| Q | data query |
| intersection between query Q and cell | |
| noisy count of cell | |
| L | domain length of D |
| H | domain width of D |
| a | length of Q |
| b | width of Q |
| Dataset | Num of Points | Domain Size | Query Size |
|---|---|---|---|
| Checkin | 625,123 | 354 × 133 | |
| Areas | 179,371 | 351 × 54 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhu, R.; Liu, S.; Cai, Z. Node Location Privacy Protection Based on Differentially Private Grids in Industrial Wireless Sensor Networks. Sensors 2018, 18, 410. https://doi.org/10.3390/s18020410
Wang J, Zhu R, Liu S, Cai Z. Node Location Privacy Protection Based on Differentially Private Grids in Industrial Wireless Sensor Networks. Sensors. 2018; 18(2):410. https://doi.org/10.3390/s18020410
Chicago/Turabian StyleWang, Jun, Rongbo Zhu, Shubo Liu, and Zhaohui Cai. 2018. "Node Location Privacy Protection Based on Differentially Private Grids in Industrial Wireless Sensor Networks" Sensors 18, no. 2: 410. https://doi.org/10.3390/s18020410





