1. Introduction
The Brillouin optical fiber distributed sensor is attractive for the measurement of strain and temperature change in fiber under test (FUT), based on the Brillouin frequency shift (BFS), which is a function of strain and temperature. The typical sensitivities were reported as
and
, where
is the microstrain [
1]. Therefore, one of the key issues for the sensor is to extract the peak frequency from the detected signal of the retuned optical wave, which usually contains high-level noise, since the Brillouin scattering is very weak. Obviously, the noise will deteriorate the accuracy of the peak frequency measurement. Some papers have been published discussing the accuracy of BFS. The minimum detectable peak frequency change was given earlier in Ref. [
2], expressed as
where
SNR is the signal-to-noise ratio of the detected electrical signal; and
is the FWHM of the Brillouin scattering spectrum, usually in a Lorentzian waveform. The Brillouin linewidth is typically about 40 MHz, so that the
SNR for 1 MHz resolution of BFS is required to be 58 dB. This is too high for a conventional sensor to reach. Many technical measures have to be used to suppress the noise.
Ref. [
3] presented a detailed analysis about BSF variance based on a quadratic function model, expressed as
, where the coefficients
,
, and
meet the requirement of least-square fitting. The peak frequency is estimated as
, giving the value of BFS. A different formula for the error of the estimated Brillouin peak was deduced as
where
is the frequency step of the spectrum,
SNRA is the signal-to-noise ratio of the optical signal amplitude, and
η is the fraction of peak level, over which a quadratic least-square fitting is carried out. The last expression is for the case of
. The performances of Brillouin sensors were then characterized based on the model, and consistent with the experimental results.
The difference between Equations (1) and (2) attracts attention. Ref. [
4] presented simulated comparisons of the two expressions by using Monte Carlo method with varying frequency step, signal-to-noise ratio, and
Q-factor. The last parameter is inversely proportional to the FWHM of the Brillouin scattering spectrum, which will change in the case of stimulated Brillouin scattering. It is pointed that the signal-to-noise ratios in Equations (1) and (2) have different definitions with
SNRA = SNR1/2. However, the origin of the difference between Equations (1) and (2) seems not very clear. The dependence of BFS accuracy on the data length used in data processing is not analyzed in detail, which is an important factor in quadratic fitting.
In this work, the expression of BFS uncertainty due to Gaussian noise is deduced strictly in detail based on quadratic fitting with the least-square algorithm, giving new formulas for fitted BFS variance and linewidth varying with data length and the data range’s center, noise levels, frequency step, and others. The analyses are verified by experimental signals from a Brillouin optical domain reflectometer (BOTDR), showing good agreement with each other. The deduction of the new formulas is compared with the model presented in previous publications. The reason for the differences between Formulas (1) and (2) and their applicability are discussed also.
It is shown that the data length and data range’s center deviation relative to the Brillouin peak have a direct impact on the accuracy of the extracted BFS. To mitigate this impact, a method of iterative quadratic fitting is proposed and demonstrated in this paper. It is shown, by way of practical applications to the experimental data, that the method is effective with negligible increase of calculation time.
2. Quadratic Fitting Characteristics
The quadratic fitting with
is used widely in various applications [
5,
6], and in data processing of noisy Brillouin spectra in distributed fiber sensors, typically in Lorentzian
, where
is now the spectrum of the detected Brillouin signal with noise. The accuracy of the extracted BFS depends on data noise and the data range used in fitting, including the length of data and its center, i.e., its symmetry relative to the Brillouin peak
. Signal noise will lead to fluctuations of
, and its variance is deduced to be (see
Appendix A for detail)
where
is the frequency spacing of data points,
is the length of the spectral range used in fitting.
is the FWHM of the fitted quadratic curve, and
is the noise variance. Equation (3) shows that the BFS variance is a quadratic function of
. In the case where the fitting data range is centered at the Brillouin peak, the BFS variance reaches its minimum.
Actually, even if the noise is negligibly small, the quadratic fitted peak may deviate from the Brillouin peak if the center of the data range used in the fitting does not coincide with the latter.
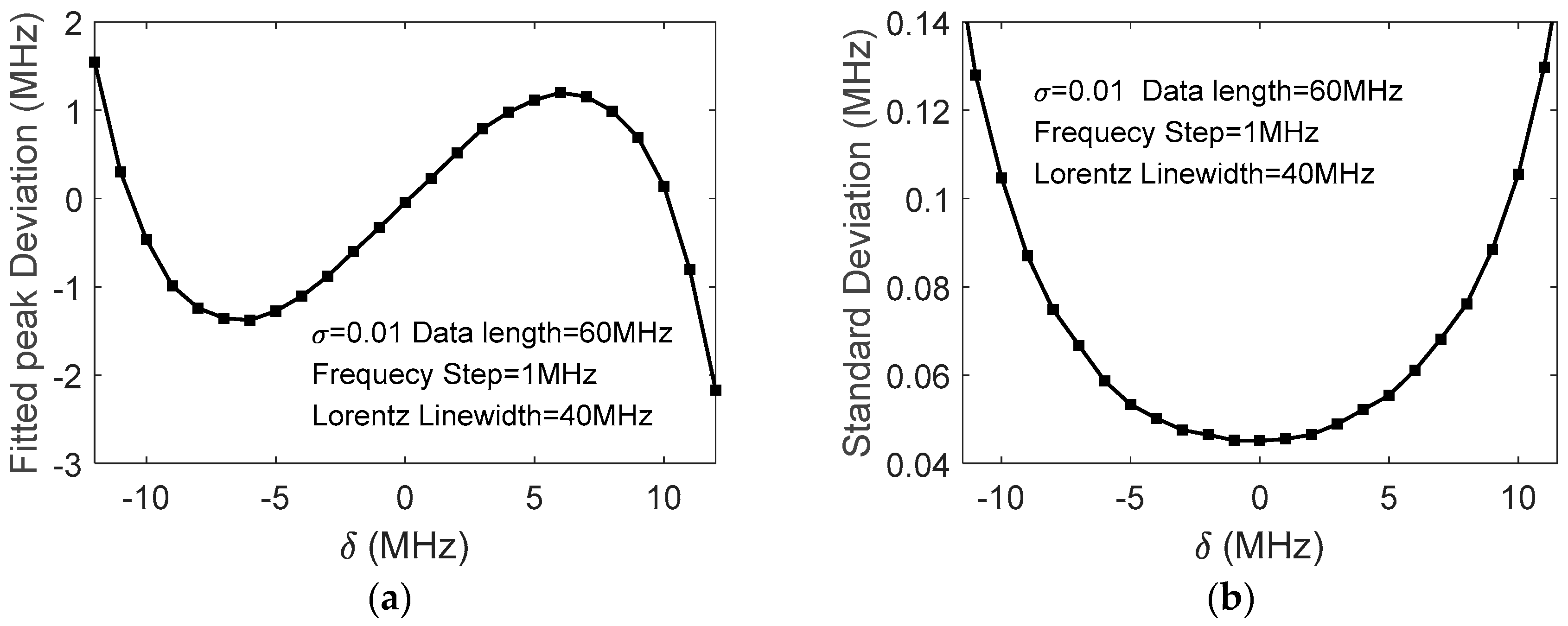
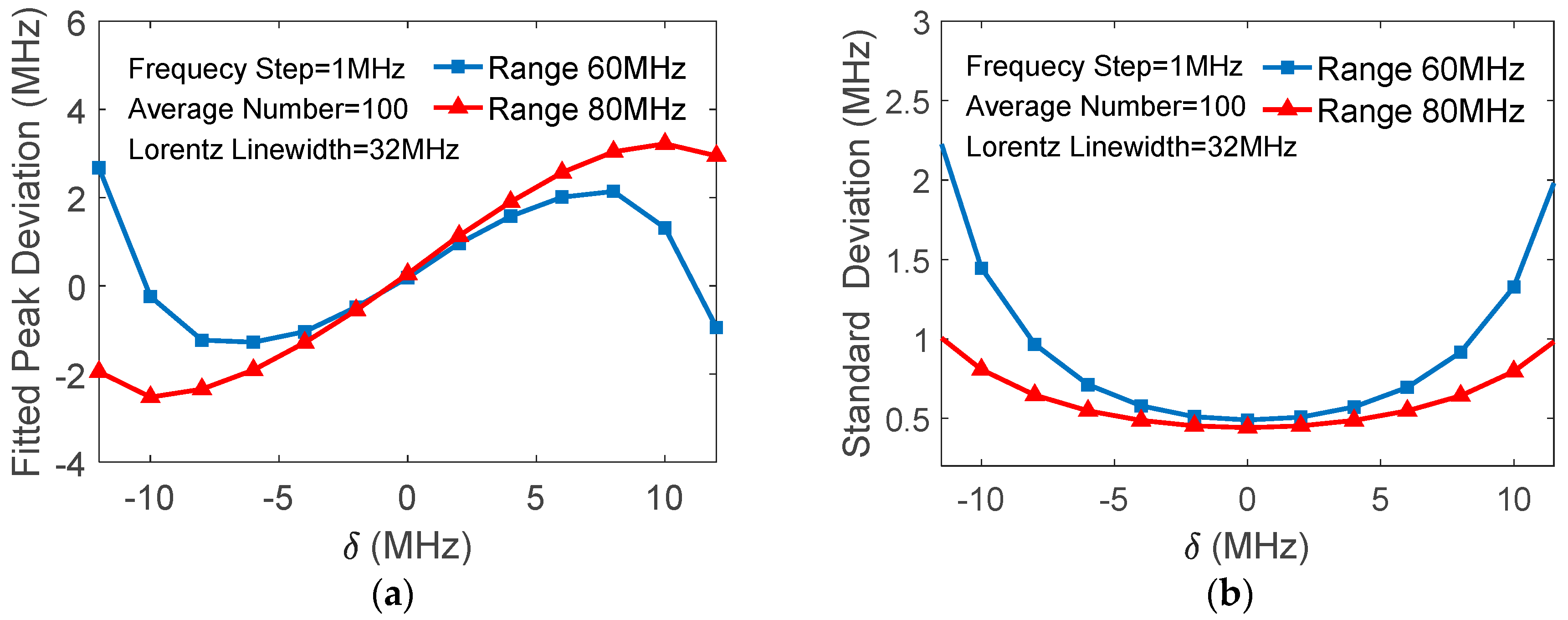
Figure 1a shows the deviation of the fitted peak
versus
, simulated with
,
, and noise level
σ = 0.01;
Figure 1b shows the standard deviations of
versus
δ. It is indicated, therefore, that the selections of the data range length and its center in quadratic fitting play important roles in the accuracy of the extracted BFS.
The BFS variances obtained by quadratic fitting are simulated with different noise levels.
Figure 2a shows an example of BFS variance versus test numbers with
,
,
, and Lorentzian peak set at the middle of the data range; the blue points are the peak frequencies for different simulation tests, and the black line is the variances obtained by averaging over the test numbers. Obviously, the fitted peaks are randomly distributed due to the noise.
Figure 2b gives the variances and standard deviations versus the noise level
σ. It is seen that the standard deviation is a straight line, showing that the BFS variance is inversely proportional to the square of
SNRA, coincident with Equation (4).
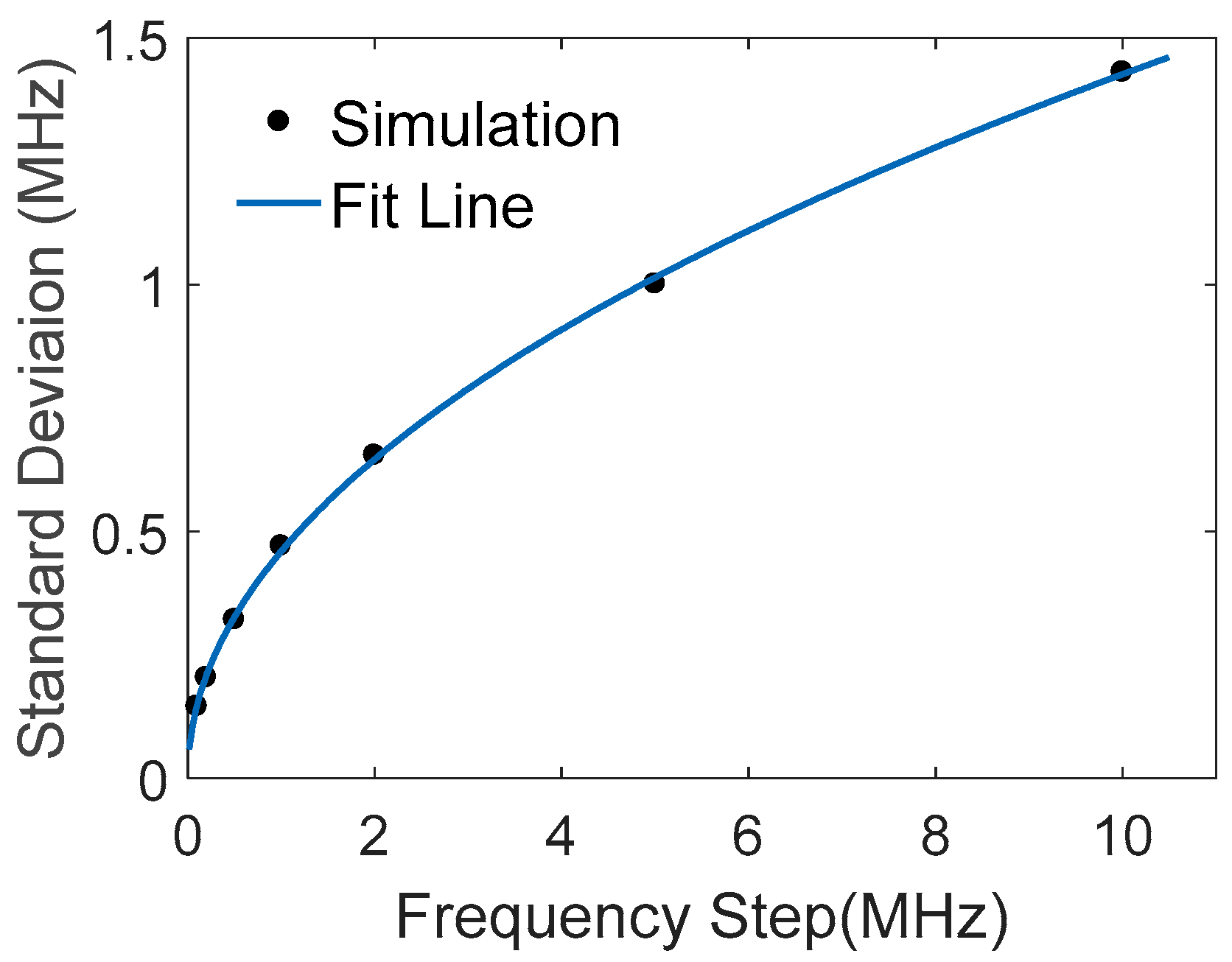
The relation between BFS variance and frequency step is also studied by simulation with
σ = 0.1 and
.
Figure 3 shows that the BFS standard deviation is the square root of the frequency step, coincident with Equation (4); therefore, a smaller step will lead to higher accuracy of the BFS measurement. However, the frequency step
is generally inversely proportional to the probe pulse width Δ
T of OTDR system, determined by FFT for the optimal spatial resolution. A trade-off has to be taken between BFS accuracy and spatial resolution.
The fitted linewidth Δ
x is an important parameter in Equations (3) and (4). In a previous publication [
3], an approximation of
was taken. In actuality, it depends on the length of the data used in fitting. The dependence of Δ
x on
and
for the case without noise and without deviation of the data range’s center is deduced to be (see
Appendix B for detail)
where
;
θ = tan
−1ρ; and the coefficients of linear approximation in the range of
are calculated to be
,
.
Figure 4 shows a simulation example, where the frequency step is taken as
, Lorentzian FWHM is 40 MHz, and the noise level is
σ = 0.02. The coefficients are estimated to be
and
for this simulation example, in good agreement with the results of Equation (5). The point at
is the theoretical limitation of
. Simulations show that this linear relation and the coefficients do not change much for different noise levels.
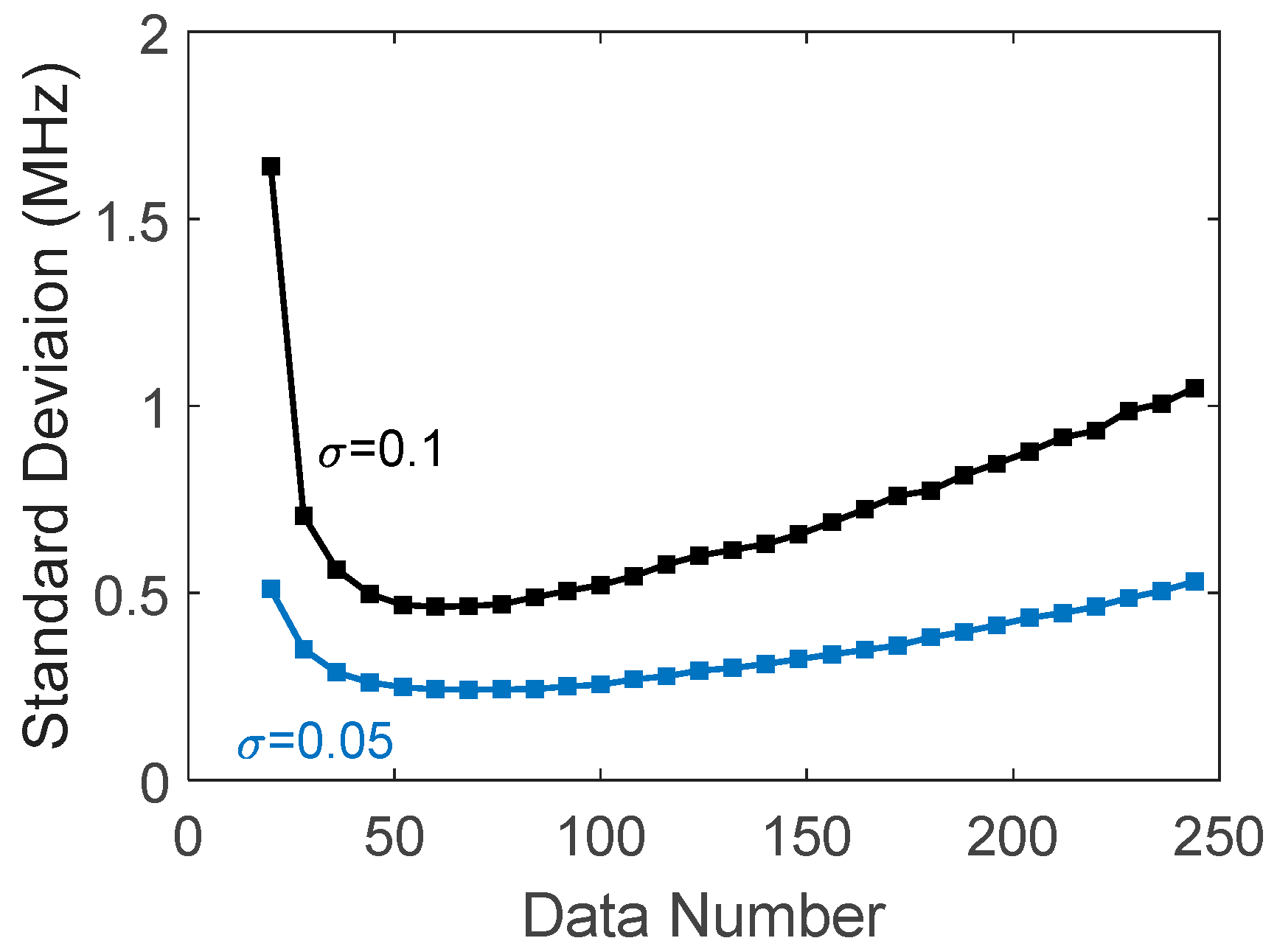
It is then seen that factor
in Equation (4) will go up towards infinity when
goes down towards zero, and the rising slope depends on
SNRA. It is reasonable that a decrease in the data number used in fitting will weaken their role in noise reduction, and thus increase the BFS variance, as shown in
Figure 5. On the other hand, in the range of
, the BFS variance will increase linearly with
; therefore, a minimum is reached at
, and the standard deviation of the peak frequency can then be expressed as
It is estimated by the analyzed result and the experimental data that
and
.
Figure 5 shows simulated curves of the BFS standard deviation versus data number for two noise levels as examples, where
and
are taken in the simulation, showing the existence of a minimum.
3. Experimental Results and Data Processing
The characteristics analyzed above are found to be in good agreement with our experimental results from a Brillouin optical time domain reflectometer (BOTDR). A narrow linewidth laser with frequency shifted by acousto-optic modulator (AOM) was used as the probe in the experiment; and a Brillouin fiber laser was used as the local oscillator for heterodyne detection, as described in [
7,
8,
9]. A 30 km long sensing fiber (SMF-28) was used in the experiments. The pulse width of the probe was set up as 100 ns; digital signals were given by using a data acquisition card with a sampling rate of 2 GS/s. Then, the Brillouin spectra were obtained by FFT with a frequency step of 1 MHz. The spectra usually contain high-level noise, especially for the signals from longer fiber distances. The frequency difference between Brillouin scattering from fiber and the local oscillation is typically 331 MHz in our BOTDR system.
The
SNR can be enhanced directly by averaging
M multiple traces, as
.
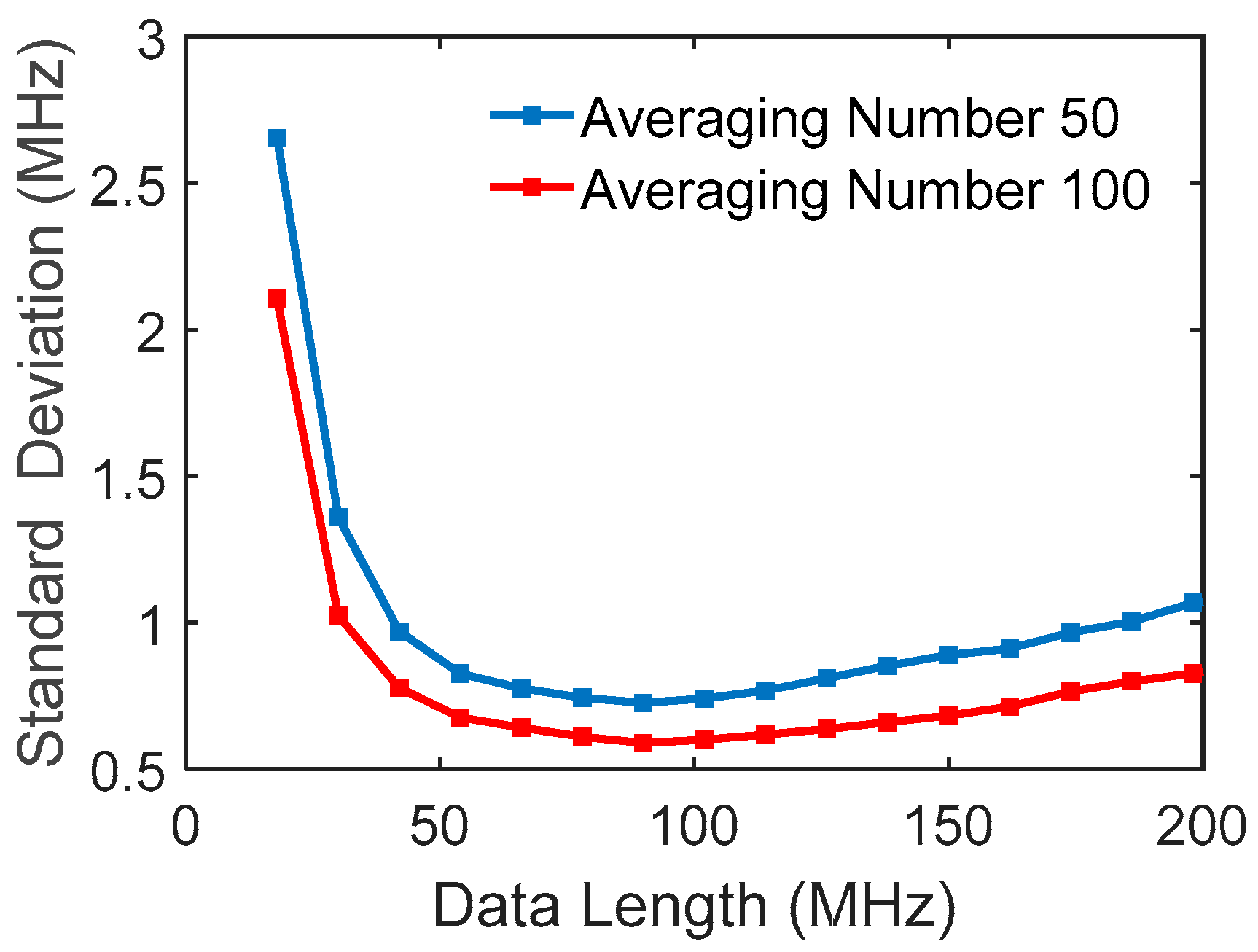
Figure 6 gives the standard deviation of the fitted peak frequency versus the averaging number
M, showing behavior of
, consistent with Equation (6).
The frequency step is related to the pulse width of the laser probe, which is set for the optimal spatial resolution. In this study, the spatial resolution is assumed to be not critical; the step can be adjusted in FFT by changing the signal range in the time domain.
Figure 7 gives an example of peak frequency standard deviation versus frequency step, where the data are averaged over 10 traces of the BOTDR signal, showing a square root relation as the analysis and simulation described.
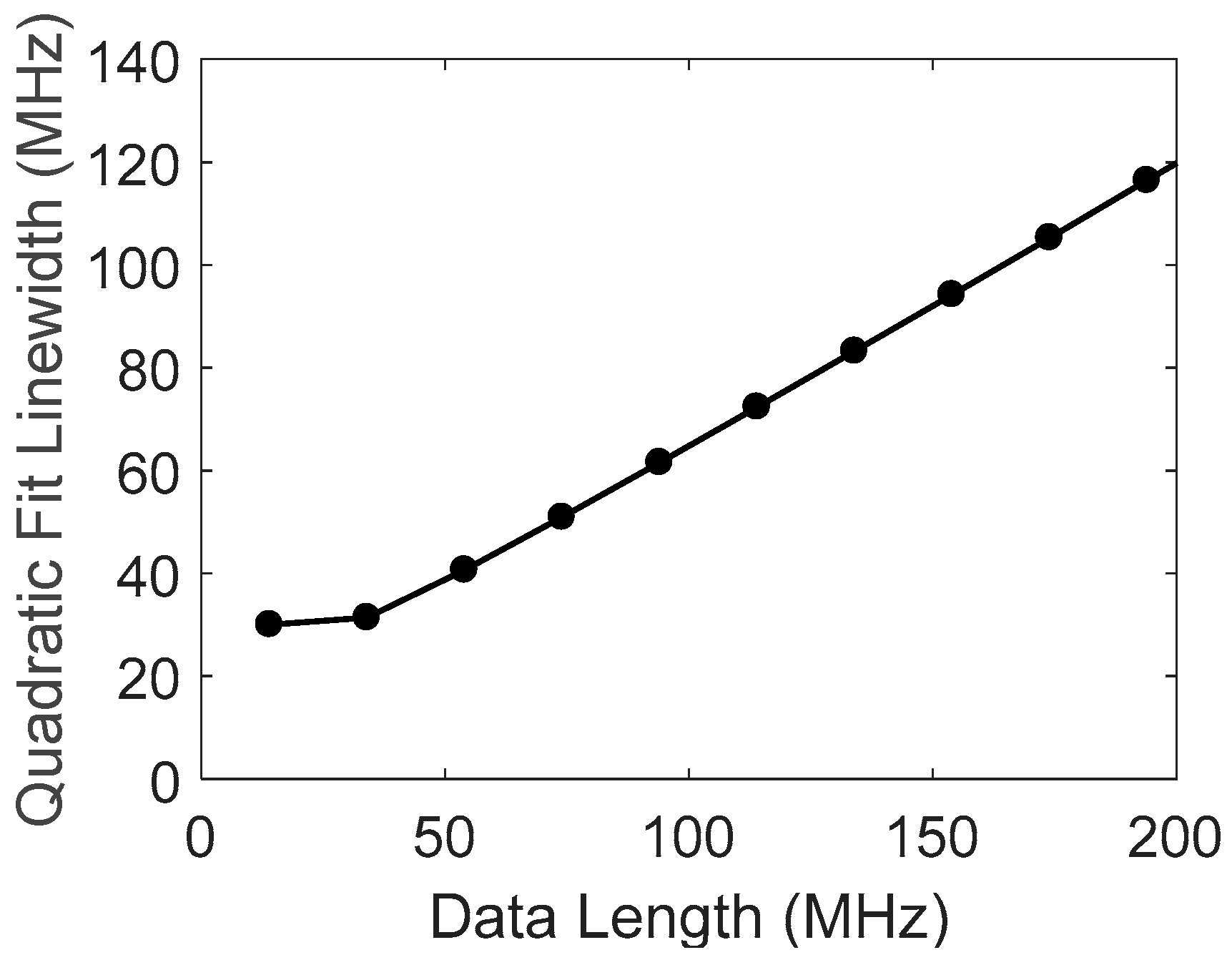
The FWHM obtained by the quadratic fitting is calculated for different data lengths by using the same spectral signals from the returned wave at a position of 6 km, as shown in
Figure 8. The curve is calculated by averaging 10 traces, showing good coincidence with the simulated results of
Figure 4. A linear relation appears in the range larger than 50 MHz; the coefficients are obtained as
,
; and the FWHM of Brillouin spectrum is estimated to be
.
The data length used in the fitting is an important parameter which affects the variance of the fitting peak frequency.
Figure 9 shows the standard deviation of the fitted peak varied with the data length, where multiple trace signals are used for data processing, and the two curves are for the different averaging numbers. The experimental data were obtained from the returned wave at a fiber distance of 30 km. The data range is centered at the Brillouin peak obtained by averaging 10,000 traces, giving the expected Brillouin peak. They resemble well the simulated curves in
Figure 5.
The effects of deviation of the data range’s center are verified experimentally. With the same expected Brillouin peak as used in
Figure 9, the frequencies and variances of the fitted peaks are calculated for 100 averaged traces, as observed in
Figure 10, and are in good agreement with the theoretical analyses.
4. Iterative Quadratic Fitting for BFS Measurement
Theoretical and experimental results show that the selection of the data range’s center directly affects the accuracy of the extracted BFS. However, the measured data usually contain high noise and the selected data range’s center in quadratic fitting often deviates from the optimization.
In this work, we propose an iterative quadratic fitting method to reduce the error of the extracted BFS. It is composed of the following steps:
- Step 1
Take the frequency at the maximum of the signal amplitude obtained by averaging of M traces as the data range’s center . The averaging number M can be adjusted according to the signal noise level.
- Step 2
Carry out quadratic fitting for the averaged signal with a selected data range centered at . A new peak frequency is then obtained.
- Step 3
Replace by and repeat Step 2 until the fitted peak converges to a stationary value.
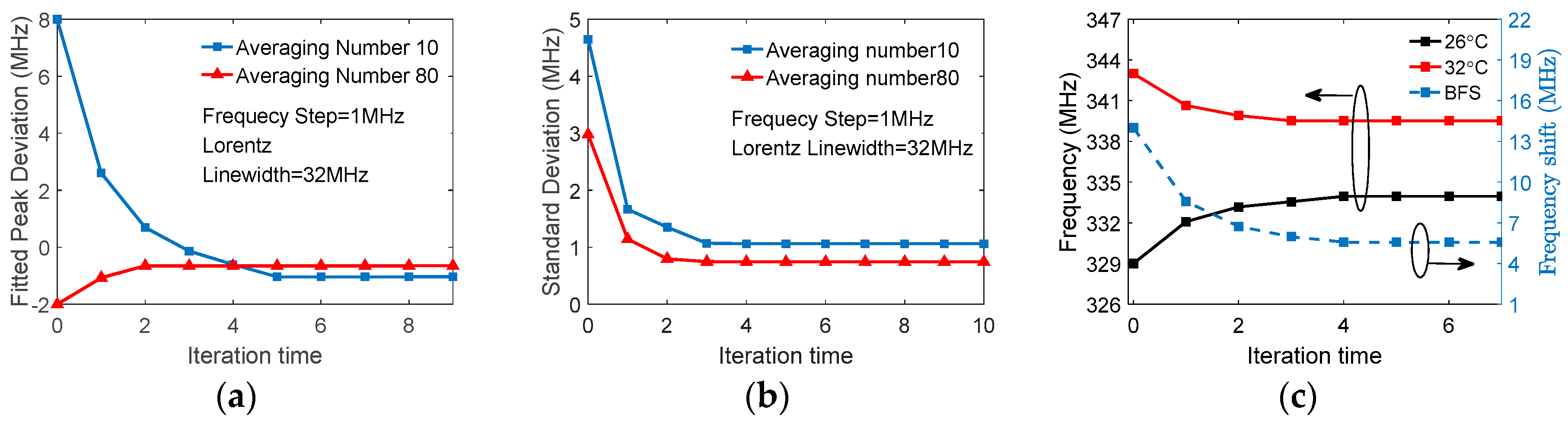
Figure 11a shows the effect of the iterative quadratic fitting method where the experimental data of BOTDR are used; results with two averaging numbers are displayed as examples. For the case of averaging 80 traces at Step 1, the peak frequency convergence is obtained in only two iterations, while five iterations are needed for averaging number of 10. It is noticed that the peak frequency estimated at Step 1 may deviate largely from the converged peak frequency, even positively or negatively, due to the randomness of noise. The two converged results have small differences between each other; this is also due to the noise. To ensure convergence, the initial data center should be selected in the range between two poles with positive slope in
Figure 10a.
The effect of the iterative quadratic fitting method can also be examined using the standard deviation of the fitted peak frequencies, as shown in
Figure 11b, where the experimental data are divided into multiple groups (e.g., 100–1000) with
M traces in each, and the fitted peak is then calculated for the multiple groups, giving the multiple results. It is seen that the standard deviations decrease and converge as the iteration time increases. In practical applications, the iterations are stopped when the fitted peak converges under a required accuracy.
Compared with the conventional fitting method, the iteration method requires fewer averaging numbers for the same accuracy. In our system (Matlab 2016b, 4 CORE I7-4770S, 8 G RAM) the data acquisition and FFT for each trace need 0.03 s, whereas a single quadratic fitting takes only 0.000017 s, which can be negligible. For example, it takes 80 × 0.03 s = 2.4 s and 10 × 0.03 s = 0.3 s, respectively, to get the two curves of
Figure 11a. Obviously, the iteration method will improve system speed. The same accuracy of the BFS by the iterative quadratic fitting is demonstrated experimentally in the BOTDR temperature sensor, as shown in
Figure 11c. A section of FUT was intentionally heated and the detected signals are averaged over 200 traces with a 1 MHz frequency step. The extracted frequencies converge at 333.9 MHz for a temperature of 26 °C and at 339.5 MHz for 32 °C after three iterations. The obtained BFS of 5.6 MHz is almost the same as that obtained with Lorentzian fitting provided by Matlab (5.5 MHz).
5. Discussions
In this work, we proposed a new formula for the minimum detectable peak frequency change. It is in a similar form to that given by Ref. [
3], but some different arguments are introduced in the deduction.
Firstly, the covariance of coefficients
and
are taken into consideration, which we think should not be omitted, as shown in Equation (A5) of the
Appendix A. The introduction of the covariance led to Equation (A6), which gives a relation between the variance of the fitted peak frequency and the center of the data range. Secondly, the center of the data range used in fitting relative to the Brillouin peak is an important factor which will lead to an error in the fitted peak frequency. These characteristics have an important influence on the accuracy of the BFS, since the selection of the data range’s center is with some uncertainty due to high noise. To overcome such an effect, we proposed a method of iterative fitting. Thirdly, we noticed that the fitted linewidth of the quadratic curve depends on the data length used in fitting. A linear equation of Δ
x on
and
was deduced theoretically and verified experimentally. This relation is needed in deducing an exact formula for the minimum detectable peak frequency change.
Equation (1) given by Ref. [
2] is actually deduced from the quadratic approximation of the Lorentzian curve near the peak frequency,
, where
is the FWHM of the Lorentzian profile. The detected electrical signal
V is proportional to
. The peak is determined by its derivative
, i.e.,
, at the peak
, where
is the half width of peak uncertainty. For noisy data, the change of electrical signal depends on its electrical signal-to-noise ratio
. The full width of peak uncertainty is thus obtained as
.
In the deduction of this formula, the frequency step
and the data number
N used for the quadratic fitting are not taken into consideration. The formula may be regarded as having the limitation of
and with
finite. In practice, the accuracy of the derivative calculation is surely dependent on
and
N. The simulation presented by Ref. [
4] showed a relation of
by using 10,000 Monte Carlo simulations, which, we think, corresponds to the case of
. Therefore, Equation (1) seems to give a qualitative description in ideal cases, but may not be suitable for practical applications.
It is of note that the analyses in this paper are for Gaussian noise cases. Although the Gaussian noise surely exists, other noise types need to be taken into consideration, such as noise induced by laser sources and devices used in the system [
10] and noise due to non-perfect extinction ratio [
11]. For a BOTDR with heterodyne detection, the frequency noise and relative intensity noise (RIN) of both the probe laser and the local oscillator are important noise. Besides this, the spectrum may deviate from the strict Lorentzian, such as a convolution of Lorentzian and the pulse shape, as discussed in Ref. [
12]. Further studies are undertaken in our group.
Our study is mainly limited in applications of BOTDR; change of Brillouin linewidth, as in the sensor based on stimulated Brillouin scattering, is not involved. It is believed that the analysis presented in this paper is also useful for BOTDA applications, where the linewidth may be decreased by Brillouin gain.