The Generated Entropy Monitored by Pyroelectric Sensors
Abstract
:1. Introduction
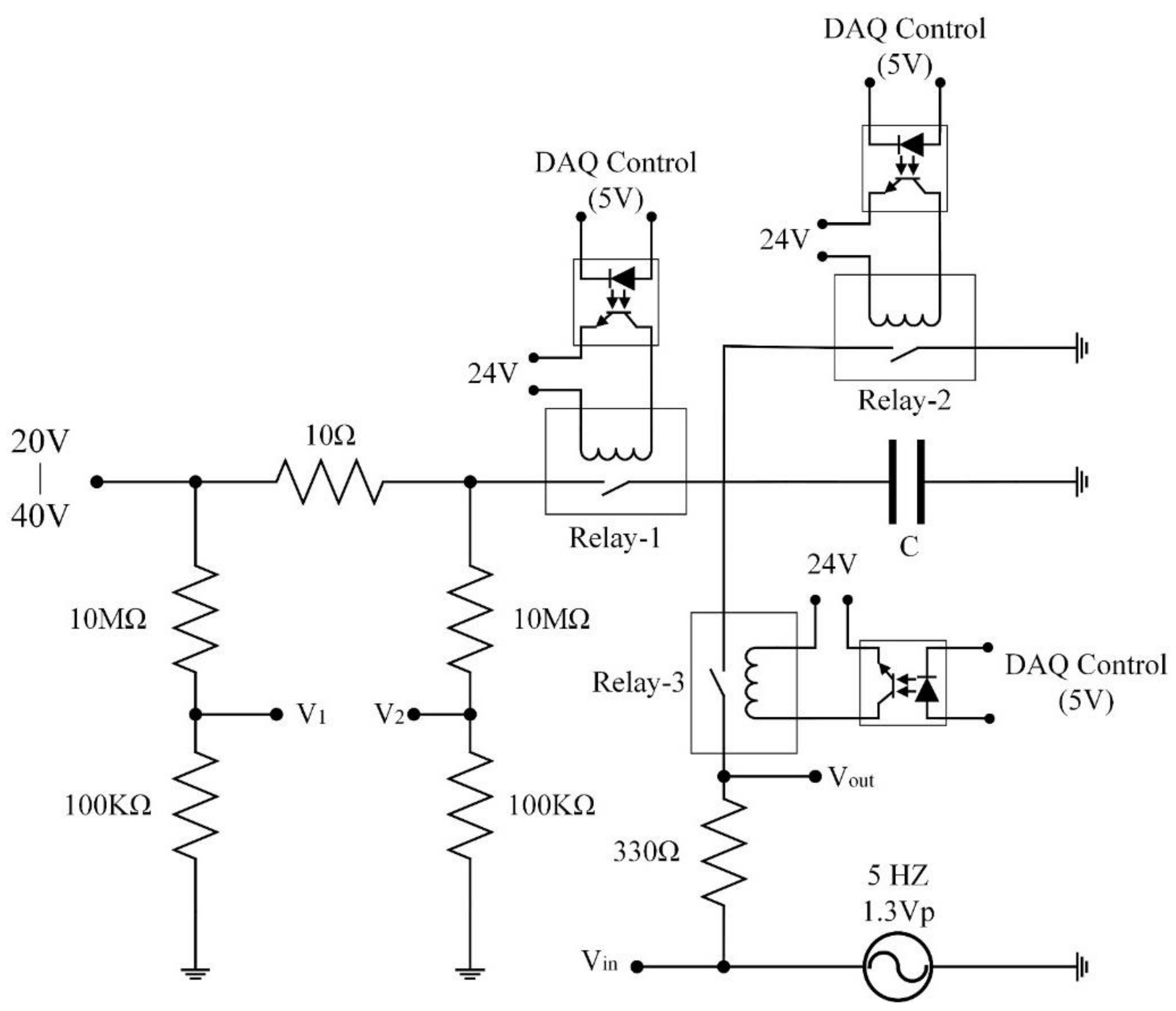
2. Materials and Methods
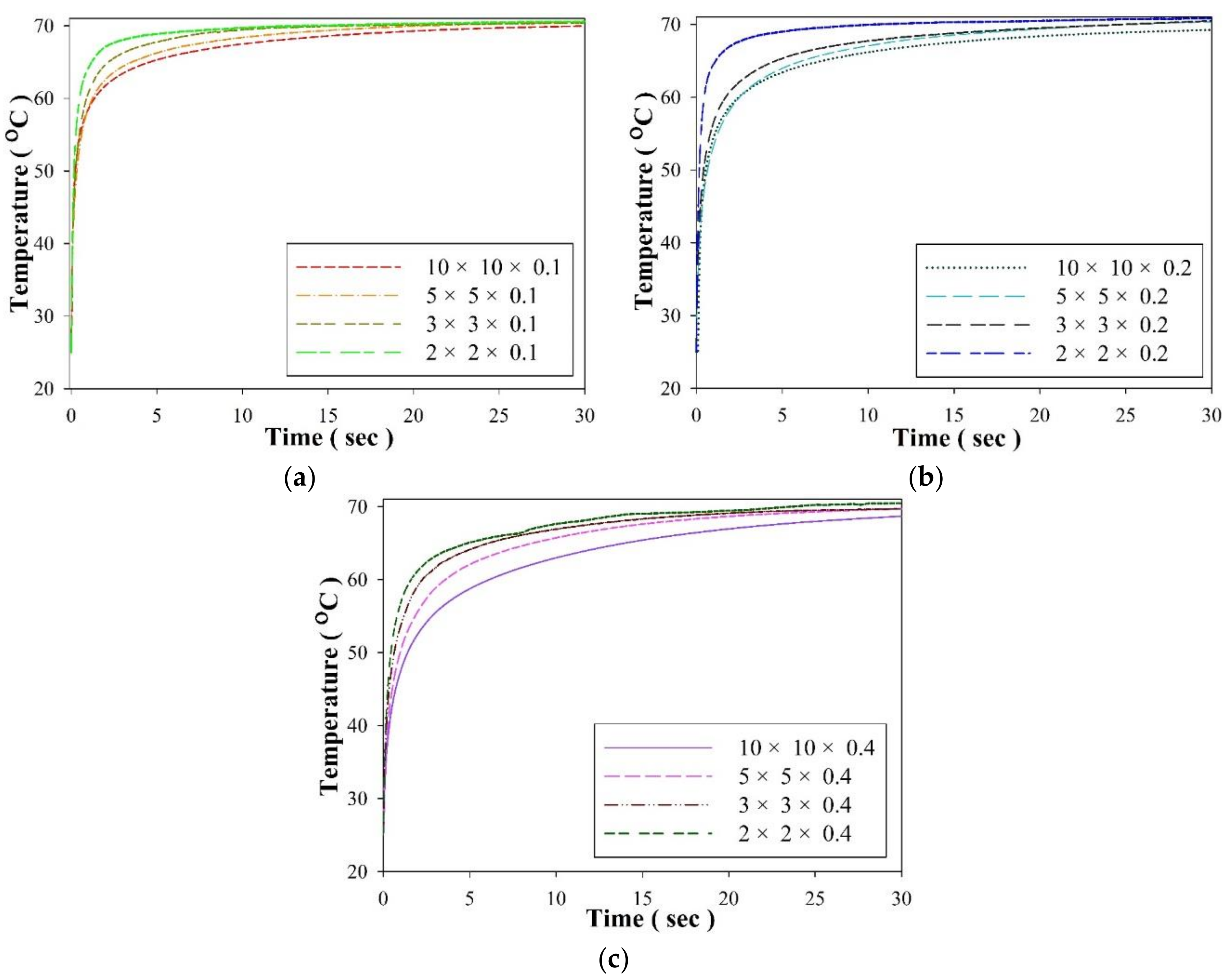
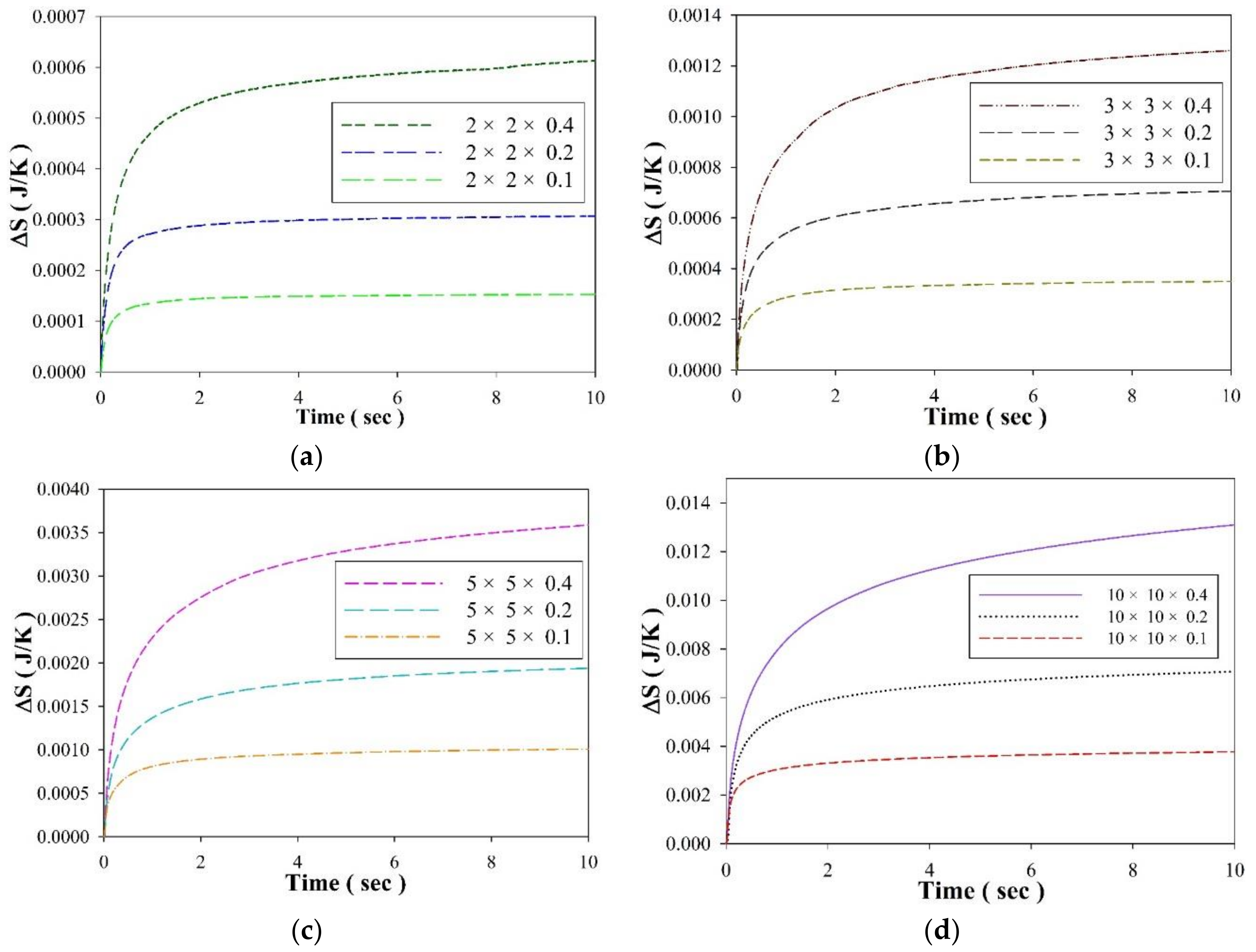
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflict of Interest
References
- Yuan, X.; Yang, F. Energy Transfer in Pyroelectric Material. In Heat Conduction; Vyacheslav, S.V., Ed.; IntechOpen: London, UK, 2011. [Google Scholar] [Green Version]
- Naderi, M.; Khonsari, M.M. Thermodynamic analysis of fatigue failure in a composite laminate. Mech. Mater. 2012, 46, 113–122. [Google Scholar] [CrossRef]
- Basaran, C.; Yan, C.Y. A Thermodynamic Framework for Damage Mechanics of Solder Joints. J. Electron. Packag. 1998, 120, 379–384. [Google Scholar] [CrossRef]
- Amiri, M.; Modarres, M. An Entropy-Based Damage Characterization. Entropy 2014, 16, 6434–6463. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Zhang, J.; Dong, L.; Zhuang, J. Determination of the entropy change of the electrode reaction by an ac electrochemical–thermal method. J. Electroanal. Chem. 1999, 469. [Google Scholar] [CrossRef]
- Basaran, C.; Nie, S. An Irreversible Thermodynamic Theory for Damage Mechanics of Solids. Int. J. Damage Mech. 2004, 13, 205–224. [Google Scholar] [CrossRef]
- Basaran, C.; Lin, M.; Ye, H. A Thermodynamic Model for Electrical Current Induced Damage. Int. J. Solids Struct. 2003, 40, 7315–7327. [Google Scholar] [CrossRef]
- Basaran, C.; Lin, M. Damage Mechanics of Electromigration Induced Failure. Mech. Mater. 2008, 40, 66–79. [Google Scholar] [CrossRef]
- Yao, W.; Basaran, C. Computational Damage Mechanics of Electromigration and Thermomigration. J. Appl. Phys. 2013, 114, 103708. [Google Scholar] [CrossRef]
- Sosnovskiy, L.A.; Sherbakov, S.S. Mechanothermodynamic Entropy and Analysis of Damage State of Complex Systems. Entropy 2016, 18, 268. [Google Scholar] [CrossRef]
- Siao, A.S.; Chao, C.K.; Hsiao, C.C. A Strip Cell in Pyroelectric Devices. Sensors 2016, 16, 375. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, C.C.; Siao, A.S. A High Aspect Ratio Micropattern in Freestanding Bulk Pyroelectric Cells. Energy Technol. 2017, 5, 883–898. [Google Scholar] [CrossRef]
- Cuadras, A.; Gasulla, M.; Ferrari, V. Thermal energy harvesting through pyroelectricity. Sens. Actuators A 2010, 158, 132–139. [Google Scholar] [CrossRef]
- Nguyen, H.; Navid, A.; Pilon, L. Pyroelectric energy converter using co-polymer P(VDF-TrFE) and Olsen cycle for waste heat energy harvesting. Appl. Therm. Eng. 2010, 30, 2127–2137. [Google Scholar] [CrossRef]
- Navid, A.; Vanderpool, D.; Bah, A.; Pilon, L. Towards optimization of a pyroelectric energy converter for harvesting waste heat. Int. J. Heat Mass Transf. 2010, 53, 4060–4070. [Google Scholar] [CrossRef]
- Mane, P.; Xie, J.; Leang, K.K.; Mossi, K. Cyclic energy harvesting from pyroelectric materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58. [Google Scholar] [CrossRef] [PubMed]
- Whatmore, R.W. Pyroelectric devices and materials. Rep. Prog. Phys. 1986, 49, 1335–1386. [Google Scholar] [CrossRef]
- Cuadras, A.; Ovejas, V.J. Determination of a System’s Entropy Using Pyroelectric Sensors. IEEE Sens. J. 2015, 15, 6890–6897. [Google Scholar] [CrossRef] [Green Version]
- Cuadras, A.; Romero, R.; Ovejas, V.J. Entropy characterisation of overstressed capacitors for lifetime prediction. J. Power Sources 2016, 336, 272–278. [Google Scholar] [CrossRef]
- Cuadras, A.; Crisóstomo, J.; Ovejas, V.J.; Quilez, M.J. Irreversible entropy model for damage diagnosis in resistors. J. Appl. Phys. 2015, 118, 165103. [Google Scholar] [CrossRef] [Green Version]
- Hsiao, C.C.; Siao, A.S. Improving Pyroelectric Energy Harvesting Using a Sandblast Etching Technique. Sensors 2013, 13, 12113–12131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Siao, A.S.; Chao, C.K.; Hsiao, C.C. Study on Pyroelectric Harvesters with Various Geometry. Sensors 2015, 15, 19633–19648. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Item | Value |
|---|---|
| Pyroelectric coefficient (10−4∙C∙m−2∙K−1) | 6.5 |
| Relative dielectric constant (ε33T/ε0) | 2100 |
| Poling field (KV/cm) | 35 |
| Resistivity (Ohm-cm) | >1012 |
| Density (g/cm3) | 7.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsiao, C.-C.; Liang, B.-H. The Generated Entropy Monitored by Pyroelectric Sensors. Sensors 2018, 18, 3320. https://doi.org/10.3390/s18103320
Hsiao C-C, Liang B-H. The Generated Entropy Monitored by Pyroelectric Sensors. Sensors. 2018; 18(10):3320. https://doi.org/10.3390/s18103320
Chicago/Turabian StyleHsiao, Chun-Ching, and Bo-Hao Liang. 2018. "The Generated Entropy Monitored by Pyroelectric Sensors" Sensors 18, no. 10: 3320. https://doi.org/10.3390/s18103320
APA StyleHsiao, C.-C., & Liang, B.-H. (2018). The Generated Entropy Monitored by Pyroelectric Sensors. Sensors, 18(10), 3320. https://doi.org/10.3390/s18103320





