N-Dimensional LLL Reduction Algorithm with Pivoted Reflection
Abstract
:1. Introduction
2. The LLL Reduction
2.1. The LLL Reduction Algorithm
- To make the column vectors in as mutually orthogonal as possible. As mentioned above, if the vectors are mutually orthogonal, then a simple rounding process will solve the ILS problem. Thus, the orthogonality of the vectors actually defines shape of search space, which will have significant influence on search efficiency;
- To minimize the length of vectors . Note that gives an upper bound of the volume of searching space, which means minimizing the vector length will shrinking the search space.
| Algorithm 1: The LLL reduction algorithm |
| Set |
| Set i = 2 |
| For |
| For j = 1 to i − 1 |
| Set = (Size reduction) |
| End |
| If then (Lovász condition) |
| Swap (, ) (Swap process) |
| Set i = max(i − 1, 2) |
| Else |
| Set i = i + 1 |
| End |
| End |
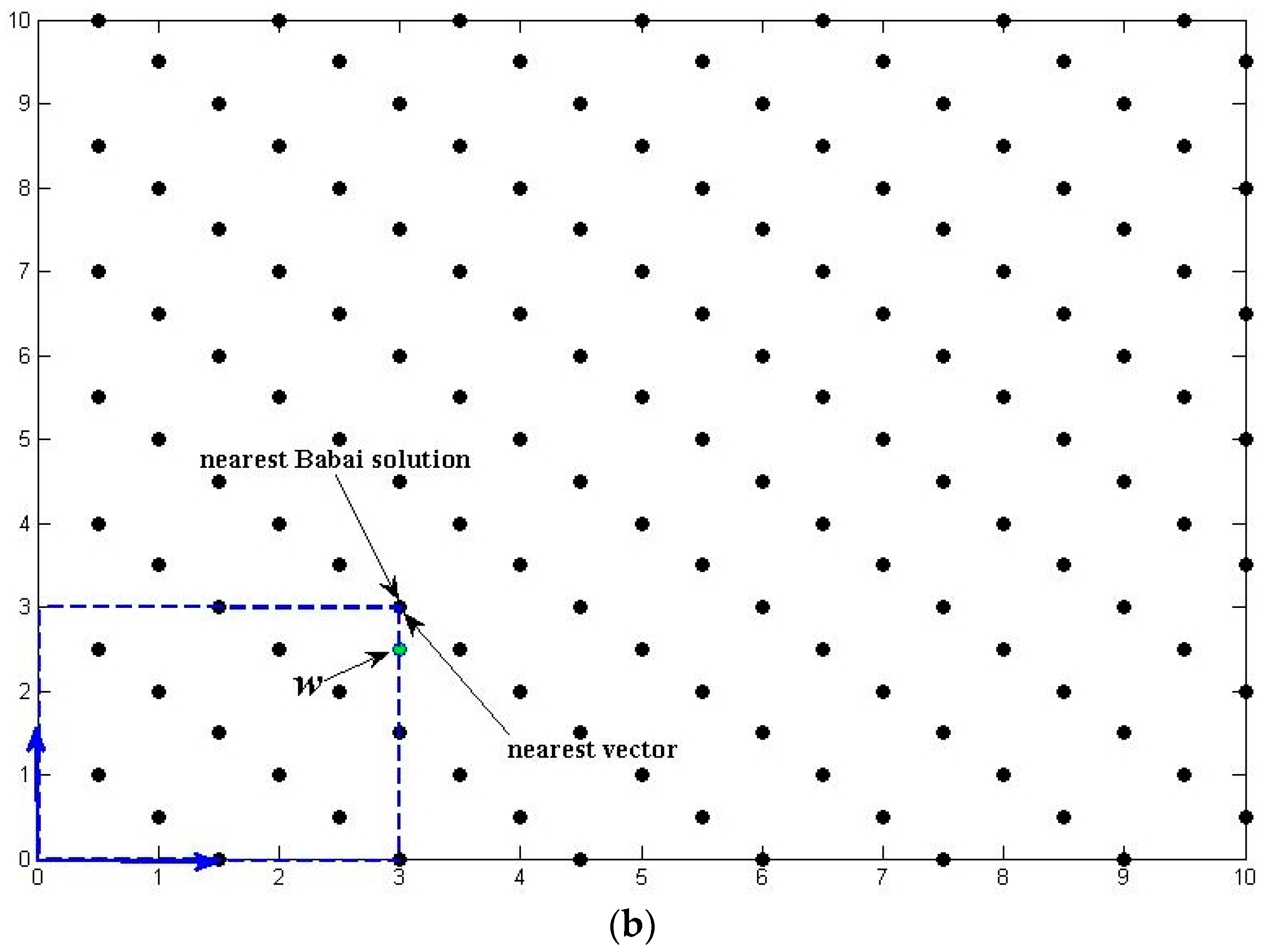
2.2. The LLL Reduction with Pivoted Reflection
| Algorithm 2: The LLL reduction with pivoted reflection |
| Set and |
| For i = 1 to m − 1 (Pivoted Householder Reflection) |
| Find the shortest vector in |
| Swap(, ) of |
| Calculate for |
| Set and |
| End |
| Set k = 2 |
| While |
| For j = k-1 down to 1 |
| Set = (Size reduction) |
| End |
| If then (Lovász condition) |
| Swap (,) (Swap process) |
| Calculate for |
| Set and |
| Set k = max(k − 1, 2) |
| Else |
| Set k = k + 1 |
| End |
| End |
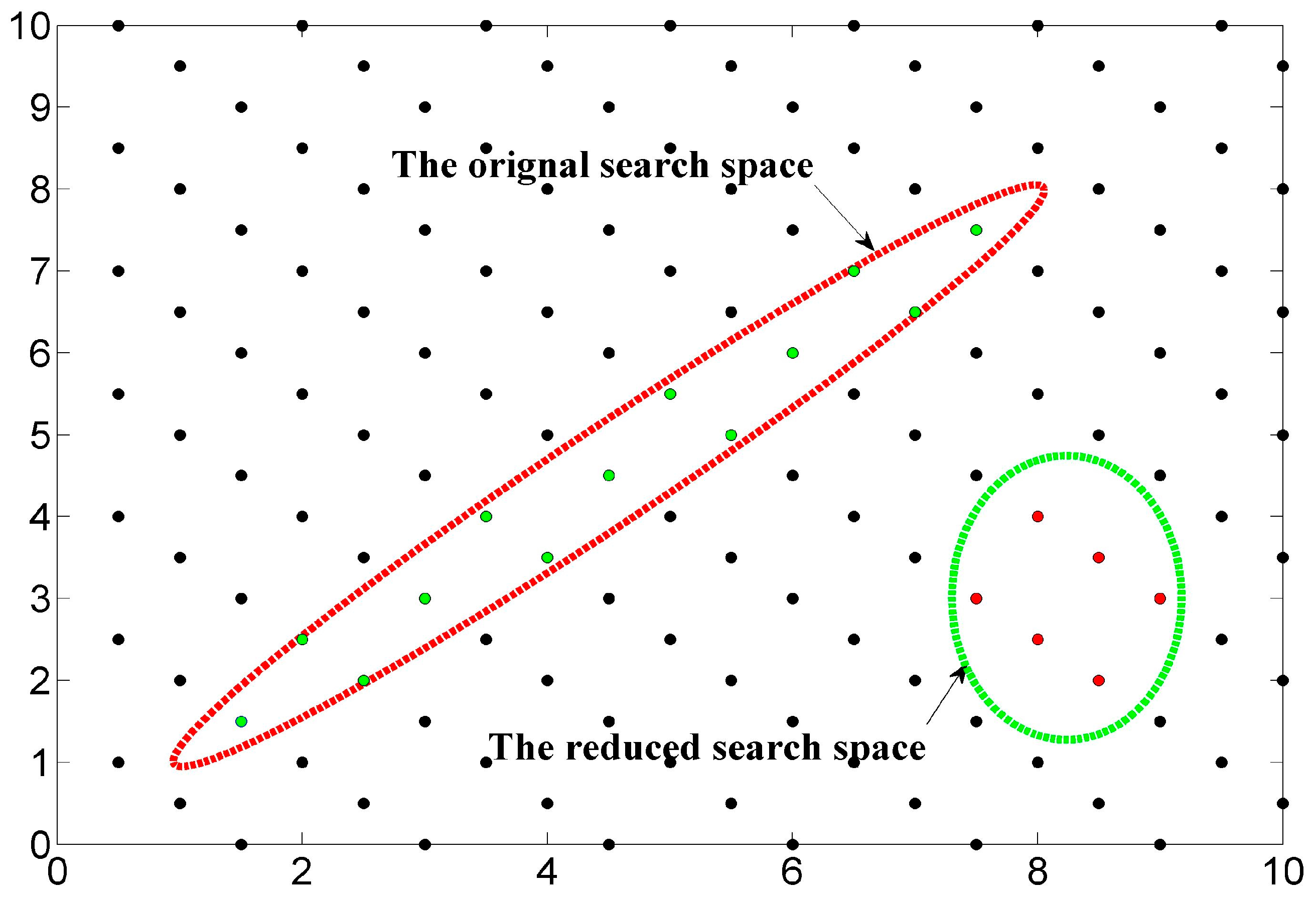
3. N-Dimensional Expansion of LLL Reduction
3.1. The N-Dimensional LLL Reduction Algorithm
| Algorithm 3: The n-LLL reduction with pivoted reflection |
| Set and |
| (Move the shortest vector to ) |
| Find the shortest vector in |
| Swap(,) of |
| Calculate for |
| Set and |
| Set i = 2 |
| While (Pivoted reflection and reduction process) |
| Find the shortest vector in |
| Swap(, ) of |
| Set temp = i |
| For j = i − 1 down to 1 |
| Set = (Size reduction) |
| If and i − j < n then (Extended Lovász condition) |
| Swap (, ) (Swap process) |
| Set temp = j |
| End |
| End |
| Calculate for |
| Set and |
| If i ! = temp then |
| i = temp |
| Else |
| Set i = i + 1 |
| End |
| End |
3.2. Analysis
3.2.1. The Performance
3.2.2. The Complexity
4. Experiments and Results
4.1. Measures of Reduction Quality
4.2. Experiment Design
4.3. Performance of N-Dimensional LLL Reduction
4.3.1. Reduction Quality
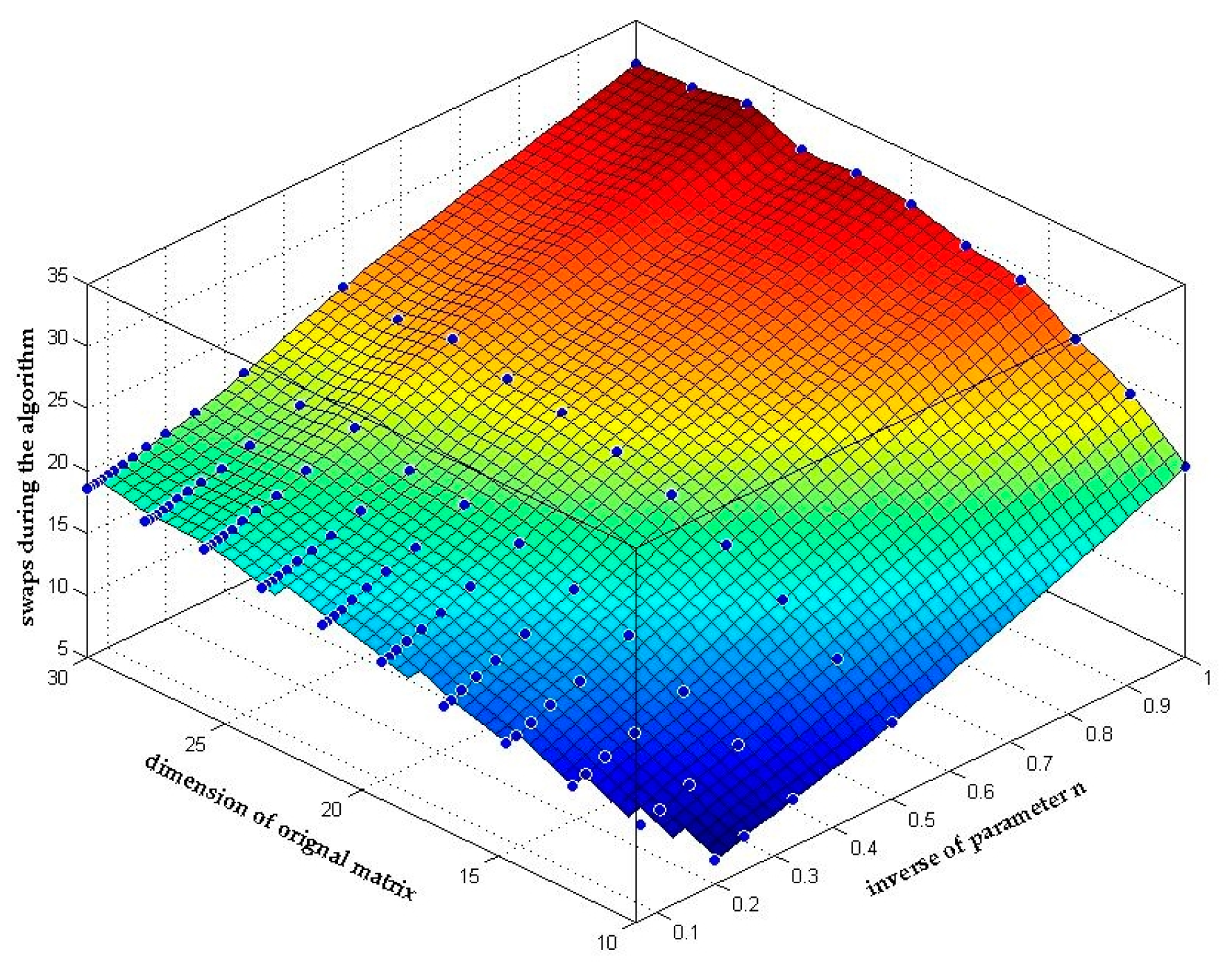
4.3.2. Complexity
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Provenzano, J.P.; Masson, A.; Journo, S.; Laramas, C.; Damidaux, J.I.; Zwolska, F. Implementation of a european infrastructure for satellite navigation: From system design to advanced technology evaluation. Int. J. Satell. Commun. Netw. 2015, 18, 223–242. [Google Scholar] [CrossRef]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The international GNSS service in a changing landscape of global navigation satellite systems. J. Geodesy 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Gerke, M.; Przybilla, H. Accuracy analysis of photogrammetric UAV image blocks: Influence of onboard RTK-GNSS and cross flight patterns. Photogramm. Fernerkund. Geoinf. 2016, 2016, 17–30. [Google Scholar] [CrossRef]
- Tahar, K.N.; Ahmad, A.; Wan, A.A.W.M.A.; Wan, M.N.W.M. Unmanned aerial vehicle photogrammetric results using different real time kinematic global positioning system approaches. In Lecture Notes in Geoinformation & Cartography; Springer: Berlin/Heidelberg, Germany, 2013; pp. 123–134. [Google Scholar]
- Woo, H.J.; Yoon, B.J.; Cho, B.G.; Kim, J.H. Research into navigation algorithm for unmanned ground vehicle using real time kinemtatic (RTK)-GPS. In Proceedings of the 2009 ICCAS-SICE, Fukuoka, Japan, 18–21 August 2009; pp. 2425–2428. [Google Scholar]
- Hatch, R. Instantaneous Ambiguity Resolution; Springer: New York, NY, USA, 1991. [Google Scholar]
- Forssell, B.; Martinneira, M.; Harrisz, R.A. Carrier phase ambiguity resolution in GNSS-2. In Proceedings of the 10th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1997), Kansas City, MO, USA, 16–19 September 1997; pp. 1727–1736. [Google Scholar]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geodesy 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Least-Squares Estimation of the Integer GPS Ambiguities. Invited lecture, Section IV “Theory and Methodology”. In Proceedings of the General Meeting of the International Association of Geodesy, Beijing, China, August 1993. [Google Scholar]
- Xu, P. Random simulation and gps decorrelation. J. Geodesy 2001, 75, 408–423. [Google Scholar] [CrossRef]
- Chang, X.W.; Yang, X.; Zhou, T. MLAMBDA: A modified LAMBDA method for integer least-squares estimation. J. Geodesy 2005, 79, 552–565. [Google Scholar] [CrossRef]
- Xu, P. Parallel cholesky-based reduction for the weighted integer least squares problem. J. Geodesy 2012, 86, 35–52. [Google Scholar] [CrossRef] [Green Version]
- Hassibi, A.; Boyd, S. Integer parameter estimation in linear models with applications to GPS. IEEE Trans. Signal Process. 1998, 46, 2938–2952. [Google Scholar] [CrossRef]
- Lenstra, A.K.; Lenstra, H.W.; Lovász, L. Factoring polynomials with rational coefficients. Math. Ann. 1982, 261, 515–534. [Google Scholar] [CrossRef]
- Wen, J.; Chang, X.W. GfcLLL: A greedy selection-based approach for fixed-complexity LLL Reduction. IEEE Commun. Lett. 2017, 21, 1965–1968. [Google Scholar] [CrossRef]
- Taherzadeh, M.; Mobasher, A.; Khandani, A.K. LLL reduction achieves the receive diversity in MIMO decoding. IEEE Trans. Inf. Theory 2007, 53, 4801–4805. [Google Scholar] [CrossRef]
- Ying, H.G.; Cong, L.; Mow, W.H. Complex lattice reduction algorithm for low-complexity MIMO detection. IEEE Trans. Signal Process. 2006, 5, 2701–2710. [Google Scholar]
- Grafarend, E.W. Mixed integer-real valued adjustment (IRA) problems: GPS initial cycle ambiguity resolution by means of the LLL algorithm. GPS Solut. 2000, 4, 31–44. [Google Scholar] [CrossRef]
- Nguên, P.Q.; Stehlé, D. Floating-Point LLL Revisited; Springer: Berlin/Heidelberg, Germany, 2005; pp. 215–233. [Google Scholar]
- Schnorr, C.P.; Euchner, M. Lattice basis reduction: Improved practical algorithms and solving subset sum problems. Math. Program. 1994, 66, 181–199. [Google Scholar] [CrossRef]
- Schnorr, C.P. A hierarchy of polynomial time basis reduction algorithms. Theor. Comput. Sci. 1987, 53, 375–386. [Google Scholar] [CrossRef]
- Fontein, F.; Schneider, M.; Wagner, U. PotLLL: A polynomial time version of LLL with deep insertions. Des. Codes Cryptogr. 2014, 73, 355–368. [Google Scholar] [CrossRef]
- Babai, L. On Lovász’ lattice reduction and the nearest lattice point problem. In Proceedings of the STACS 85 Symposium on Theoretical Aspects of Computer Science, Saarbrücken, Germany, 3–5 January 1985; pp. 13–20. [Google Scholar]
- Wübben, D.; Bohnke, R.; KüHn, V.; Kammeyer, K.D. MMSE extension of V-BLAST based on sorted QR decomposition. In Proceedings of the Vehicular Technology Conference, Orlando, FL, USA, 6–9 October 2003; Volume 501, pp. 508–512. [Google Scholar]
- Vetter, H.; Ponnampalam, V.; Sandell, M.; Hoeher, P.A. Fixed complexity LLL algorithm. IEEE Trans. Signal Process. 2009, 57, 1634–1637. [Google Scholar] [CrossRef]
- Borno, M.A.; Chang, X.W.; Xie, X.H. On “decorrelation” in solving integer least-squares problems for ambiguity determination. Emp. Surv. Rev. 2014, 46, 37–49. [Google Scholar] [CrossRef]
- Xu, P. Voronoi cells, probabilistic bounds, and hypothesis testing in mixed integer linear models. IEEE Trans. Inf. Theory 2006, 52, 3122–3138. [Google Scholar] [CrossRef]
- Jonge, P.P.D.; Tiberius, C. On the spectrum of the GPS DD-ambiguities. In Proceedings of the 7th International Technical Meeting of the Satellite Division of the Institute of Navigation, Salt Lake City, UT, USA, 20–23 September 1994. [Google Scholar]
- Teunissen, P.J.G.; Jonge, P.P.D.; Tiberius, C. The least-squares ambiguity decorrelation adjustment: Its performance on short GPS baselines and short observation spans. J. Geodesy 1997, 71, 589–602. [Google Scholar] [CrossRef]





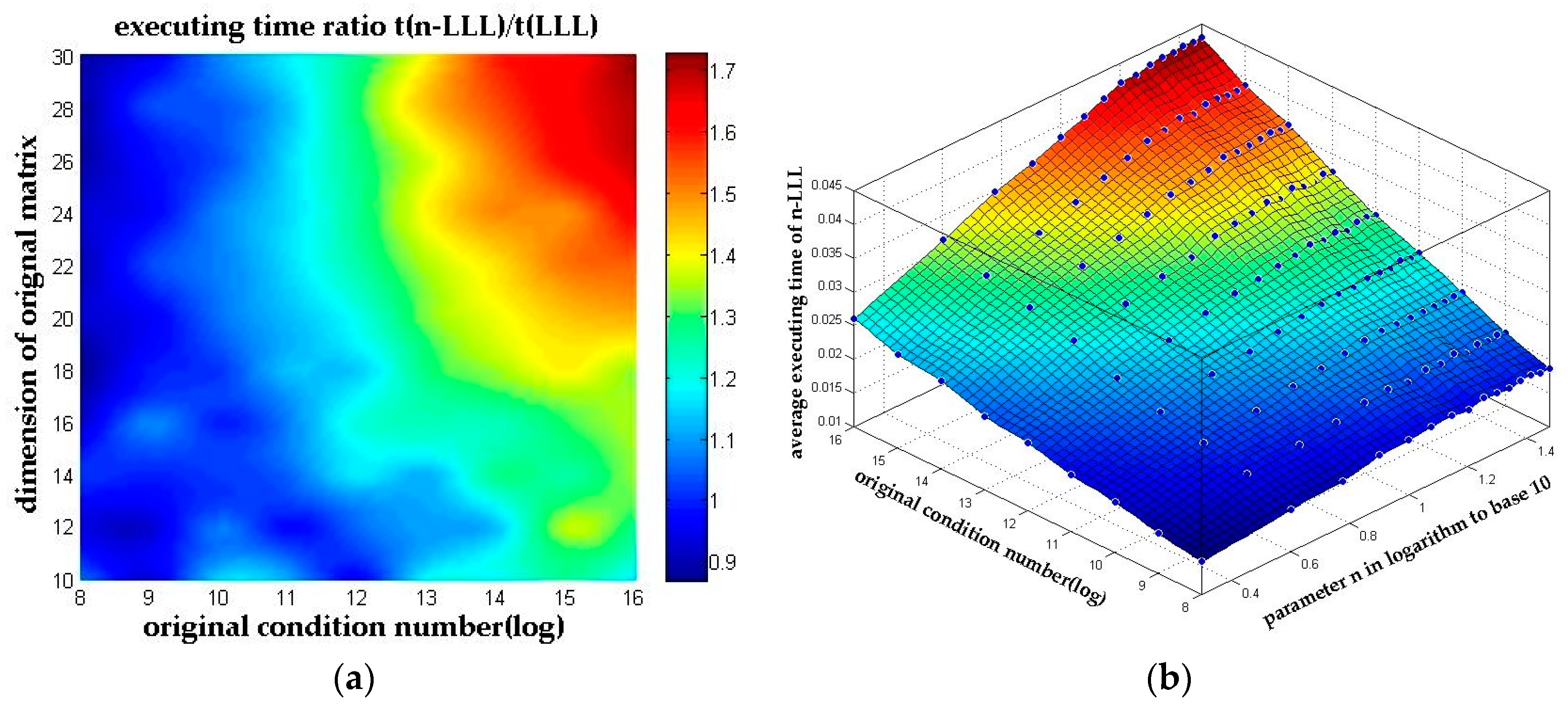
| Condition Number | n-LLL without PR | n-LLL with PR | Original LLL |
|---|---|---|---|
| 536 ms | 230 ms | 217 ms | |
| 561 ms | 251 ms | 224 ms | |
| 595 ms | 286 ms | 222 ms | |
| 628 ms | 316 ms | 220 ms | |
| 651 ms | 341 ms | 222 ms | |
| 672 ms | 369 ms | 235 ms | |
| 714 ms | 412 ms | 239 ms |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Z.; Zhu, D.; Yin, L. N-Dimensional LLL Reduction Algorithm with Pivoted Reflection. Sensors 2018, 18, 283. https://doi.org/10.3390/s18010283
Deng Z, Zhu D, Yin L. N-Dimensional LLL Reduction Algorithm with Pivoted Reflection. Sensors. 2018; 18(1):283. https://doi.org/10.3390/s18010283
Chicago/Turabian StyleDeng, Zhongliang, Di Zhu, and Lu Yin. 2018. "N-Dimensional LLL Reduction Algorithm with Pivoted Reflection" Sensors 18, no. 1: 283. https://doi.org/10.3390/s18010283





